Study on Aerodynamic Drag Reduction at Tail of 400 km/h EMU with Air Suction-Blowing Combination
Abstract
:1. Introduction
2. Calculation Model and Method
2.1. Calculation Model and Parameters
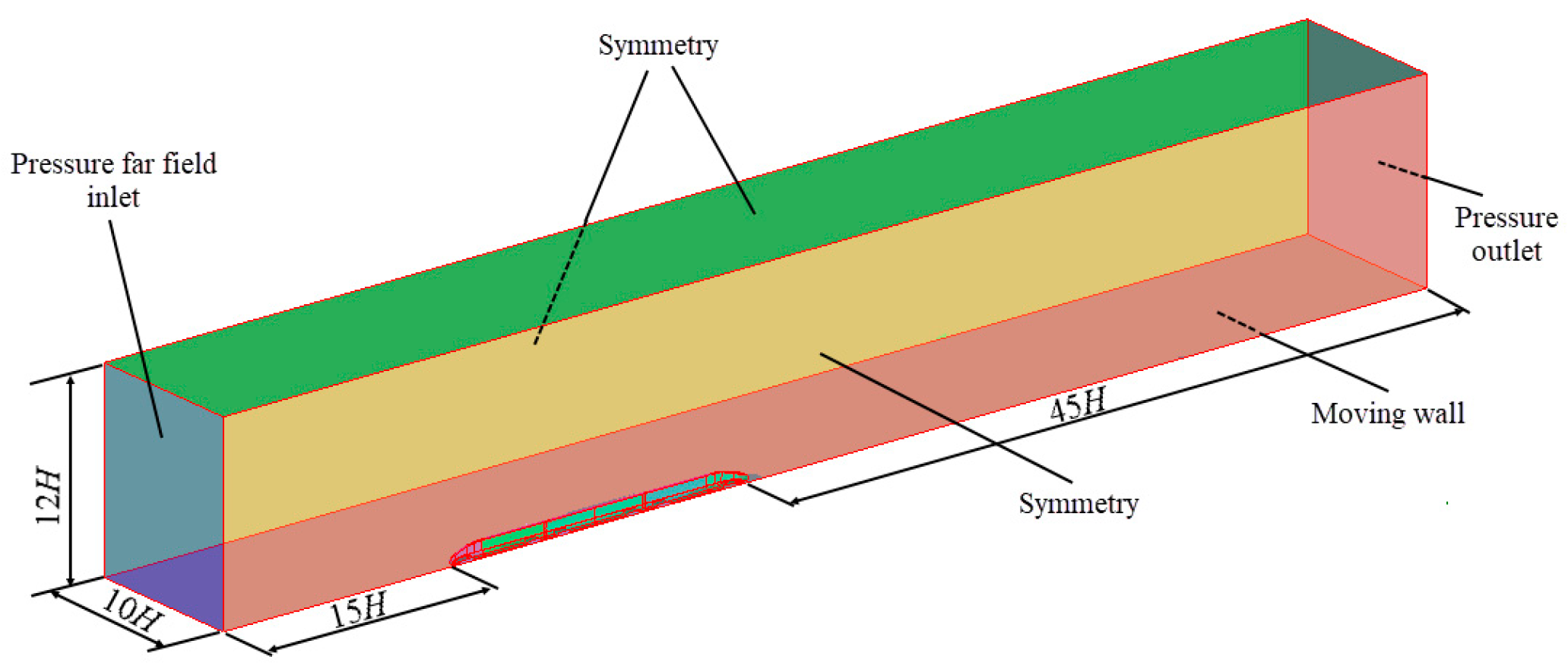
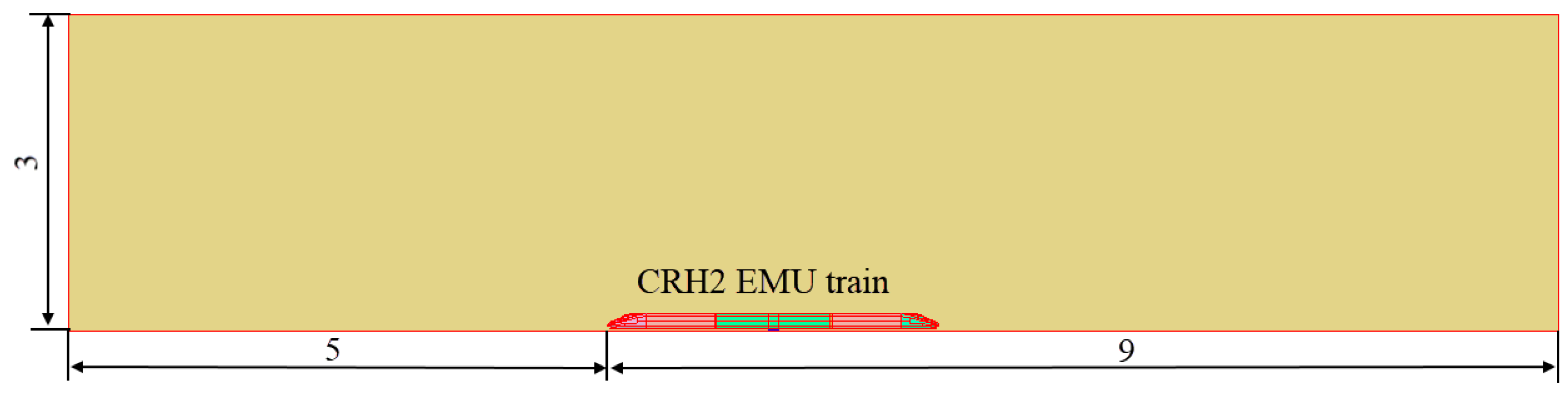
2.2. Calculation Domain and Boundary Conditions
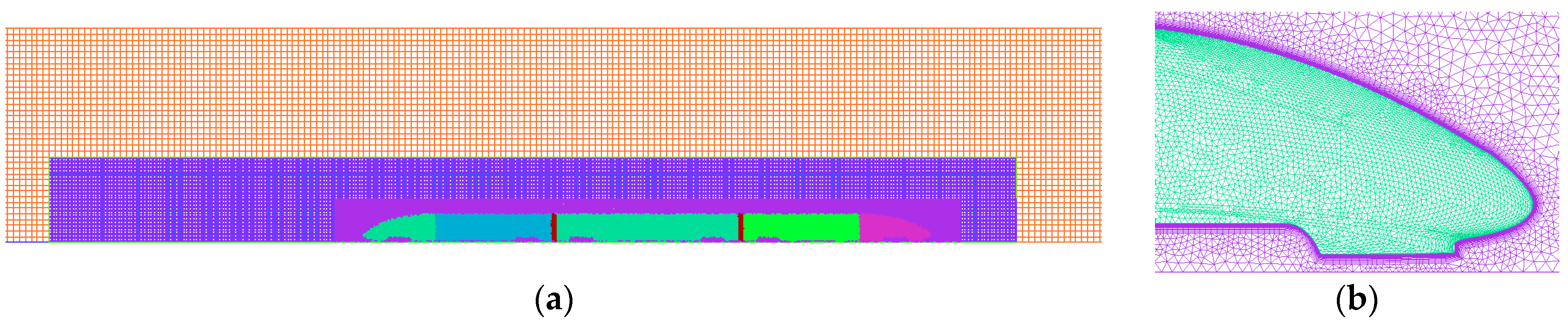
2.3. Meshing
2.4. Calculation Method and Turbulence Model
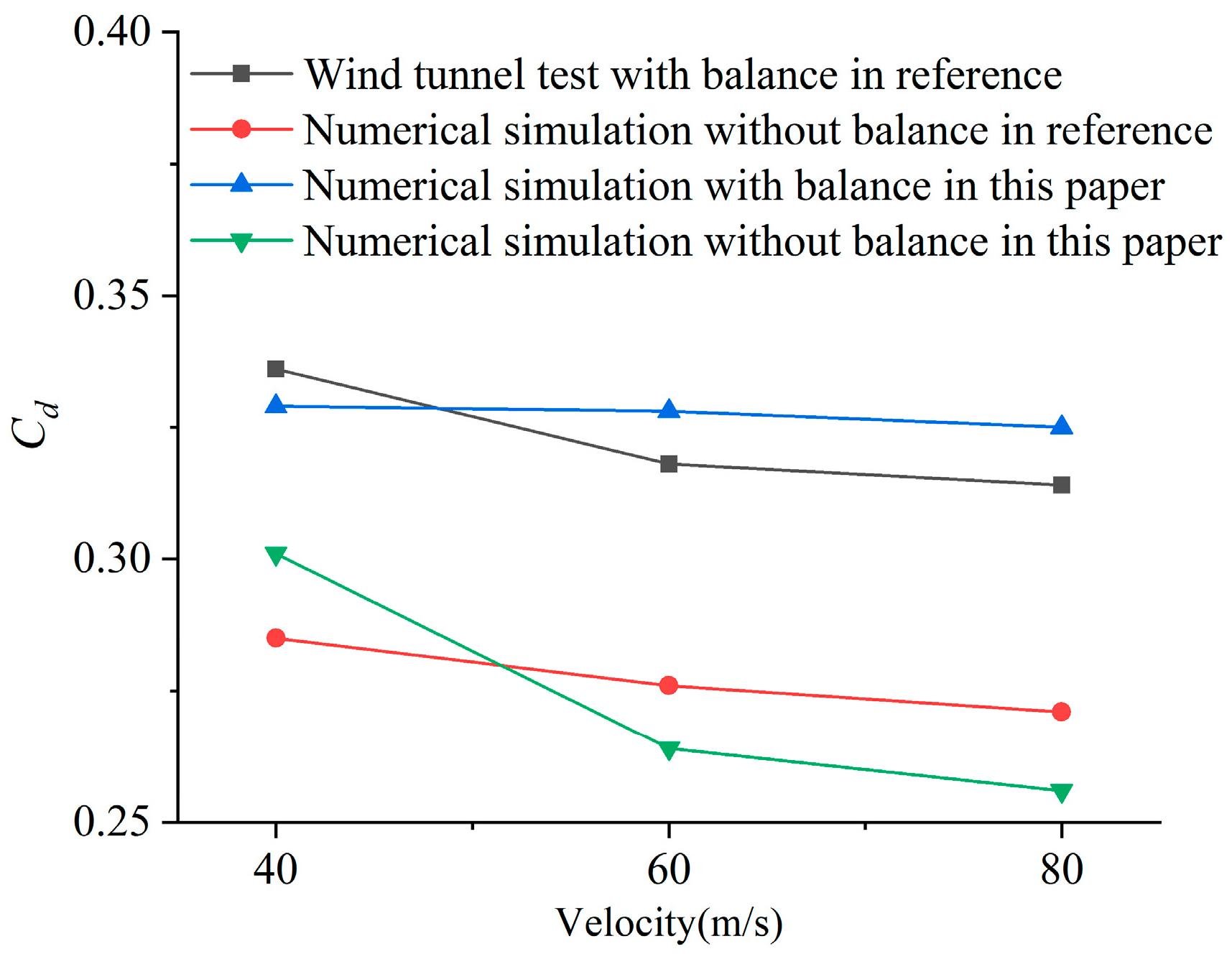
2.5. Reliability Analysis
3. Airflow Disturbance Characteristics and Setting of Suction and Blowing Ports
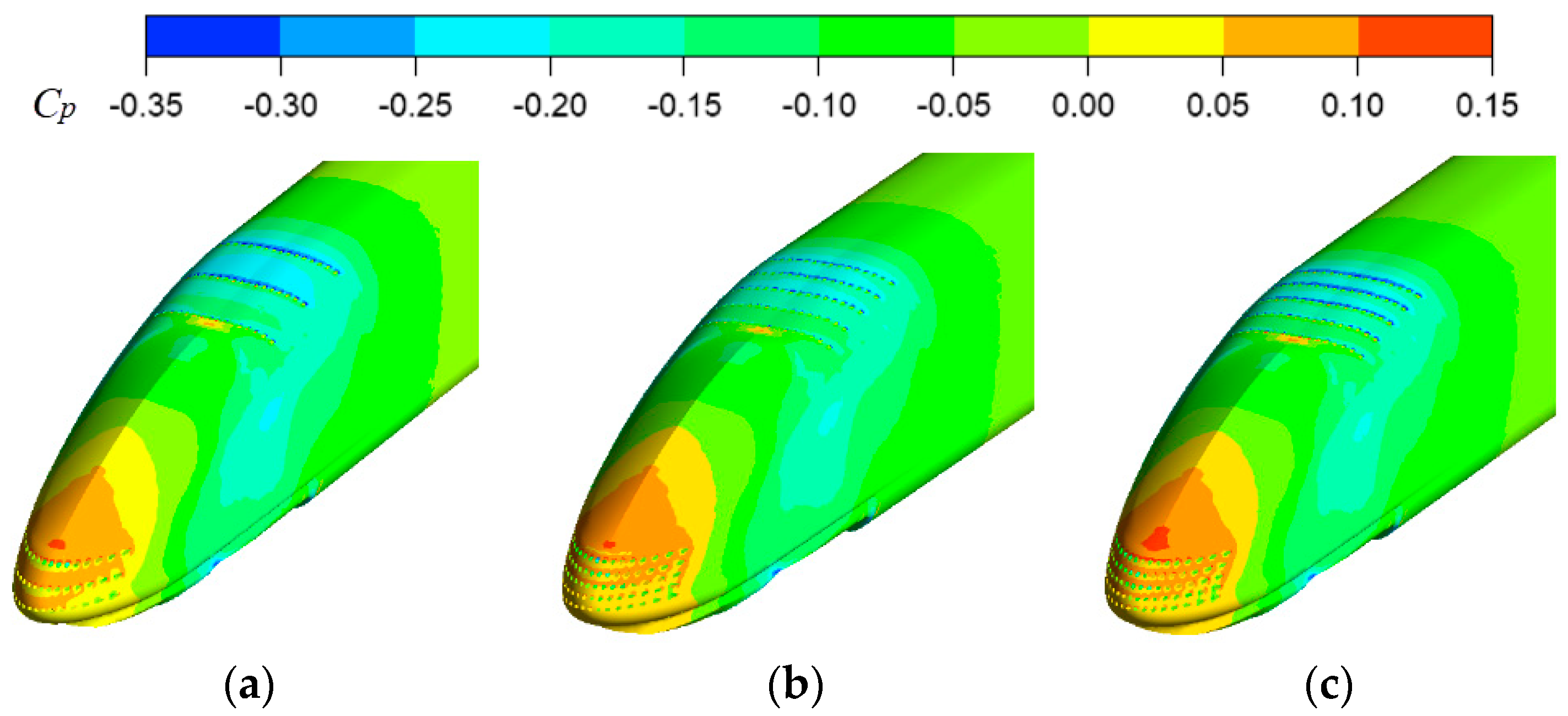
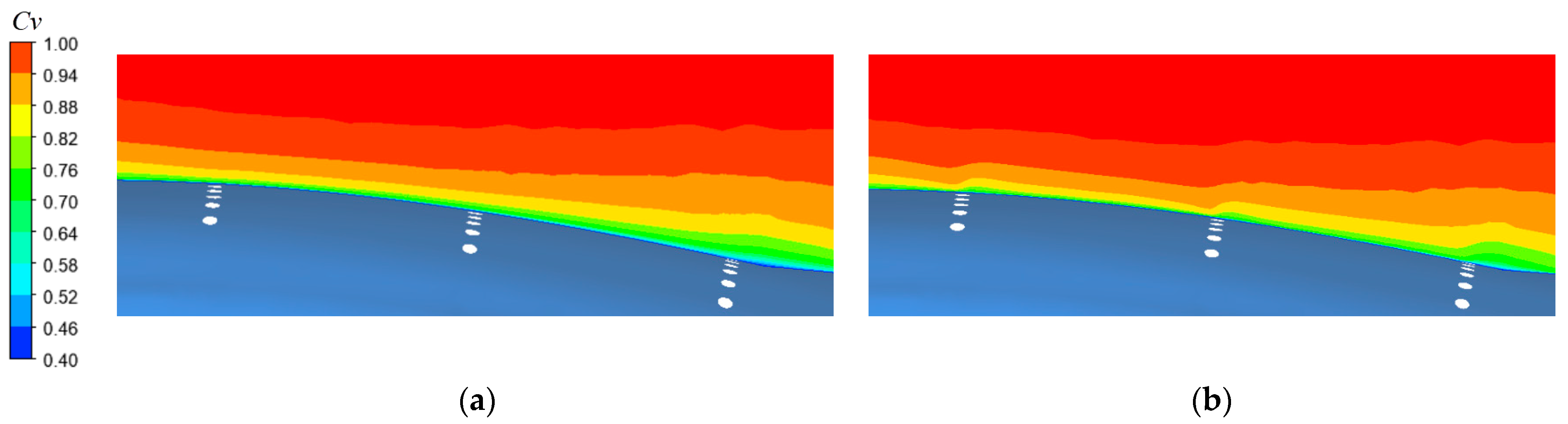
3.1. Surface Boundary Layer and Pressure Distribution of EMU
- (1)
- High-speed air strikes at the nose tip of the head car and forms a block. The speed drops sharply, and the pressure rises rapidly. Near the tip of the nose, Cv is close to 0, and Cp is about 1 at the maximum, where a strong positive pressure zone appears;
- (2)
- Due to the effect of pressure difference, on the one hand, the compressed air moves backward along the car body, forming a negative pressure zone in the transition area between the streamlined curve of the head car and the body of the equal section, and forming a boundary layer with a large velocity gradient. On the other hand, the compressed air moves to the bottom of the train, accelerating the movement between the bottom of the body and the ground to form a strong negative pressure zone, and the minimum Cp is about −1.2;
- (3)
- The airflow moves backward along the uniform section of the car body, and the pressure rises slowly and is slightly lower than the atmospheric pressure. At this time, the boundary layer gradually develops and thickens along the car body;
- (4)
- In the sudden change area where the airflow just flows through the tail section, the local vacuum above the streamlined tail causes the airflow to accelerate and form a negative pressure zone again;
- (5)
- After the airflow passes through the sudden change of the tail transverse section, the speed becomes smaller, and the pressure returns to normal, causing the boundary layer to separate from the wall surface of the EMU and forming a positive pressure near the nose end of the tail.
3.2. Setting of Suction and Blowing Ports
3.3. Expression of Related Physical Quantities
4. Results Analysis
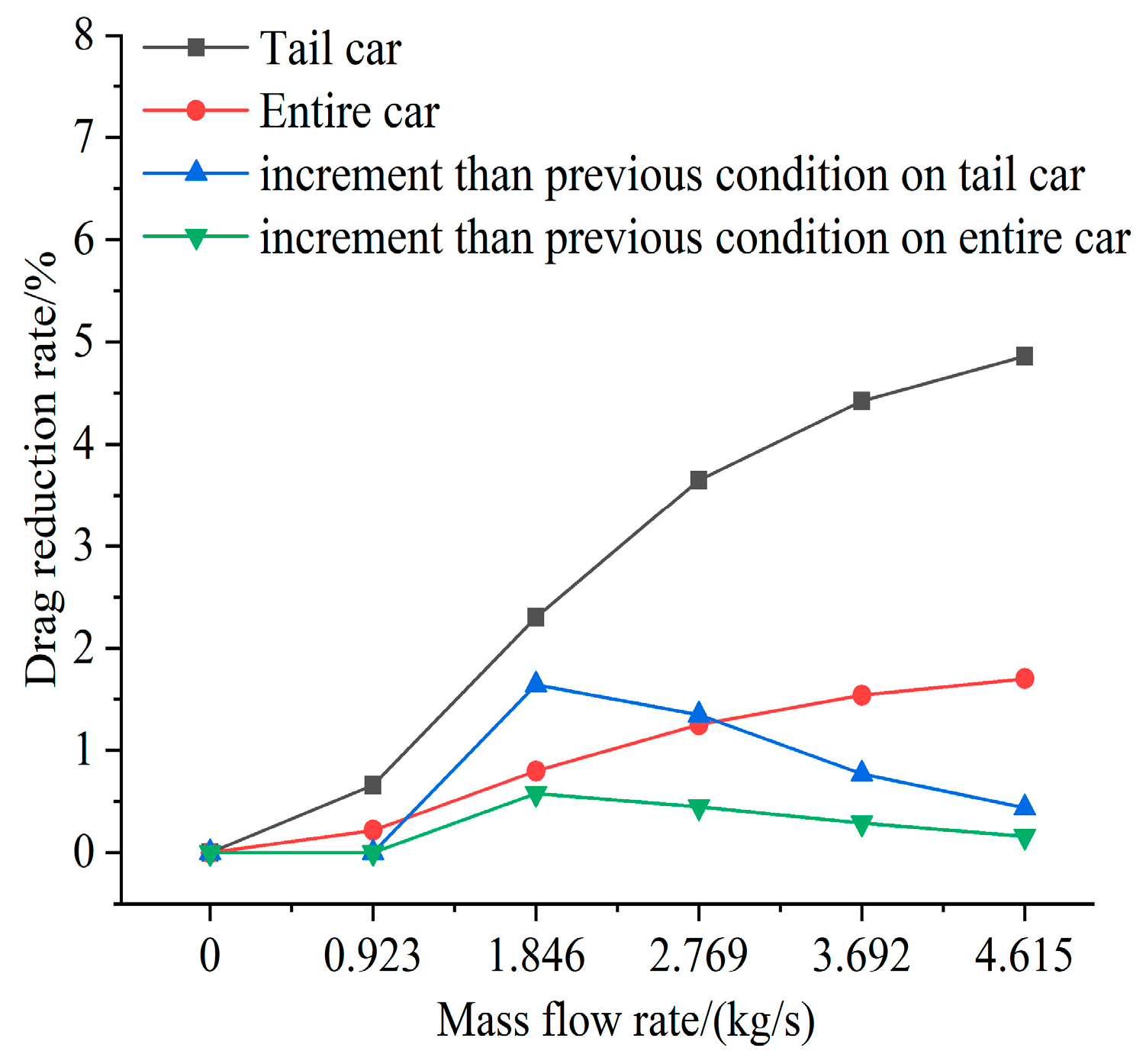
4.1. The Influence of Different Mass Flow Rate on the EMU Aerodynamic Drag
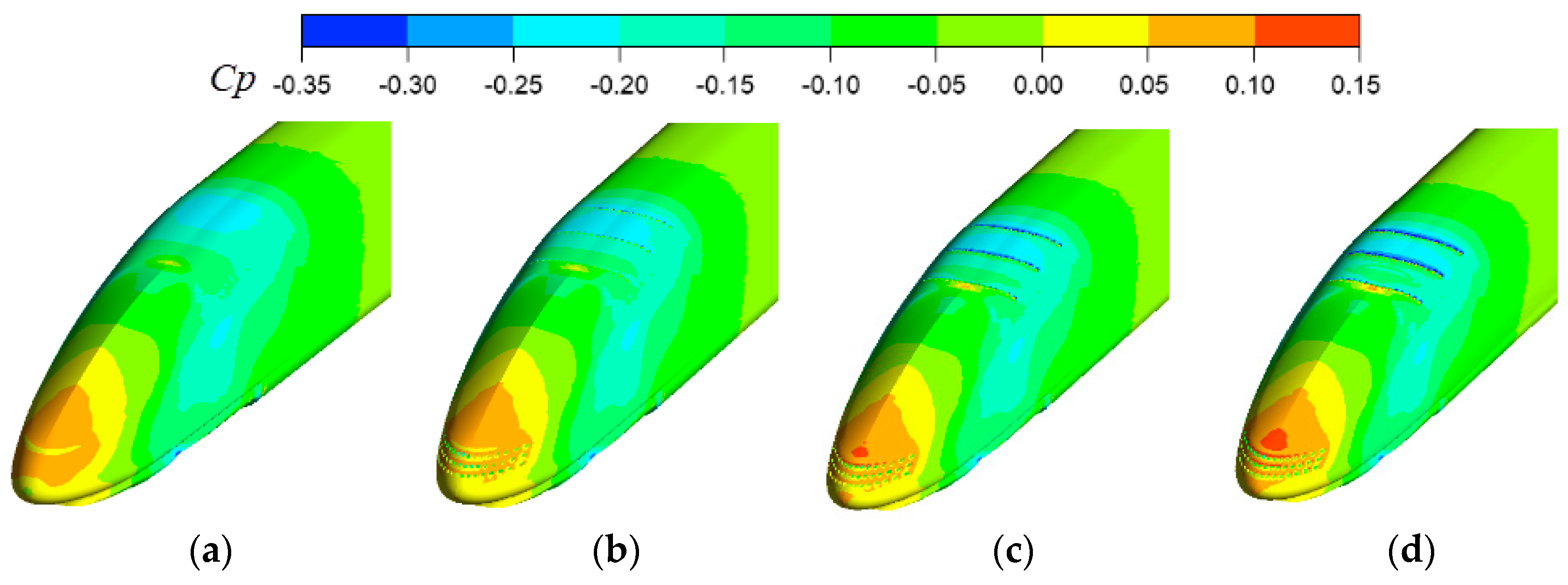
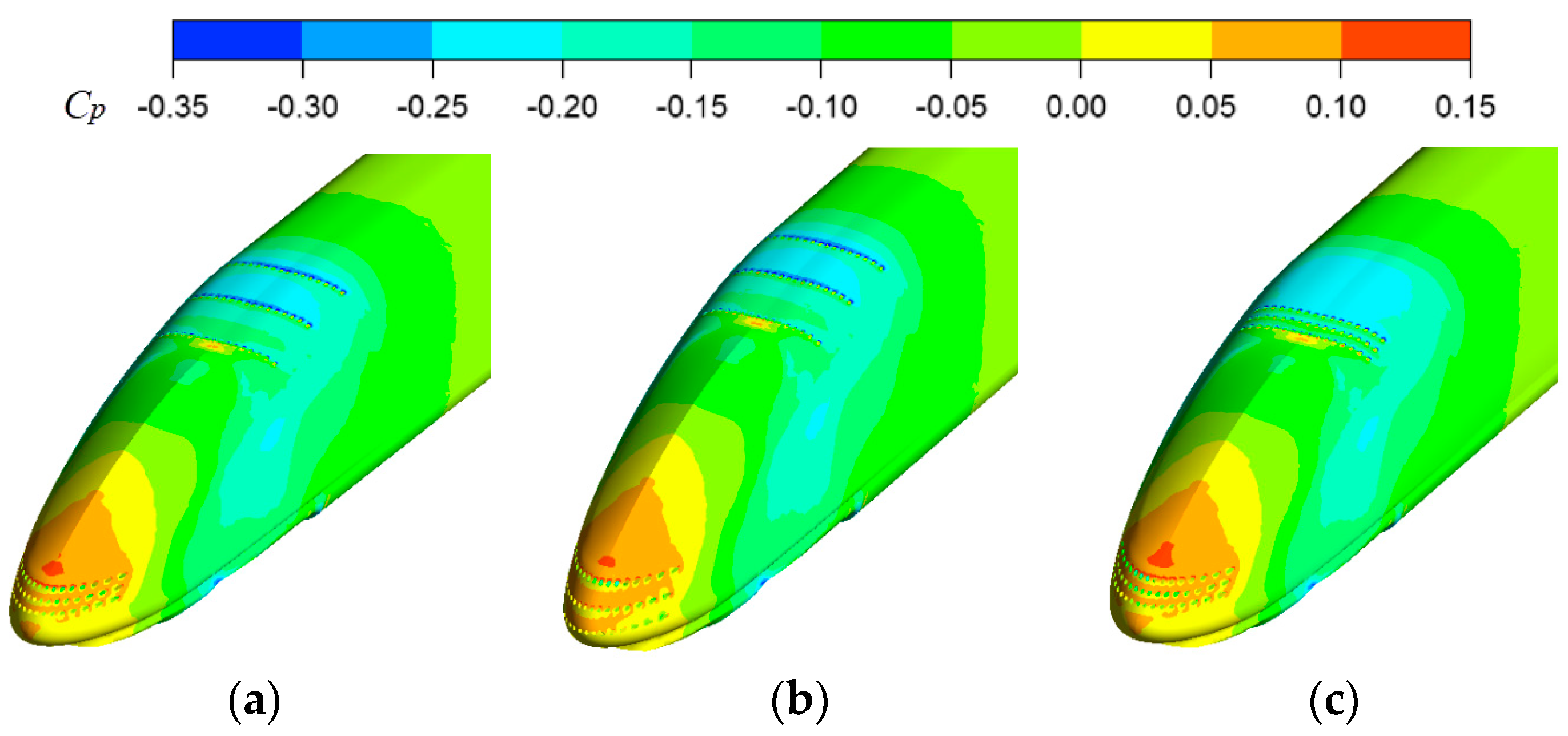
4.2. The Influence of the Distance between the Ports on the Aerodynamic Drag
4.3. The Influence of the Number of Ports on the Aerodynamic Drag
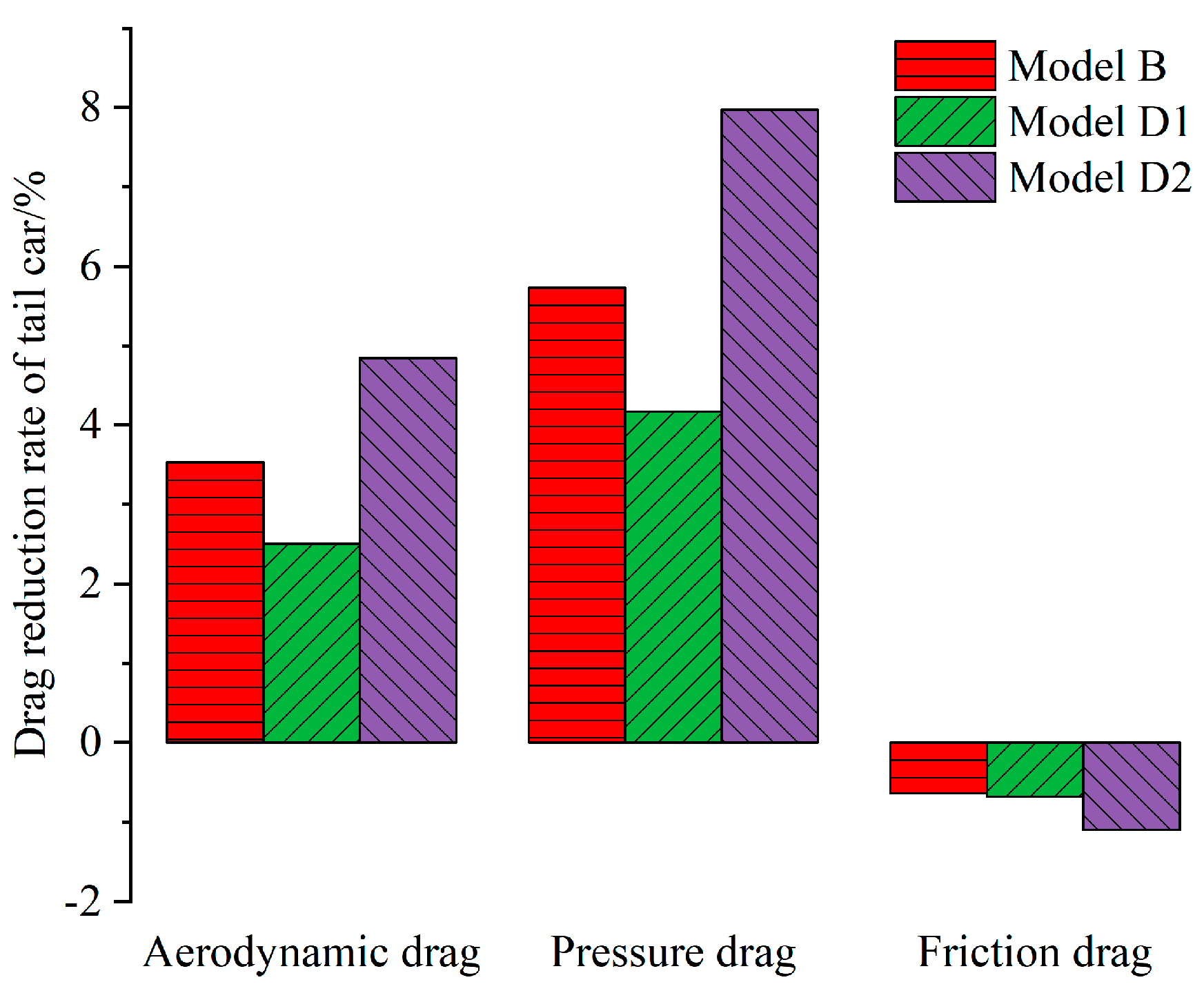
4.4. Analysis of Drag Reduction Mechanism
5. Conclusions and Prospects
- (1)
- Suction at the upper edge of the rear windscreen and blowing at the lower edge of the rear windscreen can significantly reduce the pressure drag of the tail car. The suction can remove the low-momentum fluid and transfer it to the blowing area, and the blowing can improve the vortex structure in the near wake region of the EMU. When the mass flow rate is relatively low, the aerodynamic drag reduction effect of the tail car is better. When the mass flow rate increases too much, it will reduce the drag reduction efficiency of the tail car and consume more energy;
- (2)
- Under a certain blowing and suction flow rate, the more the number of blowing and suction ports concentrated on the upper and lower edges of the windscreen, and the smaller the spacing, the better the drag reduction effect. If five ports are set, respectively, for the suction and blowing area at the EMU tail, when the suction-blow mass flow rate is 40.826 kg m−2 s−1, the pressure drag reduction rate of the tail car can reach 7.97%;
- (3)
- Due to the simplification of the model and the omission of the bogie structure, the total aerodynamic drag of the EMU is smaller, and the corresponding drag reduction rate is larger. However, it is determined that the drag reduction method combining suction and blowing is arranged at the tail of the EMU, which can effectively reduce the differential pressure drag of the tail car. In the subsequent research, the same drag reduction method can be applied to the head car, bogie cavity, and other areas of the EMU to further reduce the differential pressure of the entire car;
- (4)
- In view of different types of train heads, the setting of air-blowing and suction ports shall be analyzed according to specific conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | Symbol | Description |
| Cd | Drag coefficient | p | Pressure at any point in flow field |
| Fd | Aerodynamic drag | p∞ | Atmospheric pressure |
| ρ | Air density | qj | Mass flow rate |
| U | Speed of EMU | Vj | Speed of air blowing and suction |
| S | Cross-sectional area of EMU | A | Total cross-sectional area of all air-blowing holes or suction holes |
| Cv | Dimensionless velocity | Gj | Mass flux |
| V | Velocity of any point in flow field | α | Drag reduction rate |
| V∞ | Inlet flow velocity | Fd(n−S−B) | Aerodynamic drag of EMU without blowing and suction |
| Cp | Pressure coefficient | Fd(S−B) | Aerodynamic drag of EMU under a certain suction-blowing condition. |
References
- Tian, H. Train Aerodynamics; China Railway Publishing House: Beijing, China, 2007; pp. 1–3. [Google Scholar]
- Li, T.; Dai, Z.; Liu, J.; Wu, N.; Zhang, W. Review on aerodynamic drag reduction optimization of high-speed trains in China. J. Traff. Transp. Eng. 2021, 21, 59–80. [Google Scholar]
- Wei, Y.Y.; Zhou, Y.Q.; Luo, Q.F.; Deng, W. Optimal reactive power dispatch using an improved slime Mould algorithm. Energy Rep. 2021, 7, 8742–8759. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.J.; Liu, Y.; Deng, W.Q.; Deng, W. Co-evolutionary competitive swarm optimizer with three-phase for large-scale complex optimization problem. Inf. Sci. 2022, 619, 2–18. [Google Scholar] [CrossRef]
- Chen, H.; Miao, F.; Chen, Y.; Xiong, Y.; Chen, T. A Hyperspectral Image Classification Method Using Multifeature Vectors and Optimized KELM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2781–2795. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Du, C.; Fan, X.; Cui, L.; Chen, H.; Deng, F.; Tong, Q.; He, M.; Yang, M.; et al. Custom-molded offloading footwear effectively prevents recurrence and amputation, and lowers mortality rates in high-risk diabetic foot patients: A multicenter, prospective observational study. Diabetes Metab. Syndr. Obes. Targets Ther. 2022, 15, 103–109. [Google Scholar] [CrossRef]
- He, Z.Y.; Shao, H.D.; Wang, P.; Janet, L.; Cheng, J.S.; Yang, Y. Deep transfer multi-wavelet auto-encoder for intelligent fault diagnosis of gearbox with few target training samples. Knowl.-Based Syst. 2020, 191, 105313. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, J.; Chen, H.; Chen, J.; Li, Y.; Xu, J.; Deng, W. Intelligent Diagnosis Using Continuous Wavelet Transform and Gauss Convolutional Deep Belief Network. In IEEE Transactions on Reliability; IEEE: Toulouse, France, 2022. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, L.; Zhou, X.; Zhou, Y.; Sun, Y.; Zhu, W.; Chen, H.; Deng, W.; Chen, H.; Zhao, H. Multi-strategy particle swarm and ant colony hybrid optimization for airport taxiway planning problem. Inf. Sci. 2022, 612, 576–593. [Google Scholar] [CrossRef]
- Jin, T.; Zhu, Y.; Shu, Y.; Cao, J.; Yan, H.; Jiang, D. Uncertain optimal control problem with the first hitting time objective and application to a portfolio selection model. J. Intell. Fuzzy Syst. 2022, Preprint, 1–15. [Google Scholar] [CrossRef]
- Song, Y.; Cai, X.; Zhou, X.; Zhang, B.; Chen, H.; Li, Y.; Deng, W.; Deng, W. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst. Appl. 2022, 213, 118834. [Google Scholar] [CrossRef]
- Li, W.; Zhong, X.; Shao, H.; Cai, B.; Yang, X. Multi-mode data augmentation and fault diagnosis of rotating machinery using modified ACGAN designed with new framework. Adv. Eng. Inform. 2022, 52, 101552. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, T.; Xia, Y.; Yang, M.; Liu, H. Development and prospect of aerodynamic drag-reduction technologies for trains at higher speed (400+ km/h). Acta Aerodyn. Sin. 2021, 39, 83–94. [Google Scholar]
- Zhao, H.M.; Zhang, P.P.; Zhang, R.C.; Yao, R.; Deng, W. A novel performance trend prediction approach using ENBLS with GWO. Meas. Sci. Technol. 2023, 34, 025018. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, Z.; Li, G.; Liu, Y.; Yang, R.; Liu, H. Optimal search mapping among sensors in heterogeneous smart homes. Math. Biosci. Eng. 2023, 20, 1960–1980. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.J.; Gao, X.Z.; Zhao, H.M. An enhanced MSIQDE algorithm with novel multiple strategies for global optimization problems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1578–1587. [Google Scholar] [CrossRef]
- Ren, Z.; Han, X.; Yu, X.; Skjetne, R.; Leira, B.J.; Sævik, S.; Zhu, M. Data-driven simultaneous identification of the 6DOF dynamic model and wave load for a ship in waves. Mech. Syst. Signal Process. 2023, 184, 109422. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, W.G.; Liao, Y.; Song, Z.; Shi, J.; Jiang, X.; Shen, C.; Zhu, Z. Bearing fault diagnosis via generalized logarithm sparse regularization. Mech. Syst. Signal Process. 2022, 167, 108576. [Google Scholar] [CrossRef]
- Jin, T.; Gao, S.; Xia, H.; Ding, H. Reliability analysis for the fractional-order circuit system subject to the uncertain random fractional-order model with Caputo type. J. Adv. Res. 2021, 32, 15–26. [Google Scholar] [CrossRef]
- Zhu, H.; Hao, W.; Li, C.; Ding, Q.; Wu, B. A critical study on passive flow control techniques for straight-bladed vertical axis wind turbine. Energy 2018, 165, 12–25. [Google Scholar] [CrossRef]
- Cai, J.; Gao, Z. Numerical study on drag reduction by micro-blowing/suction compounding flow control on supercritical airfoil. Procedia Eng. 2015, 99, 613–617. [Google Scholar]
- Chen, H.Y.; Fang, M.; Xu, S. Hyperspectral remote sensing image classification with CNN based on quantum genetic-optimized sparse representation. IEEE Access 2020, 8, 99900–99909. [Google Scholar] [CrossRef]
- Zhao, H.M.; Zhang, P.P.; Chen, B.J.; Chen, H.Y.; Deng, W. Bearing fault diagnosis using transfer learning and optimized deep belief network. Meas. Sci. Technol. 2022, 33, 065009. [Google Scholar] [CrossRef]
- Collis, S.S.; Joslin, R.D.; Seifert, A.; Theofilis, V. Issues in active flow control: Theory, control, simulation, and experiment. Prog. Aeronaut. Sci. 2004, 40, 237–289. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, G.; Deng, W.; Zhou, Y.; Luo, Q. MOMPA: Multi-objective marine predator algorithm. Comput. Methods Appl. Mech. Eng. 2021, 385, 114029. [Google Scholar] [CrossRef]
- Jin, T.; Yang, X. Monotonicity theorem for the uncertain fractional differential equation and application to uncertain financial market. Math. Comput. Simul. 2021, 190, 203–221. [Google Scholar] [CrossRef]
- Yu, C.; Zhou, S.; Song, M.; Chang, C.-I. Semisupervised Hyperspectral Band Selection Based on Dual-Constrained Low-Rank Representation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5503005. [Google Scholar] [CrossRef]
- Luo, S.; Miao, W.; Liu, Q.; Li, C. Research on lift increase and drag reduction of S809 airfoil based on Suction-Blow Combined Jet. J. Chin. Soc. Power Eng. 2021, 41, 883–891. [Google Scholar]
- Xu, K.; Zha, G. Investigation of coflow jet active flow control for wind turbine airfoil. In AIAA Aviation 2020 Forum; AIAA: Reston, VA, USA, 2020; p. 2942. [Google Scholar]
- Aubrun, S.; Mcnally, J.; Alvi, F.; Kourta, A. Separation flow control on a generic ground vehicle using steady microjet arrays. Exp. Fluids 2011, 51, 1177–1187. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, G.; Tian, S.; Zhang, Z. Active flow control of 35°Ahmed model to reduce aerodynamic drag with steady jet. J. Jilin Univ. Eng. Technol. Ed. 2019, 49, 351–358. [Google Scholar]
- Yang, Y.; Zheng, M.; Huang, J.; Nie, Y. Aerodynamic drag reduction method of vehicle body based on non-smooth surface and vortex interference. China Mech. Eng. 2016, 27, 982–988. [Google Scholar]
- Lin, P.; Li, G. Numerical study on the aerodynamic drag reduction characteristics of high speed train suction based on the drag reduction theory of boundary layer. China Railw. 2020, 10, 71–77. [Google Scholar]
- Huang, S.; Yu, Y.; Li, Z.; Che, Z. Study of aerodynamic drag reduction of high-speed train based on tail jet-flow control. J. China Railw. Soc. 2021, 43, 38–46. [Google Scholar]
- Liang, X.; Luo, Z.; Li, X.; Xiong, X.; Zhang, X. Drag reduction of high-speed trains via low-density gas injection. AIP Adv. 2022, 12, 065115. [Google Scholar] [CrossRef]
- Shkvar, E.O.; Jamea, A.E.S.-J.; Cai, J.-C.; Kryzhanovskyi, A.S. Effectiveness of blowing for improving the high-speed trains aerodynamics. Thermophys. Aeromech. 2018, 25, 675–686. [Google Scholar] [CrossRef]
- Ikeda, M.; Yoshida, K.; Suzuki, M. A Flow Control Technique Utilizing Air Blowing to Modify the Aerodynamic Characteristics of Pantograph for High-speed Train. J. Mech. Syst. Transp. Logist. 2008, 1, 264–271. [Google Scholar] [CrossRef]
- Chen, H.L.; Li, C.Y.; Mafarja, M.; Heidari, A.A.; Chen, Y.; Cai, Z.N. Slime mould algorithm: A comprehensive review of recent variants and applications. Int. J. Syst. Sci. 2023, 54, 204–235. [Google Scholar] [CrossRef]
- Xu, J.J.; Zhao, Y.L.; Chen, H.Y.; Deng, W. ABC-GSPBFT: PBFT with grouping score mechanism and optimized consensus process for flight operation data-sharing. Inf. Sci. 2023, 624, 110–127. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, G.; Zhou, Y.; Luo, Q.; Deng, W. Artificial Electric Field Algorithm with Greedy State Transition Strategy for Spherical Multiple Traveling Salesmen Problem. Int. J. Comput. Intell. Syst. 2022, 15, 5. [Google Scholar] [CrossRef]
- Duan, Z.; Song, P.; Yang, C.; Deng, L.; Jiang, Y.; Deng, F.; Jiang, X.; Chen, Y.; Yang, G.; Ma, Y.; et al. The impact of hyperglycaemic crisis episodes on long-term outcomes for inpatients presenting with acute organ injury: A prospective, multicentre follow-up study. Front. Endocrinol. 2022, 13, 1057089. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Yu, L.; Chen, H.; Deng, W.; Deng, W. Feature extraction using parameterized multi-synchrosqueezing transform. IEEE Sens. J. 2022, 22, 14263–14272. [Google Scholar] [CrossRef]
- Li, T.Y.; Shi, J.Y.; Deng, W.; Hu, Z.D. Pyramid particle swarm optimization with novel strategies of competition and cooperation. Appl. Soft Comput. 2022, 121, 108731. [Google Scholar] [CrossRef]
- Deng, W.; Ni, H.; Liu, Y.; Chen, H.; Zhao, H. An adaptive differential evolution algorithm based on belief space and generalized opposition-based learning for resource allocation. Appl. Soft Comput. 2022, 127, 109419. [Google Scholar] [CrossRef]
- Yao, R.; Guo, C.; Deng, W.; Zhao, H. A novel mathematical morphology spectrum entropy based on scale-adaptive techniques. ISA Trans. 2022, 126, 691–702. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Qian, Z.; Deng, W.; Zhang, D.Z.; Lu, H.; Wang, S. Forecasting crude oil prices based on variational mode decomposition and random sparse Bayesian learning. Appl. Soft Comput. 2021, 113, 108032. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Jin, T.; Xia, H.; Deng, W.; Li, Y.; Chen, H. Uncertain Fractional-Order Multi-Objective Optimization Based on Reliability Analysis and Application to Fractional-Order Circuit with Caputo Type. Circuits Syst. Signal Process. 2021, 40, 5955–5982. [Google Scholar] [CrossRef]
- Liu, Y.; Heidari, A.A.; Cai, Z.N.; Liang, G.X.; Chen, H.L.; Pan, Z.F.; Alsufyani, A.; Bourouis, S. Simulated annealing-based dynamic step shuffled frog leaping algorithm: Optimal performance design and feature selection. Neurocomputing 2022, 503, 325–362. [Google Scholar] [CrossRef]
- Tian, C.; Jin, T.; Yang, X.; Liu, Q. Reliability analysis of the uncertain heat conduction model. Comput. Math. Appl. 2022, 119, 131–140. [Google Scholar] [CrossRef]
- Li, B.; Xu, J.; Jin, T.; Shu, Y. Piecewise parameterization for multifactor uncertain system and uncertain inventory-promotion optimization. Knowl.-Based Syst. 2022, 255, 109683. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.W.; Tu, L.P. A modified particle swarm optimization using adaptive strategy. Expert Syst. Appl. 2020, 152, 113353. [Google Scholar] [CrossRef]
- Silva, Y.; Herthel, A.B.; Subramanian, A. A multi-objective evolutionary algorithm for a class of mean-variance portfolio selection problems. Expert Syst. Appl. 2019, 133, 225–241. [Google Scholar] [CrossRef]
- Jin, T.; Xia, H. Lookback option pricing models based on the uncertain fractional-order differential equation with Caputo type. J. Ambient. Intell. Humaniz. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Wang, L.; Yu, D.; Ding, Y. Feasibility study on raising the operation speed of EMU from 350 km/h to 400 km/h. Electr. Drives Locomot. 2020, 2, 17–22. [Google Scholar]
- Pan, Y.; Yao, J.; Liu, T.; Li, C. Discussion on the wake vortex structure of a high speed train by vortex identification methods. Chin. J. Mech. 2018, 50, 667–676. [Google Scholar]
- Zhu, H.; Zhang, Y.; Zhao, H.; Wu, P.; Shao, X. Drag reduction on technology of high-speed train based boundary layer control. J. Traff. Transp. Eng. 2017, 17, 64–72. [Google Scholar]
- Zhou, J.; Ou, P.; Liu, P.; Guo, H. Numerical study of ground effects on high speed train aerodynamic drag. J. Exp. Fluid Mech. 2016, 30, 26–31&55. [Google Scholar]







| Mesh Density | Mesh Number (106) | Aerodynamic Drag Coefficient | ||
|---|---|---|---|---|
| Head Car | Middle Car | Tail Car | ||
| coarse | 5.41 | 0.120 | 0.051 | 0.092 |
| medium | 10.55 | 0.115 | 0.050 | 0.090 |
| fine | 16.00 | 0.114 | 0.050 | 0.090 |
| Position | Drag Coefficient Under Different Mass Flow Rate | |||||
|---|---|---|---|---|---|---|
| 0 | 0.923 kg/s | 1.846 kg/s | 2.769 kg/s | 3.692 kg/s | 4.615 kg/s | |
| Entire car | 0.2571 | 0.2565 | 0.2551 | 0.2539 | 0.2531 | 0.2527 |
| Head car | 0.1151 | 0.1151 | 0.1151 | 0.1151 | 0.1151 | 0.1151 |
| Middle car | 0.0502 | 0.0503 | 0.0502 | 0.0503 | 0.0502 | 0.0502 |
| Tail car | 0.0897 | 0.0891 | 0.0876 | 0.0864 | 0.0857 | 0.0853 |
| Windshield | 0.0021 | 0.0020 | 0.0022 | 0.0021 | 0.0021 | 0.0021 |
| Model | Spacing of Suction Ports along the Surface of Car Body (mm) | Spacing of Blowing Ports in Vertical Direction (mm) |
|---|---|---|
| A | 1060 | 150 |
| B | 1060 | 300 |
| C | 265 | 150 |
| Model | Total Mass Flow Rate (kg s−1) | Mass Flux (kg m−2 s−1) | Ports × Holes (for Semi-Body Model) |
|---|---|---|---|
| B | 2.769 | 40.826 | 3 × 8 |
| D1 | 2.769 | 24.496 | 5 × 8 |
| D2 | 4.615 | 40.826 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Chen, G.; Guan, Y.; Deng, W. Study on Aerodynamic Drag Reduction at Tail of 400 km/h EMU with Air Suction-Blowing Combination. Machines 2023, 11, 222. https://doi.org/10.3390/machines11020222
Cui H, Chen G, Guan Y, Deng W. Study on Aerodynamic Drag Reduction at Tail of 400 km/h EMU with Air Suction-Blowing Combination. Machines. 2023; 11(2):222. https://doi.org/10.3390/machines11020222
Chicago/Turabian StyleCui, Hongjiang, Guanxin Chen, Ying Guan, and Wu Deng. 2023. "Study on Aerodynamic Drag Reduction at Tail of 400 km/h EMU with Air Suction-Blowing Combination" Machines 11, no. 2: 222. https://doi.org/10.3390/machines11020222
APA StyleCui, H., Chen, G., Guan, Y., & Deng, W. (2023). Study on Aerodynamic Drag Reduction at Tail of 400 km/h EMU with Air Suction-Blowing Combination. Machines, 11(2), 222. https://doi.org/10.3390/machines11020222







