Design of a High-Gap Plant Protection Machine (HGPM) with Stepless Variable Speed and Power Adjustable Function
Abstract
:1. Introduction
- This paper designs a chassis power transmission system of HGPM based on hydrostatic transmission and time-sharing 4WD transfer gear and analyzes the walking performance and stability of HGPM in detail, which provides a basis for the development of a chassis power transmission system of HGPM.
- Based on the simulation software, an undercarriage dynamics model of upland gap planters is established for multi-condition performance simulation tests. Then, the real vehicle test is carried out to verify the rationality and realism of the theoretical design of the plant protection machine and related dynamics analysis and other data.
- This paper presents an important reference for engineering applications such as optimizing agricultural machinery dynamics, driving stability, and ensuring fuel economy.
2. Dynamics Switching Principle
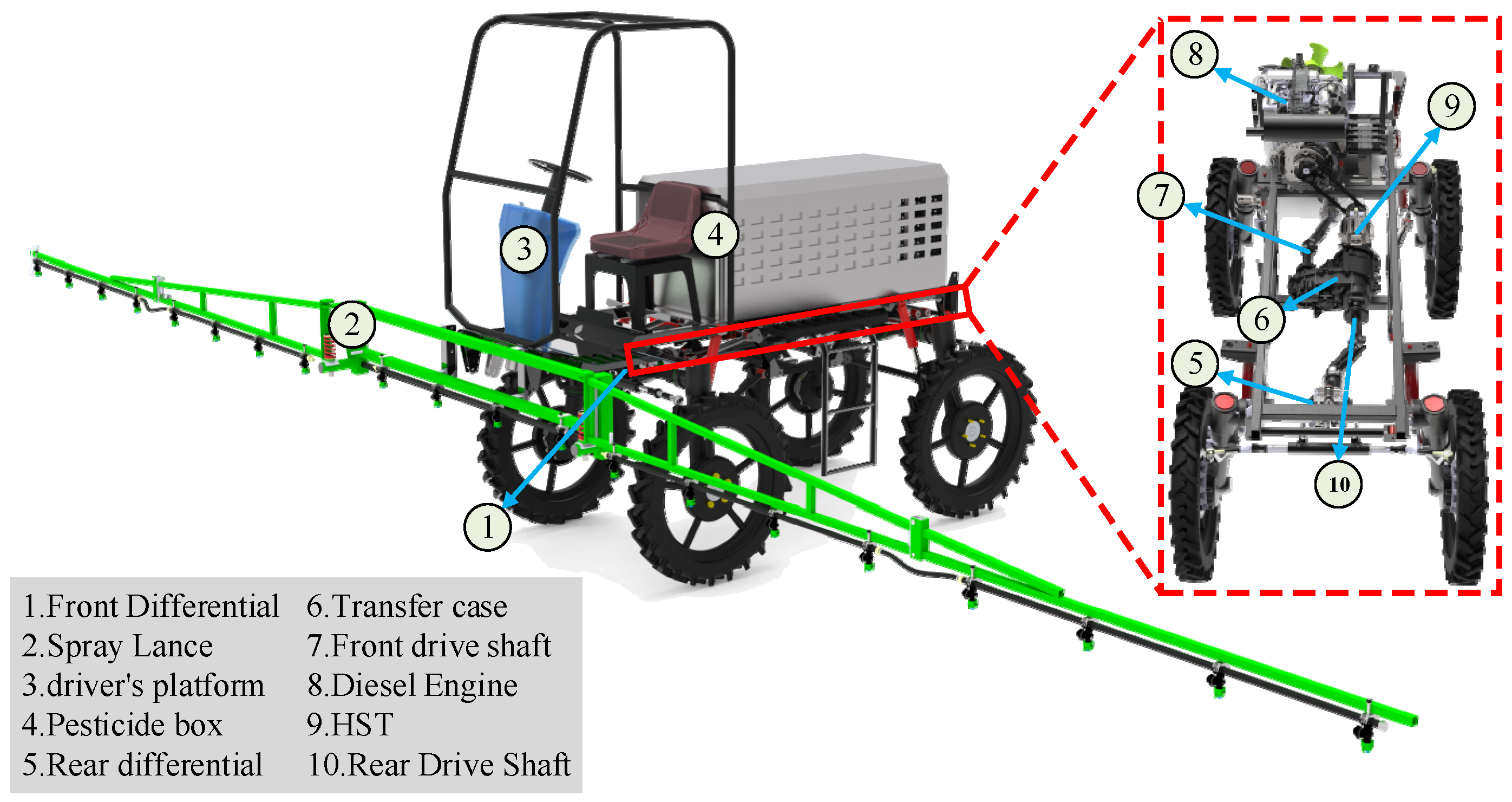
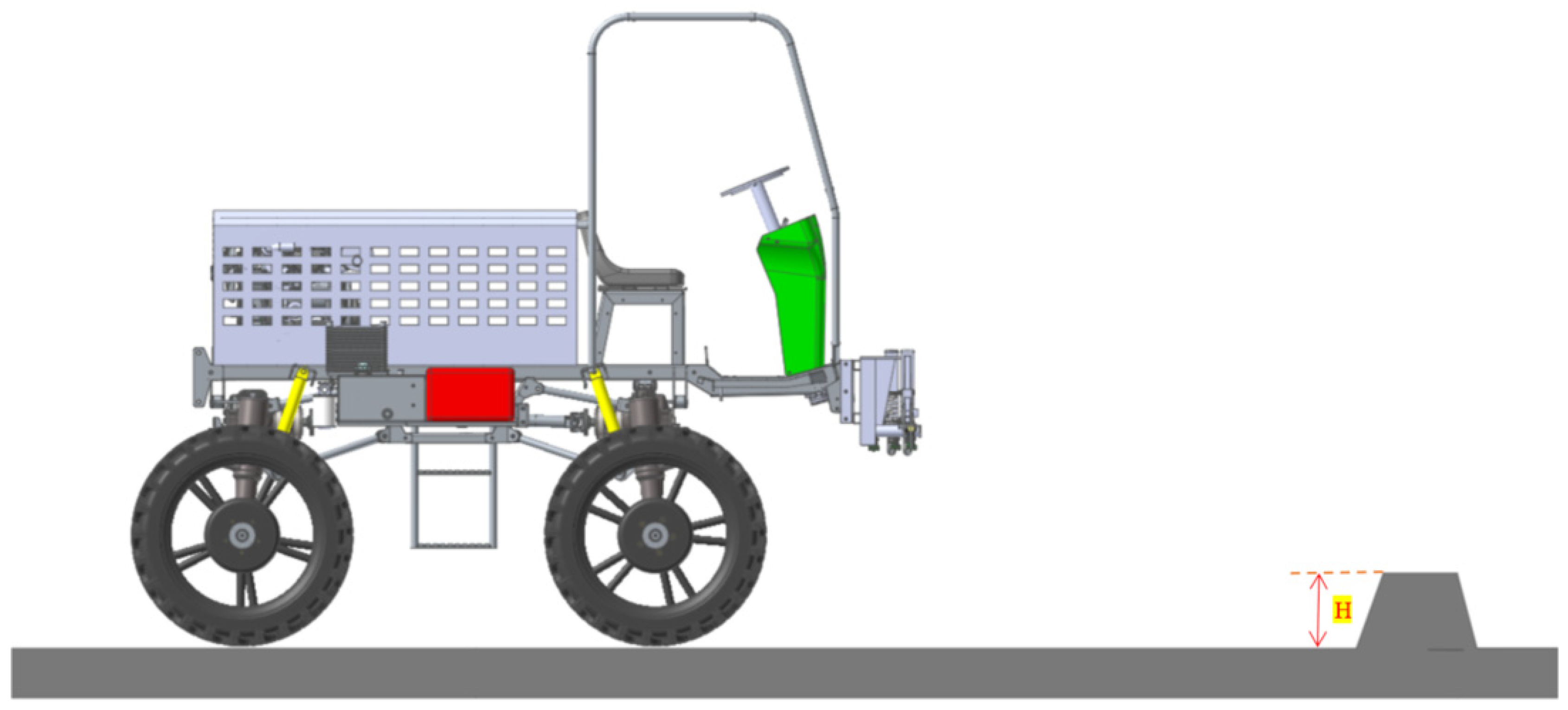
2.1. Whole Machine Structure and Working Principle
2.2. Transmission System Design
2.2.1. Transmission Characteristics of HST
2.2.2. Transmission Characteristics of the Splitter
2.3. System Configuration
3. Chassis Performance Simulation Analysis
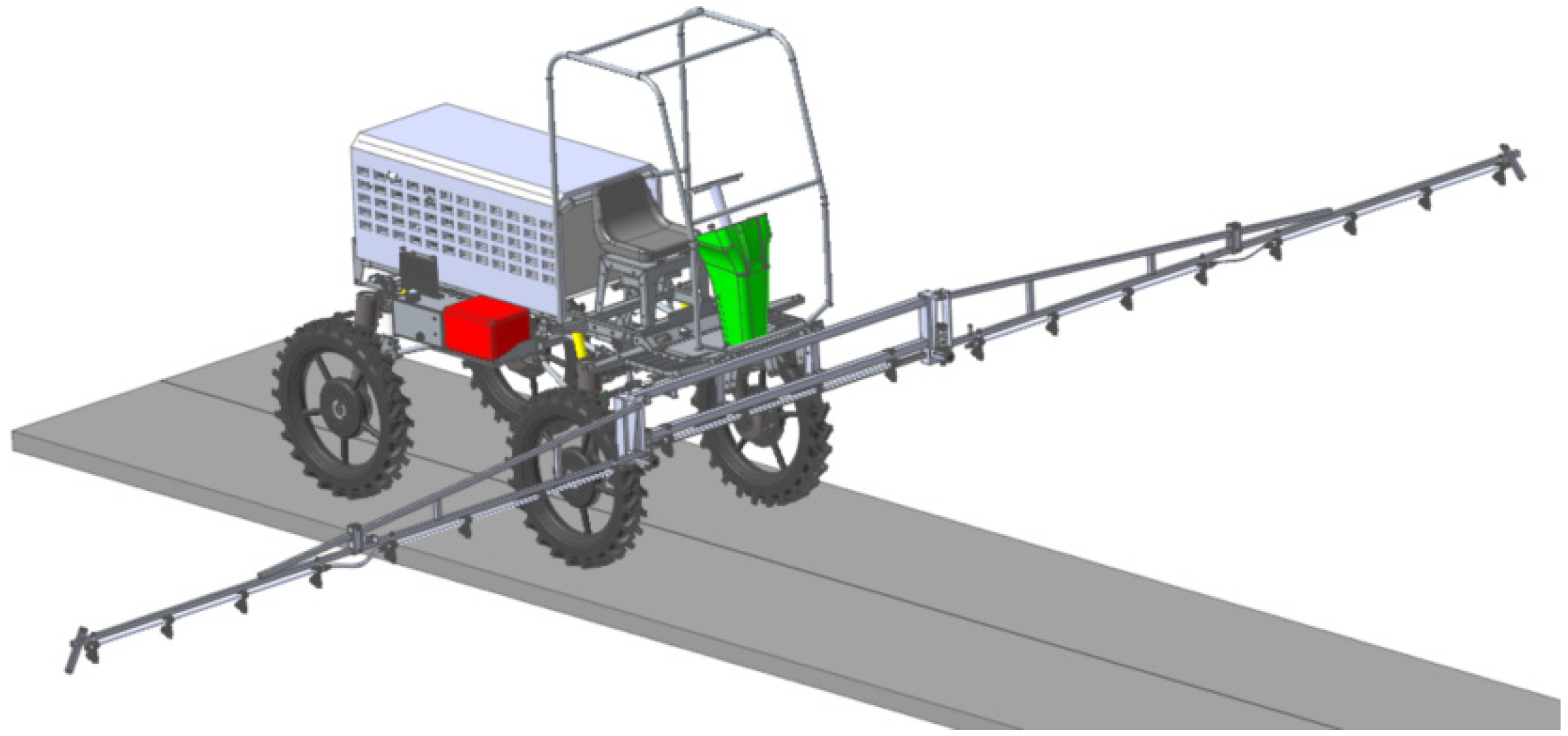
3.1. Dynamics Modelling
3.2. Chassis Performance Analysis
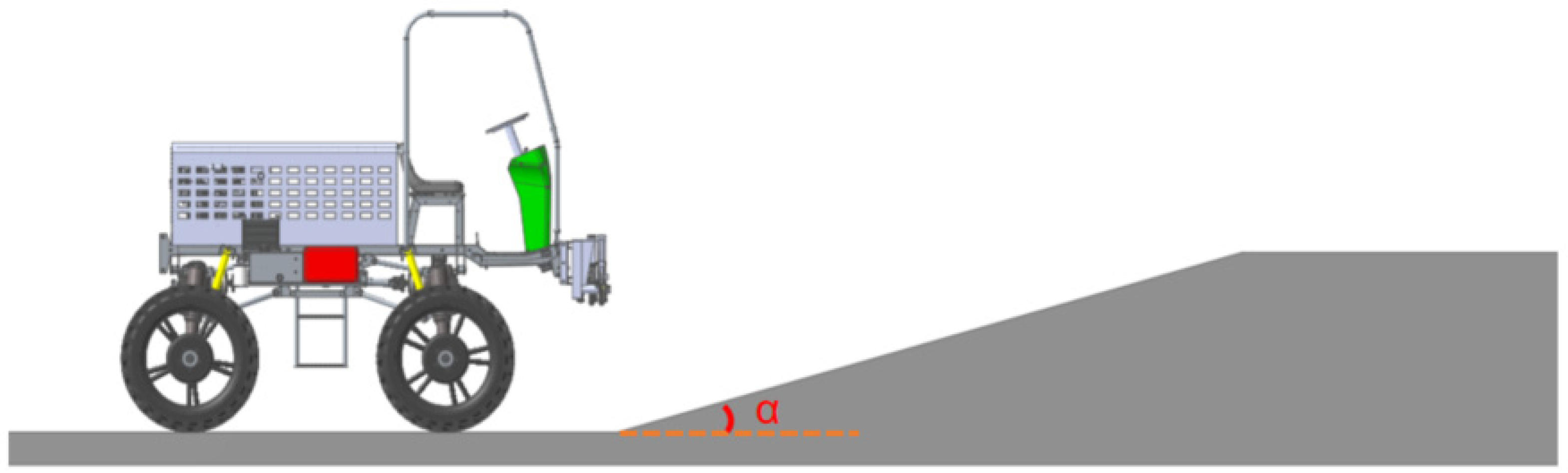
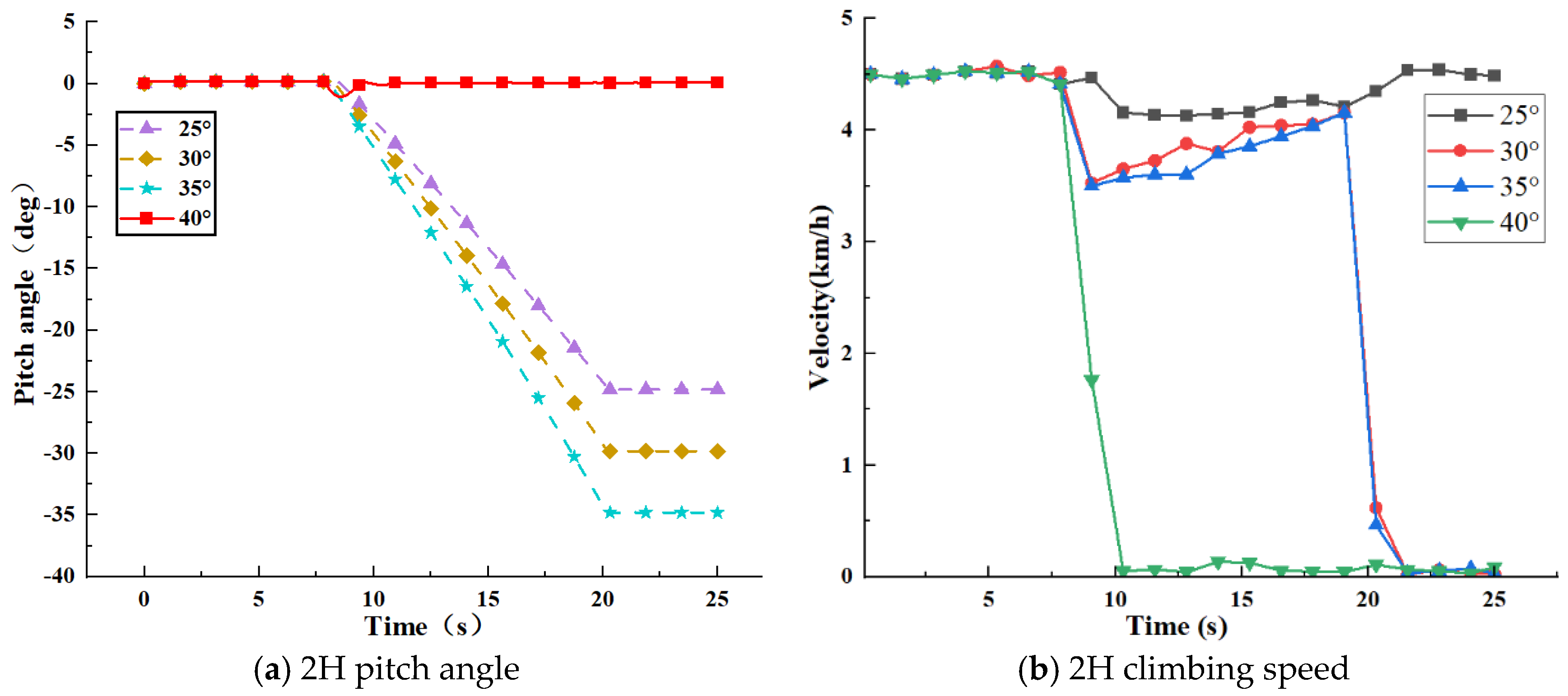
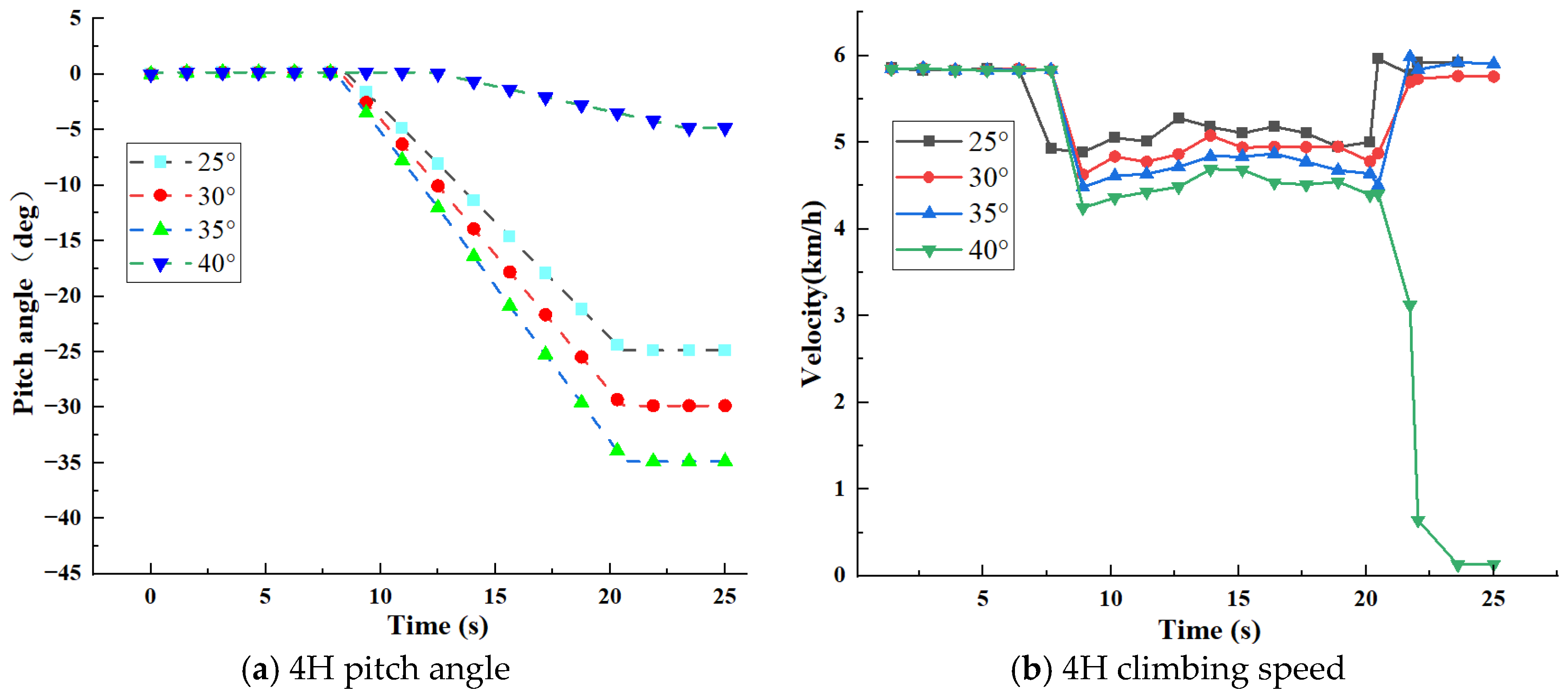
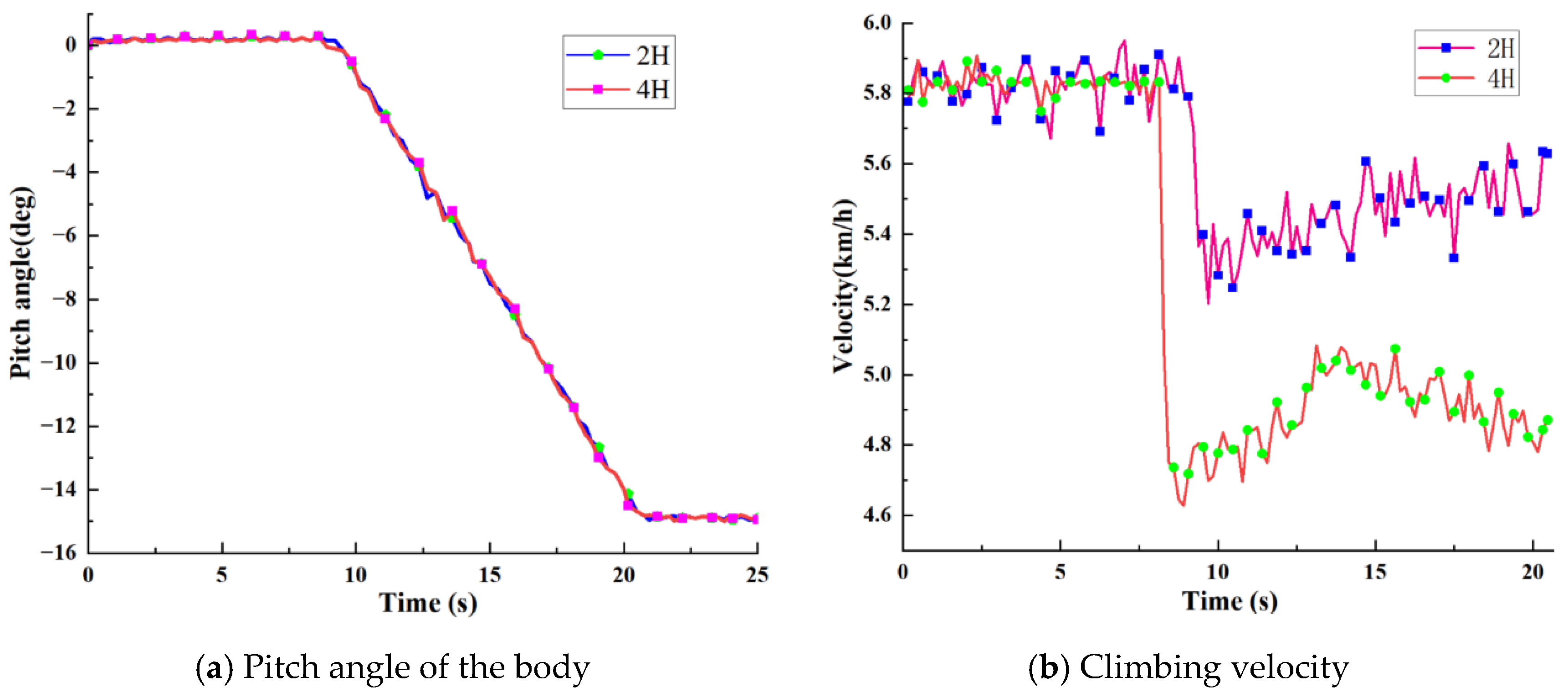
3.2.1. Climbing Performance Analysis
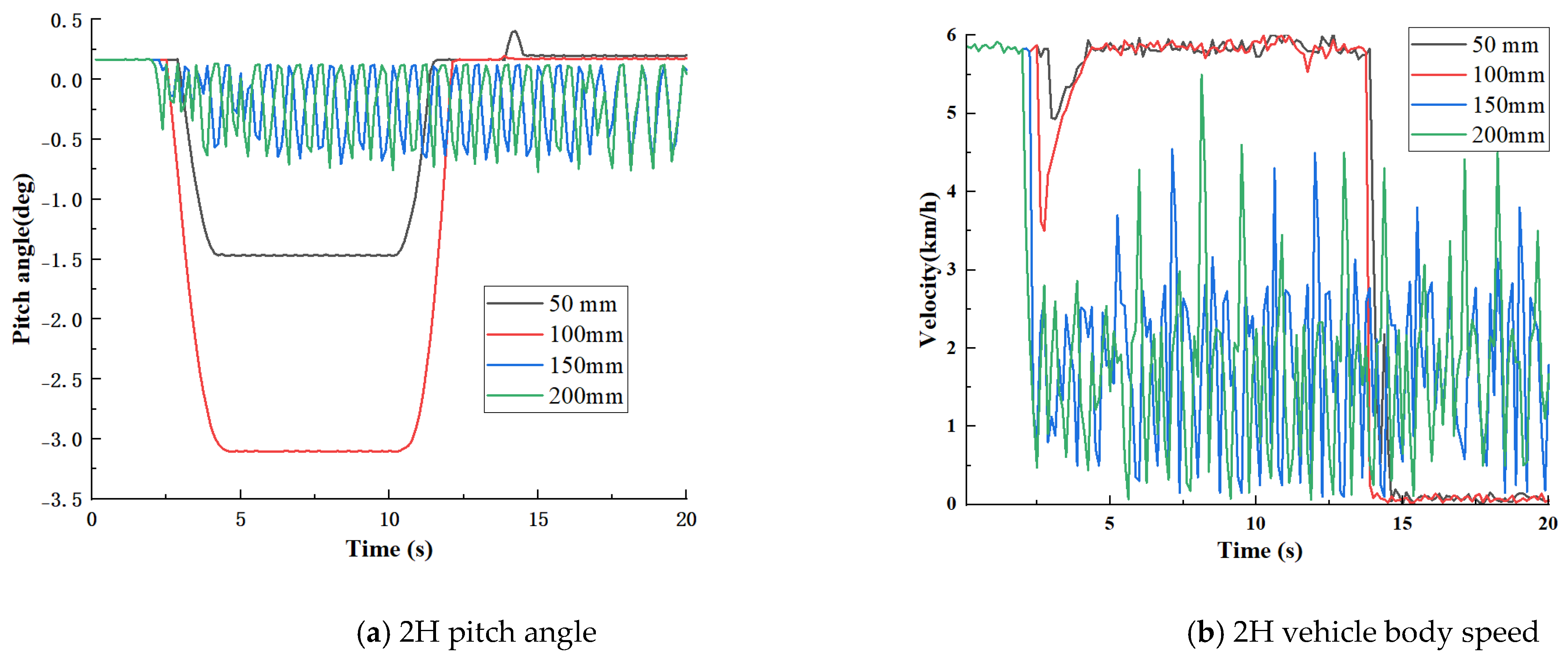
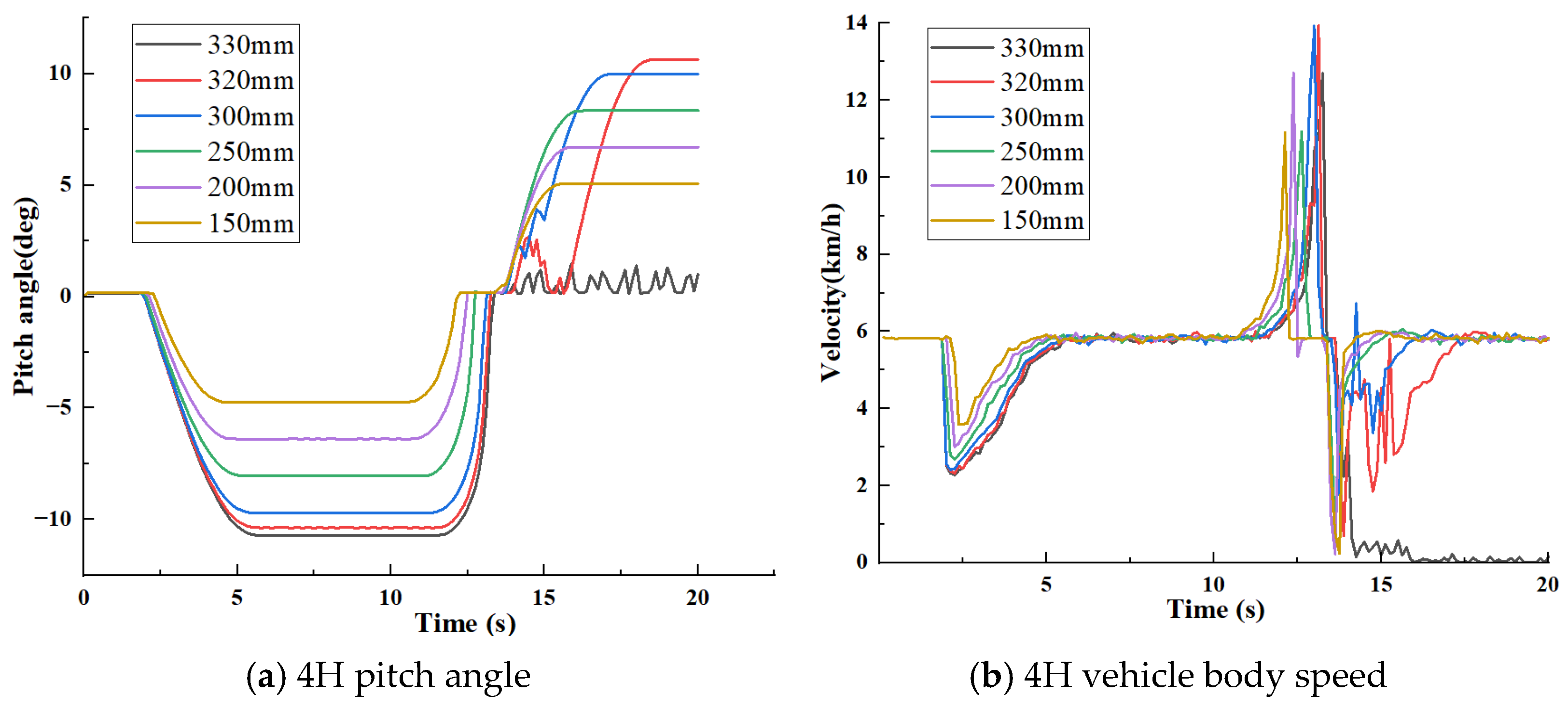
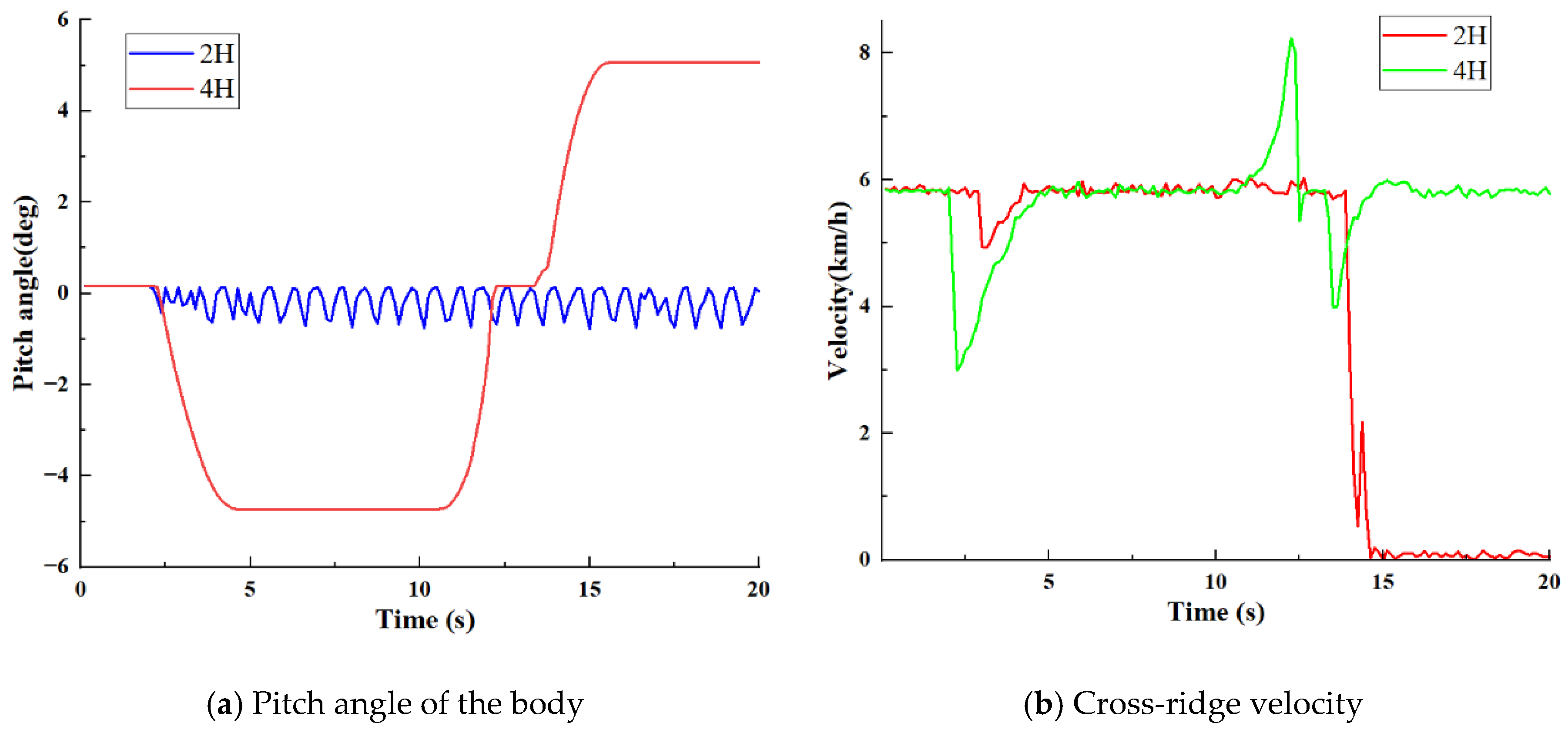
3.2.2. Cross-Ridge Performance Analysis
3.2.3. Performance Analysis of Opposite Pavement
4. Experiments
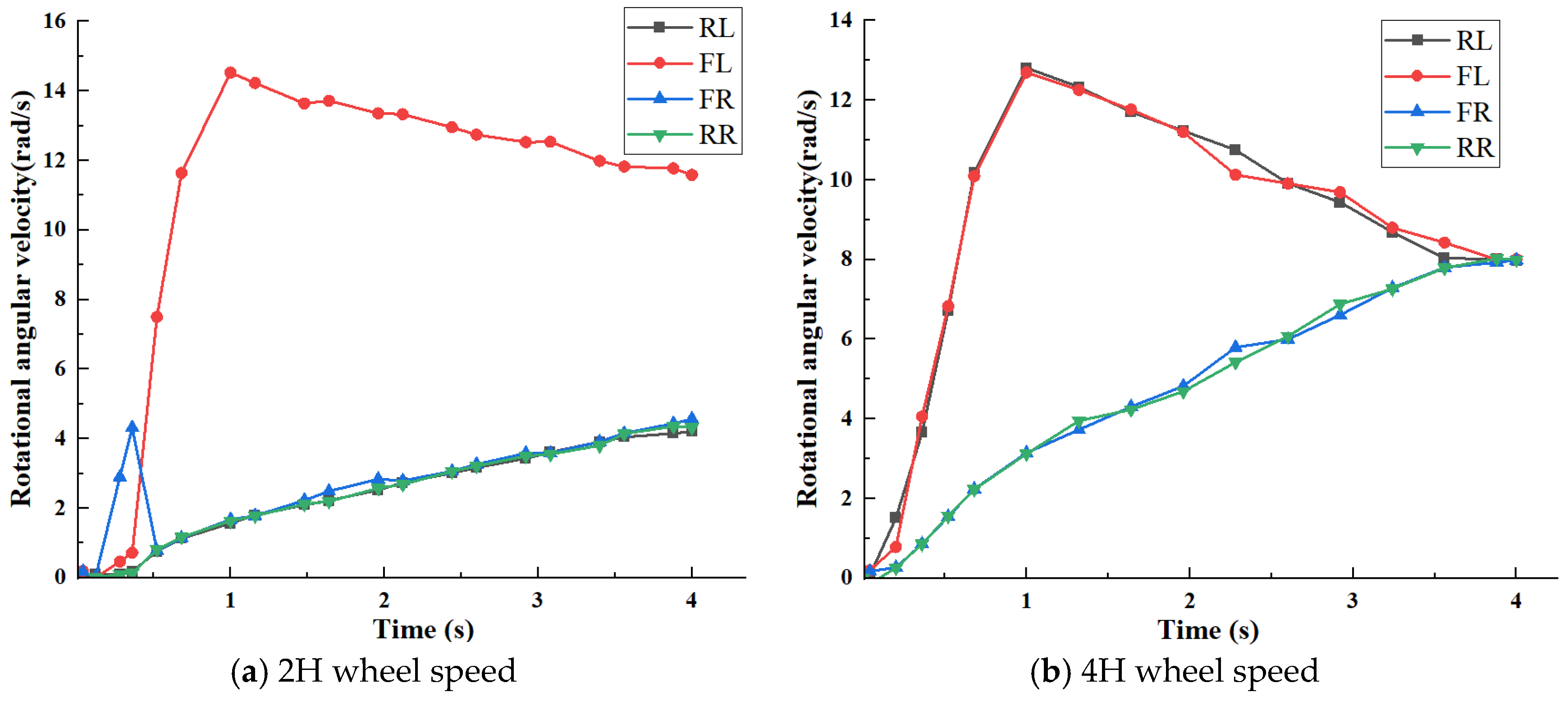
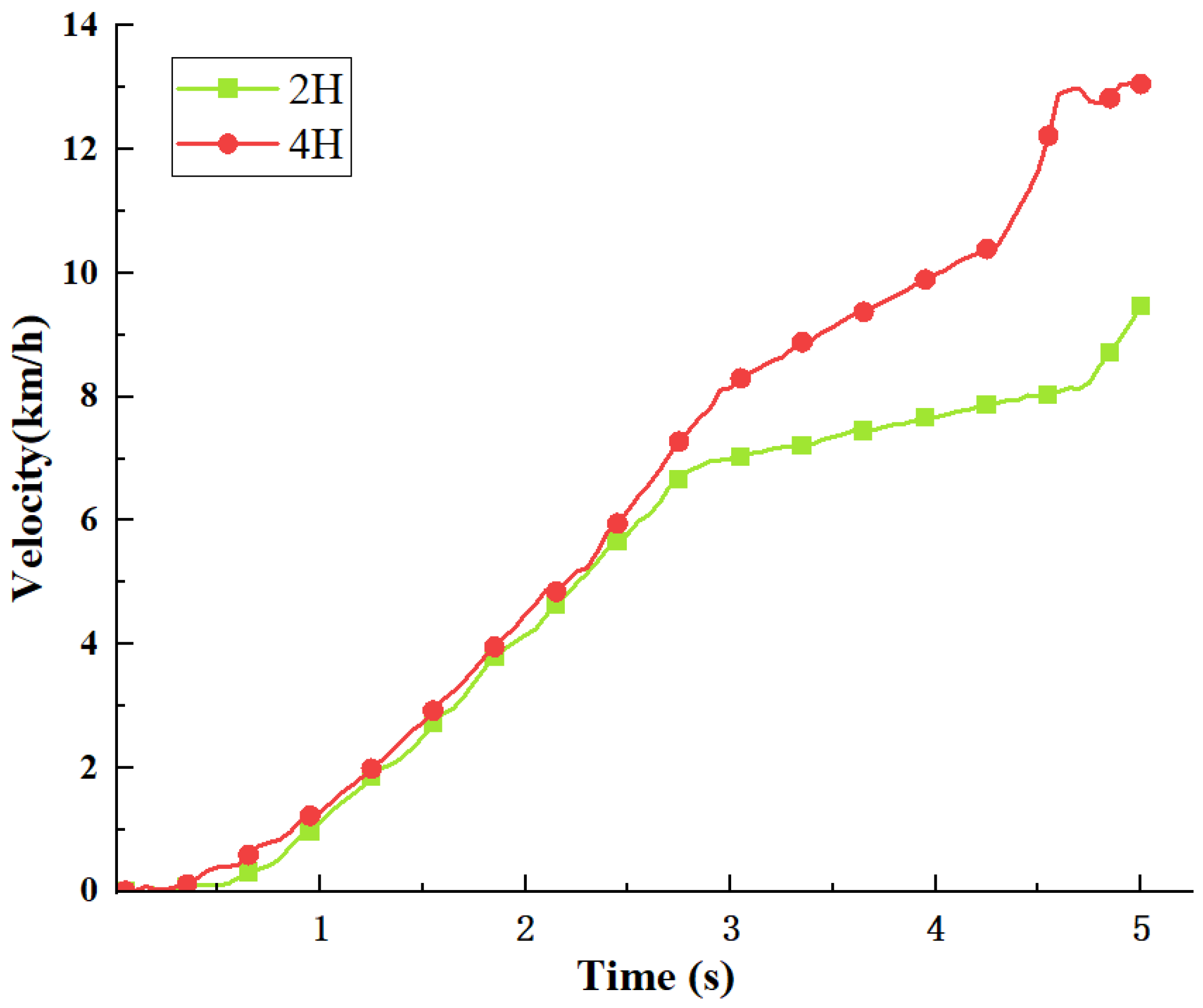
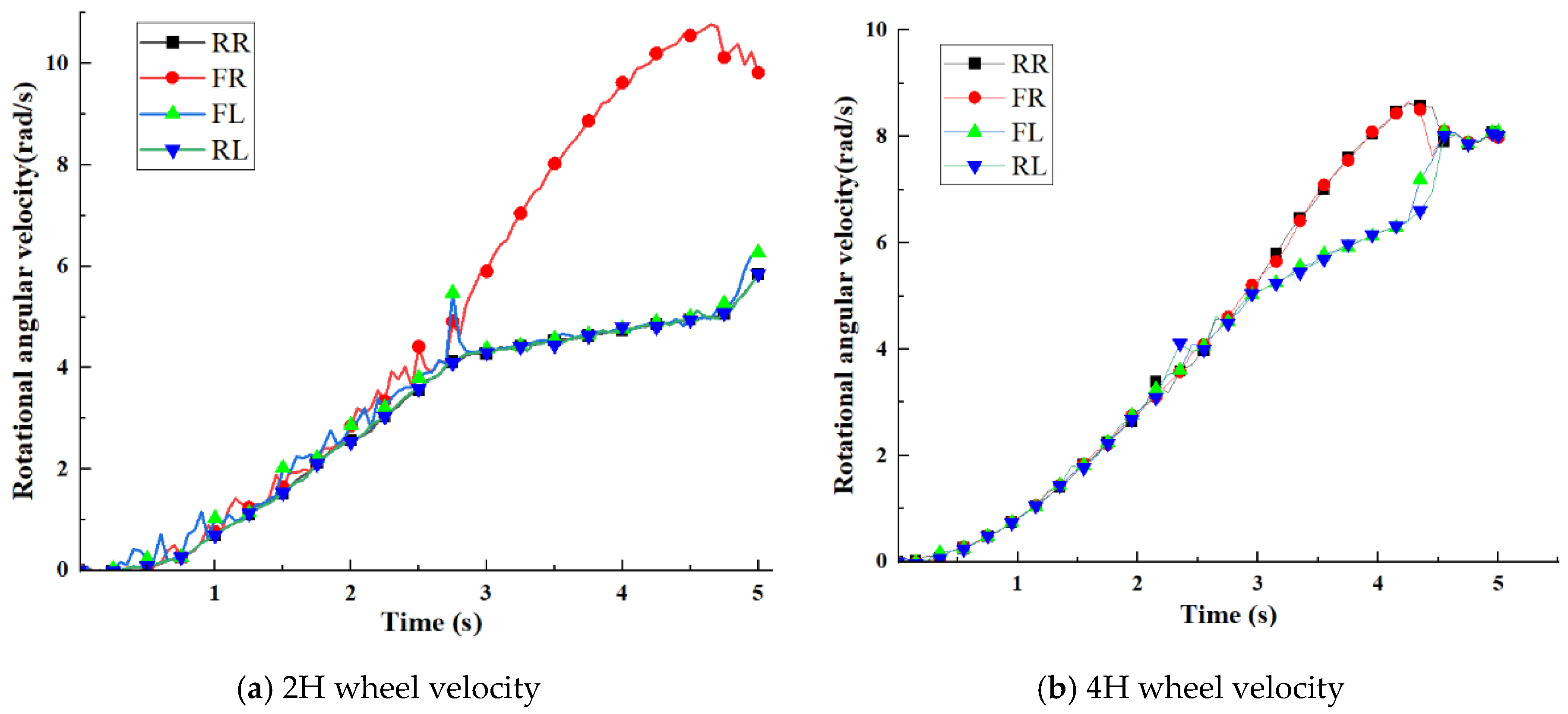
4.1. Climbing and Ridge Crossing Performance Test
4.2. Real-World Test of Rapid Acceleration on Variable-Access Roads
5. Discussion
- (1)
- The influence of dynamics control on operational performance
- (2)
- The impact of anti-skid braking on safety performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Zhou, Y.; Yue, X.; Zhang, G.; Wen, X.; Ma, B.; Xu, L.; Chen, L. Real-time detection of crop rows in maize fields based on autonomous extraction of ROI. Expert Syst. Appl. 2023, 213, 118826. [Google Scholar] [CrossRef]
- Xie, D.; Chen, L.; Liu, L.; Chen, L.; Wang, H. Actuators and sensors for application in agricultural robots: A review. Machines 2022, 10, 913. [Google Scholar] [CrossRef]
- Malkani, P.; Rathod, S.K.; Asha, K.R.; Khura, T.K.; Khuswaha, H.L. Design, analysis and fabrication of high clearance self-propelled foliar applicator. Curr. J. Appl. Sci. Technol. 2020, 39, 367–378. [Google Scholar] [CrossRef]
- Zeng, S.; Liu, J.; Luo, X.; Liu, S.; Huang, D.; Zewen, M.O. Design and experiment of wheel-track compound power chassis for high clearance sprayer in paddy field. J. South China Agric. Univ. 2019, 40, 14–22. [Google Scholar]
- Wang, W.; Feng, J.; Wan, W.; Zhang, P.; Yang, S. Modeling and Analysis of the Kinetic Influence of Liquid Sloshing Characteristics on High-Clearance Sprayers. Discret. Dyn. Nat. Soc. 2021, 2021, 9926962. [Google Scholar] [CrossRef]
- Shu, X.; Jiang, P.; Wenwu, H.U.; Shi, Y.; Lin, W.; Dong, C.; University, H.A. Design and test of the chassis leveling system for the high ground gap plant protection machine. J. Hunan Agric. Univ. 2019, 45, 321–326. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, Y.; Zhang, B.; Wen, X.; Yue, X.; Chen, L. Autonomous detection of crop rows based on adaptive multi-ROI in maize fields. Int. J. Agric. Biol. Eng. 2021, 14, 217–225. [Google Scholar] [CrossRef]
- Zhang, C.; Li, C.; Zhao, C.; Li, L.; Gao, G.; Chen, X. Design of hydrostatic chassis drive system for large plant protection machine. Agriculture 2022, 12, 1118. [Google Scholar] [CrossRef]
- Chen, Y.; Mao, E.; Li, W.; Zhang, S.; Song, Z.; Yang, S.; Chen, J. Design and experiment of a high-clearance self-propelled sprayer chassis. Int. J. Agric. Biol. Eng. 2020, 13, 71–80. [Google Scholar] [CrossRef]
- Chen, Z.; Gu, J.; Yang, X. A novel rigid wheel for agricultural machinery applicable to paddy field with muddy soil. J. Terramechan. 2019, 87, 21–27. [Google Scholar] [CrossRef]
- Fernandes, H.R.; Garcia, A.P. Design and control of an active suspension system for unmanned agricultural vehicles for field operations. Biosyst. Eng. 2018, 174, 107–114. [Google Scholar] [CrossRef]
- Li, Z.; Chen, L.; Zheng, Q.; Dou, X.; Yang, L. Control of a path following caterpillar robot based on a sliding mode variable structure algorithm. Biosyst. Eng. 2019, 186, 293–306. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Zhang, C.; Zheng, Q.; Liu, L. Fault-tolerant control based on fractional sliding mode: Crawler plant protection robot. Comput. Electr. Eng. 2023, 105, 108527. [Google Scholar] [CrossRef]
- Sun, D.; Chen, D.; Wang, S.; Wang, X. A dynamic instability detection and prediction system for high clearance tractor. IFAC-PapersOnLine 2016, 49, 50–54. [Google Scholar] [CrossRef]
- Zhang, Z.; Jia, X.; Yang, T.; Gu, Y.; Wang, W.; Chen, L. Multi-objective optimization of lubricant volume in an ELSD considering thermal effects. Int. J. Therm. Sci. 2021, 164, 106884. [Google Scholar] [CrossRef]
- Chen, L.; Ma, P.; Tian, J.; Liang, X. Prediction and optimization of lubrication performance for a transfer case based on computational fluid dynamics. Eng. Appl. Comput. Fluid Mech. 2019, 13, 1013–1023. [Google Scholar] [CrossRef]
- Zhu, Z.; Yang, Y.; Wang, D.; Cai, Y.; Lai, L. Energy saving performance of agricultural tractor equipped with mechanic-electronic-hydraulic powertrain system. Agriculture 2022, 12, 436. [Google Scholar] [CrossRef]
- Wang, W.; Chen, L.; Yang, Y.; Liu, L. Current status and prospects of chassis technology research in agricultural machinery. J. Agric. Mach. 2021, 52, 1–15. [Google Scholar]
- Gonzalez-de-Soto, M.; Emmi, L.; Perez-Ruiz, M.; Aguera, J.; Gonzalez-de-Santos, P. Autonomous systems for precise spray-ing—Evaluation of a robotized patch sprayer. Biosyst. Eng. 2016, 146, 165–182. [Google Scholar] [CrossRef]
- Liu, H.; Long, Y.N.; He, S.W.; Cui, Y.M.; Sheng, Y. Design and experiment of the auxiliary steering system for a four-wheel independent electrically driven high clearance sprayer. Trans. Chin. Soc. Agric. Eng. 2021, 37, 30–37. [Google Scholar]
- Zhou, Q.Q.; Wen, H.J.; Li, Z.X.; Zhang, W.R.; Yi, Z.T.; Wang, G.T. Design and test of fuzzy anti-skid control of four-wheel drive hydraulically driven sprayer. Trans. Chin. Soc. Agric. Mach. 2020, 51, 283–288. [Google Scholar]
- Pontelli, C.O.; Mucheroni, M.F.; Balthazar, J.M.; Pontes, B.R. Comparison between two types of passive boom suspension under simulated conditions of track test. Eng. Agric. 2010, 30, 761–775. [Google Scholar]
- Guo, X.; Vacca, A. Advanced design and optimal sizing of hydrostatic transmission systems. Actuators 2021, 10, 243. [Google Scholar] [CrossRef]
- Mistry, K.A.; Patel, B.A.; Patel, D.J.; Parsana, P.M.; Patel, J.P. Design and analysis of hydrostatic transmission system. IOP Conf. Ser. Mater. Sci. Eng. 2018, 310, 012048. [Google Scholar] [CrossRef]
- Xue, L.; Jiang, H.; Zhao, Y.; Wang, J.; Wang, G.; Xiao, M. Fault diagnosis of wet clutch control system of tractor hydrostatic power split continuously variable transmission. Comput. Electron. Agric. 2022, 194, 106778. [Google Scholar] [CrossRef]
- Comellas, M.; Pijuan, J.; Potau, X.; Nogués, M.; Roca, J. Analysis of a hydrostatic transmission driveline for its use in off-road multiple axle vehicles. J. Terramechan. 2012, 49, 245–254. [Google Scholar] [CrossRef]
- Xupeng, H.; Wenbin, S.; Hang, Z.; Yanni, Z.; Qiao, H.; Chaohui, W. Research of the hydrostatic transmission for deep-sea current energy converter. Energy Convers. Manag. 2020, 207, 112544. [Google Scholar] [CrossRef]
- Chen, L.; Li, Z.; Yang, J.; Song, Y. Lateral stability control of four-wheel-drive electric vehicle based on coordinated control of torque distribution and ESP differential braking. Actuators 2021, 10, 135. [Google Scholar] [CrossRef]
- Meng, J.; Zheng, Q.; Chen, L. Multi-objective optimization design of splitter for time-division four-wheel drive vehicle. Mech. Sci. Technol. 2016, 35, 1756–1760. [Google Scholar] [CrossRef]
- Liang, X.; Chen, L.; Wang, Y.; Wan, L. A proposed torque calculation model for multi-plate clutch considering boundary lubrication conditions and heat transfer. Int. J. Heat Mass Transf. 2020, 157, 119732. [Google Scholar] [CrossRef]
- Huang, C.; Xu, Z.; Zhang, Y.; Xue, Z.; Wang, X.; Li, L. A model-based temperature estimation method and experimental ver-ification for 4WD vehicle transfer case clutch. IFAC-PapersOnLine 2021, 54, 209–214. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, K.; Xiao, M.; Zhou, M. Research on steady-state transmission efficiency of HMCVT based on hydraulic me-chanical transmission torque ratio. J. Agric. Mach. 2021, 52, 9. [Google Scholar]
- Wang, Q.; Zhang, Q.; Zhang, Y.; Zhou, G.; Li, Z.; Chen, L. Lodged sugarcane/crop dividers interaction: Analysis of robotic sugarcane harvester in agriculture via a rigid-flexible coupled simulation method. Actuators 2022, 11, 23. [Google Scholar] [CrossRef]
- Wang, Q.; Bai, Z.; Li, Z.; Xie, D.; Chen, L.; Wang, H. Straw/spring teeth interaction analysis of baler picker in smart agriculture via an ADAMS-DEM coupled simulation method. Machines 2021, 9, 296. [Google Scholar] [CrossRef]
- Yan, X.; Nie, J.; Ma, Z. Intelligent mobile chassis modeling and climbing process simulation based on Recurdyn. J. Zhongyuan Inst. Technol. 2021, 32, 27–31. [Google Scholar]
- Fu, X.; Wang, Y.; Liu, D.; Wang, J. Research on the drive force control of wheel motor-driven off-road vehicles. China Mech. Eng. 2022, 1–12. Available online: http://kns.cnki.net/kcms/detail/42.1294.TH.20220923.1705.012.html (accessed on 7 February 2023).
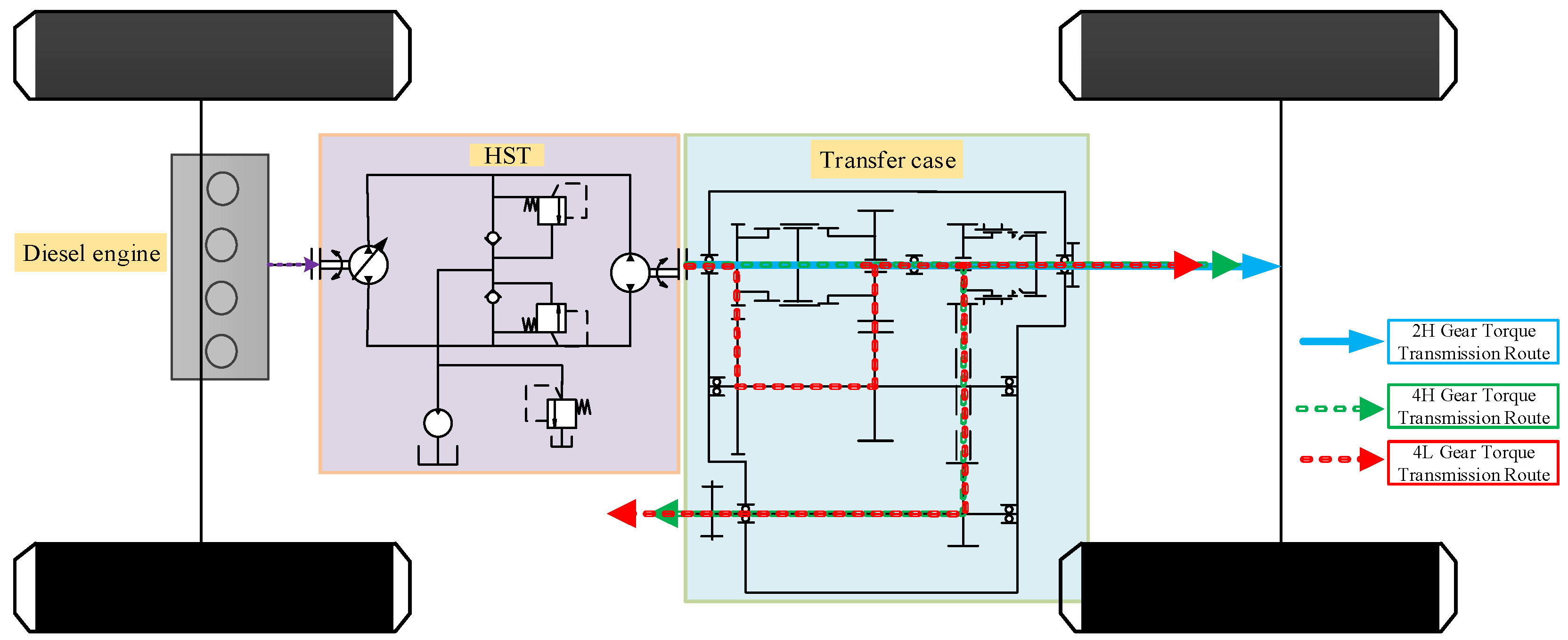




| Drive Mode | Gear Level | Transmission Ratio | Drive Form |
|---|---|---|---|
| 2WD | 2H | 1:1 | Two-wheel-drive status |
| 4WD | 4H | 1:1 | Four-wheel high-speed drive status |
| 4L | 2.48:1 | Four-wheel low-speed drive status |
| Parameters | Number of Values |
|---|---|
| Full load mass | 1500 kg |
| Overall dimension | 2200 mm × 1400 mm × 1800 mm |
| Spraying width | 8000 mm |
| The volume of medicine box | 200 L |
| Operating speed | 0~10 km/h |
| Unloaded mass | 1200 kg |
| Number of axes | 2 |
| Axis distance | 1200 mm |
| Wheel distance | 1650 mm |
| Distance from center of mass to front axis | 800 mm |
| Ground clearance | 980 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.; Xie, D.; Liu, T.; Hu, P.; Liu, H.; Zheng, Q. Design of a High-Gap Plant Protection Machine (HGPM) with Stepless Variable Speed and Power Adjustable Function. Machines 2023, 11, 265. https://doi.org/10.3390/machines11020265
Cai Z, Xie D, Liu T, Hu P, Liu H, Zheng Q. Design of a High-Gap Plant Protection Machine (HGPM) with Stepless Variable Speed and Power Adjustable Function. Machines. 2023; 11(2):265. https://doi.org/10.3390/machines11020265
Chicago/Turabian StyleCai, Zengbin, Dongbo Xie, Tao Liu, Peiyu Hu, Hongji Liu, and Quan Zheng. 2023. "Design of a High-Gap Plant Protection Machine (HGPM) with Stepless Variable Speed and Power Adjustable Function" Machines 11, no. 2: 265. https://doi.org/10.3390/machines11020265
APA StyleCai, Z., Xie, D., Liu, T., Hu, P., Liu, H., & Zheng, Q. (2023). Design of a High-Gap Plant Protection Machine (HGPM) with Stepless Variable Speed and Power Adjustable Function. Machines, 11(2), 265. https://doi.org/10.3390/machines11020265






