Effects of Tooth Modification in the Involute Helical Gear Form-Grinding Process on Loaded Transmission Character with Consideration of Tooth Axial Inclination Error
Abstract
:1. Introduction
2. Tooth Modification Model Based on Tooth Axial Inclination Error
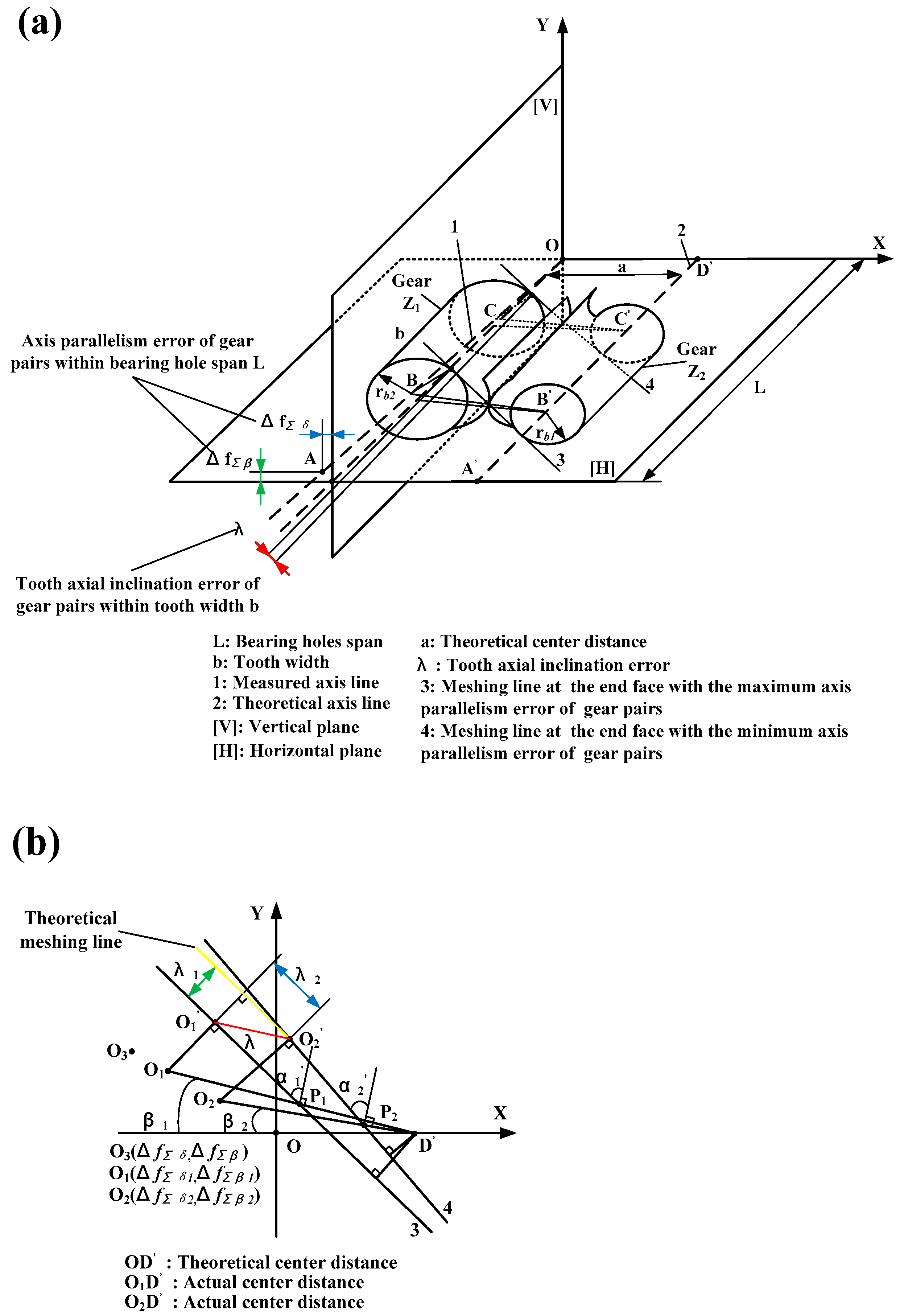
2.1. Axis Parallelism Error of Gear Pairs
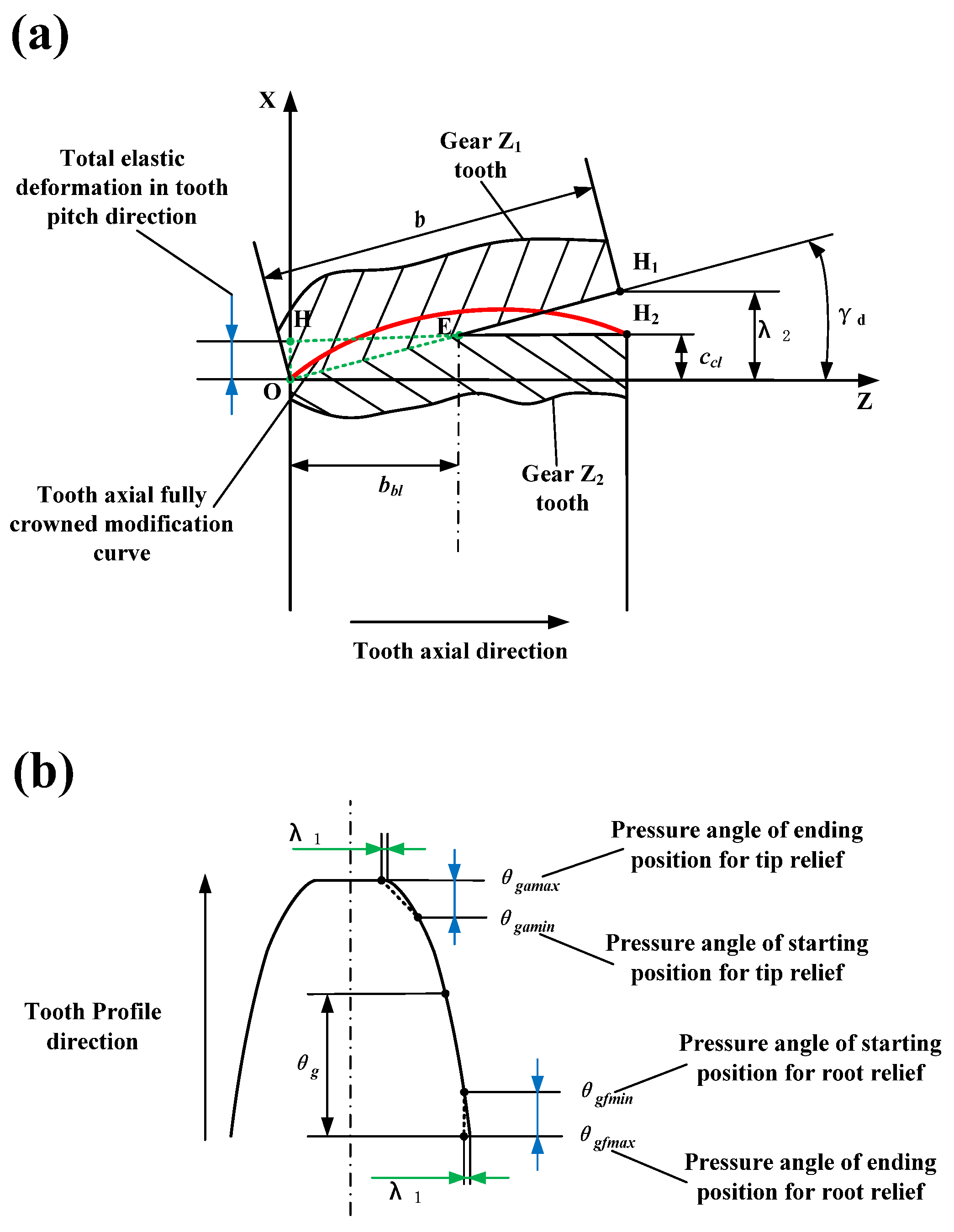
2.2. Tooth Modification Model Based on Tooth Axial Inclination Error
3. Involute Helical Gear Form Grinding with Tooth Modification
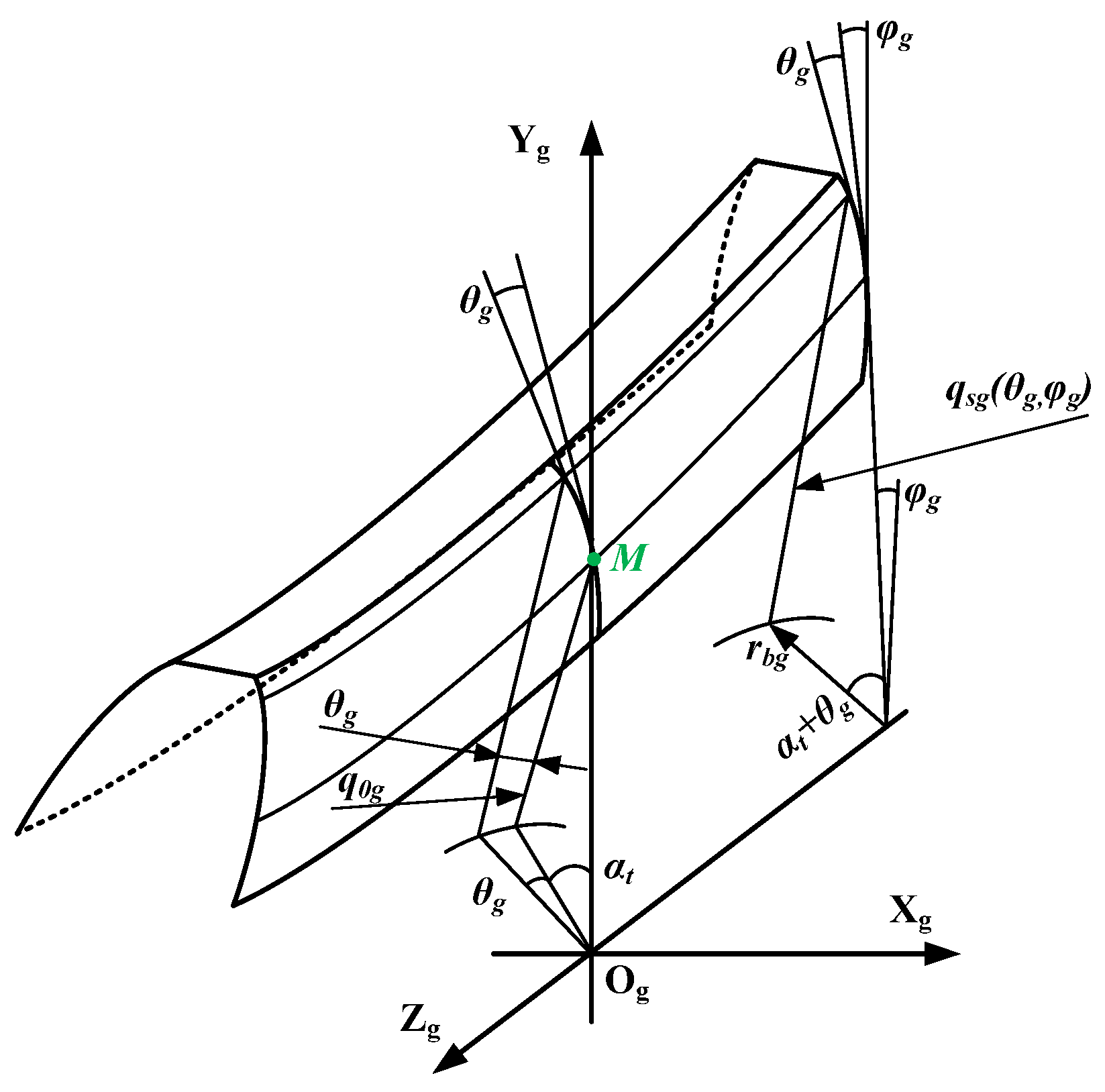
3.1. Tooth Surface Equation of Involute helical Gear with Tooth Modification
3.2. Involute Helical Gear Form-Grinding Process with Tooth Modification
3.3. Calculation of Cross-Sectional Profile of Grinding Wheel
3.4. Tooth Surface Modified Error of Involute Helical Gear with Different Tooth Modification Parameters
4. Finite Element Simulation of Involute Helical Gearbox with Tooth Modification
4.1. Influence of Tooth Modification on Tooth Surface Contact Stress
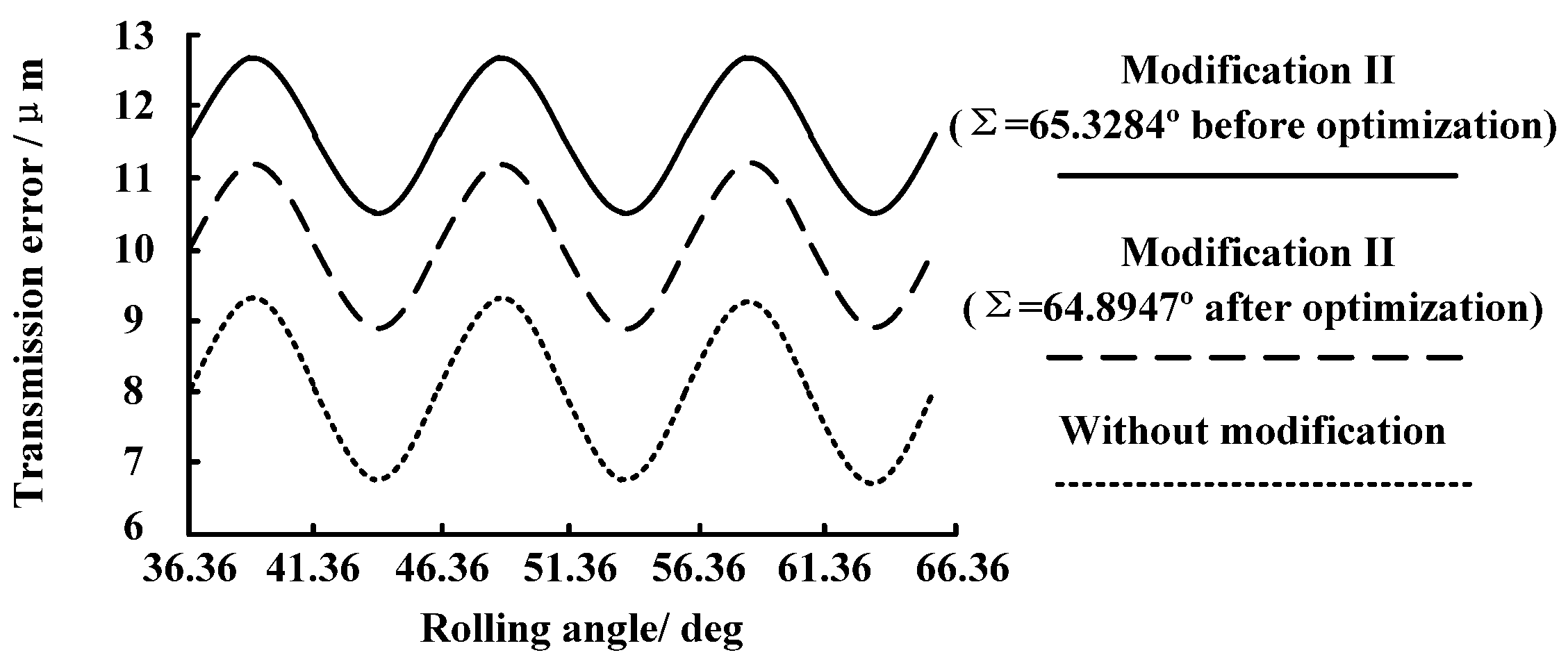
4.2. Influence of Tooth Modification on Gearbox Transmission Error
5. Experimental Verification
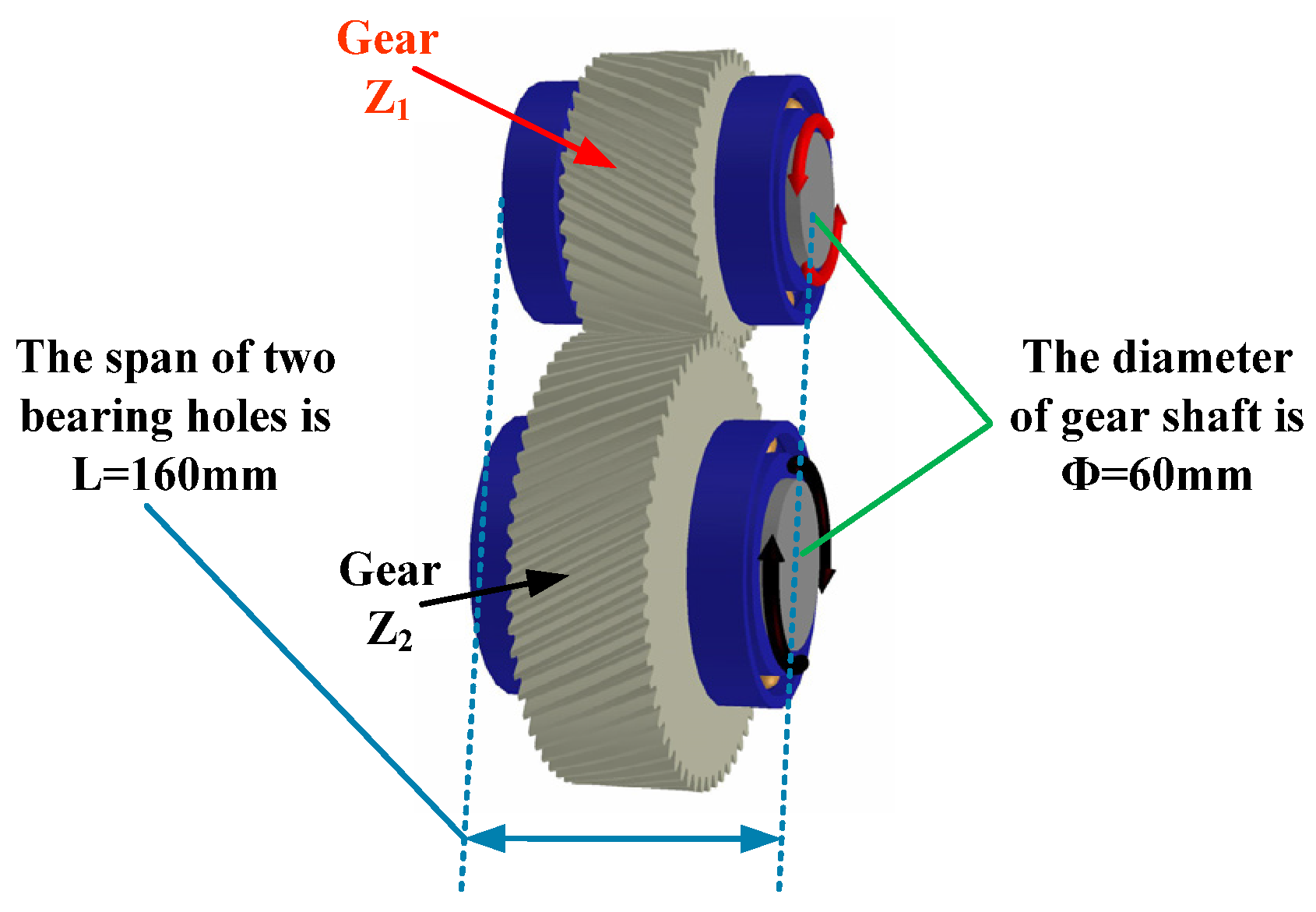
5.1. Static Accuracy Measuring Experiment of Machine Tools
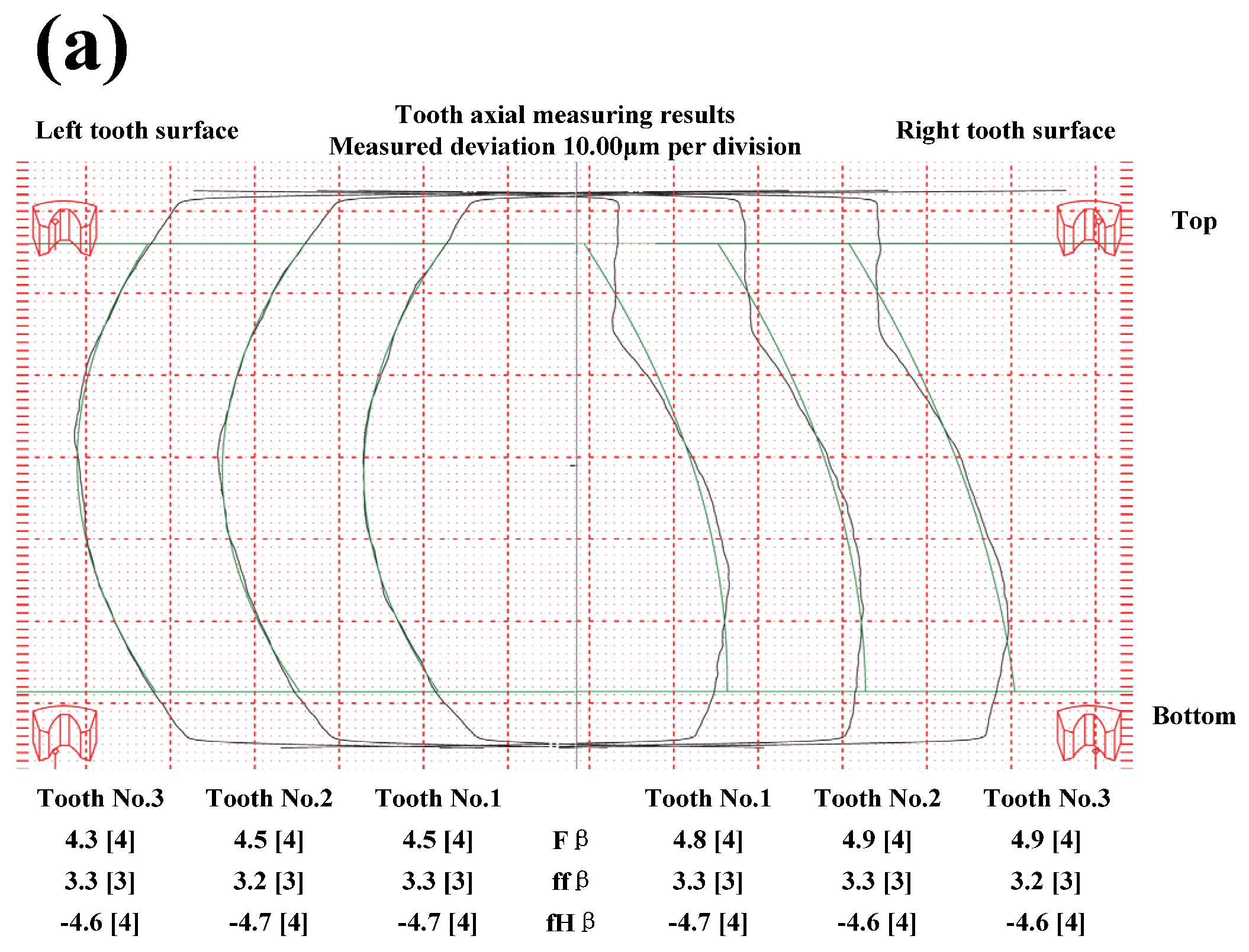
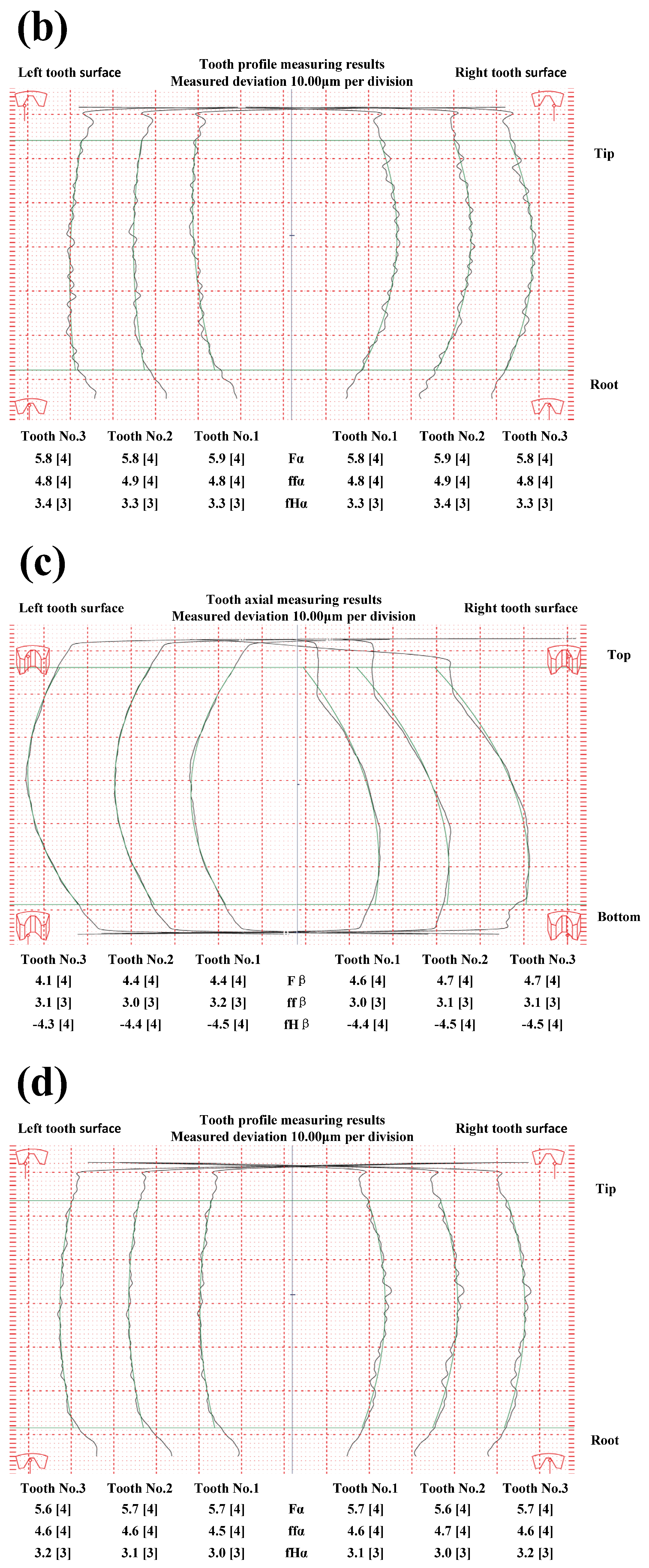
5.2. Grinding and Measuring Experiment of Involute Helical Gear with Different Tooth Modification Parameters
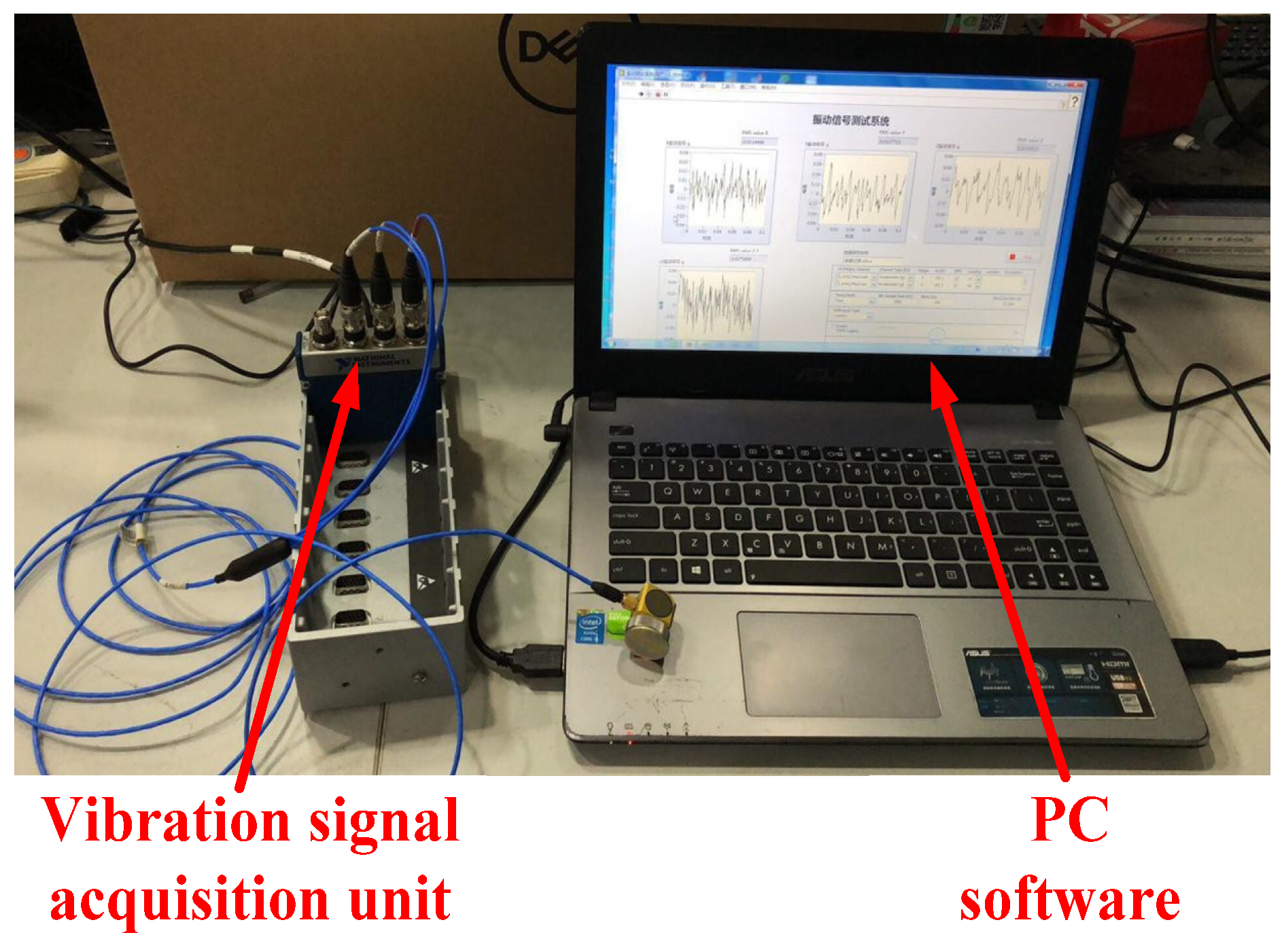
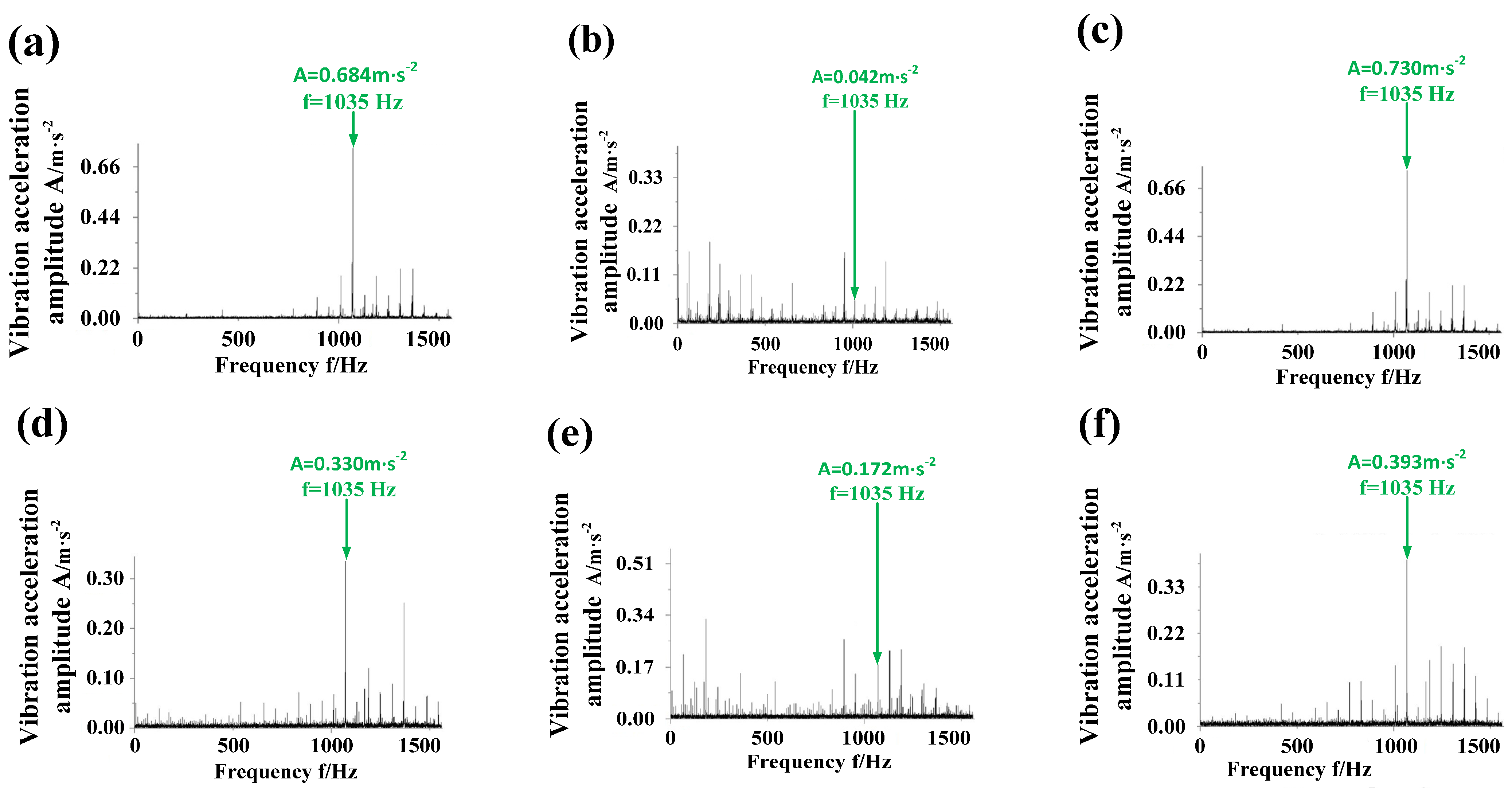
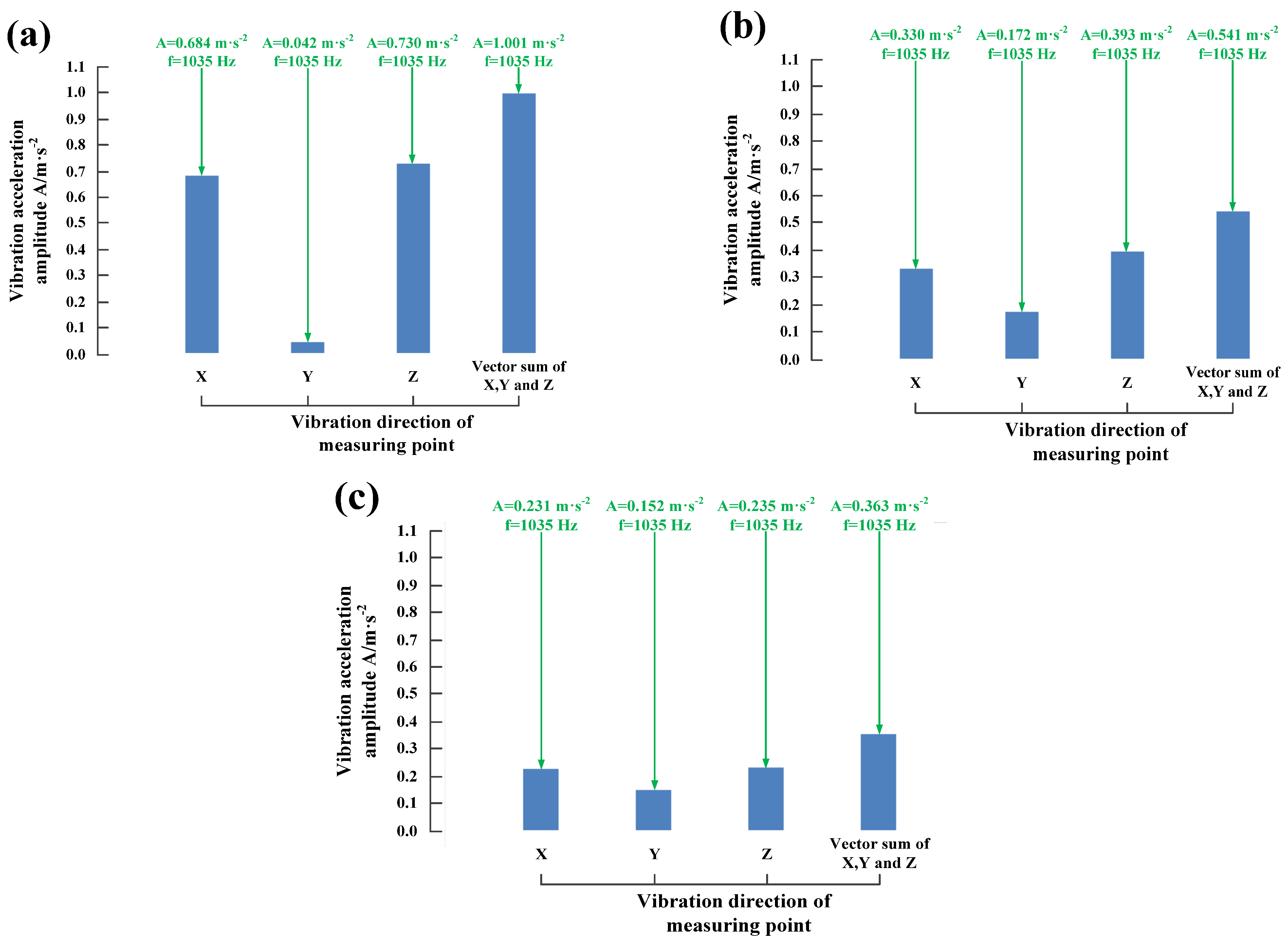
5.3. Gearbox Vibration Measuring Experiment
6. Conclusions
- (1)
- Compared with the existing method, the method proposed in this paper can effectively reduce “tooth profile distortion” and “tooth axial twist” of the involute helical gear form-grinding process, thus improving loaded transmission character. In particular, the tooth surface modified error data show that “tooth profile distortion” of modification II ( after optimization) is reduced significantly, where the tooth profile modification rate is about 98.6%; and the “tooth axial twist” of modification II ( after optimization) is reduced significantly, where the tooth axial modification rate is about 95.7%;
- (2)
- According to the grinding and measuring experiment, the Gleason measuring accuracy is level 4. Compared with modification II ( before optimization), the “tooth profile distortion” and “tooth axial twist” of modification II ( after optimization) are effectively reduced, and the offset of the “tooth profile distortion” and “tooth axial twist” are, respectively, lower by 31.6% and 31.7%. Moreover, the tooth modification of modification II ( after optimization) is significantly realized, and the tooth modification rates of the tooth profile and tooth axial are about 97.6% and 94.7%, respectively;
- (3)
- According to the gearbox vibration measuring experiment, loaded transmission character is improved significantly. Compared to the gearbox without modification, the reduction rate of the vector sum of the gearbox vibration amplitude of modification II ( before optimization) is 46.0%, and the reduction rate of the vector sum of the gearbox vibration amplitude of modification II ( after optimization) is 63.7%. Furthermore, there is an obvious eccentric load on the tooth surface of the gearbox without modification; there is almost no eccentric load on the tooth surface of the gearbox with modification II ( after optimization). Therefore, this paper can provide a theoretical and experimental basis for the research of high-performance gear-grinding technology of gear-grinding machines.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, J.; Wei, J.J.; Shi, Z.Y. An evaluation method of gear profile deviations based on the consideration of installation errors. Measurement 2019, 146, 806–814. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Feng, R.J.; Pang, X.; Wen, B.C. An improved analytical method for mesh stiffness calculation of spur gears with tip relief. Mech. Mach. Theory 2016, 98, 64–80. [Google Scholar] [CrossRef]
- Galym, Z.; Spitas, C. Analysis of a misalignment-insensitive spur gear transmission using a Rzeppa joint. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1670–1683. [Google Scholar] [CrossRef]
- Duezcuekoglu, H. PA 66 spur gear durability improvement with tooth width modification. Mater. Des. 2009, 30, 1060–1067. [Google Scholar] [CrossRef]
- Pedersen, N.L.; Jorgensen, M.F. On gear tooth stiffness evaluation. Comput. Struct. 2014, 135, 109–117. [Google Scholar] [CrossRef]
- Lin, H.H.; Oswald, F.B.; Townsend, D.P. Dynamic loading of spur gears with linear or parabolic tooth profile modifications. Mech. Mach. Theory 1994, 29, 1115–1129. [Google Scholar] [CrossRef]
- Tian, X.Q.; Zhou, L.; Han, J.; Xia, L. Research on gear flank twist compensation of continuous generating grinding gear based on flexible electronic gearbox. IEEE Access 2021, 9, 151080–151088. [Google Scholar] [CrossRef]
- Tran, V.Q.; Wu, Y.R. A novel method for closed-loop topology modification of helical gears using internal-meshing gear honing. Mech. Mach. Theory 2020, 145, 103691. [Google Scholar] [CrossRef]
- Tran, V.T.; Hsu, R.H.; Tsay, C.B. Tooth contact analysis of double-crowned involute helical pairs shaved by a crowning mechanism with parallel shaving cutters. Mech. Mach. Theory 2014, 79, 198–216. [Google Scholar] [CrossRef]
- Liu, J.; Ding, S.Z.; Pang, R.K.; Li, X.B. Influence of the roller profile modification of planet bearing on the vibrations of a planetary gear system. Measurement 2021, 180, 109612. [Google Scholar] [CrossRef]
- Shen, Y.B.; Fang, Z.D.; Zhao, N.; Guo, H.; Zeng, X.C. Application of modified geometry of face-gear drive with double crowned helical pinion. In Advanced Design and Manufacture to Gain a Competitive Edge: New Manufacturing Techniques and Their Role in Improving Enterprise Performance; Springer: London, UK, 2008; Volume 1, pp. 579–588. [Google Scholar] [CrossRef]
- Wang, Z.H.; Song, X.M.; He, W.M.; Li, G.; Zhu, W.M.; Geng, Z. Tooth surface model construction and error evaluation for tooth-trace modification of helical gear by form grinding. China Mech. Eng. 2015, 26, 2841–2847. [Google Scholar] [CrossRef]
- Lee, C.K. Manufacturing process for a cylindrical crown gear drive with a controllable fourth order polynomial function of transmission error. J. Mater. Process. Technol. 2009, 209, 3–13. [Google Scholar] [CrossRef]
- Shih, Y.P.; Chen, S.D. A flank correction methodology for a five-axis CNC gear profile grinding machine. Mech. Mach. Theory 2012, 47, 31–45. [Google Scholar] [CrossRef]
- Xia, Z.; Huang, X.D.; Yuan, H. A kind of exactitude algorithm for wheel profile of the helical-gear form grinding. Mech. Sci. Technol. Aerosp. Eng. 2012, 31, 1311–1314. [Google Scholar] [CrossRef]
- Guo, E.K.; Huang, X.D.; Yuan, H.; Fang, C.G.; Zhang, H. Contact line optimization for improving efficiency and precision of form grinding. Comput. Integr. Manuf. Syst. 2013, 19, 67–74. [Google Scholar] [CrossRef]
- Guo, E.K.; Huang, X.D.; Yuan, H.; Fang, C.G. Optimization of contact line for form grinding of involute helical gears. Mech. Sci. Technol. Aerosp. Eng. 2012, 31, 1320–1324. [Google Scholar] [CrossRef]
- Ding, G.L.; Zhang, S.; Zhao, D.X.; Zhao, D.; Zhao, D.X. Optimization of grinding wheel profile for gear form grinding. China Mech. Eng. 2015, 26, 743–748. [Google Scholar] [CrossRef]
- Fang, C.G.; Huang, X.D.; Guo, E.K.; Zhang, H. Tool path planning for lead modification of form grinding based on wheel configuration optimization. J. Nanjing Univ. Technol. (Nat. Sci. Ed.) 2013, 35, 87–93. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhu, W.M.; Li, G.; Geng, Z. Optimization of contact line for form-grinding modified helical gears based on neural network. China Mech. Eng. 2014, 25, 1665–1671. [Google Scholar] [CrossRef]
- Seol, I.H.; Kim, D.H. The kinematic and dynamic analysis of crowned spur gear drive. Comput. Methods Appl. Mech. Eng. 1998, 167, 109–118. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, Z. Analysis of transmission errors under load of helical gears with modified tooth surfaces. J. Mech. Des. 1997, 119, 120–126. [Google Scholar] [CrossRef]
- Chang, S.; Houser, D.R.; Harianto, J. Tooth flank corrections of wide face width helical gears that account for shaft deflections. ASME Int. Des. Eng. Tech. Conf. Comput. Inf. Eng. Conf. 2003, 4, 567–574. [Google Scholar]
- Imrek, H.; Duzcukoglu, H. Relation between wear and tooth width modification in spur gears. Wear 2007, 262, 390–394. [Google Scholar] [CrossRef]
- Chen, S.Y.; Tang, J.Y.; Wang, Z.W.; Hu, Z.H. Effect of modification on dynamic characteristics of gear transmissions system. J. Mech. Eng. 2014, 50, 59–65. [Google Scholar] [CrossRef]
- Zhang, B.F.; Cui, Y.H.; Liu, K.; Dong, Y.W. Effects of involute spur gear structure parameters on meshing efficiency. J. Mech. Strength 2015, 37, 122–127. [Google Scholar] [CrossRef]
- Song, L.M. Tooth Profile and Gear Strength; National Defense Press: Beijing, China, 1987. [Google Scholar]
- Sun, Z.; Chen, S.Y.; Hu, Z.H.; Tao, X. Improved mesh stiffness calculation model of comprehensive modification gears considering actual manufacturing. Mech. Mach. Theory 2022, 167, 104470. [Google Scholar] [CrossRef]
- Yan, P.F.; Liu, H.; Gao, P.; Zhang, X.; Zhan, Z.B.; Zhang, C. Optimization of distributed axial dynamic modification based on the dynamic characteristics of a helical gear pair and a test verification. Mech. Mach. Theory 2021, 163, 104371. [Google Scholar] [CrossRef]
- Umeyama, M.; Kato, M.; Inoue, K. Effects of gear dimensions and tooth surface modifications on the loaded transmission error of a helical gear pair. J. Mech. Des. 1998, 120, 119–125. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.H.; Liu, L.; Diao, X.W.; Wang, X.J. Effect of gear transmission on tooth surface of topographic profile error in double-sided grinding by forming method. China Mech. Eng. 2021, 33, 1661. [Google Scholar]
- Li, Y.; Wang, Z.H.; Liu, L.; Diao, X.W.; Zhu, X.Y. Analysis and optimization of the properties of the grinding contact line for form-grinding modified helical gears. Int. J. Adv. Manuf. Technol. 2022, 120, 403–413. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, W.G.; Liu, X.R.; Qian, X.Q.; He, Z.Y. Gear modification fast algorithm based on shaft angle error. J. Mech. Strength 2021, 43, 175–182. [Google Scholar] [CrossRef]









| Name | Symbol | Unit | Value |
|---|---|---|---|
| Normal module | 2.4 | ||
| Tooth modification right-hand gear | 39 | ||
| Mating left-hand gear | 50 | ||
| Normal pressure angle | 19.5 | ||
| Spiral angle | 25 | ||
| Tooth width | 22 | ||
| Addendum modification coefficient | 0 | ||
| Grinding wheel radius | 120 | ||
| Addendum coefficient | 1 | ||
| Bottom clearance coefficient | 0.25 | ||
| Material | 20CrMnTi | ||
| Tooth surface hardness | HRC | 59~63 | |
| Elasticity modulus | 207 |
| Transmission Torque /N·m | Grinding Wheel Mounting Angle/° | Modification | Tooth Profile Tip Relief and Root Relief/μm | Tooth Axial Fully Crowned Modification/μm |
|---|---|---|---|---|
| I | 14 | 14 | ||
| 65.3284 | II | 5.2 | 6.5 | |
| I | 14 | 14 | ||
| 50 | 64.8947 | II | 5.2 | 6.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Wu, Y.; Li, Y.; Liu, X. Effects of Tooth Modification in the Involute Helical Gear Form-Grinding Process on Loaded Transmission Character with Consideration of Tooth Axial Inclination Error. Machines 2023, 11, 305. https://doi.org/10.3390/machines11020305
Yang Y, Wu Y, Li Y, Liu X. Effects of Tooth Modification in the Involute Helical Gear Form-Grinding Process on Loaded Transmission Character with Consideration of Tooth Axial Inclination Error. Machines. 2023; 11(2):305. https://doi.org/10.3390/machines11020305
Chicago/Turabian StyleYang, Yongming, Yunlong Wu, Yan Li, and Xinrong Liu. 2023. "Effects of Tooth Modification in the Involute Helical Gear Form-Grinding Process on Loaded Transmission Character with Consideration of Tooth Axial Inclination Error" Machines 11, no. 2: 305. https://doi.org/10.3390/machines11020305
APA StyleYang, Y., Wu, Y., Li, Y., & Liu, X. (2023). Effects of Tooth Modification in the Involute Helical Gear Form-Grinding Process on Loaded Transmission Character with Consideration of Tooth Axial Inclination Error. Machines, 11(2), 305. https://doi.org/10.3390/machines11020305








