Euler Representation-Based Structural Balance Discriminant Projection for Machinery Fault Diagnosis
Abstract
1. Introduction
2. Review of Locality Preserving Projection
3. Proposed Method
3.1. Euler Representation
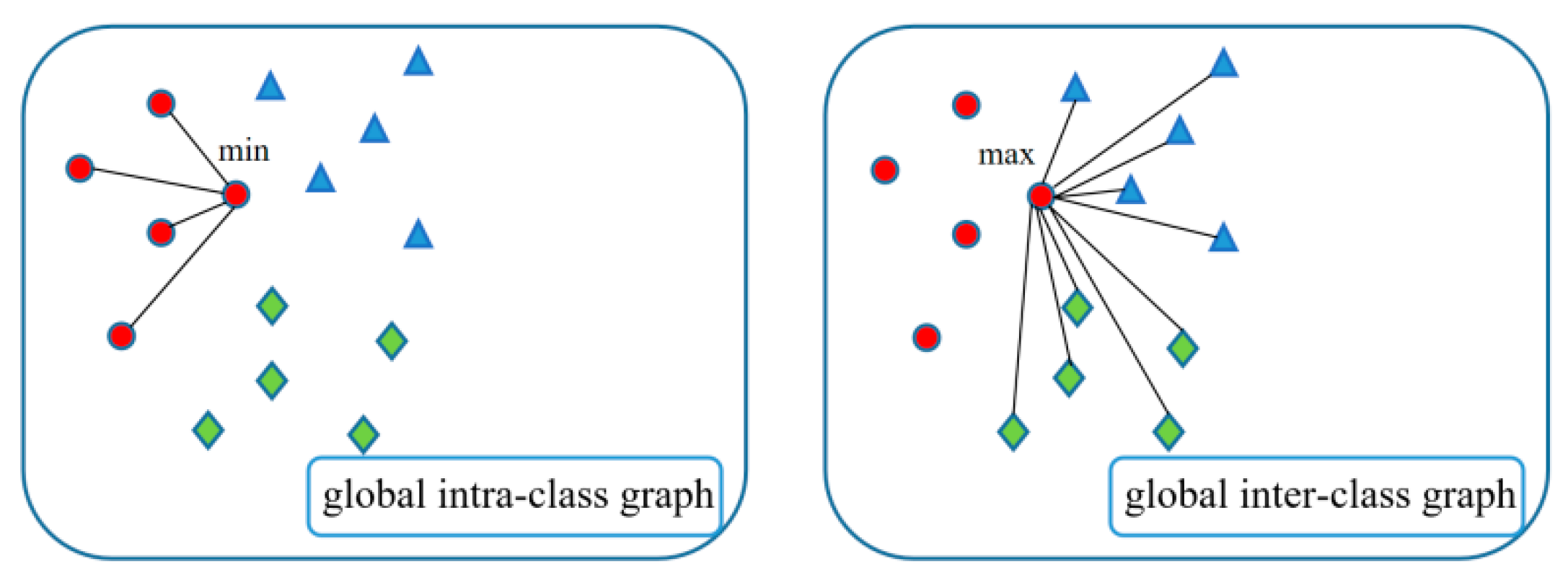
3.2. Construction of Local Objective Function
3.3. Construction of Global Objective Function
3.4. The Uniform Object Function of ESBDP
3.5. Optimization of the Uniform Objective Function
| Algorithm 1 Euler Representation Based Structural Balance Discriminant Projection |
| Input: Training fault sample set |
| Output: projection matrix |
| (1) Conversion of the original feature data into Euler representation data by Equation (9). |
| (2) Construction the weight matrix , , and . |
| (3) Fixing the balance parameters and , update . |
| (4) Fixing the projection matrices , update and . |
| (5) Repeat (3) and (4) until convergence. |
4. Fault Diagnosis Process Based on ESBDP Algorithm
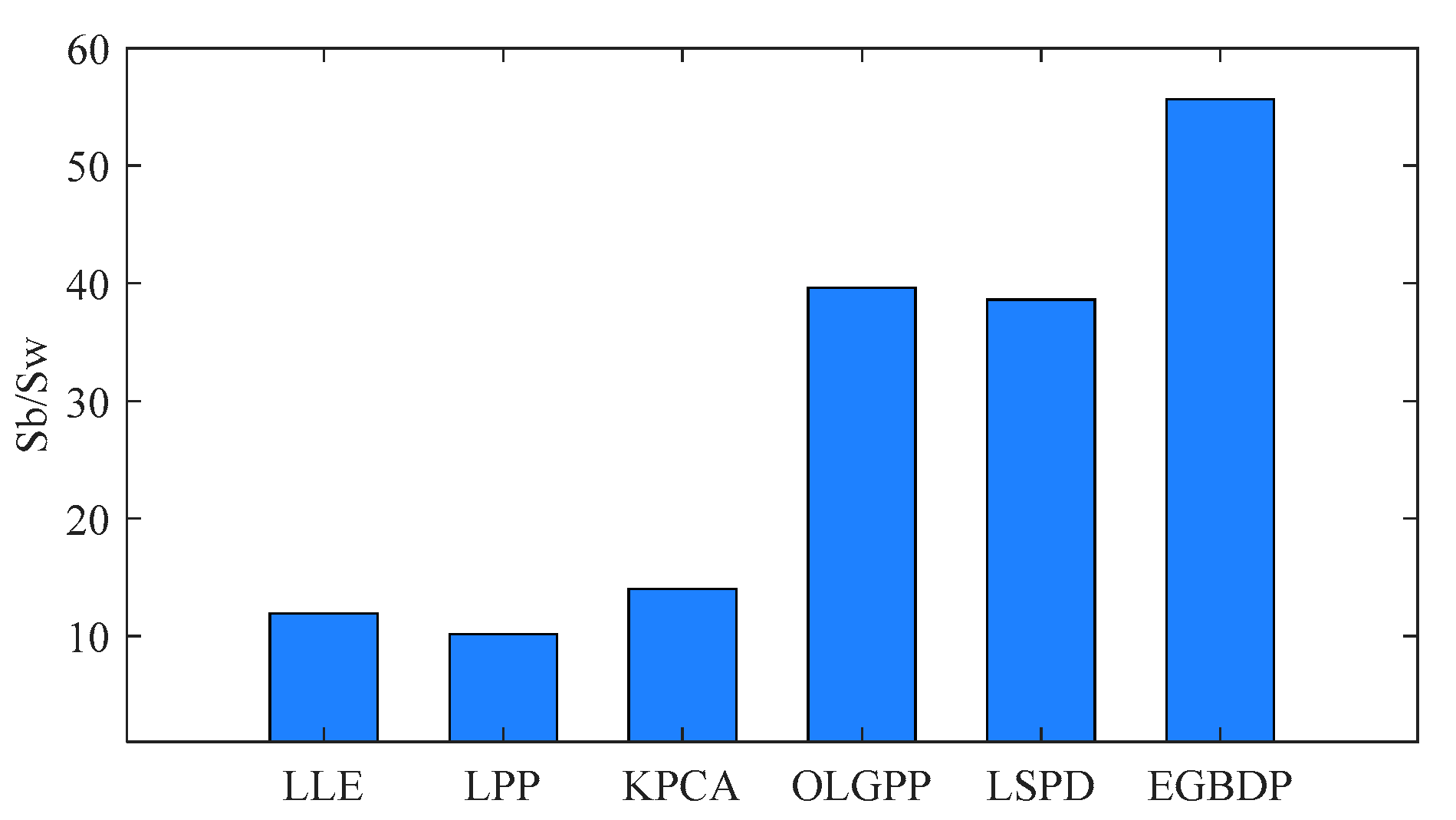
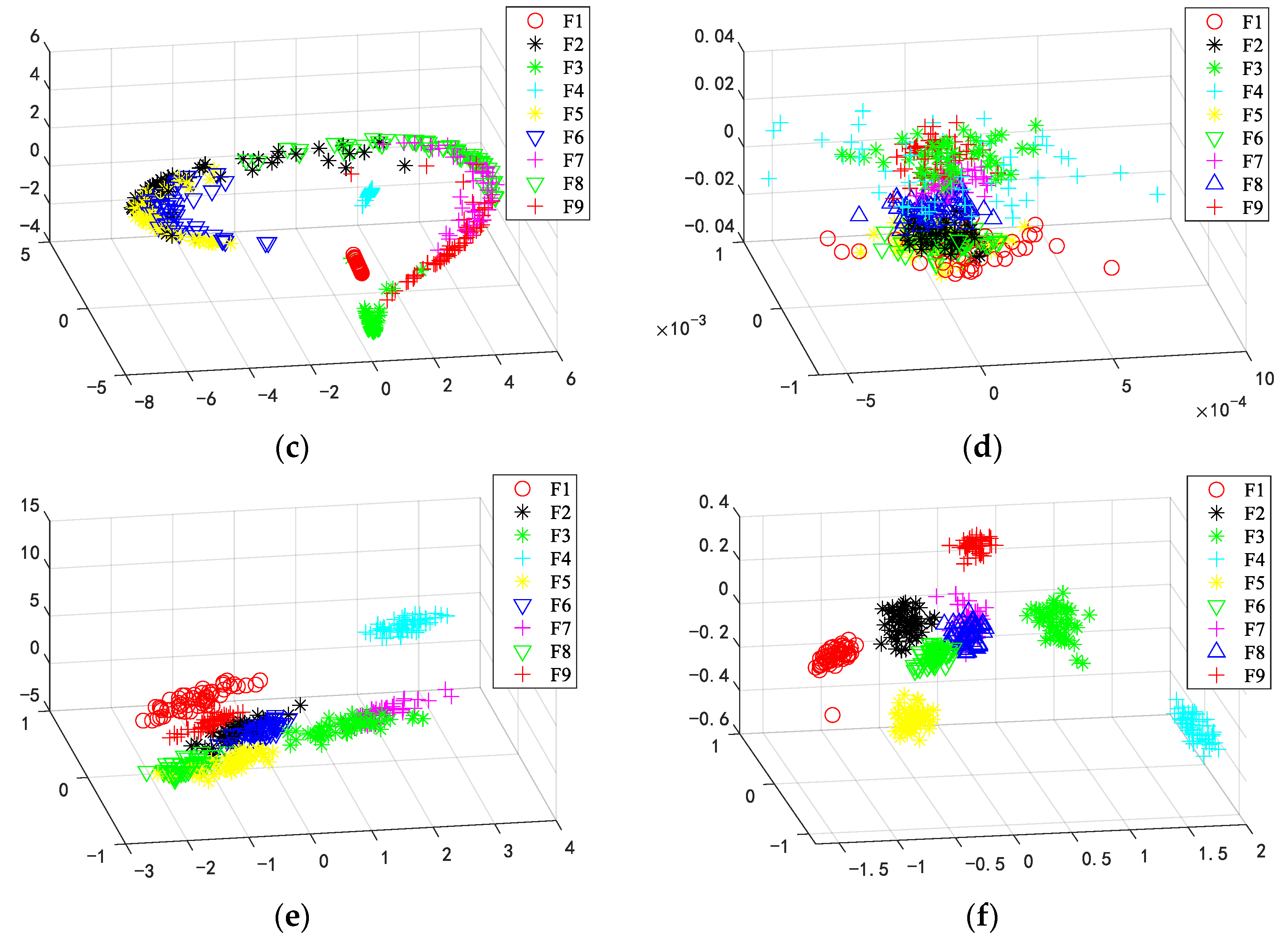
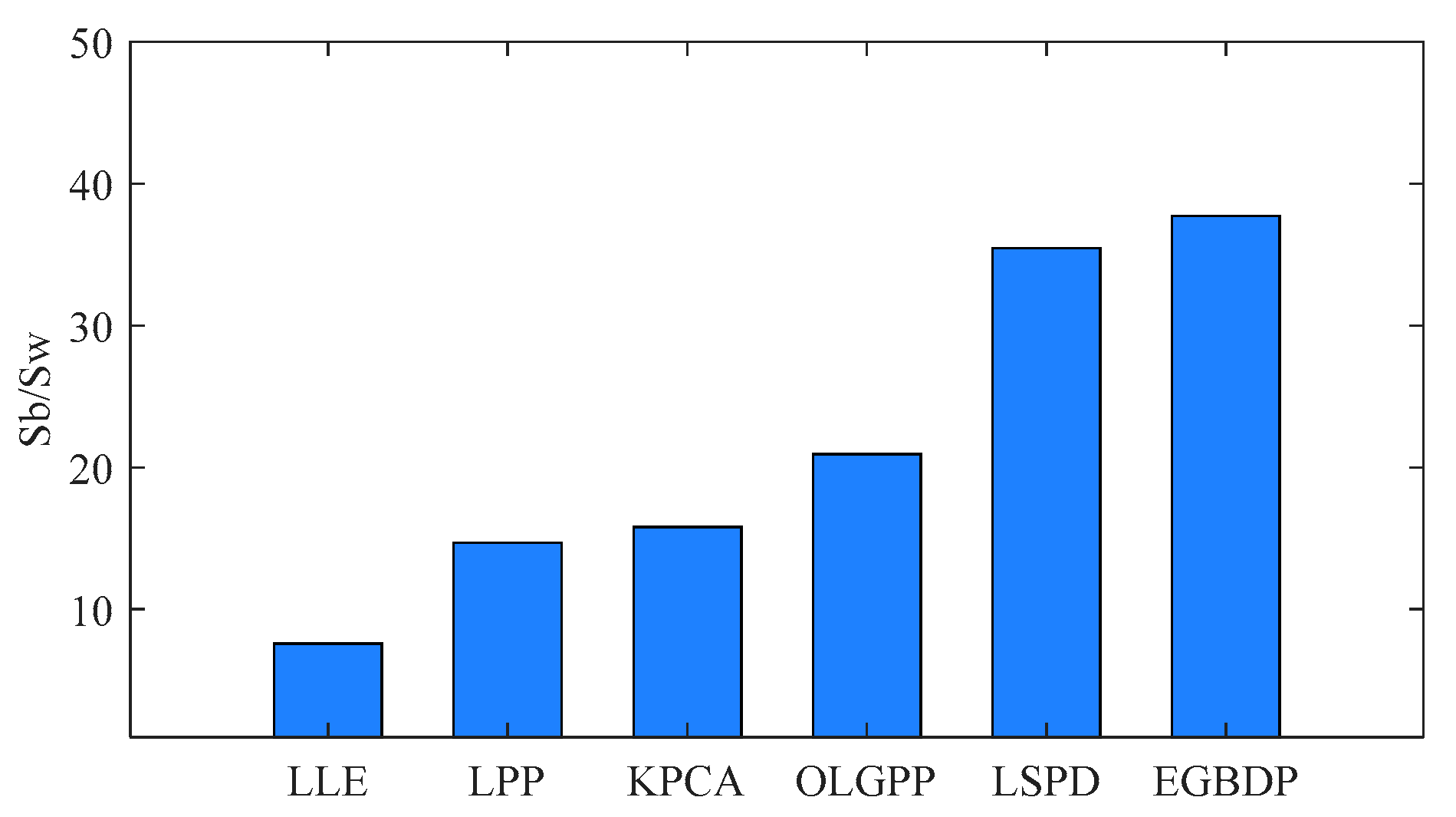
5. Experimental Results and Analysis
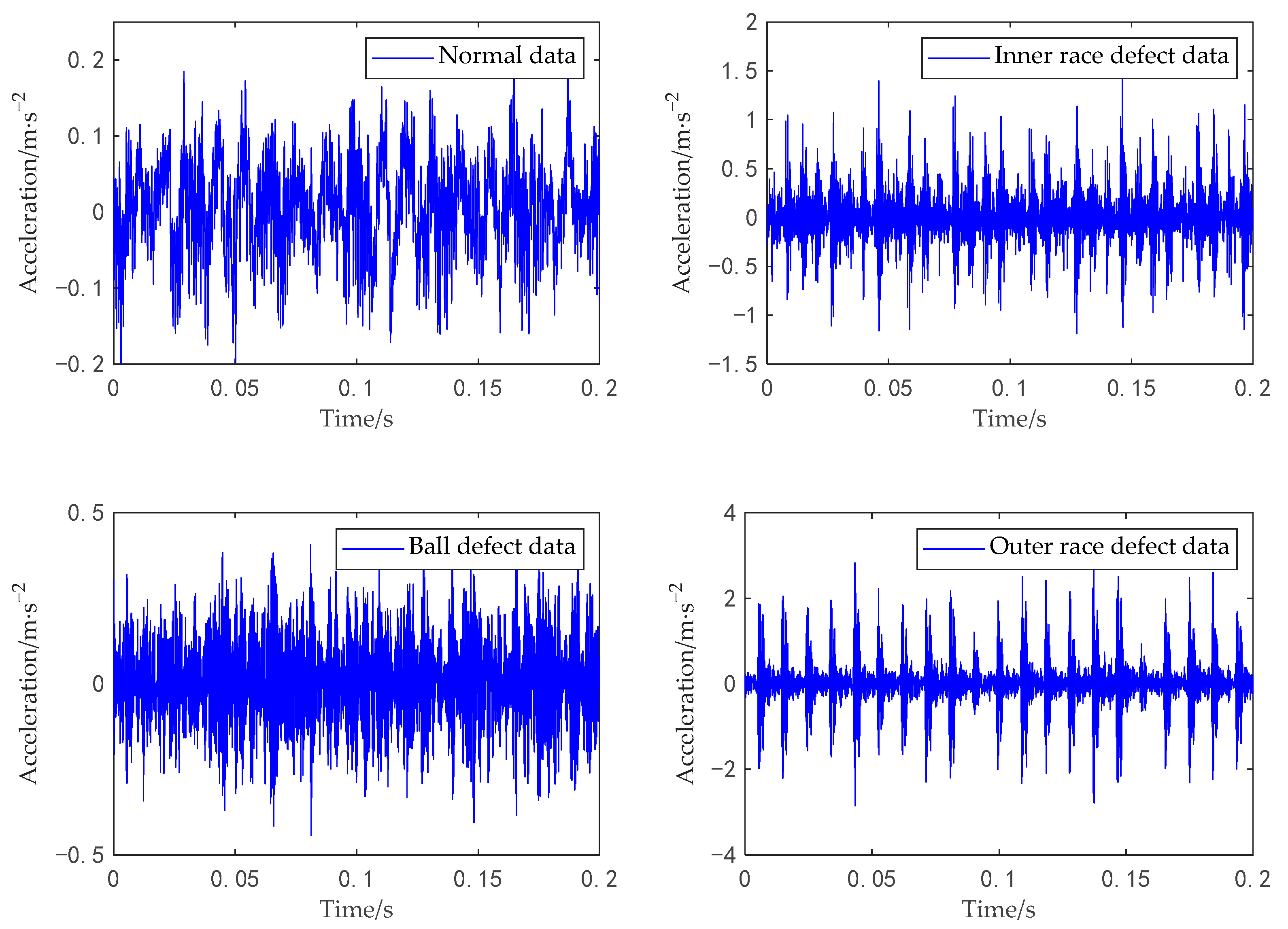
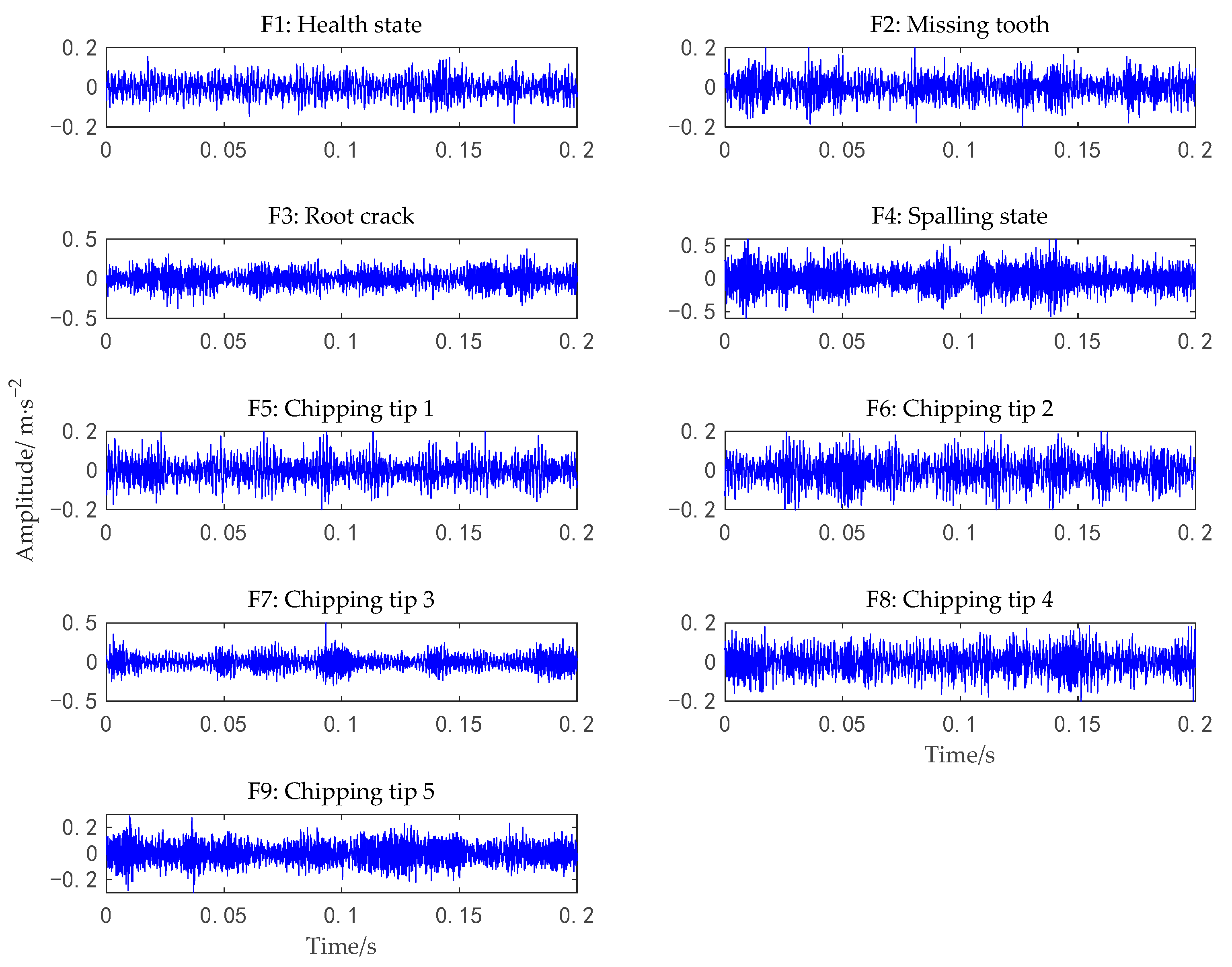
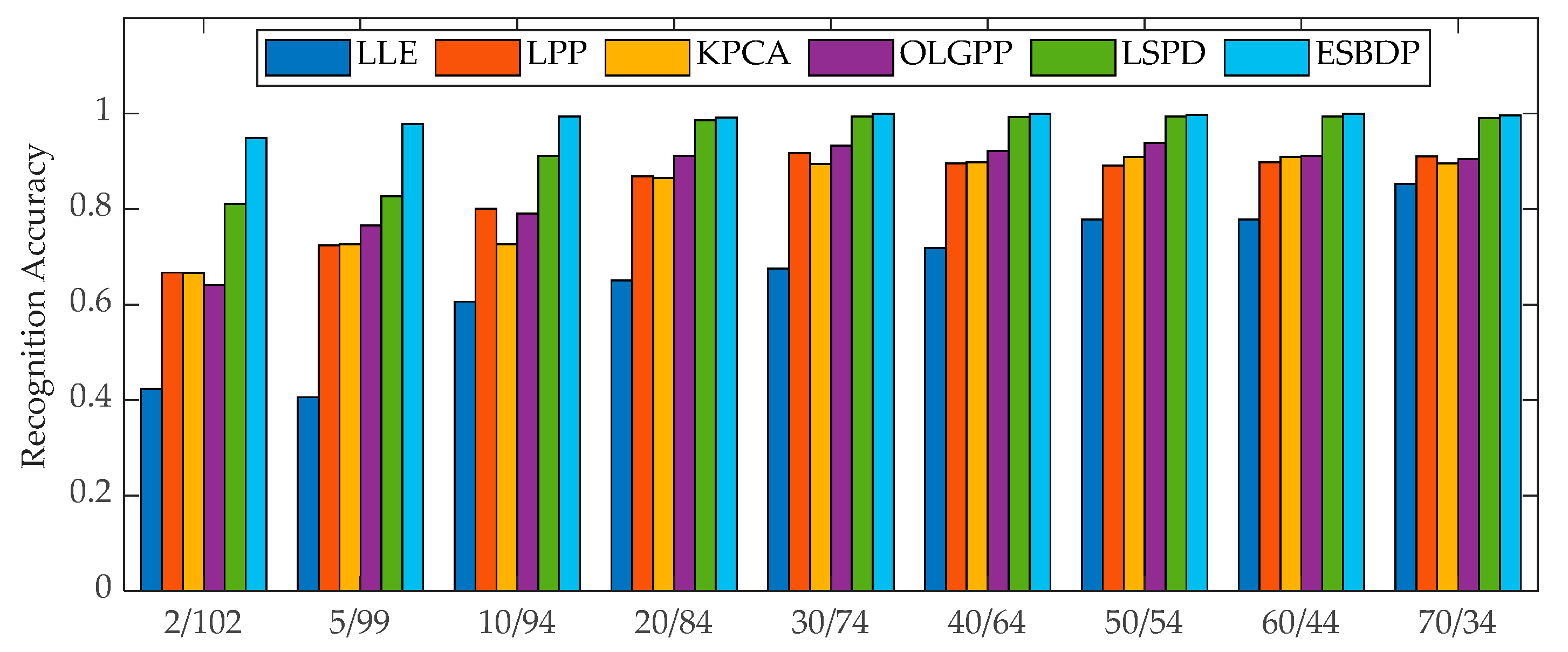
5.1. Experiments on the Bearing Dataset
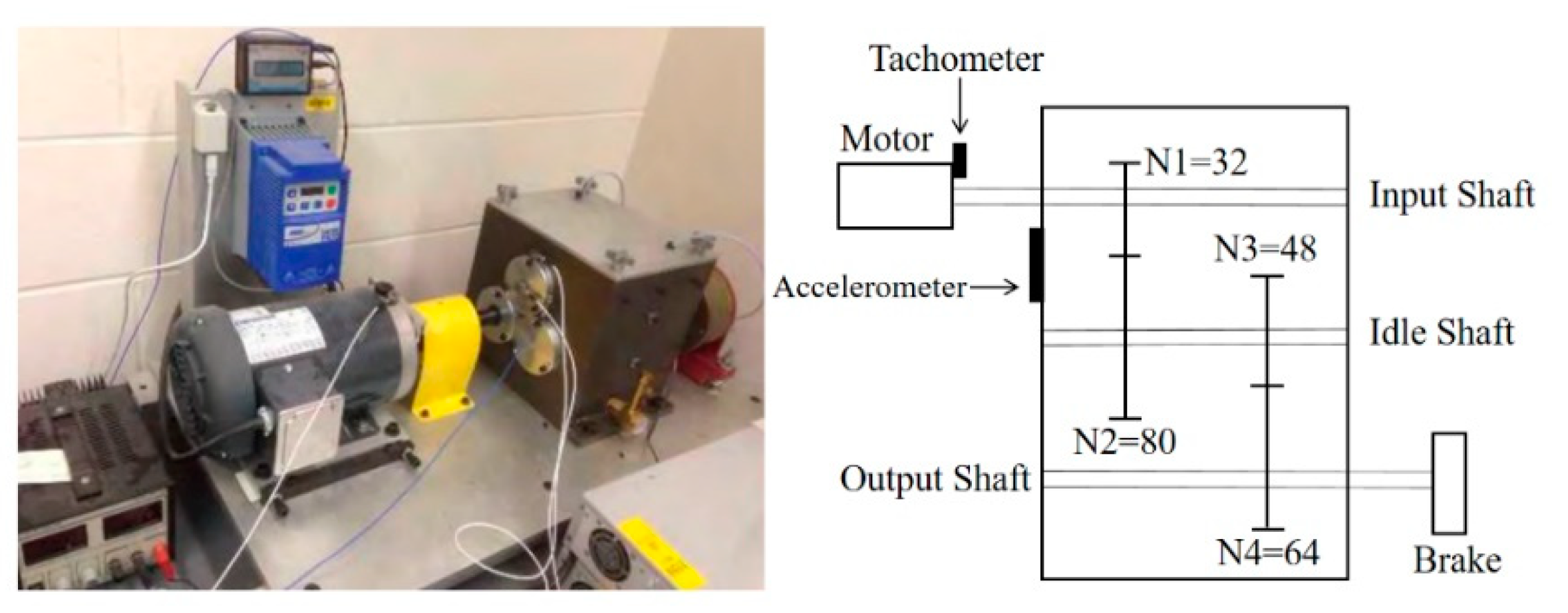
5.2. Experiments on the Gear Dataset
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PCA | principal components analysis |
| KPCA | kernel principal components analysis |
| LLE | local linear embedding |
| MFA | marginal fisher analysis |
| NPE | neighborhood preserving embedding |
| LPP | locality preserving projection |
| NLSPP | nonlocal and local structure preserving projection |
| FDGLPP | Fisher discriminative global local preserving projection |
| GLMDPP | global–local marginal discriminative preserving projection |
| GLMFA | global–local margin Fisher analysis |
| OLGPP | orthogonal locality and globality preserving projection |
| LGBODP | local–global balanced orthogonal discriminant projection |
| ESBDP | Euler representation-based structural balance discriminant projection |
| CWRU | Case Western Reserve University |
| LSPD | local similarity preserving discriminant |
| SVM | support vector machine |
References
- Liu, Y.; Hu, Z.; Zhang, Y. Symmetric positive definite manifold learning and its application in fault diagnosis. Neural Netw. 2022, 147, 163–174. [Google Scholar] [CrossRef] [PubMed]
- Qi, R.; Zhang, J.; Spencer, K. A Review on Data-Driven Condition Monitoring of Industrial Equipment. Algorithms 2022, 16, 9. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, W.; Liao, Y.; Song, Z.; Shi, J.; Jiang, X.; Shen, C.; Zhu, Z. Bearing fault diagnosis via generalized logarithm sparse regularization. Mech. Syst. Signal Process. 2022, 167, 108576. [Google Scholar] [CrossRef]
- Fekih, A.; Habibi, H.; Simani, S. Fault Diagnosis and Fault Tolerant Control of Wind Turbines: An Overview. Energies 2022, 15, 7186. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, F.; Liu, Z. Sparsity discriminant preserving projection for machinery fault diagnosis. Measurement 2021, 173, 108488. [Google Scholar] [CrossRef]
- Su, Z.; Tang, B.; Liu, Z.; Qin, Y. Multi-fault diagnosis for rotating machinery based on orthogonal supervised linear local tangent space alignment and least square support vector machine. Neurocomputing 2015, 157, 208–222. [Google Scholar] [CrossRef]
- Peng, B.; Bi, Y.; Xue, B.; Zhang, M.; Wan, S. A Survey on Fault Diagnosis of Rolling Bearings. Algorithms 2022, 15, 347. [Google Scholar] [CrossRef]
- Brusa, E.; Cibrario, L.; Delprete, C.; Maggio, L.G.D. Explainable AI for Machine Fault Diagnosis: Understanding Features’ Contribution in Machine Learning Models for Industrial Condition Monitoring. Appl. Sci. 2023, 13, 2038. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A review on vibration-based condition monitoring of rotating machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Cen, J.; Yang, Z.; Liu, X.; Xiong, J.; Chen, H. A review of data-driven machinery fault diagnosis using machine learning algorithms. J. Vib. Eng. Technol. 2022, 10, 2481–2507. [Google Scholar] [CrossRef]
- Reddy, G.T.; Reddy, M.P.K.; Lakshmanna, K.; Kaluri, R.; Rajput, D.S.; Srivastava, G.; Baker, T. Analysis of dimensionality reduction techniques on big data. IEEE Access 2020, 8, 54776–54788. [Google Scholar] [CrossRef]
- Jia, W.; Sun, M.; Lian, J.; Hou, S. Feature dimensionality reduction: A review. Complex Intell. Syst. 2022, 8, 2663–2693. [Google Scholar] [CrossRef]
- Wang, H.; Ni, G.; Chen, J. Research on rolling bearing state health monitoring and life prediction based on PCA and internet of things with multi-sensor. Measurement 2020, 157, 107657. [Google Scholar] [CrossRef]
- Wang, H.; Huang, H.; Yu, S.; Gu, W. Size and Location Diagnosis of Rolling Bearing Faults: An Approach of Kernel Principal Component Analysis and Deep Belief Network. Int. J. Comput. Intell. Syst. 2021, 14, 1672–1686. [Google Scholar] [CrossRef]
- Zhong, K.; Han, M.; Qiu, T.; Han, B. Fault diagnosis of complex processes using sparse kernel local Fisher discriminant analysis. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1581–1591. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, Y.; Zhang, F.; Ai, X.; Wang, Z. A novel intelligent method for inter-shaft bearing-fault diagnosis based on hierarchical permutation entropy and LLE-RF. J. Vib. Control 2022, 1, 10775463221134166. [Google Scholar] [CrossRef]
- Jiang, L.; Xuan, J.; Shi, T. Feature extraction based on semi-supervised kernel Marginal Fisher analysis and its application in bearing fault diagnosis. Mech. Syst. Signal Process. 2013, 1, 113–126. [Google Scholar] [CrossRef]
- Wang, W.; Aggarwal, V.; Aeron, S. Tensor train neighborhood preserving embedding. IEEE Trans. Signal Process. 2018, 66, 2724–2732. [Google Scholar] [CrossRef]
- Ran, R.; Ren, Y.; Zhang, S.; Fang, B. A novel discriminant locality preserving projections method. J. Math. Imaging Vis. 2021, 63, 541–554. [Google Scholar] [CrossRef]
- He, Y.L.; Zhao, Y.; Hu, X.; Yan, X.N.; Zhu, Q.X.; Xu, Y. Fault diagnosis using novel AdaBoost based discriminant locality preserving projection with resamples. Eng. Appl. Artif. Intell. 2020, 91, 103631. [Google Scholar] [CrossRef]
- Yang, C.; Ma, S.; Han, Q. Unified discriminant manifold learning for rotating machinery fault diagnosis. J. Intell. Manuf. 2022, 91, 1–12. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, R.; Yin, J.; Li, Y.; Lu, H.; Xu, M. A new intelligent fault identification method based on transfer locality preserving projection for actual diagnosis scenario of rotating machinery. Mech. Syst. Signal Process. 2020, 135, 106344. [Google Scholar] [CrossRef]
- Li, Y.; Lekamalage, C.K.L.; Liu, T.; Chen, P.A.; Huang, G.B. Learning representations with local and global geometries preserved for machine fault diagnosis. IEEE Trans. Ind. Electron. 2019, 67, 2360–2370. [Google Scholar] [CrossRef]
- Fu, Y. Local coordinates and global structure preservation for fault detection and diagnosis. Meas. Sci. Technol. 2021, 32, 115111. [Google Scholar] [CrossRef]
- Luo, L.; Bao, S.; Mao, J.; Tang, D. Nonlocal and local structure preserving projection and its application to fault detection. Chemom. Intell. Lab. Syst. 2016, 157, 177–188. [Google Scholar] [CrossRef]
- Tang, Q.; Chai, Y.; Qu, J.; Fang, X. Industrial process monitoring based on Fisher discriminant global-local preserving projection. J. Process Control 2019, 81, 76–86. [Google Scholar] [CrossRef]
- Li, Y.; Ma, F.; Ji, C.; Wang, J.; Sun, W. Fault Detection Method Based on Global-Local Marginal Discriminant Preserving Projection for Chemical Process. Processes 2022, 10, 122. [Google Scholar] [CrossRef]
- Huang, Z.; Zhu, H.; Zhou, J.T.; Peng, X. Multiple marginal fisher analysis. IEEE Trans. Ind. Electron. 2018, 66, 9798–9807. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M. Fault diagnosis of rolling bearing based on feature reduction with global-local margin Fisher analysis. Neurocomputing 2018, 315, 447–464. [Google Scholar] [CrossRef]
- Su, S.; Zhu, G.; Zhu, Y. An orthogonal locality and globality dimensionality reduction method based on twin eigen decomposition. IEEE Access 2021, 9, 55714–55725. [Google Scholar] [CrossRef]
- Zhang, S.; Lei, Y.; Zhang, C.; Hu, Y. Semi-supervised orthogonal discriminant projection for plant leaf classification. Pattern Anal. Appl. 2016, 19, 953–961. [Google Scholar] [CrossRef]
- Shi, M.; Zhao, R.; Wu, Y.; He, T. Fault diagnosis of rotor based on local-global balanced orthogonal discriminant projection. Measurement 2021, 168, 108320. [Google Scholar] [CrossRef]
- Chou, J.; Zhao, S.; Chen, Y.; Jing, L. Unsupervised double weighted graphs via good neighbours for dimension reduction of hyperspectral image. Int. J. Remote Sens. 2022, 43, 6152–6175. [Google Scholar] [CrossRef]
- Yan, T.; Shen, S.L.; Zhou, A.; Chen, X. Prediction of geological characteristics from shield operational parameters by integrating grid search and K-fold cross validation into stacking classification algorithm. J. Rock Mech. Geotech. Eng. 2022, 14, 1292–1303. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Q.; Han, J.; Wang, S. Euler sparse representation for image classification. Proc. AAAI Conf. Artif. Intell. 2018, 32, 3691–3697. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, H.; Gao, R.; Zhang, H.; Wang, Y. K-nearest neighbors rule combining prototype selection and local feature weighting for classification. Knowl. Based Syst. 2022, 243, 108451. [Google Scholar] [CrossRef]
- Su, W.; Wang, Y. Estimating the Gerber-Shiu function in Lévy insurance risk model by Fourier-cosine series expansion. Mathematics 2021, 9, 1402. [Google Scholar] [CrossRef]
- Mekonen, B.D.; Salilew, G.A. Geometric Series on Fourier Cosine-Sine Transform. J. Adv. Math. Comput. Sci. 2018, 28, 1–4. [Google Scholar] [CrossRef]
- Fitch, A.; Kadyrov, A.; Christmas, W.; Kittler, J. Fast robust correlation. IEEE Trans. Image Process. 2005, 70, 1063–1073. [Google Scholar] [CrossRef]
- Peng, L.; Yao, Q. Least absolute deviations estimation for ARCH and GARCH Models. Biometrika 2003, 90, 967–975. [Google Scholar] [CrossRef]
- Zhong, H.; Lv, Y.; Yuan, R.; Yang, D. Bearing fault diagnosis using transfer learning and self-attention ensemble lightweight convolutional neural network. Neurocomputing 2022, 501, 765–777. [Google Scholar] [CrossRef]
- Yang, X.; Shao, H.; Zhong, X.; Cheng, J. Symplectic weighted sparse support matrix machine for gear fault diagnosis. Measurement 2021, 168, 108392. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, Z.; Zhang, Y. Bearing feature extraction using multi-structure locally linear embedding. Neurocomputing 2021, 428, 280–290. [Google Scholar] [CrossRef]
- Altaf, M.; Akram, T.; Khan, M.A.; Iqbal, M.; Ch, M.M.I.; Hsu, C.H. A new statistical features based approach for bearing fault diagnosis using vibration signals. Sensors 2022, 22, 2012. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Ding, C.; Hsu, C.H.; Yang, F. Dimensionality reduction via preserving local information. Future Generat. Comput. Syst. 2020, 108, 967–975. [Google Scholar] [CrossRef]










| Metric Method | Bearing Dataset | Gear Dataset | ||
|---|---|---|---|---|
| Same | Different | Same | Different | |
| Euclidean distance | 0.14 | 2.06 | 1.11 | 2.28 |
| Euler distance | 1.99 | 29.63 | 11.92 | 31.68 |
| No. | Parameters | No. | Parameters | No. | Parameters |
|---|---|---|---|---|---|
| 1 | 9 | 17 | |||
| 2 | 10 | 18 | |||
| 3 | 11 | 19 | |||
| 4 | 12 | 20 | |||
| 5 | 13 | 21 | |||
| 6 | 14 | 22~29 | Three-layer wavelet packet decomposition band energy characteristic. | ||
| 7 | 15 | ||||
| 8 | 16 |
| Fault Type | Recognition Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| LLE | LPP | KPCA | OLGPP | LSPD | ESBDP | |
| Normal | 100 | 100 | 100 | 100 | 99.83 | 100 |
| Inner race | 93.33 | 83.67 | 96.17 | 98.17 | 100 | 100 |
| Ball | 88.83 | 83.83 | 82.33 | 96.67 | 100 | 100 |
| Outer race | 91.0 | 99.67 | 100 | 96.67 | 100 | 100 |
| Average recognition rate | 93.29 | 91.79 | 94.63 | 98.63 | 99.96 | 100 |
| Standard deviation | 0.95 | 6.55 | 0.72 | 0.94 | 0.13 | 0.00 |
| Processing time (s) | 0.80 | 0.32 | 0.33 | 0.71 | 0.50 | 0.34 |
| Fault Type | Recognition Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| LLE | LPP | KPCA | OLGPP | LSPD | ESBDP | |
| Health state | 92.59 | 100 | 100 | 100 | 100 | 100 |
| Missing tooth | 57.41 | 66.67 | 74.07 | 77.78 | 100 | 100 |
| Root crack | 74.07 | 98.15 | 94.44 | 96.30 | 100 | 100 |
| Spalling | 88.89 | 100 | 100 | 100 | 100 | 100 |
| Chipping tip 1 | 64.81 | 88.89 | 81.48 | 81.48 | 96.30 | 100 |
| Chipping tip 2 | 92.59 | 96.30 | 100 | 100 | 100 | 100 |
| Chipping tip 3 | 79.63 | 87.04 | 83.33 | 92.59 | 100 | 100 |
| Chipping tip 4 | 87.04 | 87.04 | 88.89 | 98.15 | 100 | 100 |
| Chipping tip 5 | 62.96 | 77.78 | 96.30 | 100 | 98.15 | 100 |
| Average recognition accuracy | 77.78 | 89.09 | 90.95 | 93.83 | 99.38 | 100 |
| Processing time (s) | 0.57 | 0.39 | 0.24 | 0.51 | 0.33 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Zhu, Y.; Su, S.; Fang, X.; Wang, T. Euler Representation-Based Structural Balance Discriminant Projection for Machinery Fault Diagnosis. Machines 2023, 11, 307. https://doi.org/10.3390/machines11020307
Zhang M, Zhu Y, Su S, Fang X, Wang T. Euler Representation-Based Structural Balance Discriminant Projection for Machinery Fault Diagnosis. Machines. 2023; 11(2):307. https://doi.org/10.3390/machines11020307
Chicago/Turabian StyleZhang, Maoyan, Yanmin Zhu, Shuzhi Su, Xianjin Fang, and Ting Wang. 2023. "Euler Representation-Based Structural Balance Discriminant Projection for Machinery Fault Diagnosis" Machines 11, no. 2: 307. https://doi.org/10.3390/machines11020307
APA StyleZhang, M., Zhu, Y., Su, S., Fang, X., & Wang, T. (2023). Euler Representation-Based Structural Balance Discriminant Projection for Machinery Fault Diagnosis. Machines, 11(2), 307. https://doi.org/10.3390/machines11020307






