Wear Parameter Diagnostics of Industrial Milling Machine with Support Vector Regression
Abstract
:1. Introduction
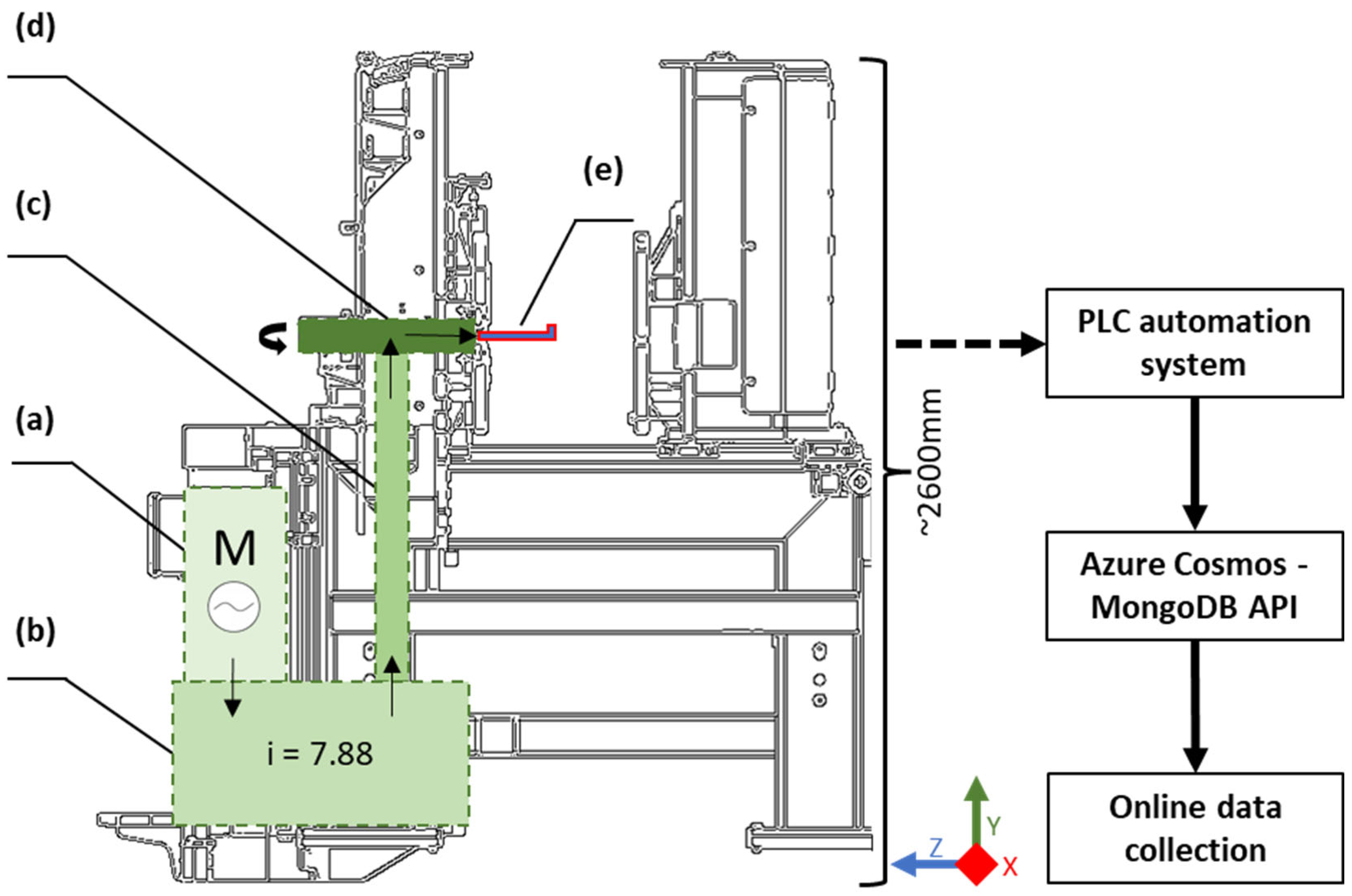
2. Methods: Peripheral Milling Machine Architecture and Data Acquisition
2.1. Operation and the Architecture of the Milling Machine
2.2. Data Acquisition
3. Data Pre-Processing and Feature Reduction Process
3.1. Pearson Correlation Coefficient (PCC)
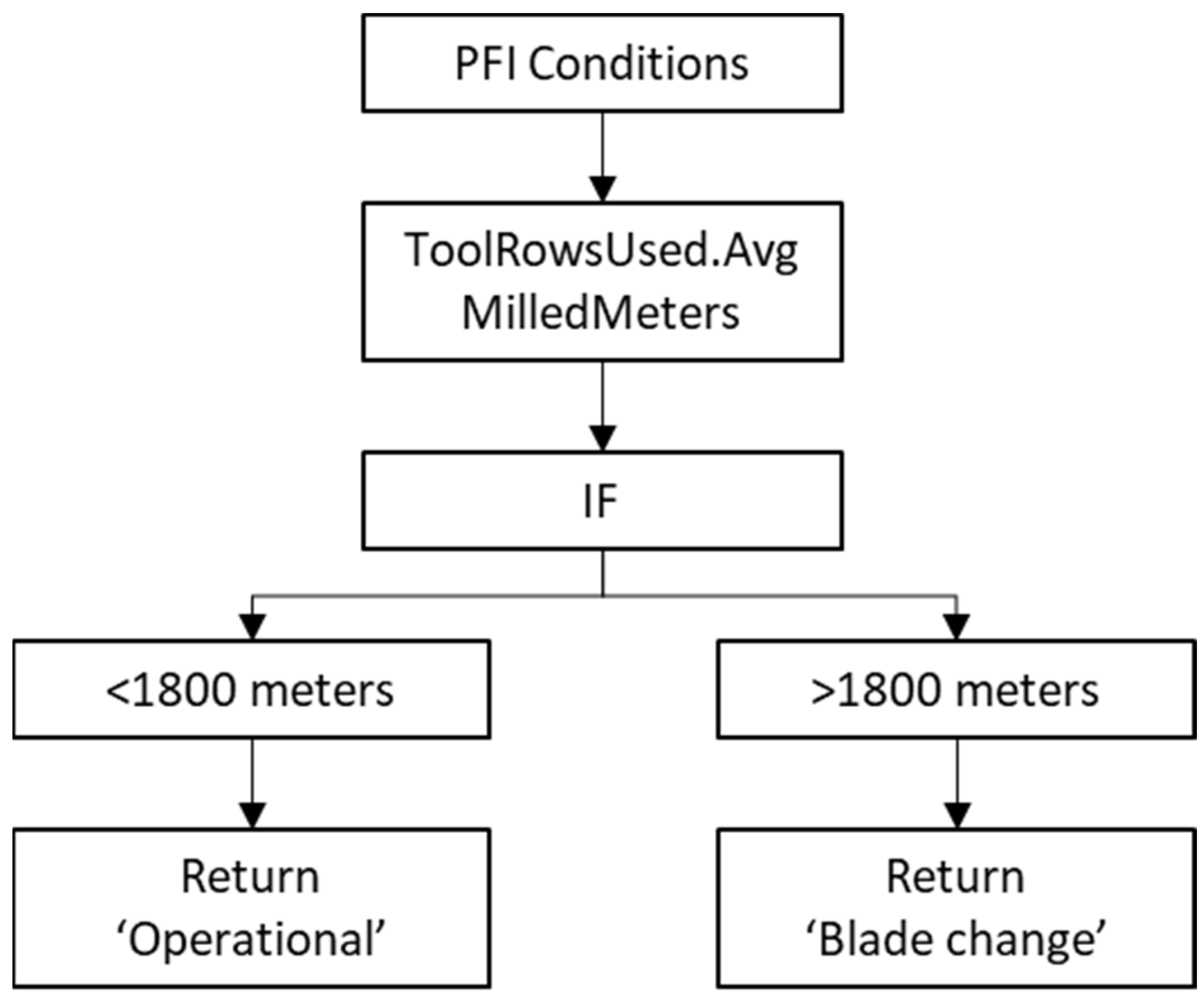
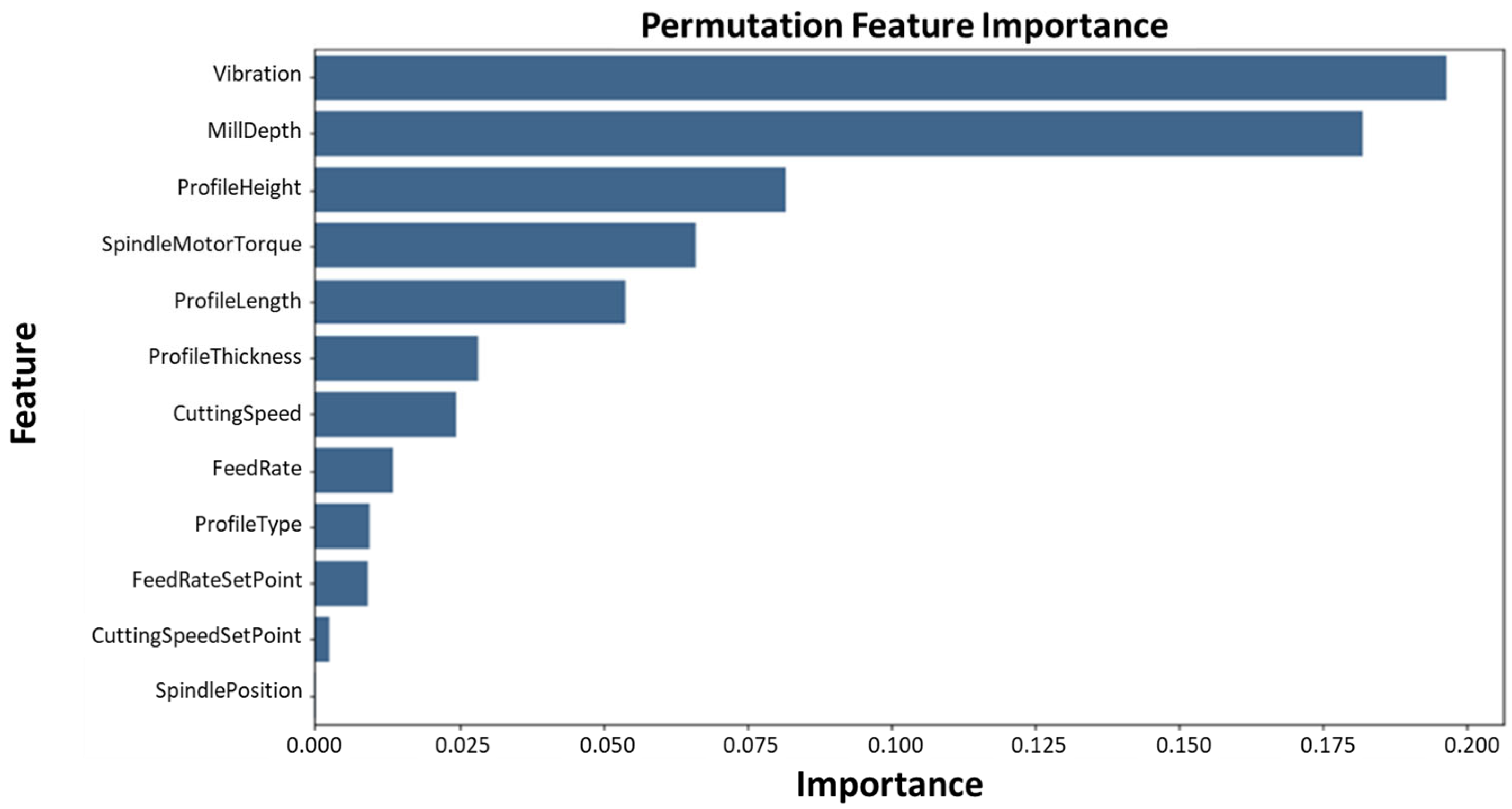
3.2. Permutation Feature Importance (PFI)
4. Supervised Wear Feature Analysis with Support Vector Regression
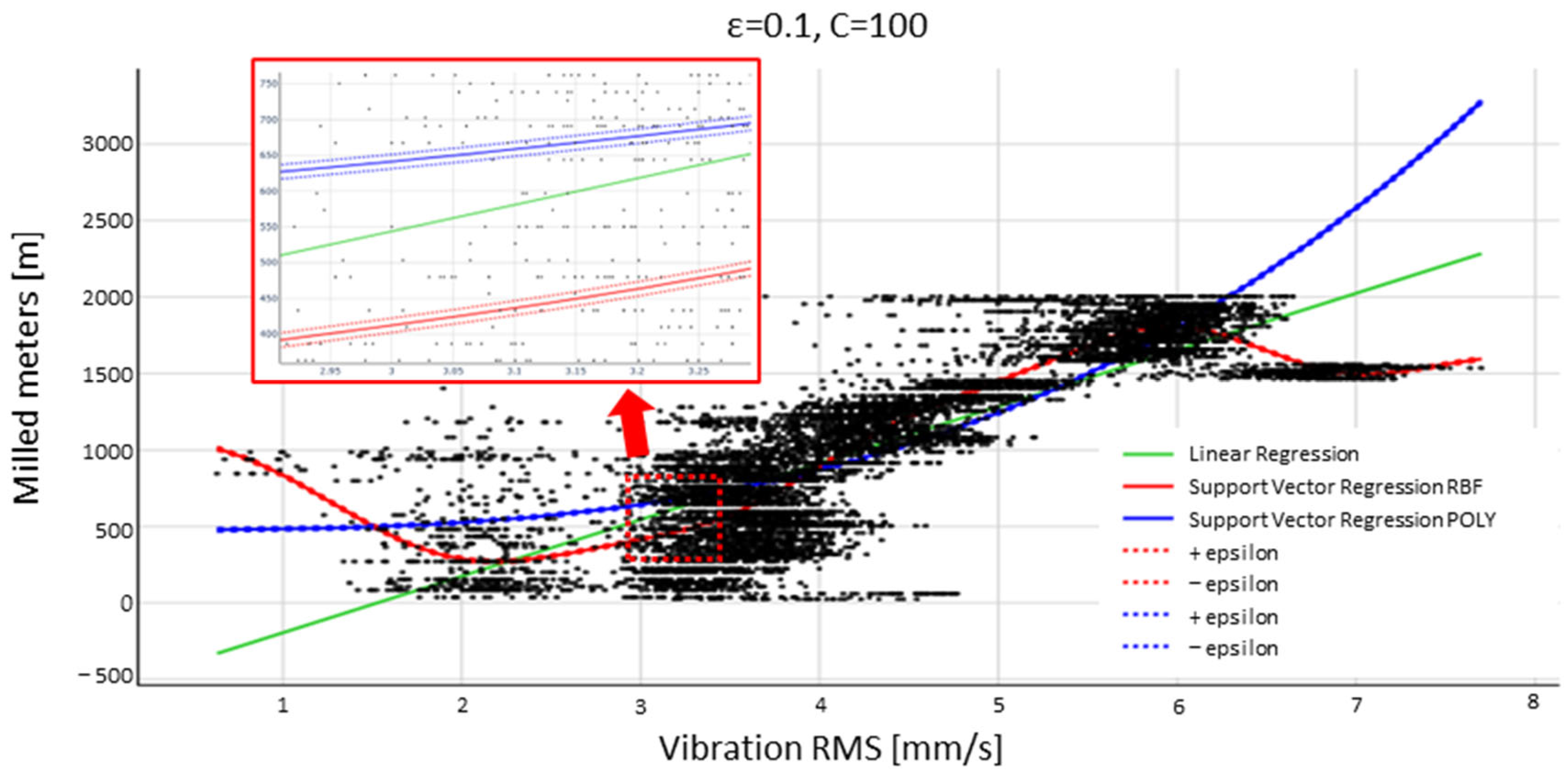
4.1. Kernel Classifier Selection
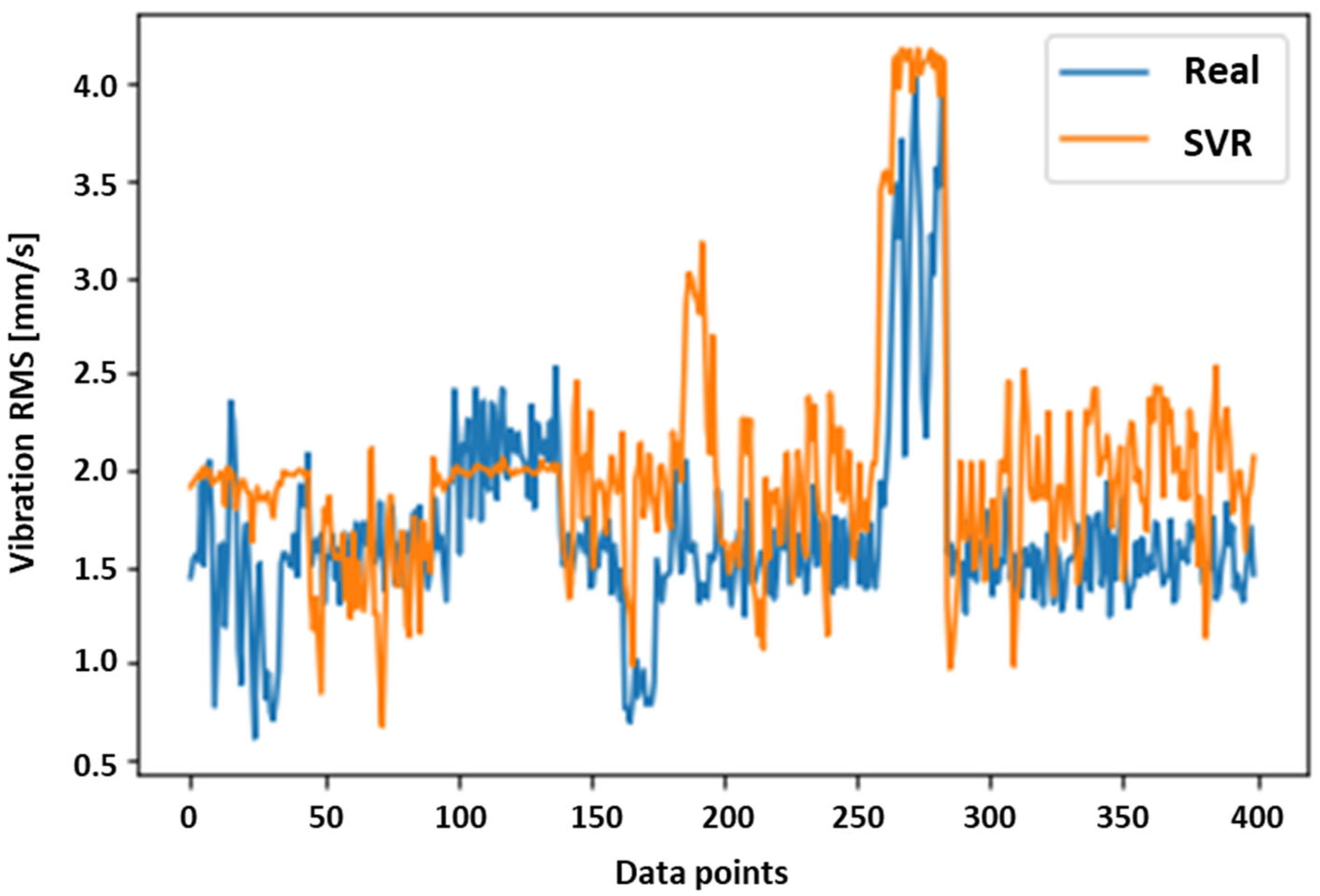
4.2. Vibration Analysis with the SVR (RBF)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive Network-Based Fuzzy Inference System |
| API | Application Programming Interface |
| AUC | Area Under Curve |
| b | Bias |
| BPNN | Back Propagation Neural Network |
| CBM | Condition-Based Maintenance |
| GenSVM | Generalised Multiclass Support Vector Machine |
| HI | Health Index |
| KNN | K-Nearest Neighbour |
| LSSVM | Least Squares Support Vector Machines |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MSE | Mean Square Error |
| n | Identification Number of a Single Data Point |
| OEM | Original Equipment Manufacturer |
| PCC | Pearson Correlation Coefficient |
| Phi φ | Dot Product From Input Space to Feature Space |
| PLC | Programmable Logic Controller |
| PPX | Pay-Per-X |
| R2 | Squared Correlation Coefficient |
| RBF | Gaussian Radial Basis Function |
| RF | Random Forest |
| RMS | Root Mean Square |
| ROC | Receiver Operating Characteristics |
| RUL | Remaining Useful Life |
| SVM | Support Vector Machines |
| SVR | Support Vector Regression |
| w | w is A Weight Vector in |
| xi | First Individual Data Point |
| yi | First Individual Data Point of the Comparable Variable |
| Corresponding Arithmetic Mean of the First Sample | |
| Corresponding Arithmetic Mean of the Comparable Variable |
References
- Schroderus, J.; Allan, L.; Menon, K.; Kärkkäinen, H. Towards a Pay-Per-X Maturity Model for Equipment Manufacturing Companies. Procedia Comput. Sci. 2022, 196, 226–234. [Google Scholar] [CrossRef]
- Menon, K. Industrial Internet Enabled Value Creation for Manufacturing Companies; Tampere University: Tampere, Finland, 2020. [Google Scholar]
- Singh, H.; Matharu, G.S.; Dardi, A.K.; Matharu, J.S. Empirical Investigation of Big Data Analytical Tools: Comparative Analysis. In Proceedings of the 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 23–25 April 2019; pp. 1264–1269. [Google Scholar] [CrossRef]
- Roy, S.K.; Misra, S.; Raghuwanshi, N.S. SensPnP: Seamless Integration of Heterogeneous Sensors with IoT Devices. IEEE Trans. Consum. Electron. 2019, 65, 205–214. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Li, Z.; Dong, L.; Li, Q. A novel approach for predicting tool remaining useful life using limited data. Mech. Syst. Signal Process. 2020, 143, 106832. [Google Scholar] [CrossRef]
- Van der Voort, H.; van Bulderen, S.; Cunningham, S.; Janssen, M. Data science as knowledge creation a framework for synergies between data analysts and domain professionals. Technol. Forecast. Soc. Change 2021, 173, 121160. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Kanellopoulos, D.; Pintelas, P.E. Data preprocessing for supervised leaning. Int. J. Comput. Sci. 2006, 1, 111–117. [Google Scholar]
- Zhang, Y.; Zhu, K.; Duan, X.; Li, S. Tool wear estimation and life prognostics in milling: Model extension and generalization. Mech. Syst. Signal Process. 2021, 155, 107617. [Google Scholar] [CrossRef]
- Liu, M.; Yao, X.; Zhang, J.; Chen, W.; Jing, X.; Wang, K. Multi-Sensor Data Fusion for Remaining Useful Life Prediction of Machining Tools by IABC-BPNN in Dry Milling Operations. Sensors 2020, 20, 4657. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yao, X.; Zhang, J.; Jin, H. Tool Condition Monitoring and Remaining Useful Life Prognostic Based on a Wireless Sensor in Dry Milling Operations. Sensors 2016, 16, 795. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Shi, T.; Xuan, J. Milling tool wear prediction using multi-sensor feature fusion based on stacked sparse autoencoders. Measurement 2022, 190, 110719. [Google Scholar] [CrossRef]
- Usui, E.; Hirota, A.; Masuko, M. Analytical Prediction of Three Dimensional Cutting Process—Part 1: Basic Cutting Model and Energy Approach. J. Eng. Ind. 1978, 100, 222–228. [Google Scholar] [CrossRef]
- Takeyama, H.; Murata, R. Basic Investigation of Tool Wear. J. Eng. Ind. 1963, 85, 33–37. [Google Scholar] [CrossRef]
- Ochoa, L.E.E.; Quinde, I.B.R.; Sumba, J.P.C.; Guevara, A.V.; Morales-Menendez, R. New Approach based on Autoencoders to Monitor the Tool Wear Condition in HSM. IFAC-PapersOnLine 2019, 52, 206–211. [Google Scholar] [CrossRef]
- Panda, S.; Chakraborty, D.; Pal, S. Flank wear prediction in drilling using back propagation neural network and radial basis function network. Appl. Soft Comput. 2008, 8, 858–871. [Google Scholar] [CrossRef]
- Rahimi, M.H.; Huynh, H.N.; Altintas, Y. On-line chatter detection in milling with hybrid machine learning and physics-based model. CIRP J. Manuf. Sci. Technol. 2021, 35, 25–40. [Google Scholar] [CrossRef]
- Chen, Q.; Xie, Q.; Yuan, Q.; Huang, H.; Li, Y. Research on a Real-Time Monitoring Method for the Wear State of a Tool Based on a Convolutional Bidirectional LSTM Model. Symmetry 2019, 11, 1233. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Jennings, C.; Terpenny, J.; Gao, R.X.; Kumara, S. A Comparative Study on Machine Learning Algorithms for Smart Manufacturing: Tool Wear Prediction Using Random Forests. J. Manuf. Sci. Eng. 2017, 139, 071018. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Zhu, H.; Hu, K.; Wu, J.; Shao, X.; Wang, Y. Multisensory Data-Driven Health Degradation Monitoring of Machining Tools by Generalized Multiclass Support Vector Machine. IEEE Access 2019, 7, 47102–47113. [Google Scholar] [CrossRef]
- Benkedjouh, T.; Medjaher, K.; Zerhouni, N.; Rechak, S. Health Assessment and Life Prediction of Cutting Tools Based on Support Vector Regression. J. Intell. Manuf. 2015, 26, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Nee, A.Y.C. Handbook of Manufacturing Engineering and Technology; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Pecht, M.G.; Kang, M. Prognostics and Health Management of Electronics; IEEE Press: Piscataway, NJ, USA, 2018. [Google Scholar]
- Wan, Z.; Xu, Y.; Šavija, B. On the Use of Machine Learning Models for Prediction of Compressive Strength of Concrete: Influence of Dimensionality Reduction on the Model Performance. Materials 2021, 14, 713. [Google Scholar] [CrossRef]
- Gruosso, G.; Gajani, G.S.; Ruiz, F.; Valladolid, J.D.; Patino, D. A Virtual Sensor for Electric Vehicles’ State of Charge Estimation. Electronics 2020, 9, 278. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.; Lin, C. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2013, 2, 27. [Google Scholar] [CrossRef]
- Santos, C.E.D.S.; Sampaio, R.C.; Coelho, L.D.S.; Bestard, G.A.; Llanos, C.H. Multi-objective adaptive differential evolution for SVM/SVR hyperparameters selection. Pattern Recognit. 2020, 110, 107649. [Google Scholar] [CrossRef]
- Rivas-Perea, P.; Cota-Ruiz, J.; Chaparro, D.G.; Venzor, J.A.P.; Carreón, A.Q.; Rosiles, J.G. Support Vector Machines for Regression: A Succinct Review of Large-Scale and Linear Programming Formulations. Int. J. Intell. Sci. 2013, 03, 5–14. [Google Scholar] [CrossRef] [Green Version]
- Sabzekar, M.; Hasheminejad, S.M.H. Robust regression using support vector regressions. Chaos Solitons Fractals 2021, 144, 110738. [Google Scholar] [CrossRef]
- Stapelberg, R.F. Handbook of Reliability, Availability, Maintainability and Safety in Engineering Design; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Boyes, H.; Hallaq, B.; Cunningham, J.; Watson, T. The industrial internet of things (IIoT): An analysis framework. Comput. Ind. 2018, 101, 1–12. [Google Scholar] [CrossRef]
- Omri, N.; Al Masry, Z.; Mairot, N.; Giampiccolo, S.; Zerhouni, N. Industrial data management strategy towards an SME-oriented PHM. J. Manuf. Syst. 2020, 56, 23–36. [Google Scholar] [CrossRef]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python and Scikit-Learn. 2015. Available online: http://kukuruku.co/hub/python/introduction-to-machine-learning-with-python-andscikit-learn (accessed on 1 June 2022).
- Kadiyala, A.; Kumar, A. Applications of Python to evaluate environmental data science problems. Environ. Prog. Sustain. Energy 2017, 36, 1580–1586. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn & TensorFlow; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019; Volume 53. [Google Scholar]
- Tschätsch, H. Applied Machining Technology; Springer: Berlin/Heidelberg, Germany, 2009; pp. 5–23. [Google Scholar] [CrossRef]
- Adler, J.; Parmryd, I. Quantifying colocalization by correlation: The Pearson correlation coefficient is superior to the Mander’s overlap coefficient. Cytom. Part A 2010, 77A, 733–742. [Google Scholar] [CrossRef]
- Jiang, J.-R.; Kao, J.-B.; Li, Y.-L. Semi-Supervised Time Series Anomaly Detection Based on Statistics and Deep Learning. Appl. Sci. 2021, 11, 6698. [Google Scholar] [CrossRef]
- Molnar, C.; Freiesleben, T.; König, G.; Casalicchio, G.; Wright, M.N.; Bischl, B. Relating the Partial Dependence Plot and Permutation Feature Importance to the Data Generating Process. arXiv 2021, arXiv:2109.01433. [Google Scholar] [CrossRef]
- Van Calster, B.; Wynants, L.; Collins, G.S.; Verbakel, J.Y.; Steyerberg, E.W. ROC curves for clinical prediction models part 3. The ROC plot: A picture that needs a 1000 words. J. Clin. Epidemiol. 2020, 126, 220–223. [Google Scholar] [CrossRef]
- Hand, D.J. Measuring classifier performance: A coherent alternative to the area under the ROC curve. Mach. Learn. 2009, 77, 103–123. [Google Scholar] [CrossRef] [Green Version]
- Carter, J.V.; Pan, J.; Rai, S.N.; Galandiuk, S. ROC-ing along: Evaluation and interpretation of receiver operating characteristic curves. Surgery 2016, 159, 1638–1645. [Google Scholar] [CrossRef]
- Blanco, V.; Puerto, J.; Rodriguez-Chia, A.M. On p-Support Vector Machines and Multidimensional Kernels. J. Mach. Learn. Res. 2020, 21, 469–497. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Klein, S.; Schorr, S.; Bähre, D. Quality Prediction of Honed Bores with Machine Learning Based on Machining and Quality Data to Improve the Honing Process Control. Procedia CIRP 2020, 93, 1322–1327. [Google Scholar] [CrossRef]
- Teti, R.; Segreto, T.; Caggiano, A.; Nele, L. Smart Multi-Sensor Monitoring in Drilling of CFRP/CFRP Composite Material Stacks for Aerospace Assembly Applications. Appl. Sci. 2020, 10, 758. [Google Scholar] [CrossRef] [Green Version]
- Wan, X. Influence of feature scaling on convergence of gradient iterative algorithm. J. Phys. Conf. Ser. 2019, 1213, 032021. [Google Scholar] [CrossRef] [Green Version]





| Manual Setup Data | PLC Automation Control |
|---|---|
| Milling Part ID | Cutting Speed Set Point [220–240 rpm] |
| Profile Height [70–200 mm] | Feed Rate Set Point [5000–8000 mm/min] |
| Profile Length [6000–23,800 mm] | Feed Motor Torque Set Point [% of nominal] |
| Profile Thickness [5–30 mm] | Frame Position Set Point [0…3] |
| Profile Type [I or L] | Machine Active [T/F] |
| Spindle Position [0…3] | Mill Depth Set Point [1.5–3.03 mm] |
| Tool Number [1 or 2] | Milling Status [T/F] |
| Time Stamp [yyyy-mm-dd-hh-mm-ss] |
| Calculated Parameters | Measured Parameters |
|---|---|
| Cutting Speed Ratio [0…1] | Cutting Speed [rpm] |
| Feed Rate Ratio [0…1] | Feed Rate [mm/min] |
| Num. Of Tool Rows Used [1 or 2] | Milling End Time [yyyy-mm-dd-hh-mm-ss] |
| ToolRows0.MilledMeters [m] | Milling Start Time [yyyy-mm-dd-hh-mm-ss] |
| ToolRows0.MilledTime [s] | Spindle Motor Torque [% of nominal] |
| ToolRows0.Used [T/F] | Vibration [mm/s RMS] |
| ToolRows1.MilledMeters [m] | |
| ToolRows1.MilledTime [s] | |
| ToolRows1.Used [T/F] | |
| ToolRows2.MilledMeters [m] | |
| ToolRows2.MilledTime [s] | |
| ToolRows2.Used [T/F] | |
| ToolRows3.MilledMeters [m] | |
| ToolRows3.MilledTime [s] | |
| ToolRows3.Used [T/F] | |
| ToolRowsUsed.MaxMilledMeters [m] | |
| ToolRowsUsed.AvgMilledMeters [m] | |
| ToolRowsUsed.MinMilledMeters [m] |
| Error Scoring Metric | Linear | SVR POLY | SVR RBF |
|---|---|---|---|
| Train score R2 | 0.649464505 | 0.819797848 | 0.856560515 |
| Test score R2 | 0.646896683 | 0.803223516 | 0.846645929 |
| Train mean absolute error (MAE) | 0.080181311 | 0.056275051 | 0.049610738 |
| Train MSE [%] | 0.010790393 | 0.006013242 | 0.004686307 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mäkiaho, T.; Vainio, H.; Koskinen, K.T. Wear Parameter Diagnostics of Industrial Milling Machine with Support Vector Regression. Machines 2023, 11, 395. https://doi.org/10.3390/machines11030395
Mäkiaho T, Vainio H, Koskinen KT. Wear Parameter Diagnostics of Industrial Milling Machine with Support Vector Regression. Machines. 2023; 11(3):395. https://doi.org/10.3390/machines11030395
Chicago/Turabian StyleMäkiaho, Teemu, Henri Vainio, and Kari T. Koskinen. 2023. "Wear Parameter Diagnostics of Industrial Milling Machine with Support Vector Regression" Machines 11, no. 3: 395. https://doi.org/10.3390/machines11030395
APA StyleMäkiaho, T., Vainio, H., & Koskinen, K. T. (2023). Wear Parameter Diagnostics of Industrial Milling Machine with Support Vector Regression. Machines, 11(3), 395. https://doi.org/10.3390/machines11030395






