Simulation and Validation of Cavitating Flow in a Torque Converter with Scale-Resolving Methods
Abstract
1. Introduction
2. Computational Model
2.1. Turbulence Model
2.1.1. SST Model
2.1.2. DDES Model
2.1.3. SBES Model
2.1.4. SAS-SST Model
2.1.5. WALE Model
2.2. Cavitation Model
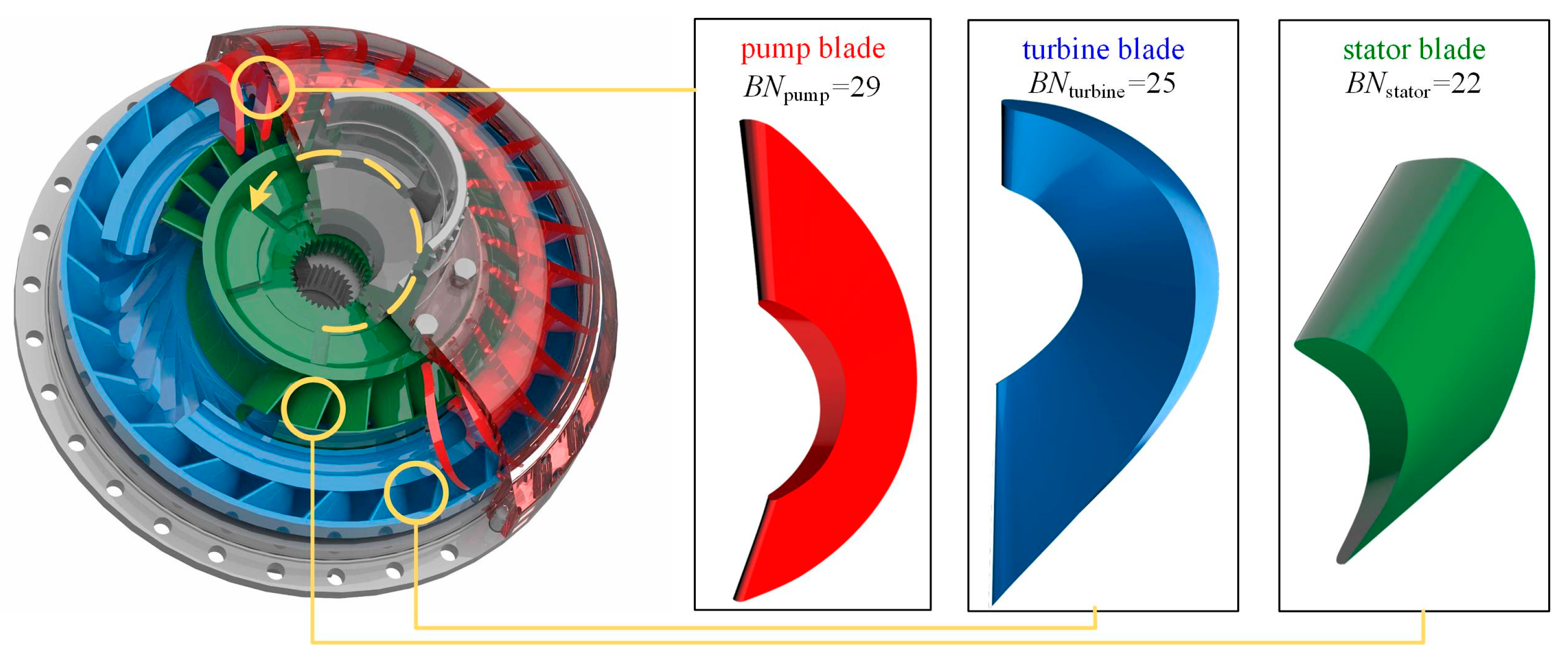
2.3. Geometry and Mesh Model
2.4. Simulation Settings
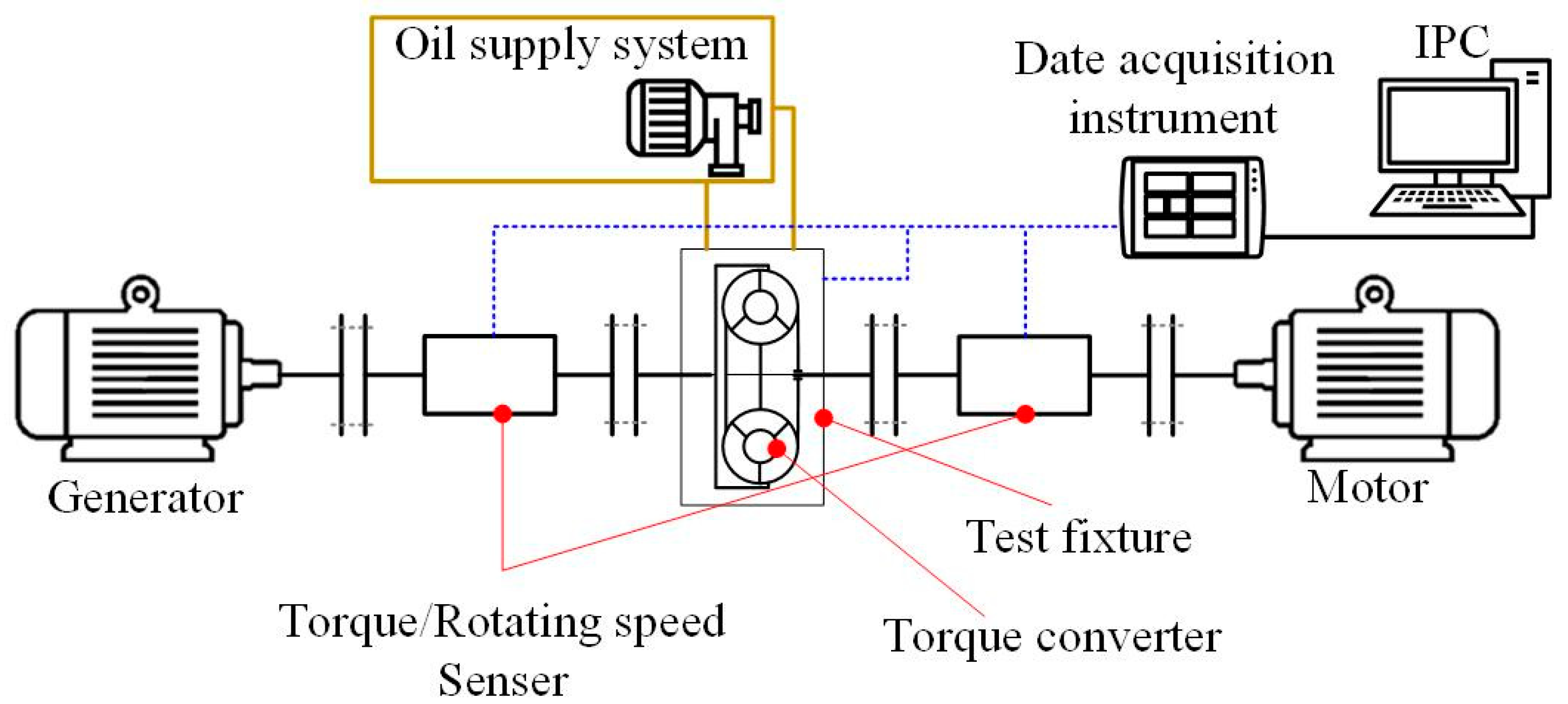
3. Hydraulic Torque Converter Test Rig
3.1. Hydrodynamic Performance Test of Hydraulic Torque Converter
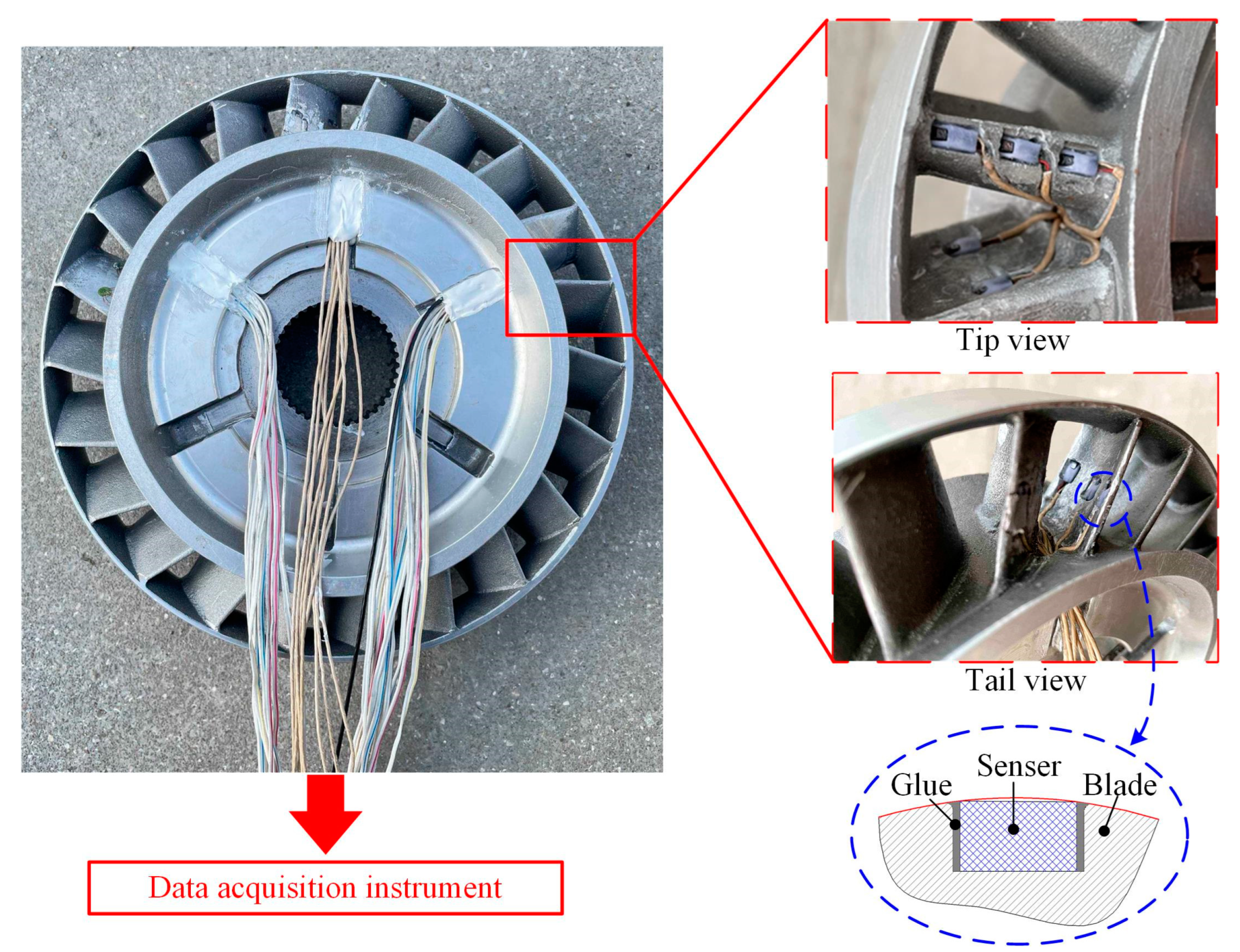
3.2. Blade Surface Pressure Test Inside Hydraulic Torque Converter
4. Results
5. Flow Field Analysis
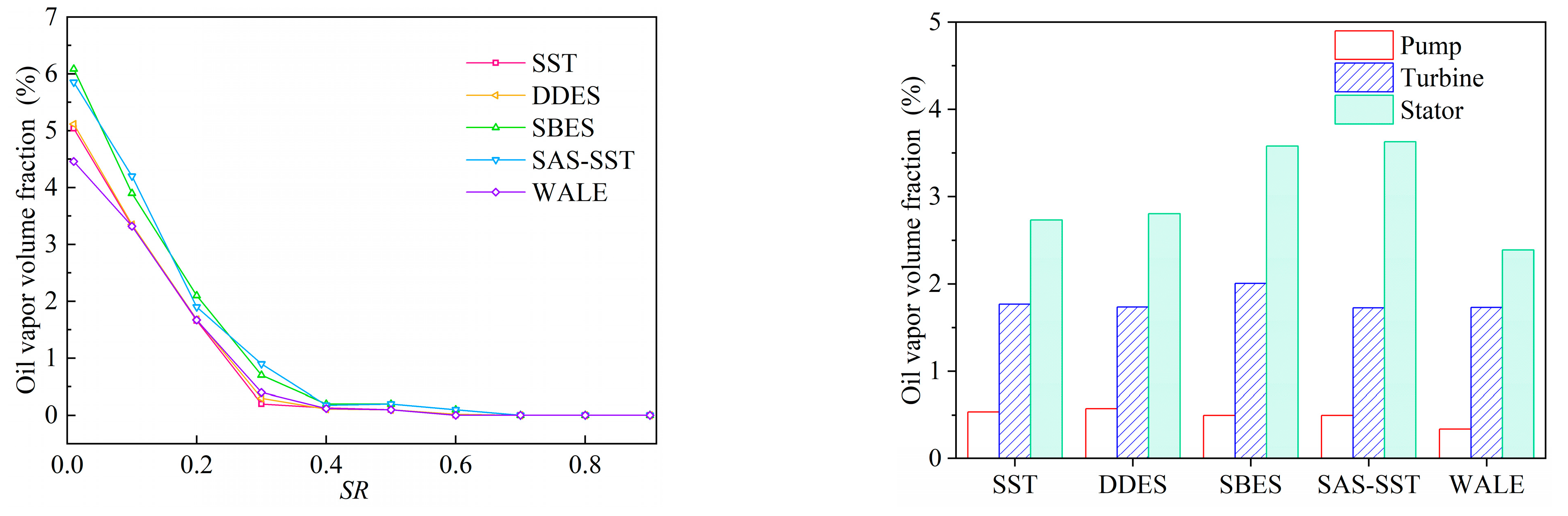
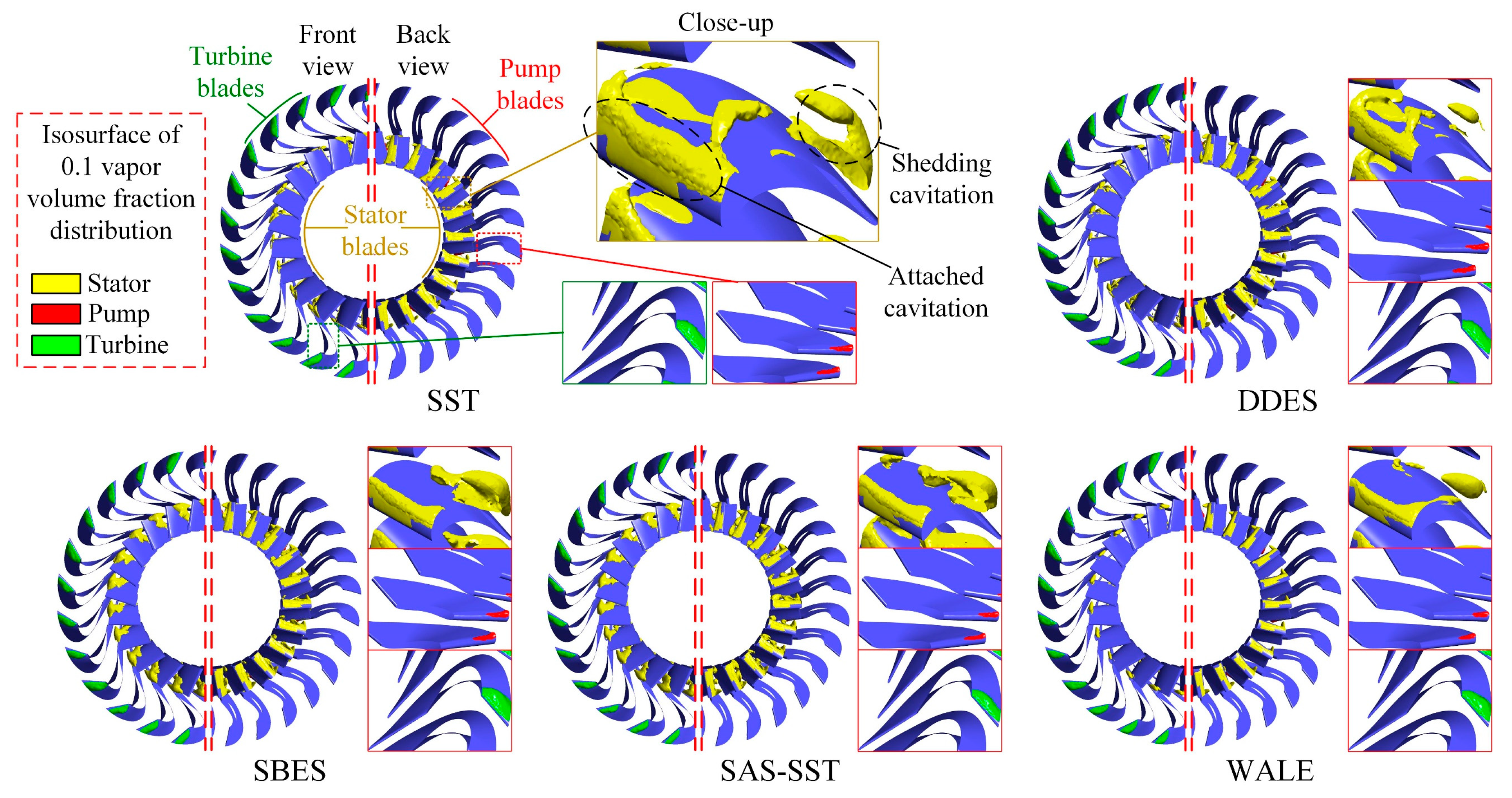
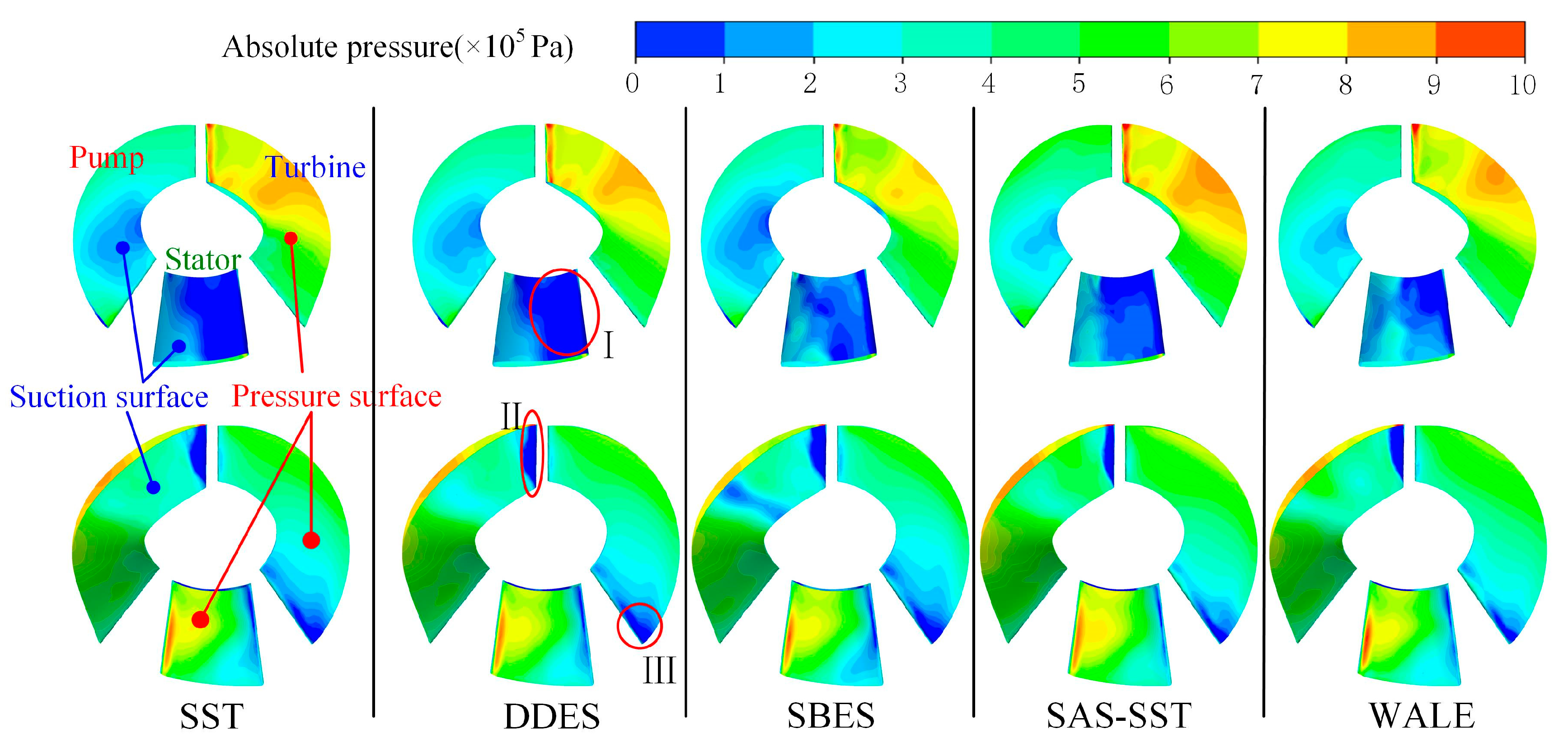
5.1. Overall Cavitation Characteristics
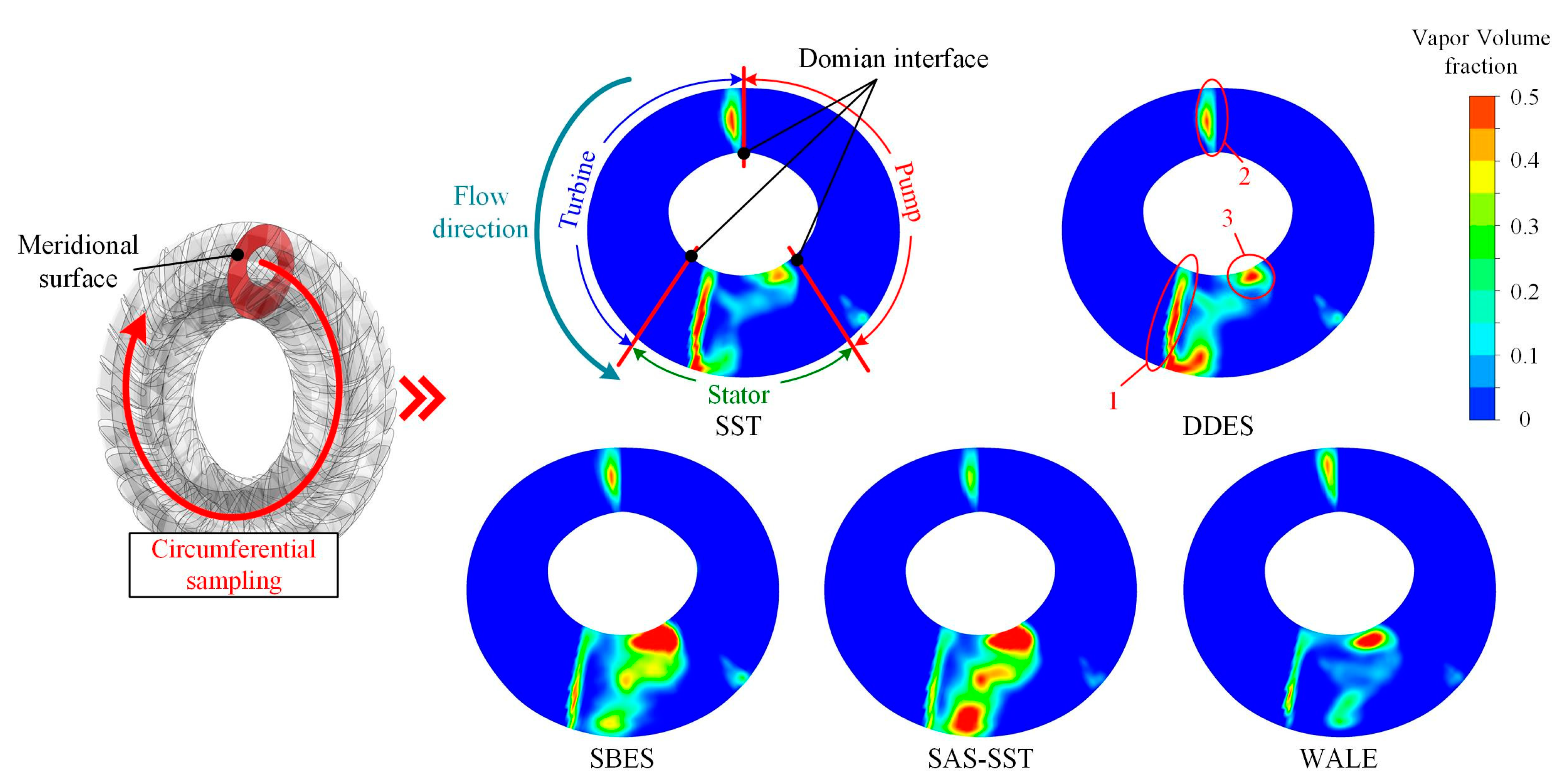
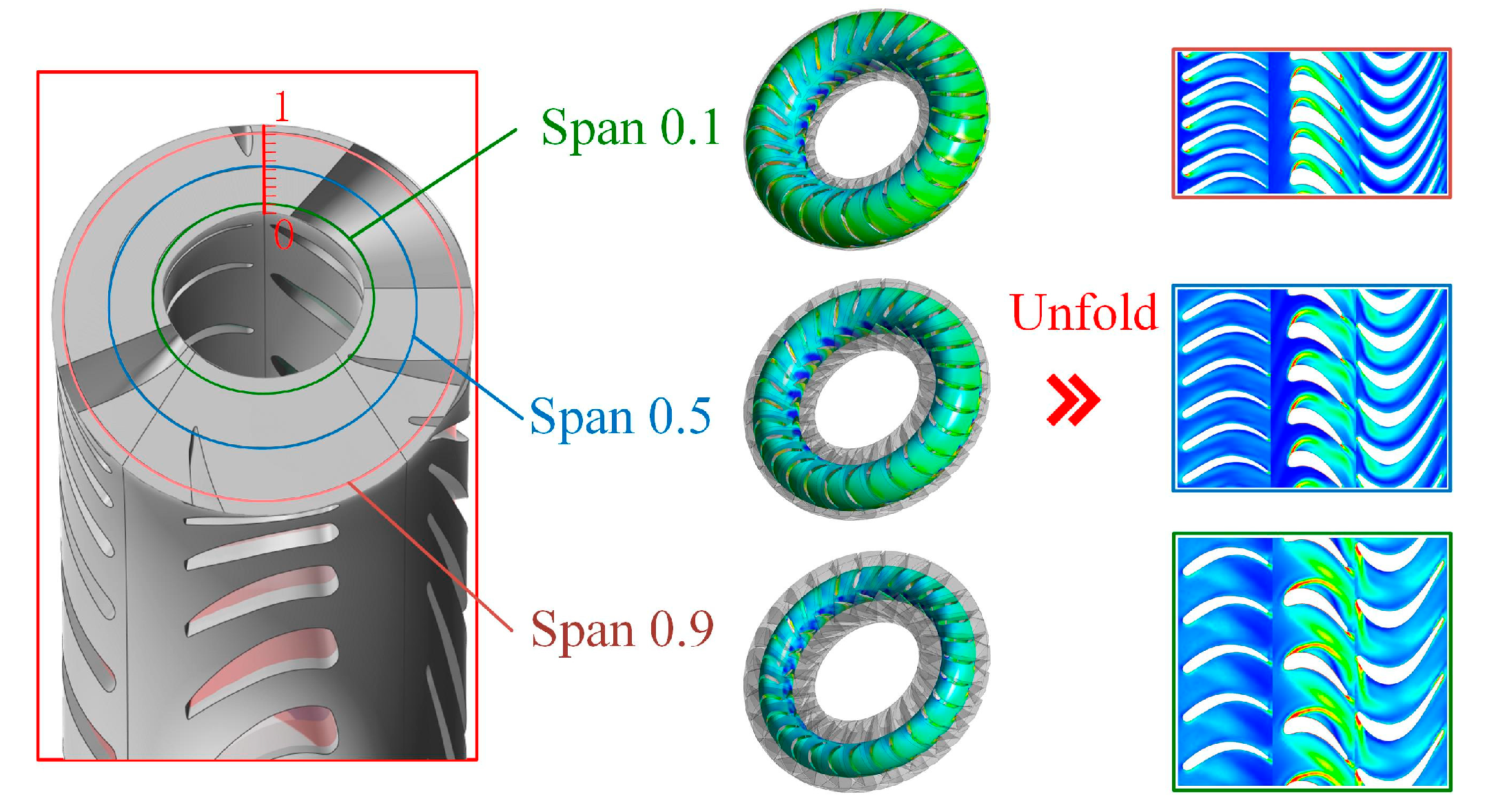
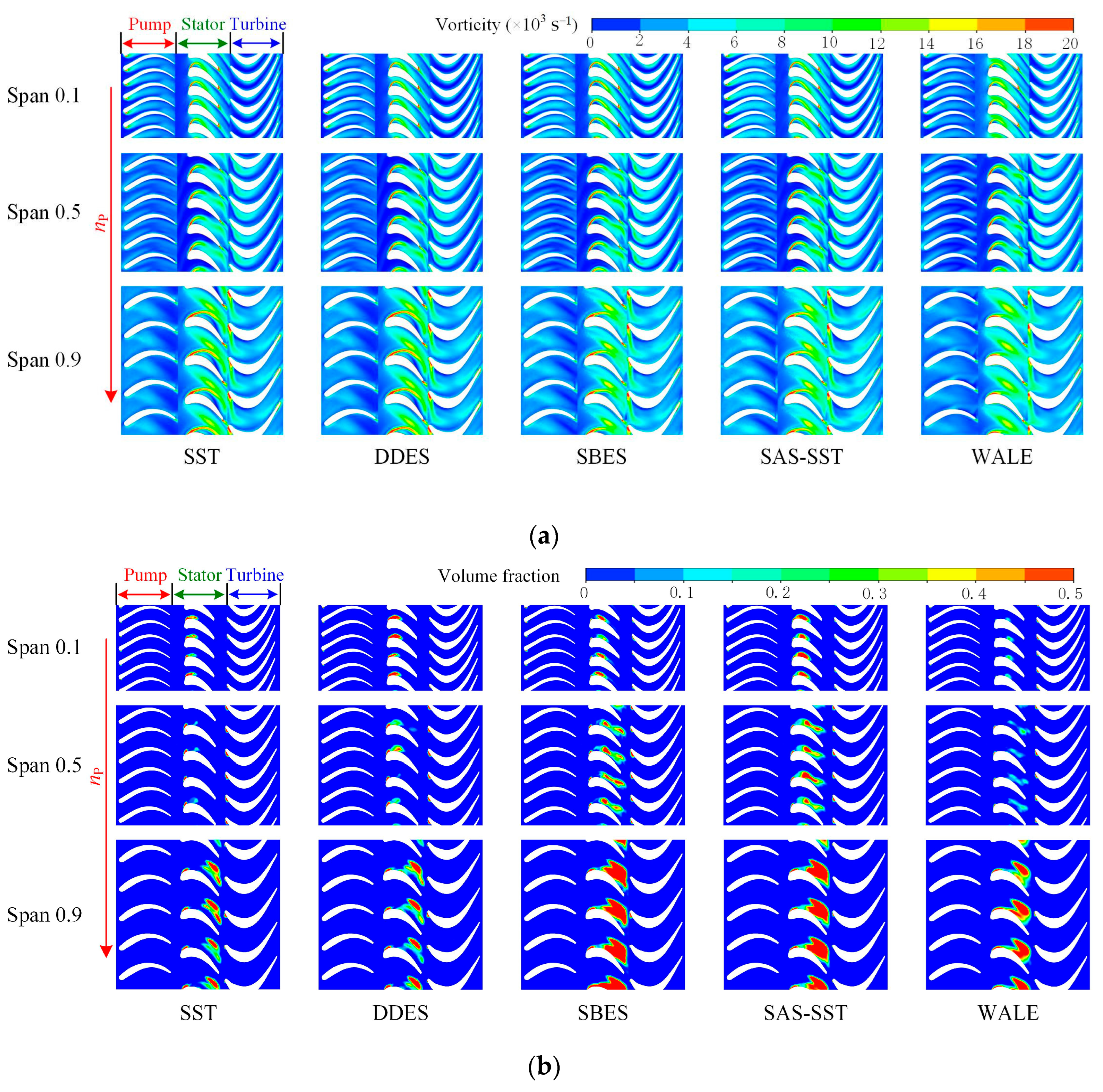
5.2. Cavitation and Vortex Analysis of the Chord Surface
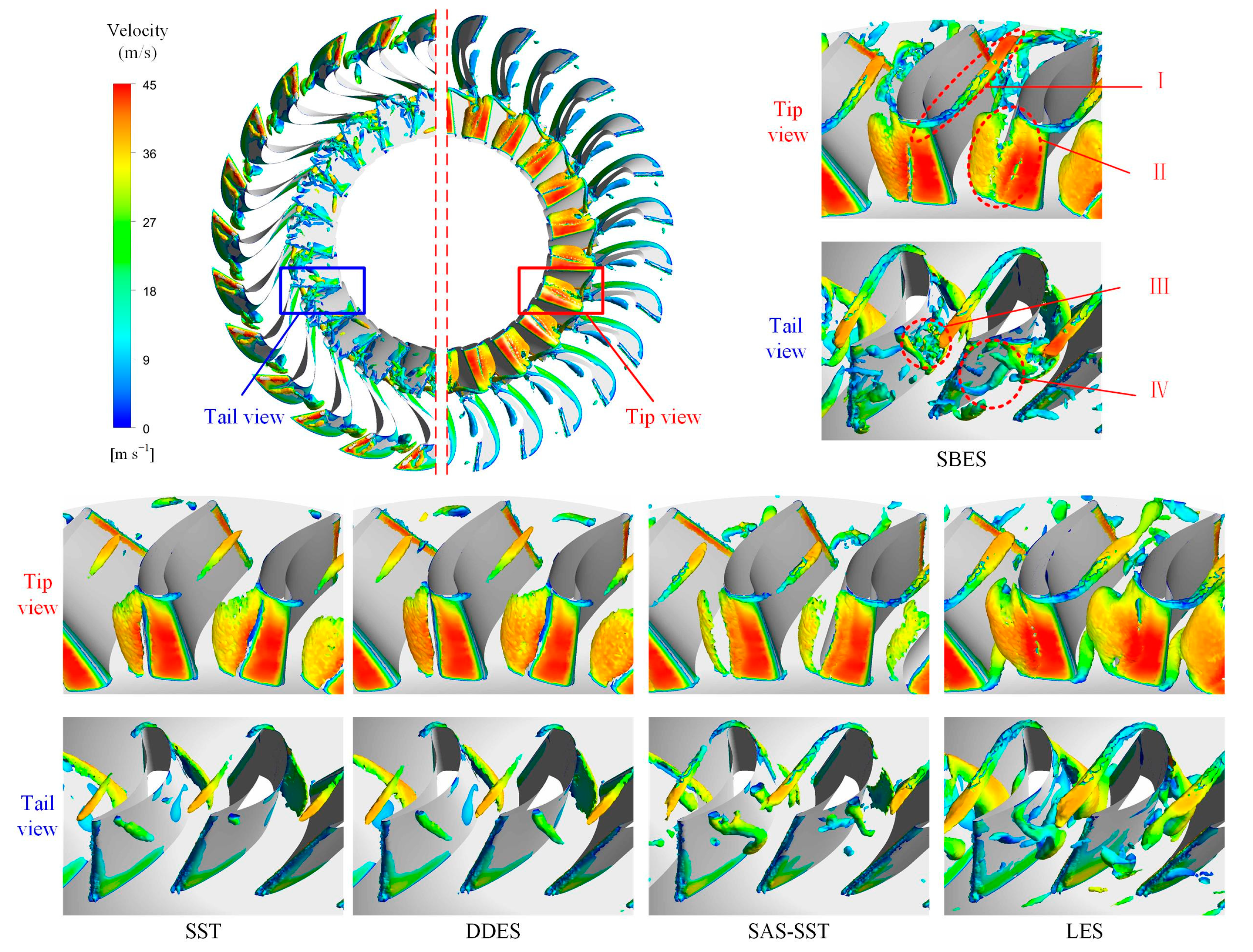
5.3. D Vortex Structure in the Stator Flow Field
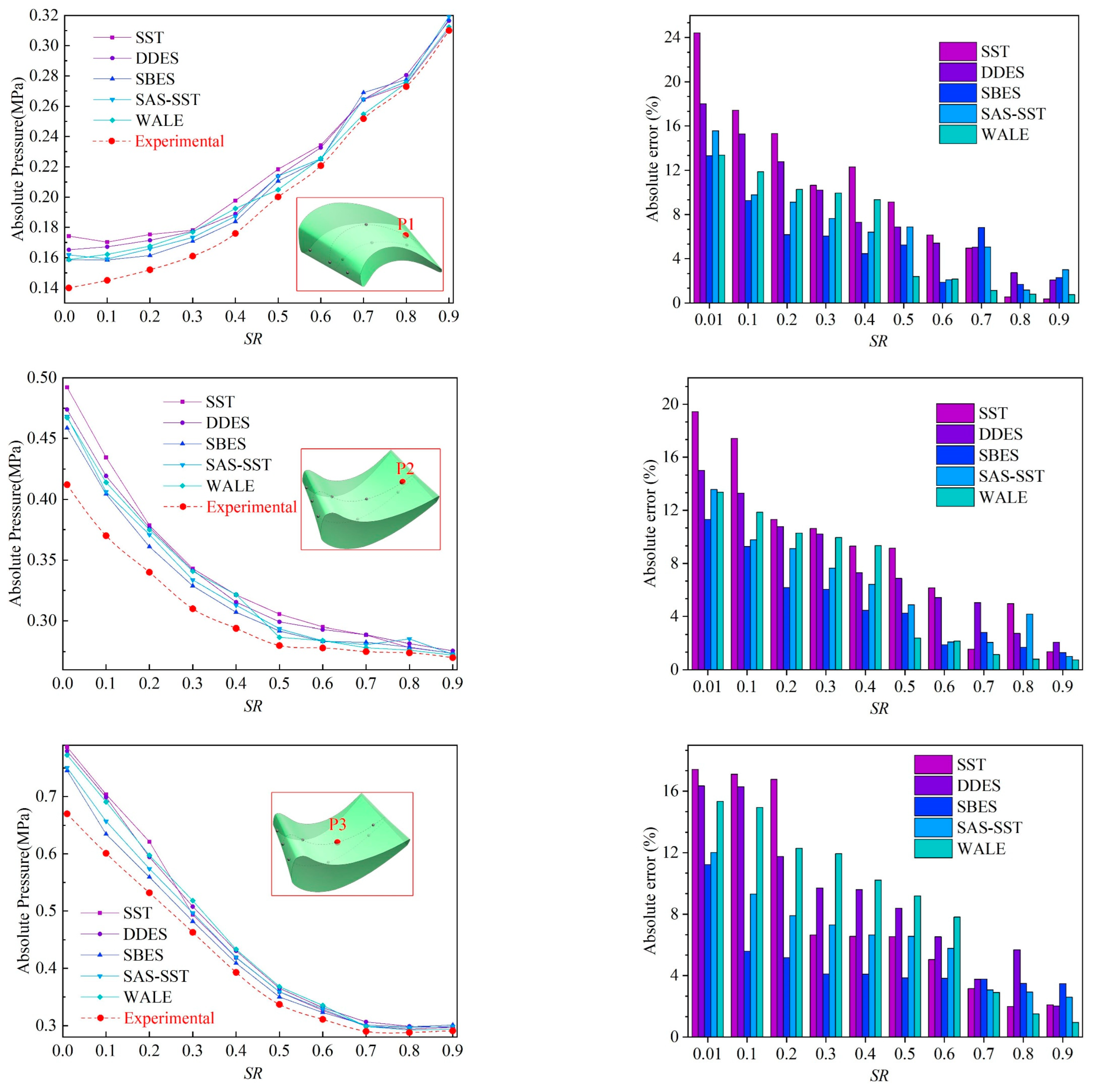
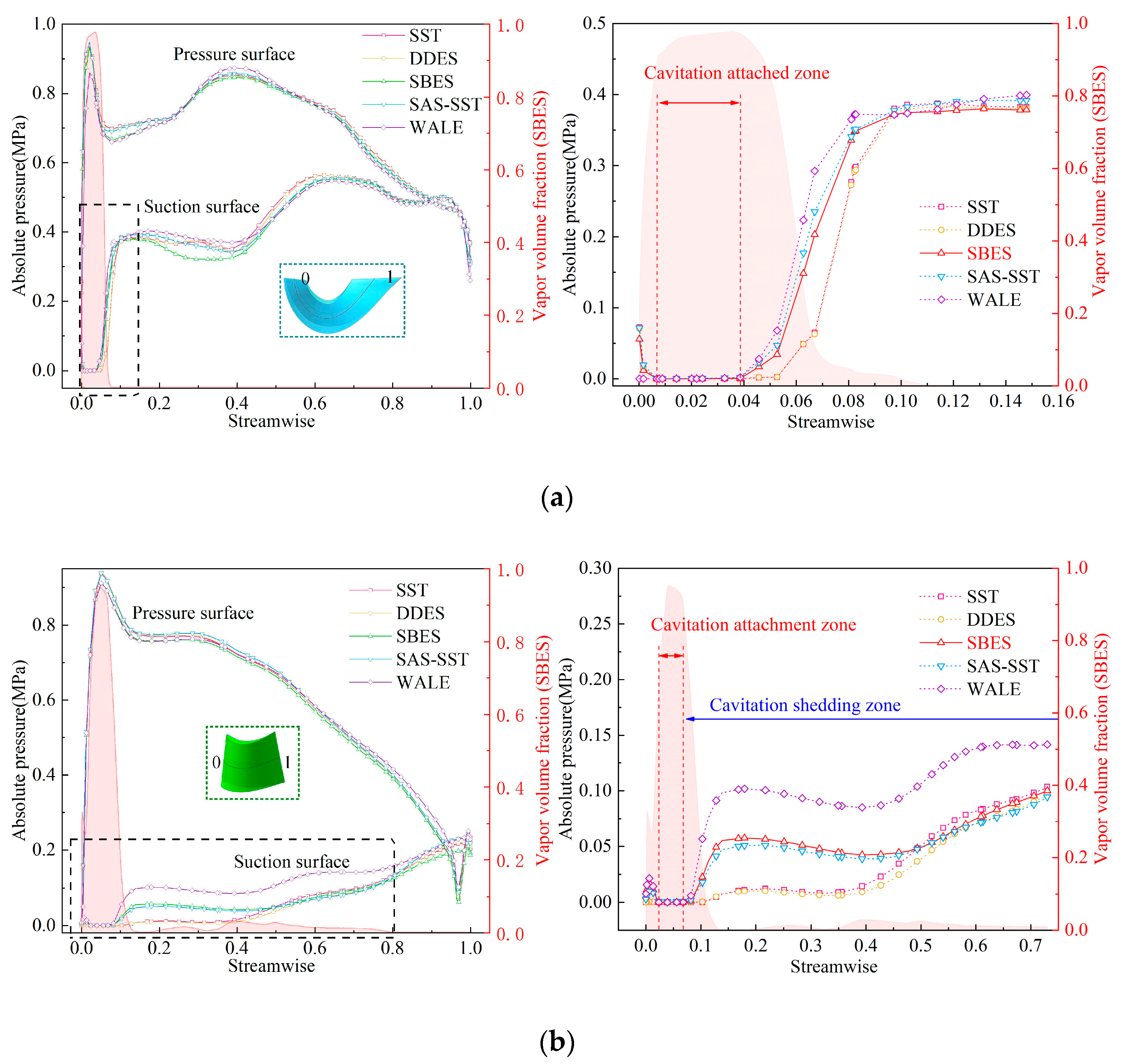
5.4. Quantitative Analysis of Blade Pressure
6. Analysis of Transient Cavitation Evolution in the Stator
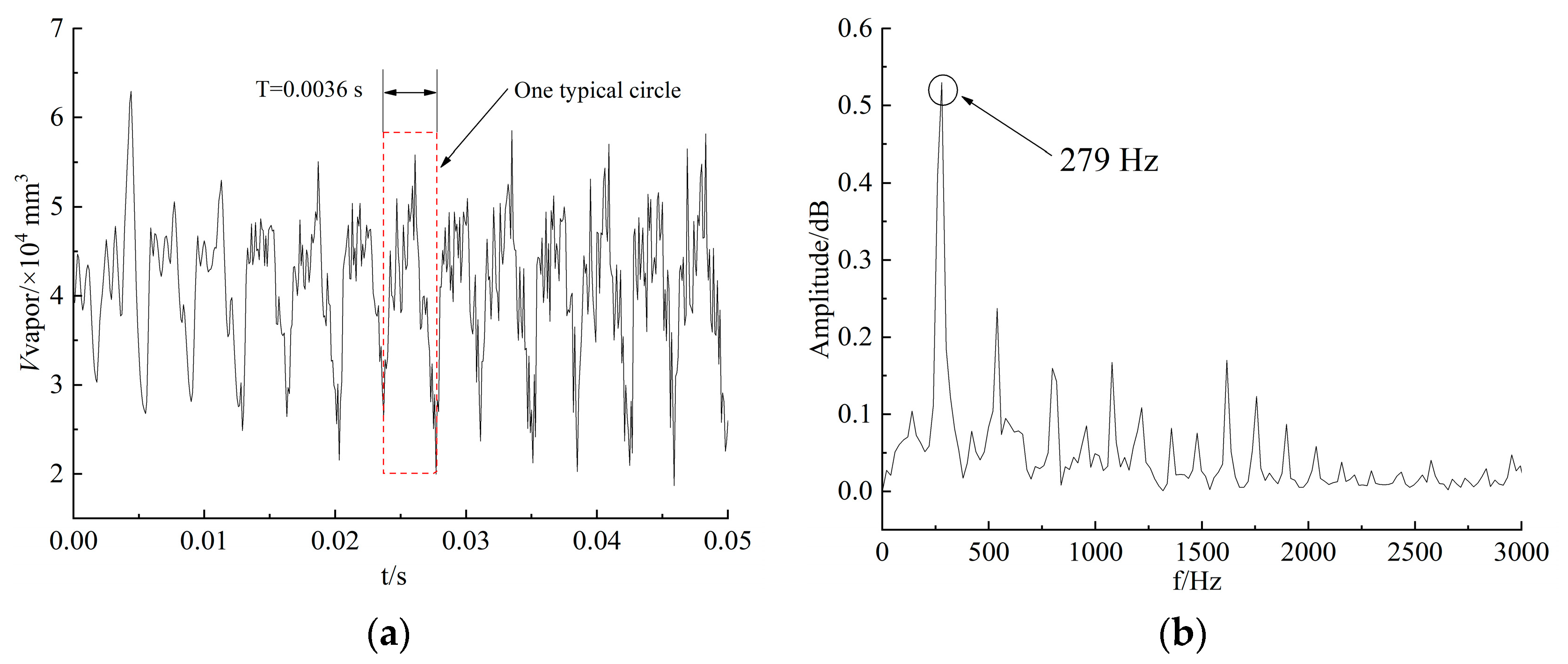
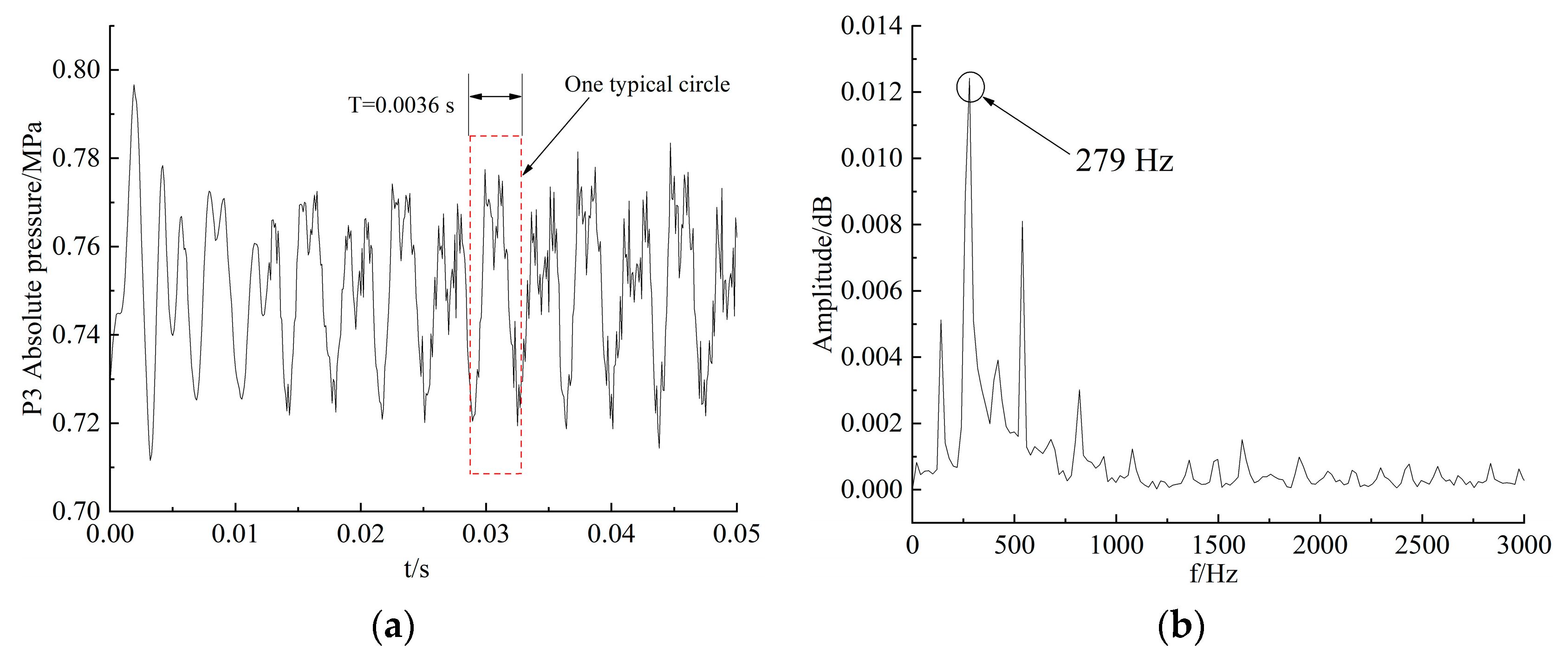
6.1. Spectral Analysis of Vapor Volume and Pressure
6.2. Evolution of Cavitation
6.3. Transient Shedding Cavitation Flow Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| BNpump | Blade number of pump |
| BNturbine | Blade number of turbine |
| BNstator | Blade number of stator |
| RB | bubble radius, m |
| pg | vapor pressure, Pa |
| p | local pressure, Pa |
| ρf | liquid density, kg m−3 |
| t | time, s |
| F | mass transfer empirical factor |
| ṁfg | interphase mass transfer per unit, kg s−1 |
| ρg | vapor density, kg m−3 |
| NB | bubble count per unit volume |
| rnuc | volume fraction of the nucleation site |
| μf | dynamic viscosity of oil, Pa s |
| μg | dynamic viscosity of vapor, Pa s |
| pref | Reference pressure, MPa |
| NP | Rotating speed of pump, rpm |
| NT | Rotating speed of turbine, rpm |
| Ns | Rotating speed of stator, rpm |
| SR | Rotation speed ratio |
| K | Torque ratio |
| CC | Capacity constant, kg/rad2/m3 |
| η | Efficiency |
| Vvapor | Vapor volume, mm3 |
References
- Ran, Z.; Ma, W.; Liu, C. 3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter. Appl. Sci. 2021, 11, 2798. [Google Scholar] [CrossRef]
- Yin, Z.; Gu, Y.; Fan, T.; Li, Z.; Wang, W.; Wu, D.; Mou, J.; Zheng, S. Effect of the Inclined Part Length of an Inclined Blade on the Cavitation Characteristics of Vortex Pumps. Machines 2023, 11, 21. [Google Scholar] [CrossRef]
- Liu, C.; Guo, M.; Yan, Q.; Wei, W. Influence of Charging Oil Condition on Torque Converter Cavitation Characteristics. Chin. J. Mech. Eng. 2022, 35, 49. [Google Scholar] [CrossRef]
- Ran, Z.; Ma, W.; Liu, C. Design Approach and Mechanism Analysis for Cavitation-Tolerant Torque Converter Blades. Appl. Sci. 2022, 12, 3405. [Google Scholar] [CrossRef]
- Guo, M.; Liu, C.; Yan, Q.; Wei, W.; Khoo, B.C. The Effect of Rotating Speeds on the Cavitation Characteristics in Hydraulic Torque Converter. Machines 2022, 10, 80. [Google Scholar] [CrossRef]
- Pan, X.; Xinyuan, C.; Hongjun, S.; Jiping, Z.; Lin, W.; Huichao, G. Effect of the blade shaped by Joukowsky airfoil transformation on the characteristics of the torque converter. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 3314–3321. [Google Scholar] [CrossRef]
- Ghadimi, A.; Ghassemi, H. Comparative assessment of hydrodynamic performance of two-dimensional Naca0012 and Naca6612 hydrofoils under different cavitation and non-cavitation conditions. Int. J. Hydromechatronics 2020, 3, 349–367. [Google Scholar] [CrossRef]
- Yang, K.; Liu, C.; Li, J.; Xiong, J. Calculation and analysis of thermal flow field in hydrodynamic torque converter with a new developed stress-blended eddy simulation. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 3436–3460. [Google Scholar] [CrossRef]
- Zheng, Z.-Y.; Liu, Q.-Z.; Deng, Y.-K.; Li, B. Multi-objective optimization design for the blade angles of hydraulic torque converter with adjustable pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 2523–2536. [Google Scholar] [CrossRef]
- Liu Cheng Guo, M.; Wei, W.; Yan, Q.; Li, P. Investigation on the Effects of Torque Converter Blade Thickness Based on FSI Simulation. Volume 3A: Fluid Applications and Systems (p. V03AT03A017). In Proceedings of the ASME-JSME-KSME 2019 8th Joint Fluids Engineering Conference, San Francisco, CA, USA, 28 July–1 August 2019. [Google Scholar]
- Chen, J.; Wu, G. Kriging-assisted design optimization of the impeller geometry for an automotive torque converter. Struct. Multidiscip. Optim. 2018, 57, 2503–2514. [Google Scholar] [CrossRef]
- Hayashi, T.; Nakamura, Y.; Miyagawa, K. Design optimization of a low specific speed centrifugal pump with an unshrouded impeller for cryogenic liquid flow. In Proceedings of the 29th Iahr Symposium on Hydraulic Machinery and Systems, Kyoto, Japan, 16–21 September 2018. [Google Scholar]
- Namazizadeh, M.; Gevari, M.T.; Mojaddam, M.; Vajdi, M. Optimization of the Splitter Blade Configuration and Geometry of a Centrifugal Pump Impeller using Design of Experiment. J. Appl. Fluid Mech. 2020, 13, 89–101. [Google Scholar] [CrossRef]
- Tang, X.; Gu, N.; Wang, W.; Wang, Z.; Peng, R. Aerodynamic robustness optimization and design exploration of centrifugal compressor impeller under uncertainties. Int. J. Heat Mass Transf. 2021, 180, 121799. [Google Scholar] [CrossRef]
- Wu, G.-Q.; Chen, J.; Zhu, W.-J. Performance Analysis and Improvement of Flat Torque Converters Using DOE Method. Chin. J. Mech. Eng. 2018, 31, 60. [Google Scholar] [CrossRef]
- Menter, F.; Hüppe, A.; Matyushenko, A.; Kolmogorov, D. An Overview of Hybrid RANS–LES Models Developed for Industrial CFD. Appl. Sci. 2021, 11, 2459. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Bai, X.R.; Long, X.P.; Ji, B.; Peng, X.X.; Farhat, M. Large eddy simulation of the tip-leakage cavitating flow with an insight on how cavitation influences vorticity and turbulence. Appl. Math. Model. 2020, 77, 788–809. [Google Scholar] [CrossRef]
- Li, J.; Sui, T.; Dong, X.; Gu, F.; Su, N.; Liu, J.; Xu, C. Large eddy simulation studies of two-phase flow characteristics in the abrasive flow machining of complex flow ways with a cross-section of cycloidal lobes. Int. J. Hydromechatronics 2022, 5, 136–166. [Google Scholar] [CrossRef]
- Wang, Z.; Li, L.; Li, X.; Zhu, Z. Large eddy simulation of cavitating flow around a twist hydrofoil and investigation on force element evolution using a multiscale cavitation model. Phys. Fluids 2022, 34, 023303. [Google Scholar] [CrossRef]
- Li, X.; Wu, Q.; Miao, L.; Yak, Y.; Liu, C. Scale-resolving simulations and investigations of the flow in a hydraulic retarder considering cavitation. J. Zhejiang Univ.-Sci. A 2020, 21, 817–833. [Google Scholar] [CrossRef]
- Liu, C.B.; Li, J.; Bu, W.Y.; Xu, Z.X.; Xu, D.; Ma, W.X. Application of scale-resolving simulation to a hydraulic coupling, a hydraulic retarder, and a hydraulic torque converter. J. Zhejiang Univ.-Sci. A 2018, 19, 904–925. [Google Scholar] [CrossRef]
- Xie, C.; Liu, J.; Jiang, J.-W.; Huang, W.-X. Numerical study on wetted and cavitating tip-vortical flows around an elliptical hydrofoil: Interplay of cavitation, vortices, and turbulence. Phys. Fluids 2021, 33, 093316. [Google Scholar] [CrossRef]
- Wu, J.; Deijlen, L.; Bhatt, A.; Ganesh, H.; Ceccio, S.L. Cavitation dynamics and vortex shedding in the wake of a bluff body. J. Fluid Mech. 2021, 917, A26. [Google Scholar] [CrossRef]
- Sezen, S.; Uzun, D.; Turan, O.; Atlar, M. Influence of roughness on propeller performance with a view to mitigating tip vortex cavitation. Ocean Eng. 2021, 239, 109703. [Google Scholar] [CrossRef]
- Yu, A.; Qian, Z.; Wang, X.; Tang, Q.; Zhou, D. Large Eddy simulation of ventilated cavitation with an insight on the correlation mechanism between ventilation and vortex evolutions. Appl. Math. Model. 2021, 89, 1055–1073. [Google Scholar] [CrossRef]
- Chen, J.; Geng, L.; De la Torre, O.; Escaler, X. Assessment of turbulence models for the prediction of Benard-Von Karman vortex shedding behind a truncated hydrofoil in cavitation conditions. In Proceedings of the 30th Iahr Symposium on Hydraulic Machinery and Systems (Iahr 2020), Lausanne, Switzerland, 21–26 March 2021; Volume 774, p. 012025. [Google Scholar]
- Menter, F.R. Best Practice: Scale-Resolving Simulations in Ansys CFD; ANSYS Germany GmbH: Darmstadt, Germany, 2012. [Google Scholar]
- Menter, F.R.; Lechner, R.; Matyushenko, A. Best Practice: RANS Turbulence Modeling in Ansys CFD; ANSYS Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Orszag, S.A.; Yakhot; Flannery, W.S.; Boysan, F.; Choudhury, D.; Maruzewski, J.; Patel, B. Renormalization Group Modeling and Turbulence Simulations. In Proceedings of International Conference on Near -Wall Turbulent Flows, Tempe, AZ, USA, 15–17 March 1993. [Google Scholar]
- Wilcox, D.C. Multiscale model for turbulent flows. AIAA J. 1988, 26, 1311–1320. [Google Scholar] [CrossRef]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar]
- Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Rotta, J.C. Turbulente Strömumgen; BG Teubner: Stuttgart, Germany, 1972. [Google Scholar]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Zwart, P.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. Fifth International Conference on Multiphase Flow. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and Numerical Modeling of Unsteady Cavitation Dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Singhal, A.; Athavale, M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Ansys, Inc. ANSYS CFX-Solver Theory Guide Release 2020-R1; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Liu, B.; Tan, L.; Li, J. Influence of Pump Rotation Speed on Hydrodynamic Performance and Stator Blade Surface Pressure Pulsation in Torque Converter. J. Fluids Eng. 2020, 142, 101207. [Google Scholar] [CrossRef]






| Model | Feature |
|---|---|
| SST (Shear Stress Transport model) | Based on the RANS ideology. Widely used in the flow field calculation of fluid machinery, with low grid fineness requirements and short calculation time, and the calculation error is large. |
| WALE (wall-adapting local eddy-viscosity model) | Belongs to the LES subgrid model. Has the capability to reproduce laminar to turbulent transition. The amount of calculation is too large, while accuracy of results depends on mesh size and quality. |
| DDES (Delayed Detached Eddy Simulation) | Belongs to the HRL algorithm. DDES combines the advantages of RANS and LES, requires lower boundary layer grids than LES, and has better computational robustness and accuracy |
| SBES (Stress-Blended Eddy Simulation) | Belongs to the HRL algorithm. SBES introduces a hybrid function, which can generically combine RANS and LES model formulations. It has a rapid “transition” from RANS to LES in separating shear layers. |
| SAS-SST (SAS based on SST model) | Belongs to the HRL algorithm. SAS is an improved URANS formulation, which allows the resolution of the turbulent spectrum in unstable flow conditions. It has better robustness and must perform fewer calculations than WALE. |
| Pump | Turbine | Stator | |
|---|---|---|---|
| Blade number | 29 | 25 | 22 |
| Blade entrance angle (deg) | −31 | 46 | −23 |
| Blade exit angle (deg) | 34 | −65 | 50 |
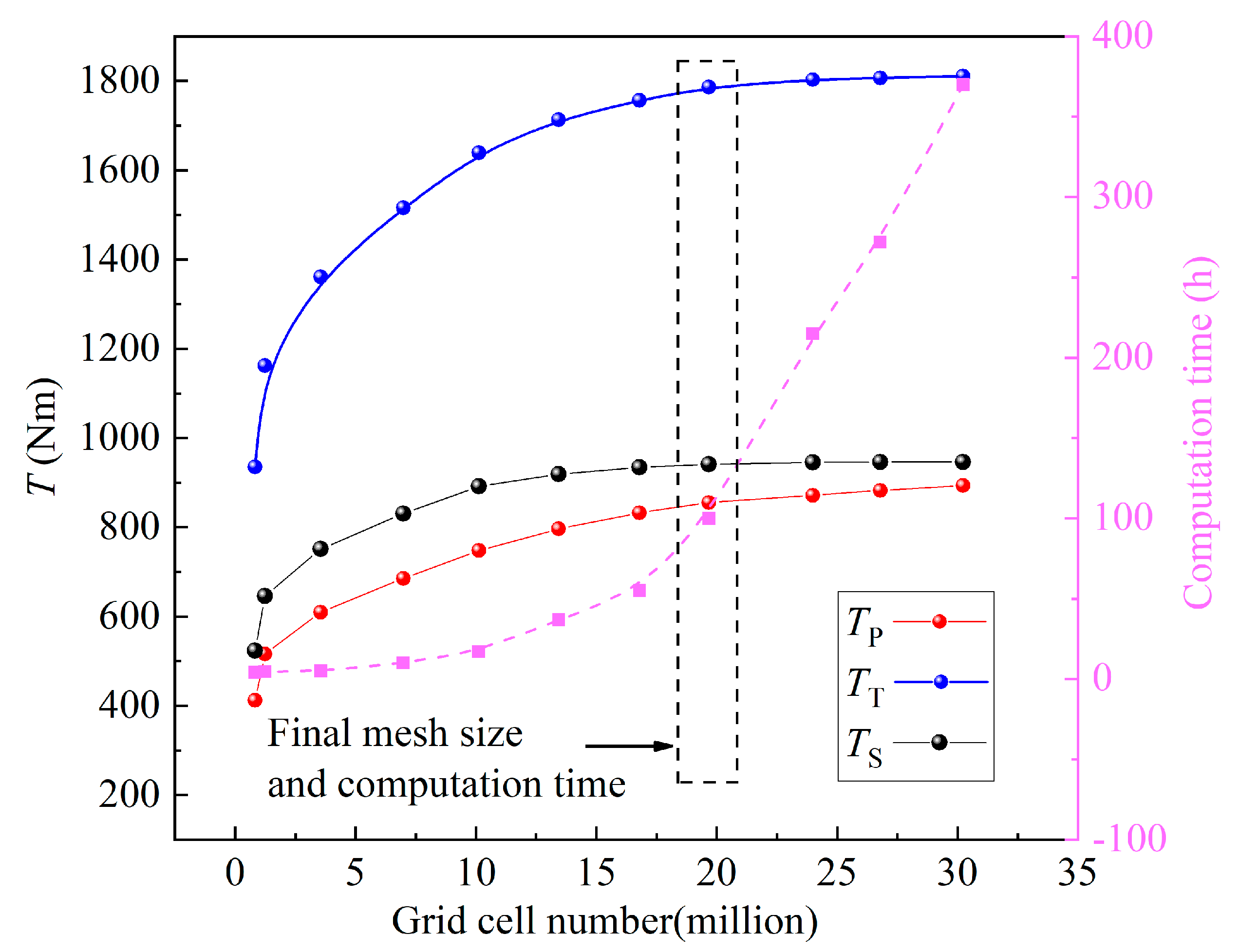
| Grid Cell Number (×106) | Computation Time (h) | TP (N m) | Div. | TT (N m) | Div. | TS (N m) | Div. |
|---|---|---|---|---|---|---|---|
| 0.82478 | 4 | 412.13 | 935.38 | 523.24 | |||
| 1.23243 | 4.5 | 516.12 | 25.23% | 1162.02 | 24.23% | 645.90 | 23.44% |
| 3.55688 | 5 | 609.69 | 18.13% | 1361.08 | 17.13% | 751.39 | 16.33% |
| 6.98908 | 10 | 685.29 | 12.39% | 1516.24 | 11.40% | 830.95 | 10.59% |
| 10.12353 | 17 | 747.79 | 9.12% | 1639.36 | 8.12% | 891.57 | 7.30% |
| 13.43893 | 37 | 796.57 | 6.52% | 1713.52 | 4.52% | 918.95 | 3.07% |
| 16.78994 | 55 | 832.52 | 4.51% | 1756.58 | 2.51% | 934.06 | 1.64% |
| 19.67383 | 100 | 855.27 | 2.73% | 1786.65 | 1.71% | 941.39 | 0.78% |
| 23.98664 | 215 | 871.78 | 1.93% | 1803.11 | 0.92% | 945.33 | 0.42% |
| 26.79305 | 272 | 882.65 | 1.25% | 1807.02 | 0.22% | 946.37 | 0.11% |
| 30.23543 | 370 | 893.42 | 1.12% | 1811.02 | 0.22% | 946.59 | 0.02% |
| Analysis Step | No Cavitation I | No Cavitation II | Cavitation III | Cavitation IV |
|---|---|---|---|---|
| Analysis type | Steady state | Steady state | Steady state | Transient |
| Advection scheme | Upwind | High resolution | High resolution | High resolution |
| Interface model | Frozen rotor | Frozen rotor | Stage | Transient Rotor-Stator |
| Cavitation model | None | None | Zwart model | Zwart model |
| Time step | 1 × 10−3 s | 1 × 10−4 s | 1 × 10−4 s | 1 × 10−5 s |
| Step number | 300 | 300 | 400 | 5000 |
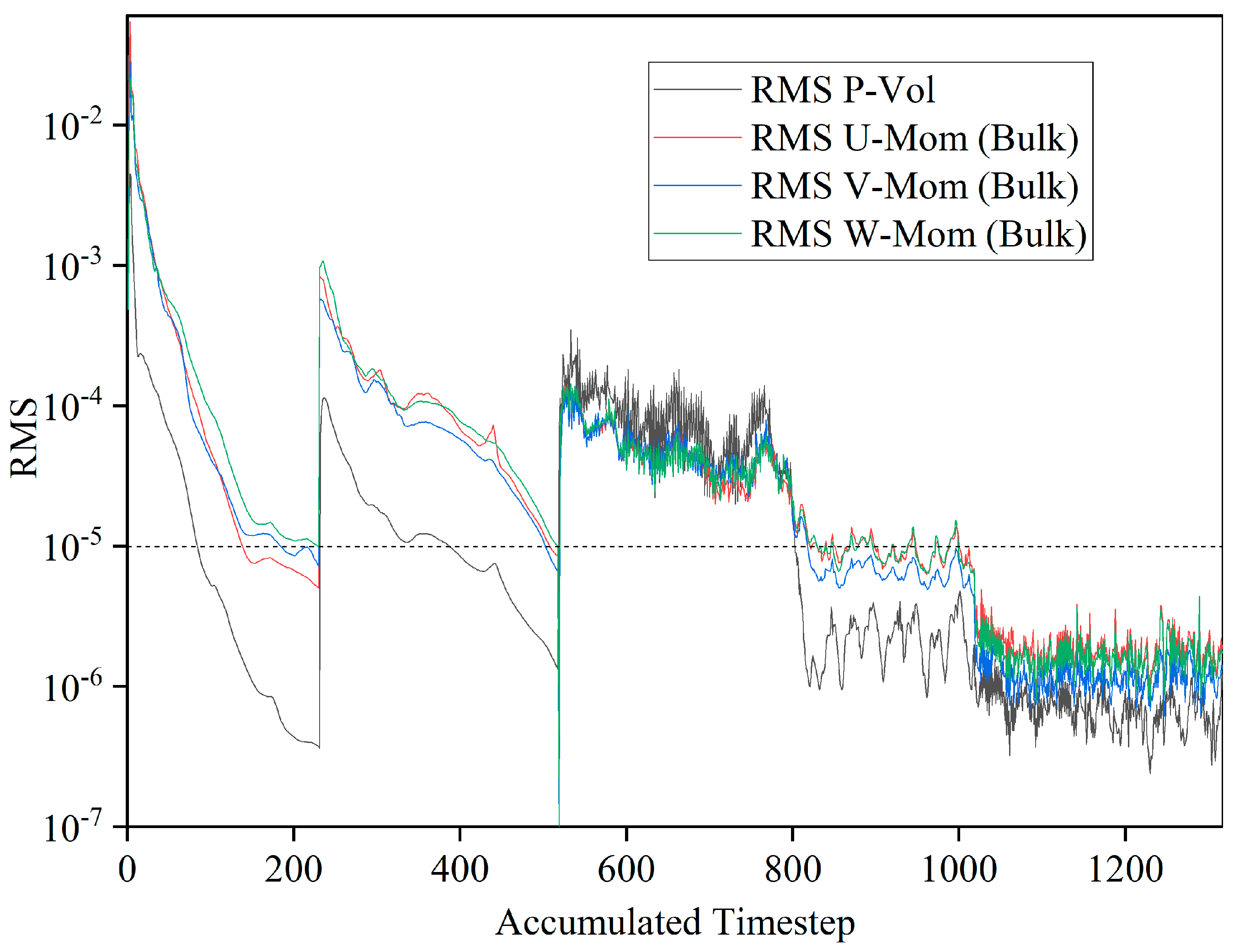
| Convergence target | RMS 1 × 10−4 | RMS 1 × 10−5 | RMS 1 × 10−5 | RMS 1 × 10−5 |
| Fluid properties | ρf = 835.2 kg·m−3, μf = 1.46 × 10−2 Pa·s | |||
| Vapor properties | ρg = 2.1 kg·m−3, μg = 1.2 × 10−5 Pa·s | |||
| Pump status | NP = 2000 rpm | |||
| Turbine status | NT = 20−1800 rpm | |||
| Stator status | NS = 0 | |||
| Reference pressure | pref = 0.4 MPa | |||
| Boundary details | No-slip and smooth wall | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yan, Q.; Liu, C.; Guo, M.; Wei, W. Simulation and Validation of Cavitating Flow in a Torque Converter with Scale-Resolving Methods. Machines 2023, 11, 489. https://doi.org/10.3390/machines11040489
Zhang J, Yan Q, Liu C, Guo M, Wei W. Simulation and Validation of Cavitating Flow in a Torque Converter with Scale-Resolving Methods. Machines. 2023; 11(4):489. https://doi.org/10.3390/machines11040489
Chicago/Turabian StyleZhang, Jiahua, Qingdong Yan, Cheng Liu, Meng Guo, and Wei Wei. 2023. "Simulation and Validation of Cavitating Flow in a Torque Converter with Scale-Resolving Methods" Machines 11, no. 4: 489. https://doi.org/10.3390/machines11040489
APA StyleZhang, J., Yan, Q., Liu, C., Guo, M., & Wei, W. (2023). Simulation and Validation of Cavitating Flow in a Torque Converter with Scale-Resolving Methods. Machines, 11(4), 489. https://doi.org/10.3390/machines11040489








