Drivetrain Response Prediction Using AI-Based Surrogate and Multibody Dynamics Model
Abstract
1. Introduction
- (1)
- The framework for predicting the response of numerical models is extended to a complex and highly nonlinear system, providing much needed insight into the obstacles that arise during the process.
- (2)
- A means of reducing the computations necessary to extract the response of an MBD system is provided through the use of the RNN. This, in turn, results in significant advantages in computation time, especially when considering iterative processes such as model optimization or data mining.
- (3)
- The proposed framework provides a solution for obtaining a smoother time-response of an MBD system by dealing with singularities arising from redundancies in the models.
2. Gear Transmission System
2.1. Vibration Response Analysis
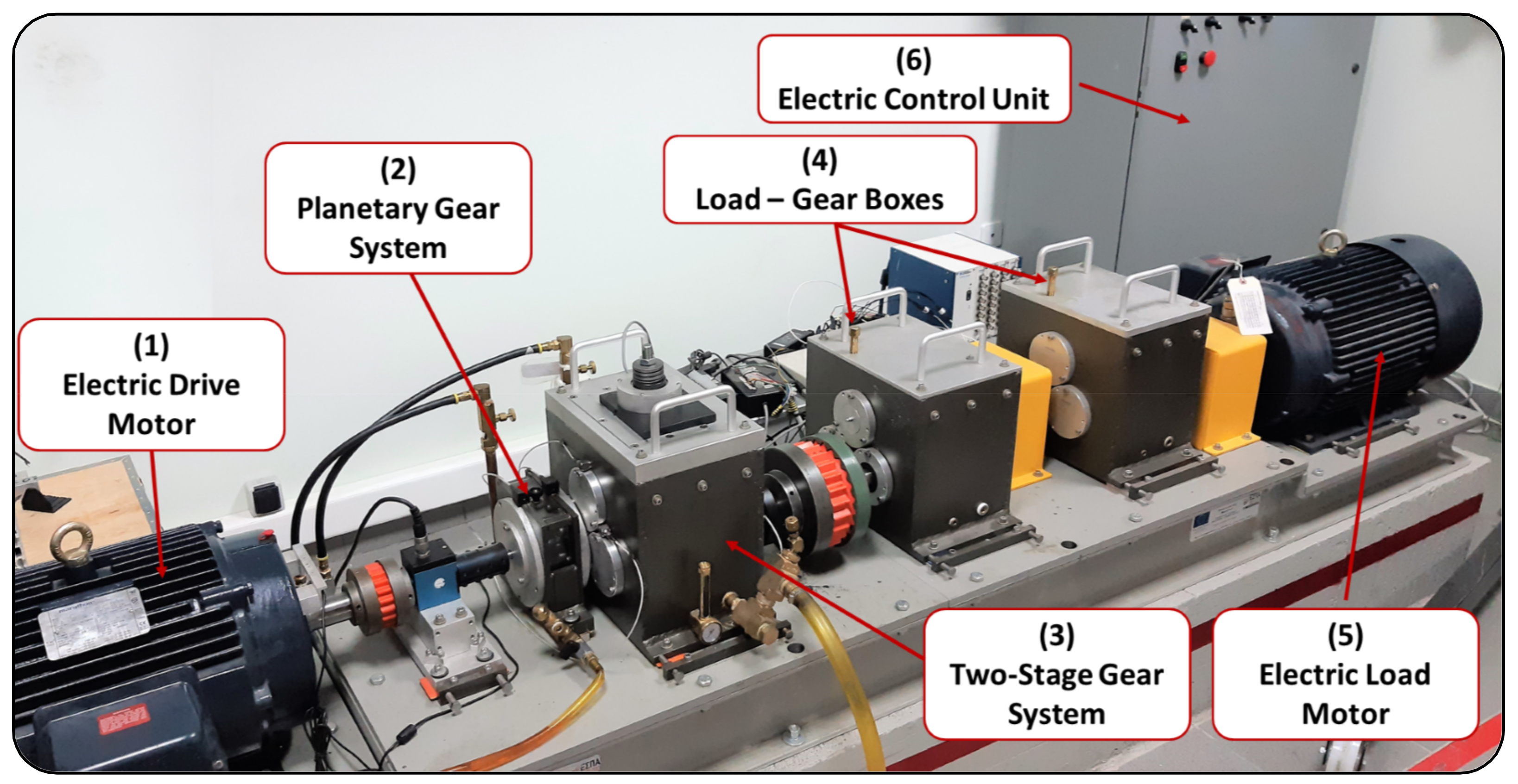
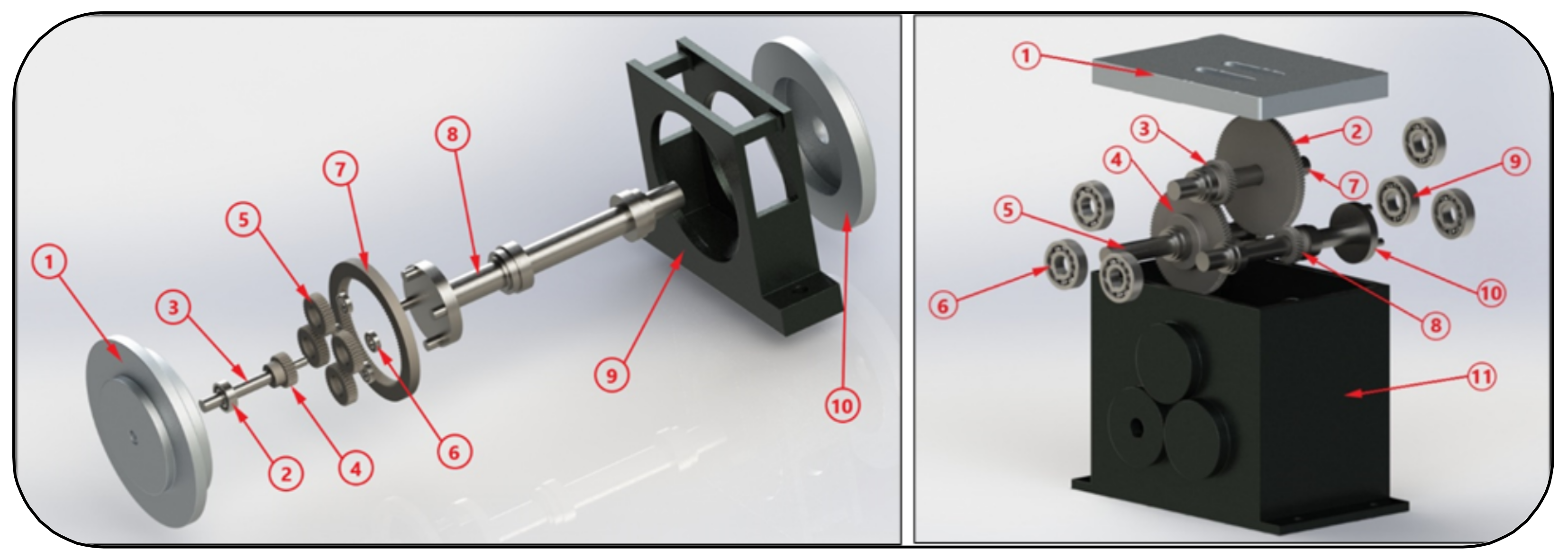
2.2. Experimental Gear Drivetrain
2.3. Gear Drivetrain Multibody Dynamics Model
3. RNN-Based Surrogate Model
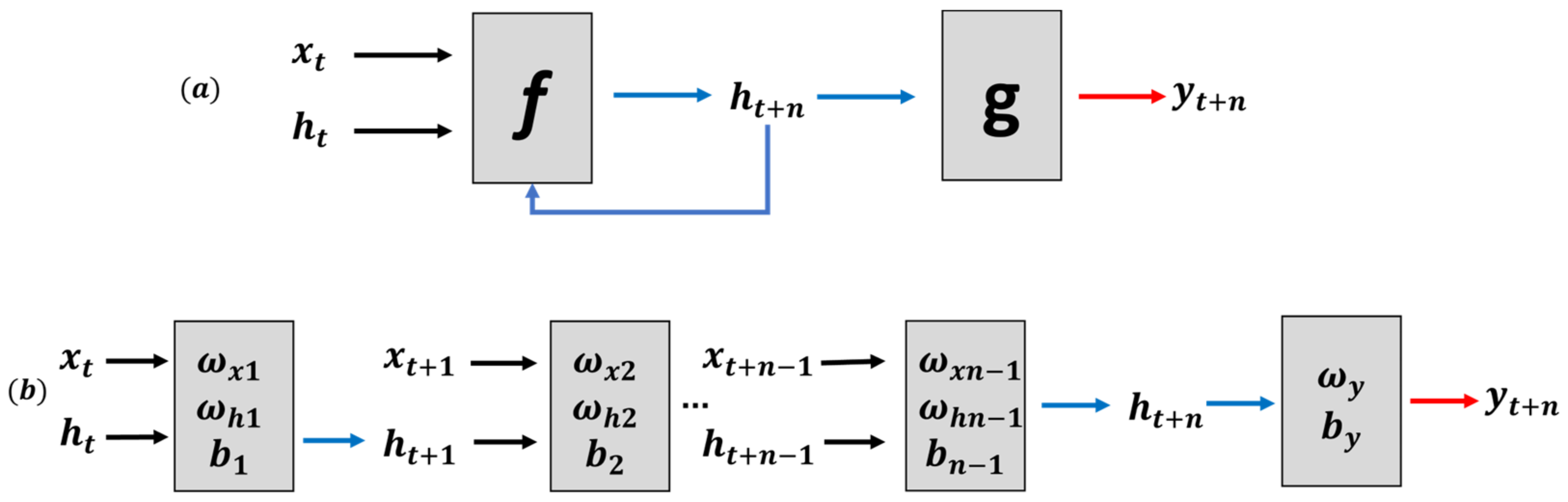
3.1. Recurrent Neural Networks
3.2. RNN Type and Data Pre-Processing
| Algorithm 1: Rolling prediction process |
|
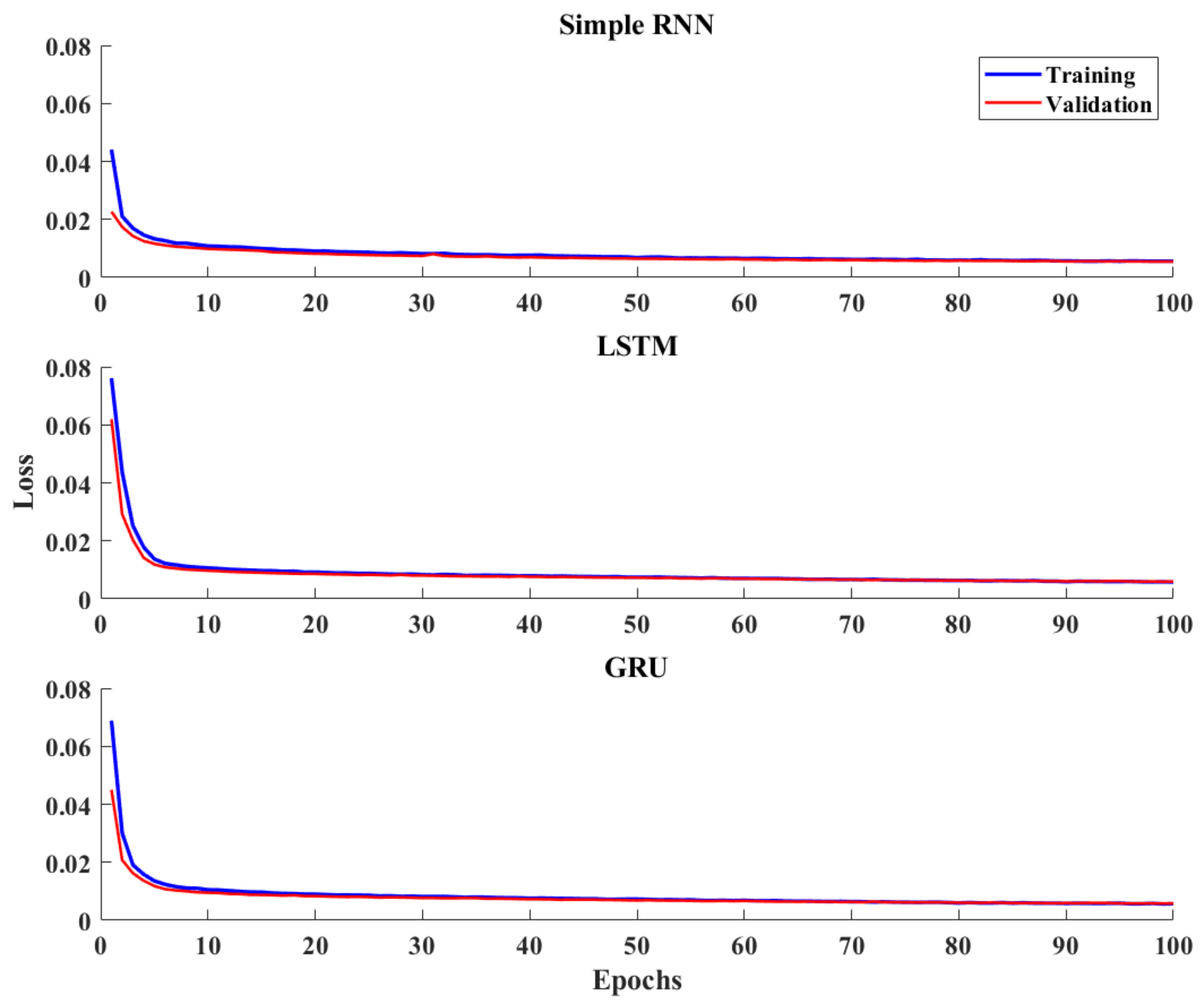
3.3. RNN-Based Model Surrogates
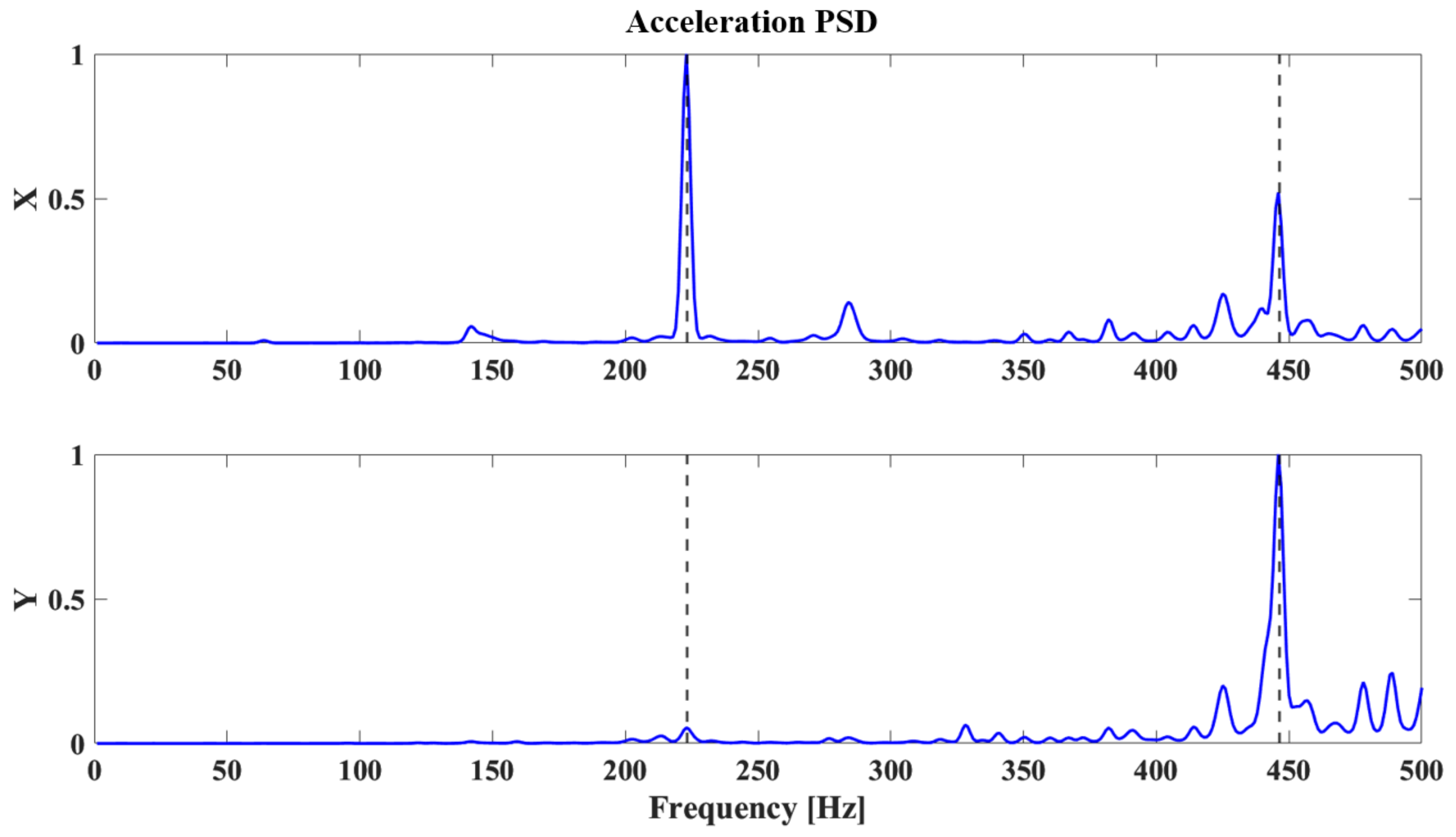
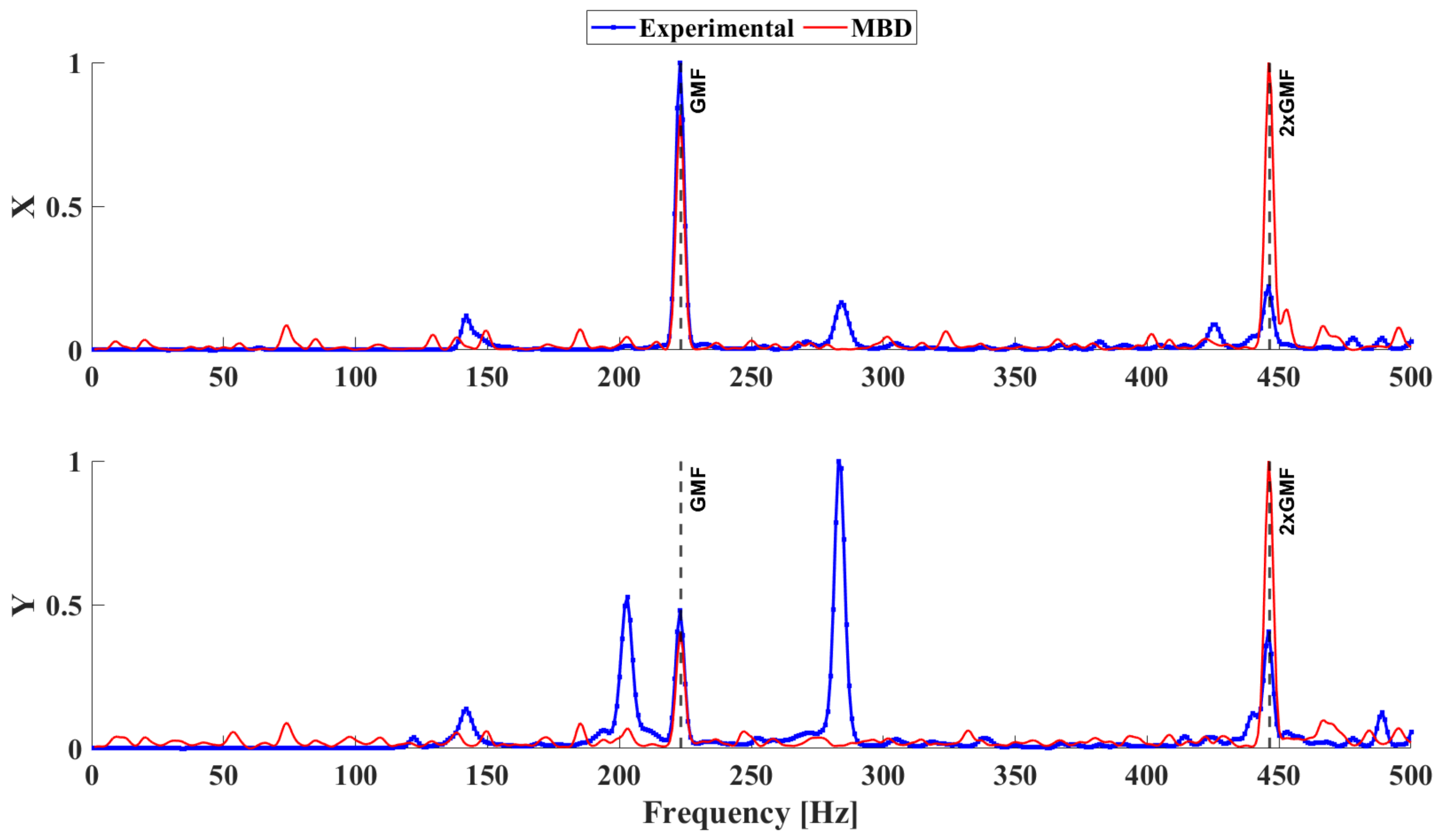
4. Experimental and MBD System Responses
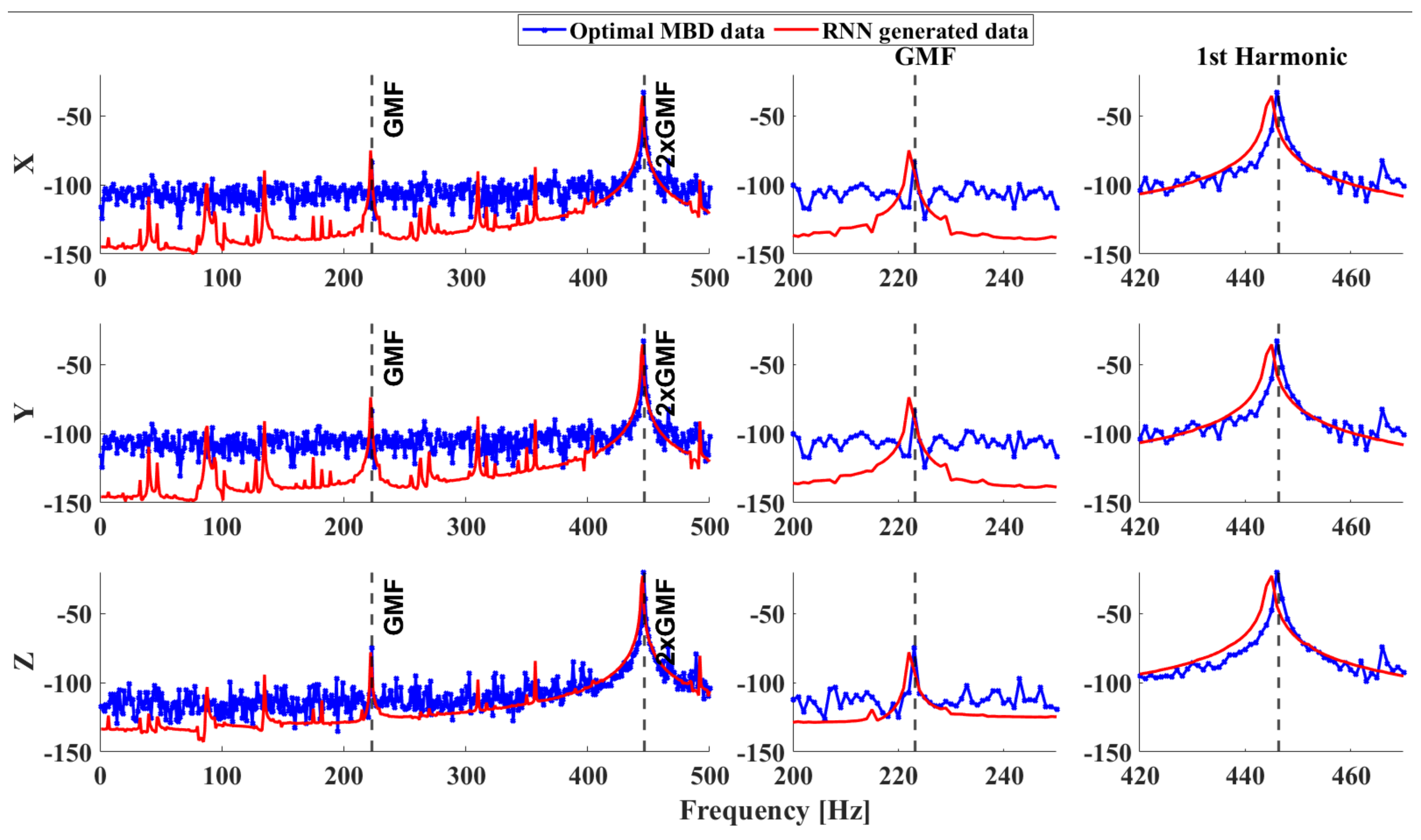
5. RNN-Surrogate Response Predictions
5.1. System Response Rolling Predictions
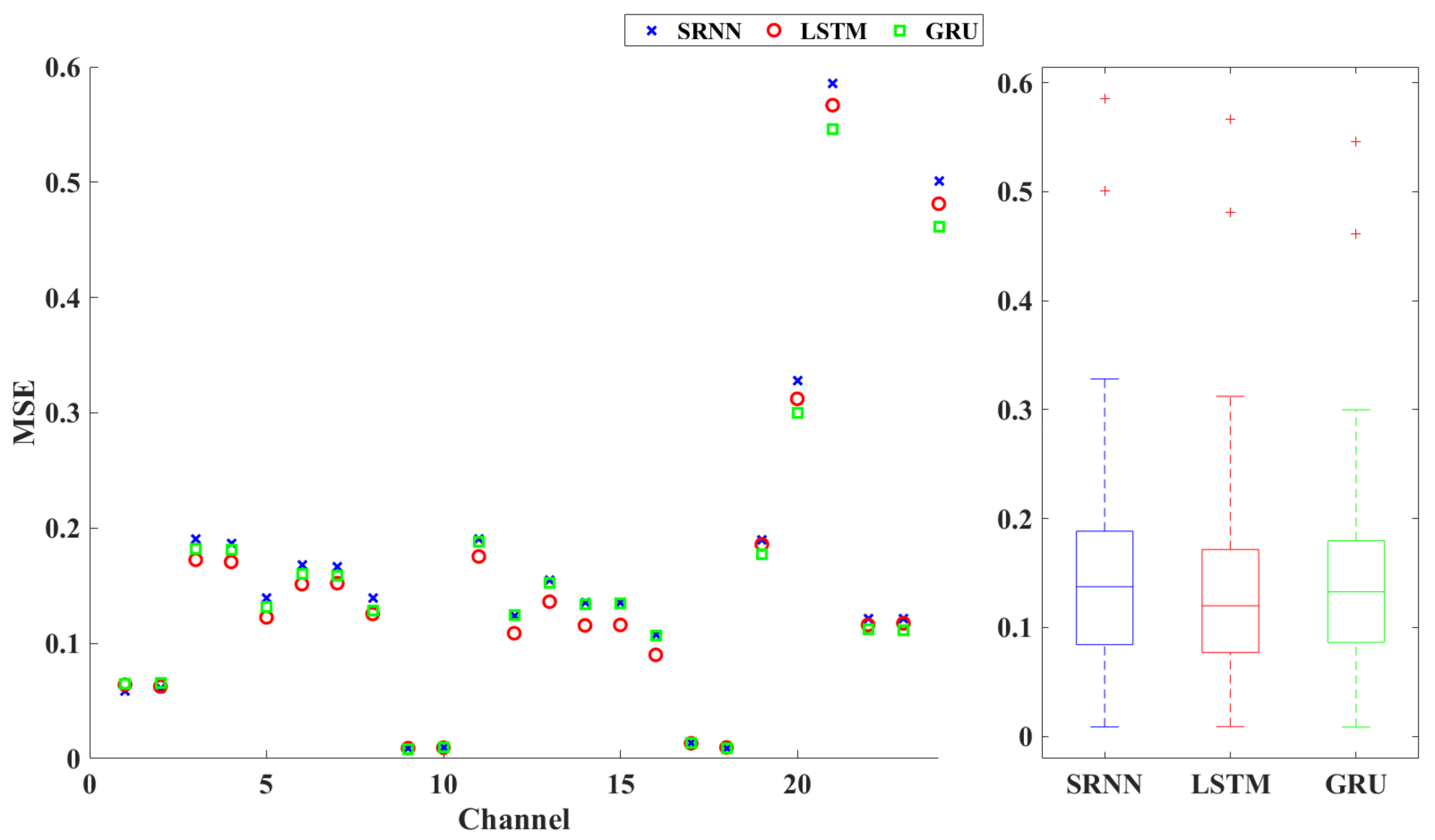
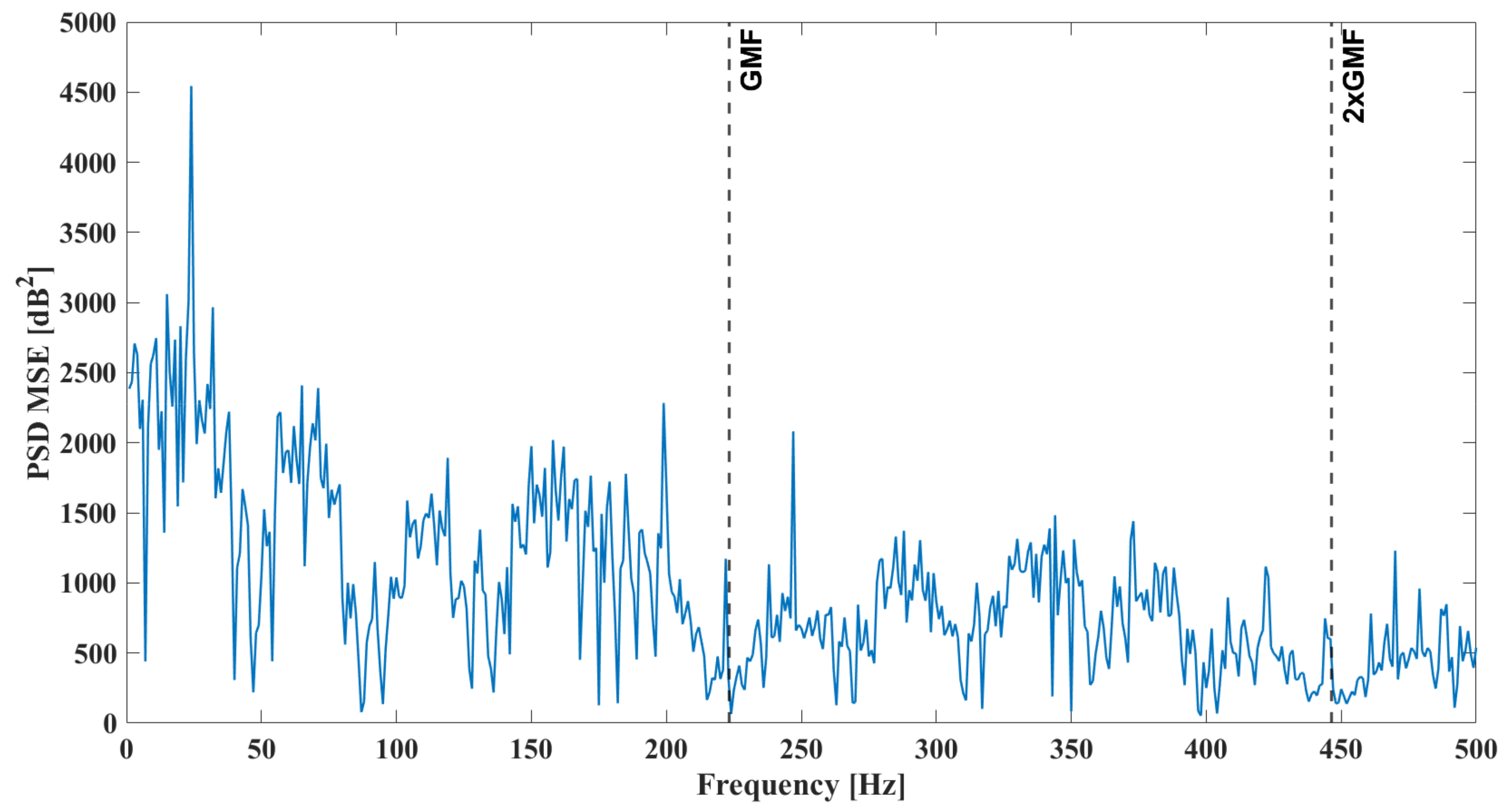
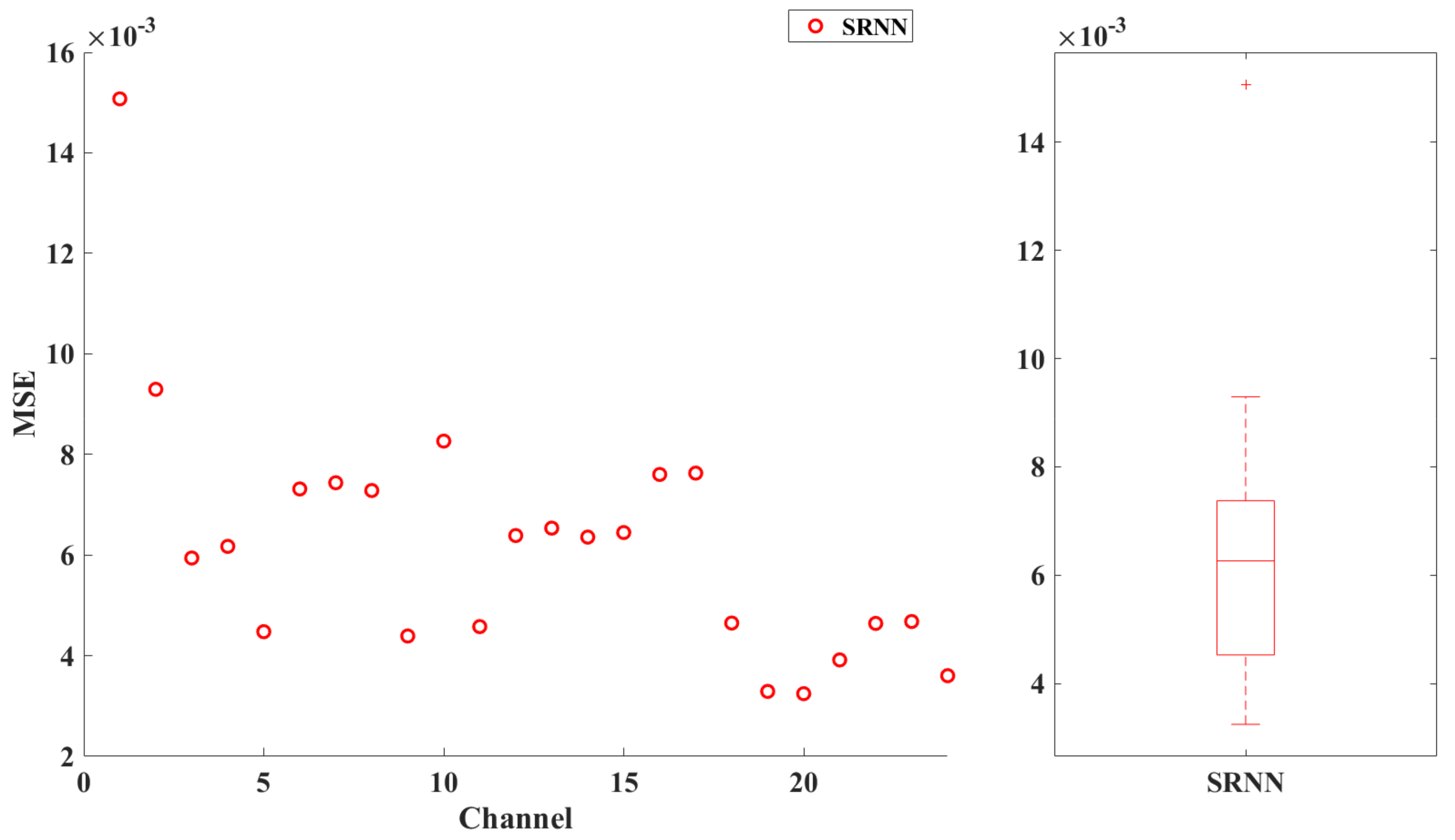
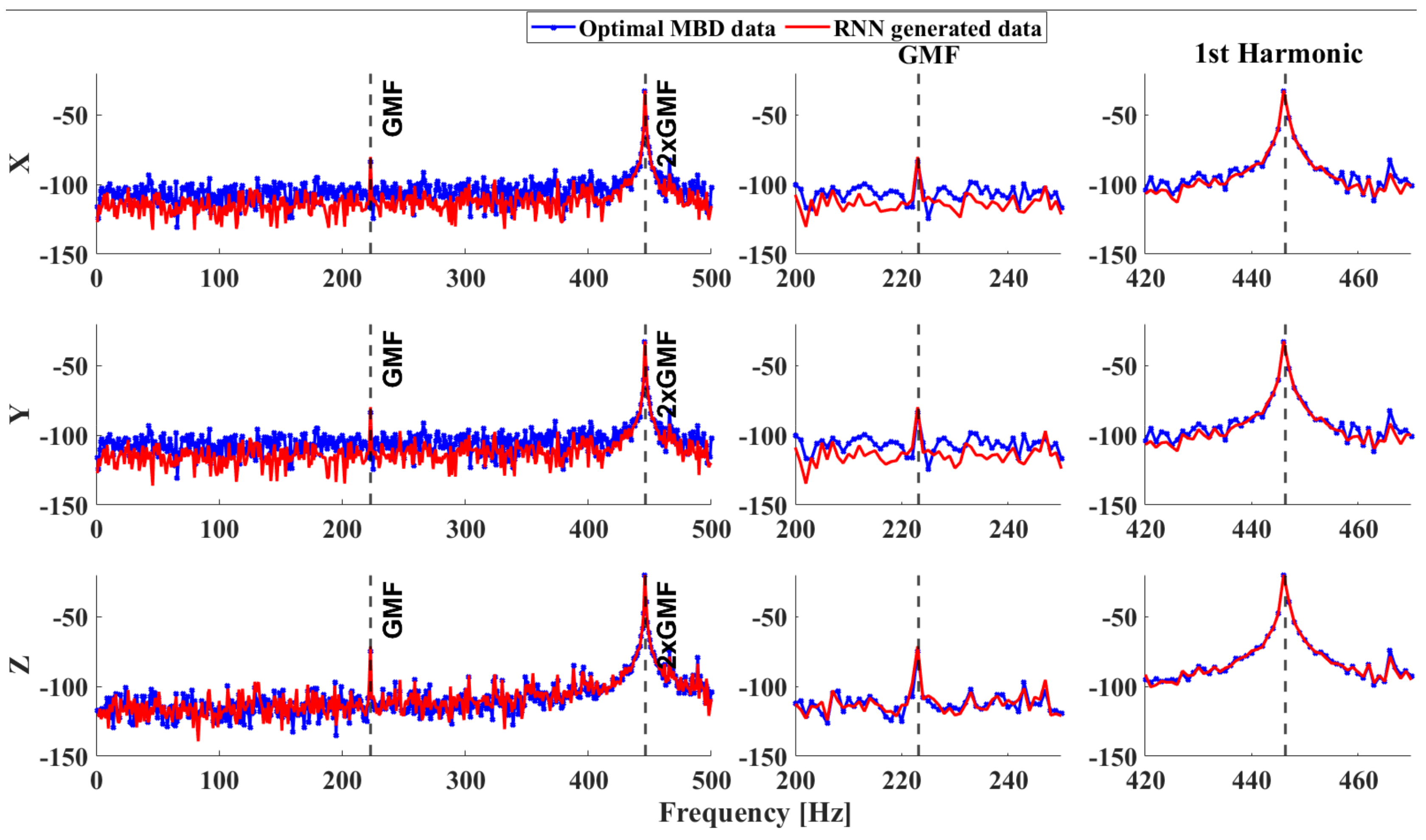
5.2. Predictions on Test Data
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ye, Y.; Huang, P.; Sun, Y.; Shi, D. MBSNet: A deep learning model for multibody dynamics simulation and its application to a vehicle-track system. Mech. Syst. Signal Process. 2021, 157, 107716. [Google Scholar] [CrossRef]
- Han, S.; Choi, H.-S.; Choi, J.; Choi, J.H.; Kim, J.-G. A DNN-based data-driven modeling employing coarse sample data for real-time flexible multibody dynamics simulations. Comput. Methods Appl. Mech. Eng. 2020, 373, 113480. [Google Scholar] [CrossRef]
- Han, X.; Xiang, H.; Li, Y.; Wang, Y. Predictions of vertical train-bridge response using artificial neural network-based surrogate model. Adv. Struct. Eng. 2019, 22, 2712–2723. [Google Scholar] [CrossRef]
- Dye, J.; Lankarani, H. Hybrid Simulation of a Dynamic Multibody Vehicle Suspension System Using Neural Network Modeling Fit of Tire Data. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016. [Google Scholar] [CrossRef]
- Hegedüs, F.; Gáspár, P.; Bécsi, T. Fast Motion Model of Road Vehicles with Artificial Neural Networks. Electronics 2021, 10, 928. [Google Scholar] [CrossRef]
- Choi, H.-S.; An, J.; Han, S.; Kim, J.-G.; Jung, J.-Y.; Choi, J.; Orzechowski, G.; Mikkola, A.; Choi, J.H. Data-driven simulation for general-purpose multibody dynamics using Deep Neural Networks. Multibody Syst. Dyn. 2020, 51, 419–454. [Google Scholar] [CrossRef]
- Greve, L.; van de Weg, B.P. Surrogate modeling of parametrized finite element simulations with varying mesh topology using recurrent neural networks. Array 2022, 14, 100137. [Google Scholar] [CrossRef]
- Singh, S.K.; Das, A.K.; Singh, S.R.; Racherla, V. Prediction of rail-wheel contact parameters for a metro coach using machine learning. Expert Syst. Appl. 2023, 215, 119343. [Google Scholar] [CrossRef]
- Pan, Y.; Sun, Y.; Li, Z.; Gardoni, P. Machine learning approaches to estimate suspension parameters for performance degradation assessment using accurate dynamic simulations. Reliab. Eng. Syst. Saf. 2023, 230, 108950. [Google Scholar] [CrossRef]
- Nie, X.; Min, C.; Pan, Y.; Li, Z.; Królczyk, G. An Improved Deep Neural Network Model of Intelligent Vehicle Dynamics via Linear Decreasing Weight Particle Swarm and Invasive Weed Optimization Algorithms. Sensors 2022, 22, 4676. [Google Scholar] [CrossRef]
- Ye, Z.; Yu, J. Deep morphological convolutional network for feature learning of vibration signals and its applications to gearbox fault diagnosis. Mech. Syst. Signal Process. 2021, 161, 107984. [Google Scholar] [CrossRef]
- Sun, R.-B.; Yang, Z.-B.; Yang, L.-D.; Qiao, B.-J.; Chen, X.-F.; Gryllias, K. Planetary gearbox spectral modeling based on the hybrid method of dynamics and LSTM. Mech. Syst. Signal Process. 2020, 138, 106611. [Google Scholar] [CrossRef]
- Rafiee, J.; Arvani, F.; Harifi, A.; Sadeghi, M. Intelligent condition monitoring of a gearbox using artificial neural network. Mech. Syst. Signal Process. 2007, 21, 1746–1754. [Google Scholar] [CrossRef]
- Azamfar, M.; Singh, J.; Bravo-Imaz, I.; Lee, J. Multisensor data fusion for gearbox fault diagnosis using 2-D convolutional neural network and motor current signature analysis. Mech. Syst. Signal Process. 2020, 144, 106861. [Google Scholar] [CrossRef]
- Shi, J.; Peng, D.; Peng, Z.; Zhang, Z.; Goebel, K.; Wu, D. Planetary gearbox fault diagnosis using bidirectional-convolutional LSTM networks. Mech. Syst. Signal Process. 2022, 162, 107996. [Google Scholar] [CrossRef]
- Wang, T.; Han, Q.; Chu, F.; Feng, Z. Vibration based condition monitoring and fault diagnosis of wind turbine planetary gearbox: A review. Mech. Syst. Signal Process. 2019, 126, 662–685. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Zhang, K.; Hu, S.; Sun, B. Intelligent fault diagnosis of planetary gearbox based on adaptive normalized CNN under complex variable working conditions and data imbalance. Measurement 2021, 180, 109565. [Google Scholar] [CrossRef]
- Sinha, J.K.; Elbhbah, K. A future possibility of vibration based condition monitoring of rotating machines. Mech. Syst. Signal Process. 2012, 34, 231–240. [Google Scholar] [CrossRef]
- Elbhbah, K.; Sinha, J.K. Vibration-based condition monitoring of rotating machines using a machine composite spectrum. J. Sound Vib. 2013, 332, 2831–2845. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, P.; Wang, X.; Liu, Y.; Liu, F.; Zhao, J. Condition monitoring and fault diagnosis of motor bearings using undersampled vibration signals from a wireless sensor network. J. Sound Vib. 2018, 414, 81–96. [Google Scholar] [CrossRef]
- Ruiz-Cárcel, C.; Jaramillo, V.; Mba, D.; Ottewill, J.; Cao, Y. Combination of process and vibration data for improved condition monitoring of industrial systems working under variable operating conditions. Mech. Syst. Signal Process. 2016, 66–67, 699–714. [Google Scholar] [CrossRef]
- Koutsoupakis, J.; Seventekidis, P.; Giagopoulos, D. Machine learning based condition monitoring for gear transmission systems using data generated by optimal multibody dynamics models. Mech. Syst. Signal Process. 2023, 190, 110130. [Google Scholar] [CrossRef]
- Arailopoulos, A.; Giagopoulos, D. Nonlinear constitutive force model selection, update and uncertainty quantification for periodically sequential impact applications. Nonlinear Dyn. 2020, 99, 2623–2646. [Google Scholar] [CrossRef]
- da Silva, M.R.; Marques, F.; da Silva, M.T.; Flores, P. A compendium of contact force models inspired by Hunt and Crossley’s cornerstone work. Mech. Mach. Theory 2021, 167, 104501. [Google Scholar] [CrossRef]
- Seventekidis, P.; Giagopoulos, D. A combined finite element and hierarchical Deep learning approach for structural health monitoring: Test on a pin-joint composite truss structure. Mech. Syst. Signal Process. 2021, 157, 107735. [Google Scholar] [CrossRef]
- Giagopoulos, D.; Arailopoulos, A. Computational framework for model updating of large scale linear and nonlinear finite element models using state of the art evolution strategy. Comput. Struct. 2017, 192, 210–232. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current status and future directions. Int. J. Forecast. 2020, 37, 388–427. [Google Scholar] [CrossRef]
- Chollet, F. Keras. GitHub. Available online: https://github.com/fchollet/keras (accessed on 1 July 2021).
- Lai, Z.; Mylonas, C.; Nagarajaiah, S.; Chatzi, E. Structural identification with physics-informed neural ordinary differential equations. J. Sound Vib. 2021, 508, 116196. [Google Scholar] [CrossRef]
- Cao, Z.; Yao, W.; Peng, W.; Zhang, X.; Bao, K. Physics-Informed MTA-UNet: Prediction of Thermal Stress and Thermal Deformation of Satellites. Aerospace 2022, 9, 603. [Google Scholar] [CrossRef]






| Gears | Teeth | Bearings | Rolling Elements | Rolling Element Diameter | Pitch Diameter |
|---|---|---|---|---|---|
| Sun | 28 | SKF No. 6200 | 8 | 4.762 | 20 |
| Planets | 36 | SKF No. 6800 | 10 | 2.381 | 14.5 |
| Ring gear | 100 | SKF ER-16K | 9 | 7.937 | 38.5 |
| Inlet gear | 29 | ||||
| Middle gear 1 | 100 | ||||
| Middle gear 2 | 36 | ||||
| Outlet gear | 90 | ||||
| Parameter | Two-Stage Gearbox (Contacts 1, 2) | Planetary Gearbox (Contacts 3–10) |
|---|---|---|
| [] | 3.4 × 105 | 1 × 106 |
| [] | 7 | 3.6 |
| [] | 4.7 × 10−3 | 6 × 10−3 |
| [-] | 2 | 2.2 |
| [-] | 0.15 | 0.15 |
| [-] | 0.081 | 0.081 |
| Model | Layer | Activation | No Units/Rate | Output Shape |
|---|---|---|---|---|
| SRNN | SRNN | tanh | 16 | [-,16] |
| Dropout | - | 0.05 | [-,16] | |
| Dense | LeakyReLU | 64 | [-,64] | |
| Dense | LeakyReLU | 64 | [-,64] | |
| Dense | tanh | 24 | [-,24] | |
| LSTM | LSTM | tanh | 16 | [-,16] |
| Dropout | - | 0.05 | [-,16] | |
| Dense | LeakyReLU | 64 | [-,64] | |
| Dense | LeakyReLU | 64 | [-,64] | |
| Dense | tanh | 24 | [-,24] | |
| GRU | GRU | tanh | 16 | [-,16] |
| Dropout | - | 0.05 | [-,16] | |
| Dense | LeakyReLU | 64 | [-,64] | |
| Dense | LeakyReLU | 32 | [-,32] | |
| Dense | tanh | 24 | [-,24] |
| Two-Stage—f1 | Two-Stage—f2 | Planetary—f3 |
|---|---|---|
| 23.251 | 64.442 | 223.125 |
| Ch. | Avg. Error [dB] | Avg. Error [%] | GMF Avg. Error [%] | Ch. | Avg. Error [dB] | Avg. Error [%] | GMF Avg. Error [%] |
|---|---|---|---|---|---|---|---|
| 1 | 30.89 | 31.52 | 2.51 | 13 | 20.56 | 20.20 | 4.05 |
| 2 | 27.83 | 28.27 | 3.25 | 14 | 20.39 | 20.39 | 5.78 |
| 3 | 20.93 | 20.44 | 6.35 | 15 | 20.38 | 20.37 | 5.88 |
| 4 | 21.33 | 20.90 | 5.91 | 16 | 22.23 | 22.29 | 5.85 |
| 5 | 20.86 | 19.92 | 7.69 | 17 | 43.34 | 43.23 | 15.72 |
| 6 | 25.02 | 25.23 | 8.29 | 18 | 40.85 | 39.56 | 25.86 |
| 7 | 25.26 | 25.47 | 7.87 | 19 | 16.33 | 15.069 | 1.82 |
| 8 | 25.90 | 25.99 | 8.87 | 20 | 11.61 | 10.61 | 0.08 |
| 9 | 40.371 | 38.73 | 21.16 | 21 | 8.15 | 7.56 | 2.27 |
| 10 | 46.81 | 45.87 | 2.97 | 22 | 22.29 | 21.36 | 9.13 |
| 11 | 17.69 | 16.95 | 4.32 | 23 | 21.96 | 21.05 | 10.46 |
| 12 | 21.65 | 21.37 | 4.07 | 24 | 8.69 | 8.03 | 2.44 |
| Ch. | Avg. Error [dB] | Avg. Error [%] | GMF Avg. Error [%] | Ch. | Avg. Error [dB] | Avg. Error [%] | GMF Avg. Error [%] |
|---|---|---|---|---|---|---|---|
| 1 | 11.54 | 12.05 | 0.61 | 13 | 4.85 | 4.95 | 0.36 |
| 2 | 9.26 | 9.59 | 0.25 | 14 | 4.30 | 4.48 | 1.40 |
| 3 | 3.93 | 4.03 | 0.35 | 15 | 4.35 | 4.53 | 1.49 |
| 4 | 4.28 | 4.39 | 0.10 | 16 | 5.37 | 5.58 | 1.78 |
| 5 | 3.58 | 3.61 | 0.68 | 17 | 11.84 | 11.93 | 0.48 |
| 6 | 6.89 | 7.07 | 1.88 | 18 | 8.80 | 8.64 | 4.60 |
| 7 | 6.73 | 6.91 | 1.65 | 19 | 4.21 | 3.98 | 1.02 |
| 8 | 7.24 | 7.40 | 0.91 | 20 | 2.76 | 2.63 | 2.30 |
| 9 | 10.16 | 9.83 | 7.49 | 21 | 0.06 | 0.17 | 3.06 |
| 10 | 18.73 | 18.54 | 8.75 | 22 | 7.18 | 6.98 | 0.66 |
| 11 | 3.04 | 3.10 | 0.26 | 23 | 7.33 | 7.12 | 1.22 |
| 12 | 5.46 | 5.54 | 0.35 | 24 | 0.18 | 0.02 | 4.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsoupakis, J.; Giagopoulos, D. Drivetrain Response Prediction Using AI-Based Surrogate and Multibody Dynamics Model. Machines 2023, 11, 514. https://doi.org/10.3390/machines11050514
Koutsoupakis J, Giagopoulos D. Drivetrain Response Prediction Using AI-Based Surrogate and Multibody Dynamics Model. Machines. 2023; 11(5):514. https://doi.org/10.3390/machines11050514
Chicago/Turabian StyleKoutsoupakis, Josef, and Dimitrios Giagopoulos. 2023. "Drivetrain Response Prediction Using AI-Based Surrogate and Multibody Dynamics Model" Machines 11, no. 5: 514. https://doi.org/10.3390/machines11050514
APA StyleKoutsoupakis, J., & Giagopoulos, D. (2023). Drivetrain Response Prediction Using AI-Based Surrogate and Multibody Dynamics Model. Machines, 11(5), 514. https://doi.org/10.3390/machines11050514






