Study on Fatigue Characteristics of Rivets in Bearing Cage for an Aeroengine Transmission System

Abstract

This study focuses on the rivet early fatigue characteristics in a deep-groove ball bearing cage for a transmission system in a turboprop engine. Nonlinear dynamic differential equations for the deep-groove ball bearing with a two-piece cage were developed. The rivet stress was used to identify the early failure mechanism of the rivets. This investigation revealed that by delivering an optimal preload of the rivet causes the two halves of the cage have less misalignment and a lower rivet stress. The fit relationship between the rivet and the rivet bore has a significant influence on the rivet stress. Excessive clearance increases the stress on the head of the rivet, while excessive interference increases the stress on the middle of the rivet. For the 1.5 mm diameter rivet analyzed in this study, the appropriate fit relationship is −0.02 mm–0 mm. A reasonable matching value of the load and the speed and the cage clearance ratio are beneficial to reducing the rivet stress. The impact load acting on the bearing and a ring misalignment can increase the rivet stress.

1. Introduction

Deep-groove ball bearings are widely used in the transmission system of a turboprop engine, in which a cage is riveted together with a cage cover and a cage seat. The two-piece cage has better processing and assembly technology than the integral machined cage. During bearing operation, the cage is disassembled when the riveted structure fails and the bearing cannot run normally. This eventually causes the transmission system to malfunction and seriously affects the safety of the aircraft.

Many scholars have studied the strength and fatigue characteristics of the cage in a rolling bearing. Crawford [1] measured the cage stress value of a deep-groove ball bearing cage by using a variety of inclined angles for the inner ring on the built test bench through a strain gauge. Fang et al. [2] presented the stress concentration factors as functions of the critical design variables for the cages. The effects of the radial balance slots on the maximum stress were studied and recommendations for the slot size and location were provided. Sakaguchi et al. [3,4] investigated the cage stress in the needle roller bearing and the tapered roller bearing by using the finite-element and a component-mode-synthesis method. The results show that one boundary point lying at the center on each bar is appropriate for the effective dynamic analysis model that focuses on the cage stress. This occurs along the pocket corners of the cage, which are broken. Weinzapfel et al. [5] developed a discrete element method and treated the cage as a flexible body to investigate the influence of a flexible cage on bearing dynamics characteristics. Ashtekar et al. [6] developed a 3D explicit finite element model of the cage to investigate the cage dynamics, deformations, and the cage stress of a ball bearing under a variety of operation conditions. Yang et al. [7] analyzed the cage dynamic characteristics of a high-speed cylindrical roller bearing through the rigid-flexible coupling method. The results show that the flexible vibration of the cage makes the cage generate an alternating stress concentration. A flexible analysis of the cage should be conducted for the optimization design during the bearing in high-speed conditions. Cui et al. [8] established a finite element analysis model of the rollers and the cage based on the dynamic analysis of the cylindrical roller bearing. The effect of roller dynamic unbalance on cage stress was investigated. The results show that the roller dynamic unbalance affects the contact status between the rollers and the cage pocket and causes the overall increase in cage stress. Li et al. [9] studied the cage stress of the cylindrical roller bearing at the stop stage. The results show that the cage stress is produced mostly by the centrifugal force when the bearing is working at a constant speed, but at the stop stage, cage stress is caused mostly by the collision force between the rollers and cage, and the value reaches several times of that at a constant speed. Huang et al. [10] researched the influences of the impact loads on the axle bearing cage dynamic characteristics, the contact force between the rollers and cage, and the stress distribution of the cage. The results show that the contact force and the contact frequency between the roller and cage increase significantly with the increase of the impact acceleration, which can speed up the fatigue failure of the cage. To sum up, the cages in these analyses are the integral cages, and the riveted cages are not studied.

He et al. [11] proposed the use of the straight-bar rivet and a double-head hot riveting process. These were selected to solve the problems in which the micro-crack propagation of the rivet semi-circular head causes the rivet head to break when the bearing is subjected to a large impact load, and it also causes a large mechanical vibration. The results show that the riveting reliability of the cage significantly improved. Zhao and He et al. [12,13] analyzed the micro- and macro-fracture morphology of the cage rivets, and they presented the main problems in the process of the cage riveting and bearing application. However, the failure mechanism of the cage rivets was not studied. Qin et al. [14] compared the failure and nonfailure rivet structure of the axle-box-bearing cage in the DF11G locomotive. The results show that an unreasonable improvement of the cage structural design is the main reason for the rivets fracturing. Li et al. [15] determined the failure causes of the rivets through a fractographic analysis, the dimension re-inspection of the rivets, and a metallographic analysis. The results indicate that the rivets fractured with a high-cycle fatigue mode. The fatigue failure was correlated with the fretting damage between the surface of the rivet bar and the wall of the mating hole. He et al. [16] analyzed the cases of the rivet head falling off in a cage for an aeroengine in terms of the structure, fracture, metallographic analysis, and the dimensions of related parts. The results indicate that the excessive clearance of the rivet hole is the main reason for the rivet head to fall off. The double-sided hot riveting process was proposed to avoid the failure of the rivet head falling off. However, only a qualitative analysis was performed in the study, which is due to the lack of a quantitative analysis of the rivet fit relationship. Gu et al. [17] analyzed the causes of the quality problems such as the shape deviation of the rivet head and the riveting process for the wave cage in a ball bearing. Specific countermeasures were given to ensure the cage riveting quality. Wang et al. [18] studied the fault features of the bearing, the physical and chemical analysis, and the size measurement. The results indicate that the ball diameter group and the additional vibration load are the main causes of the cage fracture. In summary, the failure analysis of the cage rivets is mostly carried out from the failure fracture and metallographic structure. Murashkina et al. [19] used the results of the multi-body dynamic simulation of a ball bearing in the cage strength analysis. The stress and deformation of the cage and rivets were presented. However, the fit relationship between the cage and the rivets was not investigated. Zheng et al. [20] proposed a residual stress model to predict the residual stress distribution of the riveted joints. The effects of various parameters, such as the height of the rivet drive head, the hole diameter, and the sheet material property on the residual stress distribution of the sheet faying surface, were investigated. Huang et al. [21] studied the residual stress profile in dissimilar metal sheets joined by a self-piercing rivet and compared it to experimental measurements. Jin et al. [22] presented a constitutive model with damage criteria to describe the deformation behavior during the riveting process and to predict progressive failure. By using the model, the stress distribution during the riveting process, the residual stress variation after riveting and the failure modes of the tensile test were predicted. However, these analyses focus on the riveted hinges. In summary, a few studies have been carried out on the interaction state between the cage and the rivets considering the interaction among the rolling elements, the cage, and the rivets. In practical engineering applications, the size of the rivet is often selected according to experience; however, the matching size of the rivet and the rivet hole and the preload of the two-piece of the cage will have a significant impact on the stress distribution on the rivet, it is difficult to ensure a more accurate matching size and preload in the assembly process. At present, the preload force of the two pieces of the cage and the mating relationship of the rivet are not focused on consideration in the bearing design, and there is a lack of research on the effect of rivet and rivet-hole fitting size and preload on rivet life. The preload force and fitting size range given in the paper have been verified, which can greatly increase the service life of the rivet. In this study, the dynamic analysis model of a ball bearing with a two-piece cage was established. The effect of the rivet preload, the rivet fit relationship, the bearing working conditions, and the cage clearance ratio (defined as the ratio of the cage pocket clearance to the cage guide clearance) on the rivet stress were investigated to reveal the fatigue characteristics of the rivets. The research results can provide an effective theoretical basis for improving the quality and reliability of the cage in the transmission system of the turboprop engine.

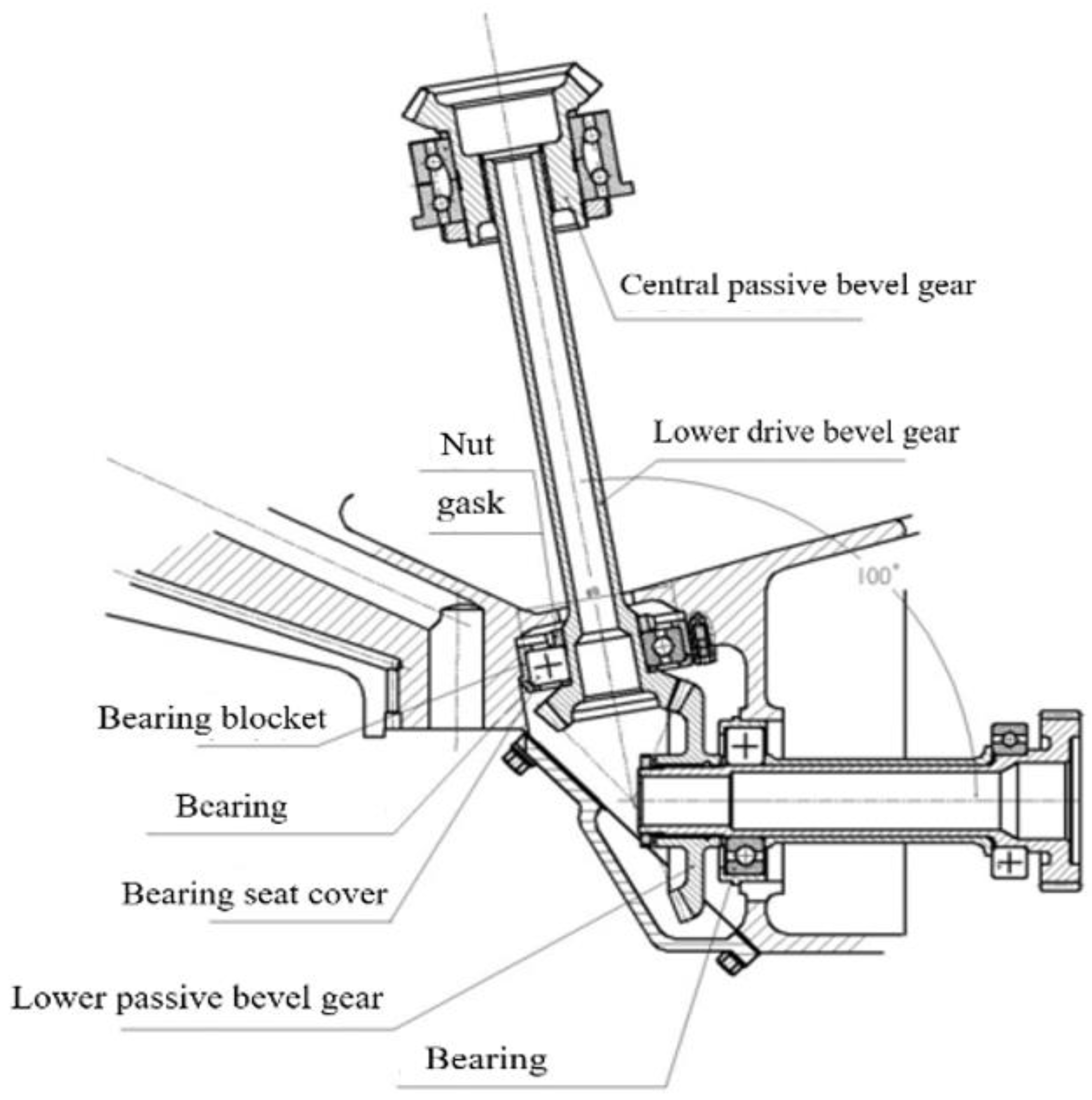
2. Early Fracture Failure Characterization of the Rivets and Cage

The power from the engine first passes through the central passive bevel gear, and the lower active bevel gear is beveled to the lower passive bevel gear through the inner cavity of the lower right rectification support plate of the subhousing, as shown in Figure 1.

The deep-groove ball bearing engine in the transmission system of an turboprop engine has the early fracture failure appearance, as shown in Figure 2. The bevel gears in the transmission system are in good meshing condition, the bearing has no temperature rise feature, and the outer ring has no abnormal damage trace. However, the rivets are broken, and the two-piece cage is separated; some extrusion wear traces can be seen in the cage pockets. According to the field survey, some rivets are broken at the chamfer of head, and the rivet head fell off. Others are broken in the middle, and some of them were bent at the break. Preliminary analysis shows that these rivets are atypical fatigue failures, which are caused by shear force that caused by the circumferential and the axial load between the ball and cage. Under normal circumstances, the fatigue life of the cage is greater than the fatigue life of the bearing raceway. Atypical failure refers to the phenomenon that the cage rivet falls off, causing the cage debris to severely wear the raceway.

In this study, we conducted research to elucidate the rivet early fracture failure mechanism of the deep-groove ball bearing cage in the transmission system.

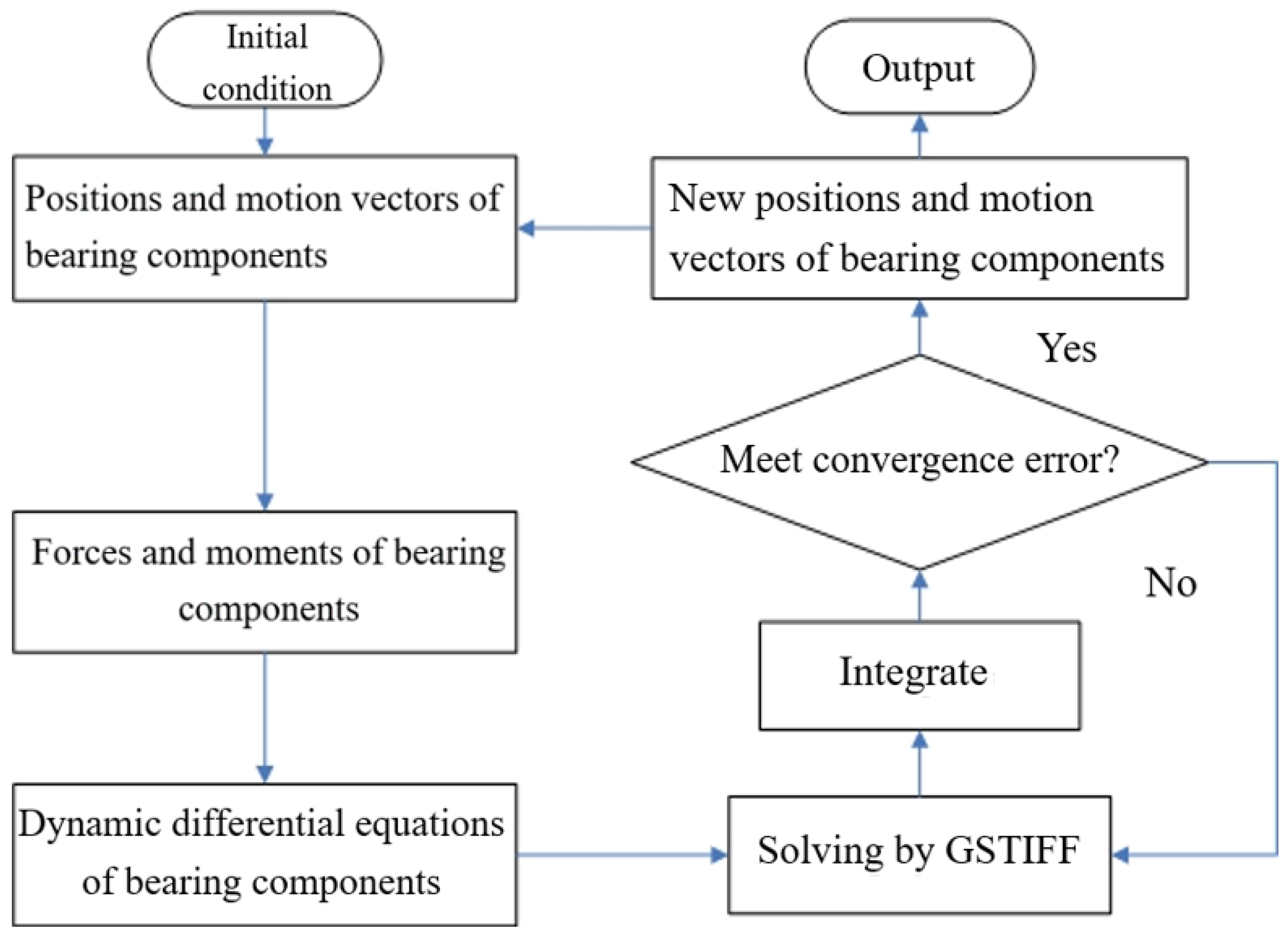
3. Dynamic Analysis Model of a Ball Bearing

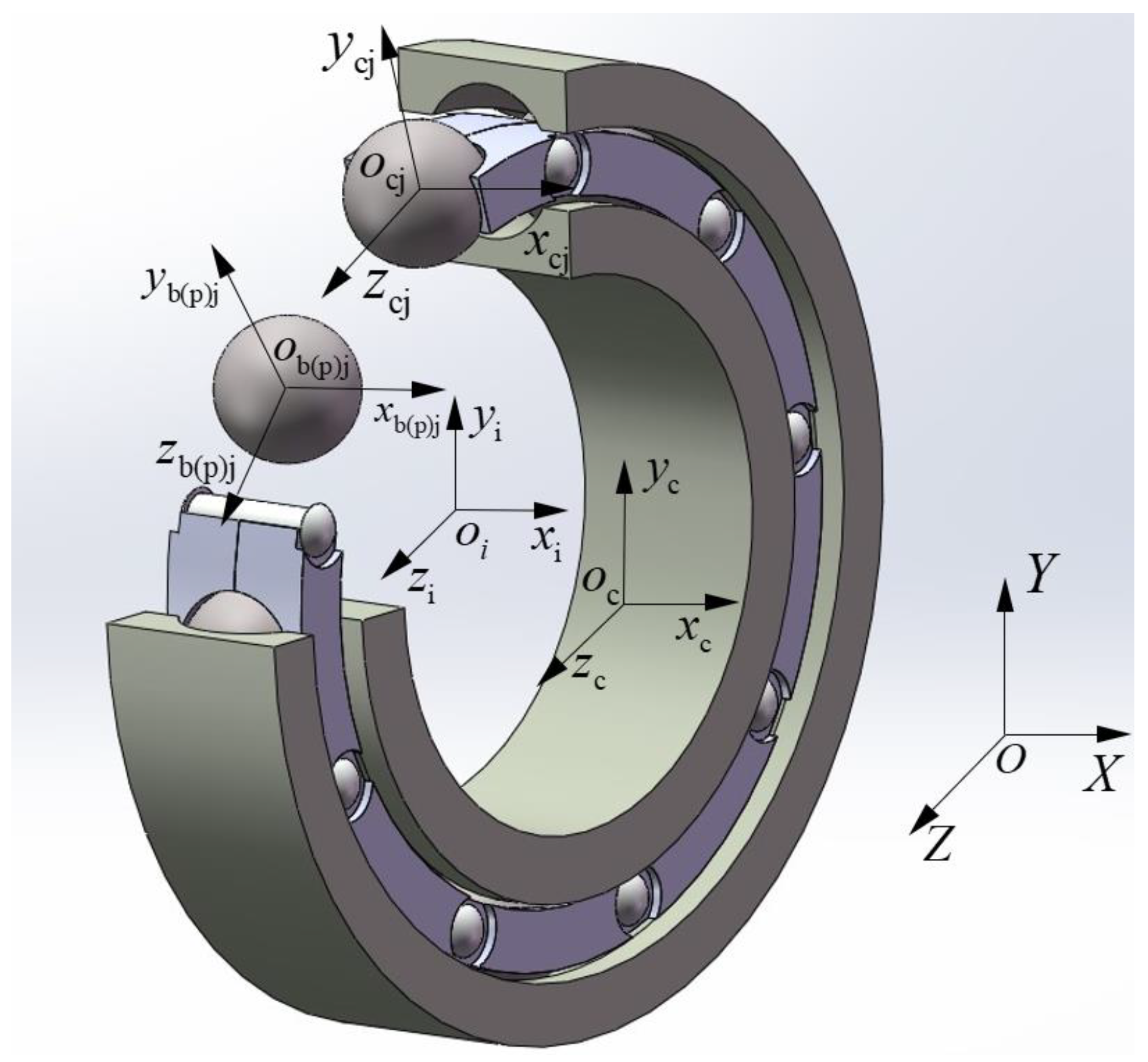
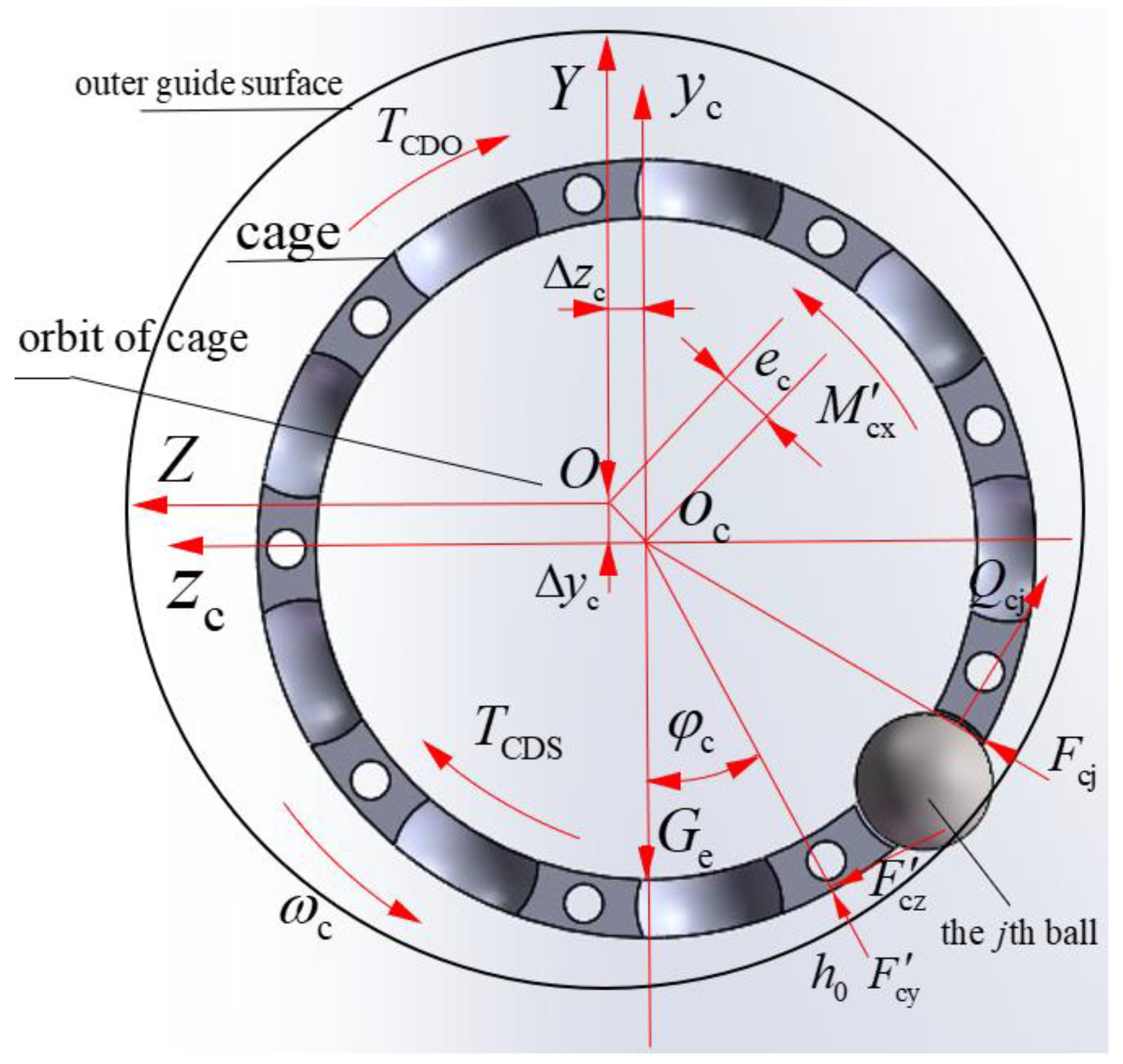
3.1. Define the Coordinate System

The bearing contact interface in line with Hertz contact theory, the bearing’s lubrication type is ‘immersion lubrication’, and the bearing components are regarded as the ideal structure. To describe the movements and interactions of the bearing, five coordinate systems are defined as shown in Figure 3.

To describe the movements and interactions of the bearing, five coordinate systems are defined as shown in Figure 3. The outer ring is fixed, and the inner ring rotates.

(1)

The inertial coordinate system {O; X, Y, Z} is fixed in space, the origin coincides with the bearing center, the X axis coincides with the bearing axis, and the YOZ plane is parallel to the radial plane through the bearing center.

(2)

The inner ring coordinate system {o_i; x_i, y_i, z_i} is fixed with the inner ring, the origin coincides with the inner ring mass center, the x_i axis coincides with the inner ring rotation axis, and the y_io_iz_i plane coincides with the inner ring radial plane through the inner ring mass center.

(3)

The cage coordinate system {o_c; x_c, y_c, z_c} is fixed with the cage, the origin coincides with the cage mass center, the x_c axis coincides with the cage rotation axis, and the y_co_cz_c plane coincides with the cage radial plane through the cage mass center.

(4)

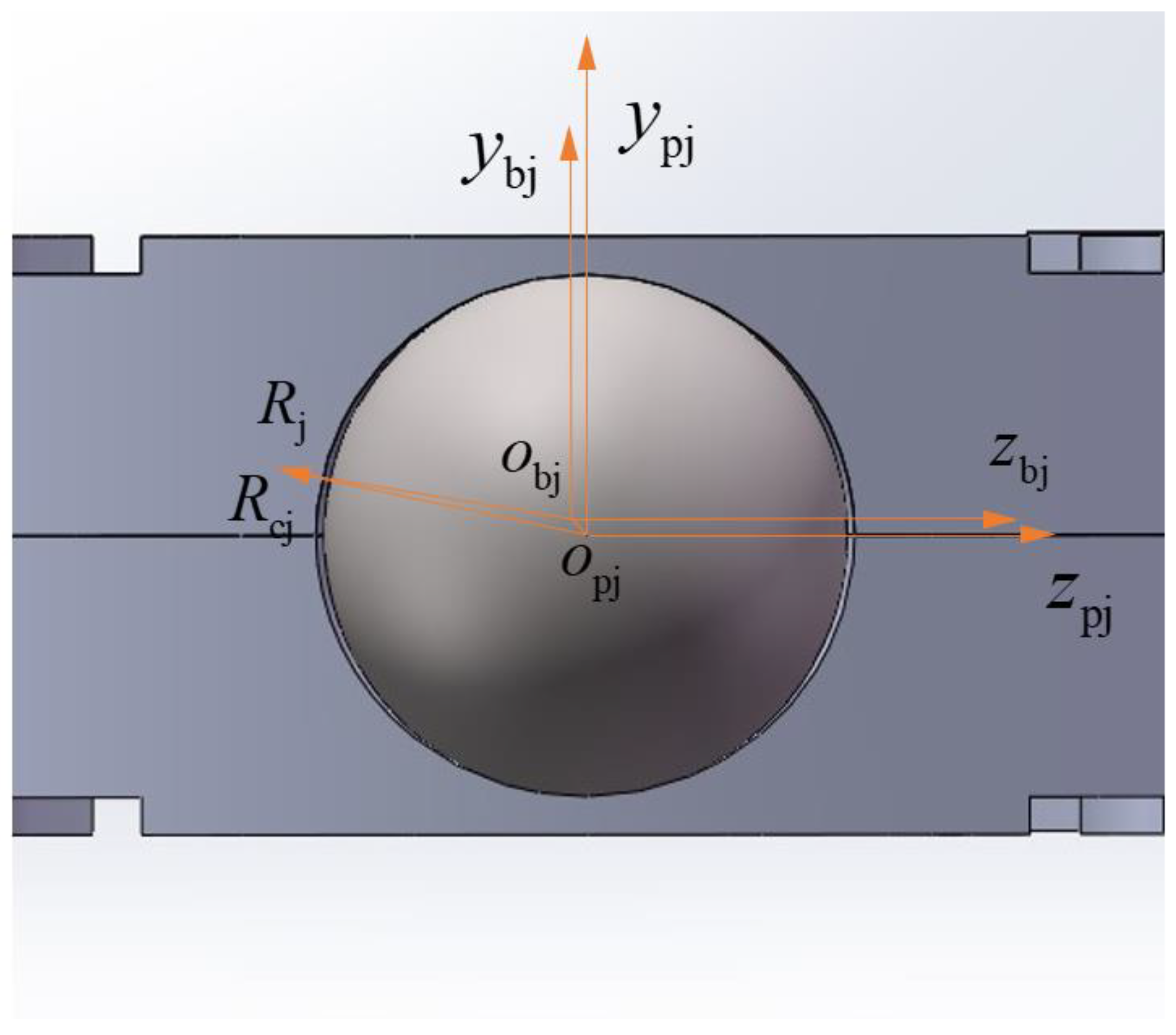
The coordinate system of the cage pocket center {o_pj; x_pj, y_pj, z_pj} is fixed in the jth cage pocket center and it moves with the cage; the origin o_pj coincides with the cage pocket geometric center, y_pj is along the radial direction of the bearing, z_pj is along the circumference direction of the bearing, x_pj is determined by y_pj and z_pj according to the right-hand rule, and each cage pocket has its own local coordinate system.

(5)

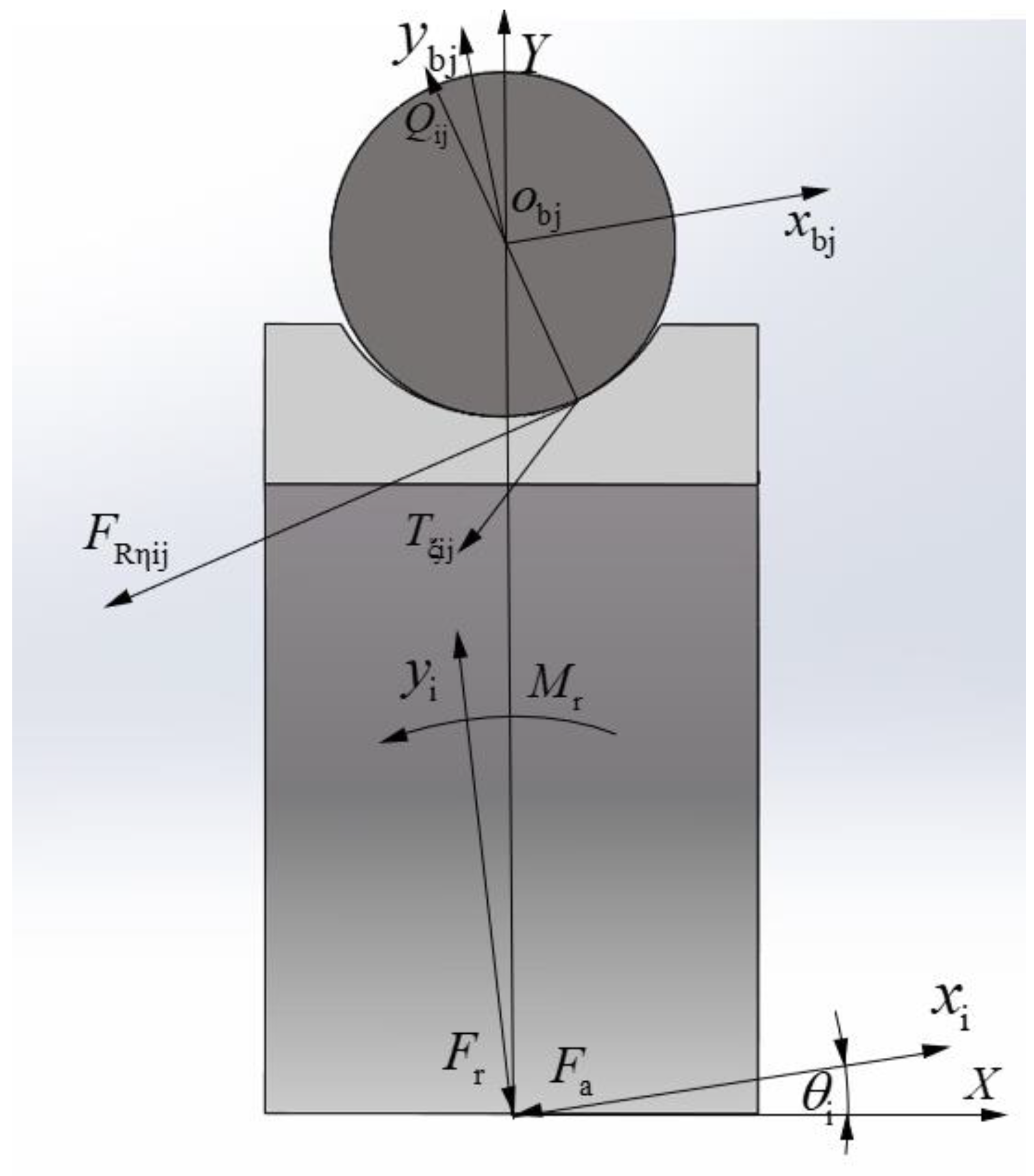
The coordinate system of the jth ball {o_bj; x_bj, y_bj, z_bj} is fixed in the jth ball mass center and it moves with the ball; the origin o_bj coincides with the ball mass center, y_bj is along the radial direction of the bearing, z_bj is along the circumference direction of the bearing, x_bj is determined by y_bj and z_bj according to the right-hand rule, and each ball has its own local coordinate system.

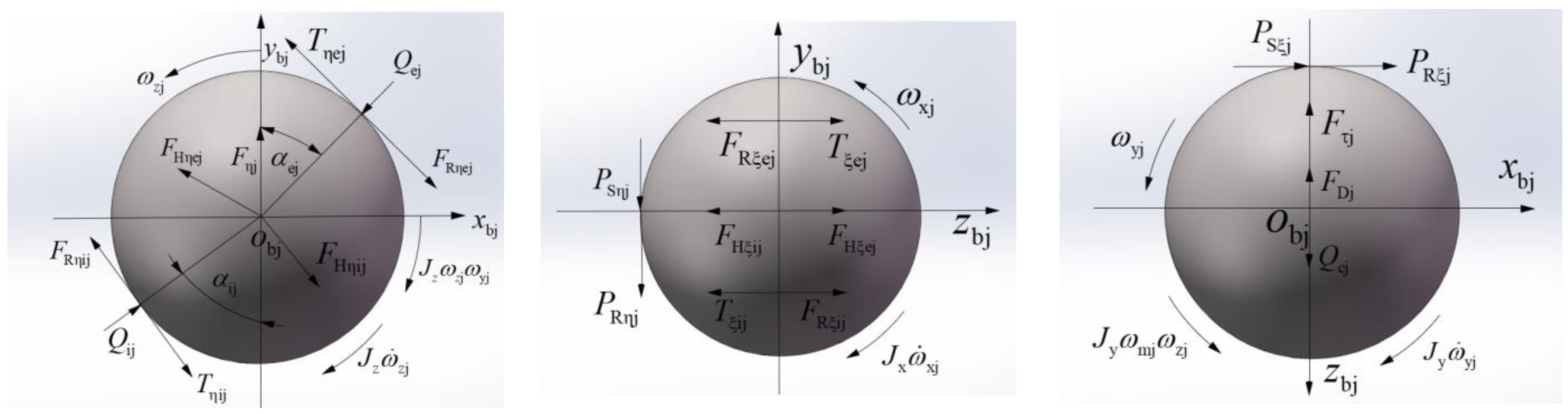
3.2. Nonlinear Dynamic Differential Equations of a Ball

Figure 4 shows the forces and moments that are acting on a ball during bearing operation. Q_ij and Q_ej are the normal contact forces between a ball and the raceway. T_ηij, T_ηej, T_ξij, T_ξej are traction forces on the contact surface, and Q_cj is contact force between a ball and a cage pocket; F_ηj and F_τj are the inertia force components of a ball. P_Rηj and P_Rξj are the rolling frictional forces acting on a ball, and P_Sηj and P_Sξj are the sliding frictional forces acting on a ball. F_Hηij, F_Hηej, F_Hξij, F_Hξej are the horizontal components of the hydrodynamic force that are acting on a ball. F_Rηij, F_Rηej, F_Rξij, F_Rξej are the hydrodynamic frictional forces at the contact inlet zone between a ball and the raceway. J_x, J_y, J_z are component moment of a ball inertia. F_Dj is the aerodynamic resistance acting on a ball by gas–oil mixture. ω_xj, ω_yj, ω_zj are the angular velocity components of a ball; $\dot{\omega }$_xj, $\dot{\omega }$_yj, $\dot{\omega }$_zj are the angular acceleration components of a ball and ω_mj is the orbit speed of the ball. The subscripts η, ξ denote the short axis and long axis of the contact zone, respectively, between the ball and the raceway. The subscripts i and e denote the inner ring and the outer ring, respectively. Finally, the subscript j denotes the jth ball.

The nonlinear dynamic differential equations of a ball in the inertia coordinate system {O; X, Y, Z} can be written as follows

$$\begin{array}{l}{Q}_{\mathrm{ij}}\left[\begin{array}{c}\sin {\alpha }_{\mathrm{ij}}\\ \cos {\alpha }_{\mathrm{ij}}\end{array}\right]-Q_{\mathrm{ej}}\left[\begin{array}{c}\sin {\alpha }_{\mathrm{ej}}\\ \cos {\alpha }_{\mathrm{ej}}\end{array}\right]-T_{\mathsf{\eta }\mathrm{ij}}\left[\begin{array}{c}-\cos {\alpha }_{\mathrm{ij}}\\ \sin {\alpha }_{\mathrm{ij}}\end{array}\right]-T_{\mathsf{\eta }\mathrm{ej}}\left[\begin{array}{c}\cos {\alpha }_{\mathrm{ej}}\\ -\sin {\alpha }_{\mathrm{ej}}\end{array}\right]-F_{\mathrm{R}\mathsf{\eta }\mathrm{ij}}\left[\begin{array}{c}\cos {\alpha }_{\mathrm{ij}}\\ -\sin {\alpha }_{\mathrm{ij}}\end{array}\right]\\ -F_{\mathrm{R}\mathsf{\eta }\mathrm{ej}}\left[\begin{array}{c}-\cos {\alpha }_{\mathrm{ej}}\\ \sin {\alpha }_{\mathrm{ej}}\end{array}\right]-F_{\mathrm{H}\mathsf{\eta }\mathrm{ij}}\left[\begin{array}{c}-\cos {\alpha }_{\mathrm{ij}}\\ \sin {\alpha }_{\mathrm{ij}}\end{array}\right]-F_{\mathrm{H}\mathsf{\eta }\mathrm{ej}}\left[\begin{array}{c}\cos {\alpha }_{\mathrm{ej}}\\ -\sin {\alpha }_{\mathrm{ej}}\end{array}\right]+P_{\mathrm{S}\mathsf{\xi }\mathrm{j}}\left[\begin{array}{c}1\\ -1\end{array}\right]+P_{\mathrm{R}\mathsf{\xi }\mathrm{j}}\left[\begin{array}{c}1\\ -1\end{array}\right]+F_{\mathsf{\eta }\mathrm{j}}\left[\begin{array}{c}0\\ 1\end{array}\right]=m_{\mathrm{b}}{\ddot{y}}_{\mathrm{bj}}\end{array}$$

(1)

$$T_{\mathsf{\xi }\mathrm{ej}}-T_{\mathsf{\xi }\mathrm{ij}}-F_{\mathrm{R}\mathsf{\xi }\mathrm{ej}}+F_{\mathrm{H}\mathsf{\xi }\mathrm{ej}}-F_{\mathrm{H}\mathsf{\xi }\mathrm{ij}}+Q_{\mathrm{cj}}-F_{\mathrm{Dj}}-F_{\mathsf{\tau }\mathrm{j}}=m_{\mathrm{b}}{\ddot{z}}_{\mathrm{bj}}$$

(2)

$$\frac{D_{\mathrm{w}}}{2}\left(\left[\begin{array}{c}\cos {\alpha }_{\mathrm{ej}}\left(T_{\mathsf{\xi }\mathrm{ej}}-T_{\mathrm{R}\mathsf{\xi }\mathrm{ej}}\right)\\ \sin {\alpha }_{\mathrm{ej}}\left(F_{\mathrm{R}\mathsf{\xi }\mathrm{ej}}-T_{\mathsf{\xi }\mathrm{ej}}\right)\\ 0\end{array}\right]+\left[\begin{array}{c}\cos {\alpha }_{\mathrm{ij}}\left(T_{\mathsf{\xi }\mathrm{ij}}-F_{\mathrm{R}\mathsf{\xi }\mathrm{ij}}\right)\\ \sin {\alpha }_{\mathrm{ij}}\left(F_{\mathrm{R}\mathsf{\xi }\mathrm{ij}}-T_{\mathsf{\xi }\mathrm{ij}}\right)\\ T_{\mathsf{\eta }\mathrm{ij}}-F_{\mathrm{R}\mathsf{\eta }\mathrm{ij}}\end{array}\right]+\left[\begin{array}{c}-P_{\mathrm{S}\mathsf{\eta }\mathrm{j}}-P_{\mathrm{R}\mathsf{\eta }\mathrm{j}}\\ -P_{\mathrm{S}\mathsf{\xi }\mathrm{j}}-P_{\mathrm{R}\mathsf{\xi }\mathrm{j}}\\ T_{\mathsf{\eta }\mathrm{ej}}-F_{\mathrm{R}\mathsf{\eta }\mathrm{ej}}\end{array}\right]\right)=\left[\begin{array}{c}{J}_{\mathrm{x}}{\dot{\omega }}_{\mathrm{xj}}\\ -J_{\mathrm{y}}{\dot{\omega }}_{\mathrm{yj}}\\ -J_{\mathrm{z}}{\dot{\omega }}_{\mathrm{zj}}\end{array}\right]+\left[\begin{array}{c}0\\ J_{\mathrm{y}}{\omega }_{\mathrm{mj}}{\omega }_{\mathrm{zj}}\\ -J_{\mathrm{z}}{\omega }_{\mathrm{mj}}{\omega }_{\mathrm{yj}}\end{array}\right]$$

(3)

where m_b is the ball mass; ${\ddot{x}}_{\mathrm{b}\mathrm{y}}$, ${\ddot{y}}_{\mathrm{b}\mathrm{y}}$, ${\ddot{z}}_{\mathrm{b}\mathrm{y}}$ are the accelerate components of a ball mass center; and D_w is the ball diameter.

3.3. Nonlinear Dynamic Differential Equations of the Cage

Assuming the displacements of the ball center coordinate {o_bj; x_bj, y_bj, z_bj} relative to the cage pocket center coordinate {o_pj; x_pj, y_pj, z_pj} is Δx_bcj, Δy_bcj, Δz_bcj, which is expressed as follows.

$$S_{\mathrm{bcj}}=\sqrt{x_{\mathrm{bcj}}^2+y_{\mathrm{bcj}}^2+z_{\mathrm{bcj}}^2}$$

(4)

Because the shape of cage pocket is cylindrical, the elastic deformation between the ball and the pocket can be expressed by the overlap of the contact surface between the pocket hole and the ball, as shown in Figure 5. The elastic deformation can be written as follows.

$${\delta }_{\mathrm{cj}}=S_{\mathrm{bcj}}-\left(R_{\mathrm{cj}}-R_{\mathrm{j}}\right)$$

(5)

where δ_cj is the elastic deformation, R_cj and R_j are the pocket radius and the ball radius, respectively.

Due to the misalignment of the bearing rings in the installation process and the overturning moment during operation, contact between the ball and the cage pocket does not always occur along the middle part of the pocket. However, it will generate a certain axial offset as shown in Figure 6. The normal force Q_cj between the ball and the cage pocket can be divided into the axial load Q_cxj and the circumferential load Q_czj. A certain amount of dislocation that is generated between the two-piece cage under the action of the contact load Q_cj, is expressed as δ_bj.

The way of the cage is guided by the outer ring is widely used in high-speed ball bearings. The forces between the cage and the guiding ring are caused by hydrodynamic effect of the lubricant, which can be analyzed by the short sliding bearing theory, as illustrated in Figure 7. $F_{\mathrm{c}\mathrm{y}}^{\prime }$, $F_{\mathrm{c}\mathrm{z}}^{\prime }$, and $M_{\mathrm{c}\mathrm{x}}^{\prime }$ represent the two orthogonal components and moments of the distribution pressure of the hydrodynamic oil film that is acting on the cage. F_cj is the friction force between the ball and the cage pocket. F_cj is the vector sum of P_Rηj and P_Rξj. T_CDO and T_CDS represent the retardation moment that acts on the cylinder face and end face of the cage. G_c is the cage gravity. e_c is the cage eccentricity. Δy_c and Δz_c are the cage displacements, and φ_c is the azimuth angle of the cage. Finally, h₀ is the minimum oil film thickness between the cage and the guiding ring. The variation of the lubrication state between the cage and the guide surface is determined and changed by analyzing the time of the oil film state.

The nonlinear dynamic differential equations of the cage in the inertia coordinate system {O; X, Y, Z} are written as follows.

$${\displaystyle \sum _{j=1}^Z(\left[\begin{array}{c}{P}_{\mathrm{S}\mathsf{\eta }\mathrm{j}}\\ P_{\mathrm{S}\mathsf{\xi }\mathrm{j}}\cos {\phi }_{\mathrm{j}}\\ P_{\mathrm{S}\mathsf{\xi }\mathrm{j}}\sin {\phi }_{\mathrm{j}}\end{array}\right]+\left[\begin{array}{c}{P}_{\mathrm{R}\mathsf{\eta }\mathrm{j}}\\ P_{\mathrm{R}\mathsf{\xi }\mathrm{j}}\cos {\phi }_{\mathrm{j}}\\ P_{\mathrm{R}\mathsf{\xi }\mathrm{j}}\sin {\phi }_{\mathrm{j}}\end{array}\right]+\left[\begin{array}{c}{Q}_{\mathrm{cxj}}\\ Q_{\mathrm{cyj}}\\ -Q_{\mathrm{czj}}\end{array}\right])}-\left[\begin{array}{c}0\\ G_{\mathrm{c}}\\ 0\end{array}\right]=\left[\begin{array}{c}{m}_{\mathrm{c}}{\ddot{x}}_{\mathrm{cx}}\\ m_{\mathrm{c}}{\ddot{y}}_{\mathrm{cy}}\\ m_{\mathrm{c}}{\ddot{z}}_{\mathrm{cz}}\end{array}\right]$$

(6)

$${\displaystyle \sum _{j=1}^Z\left[\begin{array}{c}\left(P_{\mathrm{S}\mathsf{\xi }\mathrm{j}}+P_{\mathrm{R}\mathsf{\xi }\mathrm{j}}\right)\frac{D_{\mathrm{w}}}{2}-Q_{\mathrm{cj}}\frac{d_{\mathrm{mj}}}{2}\\ \left(P_{\mathrm{S}\mathsf{\eta }\mathrm{j}}+P_{\mathrm{R}\mathsf{\eta }\mathrm{j}}\right)\frac{d_{\mathrm{mj}}}{2}\sin {\phi }_{\mathrm{j}}\\ \left(P_{\mathrm{S}\mathsf{\eta }\mathrm{j}}+P_{\mathrm{R}\mathsf{\eta }\mathrm{j}}\right)\frac{d_{\mathrm{mj}}}{2}\cos {\phi }_{\mathrm{j}}\end{array}\right]}+\left[\begin{array}{c}-T_{\mathrm{CDO}}-T_{\mathrm{CDS}}+{M^{\prime }}_{\mathrm{cx}}\\ -{F^{\prime }}_{\mathrm{cy}}\cos {\phi }_{\mathrm{c}}+{F^{\prime }}_{\mathrm{cz}}\sin {\phi }_{\mathrm{c}}\\ {F^{\prime }}_{\mathrm{cy}}\sin {\phi }_{\mathrm{c}}+{F^{\prime }}_{\mathrm{cz}}\cos {\phi }_{\mathrm{c}}\end{array}\right]=\left[\begin{array}{c}{J}_{\mathrm{cx}}{\dot{\omega }}_{\mathrm{cx}}\\ J_{\mathrm{cy}}{\dot{\omega }}_{\mathrm{cy}}\\ J_{\mathrm{cz}}{\dot{\omega }}_{\mathrm{cz}}\end{array}\right]-\left[\begin{array}{c}\left(J_{\mathrm{cy}}-J_{\mathrm{cz}}\right){\omega }_{\mathrm{cy}}{\omega }_{\mathrm{cz}}\\ \left(J_{\mathrm{cz}}-J_{\mathrm{cx}}\right){\omega }_{\mathrm{cx}}{\omega }_{\mathrm{cz}}\\ \left(J_{\mathrm{cx}}-J_{\mathrm{cy}}\right){\omega }_{\mathrm{cx}}{\omega }_{\mathrm{cy}}\end{array}\right]$$

(7)

where m_c is the cage mass; ${\ddot{x}}_{\mathrm{c}\mathrm{x}}$, ${\ddot{y}}_{\mathrm{c}\mathrm{y}}$, ${\ddot{z}}_{\mathrm{c}\mathrm{z}}$ are the acceleration components of the cage; J_cx, J_cy, J_cz represent the component moment of the cage inertia; ω_cx, ω_cy, ω_cz are angular velocity components of the cage; ${\dot{\omega }}_{\mathrm{c}\mathrm{x}}$, ${\dot{\omega }}_{\mathrm{c}\mathrm{y}}$, ${\dot{\omega }}_{\mathrm{c}\mathrm{z}}$ are the angular acceleration components of the cage; Z is the number of balls; d_mj is the pitch diameter of the ball during operation; and φ_j is azimuth angle of the ball.

3.4. Nonlinear Dynamic Differential Equations of the Inner Ring

Figure 8 shows the forces acting on inner ring during operation. F_r, F_a, and M_r are the external loads that are acting on the inner ring, and θ_i is the tilt angle of the inner ring.

The nonlinear dynamic differential equations of the inner ring in the inertia coordinate system {O; X, Y, Z} are written as follows.

$${\displaystyle \sum _{j=1}^Z\left[\begin{array}{c}{Q}_{\mathrm{ij}}\sin {\alpha }_{\mathrm{ij}}-F_{\mathrm{R}\mathsf{\eta }\mathrm{ij}}\cos {\alpha }_{\mathrm{ij}}\\ \left(Q_{\mathrm{ij}}\cos {\alpha }_{\mathrm{ij}}+F_{\mathrm{R}\mathsf{\eta }\mathrm{ij}}\sin {\alpha }_{\mathrm{ij}}\right)\cos {\phi }_{\mathrm{j}}\\ \left(Q_{\mathrm{ij}}\cos {\alpha }_{\mathrm{ij}}+F_{\mathrm{R}\mathsf{\eta }\mathrm{ij}}\sin {\alpha }_{\mathrm{ij}}\right)\sin {\phi }_{\mathrm{j}}\end{array}\right]}+\left[\begin{array}{c}{F}_{\mathrm{rx}}\\ F_{\mathrm{ry}}\\ F_{\mathrm{rz}}\end{array}\right]+\left(T_{\mathsf{\xi }\mathrm{ij}}-F_{\mathrm{R}\mathsf{\xi }\mathrm{ij}}\right)\left[\begin{array}{c}0\\ \sin {\phi }_{\mathrm{j}}\\ \cos {\phi }_{\mathrm{j}}\end{array}\right]=\left[\begin{array}{c}{m}_{\mathrm{i}}{\ddot{x}}_{\mathrm{i}}\\ m_{\mathrm{i}}{\ddot{y}}_{\mathrm{i}}\\ m_{\mathrm{i}}{\ddot{z}}_{\mathrm{i}}\end{array}\right]$$

(8)

$$\begin{array}{l}{\displaystyle \sum _{j=1}^Z\left(0.5d_{\mathrm{mj}}-0.5D_{\mathrm{w}}{f}_{\mathrm{i}}\cos {\alpha }_{\mathrm{ij}}\right)\left[\begin{array}{c}\left(Q_{\mathrm{ij}}\sin {\alpha }_{\mathrm{ij}}-F_{\mathrm{R}\mathsf{\eta }\mathrm{ij}}\cos {\alpha }_{\mathrm{ij}}\right)\sin {\phi }_{\mathrm{j}}\\ \left(Q_{\mathrm{ij}}\sin {\alpha }_{\mathrm{ij}}-F_{\mathrm{R}\mathsf{\eta }\mathrm{ij}}\cos {\alpha }_{\mathrm{ij}}\right)\cos {\phi }_{\mathrm{j}}\end{array}\right]}+0.5D_{\mathrm{w}}{f}_{\mathrm{i}}{T}_{\mathsf{\xi }\mathrm{ij}}\sin {\alpha }_{\mathrm{ij}}\left[\begin{array}{c}\cos {\phi }_{\mathrm{j}}\\ \sin {\phi }_{\mathrm{j}}\end{array}\right]\\ +\left[\begin{array}{c}{M}_{\mathrm{y}}\\ M_{\mathrm{z}}\end{array}\right]=\left[\begin{array}{c}{J}_{\mathrm{iy}}{\dot{\omega }}_{\mathrm{iy}}\\ J_{\mathrm{iz}}{\dot{\omega }}_{\mathrm{iz}}\end{array}\right]-\left[\begin{array}{c}\left(J_{\mathrm{iz}}-J_{\mathrm{ix}}\right){\omega }_{\mathrm{iz}}{\omega }_{\mathrm{ix}}\\ \left(J_{\mathrm{ix}}-J_{\mathrm{iy}}\right){\omega }_{\mathrm{ix}}{\omega }_{\mathrm{iy}}\end{array}\right]\end{array}$$

(9)

where ${\ddot{x}}_{\mathrm{i}}$, ${\ddot{y}}_{\mathrm{i}}$, ${\ddot{z}}_{\mathrm{i}}$ are the acceleration components of the inner ring; J_ix, J_iy, J_iz are component moment of the inner ring inertia; ω_ix, ω_iy, ω_iz are the angular velocity components of the inner ring; ${\dot{\omega }}_{\mathrm{i}\mathrm{y}}$ and ${\dot{\omega }}_{\mathrm{i}\mathrm{z}}$ are the angular acceleration components of the inner ring; F_rx, F_ry, F_rz, M_ry and M_rz, are the components of the external loads and moments that act on the inner ring; f_i is the curvature radius coefficient of the inner raceway.

4. Results and Discussion

The nonlinear dynamic differential equations are solved by the gear stiff (GSTIFF) [23] integration algorithm with variable steps. The procedure is presented in Figure 9. The results of the bearing kinematics and the quasi-static are used as the initial conditions that are applied to bearing elements. In this study, the solution time is 0.4 s and there are 10,000 steps, i.e., the inner ring rotates about 120 revolutions. The dynamic equations are solved by a Lenovo computer with forty Inter^® Core™ central processing units (CPU) with 192 GB of memory. The solution time of an example is about 30 min. The main parameters of the bearing are shown in

Table 1. Main parameters of the bearing.

Item	Value
Bearing bore diameter (mm)	35
Bearing outer diameter (mm)	72
Bearing width (mm)	17
Ball diameter (mm)	11.1125
Ball number	9
Cage outer diameter (mm)	59.5
Cage bore diameter (mm)	49.7
Rivet diameter (mm)	1.5 + 0.02/−0.04
Rivet material	15CrMn
Rivet material’s Young’s modulus (Gpa)	192
Rivet material’s density (g/cm3)	7.82
Rivet bore size (mm)	1.5 + 0.05/−0.02

. The working conditions of the bearing are presented in

Table 2. Working conditions.

Item	Value
Working load combinations (N)	Fr2994, Fa515; Fr2246, Fa386; Fr1994, Fa258
Working bearing speed (r/min)	18,238

.

4.1. Analysis of the Rivet Stress

Many factors can affect the rivet stress, such as the rivet preload, the fit relationship between the rivet and the rivet hole, the working conditions, the misalignment and the cage clearance ratio (defined as the ratio of the cage pocket clearance to the cage guide clearance). The rivet stress is directly proportional to the rivet preload and the fit relationship between the rivet and the rivet hole. Thus, this investigation firstly studies the effect of the rivet preload and the fit relationship between the rivet and the rivet hole on the rivet stress. Then, the effect of working conditions, the misalignment and the cage clearance ratio on the rivet stress were studded with the optimal preloading and the fit relationship.

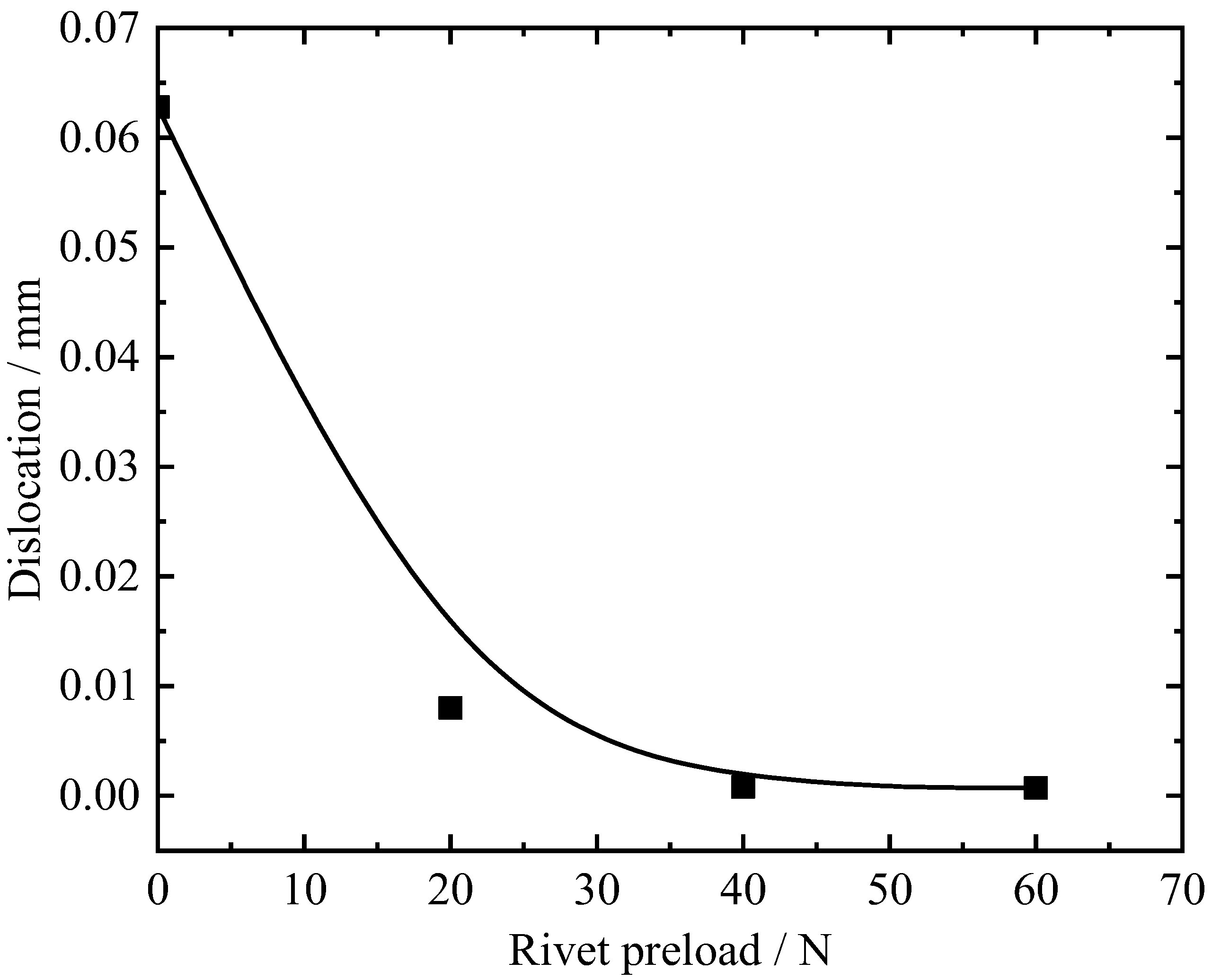
(1)

Effect of the rivet preload on rivet stress

The maximum clearance between the rivet rod and the cage was selected to eliminate the factor of the rivet hindering the dislocation of the cage. Figure 10 shows the dislocation between the two-piece cage. The preload of the rivets is defined as applying a pre-tightening force to the rivet, which is used to shorten the rivet and it compresses both pieces of the cage to prevent the two-piece cage from misplacement. As the rivet preload increases, the dislocation between the two-piece cage decreases in an inverted exponential trend. When the rivet preload exceeds 20 N, the dislocation is less than 0.01 mm. As the preload increases to 40 N, the dislocation equals 0.0 mm. This means that there is no displacement between two pieces.

In the finite element analysis, we can analyze the change of stress distribution on the rivet under different preload by controlling the size of the preload. Figure 11 presents the effect of the rivet preload on the rivet stress. The stress of the rivet head and the rod increase with an increase in the preload. When the preload reaches 60 N, the maximum stress of the rivet head exceeds 140 MPa. Therefore, there is an optimal rivet preload to prevent the cage from dislocation and to minimize the rivet stress. In this study, the optimal preload is 20 N–40 N.

(2)

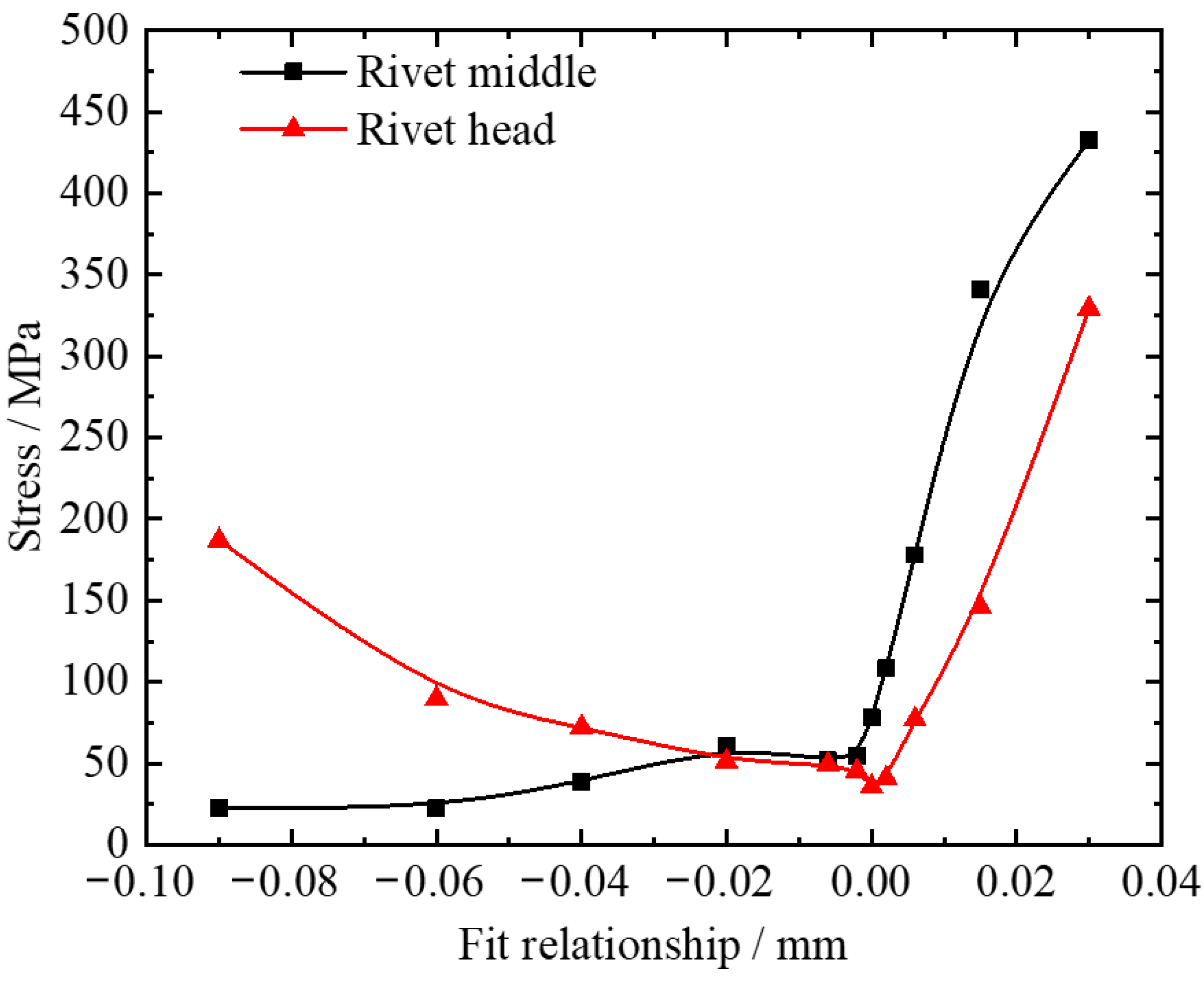
Effect of the fit relationship between the rivet and the rivet hole on the rivet stress

The fit relationship refers to the size change of the rivet and the rivet hole within the tolerance zone, and the value is the diameter of the rivet minus the diameter of the rivet hole. A negative value indicates a clearance fit, and a positive value indicates an interference fit, assuming the fit relationship between the rivet and the rivet hole is from −0.09 mm to +0.04 mm. In the finite element analysis, by changing the diameter of the rivet model to control the fit relationship, the stress generated by the rivet under different fit relationships is obtained. Figure 12 shows the effect of the fit relationship on the stress of the rivet head and the middle part. As the fit relationship changes from the clearance to the interference status, the part with the largest stress of the rivet changes from the rivet head to the middle of the rod. When the clearance is large, the stress of the rivet head is much greater than the middle of the rod. However, when the interference is large, the stress in the middle of the rod is significantly greater than that in the rivet head. The stress of the rivet head and the middle part is almost the same, and the overall stress is low when the fit relationship is −0.02 mm–0 mm. Therefore, to lower the rivet stress and to extend the service life of the cage, the fit relationship between the rivet and the rivet bore should be controlled between −0.02 mm and 0 mm for the 1.5 mm diameter rivet. (Negative values indicate the amount of interference, and positive values indicate the amount of clearance).

(3)

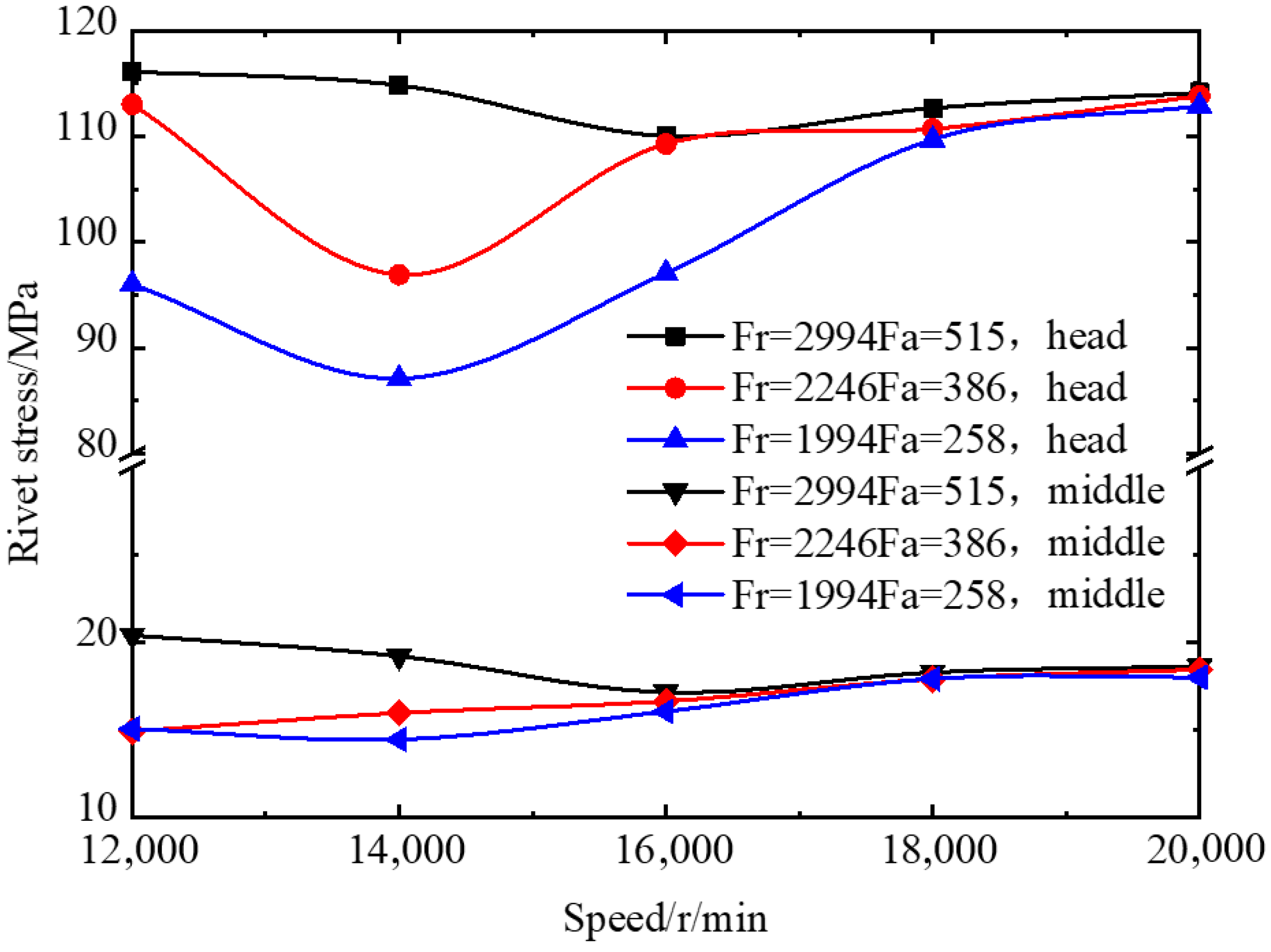
Effect of the working conditions on the rivet stress

According to the previous research results, the rivet preload in the following studies is 20 N and the fit relationship is −0.01 mm. Figure 13 shows the effect of working conditions on the rivet stress. It can be observed that the rivet stress increases as the load increases. In addition, the effect of the bearing load on the stress under a low speed is greater than that under a high-speed condition. The stress decreases and then it increases as the bearing speed increases. The difference in the rivet stress between the given three load combinations occurs when the speed is lower than 16,000 r/min; afterwards, there is basically no difference between them. A reasonable matching value of the load and the speed can reduce the rivet stress.

The impact load means a sudden radial and axial load that acts on the bearing during the operation. Assuming the radial load is 2994 N and the axial load is 515 N, the impact force on the radial and axial direction is 1401 N and 241 N, and the impact load occurs three times during 0.01 s. Figure 14 presents the influence of the impact load on the rivet stress. The results show that the rivet stress increases as the impact load increases, especially the rivet head stress. The reason is that the impact load can significantly increase the total contact force between the ball and cage when other conditions remain unchanged. The dislocation trend between the two-half-cage increases due to the contact force increases, and the rivet stress increases. An uncertain impact load on the bearing can reduce the design life of the cage and the rivets. In the process of the bearing application, attention should be paid to avoid impact on the bearing as much as possible.

(4)

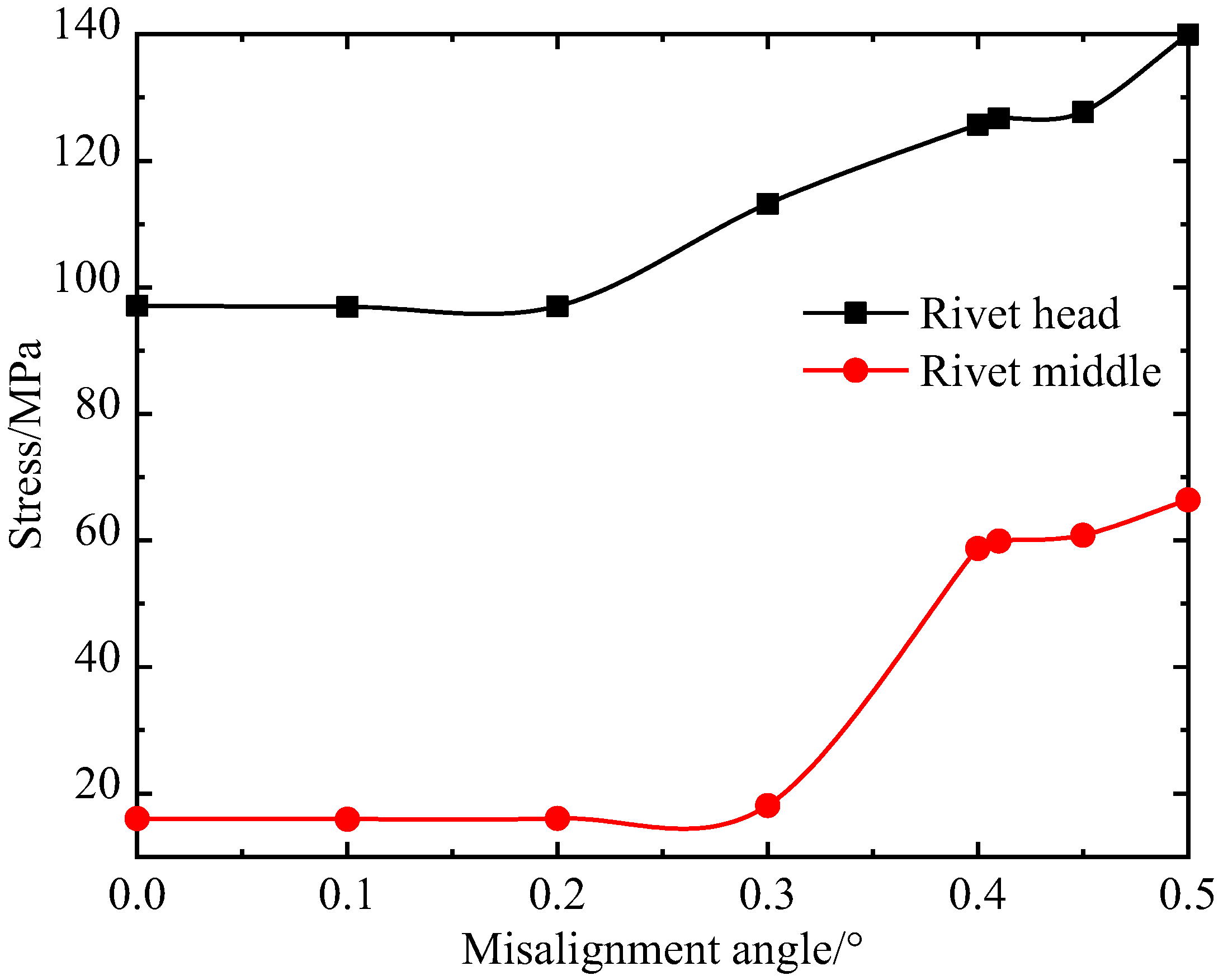
Effect of the misalignment on the rivet stress

A misalignment between the inner and outer ring will occur due to a variety of factors such as the overturning moment and the installation errors of the shaft. The title angle of the ring is used to indicate the degree of the misalignment. Assuming the bearing speed is 18,238 r/min, the radial load is 2994 N and the axial load is 515 N. The rivet stress is analyzed when the misalignment angle changes from 0.0° to 0.5°, as shown in Figure 15. The rivet stress is almost unchanged when the misalignment is less than 0.2°, while it increases sharply while the misalignment angle is greater than 0.4°, which is about 20 times of that at 0.2°. Therefore, it is necessary to avoid the overturning moment and to minimize the misalignment of the inner and outer ring during the installation and operation for the deep-groove ball bearing in the application.

(5)

Effect of the cage clearance ratio on the rivet stress

Assume the bearing speed is 18,238 r/min, and the maximum working load combination (Fr = 2994 N, Fa = 515 N). Figure 16 illustrates the effect of the cage clearance ratio on the rivet stress. With the increase of the cage clearance ratio, the rivet stress first decreases and then it increases. The rivet stress reaches the minimum when the ratio is close to 1. This is because It is challenging to form the stable coupling motion between the cage and balls can form when the ratio is close to 1 and thus the cage operation is stable. During this condition, the contact force between the cage and balls is smaller.

4.2. Comparison Validation

To verify the reliability of the analysis results, the theoretical results were compared to the early fracture failure cases. According to the research results, the failure of the rivet head easily occurs when the fit clearance between the rivet and the rivet hole is large. Figure 17 presents the comparison of the rivet and the rivet hole with a large clearance. Under this condition, the maximum stress occurs at the rivet head, as shown in Figure 17a. Because of the failure due to a large clearance, as shown in Figure 17b, five rivet heads fell off, four rivets were broken in the middle, and the rivet whose head fell off was sheared and it was stuck in one piece of the cage. When the fit relationship has an interference status, the maximus stress occurs in the middle part of the rivet, which is easy to break and fail, as demonstrated in Figure 18a. Figure 18b depicts a failure diagram with an interference relationship. Among them, seven rivets were broken from the middle part and two heads were broken. In addition, there are obvious wear marks on the side beam of the cage pocket, which indicates that the ball has an axial load on the cage. According to the results of this study, a combined load is formed with the circumferential load of the ball on the cage. The rivets are subjected to axial tension and tangential shear, thus causing the rivets fracture fatigue.

In summary, the theoretical analysis results in this study are consistent with the fracture fatigue forms of the cage. The theoretical results are more accurate, which can provide a theoretical basis for the practical application.

5. Conclusions

This paper focuses on the rivet early fatigue characteristics in a deep-groove ball bearing cage for a transmission system in a turboprop engine. The effect of the rivet preload, the rivet fit relationship, the bearing working conditions, and the cage clearance ratio on the rivet stress were investigated to reveal the fatigue characteristics of the rivets. The conclusions are as follows:

(1)

By delivering an optimal preload of the rivet, this causes the two halves of the cage to have less misalignment and a lower rivet stress. As the preload increases, the rivet stress increases. In addition, an excessive preload causes the rivet head to produce a great stress concentration. For the bearing studied in this investigation, the optimal preload of the rivet is 20 N–40 N.

(2)

The fit relationship between the rivet and the rivet bore has a significant influence on the rivet stress. There is an excessive stress on the rivet head when the fit clearance is too large, which causes the rivet head to break off. When the interference is large, the stress in the middle of the rivet rod is too large, which leads to the premature fatigue fracture in the middle of the rivet rod. For the 1.5 mm diameter rivet, we analyzed the appropriate fit relationship, which is −0.02 mm–0 mm.

(3)

The rivet stress increases with the bearing load increases. A reasonable matching value of the load and speed can reduce the rivet stress. The impact load acting on the bearing causes the rivet stress to increase. The rivet stress increases with an increase in the misalignment, and it increases sharply when the misalignment exceeds one threshold. The clearance ratio is close to 1, which is beneficial to reducing the rivet stress and increasing the cage fatigue life.