Vibration and Position Control of a Two-Link Flexible Manipulator Using Reinforcement Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Policy Gradient Method
2.2. Trust Region Policy Optimization
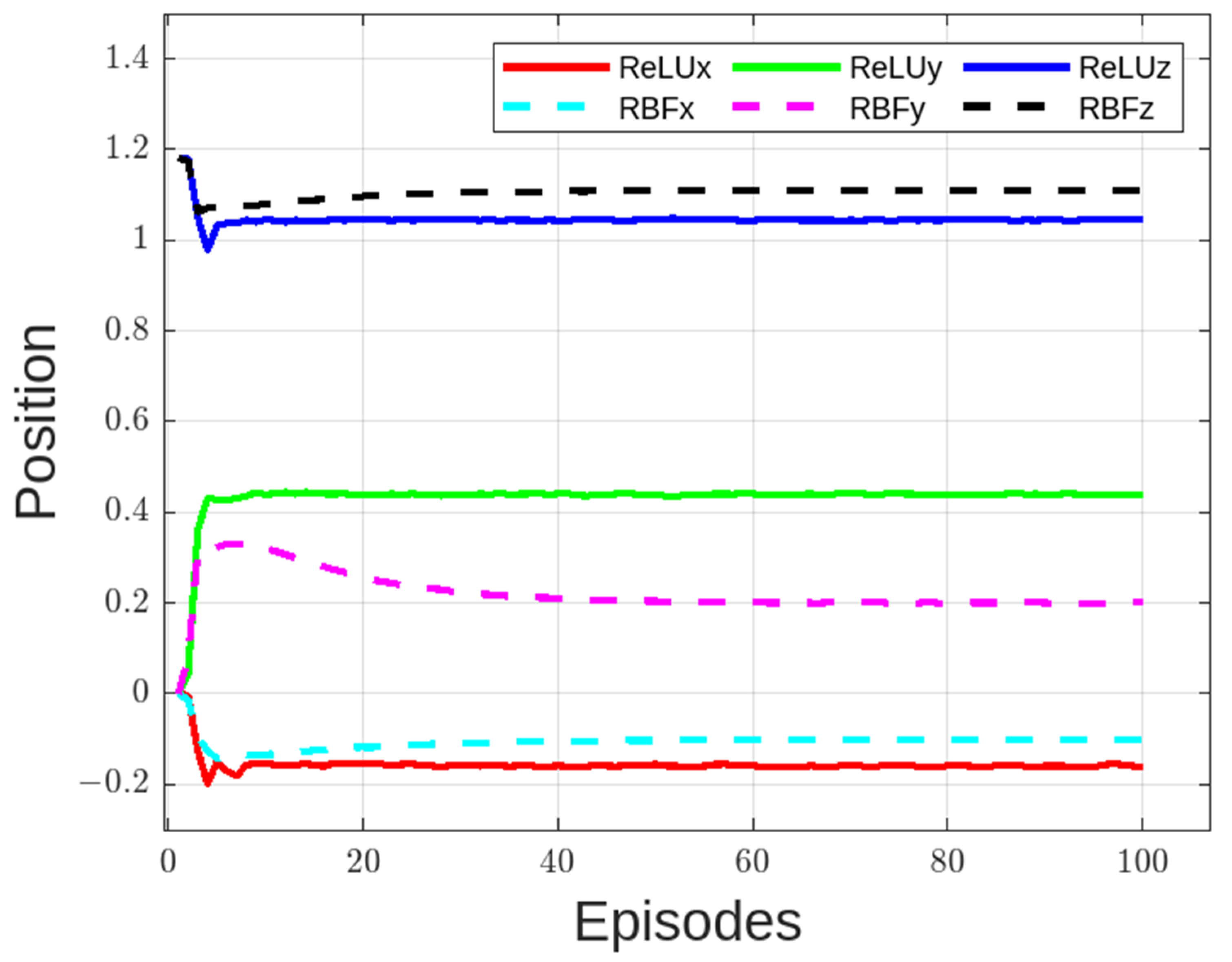
2.3. Activation Functions
3. Simulation of the Flexible Manipulator Model
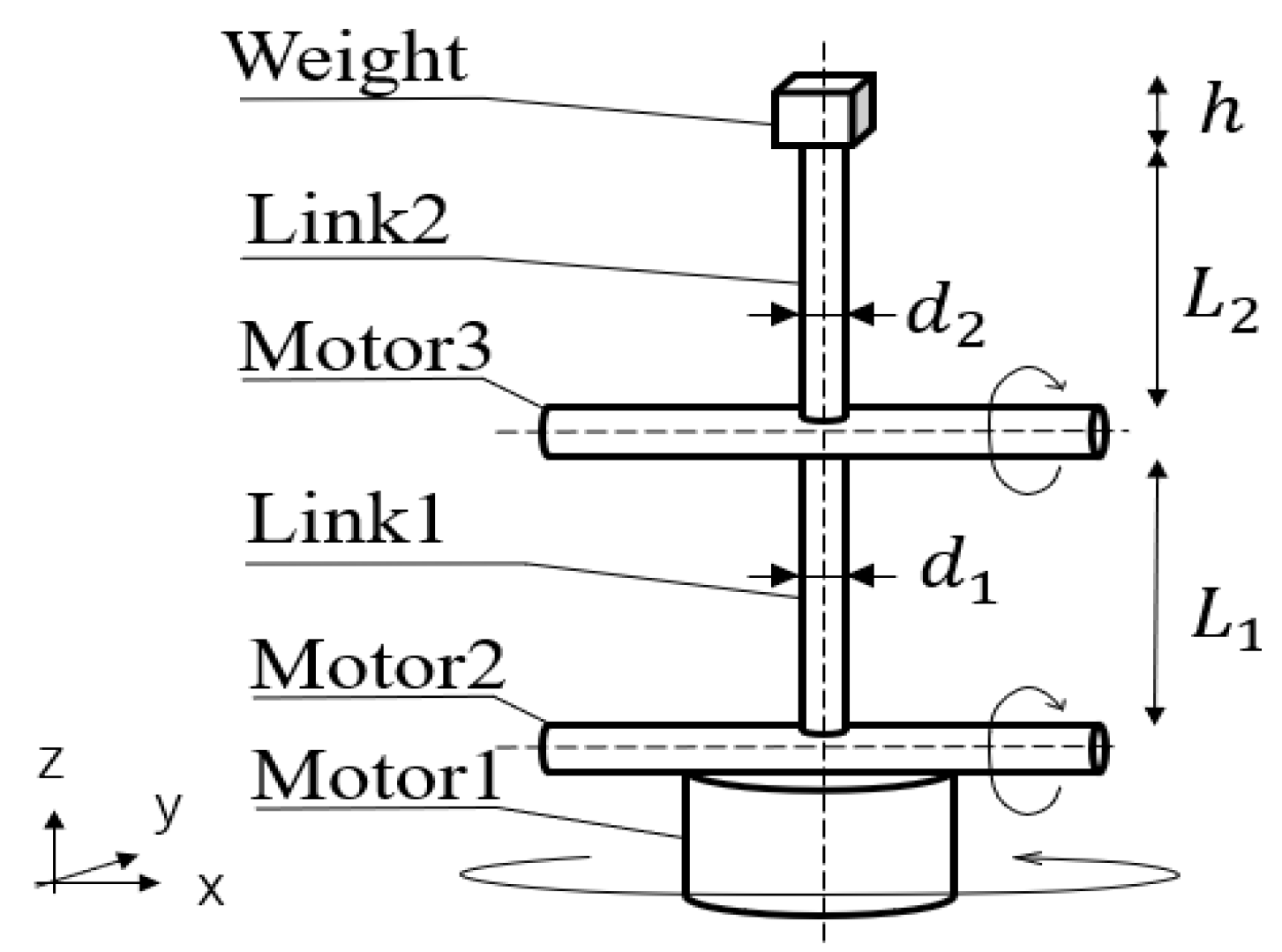
3.1. Actual Manipulator Model
3.2. Virtual Manipulator Model
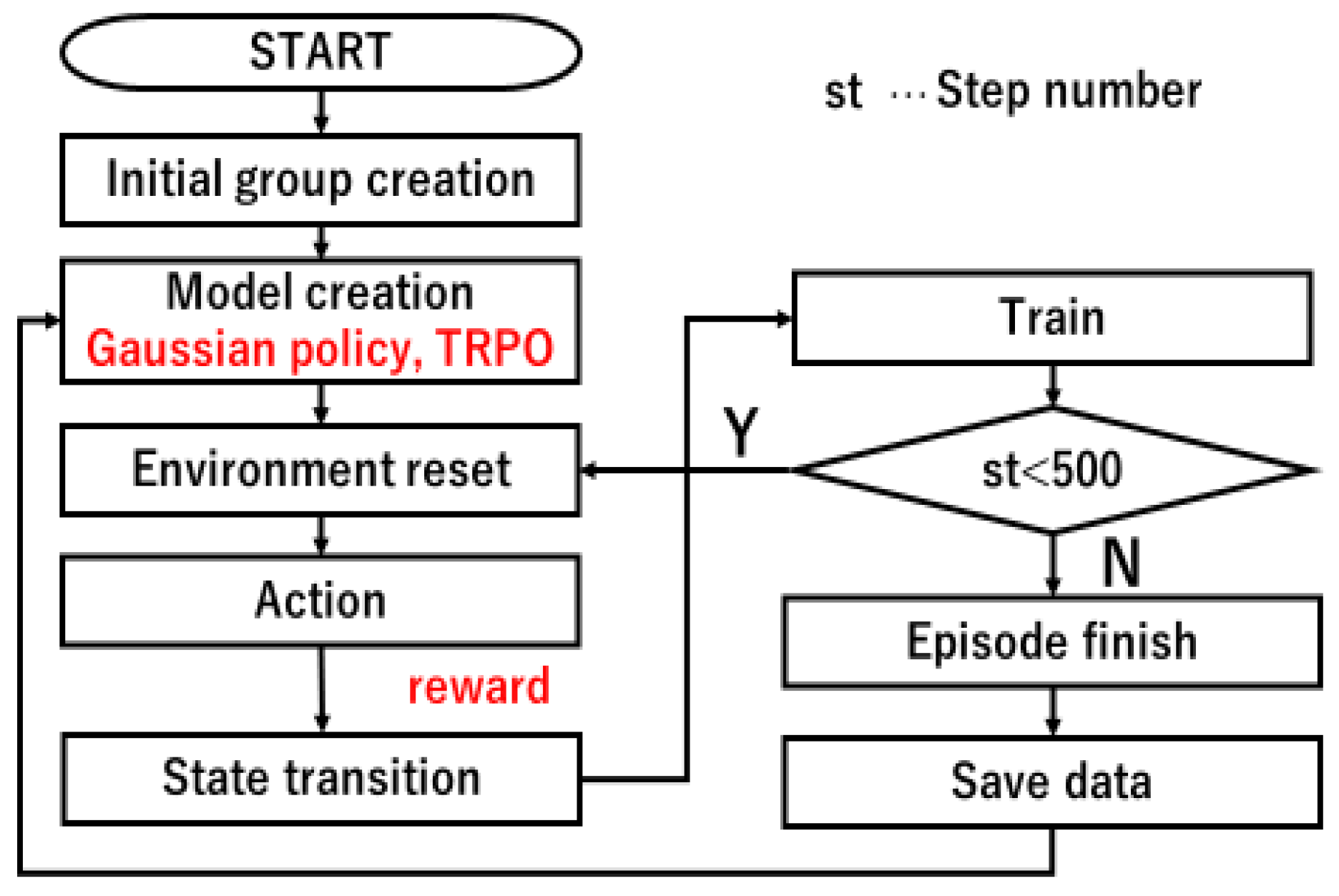
3.3. Experiment Setup
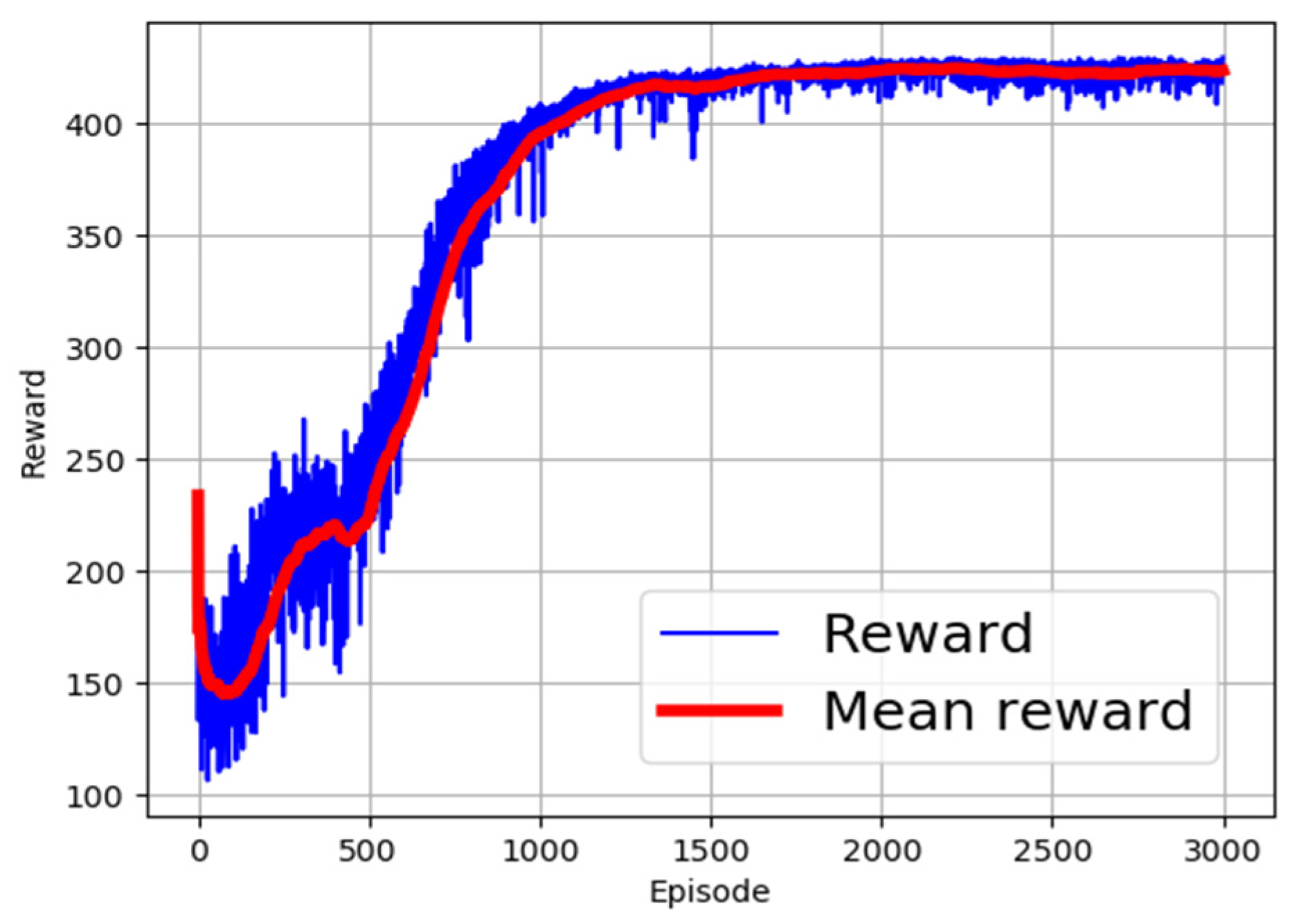
4. Results and Discussion
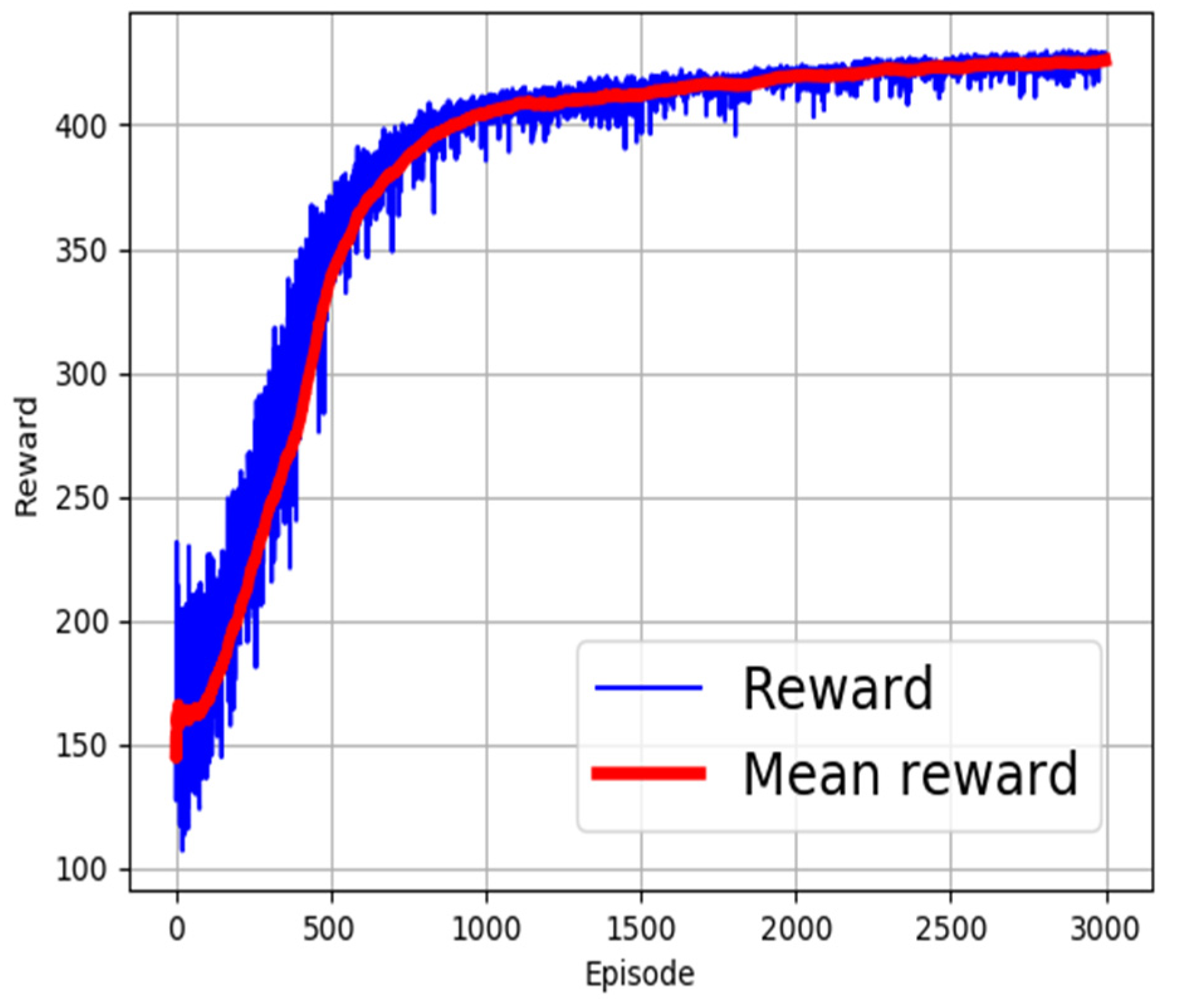
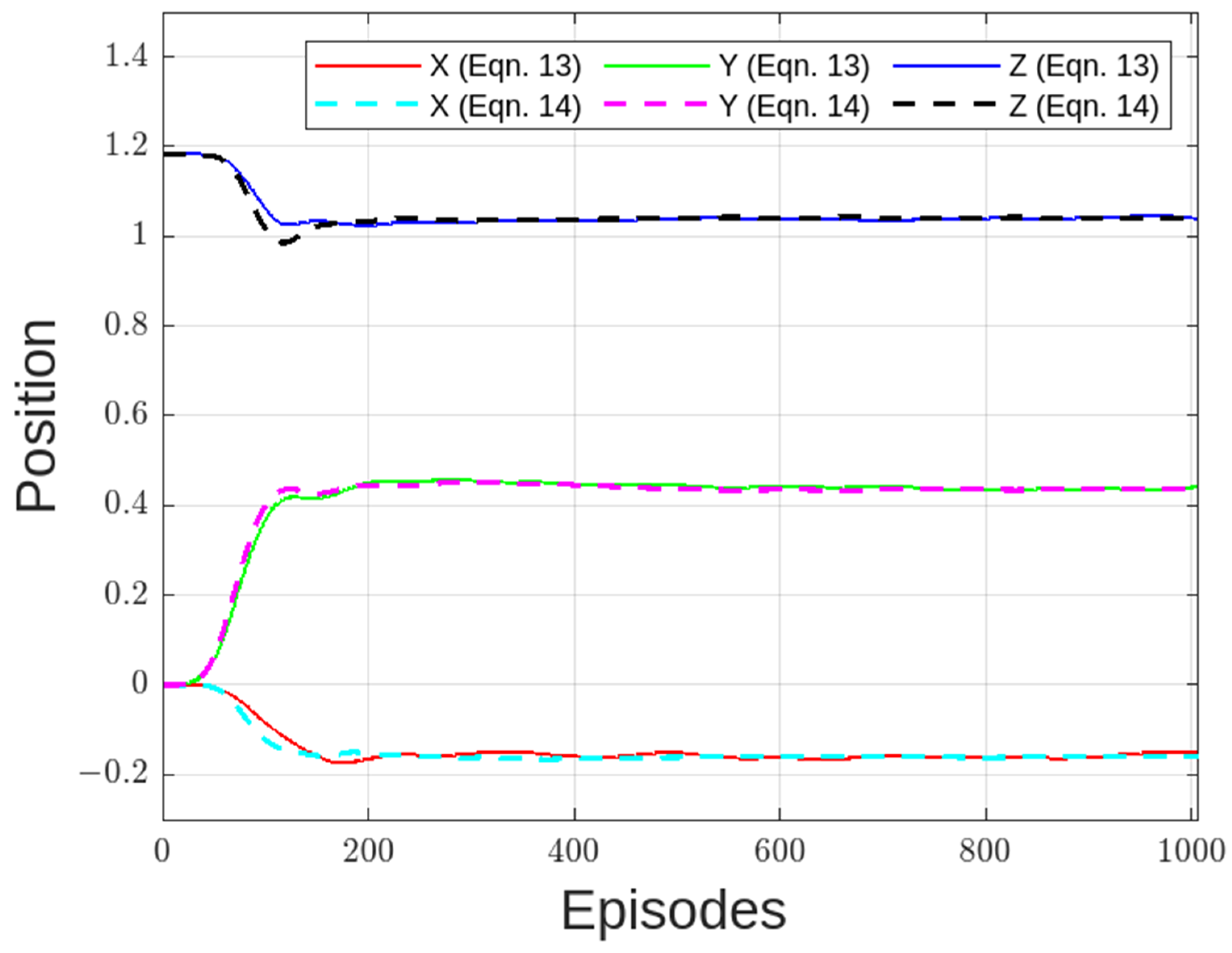
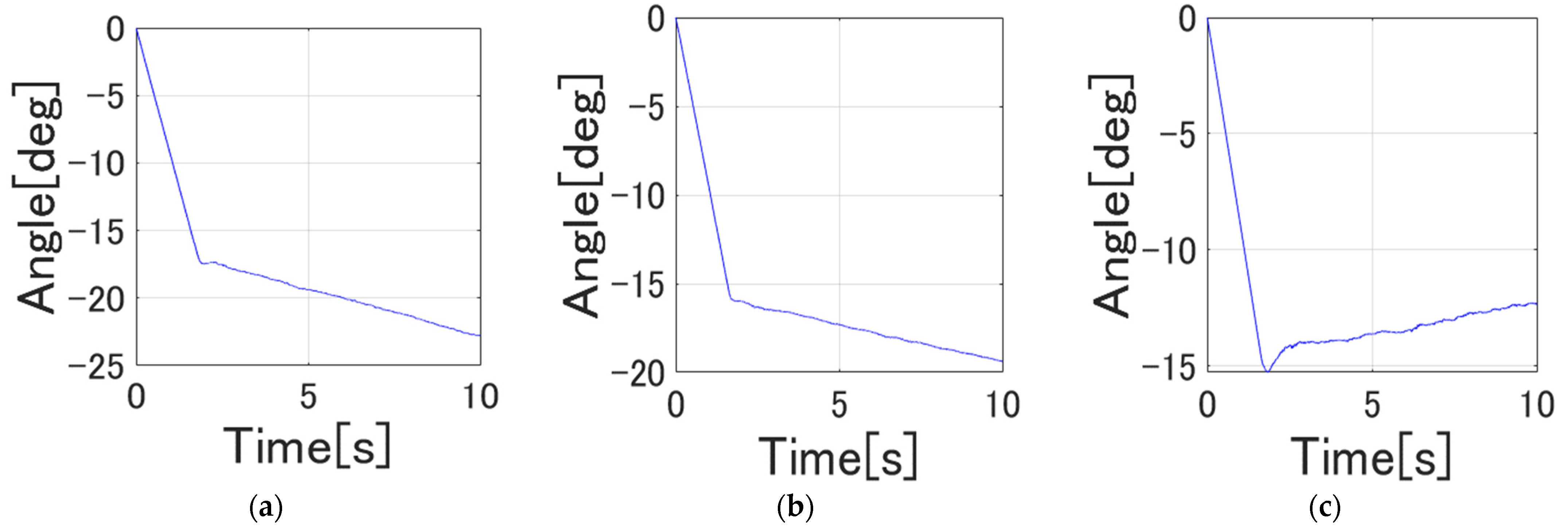
4.1. Position Control Results
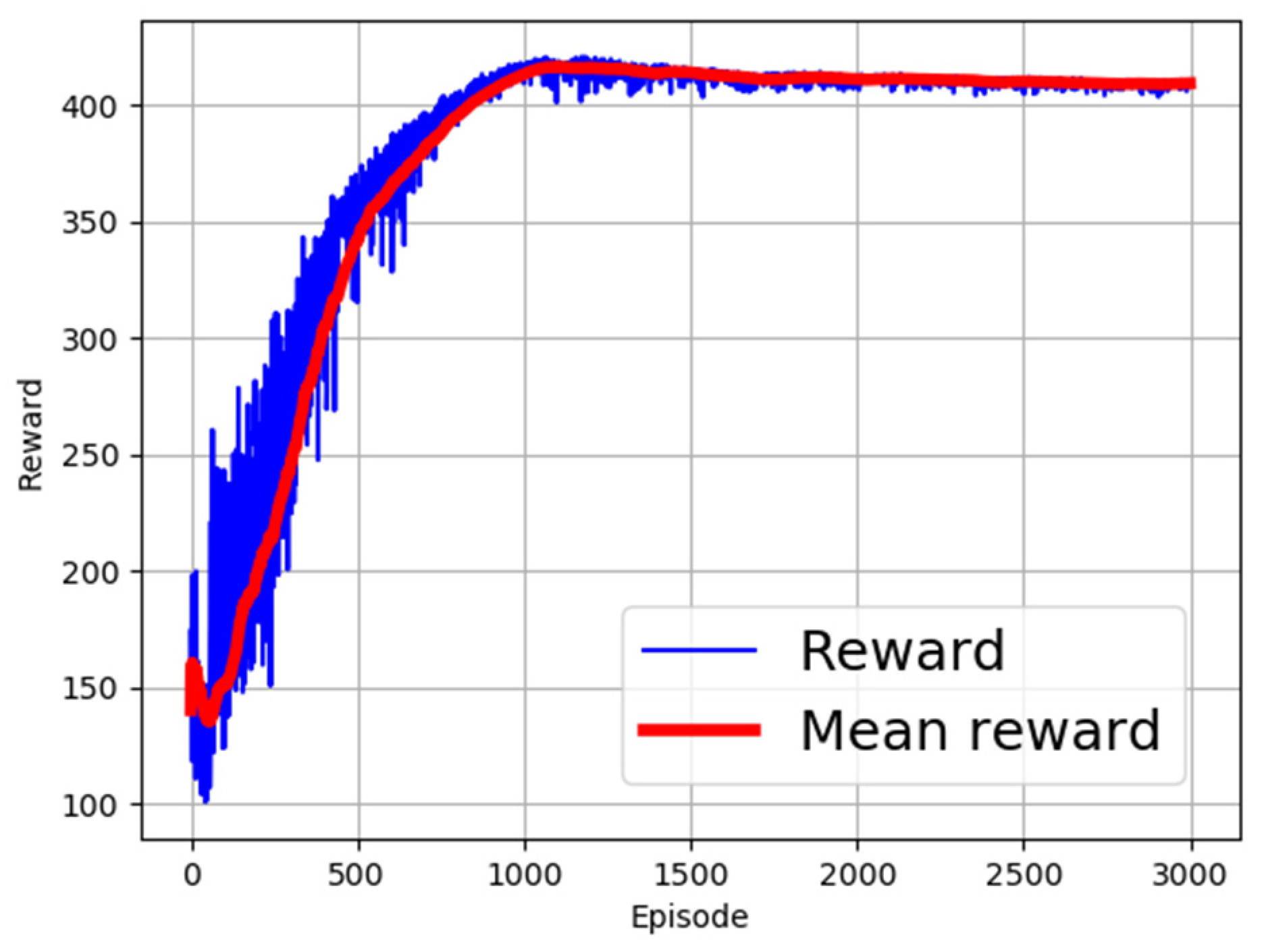
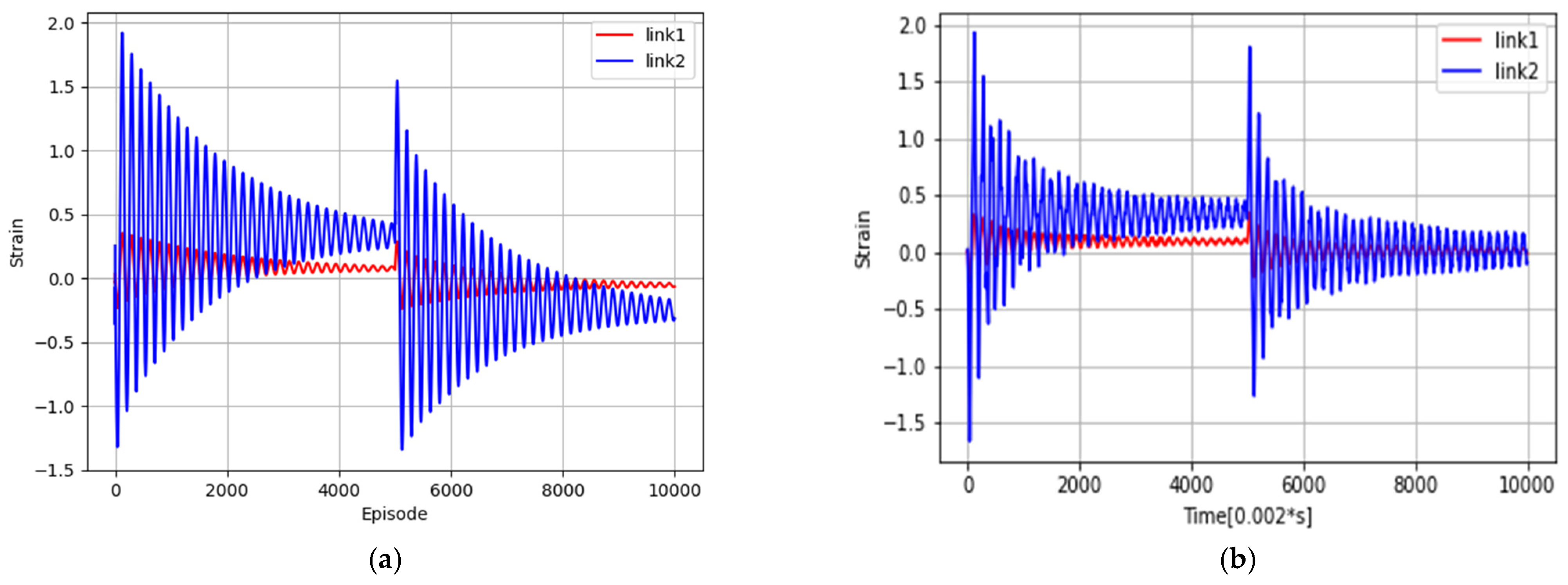
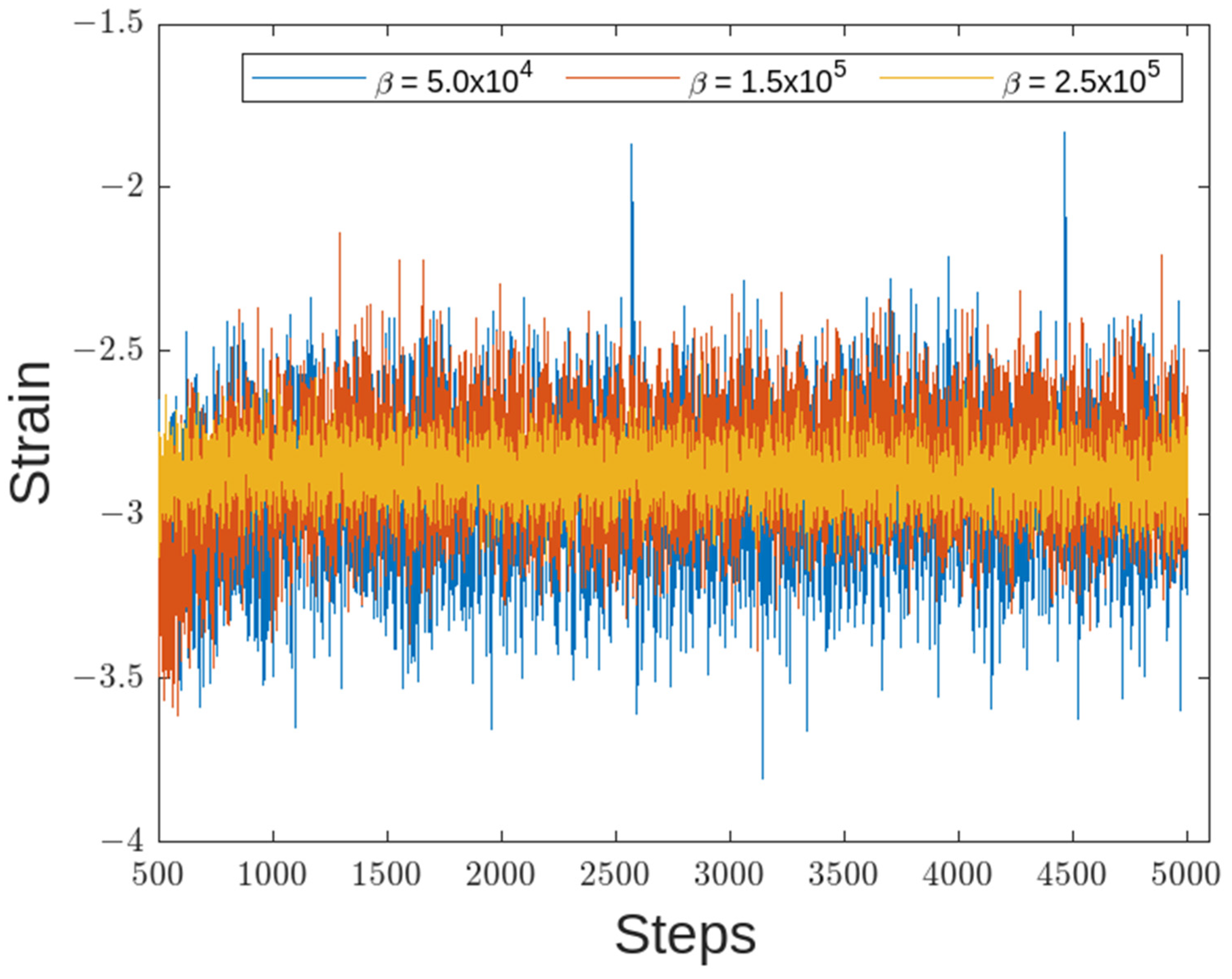
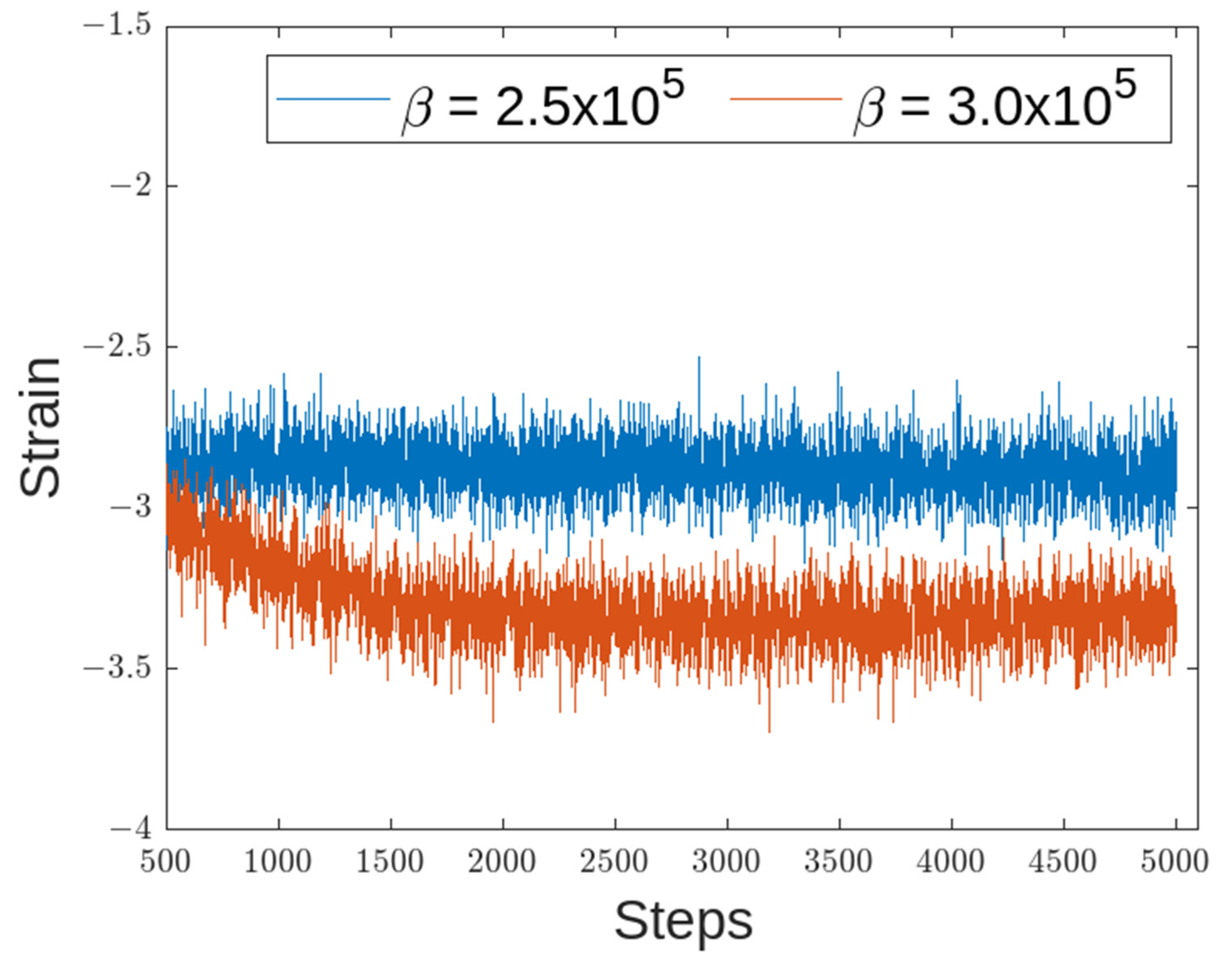
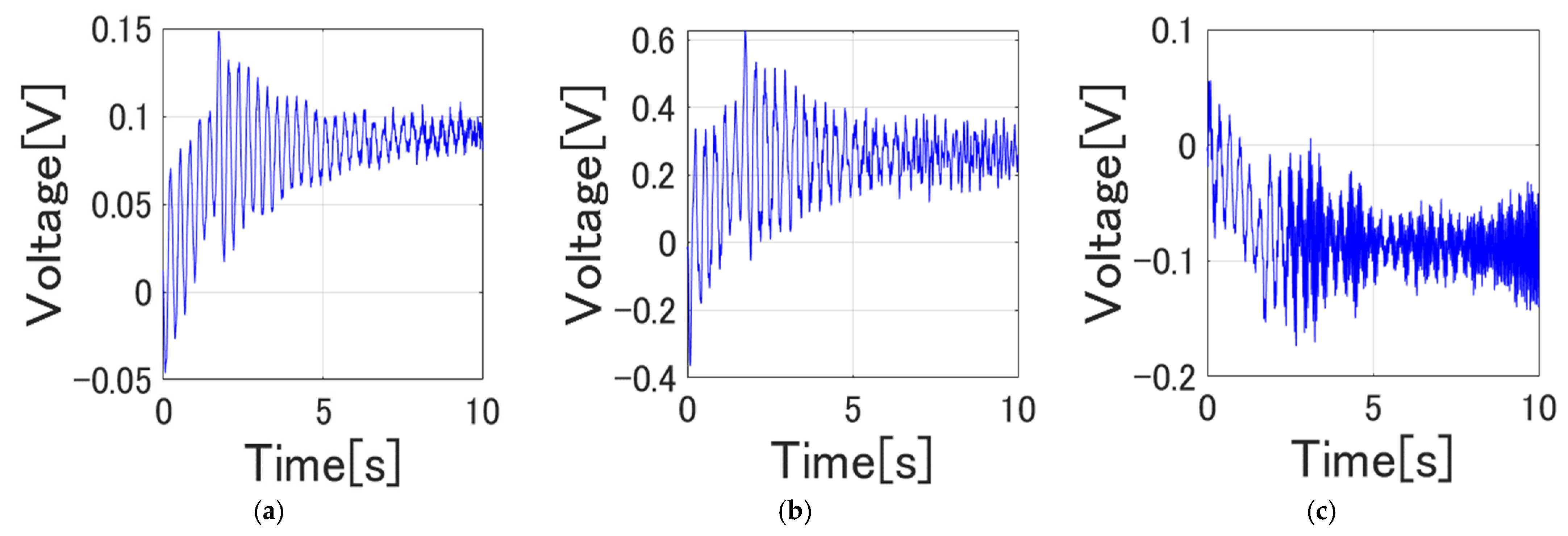
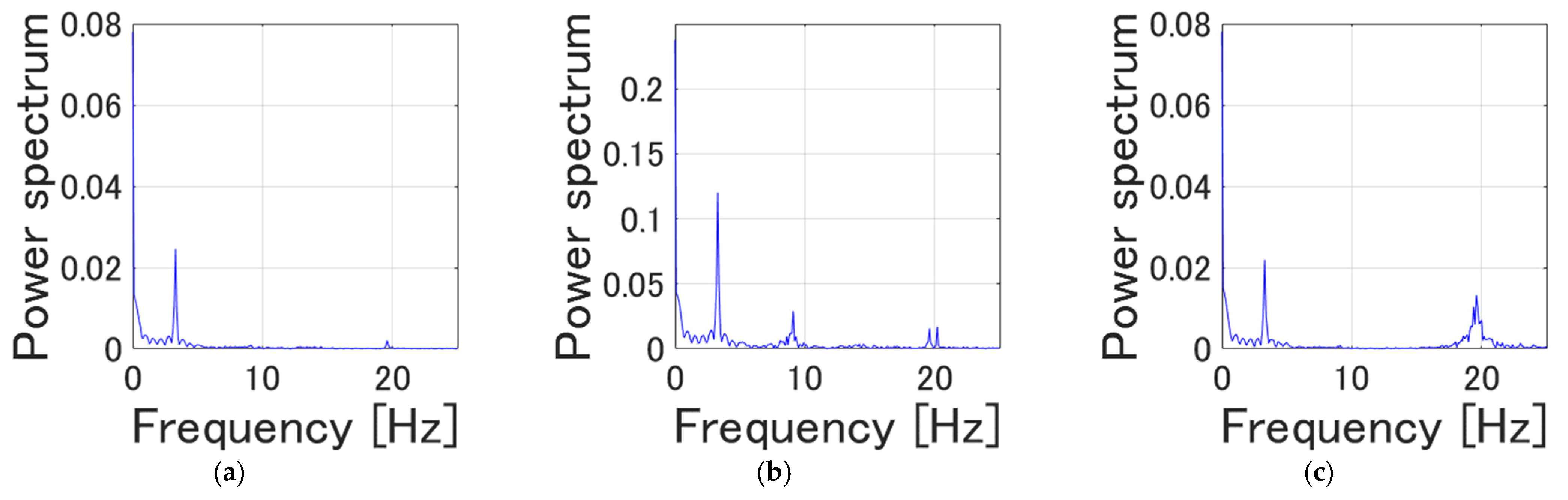
4.2. Vibration/Strain Control Results
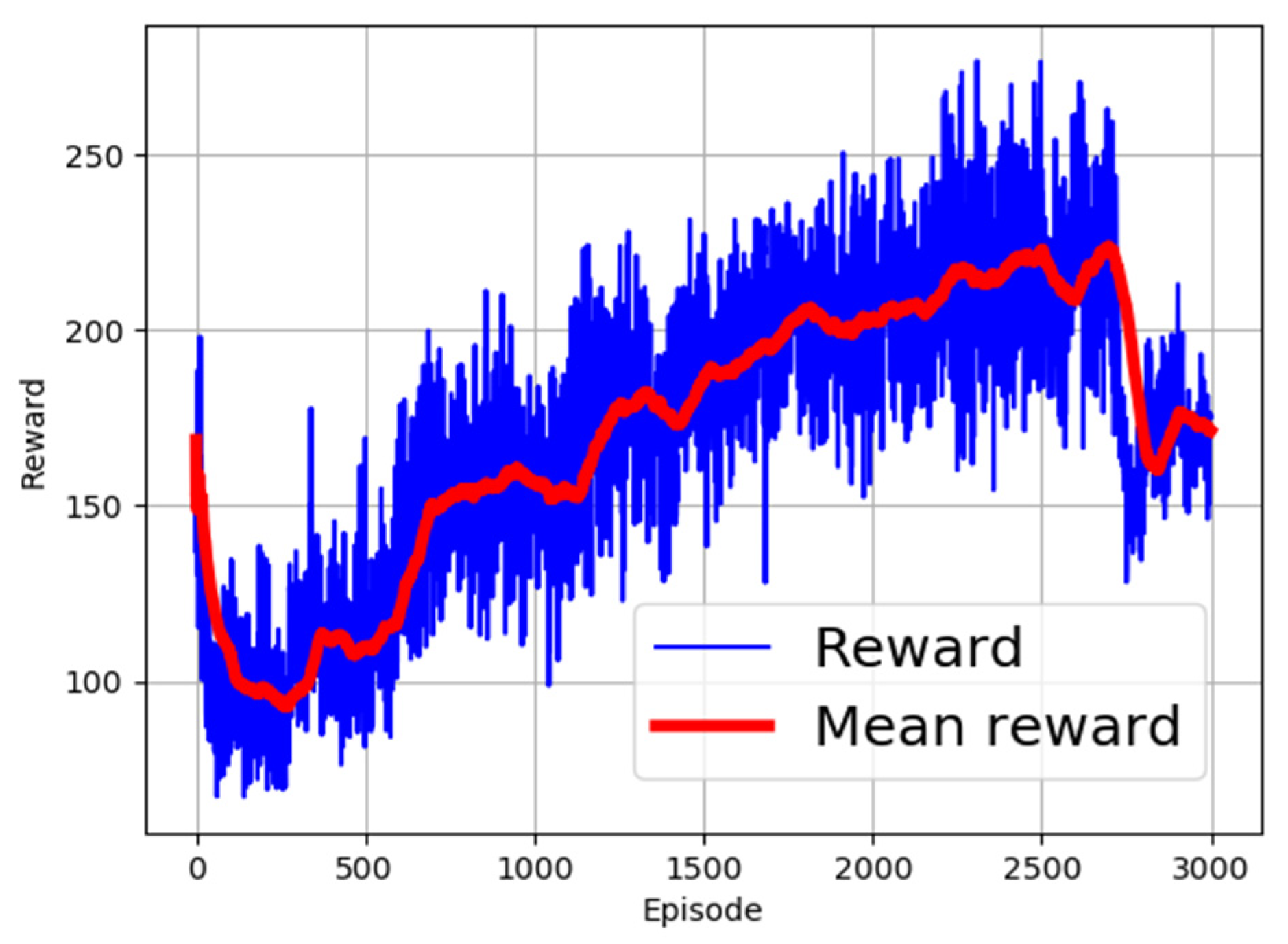
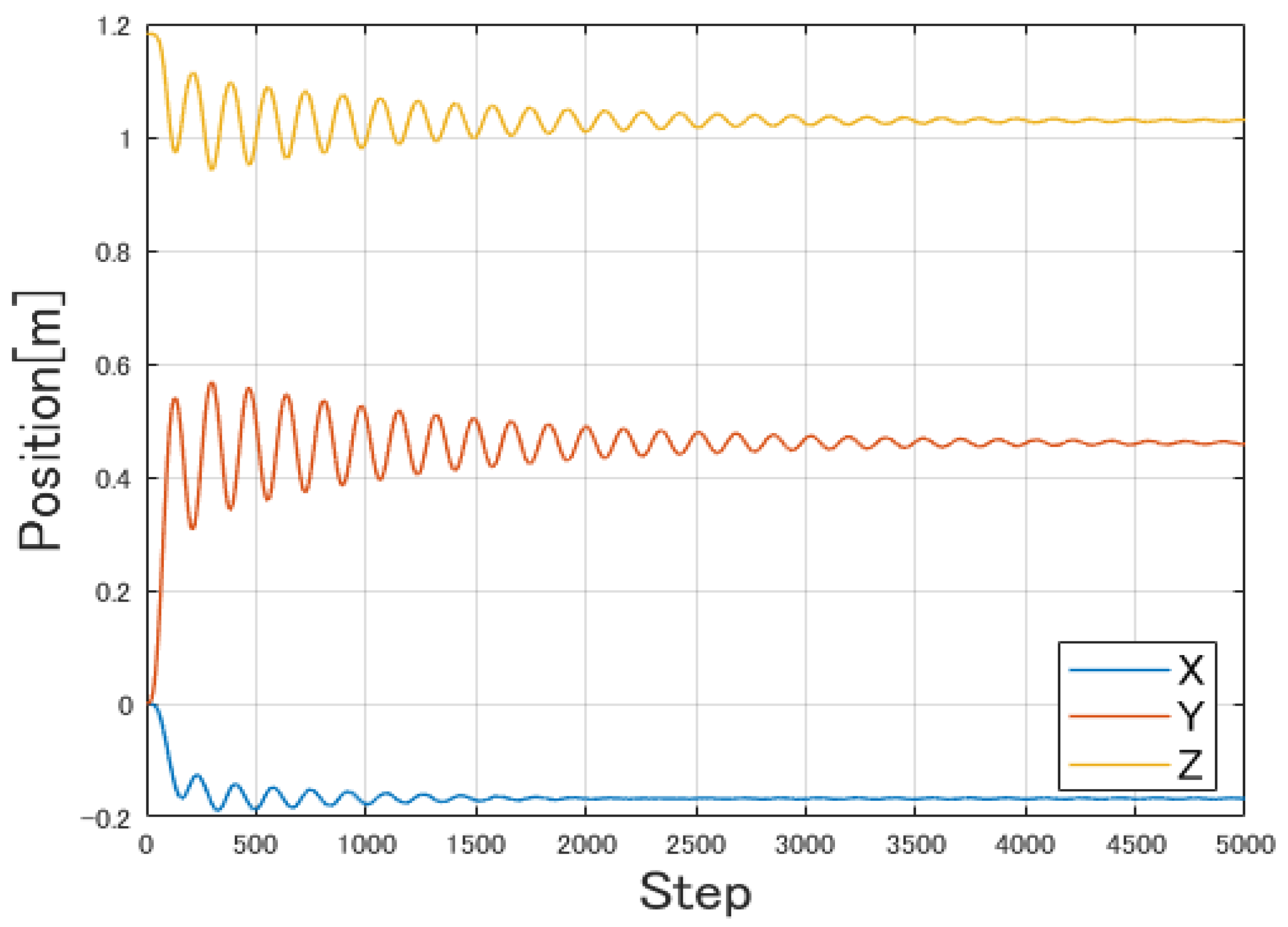
4.3. Experiment on the Actual Flexible Manipulator
- Model inaccuracies: The simulation model may not accurately capture all aspects of the real-world system, such as dynamics, friction, or other physical properties. Assumptions and simplifications made during modeling may have led to discrepancies when compared to the actual system;
- Sensor and actuator variability: Sensors and actuators used in the real-world setup may exhibit variations and uncertainties that are not adequately represented in the simulation. Differences in sensor accuracy, noise levels, actuator response, and other characteristics can contribute to deviations between the simulation and reality, leading to sim–real problems;
- Unmodeled dynamics and nonlinearities: Complex interactions and nonlinear dynamics within the system may not be fully captured in the simulation model. Structural deformations, coupling between joints, dynamic effects, and other unmodeled phenomena can result in discrepancies between the simulated and real-world behavior, leading to sim–real problems.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khaled, M.; Mohammed, A.; Ibraheem, M.S.; Ali, R. Balancing a Two Wheeled Robot; USQ Project; University of Southern Queensland: Darling Heights, QLD, Australia, 2009. [Google Scholar]
- Sasaki, M.; Kunii, E.; Uda, T.; Matsushita, K.; Muguro, J.K.; bin Suhaimi, M.S.A.; Njeri, W. Construction of an Environmental Map including Road Surface Classification Based on a Coaxial Two-Wheeled Robot. J. Sustain. Res. Eng. 2020, 5, 159–169. [Google Scholar]
- Lochan, K.; Roy, B.K.; Subudhi, B. A review on two-link flexible manipulators. Annu. Rev. Control 2016, 42, 346–367. [Google Scholar] [CrossRef]
- Yavuz, Ş. An improved vibration control method of a flexible non-uniform shaped manipulator. Simul. Model. Pract. Theory 2021, 111, 102348. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; He, W. Dynamic modeling and vibration control for a nonlinear 3-dimensional flexible manipulator. Int. J. Robust Nonlinear Control 2018, 28, 3927–3945. [Google Scholar] [CrossRef]
- Njeri, W.; Sasaki, M.; Matsushita, K. Enhanced vibration control of a multilink flexible manipulator using filtered inverse controller. ROBOMECH J. 2018, 5, 28. [Google Scholar] [CrossRef]
- Uyar, M.; Malgaca, L. Implementation of Active and Passive Vibration Control of Flexible Smart Composite Manipulators with Genetic Algorithm. Arab. J. Sci. Eng. 2023, 48, 3843–3862. [Google Scholar] [CrossRef]
- Mishra, N.; Singh, S.P. Hybrid vibration control of a Two-Link Flexible manipulator. SN Appl. Sci. 2019, 1, 715. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.B.; Bui, X.C. Hybrid Vibration Control Algorithm of a Flexible Manipulator System. Robotics 2023, 12, 73. [Google Scholar] [CrossRef]
- de Lima, J.J.; Tusset, A.M.; Janzen, F.C.; Piccirillo, V.; Nascimento, C.B.; Balthazar, J.M.; da Fonseca, R.M.L.R. SDRE applied to position and vibration control of a robot manipulator with a flexible link. J. Theor. Appl. Mech. 2016, 54, 1067–1078. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Cheng, Q.; Xiao, J.; Hao, L. Performance-based data-driven optimal tracking control of shape memory alloy actuated manipulator through reinforcement learning. Eng. Appl. Artif. Intell. 2022, 114, 105060. [Google Scholar] [CrossRef]
- Roy, S.; Kieson, E.; Abramson, C.; Crick, C. Mutual Reinforcement Learning with Robot Trainers. In Proceedings of the 2019 14th ACM/IEEE International Conference on Human-Robot Interaction (HRI), Daegu, Republic of Korea, 11–14 March 2019. [Google Scholar]
- Kober, J.; Peters, J. Reinforcement Learning in Robotics: A Survey. In Learning Motor Skills; Springer: Cham, Switzerland, 2014; Volume 97, pp. 9–67. [Google Scholar] [CrossRef] [Green Version]
- Smart, W.; Kaelbling, L. Reinforcement Learning for Robot Control. In Proceedings of the SPIE; SPIE: Philadelphia, PA, USA, 2002; Volume 4573. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Chi, J.; Jin, X.-Z.; Deng, C. Reinforcement learning approach to the control of heavy material handling manipulators for agricultural robots. Comput. Electr. Eng. 2022, 104, 108433. [Google Scholar] [CrossRef]
- Xie, Z.; Sun, T.; Kwan, T.; Wu, X. Motion control of a space manipulator using fuzzy sliding mode control with reinforcement learning. Acta Astronaut. 2020, 176, 156–172. [Google Scholar] [CrossRef]
- Qiu, Z.C.; Chen, G.H.; Zhang, X.M. Trajectory planning and vibration control of translation flexible hinged plate based on optimization and reinforcement learning algorithm. Mech. Syst. Signal Process. 2022, 179, 109362. [Google Scholar] [CrossRef]
- Sasaki, M.; Muguro, J.; Kitano, F.; Njeri, W.; Matsushita, K. Sim–Real Mapping of an Image-Based Robot Arm Controller Using Deep Reinforcement Learning. Appl. Sci. 2022, 12, 10277. [Google Scholar] [CrossRef]
- Ouyang, Y.; He, W.; Li, X.; Liu, J.-K.; Li, G. Vibration Control Based on Reinforcement Learning for a Single-link Flexible Robotic Manipulator. IFAC-PapersOnLine 2017, 50, 3476–3481. [Google Scholar] [CrossRef]
- Pane, Y.P.; Nageshrao, S.P.; Kober, J.; Babuška, R. Reinforcement learning based compensation methods for robot manipulators. Eng. Appl. Artif. Intell. 2019, 78, 236–247. [Google Scholar] [CrossRef]
- He, W.; Gao, H.; Zhou, C.; Yang, C.; Li, Z. Reinforcement Learning Control of a Flexible Two-Link Manipulator: An Experimental Investigation. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 7326–7336. [Google Scholar] [CrossRef]
- Njeri, W.; Sasaki, M.; Matsushita, K. Gain tuning for high-speed vibration control of a multilink flexible manipulator using artificial neural network. J. Vib. Acoust. Trans. ASME 2019, 141, 041011. [Google Scholar] [CrossRef]
- Nguyen, Q.C.; Vu, V.H.; Thomas, M. A Kalman filter based ARX time series modeling for force identification on flexible manipulators. Mech. Syst. Signal Process. 2022, 169, 108743. [Google Scholar] [CrossRef]
- Shang, D.; Li, X.; Yin, M.; Li, F. Dynamic modeling and fuzzy compensation sliding mode control for flexible manipulator servo system. Appl. Math. Model. 2022, 107, 530–556. [Google Scholar] [CrossRef]
- Ben Tarla, L.; Bakhti, M.; Bououlid Idrissi, B. Implementation of second order sliding mode disturbance observer for a one-link flexible manipulator using Dspace Ds1104. SN Appl. Sci. 2020, 2, 485. [Google Scholar] [CrossRef] [Green Version]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.; Kumar, R.; Singh, V.P. Reinforcement learning in robotic applications: A comprehensive survey. Artif. Intell. Rev. 2022, 55, 945–990. [Google Scholar] [CrossRef]
- Buffet, O.; Pietquin, O.; Weng, P. Reinforcement Learning. In A Guided Tour of Artificial Intelligence Research: Volume I: Knowledge Representation, Reasoning and Learning; Springer: Berlin/Heidelberg, Germany, 2020; pp. 389–414. [Google Scholar]
- Zhao, T.; Hachiya, H.; Niu, G.; Sugiyama, M. Analysis and improvement of policy gradient estimation. Adv. Neural Inf. Process. Syst. 24 2011, 26, 118–129. [Google Scholar] [CrossRef] [PubMed]
- Kubo, T. Reinforcement Learning with Python: From Introduction to Practice; Kodansha Co., Ltd.: Tokyo, Japan, 2019; pp. 140–166. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust Region Policy Optimization. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 7–9 July 2015. [Google Scholar]
- Wang, Y.; Li, Y.; Song, Y.; Rong, X. The influence of the activation function in a convolution neural network model of facial expression recognition. Appl. Sci. 2020, 10, 1897. [Google Scholar] [CrossRef] [Green Version]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation Functions: Comparison of trends in Practice and Research for Deep Learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Todorov, E. MuJoCo: Modeling, Simulation and Visualization of Multi-Joint Dynamics with Contact; Roboti Publishing: Seattle, WA, USA, 2018. [Google Scholar]
- Sasaki, M.; Muguro, J.; Njeri, W.; Doss, A.S.A. Adaptive Notch Filter in a Two-Link Flexible Manipulator for the Compensation of Vibration and Gravity-Induced Distortion. Vibration 2023, 6, 286–302. [Google Scholar] [CrossRef]
- Mishra, N.; Singh, S.P. Determination of modes of vibration for accurate modelling of the flexibility effects on dynamics of a two link flexible manipulator. Int. J. Non. Linear. Mech. 2022, 141, 103943. [Google Scholar] [CrossRef]
- Ushida, Y.; Razan, H.; Ishizuya, S.; Sakuma, T.; Kato, S. Using sim-to-real transfer learning to close gaps between simulation and real environments through reinforcement learning. Artif. Life Robot. 2022, 27, 130–136. [Google Scholar] [CrossRef]
- Du, Y.; Watkins, O.; Darrell, T.; Abbeel, P.; Pathak, D. Auto-Tuned Sim-to-Real Transfer. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 1290–1296. [Google Scholar]








| Parameter | Value |
|---|---|
| Input channels. | 215 |
| Dimensions of the action space. | 12 |
| Hidden channels. | 200 |
| Hidden layers. | 2 |
| Scale of weight initialization of the mean layer. | 0.01 |
| Initial value the var parameter. | 0 |
| Parameter | Value |
|---|---|
| Interval steps of TRPO iterations. | 5000 |
| Maximum number of iterations in the conjugate gradient method. | 20 |
| Damping factor used in the conjugate gradient method. | 0.1 |
| Discount factor [0, 1]. | 0.995 |
| Lambda-return factor [0, 1]. | 0.97 |
| Number of epochs for the value function. | 5 |
| Weight coefficient for entropy bonus [0, inf). | 0 |
| Batch size of stochastic gradient descent method for value function. | 64 |
| Maximum number of backtracking. | 10 |
| Window size used to compute statistics of value predictions. | 1000 |
| Window size used to compute statistics of entropy of action distributions. | 1000 |
| Window size used to compute statistics of KL divergence between old and new policies. | 100 |
| Window size used to compute statistics of step sizes of policy updates. | 100 |
| Function Name | Expression |
|---|---|
| ReLU | |
| Sigmoid | |
| SoftMax | |
| SoftPlus | |
| Radial Basis Function (RBF) |
| Parameter | Value |
|---|---|
| 0.44 [m] | |
| 0.44 [m] | |
| 0.027 [kg] | |
| 0.059 [kg] | |
| ] | |
| ] | |
| 0.01 [m] | |
| 0.008 [m] | |
| w | 0.1 [kg] |
| h | 0.04 [m] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sasaki, M.; Muguro, J.; Kitano, F.; Njeri, W.; Maeno, D.; Matsushita, K. Vibration and Position Control of a Two-Link Flexible Manipulator Using Reinforcement Learning. Machines 2023, 11, 754. https://doi.org/10.3390/machines11070754
Sasaki M, Muguro J, Kitano F, Njeri W, Maeno D, Matsushita K. Vibration and Position Control of a Two-Link Flexible Manipulator Using Reinforcement Learning. Machines. 2023; 11(7):754. https://doi.org/10.3390/machines11070754
Chicago/Turabian StyleSasaki, Minoru, Joseph Muguro, Fumiya Kitano, Waweru Njeri, Daiki Maeno, and Kojiro Matsushita. 2023. "Vibration and Position Control of a Two-Link Flexible Manipulator Using Reinforcement Learning" Machines 11, no. 7: 754. https://doi.org/10.3390/machines11070754
APA StyleSasaki, M., Muguro, J., Kitano, F., Njeri, W., Maeno, D., & Matsushita, K. (2023). Vibration and Position Control of a Two-Link Flexible Manipulator Using Reinforcement Learning. Machines, 11(7), 754. https://doi.org/10.3390/machines11070754






