A Novel Sleeve Design to Reduce the Eddy Current Loss of High-Speed Electrical Machines

Abstract

Demand for high-speed motors is increasing. Surface-mounted permanent magnet synchronous motors (SPMSM) used in high-speed applications have magnets attached to the rotor, so there is a risk of damage and scattering due to centrifugal force as the speed increases. For this reason, applying the retaining sleeve to the rotor is essential. However, when using sleeves, there is a problem of reducing efficiency due to eddy current loss. In this paper, a study was conducted on a motor for a 100 kW building air conditioning system operating at a speed of 20,000 rpm. The purpose of the study is to reduce eddy current loss by optimizing the sleeve geometry. To this end, 3D finite element analysis (FEA) using JMAG 22.1 was conducted to analyze eddy current loss, the minimum safety factor was analyzed through mechanical stiffness analysis using ANSYS Workbench, and the validity of sleeve shape was proved through cause analysis. Through the research results, it is expected that the shape change of the sleeve will have the effect of reducing eddy current loss.

1. Introduction

Increasing emphasis is being placed on the significance of high-power and high-efficiency motor technologies all over the world. Increasing energy consumption and environmental regulations are driving the need for high-speed permanent magnet motors. These motors offer high power density, high efficiency, a small size, and are light weight—and this is due to the development of permanent magnet and power conversion control technology. Demand for these technologies continues to increase, and their application fields are diversifying [1,2,3]. In the high-speed range, the internal permanent magnet synchronous motor (IPMSM) receives a local maximum stress at the edge of the magnet pocket as the rotor rotates, and the critical speed is limited by the mechanical stress [4,5,6]. In Ref. [7], the same comparison between surface-mounted permanent magnet synchronous motor (SPMSM) and IPMSM at the same rated operation shows that the SPMSM rotor structure has higher mechanical strength and efficiency, but the IPMSM rotor can be configured at a relatively low cost [8]. SPMSM is primarily used in high-speed applications for a wide range of driving speeds. However, SPMSM has a magnet attached to the outside of the rotor, so there is a risk of mechanical breakdown and physical scattering due to centrifugal force as the rotor rotates. To prevent this, a retaining sleeve that surrounds the permanent magnet is used to prevent mechanical yield stress and scattering [9,10]. Structurally, the retaining sleeve increases the strength of the rotor, but electromagnetically, it has an effect similar to an air gap, reducing the output [11,12]. Therefore, an optimal design of a sleeve that can structurally secure mechanical rigidity and satisfy the performance of the motor must be made [3]. There are two main types of sleeve material. One is a non-metallic material made of glass or carbon fiber, and the other is a metallic sleeve made of metal alloy. In general, metallic materials have higher strength than non-metallic materials, but because of their high conductivity, eddy current loss may occur on a larger scale, and non-metallic materials are lightweight. Depending on the designer’s convenience or application, the selection of the material of the sleeve is an important factor [12,13,14,15]. Eddy current loss affects efficiency reduction, and heat loss occurs due to heat [16]. In this paper, a motor for a 100 kW building air conditioning system operating at 20,000 rpm was targeted [17]. In this motor, an optimal tapering model and tapering slit model are proposed to reduce eddy current losses in the retaining sleeve. To verify the validity of the proposed model, JMAG 22.1 was used to determine eddy current loss through three-dimensional (3D) finite element analysis (FEA), and ANSYS Workbench was used to determine the minimum safety factor through mechanical stiffness analysis [12,18,19,20]. Finally, we propose an optimal retaining sleeve model that can minimize eddy current loss through cause analysis. Figure 1 proposes a process for optimal sleeve design. Section 2 examines a conventional model to identify various losses, efficiency, and a minimum safety factor. In this paper, the goal is to reduce eddy current loss, so the mechanical minimum safety factor is considered. Section 3 explains the causes of eddy current loss and the basic theory of mechanical stiffness due to the compression and rotational effects of a cylindrical cylinder. Section 4 proposes a sleeve tapering model to reduce eddy current loss in the sleeve of the conventional model. In Section 4.1, the sleeve tapering principles and parameters are explained. In Section 4.2, the maximum eddy current loss reduction and the minimum safety factor reduction models of the criteria selected in this paper are verified through 3D finite element analysis, and mechanical stiffness analysis for the variables. If there is a model that does not meet the selected criteria, the eddy current loss and minimum safety factor is checked with various settings and the model is then selected. In Section 5, a sleeve tapering slit model is proposed. For optimal design, sleeve slit variables are selected. In Section 5.2.1, variables are selected considering the stacking length of the sleeve. The remaining variables are selected in Section 5.2.2. The cause of eddy current loss and the reason for setting variables are explained in Section 5.2.3. The optimal sleeve shape for reducing eddy current loss is confirmed in Section 5.2.4. Likewise, loss reduction and mechanical safety are judged through 3D finite element analysis and mechanical stiffness analysis, and the final model is selected if it meets the target.

2. Conventional Model Specifications

In this study, a motor for a 100 kW building air conditioning system operating at 20,000 rpm was selected as the conventional model. The conventional model is a 2-pole 18-slot SPMSM, and the shape and name of each part can be found in Figure 2. Figure 2 is a feature modeled through JMAG 22.1. A retaining sleeve is attached to prevent the permanent magnet from scattering and experiencing mechanical stress.

Table 1. Conventional model basic specifications.

Parameter	Value	Unit
Stator outer diameter	250	mm
Stator inner diameter	108	mm
Staking length	104	mm
Air gap length	1	mm
Rotor outer diameter	106	mm
Sleeve thickness	3	mm
Number of turns per slot	7	-
Number of parallel branches	2	-
Wire diameter	4.8	mm
Fill factor	42.28	%

shows the basic specifications of the conventional model. The rotor core and stator core are made of 35PN230. The coil is made of copper, and the conductivity is 58 MS/m. The retaining sleeve is made of Inconel 718, a metallic material, and has a conductivity of 0.8 MS/m. The permanent magnet is made of NdFeB 42, and the conductivity is 0.66 MS/m. A 3D finite element analysis was performed to evaluate the loss of the conventional model. The conventional model’s performance characteristics are shown in

Table 2. Performance characteristics of the conventional model.

Parameter	Value	Unit
Current	120	Arms
Phase resistance	9.63	mΩ
Torque	50.4	N·m
Shaft torque	50	N·m
Torque ripple rate	1.6	%
Line voltage	771.6	Vpeak
Line voltage THD	1.1	%
Copper loss	208.1	W
Core loss	765.6	W
Eddy current loss	2218	W
Power	102.6	kW
Efficiency	96.9	%

. The copper loss was calculated as 208.1 W by calculating the phase resistance and taking into account the winding length and the length of the end turn. By integrating the losses of the rotor core and stator core, the iron loss was calculated to be 765.6 W. Furthermore, the eddy current loss is expressed as the total of the permanent magnet and the sleeve in the rotor, and the sleeve’s eddy current loss is 2147 W. The output is 102.6 kW, and the efficiency is assessed to be 96.9%.

3. Theoretical Analysis

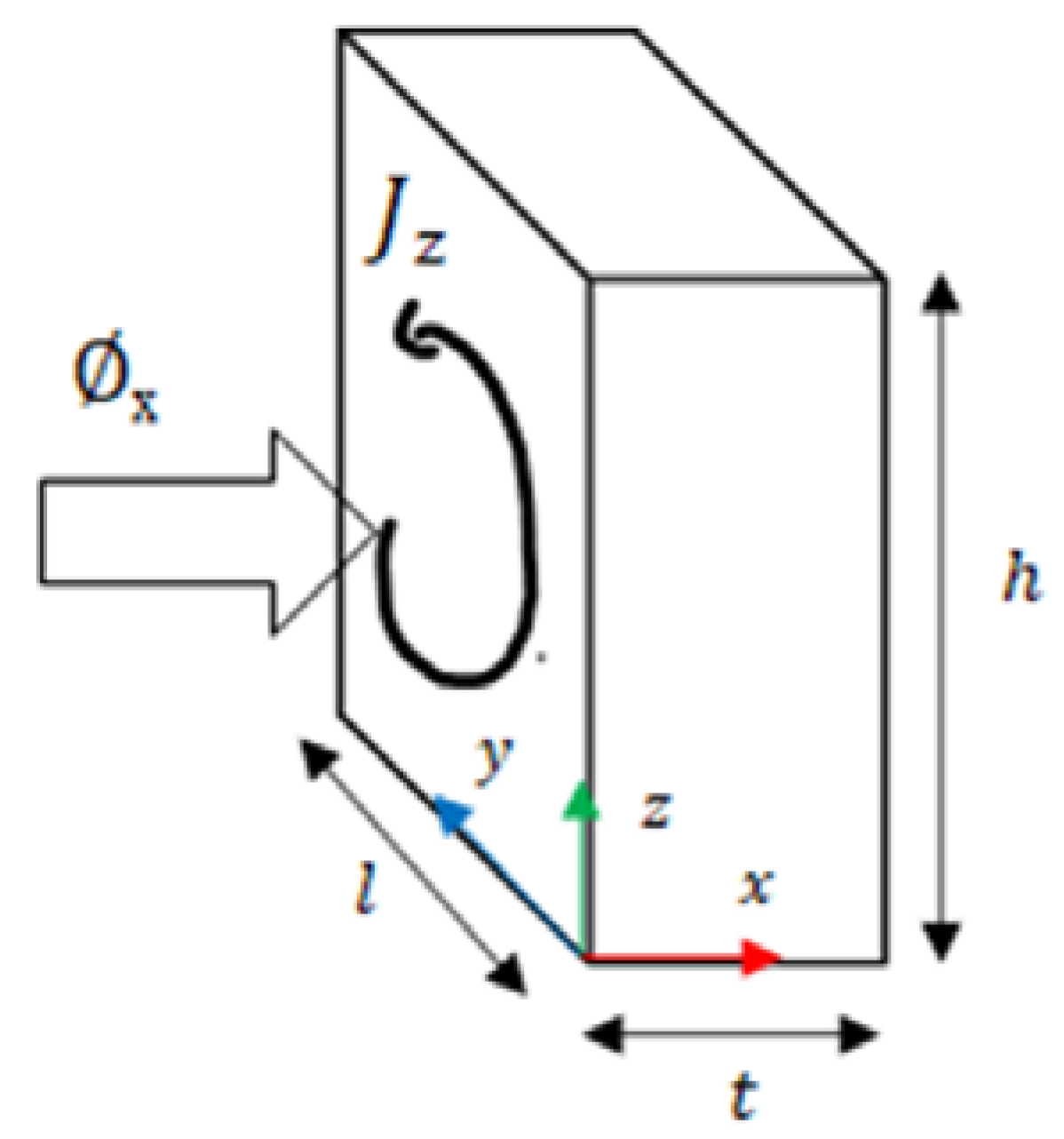
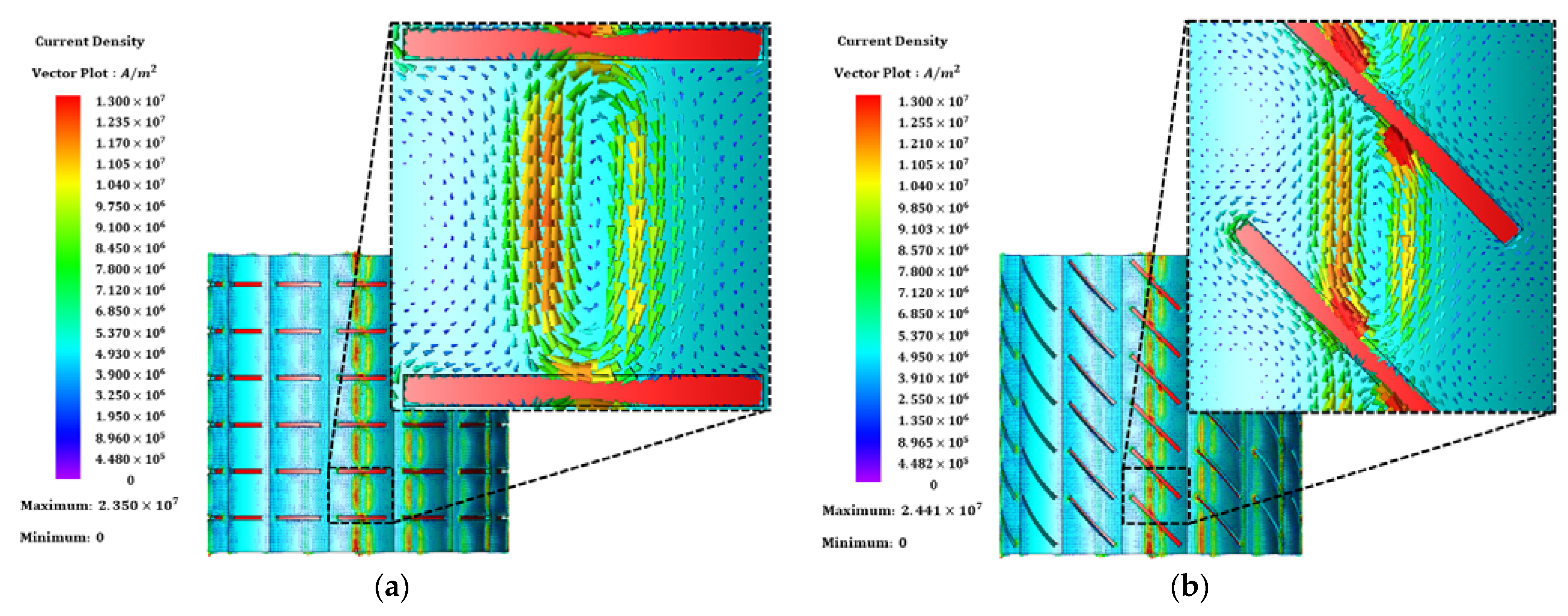
3.1. Eddy Current Loss

Three key reasons contribute to eddy current loss. The first is the PWM inverter’s carrier time harmonic component [21], the second is the spatial harmonic component caused by the change in magnetic flux density between the stator slots [22], and the final component is caused by the change in magnetic flux density caused by the change in magnetic path as the rotor rotates in the SPMSM, which is a concentrated winding [23]. It is divided into three categories. The spatial harmonic component caused by the shift in magnetic flux density between the stator slot and the slot is high in this work, so the eddy current generation is represented as follows:

$$\begin{array}{cc}\hfill P& =\int \rho J^2 dV\hfill \\ \hfill & ={{\displaystyle \int }}_{-\frac{l}{2}}^{\frac{l}{2}}\rho {\left(\frac{y}{\rho }·\frac{dB}{dt}\right)}^{2}htdy\hfill \\ \hfill & =\frac{l^{3}ht}{12\rho }{\left(\frac{dB}{dt}\right)}^2\hfill \end{array}$$

(1)

where $\rho$ is the electrical resistivity, $J$ is the current density, $l$ is the length, $t$ is the thickness, and $h$ is the height of the retaining sleeve. Figure 3 above is included to help explain the formula. The cuboid in the Figure 3 can be considered as a retaining sleeve. If there is magnetic flux from the stator to the x-axis, eddy currents will be generated due to the conductivity of the sleeve.

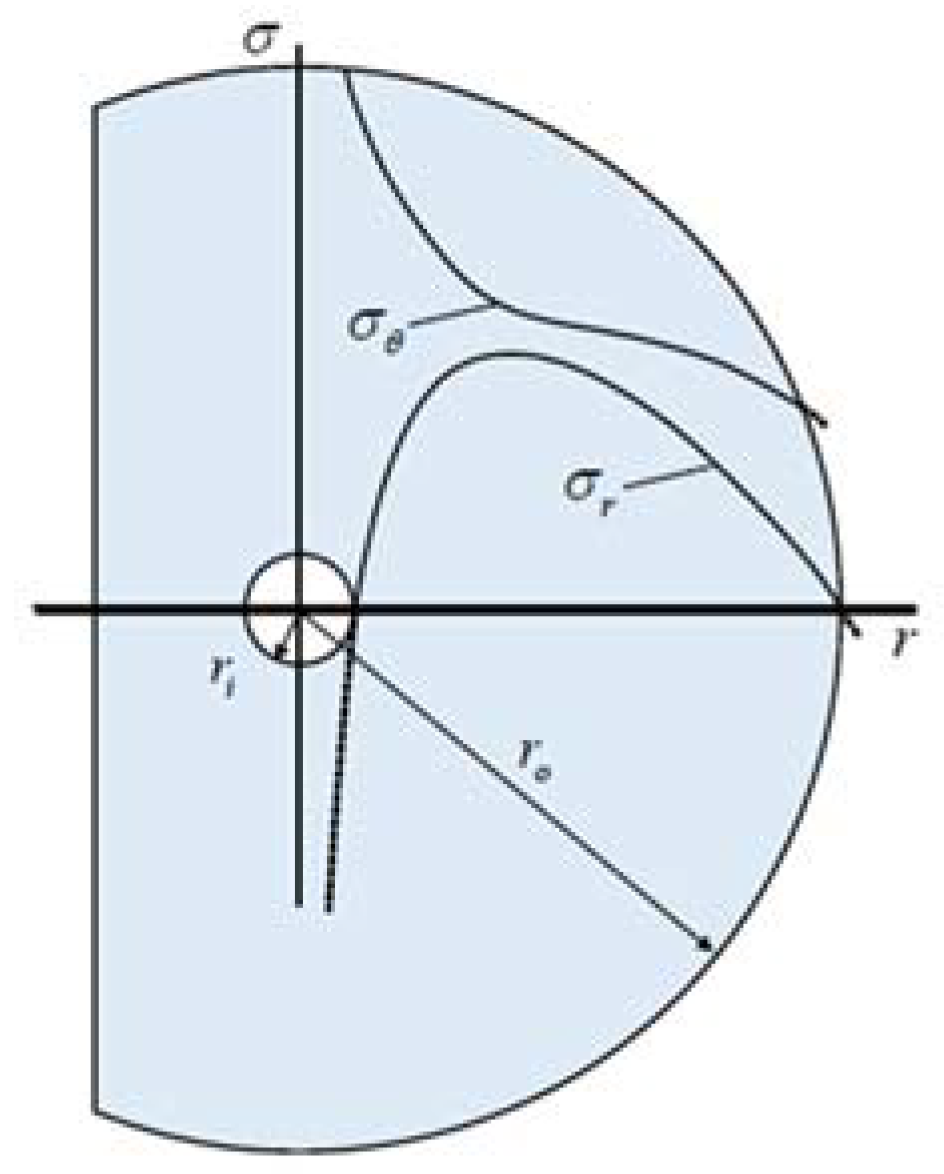
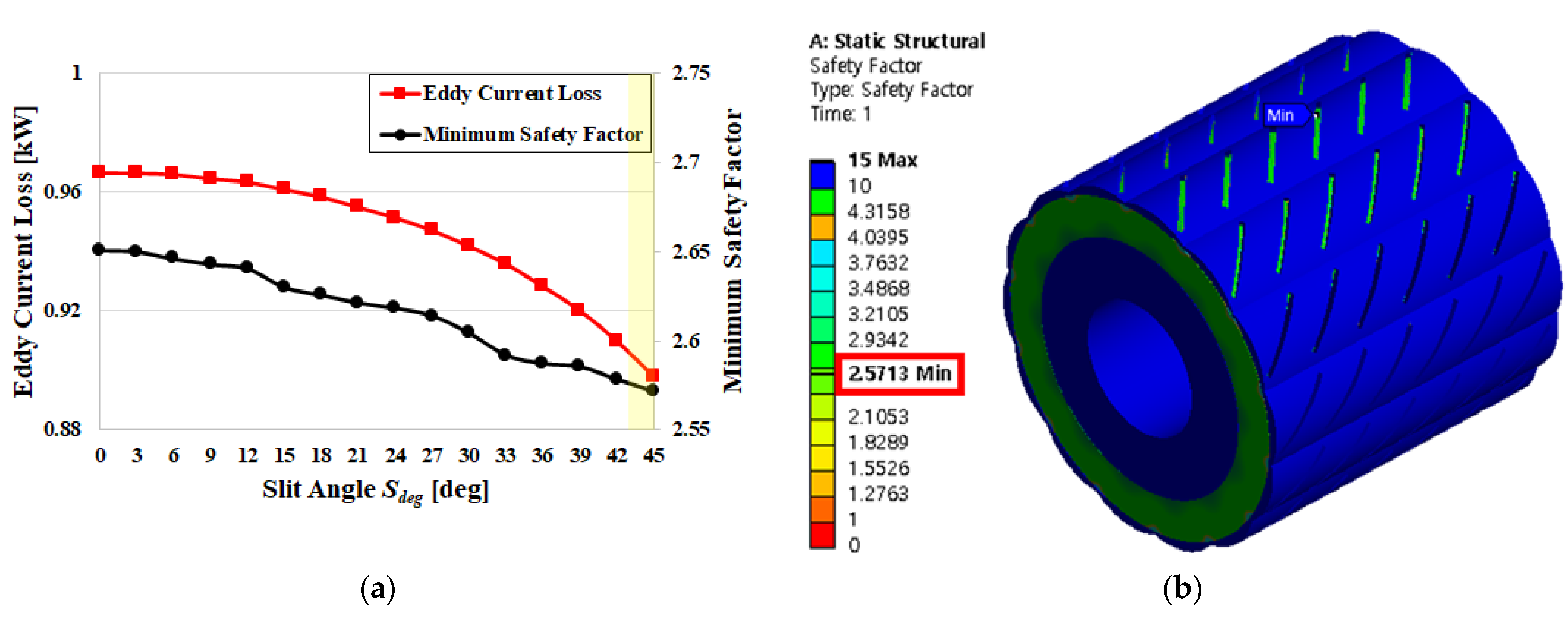
3.2. Rotor Stress and Minimum Safety Factor

Understanding the pressure and rotation effects of the cylindrical structure is required for the structural design of the surface-attached permanent magnet synchronous motor rotor. The pressure and rotation impact of the cylindrical structure are discussed in this work in order to assess the stress and safety factor when the rotor rotated. Figure 4a depicts the front view of the thick plate cylinder, whereas Figure 4b depicts the stress acting on the thick plate cylinder’s area element. If the equilibrium equation is defined as shown in Figure 4b, the equation is as follows [19]:

$$\left({\sigma }_r+d{\sigma }_r\right)\left(r+dr\right)d\theta dz-{\sigma }_{r}rd\theta dz-2{\sigma }_{\theta }\sin \left(\frac{{\sigma }_{\theta }}{2}\right)drdz=0$$

(2)

where ${\sigma }_r$ and ${\sigma }_{\theta }$ are the radial and tangential stress, respectively; and $r$, $\theta$, and $z$ are the radial, tangential, and axial direction, respectively. Since ${\sigma }_{\theta }$/2 is a very small size, when sin (${\sigma }_{\theta }$/2) ≈ ${\sigma }_{\theta }$/2 is applied, Equation (2) is rearranged as follows:

$$\frac{d{\sigma }_r}{dr}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=0$$

(3)

To calculate the stress generated only by the rotation of the cylindrical structure, the pressure inside and outside the thick plate cylinder is excluded from Equation (3) ($P_i=P_o=0$). When the thick plate cylinder as shown in Figure 4a rotates, an outward centripetal force $F_r=\rho {\omega }^{2}r$ is generated at one element of the cylinder. Applying this to the equilibrium equation in Equation (3) gives:

$$\frac{d{\sigma }_r}{dr}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}+\rho {\omega }^{2}r=0$$

(4)

where $\rho$ and $\omega$ are the volume density and angular velocity, respectively. Without considering the pressure applied to the inside and outside of the cylindrical structure, the boundary condition expression based on the rotational effect is as follows:

$$\begin{gathered} r=r_i\to {\sigma }_r=0 \\ r=r_o\to {\sigma }_r=0 \end{gathered}$$

(5)

Using the boundary condition for Equation (5), the radial and tangential stresses, and displacements due to rotational effects are calculated as follows:

$$\begin{gathered} {\sigma }_r=\frac{3+\nu }{8}\rho {\omega }^2\left(r_i^2+r_o^2-r^2-\frac{r_i^2{r}_o^2}{r^2}\right) \\ {\sigma }_{\theta }=\frac{3+\nu }{8}\rho {\omega }^2\left(r_i^2+r_o^2-\frac{1+3\nu }{3+\nu }{r}^2+\frac{r_i^2{r}_o^2}{r^2}\right) \\ {u}_r=\frac{\left(3+\nu \right)\left(1-\nu \right)}{8E}\rho {\omega }^{2}r\left(r_i^2+r_o^2-\frac{1+\nu }{3+\nu }{r}^2+\frac{1+\nu }{1-\nu }\frac{r_i^2{r}_o^2}{r^2}\right) \end{gathered}$$

(6)

where $\nu$ is the Poisson’s ratio. Figure 5 shows the radial and tangential stresses as a function of the radial position. When Equation (6) is examined, it is clear that stress in the tangential direction is greater than stress in the radial direction at all points. Therefore, considering the tangential stress ${\sigma }_{\theta }$, the tangential stress occurs maximum at $r=r_i$ and can be obtained as Equation (7) by substituting into Equation (6). The maximum radial stress occurs between $r_i$ and $r_o$, and can be obtained as in Equation (8) by differentiating with respect to the radial position $r$ in Equation (6).

$${\sigma }_{\theta ,max}=\frac{3+\nu }{4}\rho {\omega }^2\left(r_o^2+\frac{r_i^2\left(1-\nu \right)}{3+\nu }\right)$$

(7)

$${\sigma }_{r,max}=\frac{3+\nu }{8}\rho {\omega }^2{\left(r_i-r_o\right)}^2, r=\sqrt{r_i{r}_o}$$

(8)

Previously, the radial and tangential stresses caused by the pressing and rotating effects during the driving of the permanent magnet motor were obtained. However, it is difficult to judge the safety of a multi-axial structure against actual stress conditions. As a result, the equivalent stress derived by equating the directional stress state to a scalar amount is used to assess the structure’s safety. This equivalent stress is also referred to as von Mises stress [24], and is equivalent to a uniaxial tensile or compressive stress of a composite load from multiple directions. The expression for this is:

$${\sigma }_{von}=\sqrt{\frac{1}{2}\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2\right]}$$

(9)

As the rotor of SPMSM is in a state of biaxial stress in the radial and tangential directions, the equivalent stress can be obtained as follows by applying ${\sigma }_1={\sigma }_{\theta }$, ${\sigma }_1={\sigma }_r$, ${\sigma }_3=0$ in Equation (9).

$${\sigma }_{von}=\sqrt{{\sigma }_{\theta }^2-{\sigma }_{\theta }{\sigma }_r+{\sigma }_r^2}$$

(10)

The rotor structure must be designed so that the equivalent stress of the permanent magnet and the retaining sleeve calculated using Equation (10) satisfies the limited safety factor for the yield stress of each material. The formula for the minimum factor of safety to be used in this paper is expressed as:

$${\alpha }_{sf}=\frac{Yield Strength}{{\sigma }_{von,max}}\ge Limit of minimum safety factor$$

(11)

In this paper, the optimal model is selected as ${\alpha }_{sf}$ that mechanically determines safety using Equation (11).

The standard of safety factor may be different depending on the designer, but the following standard can be referred to (the suggested value of Joseph P. Vidosic) [25]:

• ${\alpha }_{sf}=1.25~1.5$: conditions and stresses can be accurately calculated, the reliability of the material quality is high, and the volume of the structure is to be reduced.
• ${\alpha }_{sf}=1.5~2$: for well-known materials that do not change load conditions and driving environments, stress can be easily calculated, and are generally applied in industry.
• ${\alpha }_{sf}=2~4$: environment, load, and stress calculations are common, and for materials that are common or not commonly used.
• ${\alpha }_{sf}=3~4$: when the operating environment fluctuates greatly, stress calculation is uncertain, or well-known materials are used.
• In this paper, the minimum safety factor for the maximum stress generated by the pressing and rotating effects on the permanent magnet and sleeve of the rotor is limited to 2 to 4.

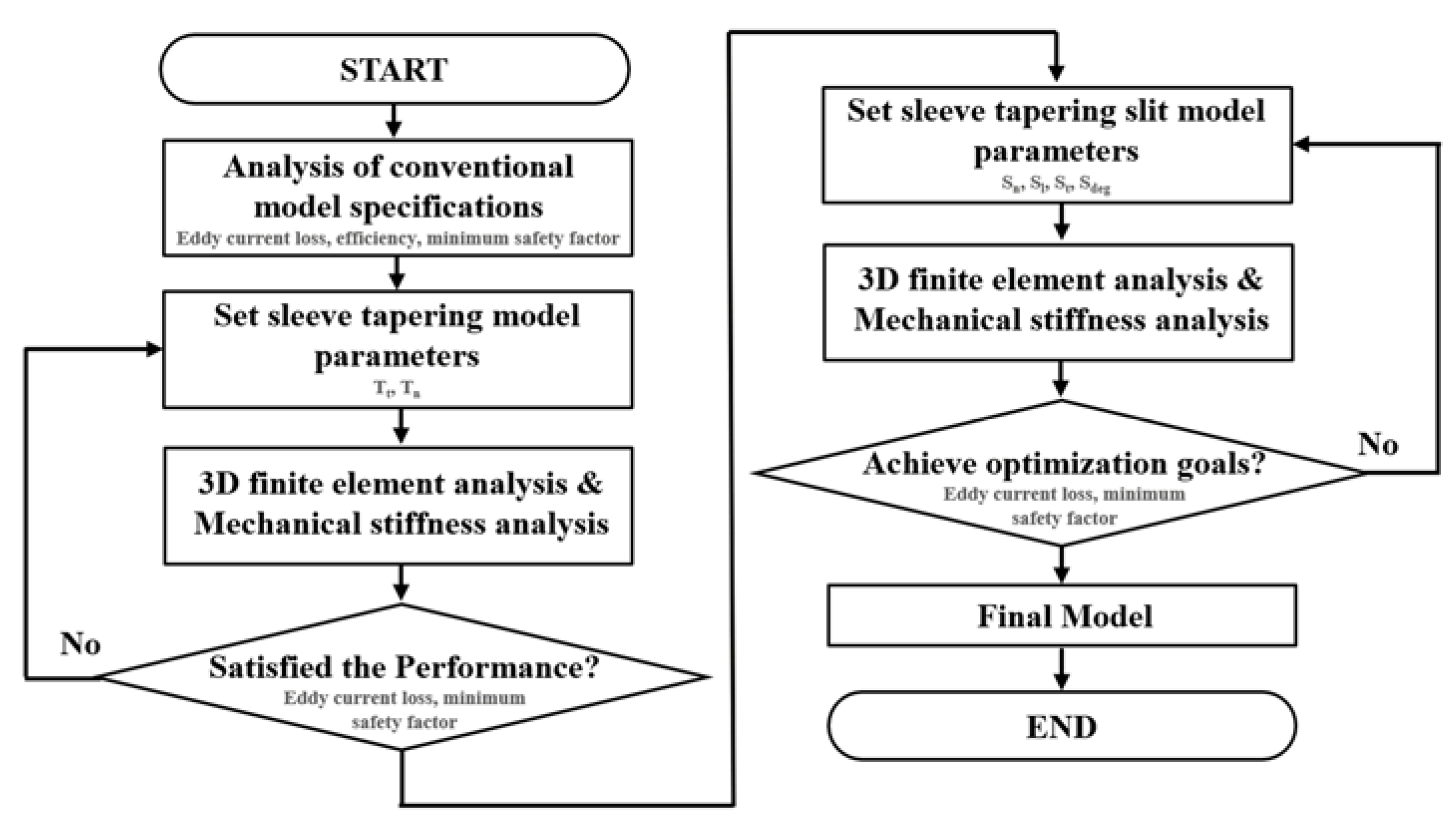
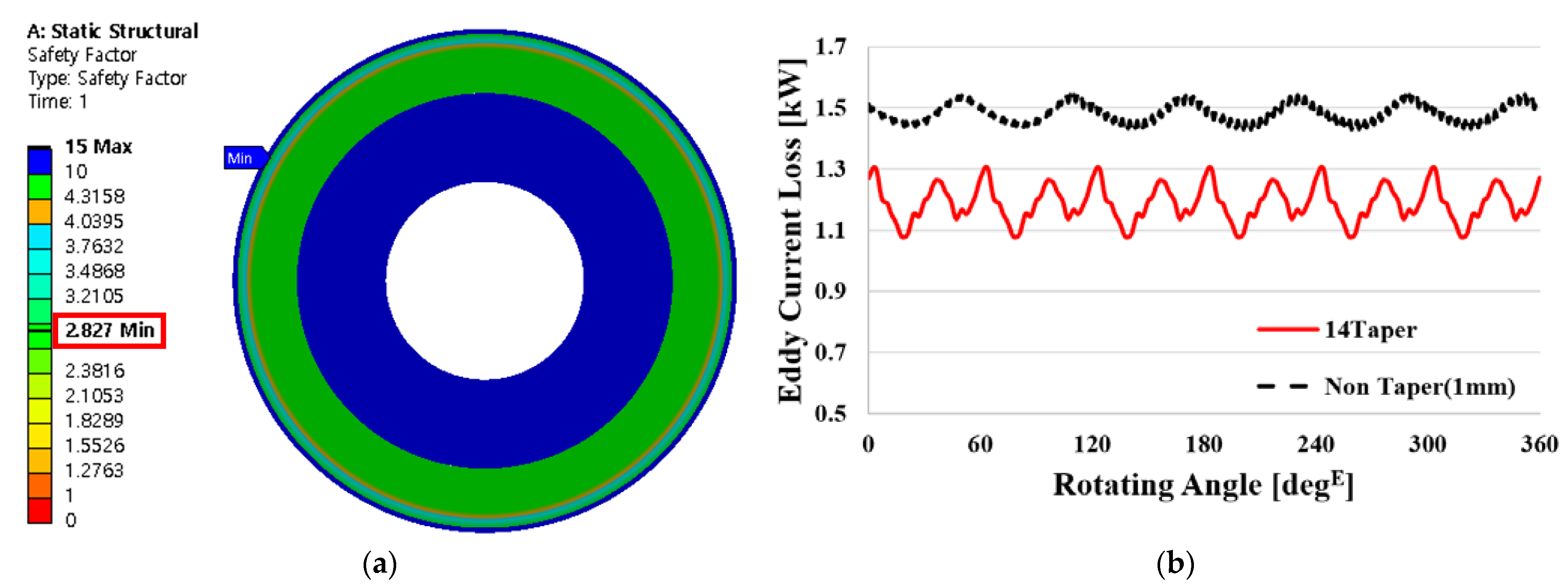
4. Sleeve Tapering Model

4.1. Proposal Sleeve Tapering Model

The reason for eddy current production in the retaining sleeve due to a change in magnetic flux density in one slot and another is examined in Equation (1). For this paper, the sleeve was tapered to create a geometric curve, as seen in Figure 6. It is a type of tapering that involves cutting the inside while keeping the sleeve’s thickness at 3 mm. As a result, the path of the eddy current created in the sleeve increases, and the resistance value increases proportionally, allowing eddy current loss to be reduced. Figure 6a depicts the proposed sleeve tapering model’s shape, while Figure 6b depicts the tapering model’s design factors. The design variables are the number of tapering ($T_n$) and the tapering thickness ($T_t$).

Table 3. Material properties in rotor.

Parameter	Inconel 718	NdFeB 42	35PN230
Mass density [kg/m3]	8220	7500	7600
Young’s modulus [Gpa]	165	160	161.4
Poisson’s ratio	0.29	0.24	0.33
Yield tensile strength [Mpa]	648	78.4	440

shows the material data for Inconel 718, NdFeB 42, and 35PN230 used in the rotor for mechanical stiffness analysis.

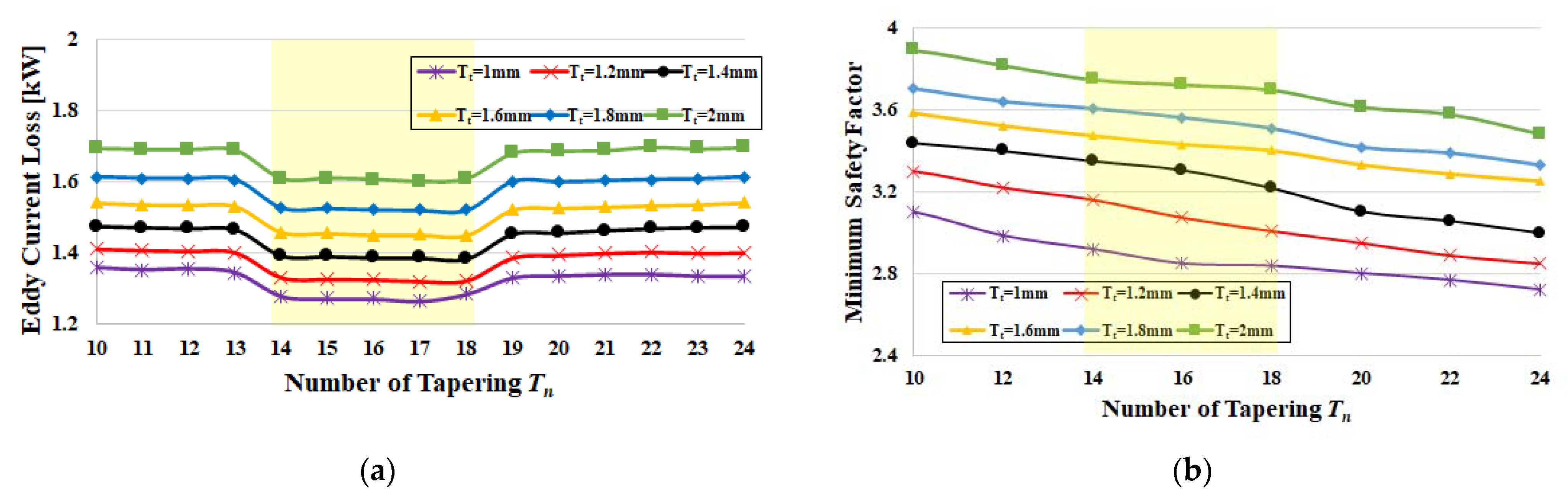
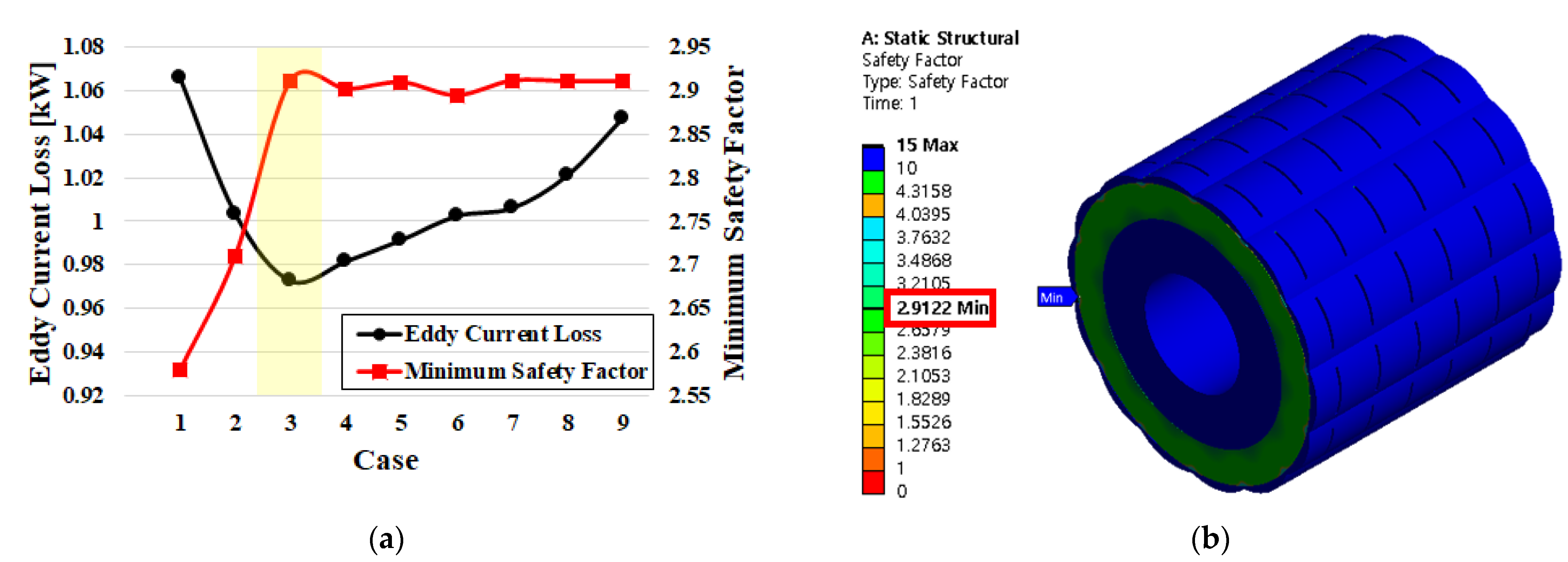
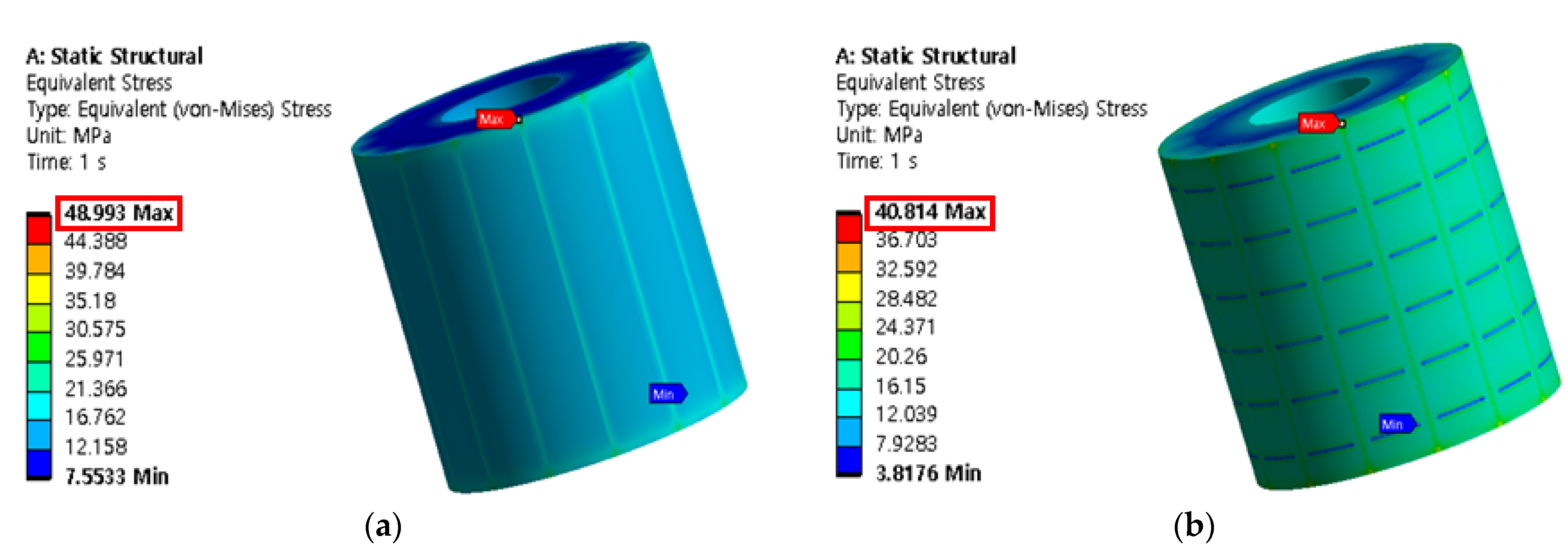
4.2. Selecting the Optimal Sleeve Tapering Model

The shape of the sleeve was proposed above, and to select the optimal sleeve tapering model considering eddy current loss and mechanical safety, the number of tapers was analyzed for each taper thickness based on the number of slots of 18. Figure 7 shows the results of eddy current loss and the minimum safety factor for the rotor. In Figure 7a, based on $T_n$ = 18, the results of eddy current loss and minimum safety factor by taper thickness are displayed. The square dotted box represents the shape of the minimum safety factor for each $T_t$. Eddy current loss and the minimal safety factor tend to grow correspondingly as taper thickness increases. JMAG 22.1 and ANSYS Workbench are used to determine these results. JMAG 22.1 was used to create the geometry. Condition established the initial angle and speed of the rotor in this software by using ‘motion: rotation’ and ‘torque: nodal force’ and holding the top and lower sides through the ‘symmetric boundary’. Based on the double layer winding, the winding was wound with a coil pitch of 9 using distributed and full-pitch winding. Mesh defined the ‘sliding mesh’, and when mesh was assigned to each part, a finite element with approximately 1.4 million mesh points was generated on a 3D basis. With this setting, the analysis was conducted in JMAG 22.1 to determine the eddy current loss. For the geometry of the rotor, ANSYS Workbench specifies rotational speed as ‘rotational velocity’, and ‘displacement’ puts limitations on the exterior of the sleeve. Each portion has a reasonable mesh setting assigned to it, and around 200,000 finite elements are produced in 3D.

The mechanical stiffness analysis findings are shown in Figure 7b. When the complete rotor, including the sleeve, was revolved at 20,000 rpm, the minimal safety factor for the maximum equivalent stress component was validated. In Figure 7b, the highest equivalent stress at the magnet’s end (marked as Min) due to centrifugal force due to rotation is approximately 19.5 Mpa, which is divided by the permanent magnet’s yield tensile strength (given in Table 3). The minimum safety factor, displayed in red, confirmed that 4.01 was obtained. Through this, the conventional model proved to be a motor with high structural safety. the goal of this paper is to reduce eddy current loss, so we chose a model that reduces eddy current loss by more than 30% (1.47 kW), and has a minimum safety factor of 2.5 or higher, when compared to a conventional model that can ensure structural safety while maximizing eddy current loss reduction. Since the conventional model is used for industrial applications, 2.5 or higher was selected in consideration of the minimum safety factor standard proposed by Joseph P. Vidosic. However, considering that the minimum safety factor of the conventional model is 4.01, a degradation of about 30% was considered. Based on the selected criteria, taper thickness was analyzed by the range (1 mm~2 mm) and the amount of tapering. Above, the appropriate taper thickness was selected based on $T_n=18$. To derive the optimal sleeve tapering model that can reduce eddy current loss, eddy current loss and minimum safety factor were analyzed up to the range of the number of tapers (10~24) and the thickness of the taper (1 mm~2 mm). Figure 8 shows the results of 3D finite element analysis and mechanical stiffness analysis for the corresponding parameter. Figure 8a shows the trend of eddy current loss for each parameter. Figure 8a shows that the eddy current is reduced more than other tapering numbers from $T_n=14$ to $T_n=18$. In the range of $T_n$ (10–13, 19–24), it was confirmed that the effect on the tapering model was not significantly affected when considering the number of slots. Figure 8b shows the minimum safety factor through mechanical stiffness analysis for each parameter. It can be seen that the thinner $T_t$ and the larger the $T_n$, the lower the structural safety. Depending on the designer’s goal, the selection model may differ. For example, if a motor has a quicker rotational speed, there is no mechanical safety margin, so a model with a high minimum safety factor should be chosen with structural safety in mind. The goal of this paper is to reduce the eddy current loss of the sleeve. The model with the lowest eddy current loss was chosen in Figure 8a, and the minimum safety factor was confirmed for that model in Figure 8b, indicating that it was structurally safe. Through this, the optimal sleeve tapering model was selected as $T_n=14$ and $T_t=1 \mathrm{m}$m. The mechanical stiffness analysis findings are shown in Figure 9. The eddy current loss of the proposed model is 1.27 kW, and, as shown in Figure 9, the minimum safety factor is 2.86. Compared to the previous model, eddy current loss was reduced by 39.5%, and the minimum safety factor was reduced by 28.6%. The proposed sleeve tapering model confirmed the reduction of eddy current loss, but the complex structure results in additional processes. Therefore, the performance feasibility of the proposed model must be verified. The eddy current loss and minimum safety factor for the sleeve tapering model were compared with the case where only the thickness of the sleeve was reduced without applying taper in the conventional model. To identify the tendency for feasibility, eddy current loss was analyzed through ANSYS MAXWELL 2D, and the minimum safety factor was analyzed through ANSYS Workbench. We designed the 2D geometry in ANSYS MAXWELL. Set ‘band’ for the rotor and enter the initial position and speed. Set boundaries in ‘Boundaries’. Set up the winding and check the sleeve part to see eddy current loss in ‘Set Eddy Effects’. By setting the mesh of each part, about 20,000 finite elements were formed. In ‘Analysis’, the first cycle of load in this software is in a transient state, so it is set to two cycles to see eddy current loss in a normal state, and ‘Time step’ is set to see one step per cycle. Figure 10 shows the results of 2D FEA results and mechanical stiffness analysis for the non-taper 1 mm model and the proposed sleeve tapering model. Figure 10a shows the minimum safety factor as a result of mechanical stiffness analysis for the non-taper 1 mm model. A local maximum stress occurs at the end of the magnet (indicated by Min), so the minimum safety factor is 2.82, as shown in the red square box. Although similar values were obtained compared to the proposed sleeve tapering model, the sleeve tapering model had a larger minimum safety factor. The reason for this is that the minimum safety factor has increased due to the non-tapered part of the sleeve tapering model, but the same is maintained at 1 mm in the tapered part, so it can be seen that a similar minimum safety factor has been obtained. Figure 10b shows the result waveform of eddy current loss analyzed according to rotor position for the 2D reference non-taper model and the proposed model. For a reasonable comparison, when the thickness was reduced in the non-taper, the length between the rotor outer diameter and the stator inner diameter was taken the same way as it was in the conventional model. The eddy current loss result from the average value of the waveform illustrated in Figure 10b was 1.48 kW for the non-taper model and 1.18 kW for the 14-taper model. It can be seen that the eddy current loss value obtained by 3D and the value obtained by 2D shown in Figure 10b are different. In the case of calculating the eddy current loss in 3D, the analysis of the finite element at each stacking part proceeds, resulting in a more accurate value. However, 2D is sufficient to see a tendency for any validity before proceeding with 3D analysis. As a result, the results of the study on the 14-taper proposed in this paper proved its performance feasibility by judging that processing may incur additional costs than non-taper 1 mm, but eddy current loss is further reduced and mechanically safer.

5. Sleeve Tapering Slit Model

5.1. Proposal Sleeve Tapering Slit Model

The reduction in eddy current loss was confirmed by changing the shape of the sleeve from the conventional model to the proposed sleeve tapering model. Furthermore, by eventually providing a straight grooved slit in the sleeve tapering structure, an ideal eddy current loss reduction model is proposed. Figure 11 depicts the shapes recommended for the rotor sleeve model. Figure 11a depicts the traditional model’s sleeve shape, Figure 11b depicts the sleeve tapering shape of $T_n=14$, $T_t=1 \mathrm{m}$m, and Figure 11c depicts the sleeve tapering slit shape and design parameters of the last proposed model. Variables include slit length ($S_l$), number of slits ($S_n$), slit thickness ($S_t$), and slit angle ($S_{deg}$).

5.2. Selecting the Optimal Sleeve Tapering Slit Model

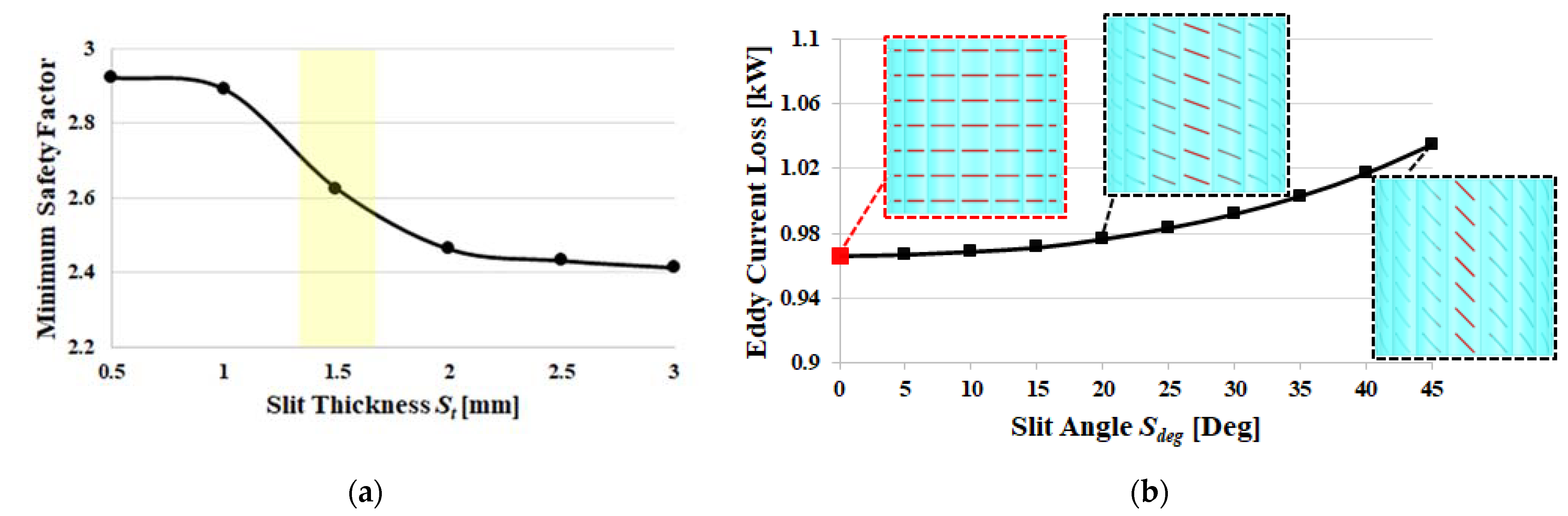
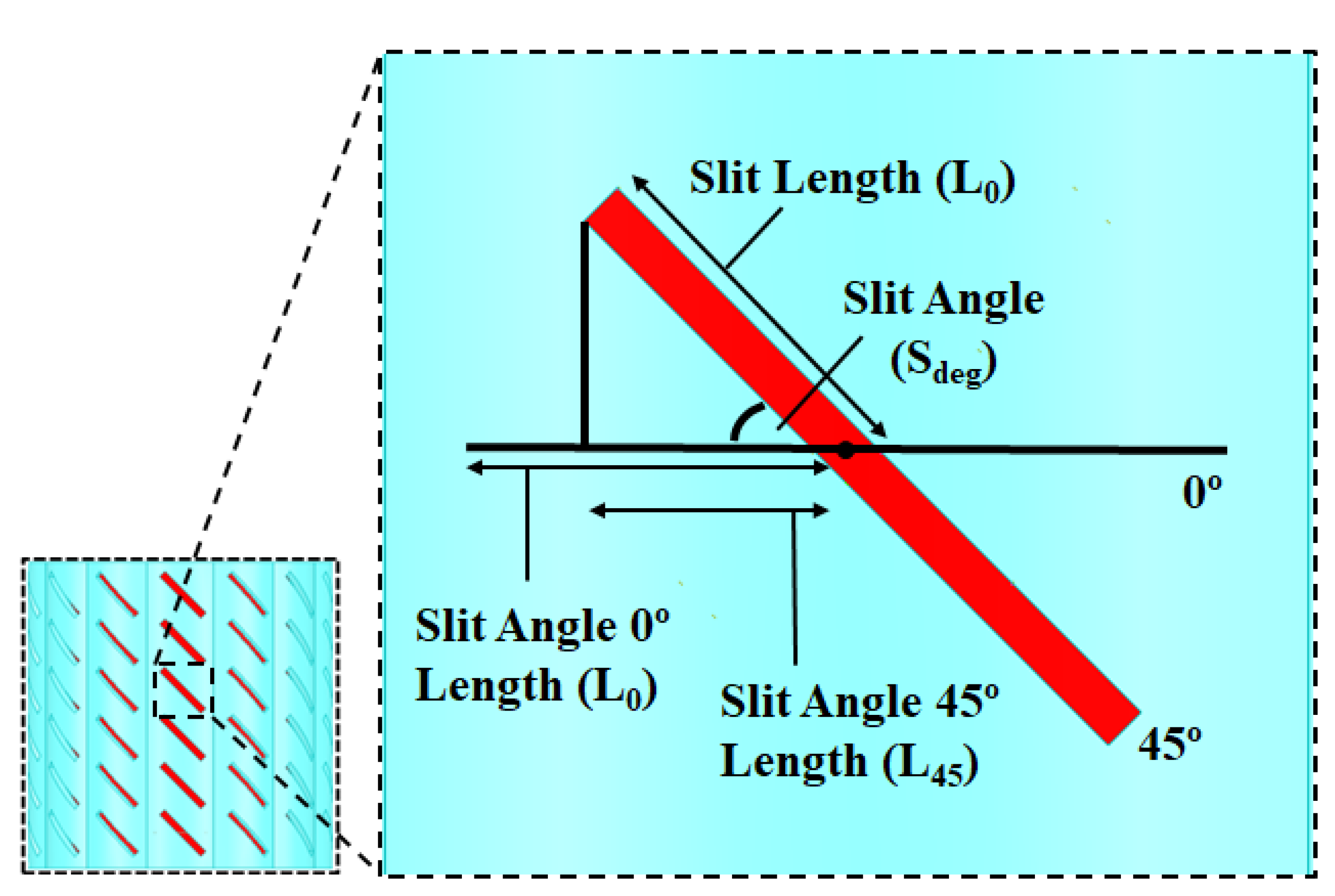
5.2.1. Selection of Slit Length ($S_l$), Number of Slit ($S_n)$

An optimal model for the sleeve tapering slit model should be derived using each variable in Figure 11c. When applying a slit to the tapering part, $S_n$ and $S_l$ are selected based on $S_t=1 \mathrm{m}$m to select the slit location. The variable $S_t$ will be optimally designed later, after $S_n$ and $S_l$ are selected.

Table 4. Case according to number of slit ($S_n)$ and slit length ($S_l)$.

Case	$\mathbf{Number}\mathbf{of}\mathbf{Slit}({\mathit{S}}_{\mathit{n}})$	$\mathbf{Slit}\mathbf{Length}({\mathit{S}}_{\mathit{l}})$
1	4	22
2	5	20
3	6	17
4	7	14
5	8	12
6	9	11
7	10	10
8	11	9
9	12	8

demonstrates that $S_n$ and $S_l$ that can be entered as maximums on the basis of the identical distance between one slit and the other slit are picked and split by case when $S_{deg}$ = 90° and the stacking length of the sleeve is 104 mm. $S_l$ = 22 is the longest length that may be entered geometrically, so 9 models were compared.

Figure 12 depicts the case’s FEA and mechanical stiffness study results. Eddy current loss analysis was performed as described in Section 4.2 for the conditions in JMAG 22.1. To obtain more precise results, the ANSYS Workbench sets the mesh condition for the slit portion to refinement. The remaining options are identical to those outlined in Section 4.2. Figure 12a shows a graphical representation of the case’s eddy current loss and minimum safety factor. The eddy current loss in case 3 follows a U-shaped curve and has the lowest eddy current loss (0.97 kW) at the inflection point. The highest equivalent stress was received as the rotor turned was different in each situation, so the minimal safety factor did not form a constant curve. case 3 was chosen, however, since it had the lowest eddy current loss (0.97 kW) and the highest minimum safety factor (2.91). Figure 12b depicts the mechanical stiffness study result for case 3. As the rotor rotates at 20,000 rpm, the maximum equivalent stress locally occurs at the tapering part of the sleeve where the permanent magnet is, resulting in a minimum safety factor of 2.91. Compared to the sleeve tapering model proposed in Section 4, the eddy current loss was reduced by 23.6% and the minimum safety factor increased by 1.7%.

The eddy current loss is minimized by giving the tapering part a slit, and the minimal safety factor is enhanced, compared to the sleeve tapering model provided in Section 4. Figure 13 demonstrates the reason for this. The mechanical stiffness analysis acquired by the magnet as the rotor rotates is depicted in Figure 13. The equivalent stress of the sleeve tapering model provided in Section 4 is shown in Figure 13a, and the corresponding stress of the case 3 model is shown in Figure 13b. The tapered slit partially disperses the tangential stress created by the centrifugal force due to rotation in Figure 13b compared to Figure 13a. As a result, the local maximum equivalent stress received by the magnet according to the rotation of the rotor occurred larger in Figure 13b, with the slit than in the tapering model. This cause is not applied to all slit models, but as shown in Figure 12a, the minimum safety factor increases by any combination of $S_n$ and $S_l$.

5.2.2. Selection of Slit Thickness ($S_t$), Slit Angle ($S_{deg})$

In the sleeve tapering slit model, two variables, $S_n$ and $S_l$, were selected among the four variables, and the thickness of the slit had to be selected. Figure 14 is the result of the minimum safety factor and eddy current loss according to each variable to select the remaining two variables. Figure 14a shows the result of the minimum safety factor according to the slit thickness ($S_t)$. The biggest factor for selecting $S_t$ is the minimum safety factor; therefore, only the minimum safety factor excluding eddy current loss is considered. It can be seen that the minimum safety factor decreases as $S_t$ increases. In Section 4.2, the minimum safety factor was set to 2.5 or higher, as a criterion selected in consideration of structural safety. Accordingly, in Figure 14a, $S_t=1.5 \mathrm{m}$m was selected, and the minimum safety factor for that condition was 2.64. In the selection of the remaining variables, the margin for the minimum safety factor was considered and selected as follows. Three variables were selected among the four variables, and finally, a variable for $S_{deg}$ was selected. Subsequently, variables were selected for $S_{deg}=0°$, and eddy current loss was analyzed in the range 0°~45° by only turning the angle at the position of the slit. Figure 14b shows the eddy current loss results in the range of $S_{deg}$, and the figure within the square dotted line shows the shape for the angle. In Figure 14b, it can be seen that the eddy current loss increases as $S_{deg}$ increases. Therefore, $S_{deg}=0°$, which reduces eddy current loss the most, was selected. In this case, the eddy current loss is 0.96 kW. In Figure 14b, it is confirmed that the reduction of eddy current loss decreases as $S_{deg}$ increases. Figure 15 shows an analysis of the cause of this. It also shows the magnetic flux diagram and eddy current path at the same step through 3D finite element analysis. Figure 15a shows the magnetic flux curve path at any position of the rotor. The armature current flows and the magnetic flux curve flows, showing the magnetic flux curves in the slot portion that passed and the slot portion that will pass while the rotor rotates. The magnetic flux curve at the corresponding rotor position is shown in the red square box. Figure 15b shows the path of the eddy current formed by the change in magnetic flux, as described in Section 3.1. Here, the sleeve, which is a material that is non-magnetic and has conductivity, can apply the disc principle of Arago, which is the principle of an induction machine. In the figure in the square dotted box in Figure 15b, which is the enlarged part of the red box in Figure 15a, an attraction force is formed in a clockwise direction (right red arrow) where the slot passed, and a repulsive force is formed in a counterclockwise direction (left red arrow) where the slot will pass. At the slot opening, the strongest eddy current path is formed in the direction where these two forces are combined (middle red arrow). That is, it was confirmed that eddy currents with high intensity were formed in the stacking direction (vertical direction) of the direction in which the magnetic flux entered in the slot opening part, which is the middle part of one slot and the other slot in the stator. When the slit is applied to the tapering, the eddy current path in the stacking direction formed by the change in magnetic flux is blocked while the rotor rotates, and a new path is formed in the blocked area. This increases, and the eddy current loss is reduced accordingly.

5.2.3. Numerical Approach to Block Length

As a result of Figure 14b, it can be confirmed that the reduction of eddy current loss decreases as $S_{deg}$ increases. The reason for this is explained in Figure 16, with reference to Figure 15b. In Section 5.2.2, it was found that as the rotor rotates, an eddy current path with high intensity is formed at the part where the sleeve meets the stator slot opening due to the change in magnetic flux. Figure 16 is an example of comparing the block length to see how much the eddy current path in the stacking direction is blocked due to $S_{deg}=0°$ and $S_{deg}=45°$. Here, the block length is defined as the length that blocks the eddy current path in the stacking direction generated in the sleeve. Since the angle of the slit rotates based on the midpoint of the slit, when $S_{deg}=0°$, the block length that blocks the eddy current path in the stacking direction is called slit angle 0° length $(L_0)$ (arrow just below $S_{deg}=0°$ block length). When $S_{deg}=45$°, the block length is called slit angle 45° length $(L_{45})$ (arrow below second of $S_{deg}=0°$ block length). $S_n$, $S_l$, and $S_t$ were selected in Section 5.2.1 and Section 5.2.2. By the same standard, only $S_{deg}$ was analyzed for eddy current loss in the range 0°~45°. As a result, it can be confirmed that the smallest eddy current loss occurs at $S_{deg}=0°$. When $S_{deg}=0°$, it can be seen that the block length blocking the path of the eddy current formed in the stacking direction is the largest. As $S_{deg}$ increases, $L_0$ (arrow indicating Slit length) decreases as much as cos ($S_{deg}$), so it is confirmed that the block length is reduced, and the eddy current loss reduction is also reduced. If the block length according to $S_{deg}$ is formulated based on $S_{deg}=0°$ with the lowest eddy current loss, it is expressed as follows.

$$L_0\cos \left(S_{deg}\right)=L_{45}$$

(12)

In Equation (12), it can be seen that as the slit angle is changed, the block length is reduced by cos ($S_{deg}$) compared to $L_0$. Block length plays a role in reducing eddy current loss according to the degree of blocking the eddy current path. A longer block length blocks more eddy current paths in the stacking direction that are formed as the rotor rotates, so eddy current loss can be reduced more effectively. This blocks more of the path for eddy currents, increasing the resistance of the overall circuit and, thus, reducing eddy current losses. Selecting an appropriate block length is very important for reducing eddy current loss.

5.2.4. Selection of Same Block Length Model

In Section 5.2.2, eddy current loss was confirmed in the range of $S_{deg}$ (0°~45°) based on the same $S_l$. Through Equation (12), it was confirmed that the block length decreases as $S_{deg}$ increases. The minimum safety factor of the model selected in Section 5.2.2 is 2.64.

Compared to the standard of 2.5 selected in this paper, the margin remains. To further reduce the eddy current loss, Equation (12) is used to make the same block length by adding $L_0$ cos ($S_{deg}$) from $S_l$ as $S_{deg}$ increases based on $S_{deg}=0°$. Figure 17 shows the results of 3D finite element analysis and mechanical stiffness analysis when only $S_{deg}$ is increased for the slit at the same location in the same block length. The reason why $S_{deg}$ is set to range 0°~45° is because of the shape aspect. In this paper, to match the same block length, as $S_{deg}$increases, the slit length increases by $L_0$ cos ($S_{deg}$). If $S_{deg}$ exceeds 45°, the top and bottom slits are not satisfactory in shape, therefore it was set up to the range of 0°~45°. Figure 17a shows eddy current loss and minimum safety factor for each $S_{deg}$ in the same block length. As $S_{deg}$ increased, eddy current loss and minimum safety factor decreased. Figure 18 shows the eddy current path at the same step as the slit angle increases for the same block length. Figure 18a shows the eddy current path for $S_{deg}=0°$. Figure 18b shows the eddy current path for $S_{deg}=45°$. In Section 5.2.2, the slit blocks the eddy current path in the stacking direction formed by the change in magnetic flux as the rotor rotates, and a new path is formed in the blocked area, increasing the eddy current path, increasing the resistance, and is said to reduce eddy current loss. In Figure 18, it can be seen that a new path is created in the area where the eddy current is blocked by the slit. It can be seen that the eddy current path in the transverse direction increases geometrically at $S_{deg}=45°$ compared to $S_{deg}=0°$. It was proved that as $S_{deg}$ increases, the eddy current path increases in the transverse direction in the region blocked by the slit in the stacking direction, increasing the resistance and reducing the eddy current loss accordingly. The $S_{deg}=45°$ model, which is larger than the minimum safety factor considering structural safety and has the most reduced eddy current loss as 0.89 kW, was selected for this paper, and is shown in Figure 17a. The mechanical stiffness results at this time can be seen in Figure 17b. In Figure. 17b, it can be seen that the largest local stress occurs in the slit part, and the minimum safety factor is 2.57 in this part. The optimal eddy current loss reduction sleeve model proposed in this paper has the shape shown in Figure 17b. Compared to the sleeve tapering model in Section 4, the eddy current loss was reduced by about 29.9% and the minimum safety factor was reduced by 2.6%. Finally, when compared with the conventional model, the eddy current loss was reduced by 57.6%, and the minimum safety factor was reduced by 35.9%. The proposed final model was able to increase the efficiency by 1.3% compared to the conventional model, because it reduced the eddy current loss in the rotor, which occupied a large part as a loss at high speed, while it was judged to be structurally safe.

6. Conclusions

In this paper, we offered an ideal model for reducing eddy current loss in a building air conditioning system motor driven at rated 100 kW and 20,000 rpm. We presented a method for optimizing sleeve design and offer two designs that can reduce sleeve eddy current loss. First, a model for sleeve tapering was proposed. By tapering and geometrically curving the sleeve, it was feasible to enhance resistance and reduce eddy current loss by lengthening the route of the eddy current created by the change in magnetic flux at the stator slot opening. Eddy current loss was reduced by 39.5% in the sleeve tapering model compared to the conventional model, but the minimal safety factor dropped to 28.6%. Finally, a model of a sleeve tapering slit was proposed. By providing a straight grooved slit to block the eddy current path with high strength in the stacking direction in the sleeve tapering structure, the eddy current path increases in the blocked area, increasing resistance and minimizing eddy current loss. The block length is defined, in this context, as the length that completely blocks the eddy current route in the stacking direction. By adjusting the angle, the best sleeve model that can reduce the eddy current loss the most for the same block length was chosen. In comparison to the prior model, eddy current loss was reduced by 57.6%, but the minimum safety factor was reduced by 35.9%. To demonstrate the study’s validity, reasonable results were obtained using 3D finite element analysis and mechanical stiffness analysis. In this paper, a study was undertaken to reduce the eddy current loss of the sleeve. Variable settings can differ depending on the type of motor, application, and designer’s preferences. It is envisaged that the proposed sleeve optimization design would serve as a crucial foundation for improving the shape of the sleeve with different types of motors and designer’s different standard settings.