Mechanical Design of a 2-PRR Parallel Manipulator for Gait Retraining System
Abstract
:1. Introduction
1.1. Motivation
1.2. Parallel Manipulators
1.3. Proposed System
- Has fewer DoFs than most commercial options, which could lead to a more economic system due to having fewer actuators.
- The kinematics of the system is relatively simple to control.
- VR task-oriented exercises can be conducted simultaneously while gait retraining.
- Assists the demand for gait retraining systems in Colombia.
- Even if the design context is specific, it could be transposed to a similar context overseas, e.g., in Latin American countries.
- A reduced number of DoFs to control the ankle’s trajectory, similar to [16], is achieved.
- A detailed description of dimensional synthesis based on kinematical performance indices, which other studies do not explicitly report [5,16]. Involving performance indices in the synthesis improves the design robustness, e.g., augmenting the workspace and dexterity with sufficient stiffness. Even when no inertial parameters are determined in this stage, a kinematically-assessed design promotes an appropriate dynamic behavior.
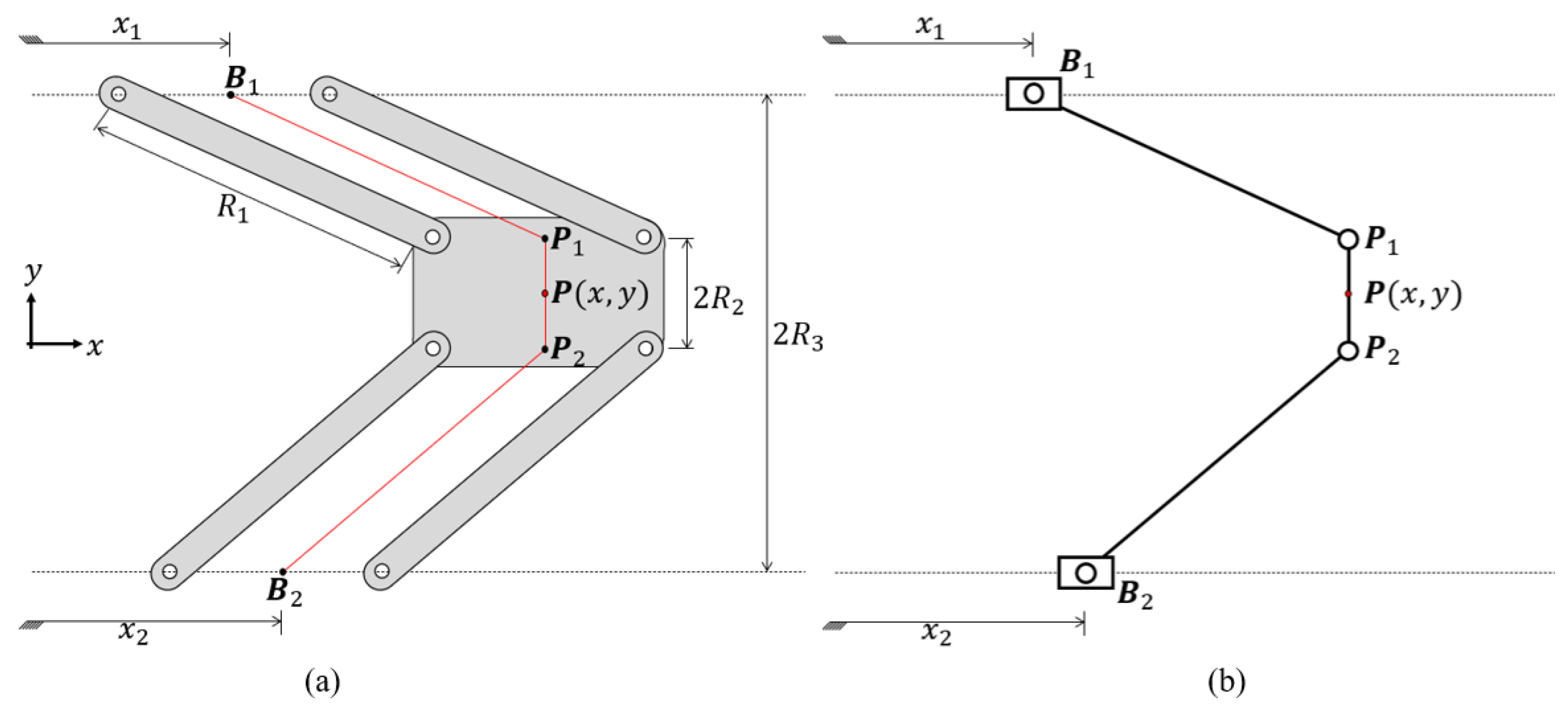
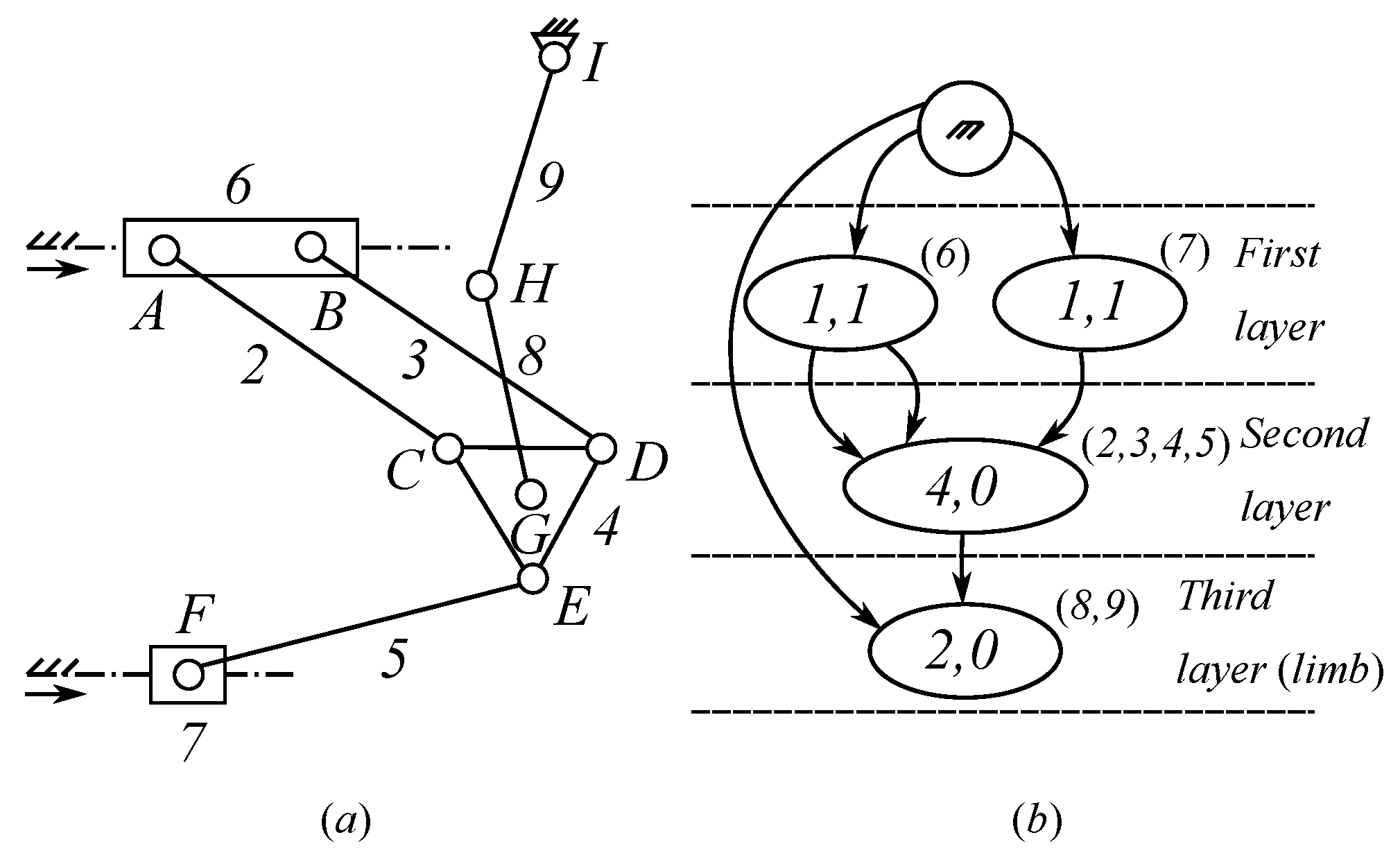
2. Kinematic Model
2.1. Inverse Kinematics
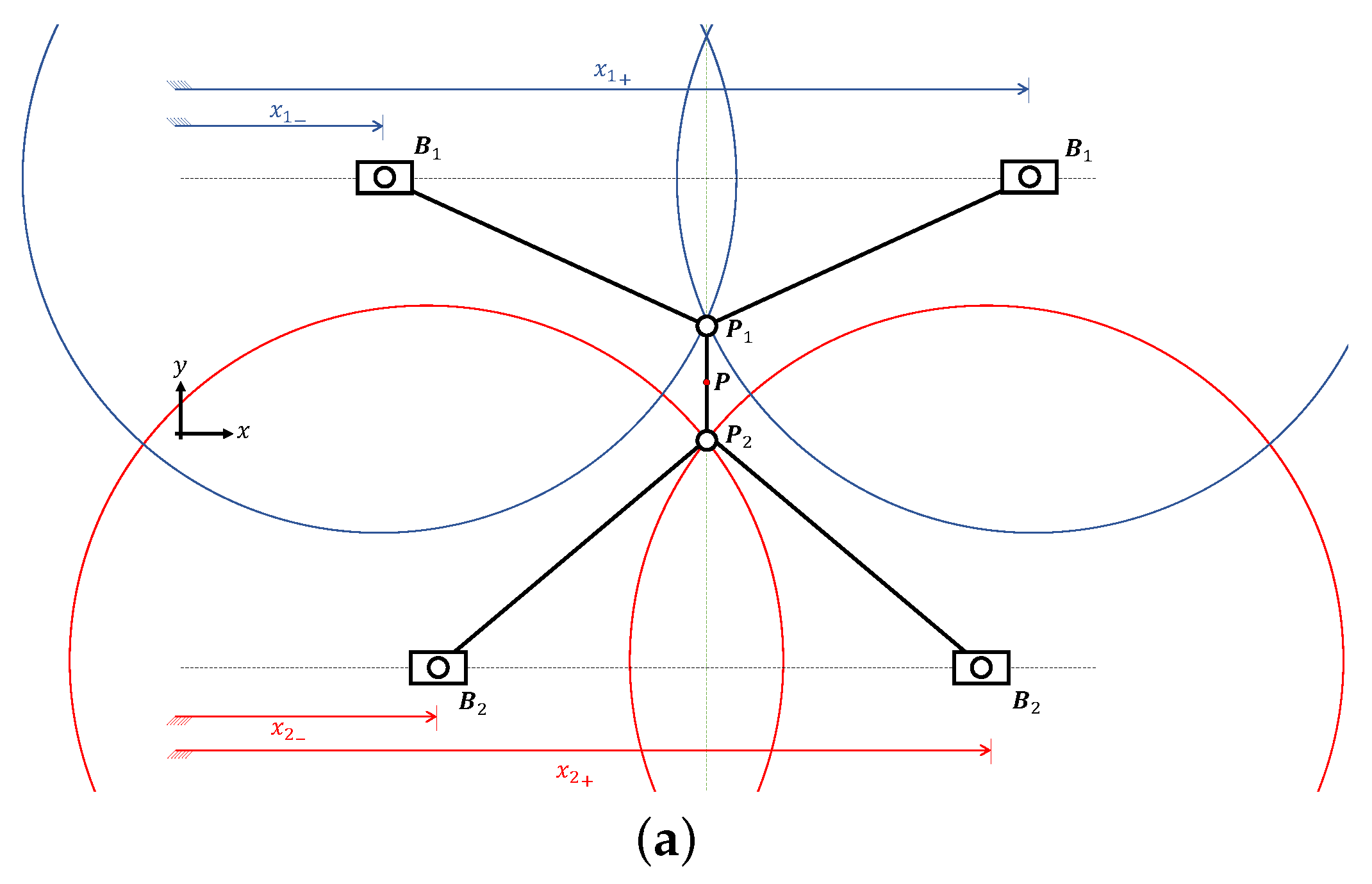
2.2. Forward Kinematics
2.3. Singularity Analysis
2.4. Parameter-Finiteness Normalization Method (PFNM)
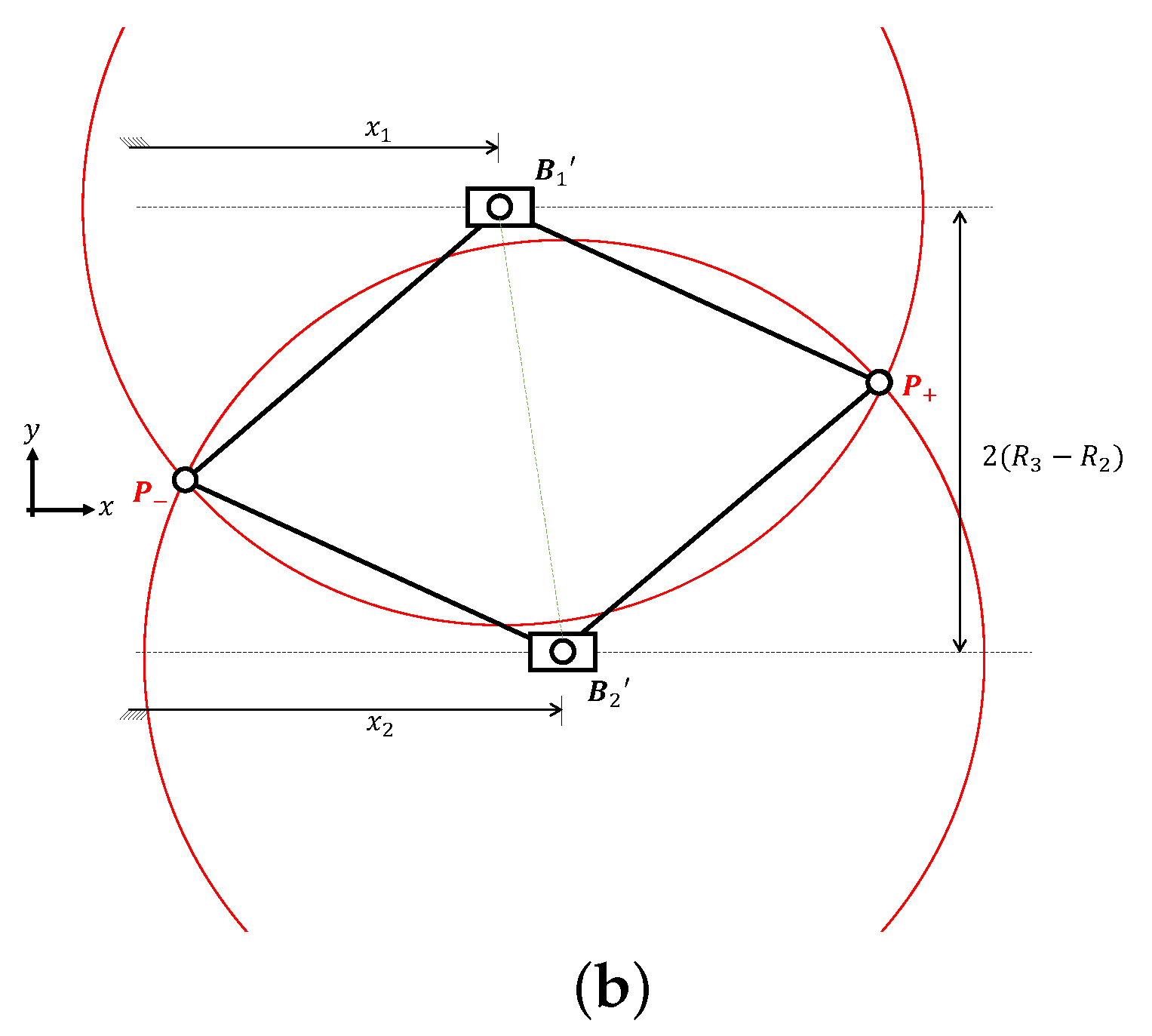
2.4.1. Non-Dimensional Translational Workspace Size
2.4.2. Minimum Linkage Length
2.4.3. Maximum and Global Conditioning Index
2.4.4. Global Rigidity Index
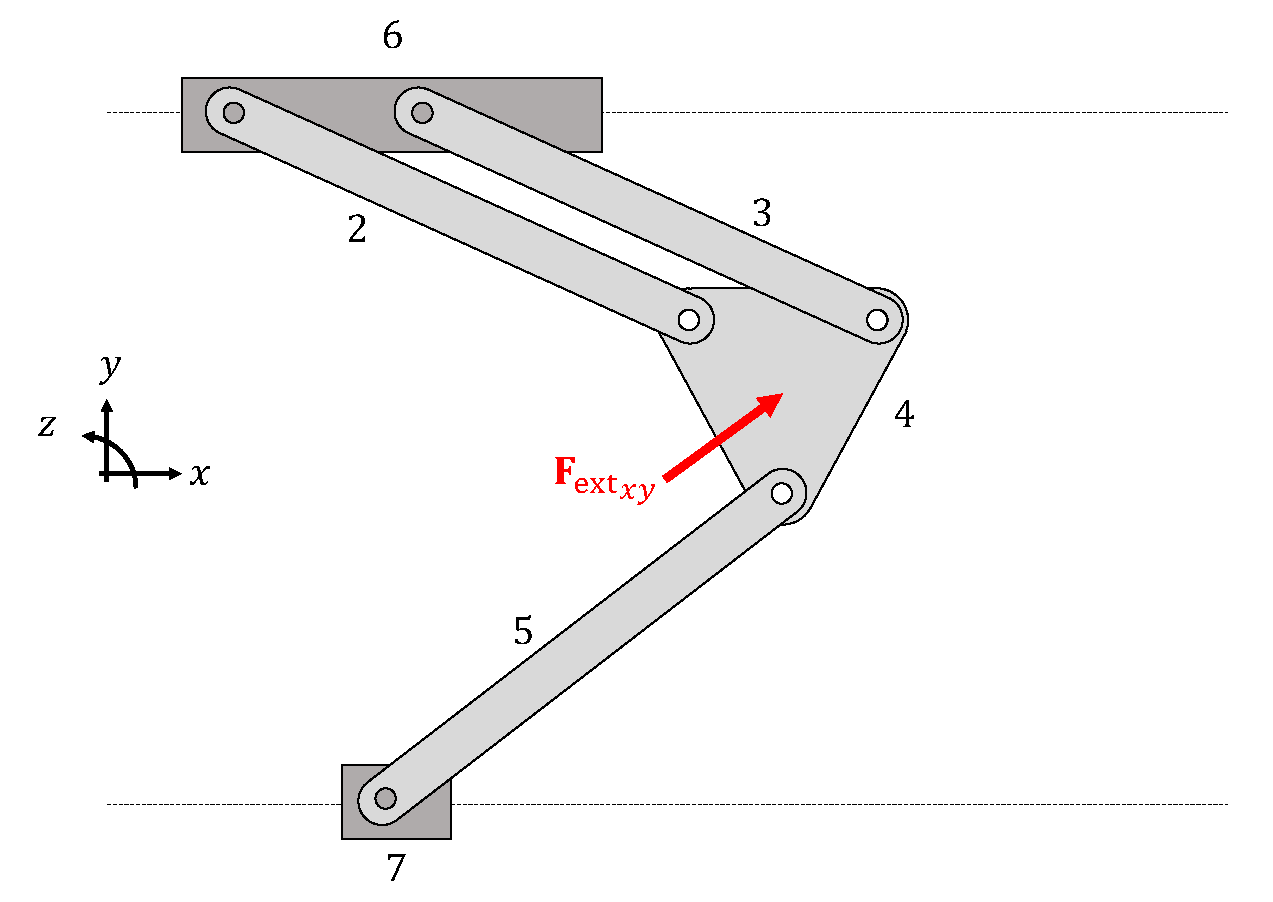
3. Force Analysis
4. Machine Design
4.1. Static Failure
4.2. Buckling Failure
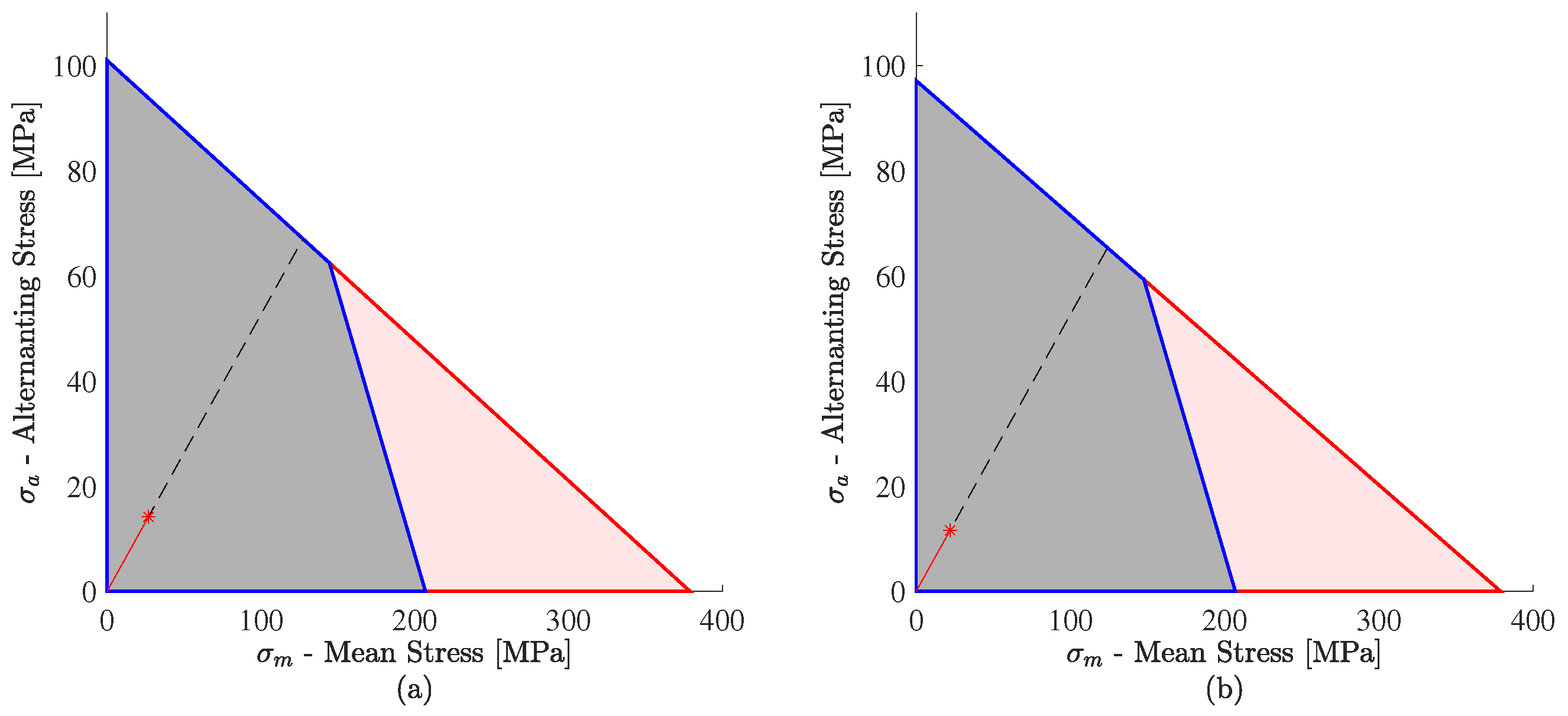
4.3. Fatigue Failure
5. Results
5.1. Performance Atlases
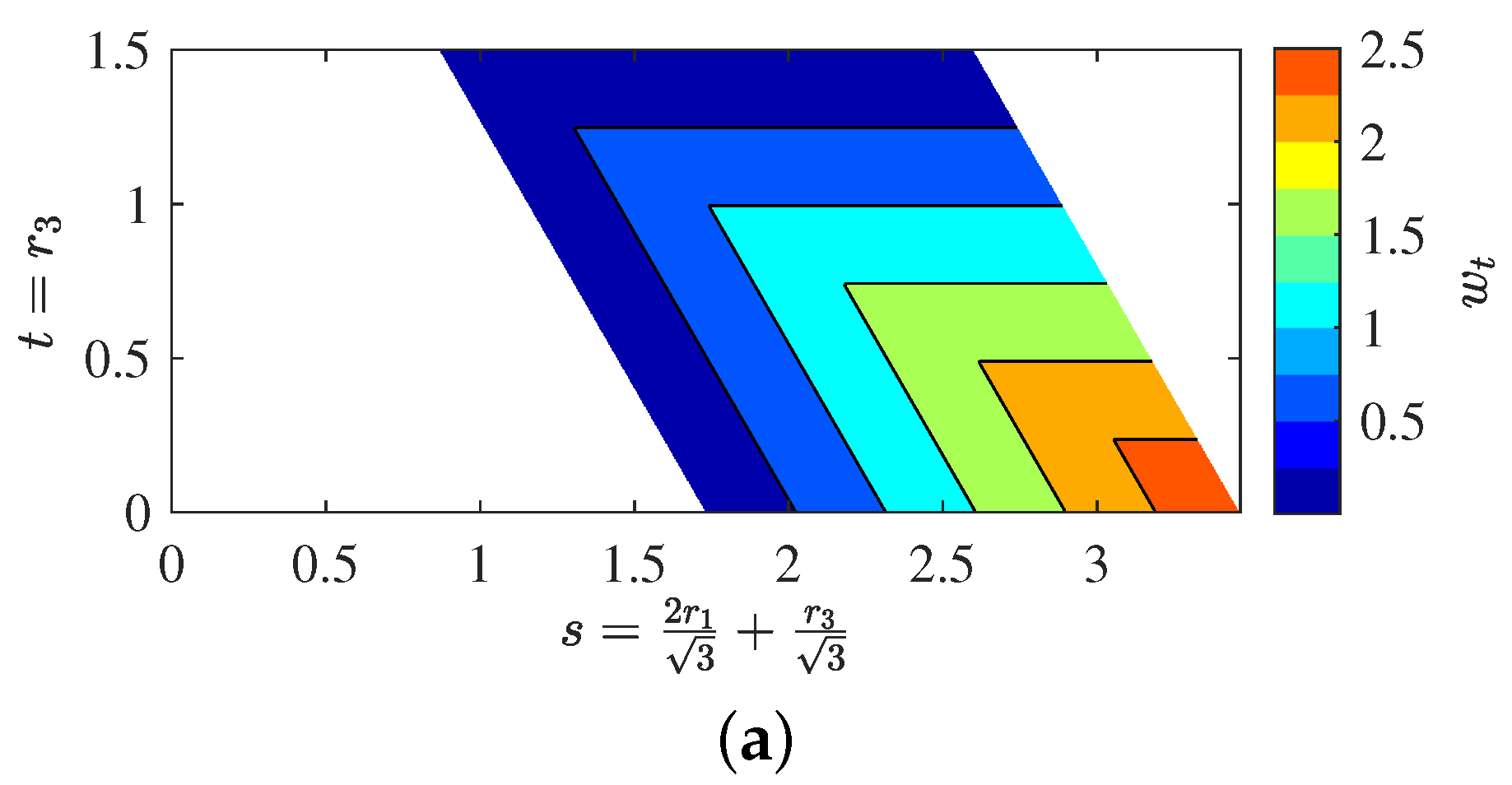
5.1.1. Non-Dimensional Workspace
5.1.2. Minimum Characteristic Length
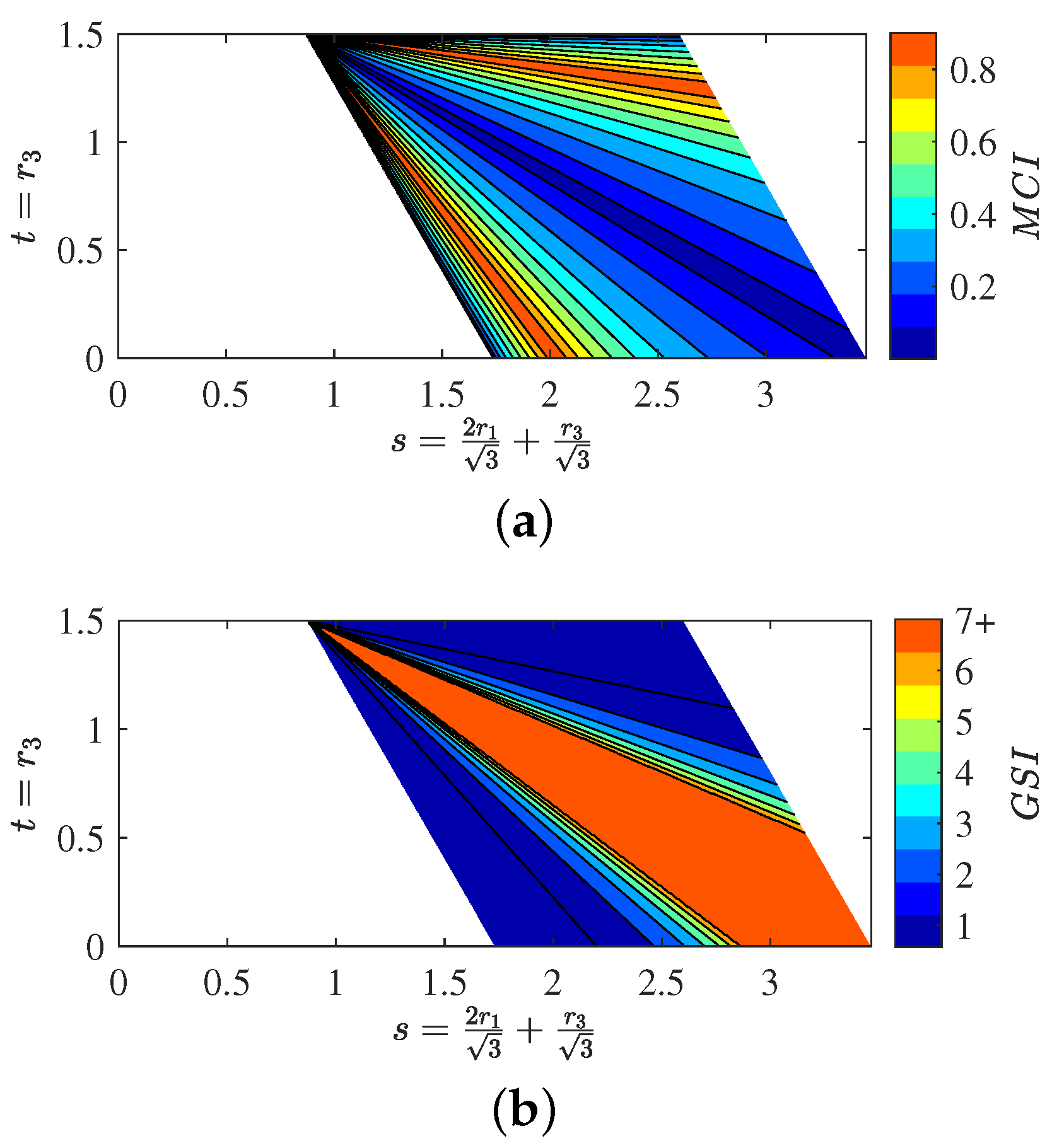
5.1.3. Maximum and Global Conditioning Index
5.1.4. Global Rigidity Index
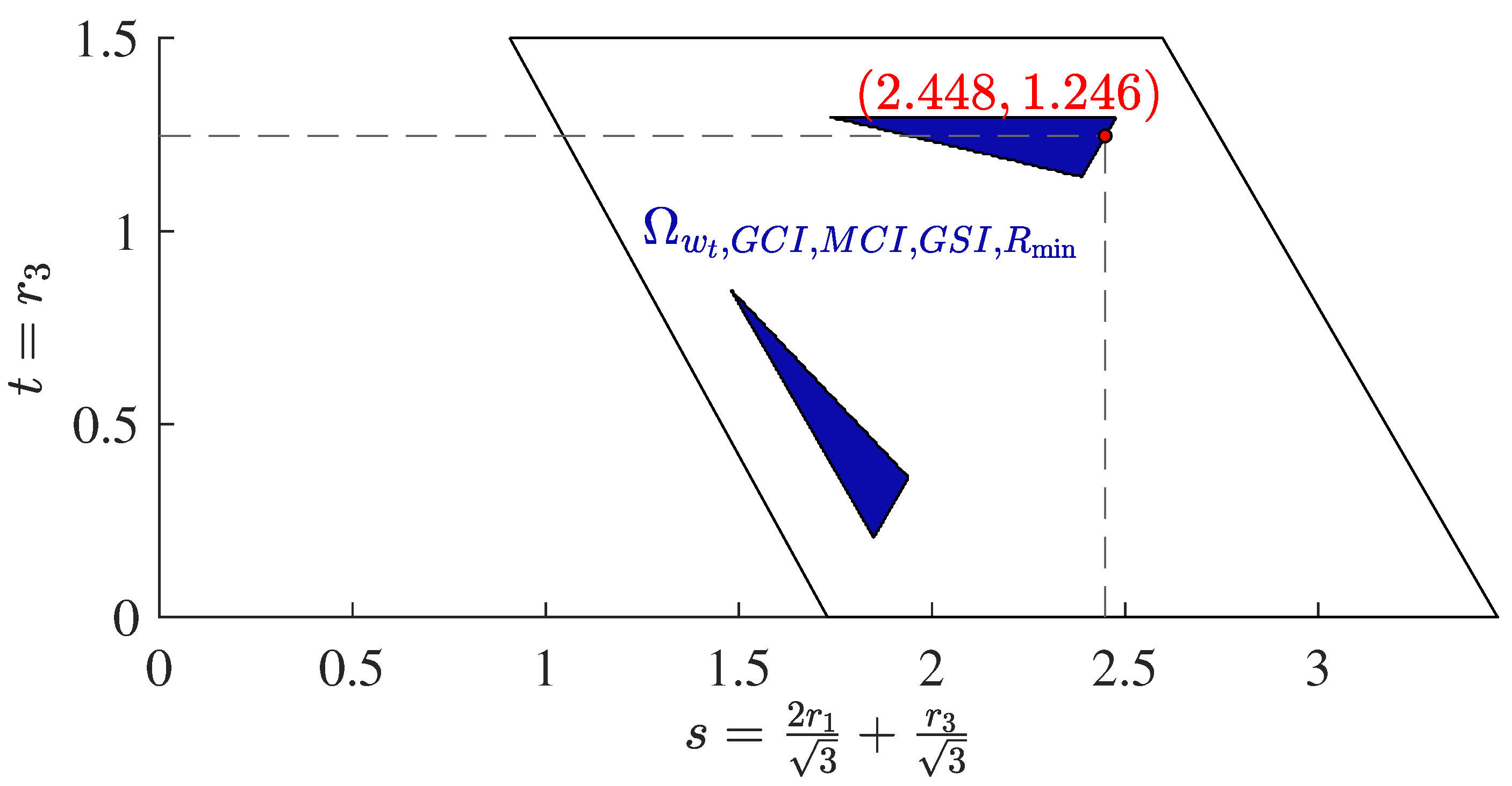
5.2. Dimensional Synthesis
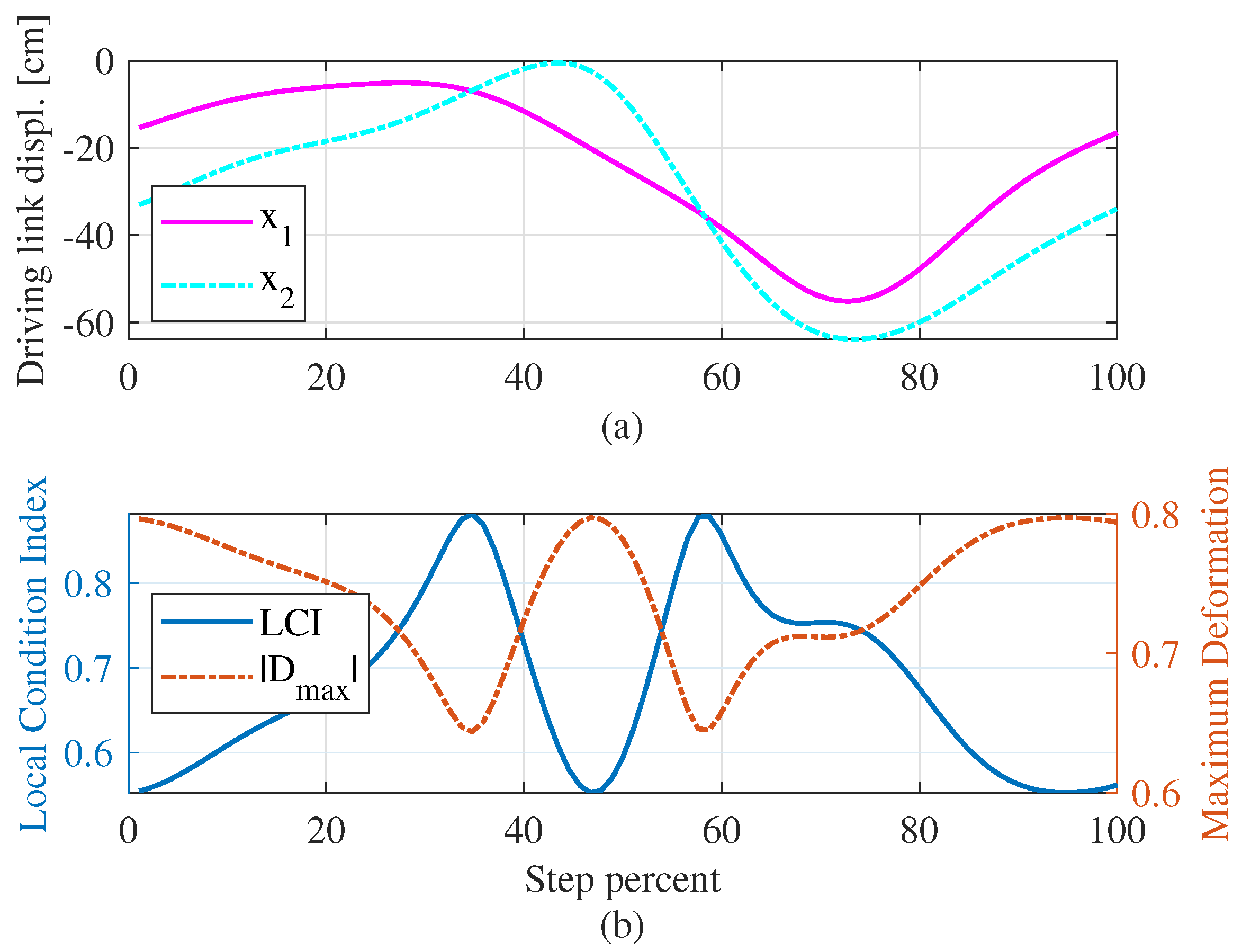
5.3. Validation of Kinematic Design Criteria
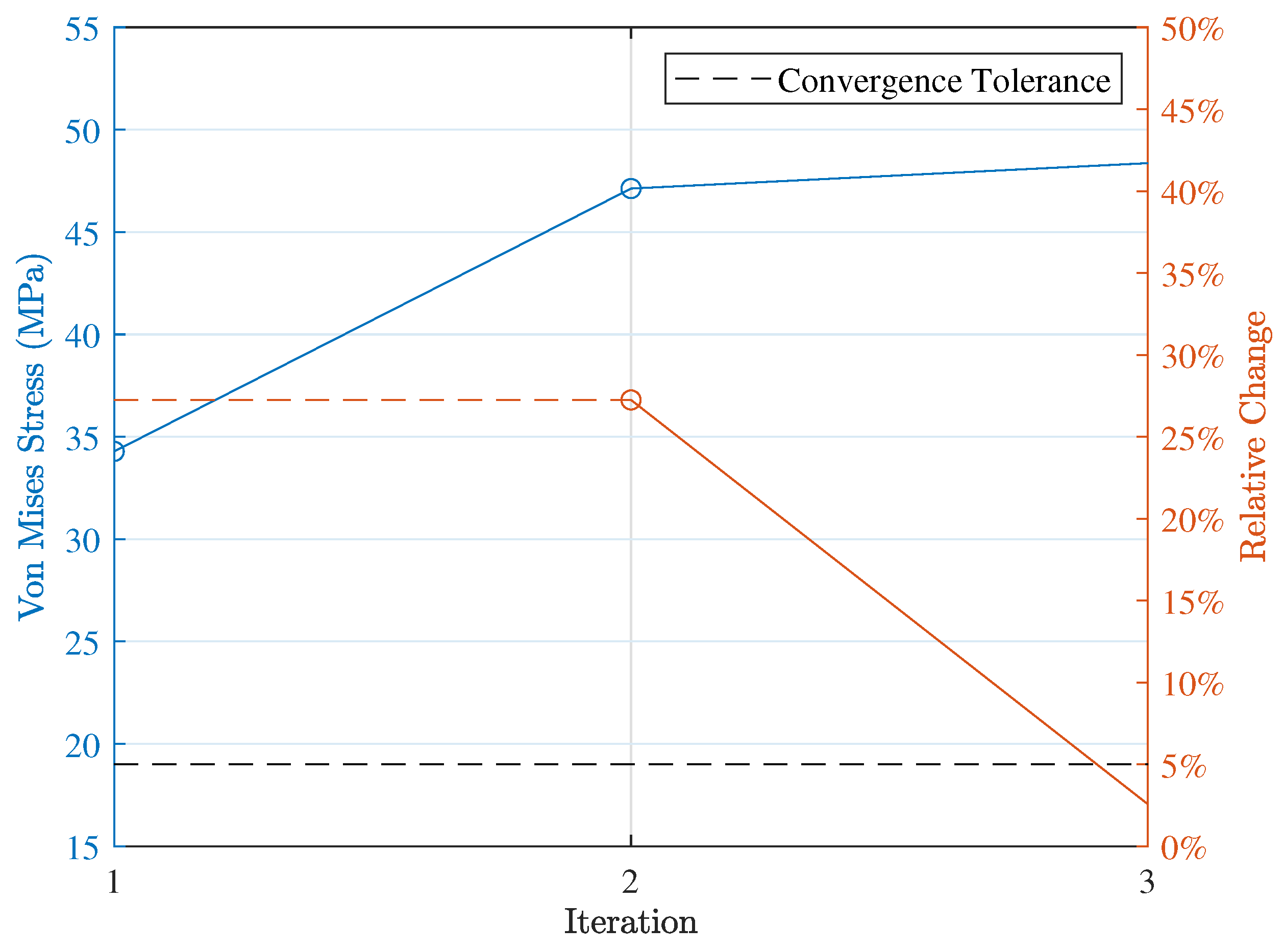
5.4. Machine Design
6. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BWS | Body Weight Support |
| PFNM | Parameter-Finiteness Normalization Method |
| PCbDM | Perfomance-Chart-based Design Methodology |
| DoF | Degree of Freedom |
| GCI | Global Conditioning Index |
| MCI | Maximum Conditioning Index |
| GSI | Global Stiffness Index |
| PDS | Parameter Design Space |
| LCF | Low-Cycle Fatigue |
| HCF | High-Cycle Fatigue |
| FEA | Finite Element Analysis |
| CAD | Computer-Aided Design |
References
- Sale, P.; Franceschini, M.; Waldner, A.; Hesse, S. Use of the robot assisted gait therapy in rehabilitation of patients with stroke and spinal cord injury. Eur. J. Phys. Rehabil. Med. 2012, 48, 21–111. [Google Scholar]
- Calabrò, R.; Cacciola, A.; Bertè, F.; Manuli, A.; Leo, A.; Bramanti, A.; Naro, A.; Milardi, D.; Bramanti, P. Robotic gait rehabilitation and substitution devices in neurological disorders: Where are we now? Neurol. Sci. 2016, 37, 503–514. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, B.; Artemiadis, P. A Review of robot-assisted lower-limb Stroke therapy: Unexplored paths and future directions in gait rehabilitation. Front. Neurorobot. 2020, 14, 19. [Google Scholar] [CrossRef] [Green Version]
- Kapsalyamov, A.; Jamwal, P.; Hussain, S.; Ghayesh, M. State of the art lower limb robotic exoskeletons for elderly assistance. IEEE Access 2019, 7, 95075–95086. [Google Scholar] [CrossRef]
- Jezernik, S.; Colombo, G.; Keller, T.; Frueh, H.; Morari, M. Robotic orthosis Lokomat: A rehabilitation and research tool. Neuromodul. Technol. Neural Interface 2003, 6, 108–115. [Google Scholar] [CrossRef] [PubMed]
- Veneman, J.; Kruidhof, R.; Hekman, E.; Ekkelenkamp, R.; Van Asseldonk, E.; Van Der Kooij, H. Design and evaluation of the LOPES exoskeleton robot for interactive gait rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 379–386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zoss, A.; Kazerooni, H.; Chu, A. Biomechanical design of the Berkeley lower extremity exoskeleton (BLEEX). IEEE/ASME Trans. Mechatron. 2006, 11, 128–138. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, B.; Yu, Z.; Yan, Y. Differential soft sensor-based measurement of interactive force and assistive torque for a robotic hip exoskeleton. Sensors 2021, 21, 6545. [Google Scholar] [CrossRef]
- Kennard, M.; Kadone, H.; Shimizu, Y.; Suzuki, K. Passive exoskeleton with gait-based knee joint support for individuals with cerebral palsy. Sensors 2022, 22, 8935. [Google Scholar] [CrossRef]
- Narayan, J.; Dwivedy, S.K. Preliminary design and development of a low-cost lower-limb exoskeleton system for paediatric rehabilitation. Proc. Inst. Mech. Eng. Part H 2021, 235, 530–545. [Google Scholar] [CrossRef]
- Sunilkumar, P.; Mohan, S.; Mohanta, J.K.; Wenger, P.; Rybak, L. Design and motion control scheme of a new stationary trainer to perform lower limb rehabilitation therapies on hip and knee joints. Int. J. Adv. Robot. Syst. 2022, 19, 17298814221075184. [Google Scholar] [CrossRef]
- Glowinski, S.; Ptak, M. A kinematic model of a humanoid lower limb exoskeleton with pneumatic actuators. Acta Bioeng. Biomech. 2022, 24, 145–157. [Google Scholar] [CrossRef]
- Hesse, S.; Schattat, N.; Mehrholz, J.; Werner, C. Evidence of end-effector based gait machines in gait rehabilitation after CNS lesion. NeuroRehabilitation 2013, 33, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Hesse, S.; Sarkodie-Gyan, T.; Uhlenbrock, D. Development of an advanced mechanised gait trainer, controlling movement of the centre of mass, for restoring gait in non-ambulant subjects—Weiterentwicklung eines mechanisierten gangtrainers mit steuerung des massenschwerpunktes zur gangrehabilitation rollstuhlpflichtiger patienten. Biomed. Tech. Eng. 1999, 44, 194–201. [Google Scholar] [CrossRef]
- Schmidt, H.; Sorowka, D.; Hesse, S.; Bernhardt, R. Entwicklung eines robotergestützten laufsimulators zur gangrehabilitation. Development of a robotic walking simulator for gait rehabilitation. Biomed. Tech. Eng. 2003, 48, 281–286. [Google Scholar] [CrossRef]
- Hesse, S.; Waldner, A.; Tomelleri, C. Innovative gait robot for the repetitive practice of floor walking and stair climbing up and down in stroke patients. J. NeuroEng. Rehabil. 2010, 7, 30. [Google Scholar] [CrossRef] [Green Version]
- Bruni, M.F.; Melegari, C.; De Cola, M.C.; Bramanti, A.; Bramanti, P.; Calabrò, R.S. What does best evidence tell us about robotic gait rehabilitation in stroke patients: A systematic review and meta-analysis. J. Clin. Neurosci. 2018, 48, 11–17. [Google Scholar] [CrossRef]
- Awad, L.; Bae, J.; O’Donnell, K.; De Rossi, S.M.M.; Hendron, K.; Sloot, L.H.; Kudzia, P.; Allen, S.; Holt, K.G.; Ellis, T.D.; et al. A soft robotic exosuit improves walking in patients after stroke. Sci. Transl. Med. 2017, 9, eaai9084. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H.; Park, G.; Cho, D.Y.; Kim, H.Y.; Lee, J.; Kim, S.; Park, S.B.; Shin, J.H. Comparisons between end-effector and exoskeleton rehabilitation robots regarding upper extremity function among chronic stroke patients with moderate-to-severe upper limb impairment. Sci. Rep. 2020, 10, 1806. [Google Scholar] [CrossRef] [Green Version]
- Li, W.Z.; Cao, G.Z.; Zhu, A.B. Review on control strategies for lower limb rehabilitation exoskeletons. IEEE Access 2021, 9, 123040–123060. [Google Scholar] [CrossRef]
- Dollar, A.M.; Herr, H. Lower extremity exoskeletons and active orthoses: Challenges and state-of-the-art. IEEE Trans. Robot. 2008, 24, 144–158. [Google Scholar] [CrossRef]
- Hamza, M.F.; Ghazilla, R.A.R.; Muhammad, B.B.; Yap, H.J. Balance and stability issues in lower extremity exoskeletons: A systematic review. Biocybern. Biomed. Eng. 2020, 40, 1666–1679. [Google Scholar] [CrossRef]
- O’Sullivan, L.; Nugent, R.; van der Vorm, J. Standards for the safety of exoskeletons used by industrial workers performing manual handling activities: A contribution from the Robo-Mate Project to their future development. Procedia Manuf. 2015, 3, 1418–1425. [Google Scholar] [CrossRef] [Green Version]
- Collo, A.; Bonnet, V.; Venture, G. A quasi-passive lower limb exoskeleton for partial body weight support. In Proceedings of the 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016. [Google Scholar] [CrossRef]
- Tsuge, B.; Mccarthy, J. Synthesis of a 10-Bar linkage to guide the gait cycle of the human leg. In Proceedings of the 39th Mechanisms and Robotics Conference, Boston, MA, USA, 2–5 August 2015. [Google Scholar] [CrossRef] [Green Version]
- Tsuge, B.; Mccarthy, J. An adjustable single degree-of-freedom system to guide natural walking movement for rehabilitation. J. Med. Devices. 2016, 10, 44501. [Google Scholar] [CrossRef] [Green Version]
- Shao, Y.; Xiang, Z.; Liu, H.; Li, L. Conceptual design and dimensional synthesis of cam-linkage mechanisms for gait rehabilitation. Mech. Mach. Theory 2016, 104, 31–42. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J.; Pritschow, G. Kinematics, singularity and workspace of planar 5R symmetrical parallel mechanisms. Mech. Mach. Theory 2006, 41, 145–169. [Google Scholar] [CrossRef]
- Merlet, J.P.; Daney, D. Appropriate design of parallel manipulators. In Smart Devices and Machines for Advanced Manufacturing; Springer: London, UK, 2008; pp. 1–25. [Google Scholar] [CrossRef] [Green Version]
- Merlet, J.P. Jacobian, manipulability, condition number, and accuracy of parallel robots. J. Mech. Des. 2005, 128, 199–206. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J. A new methodology for optimal kinematic design of parallel mechanisms. Mech. Mach. Theory 2007, 42, 1210–1224. [Google Scholar] [CrossRef]
- Mohan, S.; Mohanta, J.; Kurtenbach, S.; Paris, J.; Corves, B.; Huesing, M. Design, development and control of a 2PRP-2PPR planar parallel manipulator for lower limb rehabilitation therapies. Mech. Mach. Theory 2017, 112, 272–294. [Google Scholar] [CrossRef]
- Mohanta, J.; Mohan, S.; Deepasundar, P.; Kiruba-Shankar, R. Development and control of a new sitting-type lower limb rehabilitation robot. Comput. Electr. Eng. 2018, 67, 330–347. [Google Scholar] [CrossRef]
- Vasanthakumar, M.; Vinod, B.; Mohanta, J.K.; Mohan, S. Design and robust motion control of a planar 1P-2P RP hybrid manipulator for lower limb rehabilitation applications. J. Intell. Robot. Syst. 2019, 96, 17–30. [Google Scholar] [CrossRef]
- Baker, R. Measure Walking: A Handbook of Clinical Gait Analysis; Mac Keith Press: London, UK, 2013. [Google Scholar]
- Cross, N. Engineering Design Methods: Strategies for Product Design, 5th ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2021; ISBN 0-13-612370-8. [Google Scholar]
- Molteni, F.; Gasperini, G.; Cannaviello, G.; Guanziroli, E. Exoskeleton and end-effector robots for upper and lower limbs rehabilitation: Narrative review. PM&R. 2018, 10, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Mehrholz, J.; Pohl, M.; Platz, T.; Kugler, J.; Elsner, B. Electromechanical and robot-assisted arm training for improving activities of daily living, arm function, and arm muscle strength after stroke. Cochrane Database Syst. Rev. 2015, 9, CD006876. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Lanotte, F.; Grazi, L.; Vitiello, N.; Crea, S. Classification of lifting techniques for application of a robotic hip exoskeleton. Sensors 2019, 19, 963. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Zi, B.; Qin, L.; Pan, Q. State-of-the-art research in robotic hip exoskeletons: A general review. J. Orthop. Transl. 2020, 20, 4–13. [Google Scholar] [CrossRef]
- Barragán, J.; Ovalle, G. Entrenador de Marcha Para el Ejercicio de Miembros Inferiores Humanos. Colombian Patent Resolución No 202194, 29 April 2020. [Google Scholar]
- Manchola, M.; Serrano, D.; Gómez, D.; Ballen, F.; Casas, D.; Munera, M.; Cifuentes, C. T-FLEX: Variable stiffness ankle-foot orthosis for gait assistance. In Wearable Robotics: Challenges and Trends. WeRob 2018; Carrozza, M., Micera, S., Pons, J., Eds.; Biosystems & Biorobotics; Springer: Cham, Switzerland, 2019; Volume 22. [Google Scholar] [CrossRef]
- Prakash, C.; Gupta, K.; Mittal, M.; Kumar, R.; Laxmi, V. Passive marker based optical system for gait Kinematics for lower extremity. Procedia Comput. Sci. 2015, 45, 176–185. [Google Scholar] [CrossRef] [Green Version]
- Samson, M.; Crowe, A.; de Vreede, P.; Dessens, J.; Duursma, S.; Verhaar, H. Differences in gait parameters at a preferred walking speed in healthy subjects due to age, height and body weight. Aging Clin. Exp. Res. 2001, 13, 16–21. [Google Scholar] [CrossRef]
- Avila-Chaurand, R.; Prado-León, L.; González-Muñoz, E. Dimensiones Antropométricas de la Población Latinoamericana: México, Cuba, Colombia, Chile; Universidad de Guadalajara: Jalisco, Mexico, 2007. [Google Scholar]
- Wang, Q.; Qian, J.; Zhang, Y.; Shen, L.; Zhang, Z.; Feng, Z. Gait trajectory planning and simulation for the powered gait orthosis. In Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 15–18 December 2007; pp. 1693–1697. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J.; Pritschow, G. Performance atlases and optimum design of planar 5R symmetrical parallel mechanisms. Mech. Mach. Theory 2006, 41, 119–144. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J. A new index for the performance evaluation of parallel manipulators: A study on planar parallel manipulators. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; Volume 42. [Google Scholar] [CrossRef]
- Norton, R. Machine Design: An Integrated Approach, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2010; ISBN 0-13-612370-8. [Google Scholar]
- Nisbeth, J.; Budyna, R. Shigley’s Mechanical Engineering Design; McGraw-Hill Education: Columbus, OH, USA, 2019. [Google Scholar]
- Aziz, H.; Al-alkawi, H. An appraisal of Euler and Johnson buckling theories under dynamic compression buckling loading. Iraqi J. Mech. Mater. Eng. 2009, 9, 173–181. Available online: https://www.iasj.net/iasj/article/63758 (accessed on 15 November 2021).
- Lee, Y.L.; Pan, J.; Hathaway, R.; Barkey, M. Fatigue Testing and Analysis: Theory and Practice; Elsevier Science & Technology: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Durango, S.; Delgado, M.C.; Álvarez, C.; Flórez, R.; Flórez, M. Kinematic design of a 2-PRR parallel robot. Sci. Tech. 2020, 25, 372–379. [Google Scholar] [CrossRef]
- Kolovsky, M.; Evgrafov, A.; Semenov, Y.; Slousch, A. Geometric analysis of mechanisms. In Advanced Theory of Mechanisms and Machines; Springer: Berlin/Heidelberg, Germany, 2000; pp. 41–78. [Google Scholar]
- Saura, M.; Celdran, A.; Dopico, D.; Cuadrado, J. Computational structural analysis of planar multibody systems with lower and higher kinematic pairs. Mech. Mach. Theory 2014, 71, 79–92. [Google Scholar] [CrossRef]
- Sun, Y.; Ge, W.; Zheng, J.; Dong, D. Solving the kinematics of the planar mechanism using data structures of Assur groups. J. Mech. Robot. 2016, 8, 061002-13. [Google Scholar] [CrossRef]
- Durango, S.; Correa, J.; Ruiz, O. Graph-based structural analysis of planar mechanisms. Meccanica 2017, 52, 441–455. [Google Scholar] [CrossRef]
- Müller, A. Representation of the kinematic topology of mechanisms for kinematic analysis. Mech. Sci. 2015, 6, 137–146. [Google Scholar] [CrossRef]
- DIN Standard 71751; [Fork Joints—Synopsis]. Deutsches Institut für Normung: Berlin, Germany, 1975.
- Hesse, S.; Tomelleri, C.; Bardeleben, A.; Werner, C.; Waldner, A. Robot-assisted practice of gait and stair climbing in nonambulatory stroke patients. J. Rehabil. Res. Dev. 2012, 49, 613–622. [Google Scholar] [CrossRef] [PubMed]






| Criteria | Defined Weight |
|---|---|
| C1—Reprogrammability | 20.83% |
| C2—Adjustability to different anthropometries | 22.67% |
| C3—Easy implementation of a control system | 13.17% |
| C4—Need for a harness or additional trunk support | 13.75% |
| C5—Independent control of each lower limb | 15.83% |
| C6—Variable levels of assistance | 13.75% |
| Alternative | Global Score |
|---|---|
| A1—Stephenson III mechanism | 5.87 |
| A2—Cam-linkage mechanism | 5.79 |
| A3—Slider-crank 7 bar mechanism | 7.29 |
| A4—2-PRR mechanism | 7.58 |
| A5—2-PRR mechanism with extra DoF for foot orientation | 7.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Risk-Mora, D.Y.; Durango-Idárraga, S.; Jiménez-Cortés, H.N.; Rodríguez-Sotelo, J.L. Mechanical Design of a 2-PRR Parallel Manipulator for Gait Retraining System. Machines 2023, 11, 788. https://doi.org/10.3390/machines11080788
Risk-Mora DY, Durango-Idárraga S, Jiménez-Cortés HN, Rodríguez-Sotelo JL. Mechanical Design of a 2-PRR Parallel Manipulator for Gait Retraining System. Machines. 2023; 11(8):788. https://doi.org/10.3390/machines11080788
Chicago/Turabian StyleRisk-Mora, David Yamil, Sebastián Durango-Idárraga, Hendric Nicolás Jiménez-Cortés, and José Luis Rodríguez-Sotelo. 2023. "Mechanical Design of a 2-PRR Parallel Manipulator for Gait Retraining System" Machines 11, no. 8: 788. https://doi.org/10.3390/machines11080788
APA StyleRisk-Mora, D. Y., Durango-Idárraga, S., Jiménez-Cortés, H. N., & Rodríguez-Sotelo, J. L. (2023). Mechanical Design of a 2-PRR Parallel Manipulator for Gait Retraining System. Machines, 11(8), 788. https://doi.org/10.3390/machines11080788






