A Soft Start Method for Doubly Fed Induction Machines Based on Synchronization with the Power System at Standstill Conditions
Abstract
:1. Introduction
2. State of the Art
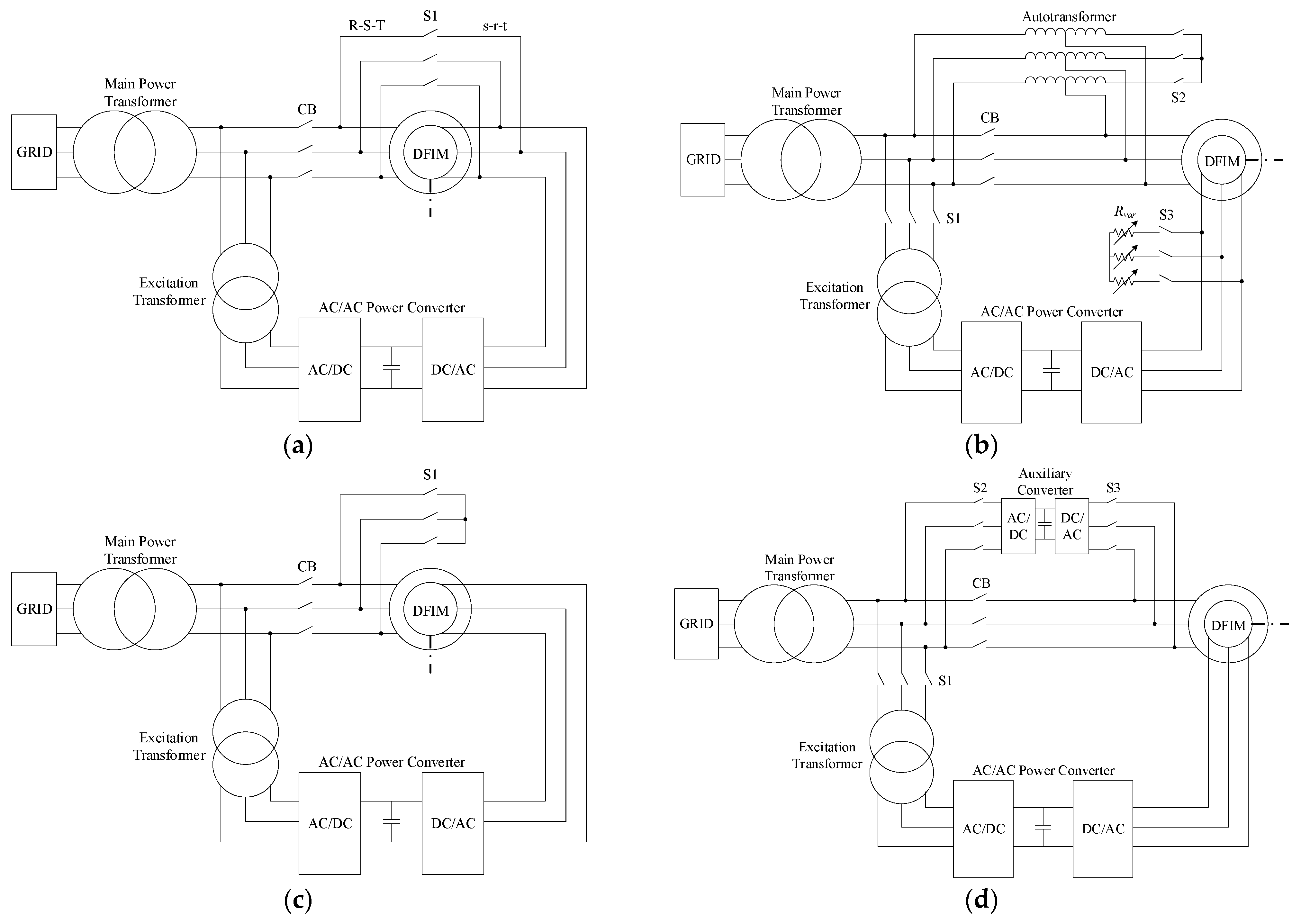
2.1. Opposite Phase Sequence-Based Start-Up Methods
2.2. Reduced Voltage-Based Start-Up Methods
2.3. Auxiliary Converter-Based Start-Up Methods
2.4. Proposed Start-Up Methods
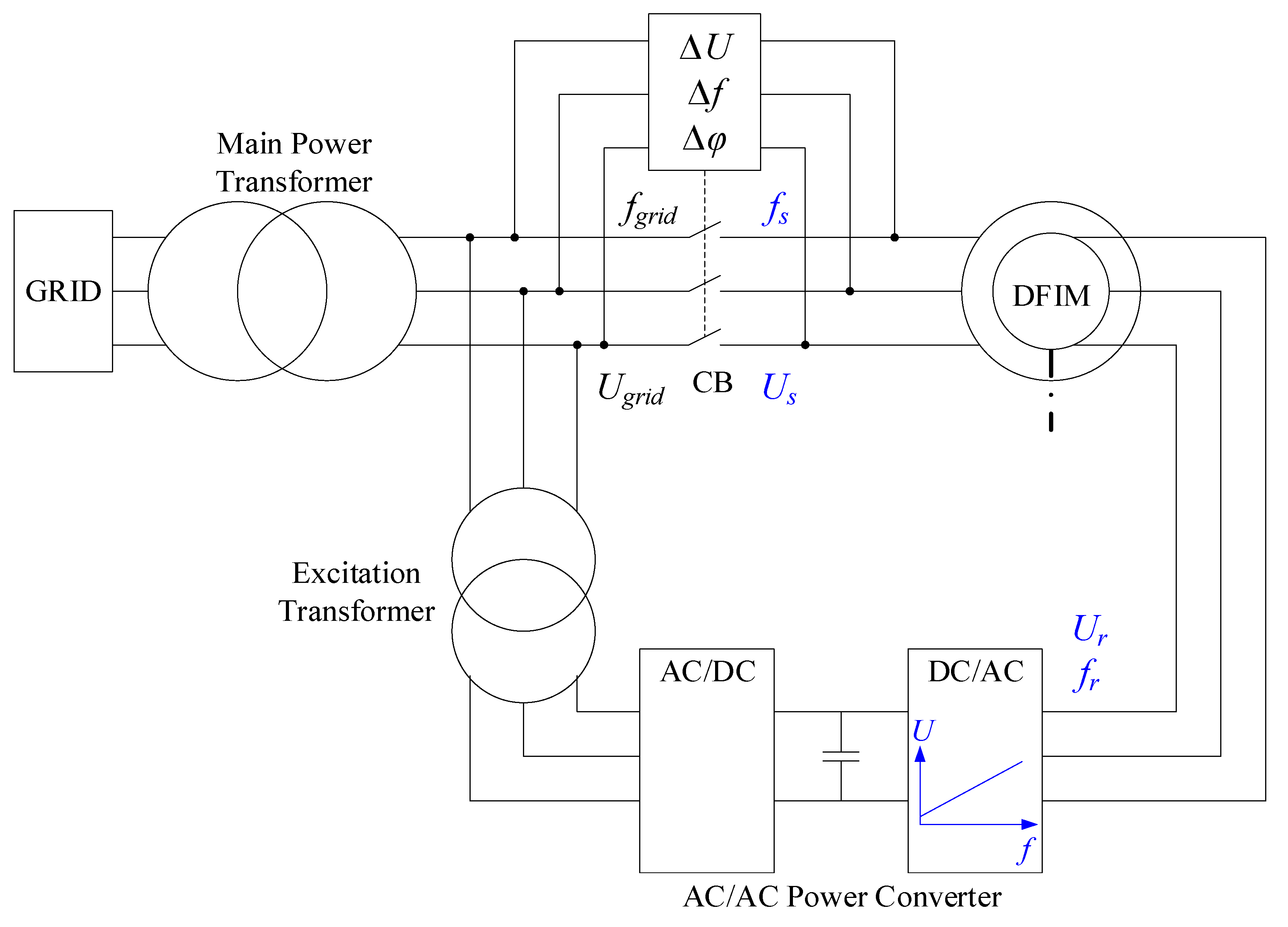
3. Description of the Proposed Soft Start-Up Method
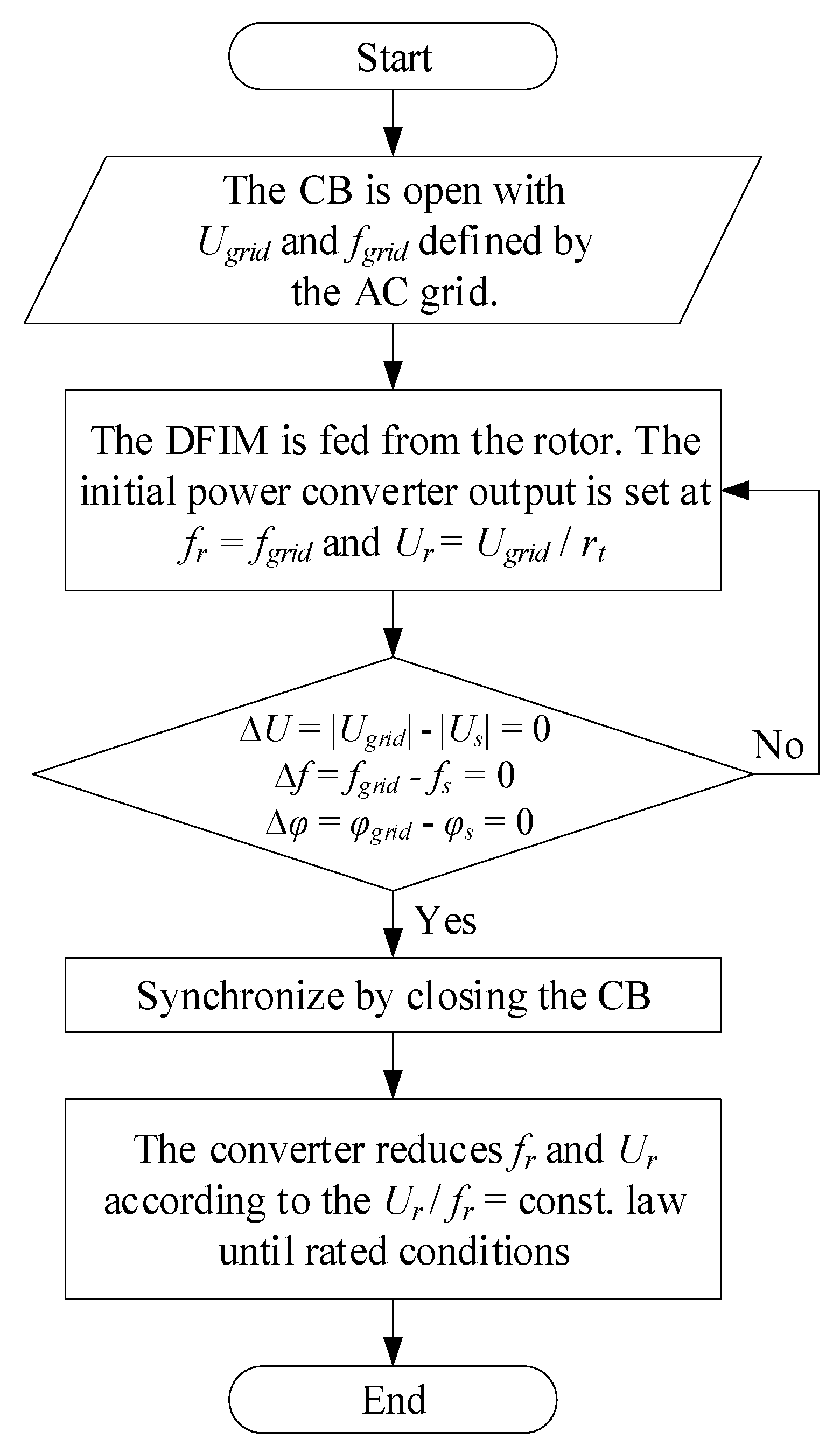
3.1. Method Overview
3.2. Dynamic Equations of the DFIM
3.3. Stator Synchronization Analysis
3.4. DFIM Acceleration
4. Computer Simulations
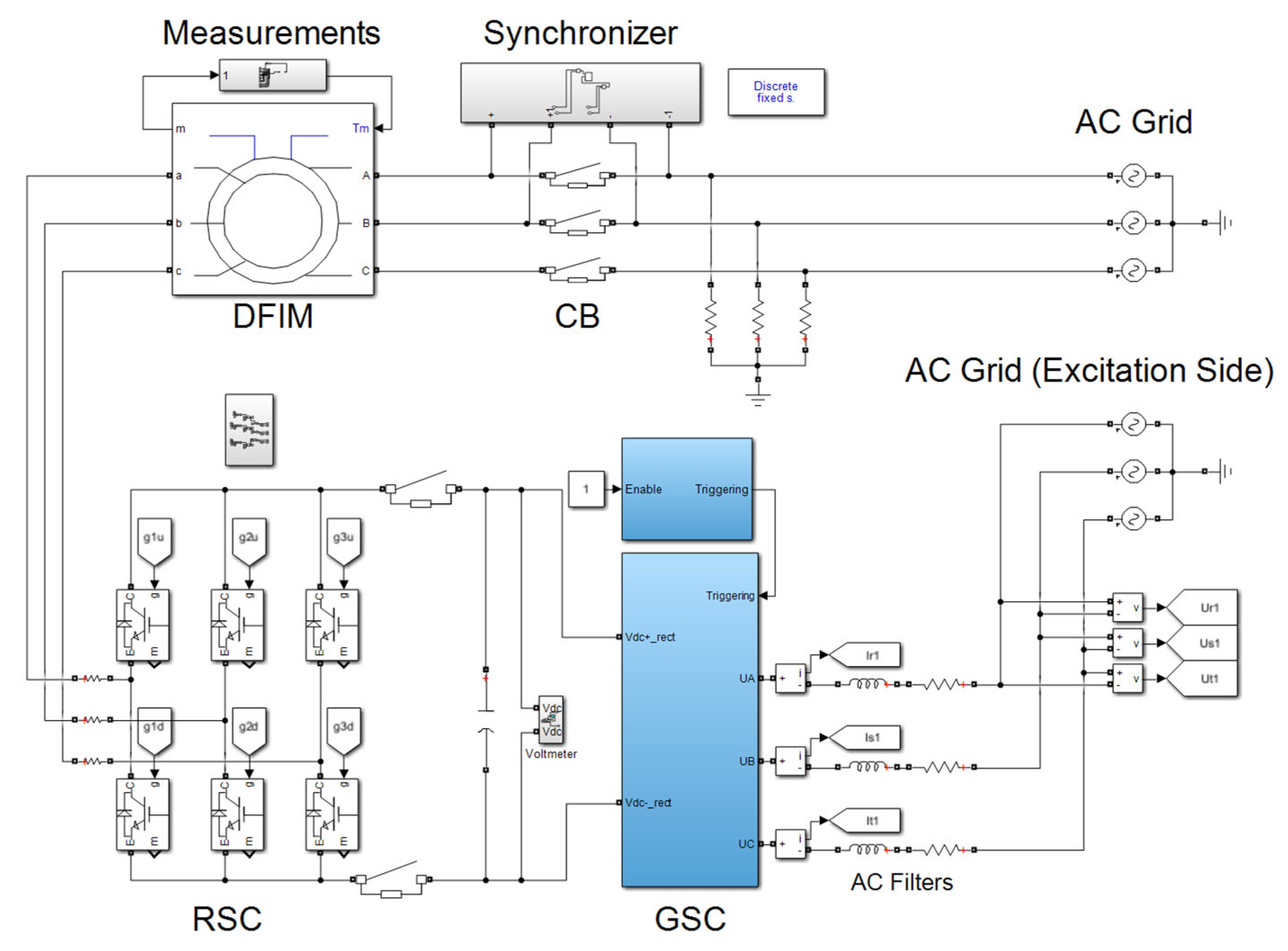
4.1. Simulation Model
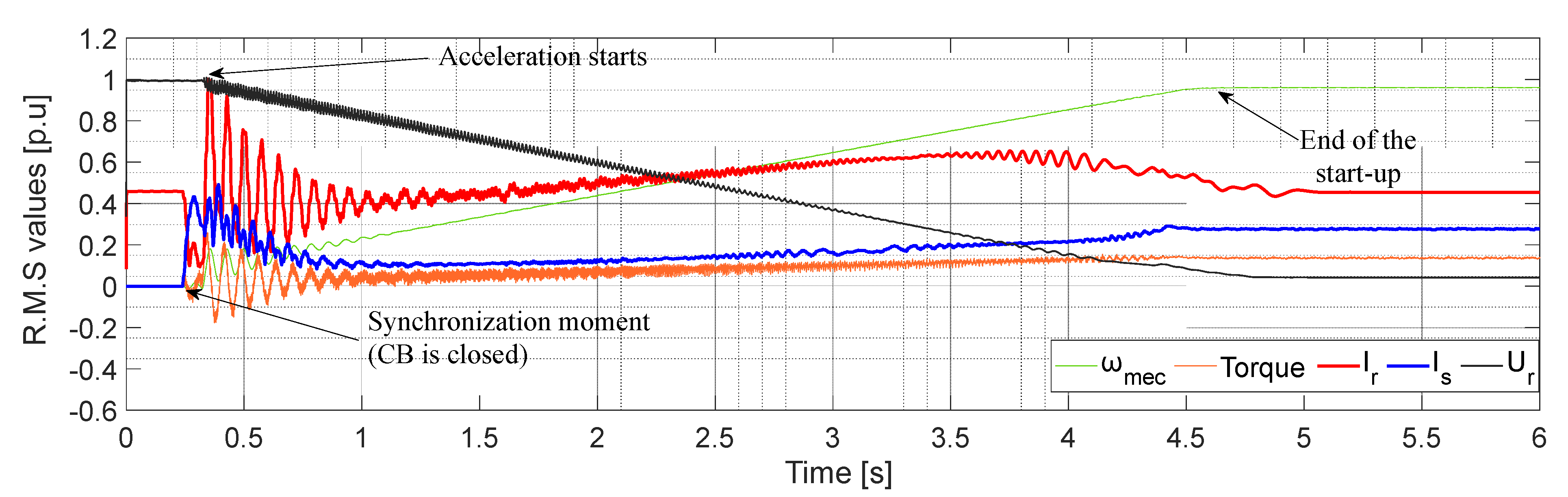
4.2. Results
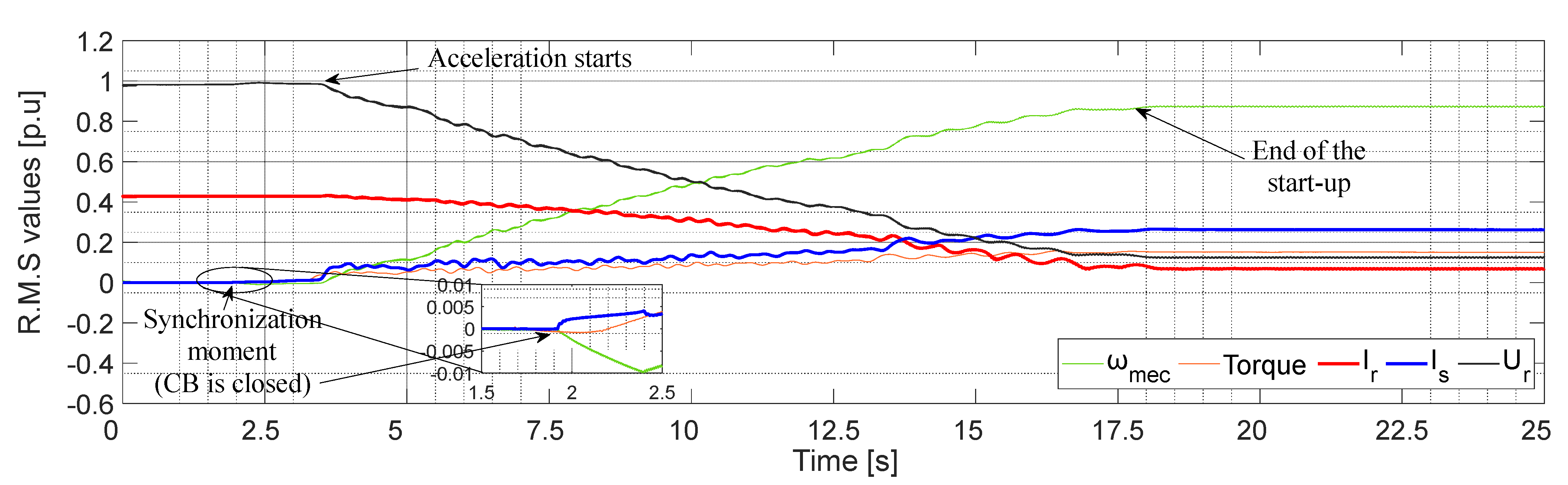
5. Experimental Tests
5.1. Experimental Setup
5.2. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature and Abbreviations
| fgrid | Grid frequency (in Hz) |
| fr | Rotor frequency (in Hz) |
| fs | Stator frequency (in Hz) |
| H | Rotor inertia constant (in s) |
| Ir | Rotor current (in A) |
| Is | Stator current (in A) |
| J | Moment of inertia (in kg·m2) |
| p | Number of pole pairs |
| Rr | Rotor resistance (in Ω) |
| Rs | Stator resistance (in Ω) |
| rt | Stator/Rotor voltage ratio |
| Rvar | Variable resistance (in Ω) |
| s | Slip |
| Tm | Mechanical torque (in N·m) |
| Tr | Mechanical counter-torque (in N·m) |
| t | Time (in s) |
| UDC | DC bus voltage (in V) |
| Ugrid | Grid voltage (in V) |
| Ur | Rotor voltage (in V) |
| Us | Stator voltage (in V) |
| Xm | Magnetizing reactance (in Ω) |
| Xr | Rotor leakage reactance (in Ω) |
| Xs | Stator leakage reactance (in Ω) |
| φ | Phase angle (in rad) |
| Ψr | Rotor flux (in Wb) |
| Ψs | Stator flux (in Wb) |
| ω0 | Angular speed (in rad/s) |
| ωmec | Mechanical rotor speed (in rad/s) |
| AC | Alternative Current |
| AT | Autotransformer |
| CB | Circuit Breaker |
| DC | Direct Current |
| DFIM | Doubly Fed Induction Machine |
| FOC | Field Oriented Control |
| GSC | Grid Side Converter |
| PWM | Pulse Width Modulation |
| RMS | Root Mean Square |
| RSC | Rotor Side Converter |
| SCIM | Squirrel Cage Induction Machine |
| SG | Synchronous Generator |
| VFD | Variable Frequency Drive |
References
- Khalid, M. Smart Grids and Renewable Energy Systems: Perspectives and Grid Integration Challenges. Energy Strategy Rev. 2024, 51, 101299. [Google Scholar] [CrossRef]
- Wang, X.; Bamisile, O.; Chen, S.; Xu, X.; Luo, S.; Huang, Q.; Hu, W. Decarbonization of China’s Electricity Systems with Hydropower Penetration and Pumped-Hydro Storage: Comparing the Policies with a Techno-Economic Analysis. Renew. Energy 2022, 196, 65–83. [Google Scholar] [CrossRef]
- Bekiroglu, E.; Yazar, M.D. MPPT Control of Grid Connected DFIG at Variable Wind Speed. Energies 2022, 15, 3146. [Google Scholar] [CrossRef]
- Abouloifa, A.; Noussi, K.; Elbouchikhi, E.; Katir, H.; Lachkar, I.; El Aroudi, A. High-Gain Observer-Based Advanced Nonlinear Control of a Grid-Connected Wind Energy Conversion System with Sensorless Maximum Power Point Tracking. Machines 2022, 10, 1074. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, X.; Zhu, D.; Zou, X.; Hu, J. Evaluation and Optimization of DFIG-Based WTs for Constant Inertia as Synchronous Generators. IEEE Trans. Power Electron. 2024, 39, 10453–10464. [Google Scholar] [CrossRef]
- Du, C.; Du, X.; Tong, C.; Li, Y.; Zhou, P. Stability Analysis for DFIG-Based Wind Farm Grid-Connected System Under All Wind Speed Conditions. IEEE Trans. Ind. Appl. 2023, 59, 2430–2445. [Google Scholar] [CrossRef]
- Gao, X.; Xie, Z.; Li, M.; Yang, S.; Zhang, X. Analysis and Mitigation of Electromechanical Oscillations in Drivetrain for Hybrid Synchronization Control of DFIG-Based Wind Turbines. IEEE Trans. Power Electron. 2024, 39, 3002–3013. [Google Scholar] [CrossRef]
- Bidgoli, M.A.; Yang, W.-J.; Ahmadian, A. DFIM versus Synchronous Machine for Variable Speed Pumped Storage Hydropower Plants: A Comparative Evaluation of Technical Performance. Renew. Energy 2020, 159, 72–86. [Google Scholar] [CrossRef]
- Mohale, V.; Chelliah, T.R.; Hote, Y.V. Analysis and Damping of Sub-Synchronous Oscillations in a 250 MW DFIM Hydro Unit Connected to Series Compensated 765 kV Transmission Lines. IEEE Trans. Ind. Appl. 2023, 59, 2234–2245. [Google Scholar] [CrossRef]
- Valavi, M.; Nysveen, A. Variable-Speed Operation of Hydropower Plants: A Look at the Past, Present, and Future. IEEE Ind. Appl. Mag. 2018, 24, 18–27. [Google Scholar] [CrossRef]
- Yang, W.-J.; Yang, J.-D. Advantage of Variable-Speed Pumped Storage Plants for Mitigating Wind Power Variations: Integrated Modelling and Performance Assessment. Appl. Energy 2019, 237, 720–732. [Google Scholar] [CrossRef]
- Lung, J.-K.; Lu, Y.; Hung, W.-L.; Kao, W.-S. Modeling and Dynamic Simulations of Doubly Fed Adjustable-Speed Pumped Storage Units. IEEE Trans. Energy Convers. 2007, 22, 250–258. [Google Scholar] [CrossRef]
- Morfín, O.; Delgado, D.; Campos, A.; Murillo, M.; Hernández, J.I.; Esquivel, P. Fault-Tolerant Controller Applied to a Wind System Using a Doubly Fed Induction Generator. Wind 2024, 4, 90–110. [Google Scholar] [CrossRef]
- Amaro Pinazo, M.; Antara Arias, R.; Mirez Tarrillo, J. Comparison of primary frequency control methods for wind turbines based on the doubly fed induction generator. Wind Eng. 2022, 46, 1923–1947. [Google Scholar] [CrossRef]
- Bahia, K.; Abdelmadjid, B. Stability analysis and study between classical sliding mode control (SMC) and super twisting algorithm (STA) for doubly fed induction generator (DFIG) under wind turbine. Energy 2021, 214, 118871. [Google Scholar]
- Hussain, H.A.; Loncarski, J.; Ristic, L.B.; Bellini, A. DFIG-Based WECS With Partial-Scale Converter: Efficiency, Cost, and Volume Comparison of SiC-Based and IGBT-Based Converter Solutions. IEEE Access 2024, 12, 89908–89920. [Google Scholar] [CrossRef]
- Nnachi, G.U.; Mosetlhe, C.T.; Hamam, Y. A Comparative Power Quality Study of DFIG and PMSG Renewable Energy Conversion Systems. In Proceedings of the 2020 5th International Conference on Renewable Energies for Developing Countries (REDEC), Marrakech, Morocco, 29–30 June 2020; pp. 1–6. [Google Scholar]
- Omodara, P.; Saavalainen, S.; Pitkäaho, E.; Pongrácz, E.; Keiski, R.L. Sustainability Assessment of Products—Case Study of Wind Turbine Generator Types. Environ. Impact Assess. Rev. 2023, 98, 106943. [Google Scholar] [CrossRef]
- Ntuli, W.K.; Kabeya, M.; Moloi, K. Review of Low Voltage Ride-Through Capabilities in Wind Energy Conversion System. Energies 2024, 17, 5321. [Google Scholar] [CrossRef]
- Hamouda, R.M.; Alolah, A.I.; Badr, M.A.; Abdel-Halim, M.A. A Comparative Study on the Starting Methods of Three Phase Wound-Rotor Induction Motors. I. IEEE Trans. Energy Convers. 1999, 14, 918–922. [Google Scholar] [CrossRef]
- Zhang, Y.; Ooi, B.T. Adapting DFIGs for Doubly-Fed Induction Motors Operation. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- IEEE Std 1010-2022 (Revision of IEEE Std 1010-2006); IEEE Guide for Control of Hydroelectric Power Plants. IEEE: New York, NY, USA, 2023; pp. 1–95.
- Yuan, X.; Chai, J.; Li, Y. A Converter-Based Starting Method and Speed Control of Doubly Fed Induction Machine With Centrifugal Loads. IEEE Trans. Ind. Appl. 2011, 47, 1409–1418. [Google Scholar] [CrossRef]
- Joseph, A.; Selvaraj, R.; Chelliah, T.R.; Sarma, S.V.A. Starting and Braking of a Large Variable Speed Hydrogenerating Unit Subjected to Converter and Sensor Faults. IEEE Trans. Ind. Appl. 2018, 54, 3372–3382. [Google Scholar] [CrossRef]
- Joseph, A.; Desingu, K.; Semwal, R.R.; Chelliah, T.R.; Khare, D. Dynamic Performance of Pumping Mode of 250 MW Variable Speed Hydro-Generating Unit Subjected to Power and Control Circuit Faults. IEEE Trans. Energy Convers. 2018, 33, 430–441. [Google Scholar] [CrossRef]
- Saiju, R.; Koutnik, J.; Krueger, K. Dynamic Analysis of Start-Up Strategies of AC Excited Double Fed Induction Machine for Pumped Storage Power Plant. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–8. [Google Scholar]
- Gong, G.; Lv, J.; Jiang, X.; Sun, X. Grid-Connection Control of Doubly Fed Variable Speed Pumped Storage Unit. In Proceedings of the 2021 5th International Conference on Green Energy and Applications (ICGEA), Singapore, 6–8 March 2021; pp. 52–57. [Google Scholar]
- Rauth, S.S.; Kastha, D.; Bajpai, P.A. Sensorless control strategy for automatic start-up and grid-synchronization of doubly fed induction generator in wind energy conversion system. Int. J. Circ. Theor. Appl. 2024, 52, 1733–1753. [Google Scholar] [CrossRef]
- Pannatier, Y.; Kawkabani, B.; Nicolet, C.; Schwery, A.; Simond, J.-J. Optimization of the Start-Up Time of a Variable Speed Pump-Turbine Unit in Pumping Mode. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2126–2132. [Google Scholar]
- Pannatier, Y.; Kawkabani, B.; Nicolet, C.; Schwery, A.; Simond, J.-J. Start-Up and Synchronization of a Variable Speed Pump-Turbine Unit in Pumping Mode. In Proceedings of the XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Li, D.; Gong, G.; Lv, J.; Jiang, X.; He, R. An Overall Control of Doubly Fed Variable Speed Pumped Storage Unit in Pumping Mode. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration, Wuhan, China, 30 October–1 November 2020; pp. 3709–3714. [Google Scholar]
- Malathy, N.; Sukhi, Y. Improved Start-Up Strategy for a Doubly Fed Induction Machine Fed Large Rated Variable Speed Pumped Storage Unit in Pumping Mode Operation. Electr. Eng. 2023, 106, 615–629. [Google Scholar] [CrossRef]
- Maendly, T.; Hodder, A.; Kawkabani, B. Start-Up of a Varspeed Group in Pump Mode: Practical Implementations and Tests. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1201–1207. [Google Scholar]
- Singh, R.R.; Baranidharan, M.; Subramaniam, U.; Bhaskar, M.S.; Rangarajan, S.S.; Abdelsalam, H.A.; Collins, E.R.; Senjyu, T. An Energy-Efficient Start-Up Strategy for Large Variable Speed Hydro Pump Turbine Equipped with Doubly Fed Asynchronous Machine. Energies 2022, 15, 3138. [Google Scholar] [CrossRef]
- Singh, R.R.; Chelliah, T.R. Energy Saving Start-Up Strategy of Pumped Storage Power Plant Equipped with Doubly-Fed Asynchronous Machine. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar]
- Anto, J.; Chelliah, T.R. Starting Performance of Doubly Fed Induction Machine Drive Serving Pumped Storage Plants Subjected to Faults in Power and Control Circuits. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–7. [Google Scholar]
- Narayanasamy, M.; Sukhi, Y. Rotor Short-Circuited Start-Up Strategy for a Doubly Fed Induction Machine-Fed Large-Rated Variable-Speed Pumped Storage Unit Operating in Pumping Mode. J. Power Electron. 2023, 23, 1733–1744. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Cavazzini, G.; Blázquez, F.; Platero, C.; Fraile-Ardanuy, J.; Sánchez, J.A.; Chazarra, M. Technological Developments for Pumped-Hydro Energy Storage; Technical Report, Mechanical Storage Subprogramme, Joint Programme on Energy Storage; European Energy Research Alliance: Brussels, Belgium, 2014; Available online: https://www.eera-energystorage.eu/ (accessed on 21 November 2024).
- Ghodbane-Cherif, M.; Skander-Mustapha, S.; Slama-Belkhodja, I. Start-Up System Design for Small Scale Autonomous DFIG Wind Turbine. Wind Eng. 2021, 45, 753–768. [Google Scholar] [CrossRef]
- Kovács, P.K. Transient Phenomena in Electrical Machines; Studies in Electrical and Electronic Engineering; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]



| Start-Up Type | Method | References | Advantages | Disadvantages |
|---|---|---|---|---|
| Opposite phase sequence-based | [20] |
|
| |
| Reduced voltage-based | With autotransformer | [21,22] |
|
|
| Stator short-circuited | [23,24,25,26,27,28,29,30,31,32,33,34,35,36] |
|
| |
| Rotor short-circuited | [23,26,37] |
|
| |
| Auxiliary converter-based | [32,38,39] |
|
| |
| Proposed start-up |
|
| ||
| Parameter | Magnitude | Units |
|---|---|---|
| Real power (Pn) | 0.52 | kW |
| Stator voltage (Un) | 400 | V |
| Frequency (fn) | 50 | Hz |
| Stator/rotor voltage ratio (rt) | 10/1 | V/V |
| Stator resistance (Rs) | 30.0 | Ω |
| Stator inductance (Ls) | 0.120 | H |
| Equivalent rotor resistance (Rr’) | 30.0 | Ω |
| Equivalent rotor inductance (Lr’) | 0.120 | H |
| Mutual inductance (Lm) | 2.432 | H |
| Moment of inertia (J) | 0.0015 | kg·m2 |
| Number of pole pairs (p) | 2 | |
| Speed (nn) | 1400 | rpm |
| Rated Parameters | Magnitude | Units |
|---|---|---|
| Real power (Pn) | 0.52 | kW |
| Frequency (fn) | 50 | Hz |
| Stator voltage (Un) | 380/660 | V |
| Stator current (In) | 1.6/0.92 | A |
| Rotor voltage (Un,r) | 65 (Y) | V |
| Rotor current (In,r) | 6 (Y) | A |
| Speed (nn) | 1400 | rpm |
| Power factor (cosφn) | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero, J.M.; Mahtani, K.; Aranzabal, I.; Gómez-Cornejo, J.; Sánchez, J.A.; Platero, C.A. A Soft Start Method for Doubly Fed Induction Machines Based on Synchronization with the Power System at Standstill Conditions. Machines 2024, 12, 847. https://doi.org/10.3390/machines12120847
Guerrero JM, Mahtani K, Aranzabal I, Gómez-Cornejo J, Sánchez JA, Platero CA. A Soft Start Method for Doubly Fed Induction Machines Based on Synchronization with the Power System at Standstill Conditions. Machines. 2024; 12(12):847. https://doi.org/10.3390/machines12120847
Chicago/Turabian StyleGuerrero, José M., Kumar Mahtani, Itxaso Aranzabal, Julen Gómez-Cornejo, José A. Sánchez, and Carlos A. Platero. 2024. "A Soft Start Method for Doubly Fed Induction Machines Based on Synchronization with the Power System at Standstill Conditions" Machines 12, no. 12: 847. https://doi.org/10.3390/machines12120847
APA StyleGuerrero, J. M., Mahtani, K., Aranzabal, I., Gómez-Cornejo, J., Sánchez, J. A., & Platero, C. A. (2024). A Soft Start Method for Doubly Fed Induction Machines Based on Synchronization with the Power System at Standstill Conditions. Machines, 12(12), 847. https://doi.org/10.3390/machines12120847








