Multi-Condition Intelligent Fault Diagnosis Based on Tree-Structured Labels and Hierarchical Multi-Granularity Diagnostic Network
Abstract
1. Introduction
- (1)
- A novel TSL method is proposed for creating multi-granularity fault labels that provide deep networks with more detailed fault attribute information.
- (2)
- An HMDN is designed to perform multi-granularity signal analysis, extracting fault information at multiple levels within a single condition. This improves the model’s ability to automatically identify common fault features in new conditions, resulting in greater adaptability across domains.
- (3)
- A multi-granularity fault loss function is developed to assist the model in learning fine-grained information while also extracting detailed features, even when using low-quality, coarse-grained labels.
2. Related Work
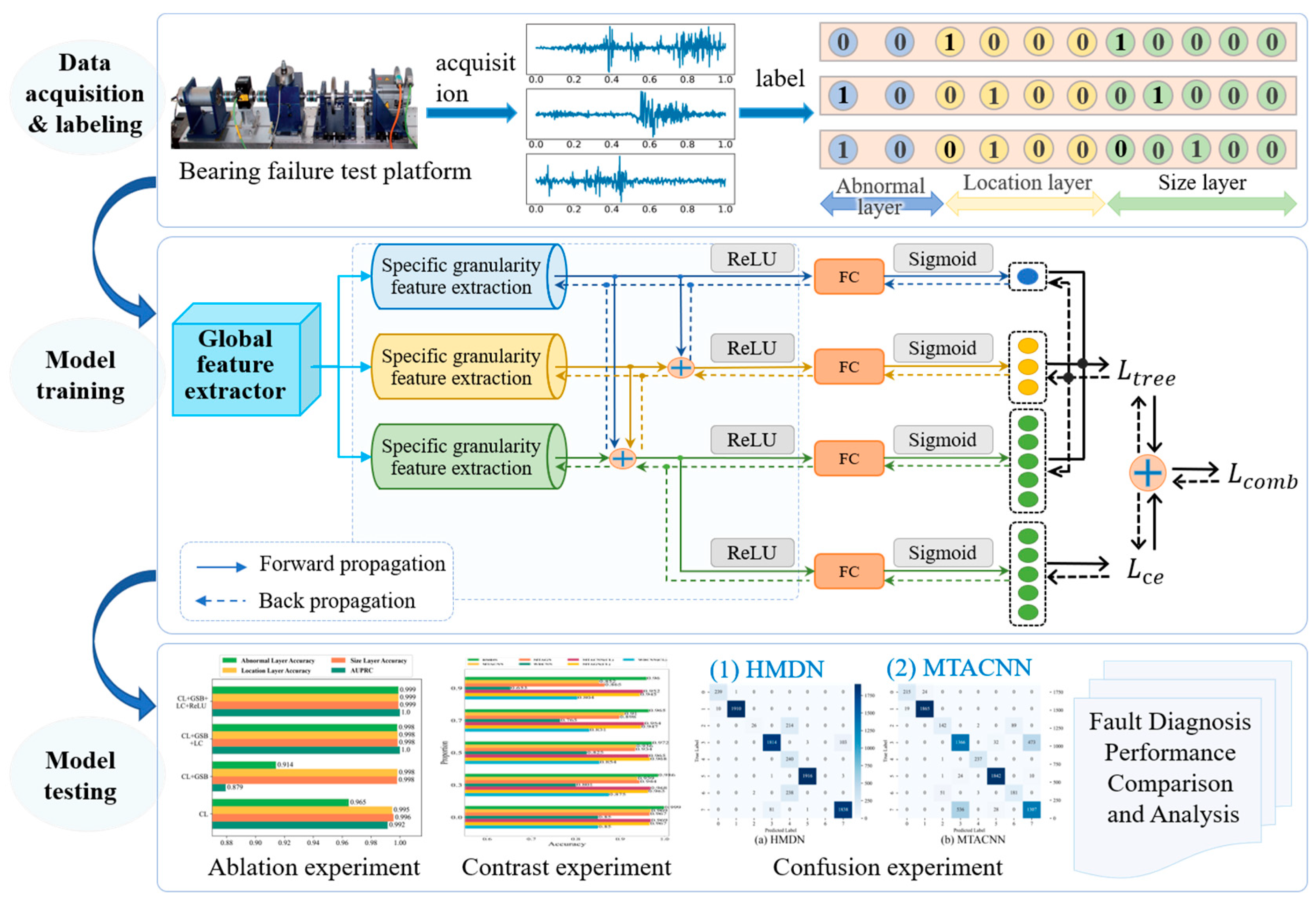
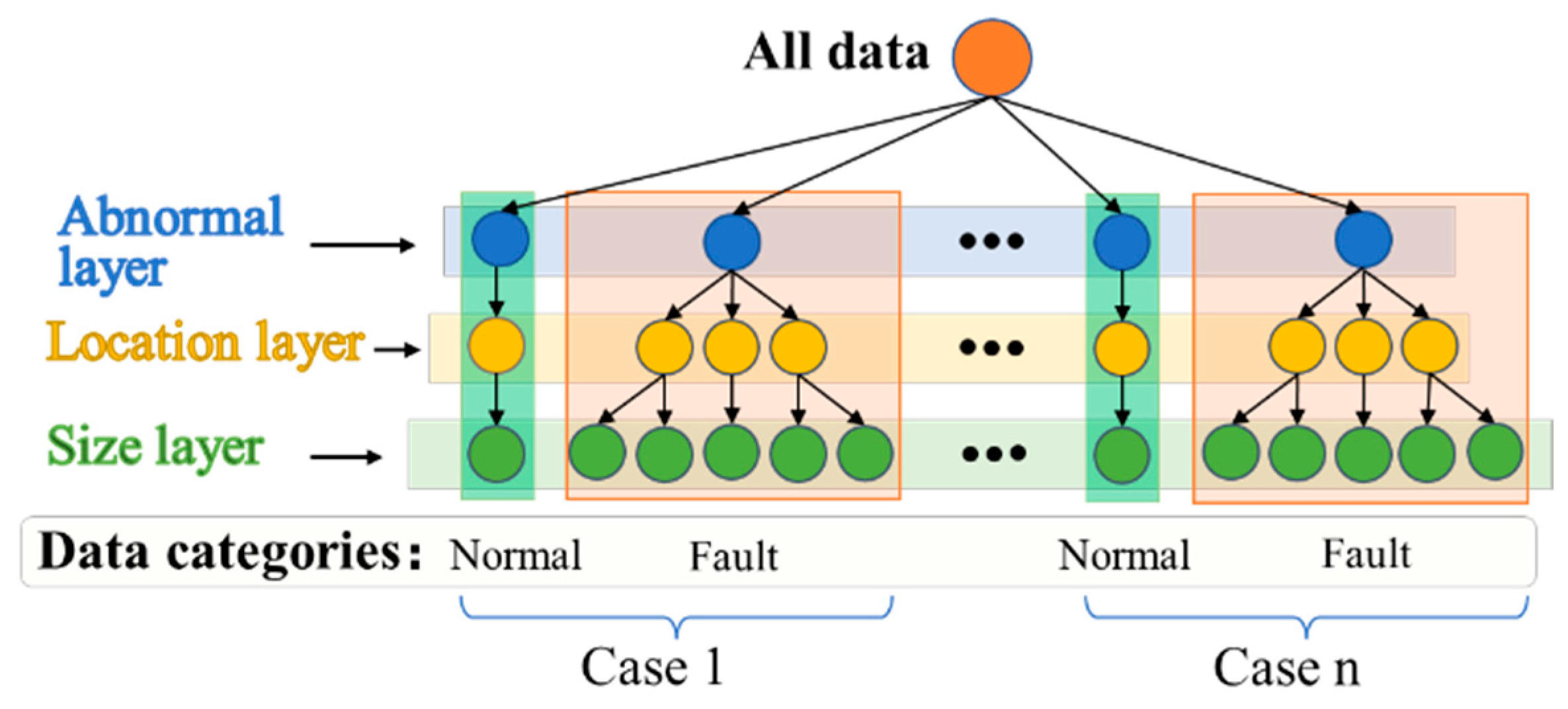
3. Proposed TLSs and HMDN
3.1. Subsection
3.2. Tree-Structured Loss
3.3. Structural Design of HMDN
4. Case Studies
4.1. Case 1: Paderborn University Dataset
4.2. Evaluation Metrics
- (1)
- Hierarchical Accuracy: The HMDN model generates probabilities for each class. The predicted label is determined by selecting the class with the highest probability at each level, and the hierarchical accuracy is calculated on the test set. Specifically, three levels of accuracy are measured: Acc-abnormal (accuracy in detecting abnormalities), Acc-location (accuracy in identifying fault locations), and Acc-size (accuracy in classifying fault sizes). This metric evaluates the model’s classification performance across multiple hierarchical levels.
- (2)
- Area Under the Precision–Recall Curve (AUPRC): AUPRC is calculated by averaging the Precision–Recall Curves (PRC) for all classes and evaluating the output probability vectors at each hierarchical level. The advantage of AUPRC is its independence from specific classification thresholds, which reduces the error rate caused by thresholds that are manually set. For a given threshold, a point (precision Pre and recall Rec) on the PRC curve is calculated as follows:where represents all classes, and , , and denote the true positives, false positives, and false negatives for class , respectively. By adjusting the threshold, the PRC curve is generated, and the area under this curve (AUPRC) is calculated.
4.3. Model Training
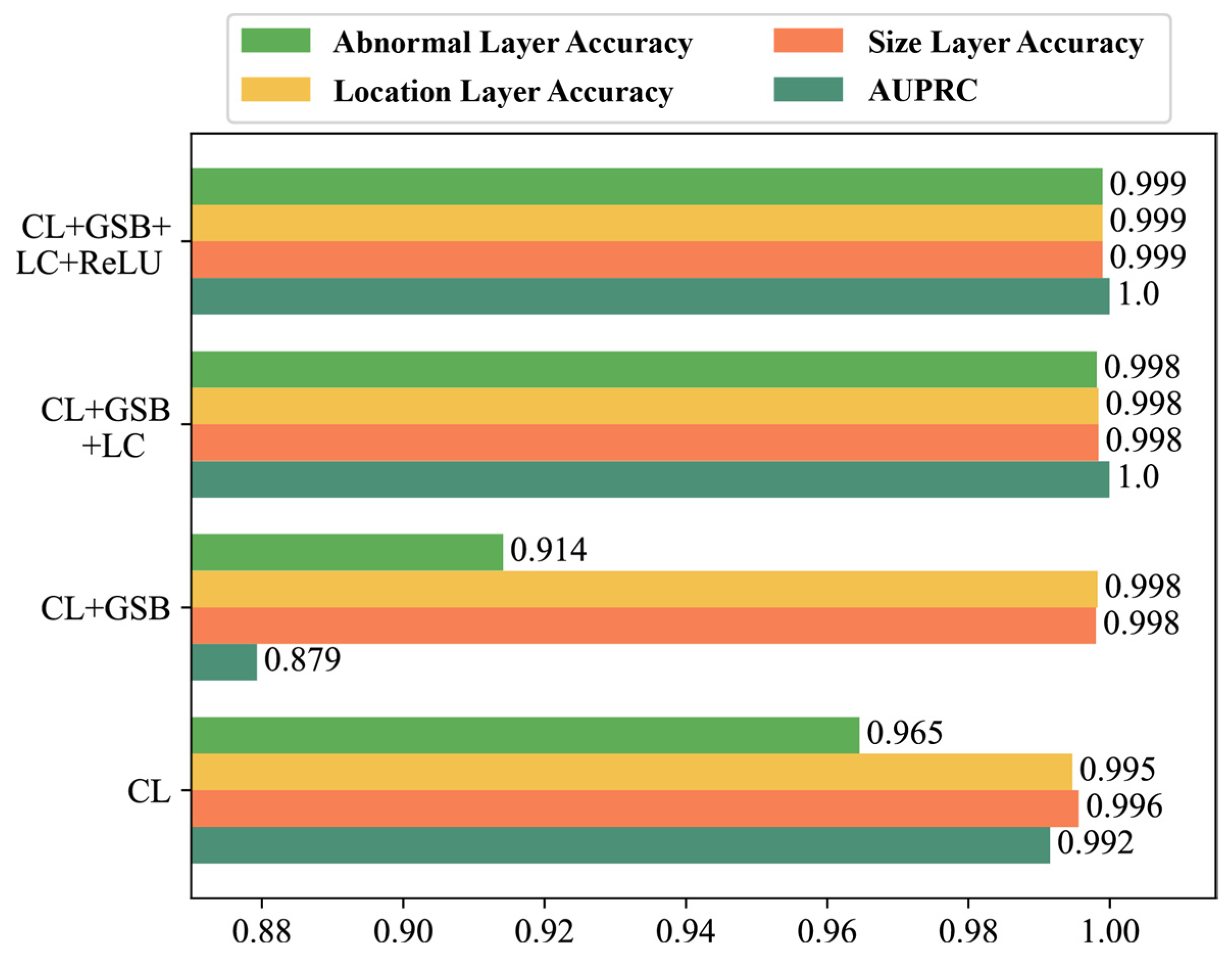
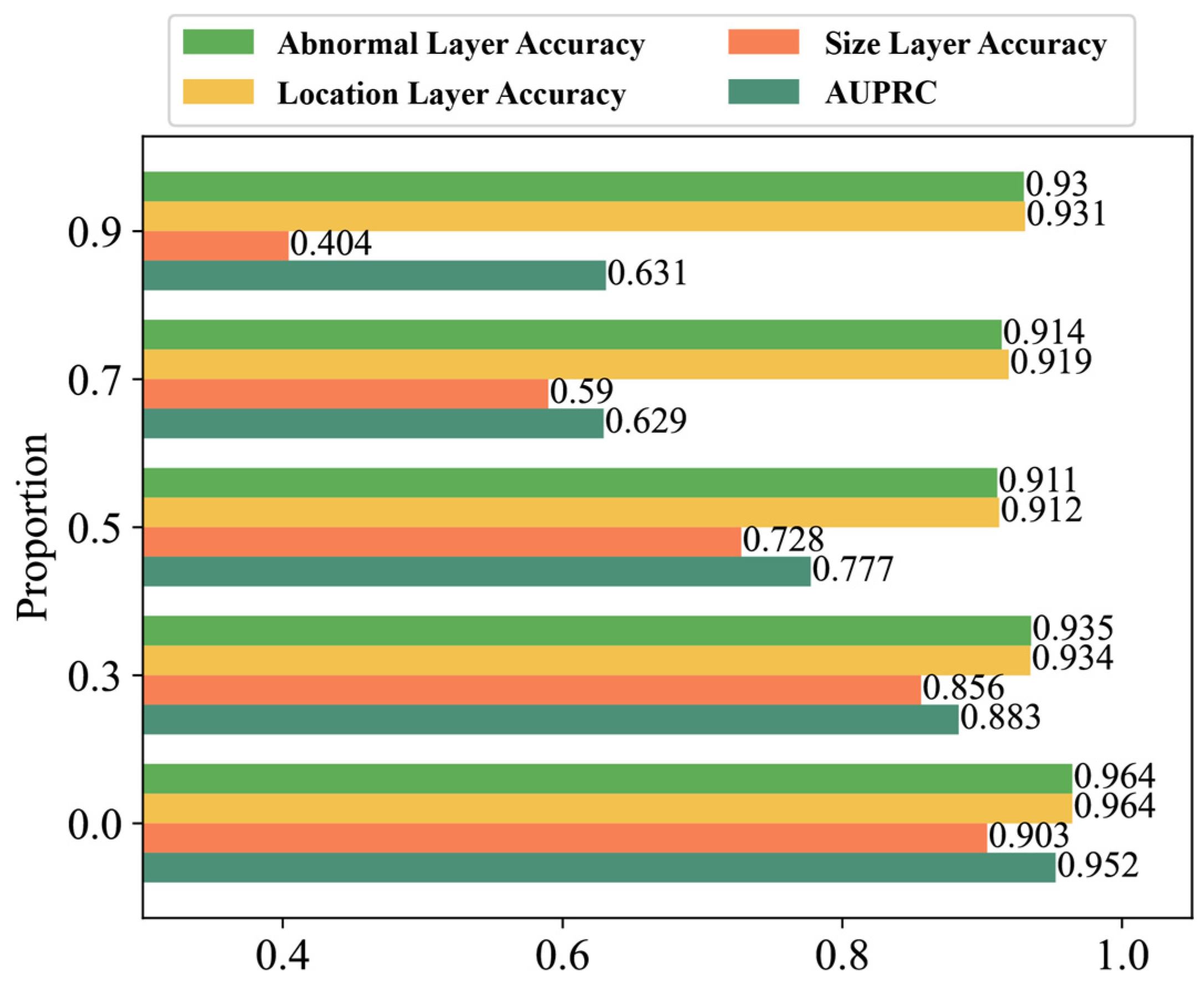
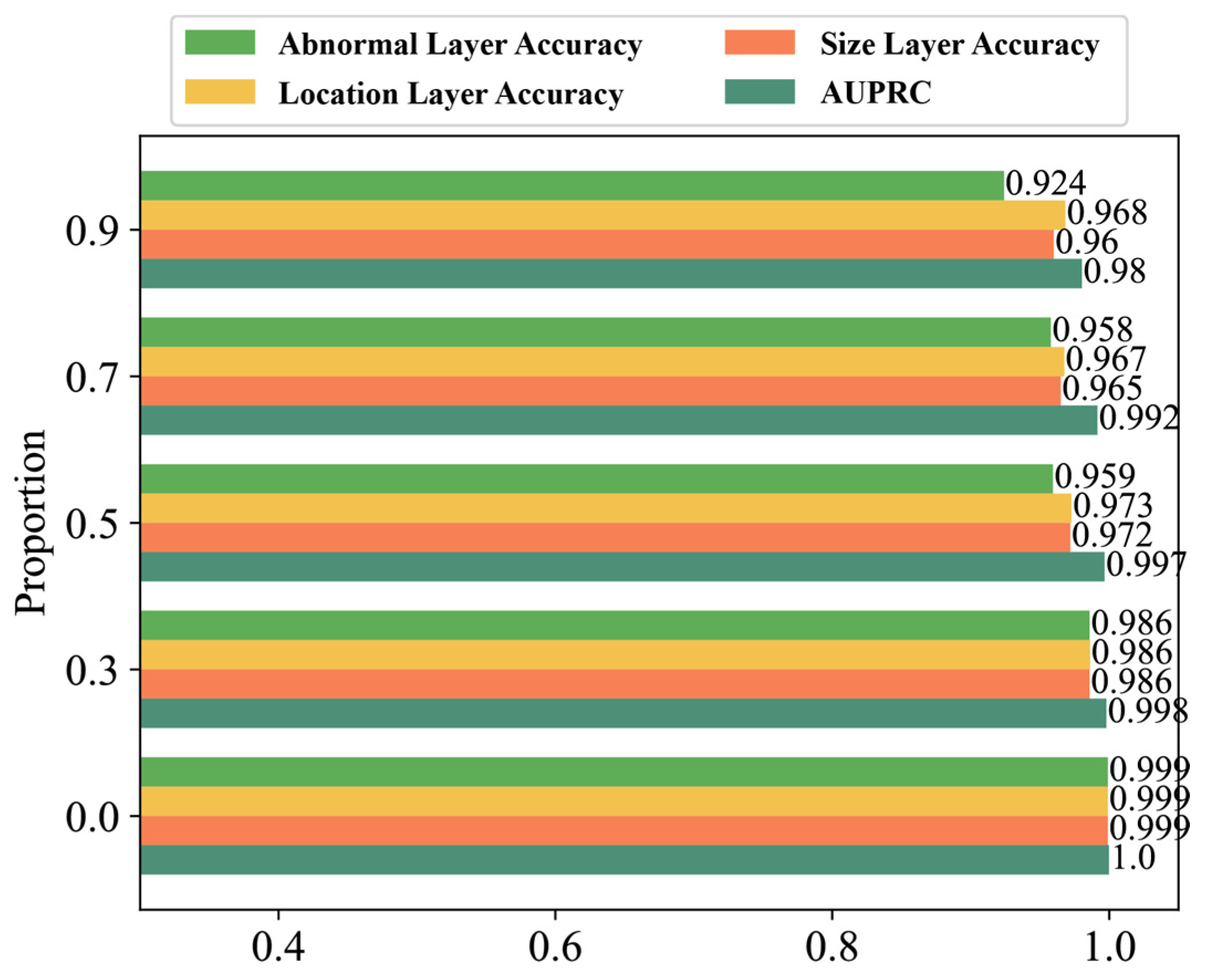
4.4. Ablation Studies on HMDN
4.5. Ablation Study on Loss Functions
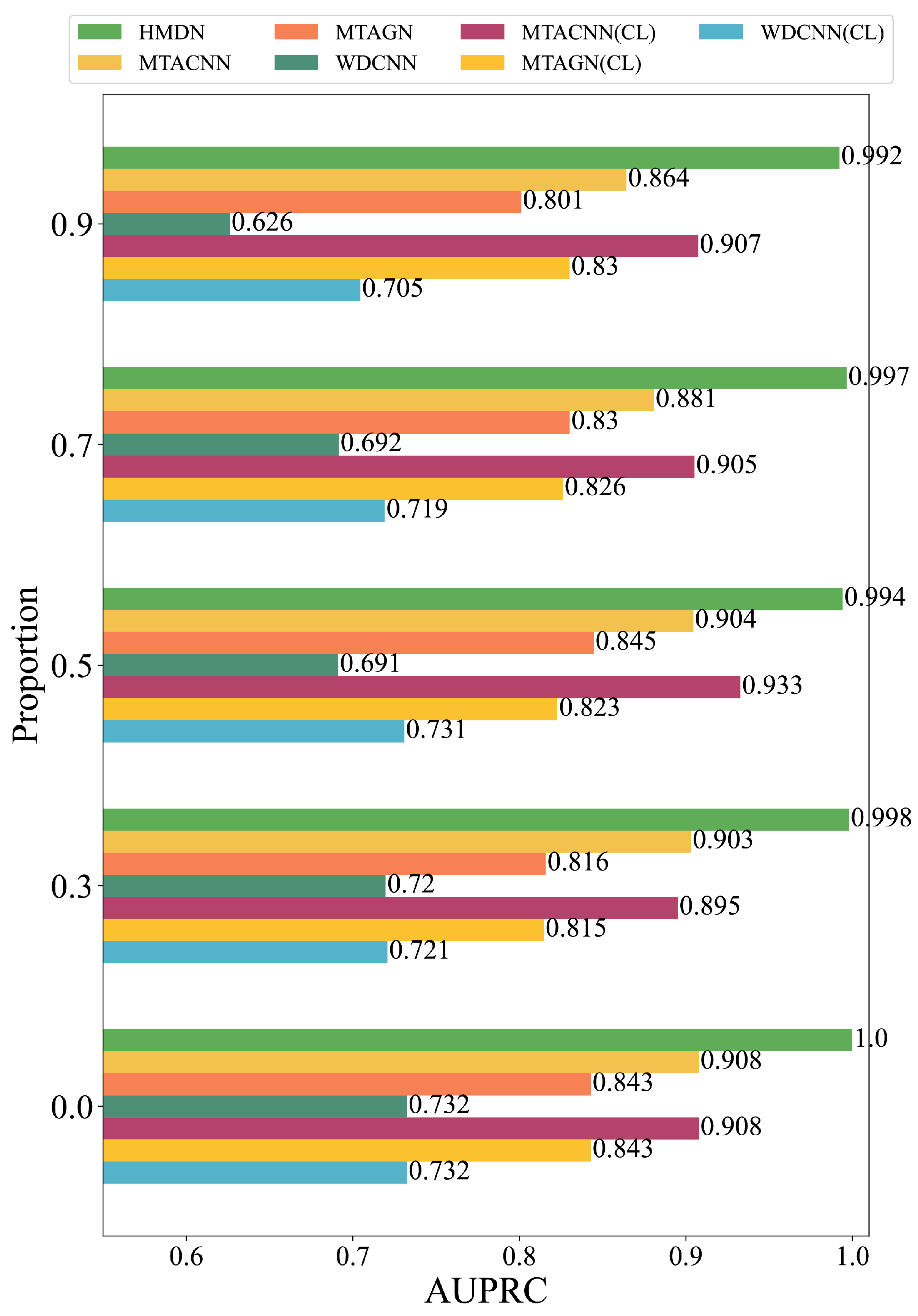
4.6. Comparative Analysis with SOTA Methods
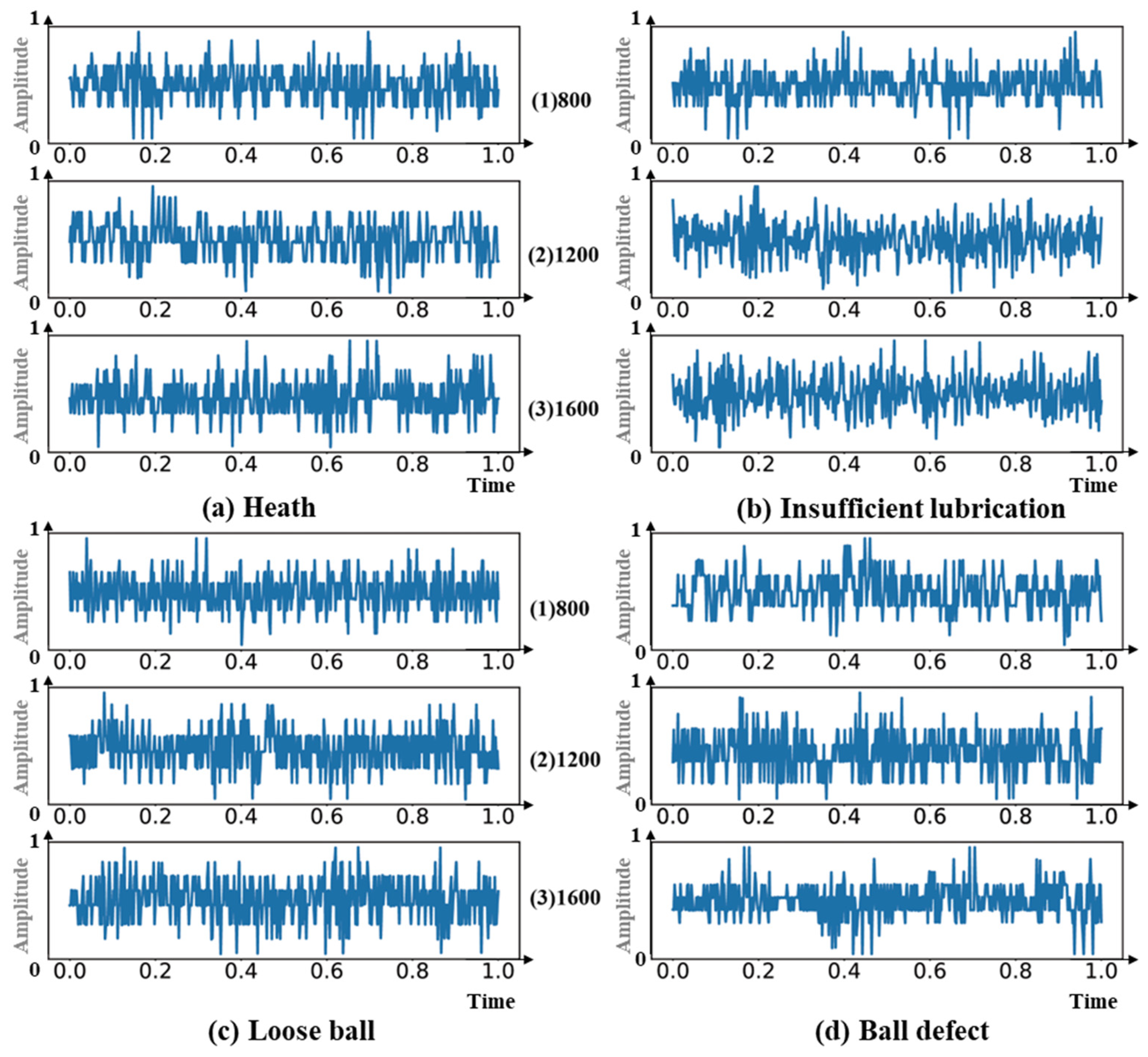
4.7. Case 2: Triple-GB Dataset
4.8. Comparative Analysis with SOTA Models
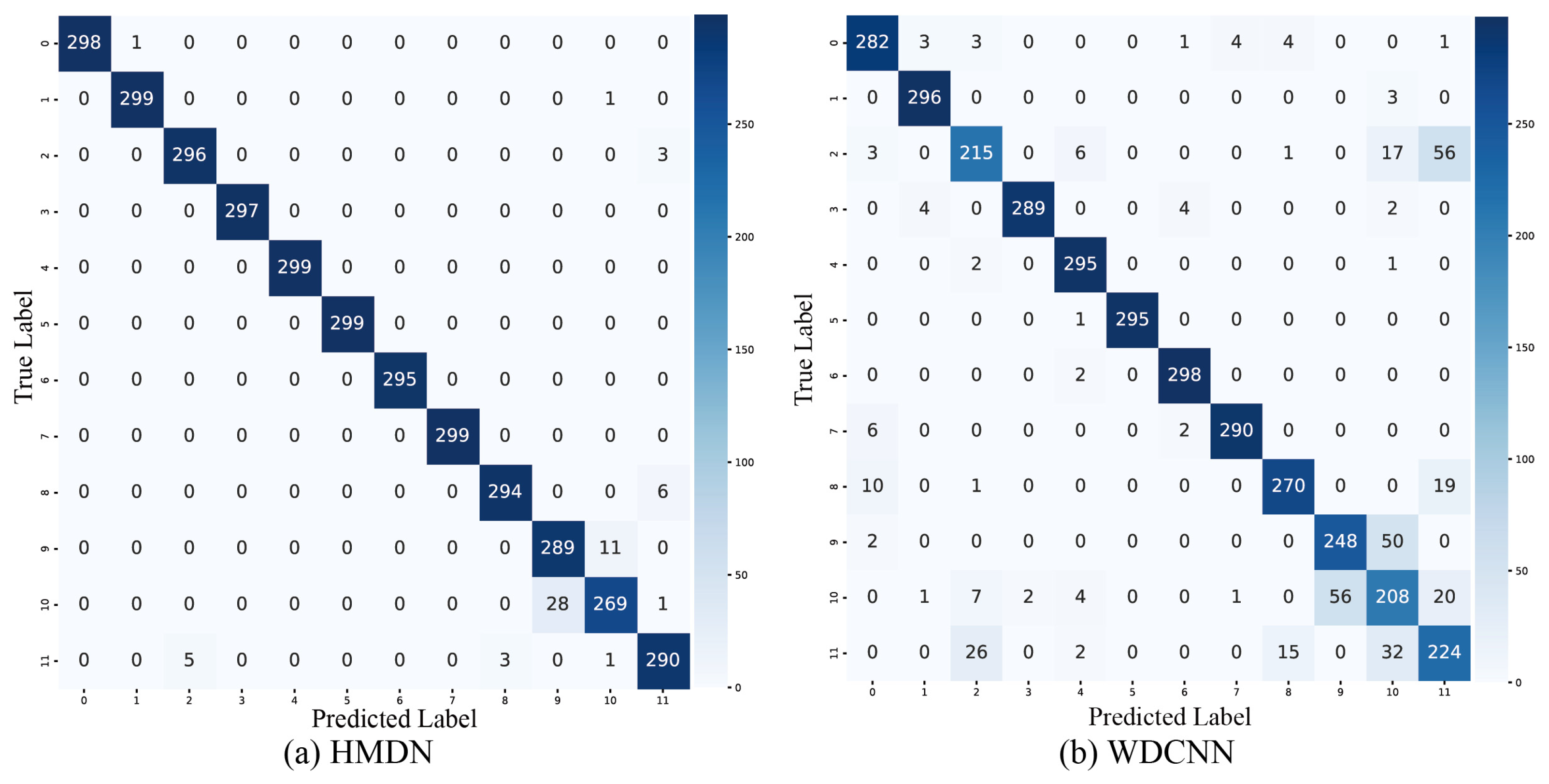
4.9. Confusion Matrix Visualization Analysis
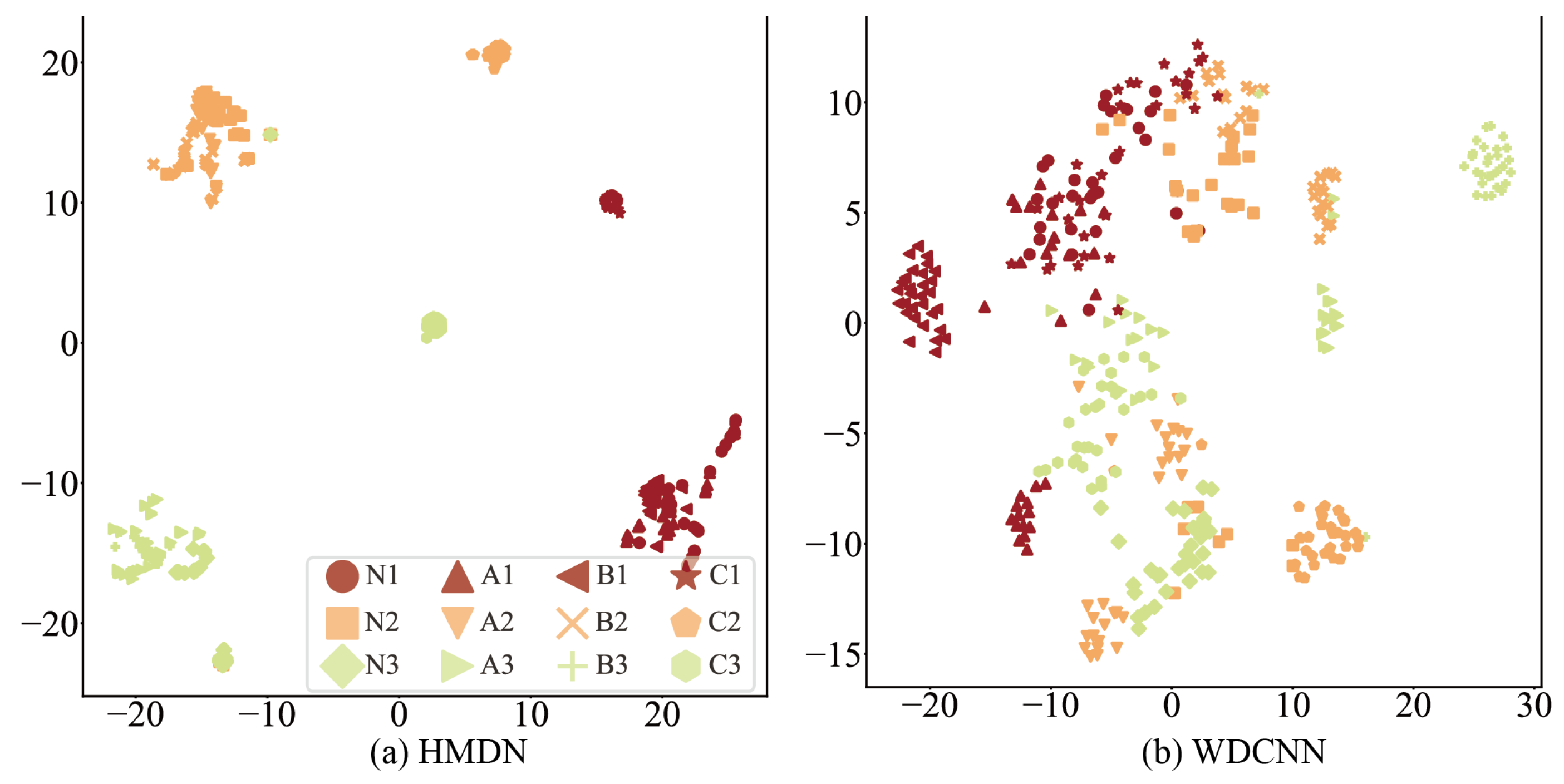
4.10. Feature Distribution Visualization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lei, Z.; Shi, J.; Luo, Z.; Cheng, M.; Wan, J. Intelligent Manufacturing from the Perspective of Industry 5.0: Application Review and Prospects. IEEE Access 2024, 12, 167436–167451. [Google Scholar] [CrossRef]
- Huang, K.; Zhu, L.; Ren, Z.; Lin, T.; Zeng, L.; Wan, J.; Zhu, Y. An Improved Fault Diagnosis Method for Rolling Bearings Based on 1D_CNN Considering Noise and Working Condition Interference. Machines 2024, 12, 383. [Google Scholar] [CrossRef]
- Tan, J.; Wan, J.; Chen, B.; Safran, M.; AlQahtani, S.A.; Zhang, R. Selective Feature Reinforcement Network for Robust Remote Fault Diagnosis of Wind Turbine Bearing Under Non-Ideal Sensor Data. IEEE Trans. Instrum. Meas. 2024, 73, 3515911. [Google Scholar] [CrossRef]
- Chettri, L.; Bera, R. A Comprehensive Survey on Internet of Things (IoT) Toward 5G Wireless Systems. IEEE Internet Things J. 2020, 7, 16–32. [Google Scholar] [CrossRef]
- Wan, J.; Li, X.; Dai, H.N.; Kusiak, A.; Martínez-García, M.; Li, D. Artificial-Intelligence-Driven Customized Manufacturing Factory: Key Technologies, Applications, and Challenges. Proc. IEEE 2021, 109, 377–398. [Google Scholar] [CrossRef]
- Ali, N.; Wang, Q.; Gao, Q.; Ma, K. Diagnosis of Multicomponent Faults in SRM Drives Based on Auxiliary Current Reconstruction Under Soft-Switching Operation. IEEE Trans. Ind. Electron. 2024, 71, 2265–2276. [Google Scholar] [CrossRef]
- Yan, S.; Shao, H.; Xiao, Y.; Liu, B.; Wan, J. Hybrid robust convolutional autoencoder for unsupervised anomaly detection of machine tools under noises. Robot. Comput.-Integr. Manuf. 2023, 79, 102441. [Google Scholar] [CrossRef]
- Gao, Q.; Huang, T.; Zhao, K.; Shao, H.; Jin, B. Multi-source weighted source-free domain transfer method for rotating machinery fault diagnosis. Expert Syst. Applications 2024, 237, 121585. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, B.; Yang, T.; Lyu, D.; Gao, W. Multitask Convolutional Neural Network with Information Fusion for Bearing Fault Diagnosis and Localization. IEEE Trans. Ind. Electron. 2020, 67, 8005–8015. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, D.; Lu, W.; Yang, J.; Li, Z.; Liang, B. A Deep Transfer Model with Wasserstein Distance Guided Multi-Adversarial Networks for Bearing Fault Diagnosis Under Different Working Conditions. IEEE Access 2019, 7, 65303–65318. [Google Scholar] [CrossRef]
- Hu, Q.; Si, X.; Qin, A.; Lv, Y.; Liu, M. Balanced Adaptation Regularization Based Transfer Learning for Unsupervised Cross-Domain Fault Diagnosis. IEEE Sens. J. 2022, 22, 12139–12151. [Google Scholar] [CrossRef]
- Tian, J.; Han, D.; Li, M.; Shi, P. A multi-source information transfer learning method with subdomain adaptation for cross-domain fault diagnosis. Knowl.-Based Syst. 2022, 243, 108466. [Google Scholar] [CrossRef]
- Kuang, J.; Xu, G.; Tao, T.; Wu, Q.; Han, C.; Wei, F. Domain Conditioned Joint Adaptation Network for Intelligent Bearing Fault Diagnosis Across Different Positions and Machines. IEEE Sens. J. 2023, 23, 4000–4010. [Google Scholar] [CrossRef]
- Xu, J.; Li, K.; Fan, Y.; Yuan, X. A label information vector generative zero-shot model for the diagnosis of compound faults. Expert Syst. Appl. 2023, 233, 120875. [Google Scholar] [CrossRef]
- Li, B.; Zhao, C. Federated Zero-Shot Industrial Fault Diagnosis with Cloud-Shared Semantic Knowledge Base. IEEE Internet Things J. 2023, 10, 11619–11630. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Cai, G. The Multiclass Fault Diagnosis of Wind Turbine Bearing Based on Multisource Signal Fusion and Deep Learning Generative Model. IEEE Trans. Instrum. Meas. 2022, 71, 3514212. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A New Deep Transfer Learning Based on Sparse Auto-Encoder for Fault Diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 136–144. [Google Scholar] [CrossRef]
- Zhang, X.; He, C.; Lu, Y.; Chen, B.; Zhu, L.; Zhang, L. Fault diagnosis for small samples based on attention mechanism. Measurement 2022, 187, 110242. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Shu, T.; Wan, J.; de Silva, C.W.; Wang, Z. A Two-Stage Approach for the Remaining Useful Life Prediction of Bearings Using Deep Neural Networks. IEEE Trans. Ind. Inform. 2019, 15, 3703–3711. [Google Scholar] [CrossRef]
- He, M.; Li, Z.; Hu, F. A Novel RUL-Centric Data Augmentation Method for Predicting the Remaining Useful Life of Bearings. Machines 2024, 12, 766. [Google Scholar] [CrossRef]
- Zhu, X.; Zhao, X.; Yao, J.; Deng, W.; Shao, H.; Liu, Z. Adaptive Multiscale Convolution Manifold Embedding Networks for Intelligent Fault Diagnosis of Servo Motor-Cylindrical Rolling Bearing Under Variable Working Conditions. IEEE/ASME Trans. Mechatron. 2024, 29, 2230–2240. [Google Scholar] [CrossRef]
- Shi, J.; Wang, X.; Lu, S.; Zheng, J.; Dong, H.; Zhang, J. An Adversarial Multisource Data Subdomain Adaptation Model: A Promising Tool for Fault Diagnosis of Induction Motor Under Cross-Operating Conditions. IEEE Trans. Instrum. Meas. 2023, 72, 3519014. [Google Scholar] [CrossRef]
- Jia, L.; Chow, T.W.S.; Yuan, Y. Causal Disentanglement Domain Generalization for time-series signal fault diagnosis. Neural Netw. 2024, 172, 106099. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wu, J.; Deng, C.; Wang, X.; Wang, Y. Deep Attention Relation Network: A Zero-Shot Learning Method for Bearing Fault Diagnosis Under Unknown Domains. IEEE Trans. Reliab. 2023, 72, 79–89. [Google Scholar] [CrossRef]
- Xing, Z.; Yi, C.; Lin, J.; Zhou, Q. A Novel Periodic Cyclic Sparse Network with Entire Domain Adaptation for Deep Transfer Fault Diagnosis of Rolling Bearing. IEEE Sens. J. 2023, 23, 13452–13468. [Google Scholar] [CrossRef]
- Xiao, Y.; Shao, H.; Han, S.; Huo, Z.; Wan, J. Novel Joint Transfer Network for Unsupervised Bearing Fault Diagnosis From Simulation Domain to Experimental Domain. IEEE/ASME Trans. Mechatron. 2022, 27, 5254–5263. [Google Scholar] [CrossRef]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition Monitoring of Bearing Damage in Electromechanical Drive Systems by Using Motor Current Signals of Electric Motors: A Benchmark Data Set for Data-Driven Classification. In Proceedings of the European Conference of the Prognostics and Health Management Society, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Shao, S.; Yan, R.; Lu, Y.; Wang, P.; Gao, R.X. DCNN-Based Multi-Signal Induction Motor Fault Diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 2658–2669. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Computer Vision—ECCV 2018, Proceedings of the 15th European Conference, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Guo, Q.; Li, Y.; Song, Y.; Wang, D.; Chen, W. Intelligent Fault Diagnosis Method Based on Full 1-D Convolutional Generative Adversarial Network. IEEE Trans. Ind. Inform. 2020, 16, 2044–2053. [Google Scholar] [CrossRef]


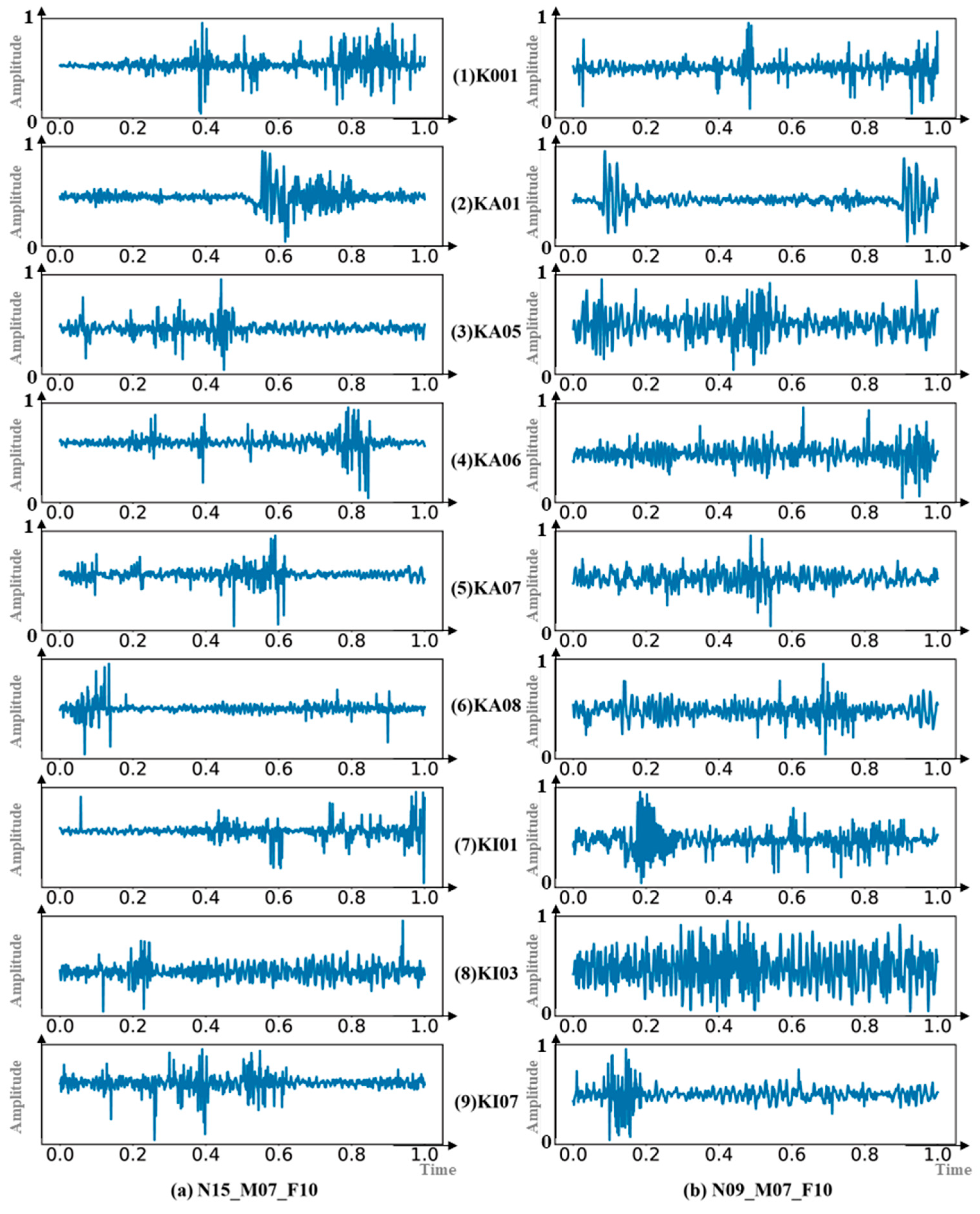



| Label | Speed (rpm) | Load Torque (Nm) | Radial Force (N) | Annotation Information |
|---|---|---|---|---|
| WC1 | 1500 | 0.7 | 1000 | N15_M07_F10 |
| WC2 | 900 | 0.7 | 1000 | N09_M07_F10 |
| WC3 | 1500 | 0.1 | 1000 | N15_M01_F10 |
| WC4 | 1500 | 0.7 | 400 | N15_M07_F04 |
| Label | ID | Defect Present | Fault Location | Cause of Defect | Fault Severity Level |
|---|---|---|---|---|---|
| Normal | K001 | NO | None | None | None |
| OR-EDM | KA01 | Yes | Inner Ring | Electrical Discharge Machining | 1 |
| OR-EE1 | KA05 | Yes | Inner Ring | Electric Engraving | 1 |
| OR-EE1 | KA06 | Yes | Inner Ring | Electric Engraving | 2 |
| OR-Drill1 | KA07 | Yes | Inner Ring | Drilling | 1 |
| OR-Drill2 | KA08 | Yes | Inner Ring | Drilling | 2 |
| IR-EDM | KI01 | Yes | Outer Ring | Electrical Discharge Machining | 1 |
| IR-EE1 | KI03 | Yes | Outer Ring | Electric Engraving | 1 |
| IR-EE2 | KI07 | Yes | Outer Ring | Electric Engraving | 2 |
| Proportion | Model | Abnormal | Location | ||
|---|---|---|---|---|---|
| Acc | Std | Acc | Std | ||
| 0.7 | MTACNN | 97.4442 | 0.01367 | 97.4442 | 0.01367 |
| MTAGN | 97.0535 | 0.01367 | 97.2488 | 0.01367 | |
| WDCNN | 90.0613 | 0.03702 | 89.4921 | 0.02845 | |
| MTACNN(CL) | 98.2421 | 0.03702 | 97.6953 | 0.01367 | |
| MTAGN(CL) | 97.4497 | 0.01367 | 97.4776 | 0.01367 | |
| WDCNN(CL) | 95.4129 | 0.02232 | 94.4977 | 0.04464 | |
| HMDN | 98.5825 | 0.01116 | 98.3314 | 0.01116 | |
| 0.9 | MTACNN | 95.5189 | 0.01367 | 95.7979 | 0.01367 |
| MTAGN | 95.8314 | 0.02232 | 95.6473 | 0.03056 | |
| WDCNN | 78.4765 | 0.02845 | 79.2745 | 0.02734 | |
| MTACNN(CL) | 97.9408 | 0.01116 | 97.3214 | 0.01367 | |
| MTAGN(CL) | 97.3046 | 0.01367 | 96.9642 | 0.01116 | |
| WDCNN(CL) | 93.9899 | 0.01367 | 90.6584 | 0.02734 | |
| HMDN | 98.8024 | 0.01367 | 98.2957 | 0.01116 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Tan, J.; Luo, Y.; Wang, S.; Wan, J. Multi-Condition Intelligent Fault Diagnosis Based on Tree-Structured Labels and Hierarchical Multi-Granularity Diagnostic Network. Machines 2024, 12, 891. https://doi.org/10.3390/machines12120891
Yan H, Tan J, Luo Y, Wang S, Wan J. Multi-Condition Intelligent Fault Diagnosis Based on Tree-Structured Labels and Hierarchical Multi-Granularity Diagnostic Network. Machines. 2024; 12(12):891. https://doi.org/10.3390/machines12120891
Chicago/Turabian StyleYan, Hehua, Jinbiao Tan, Yixiong Luo, Shiyong Wang, and Jiafu Wan. 2024. "Multi-Condition Intelligent Fault Diagnosis Based on Tree-Structured Labels and Hierarchical Multi-Granularity Diagnostic Network" Machines 12, no. 12: 891. https://doi.org/10.3390/machines12120891
APA StyleYan, H., Tan, J., Luo, Y., Wang, S., & Wan, J. (2024). Multi-Condition Intelligent Fault Diagnosis Based on Tree-Structured Labels and Hierarchical Multi-Granularity Diagnostic Network. Machines, 12(12), 891. https://doi.org/10.3390/machines12120891








