AC-Winding-Resistance Calculation of Toroidal Inductors with Solid-Round-Wire and Litz-Wire Winding Based on Complex Permeability Modeling †
Abstract
1. Introduction
2. A Literature Review of Winding Loss Calculation in Toroidal Inductor Windings
2.1. Modified Dowell’s Model
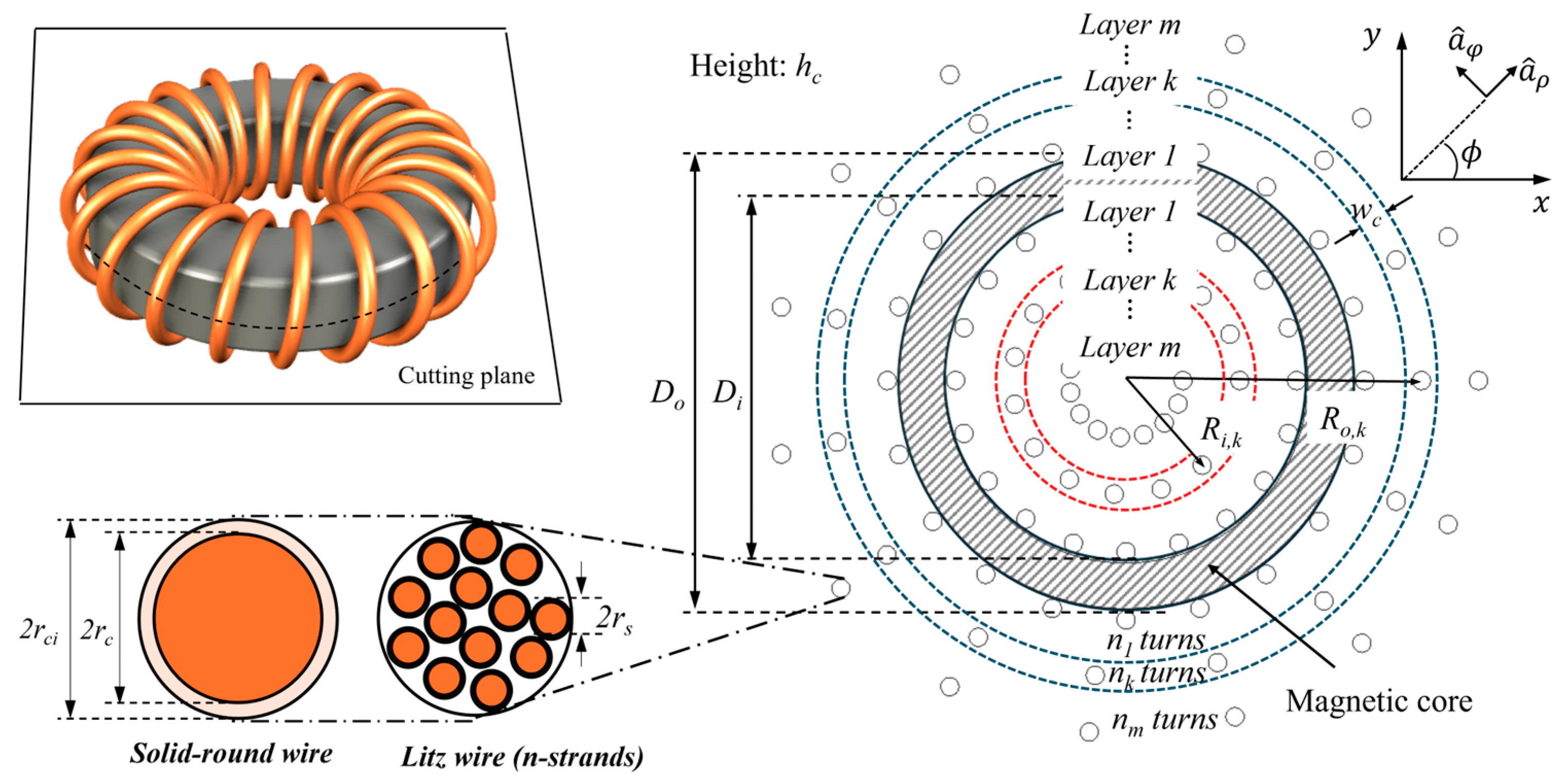
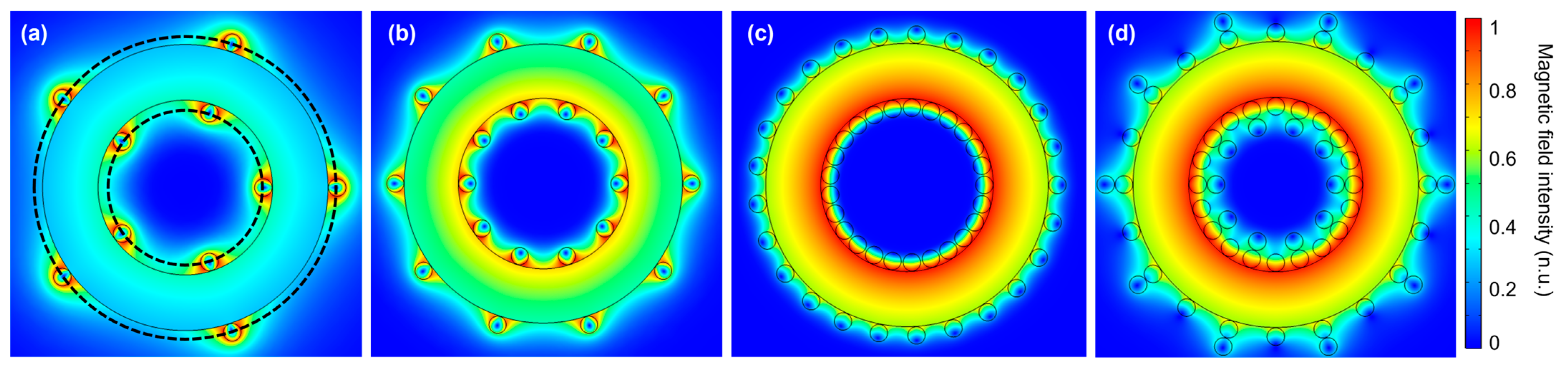
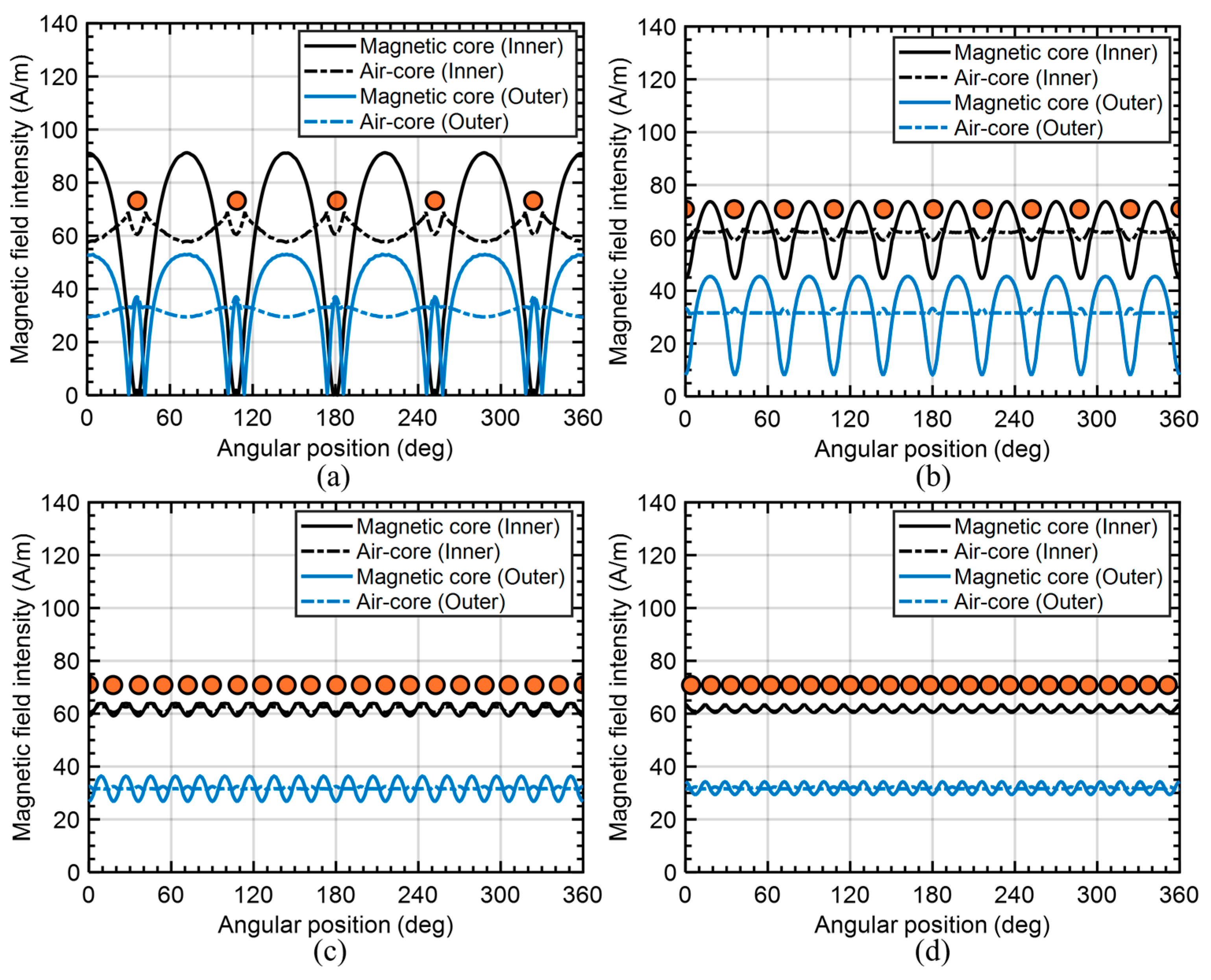
2.2. The Magnetic Field in the Winding and Its Contribution on the AC Winding Resistance
3. Complex Permeability Approach for AC-resistance Calculation
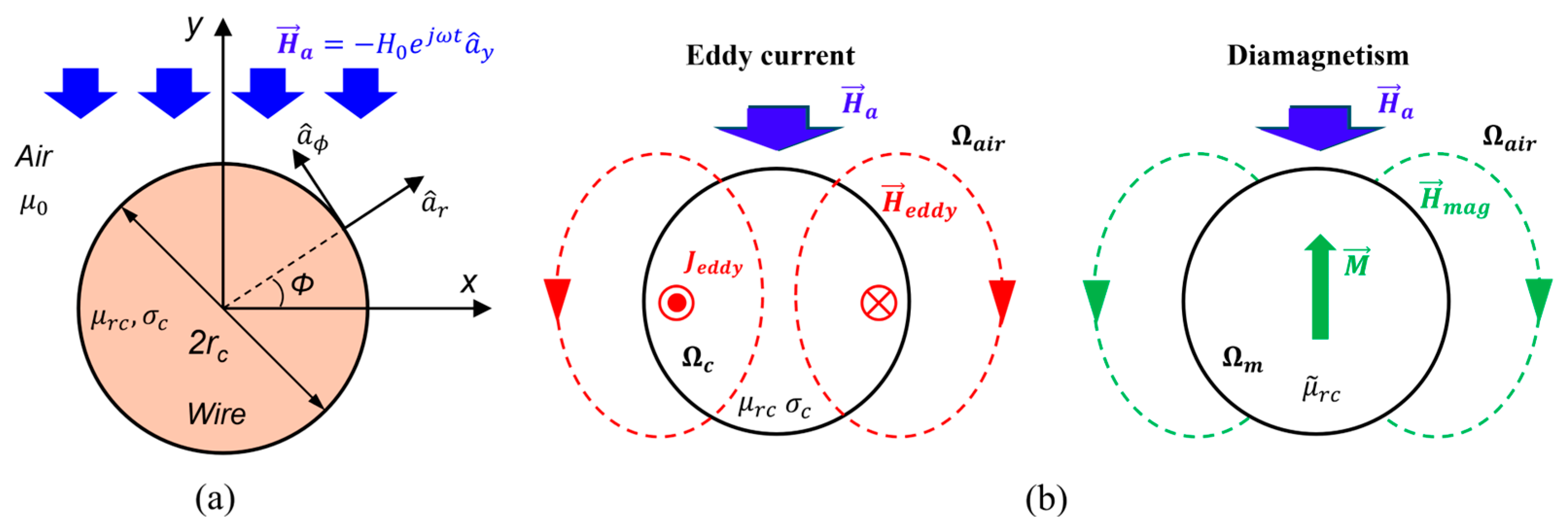
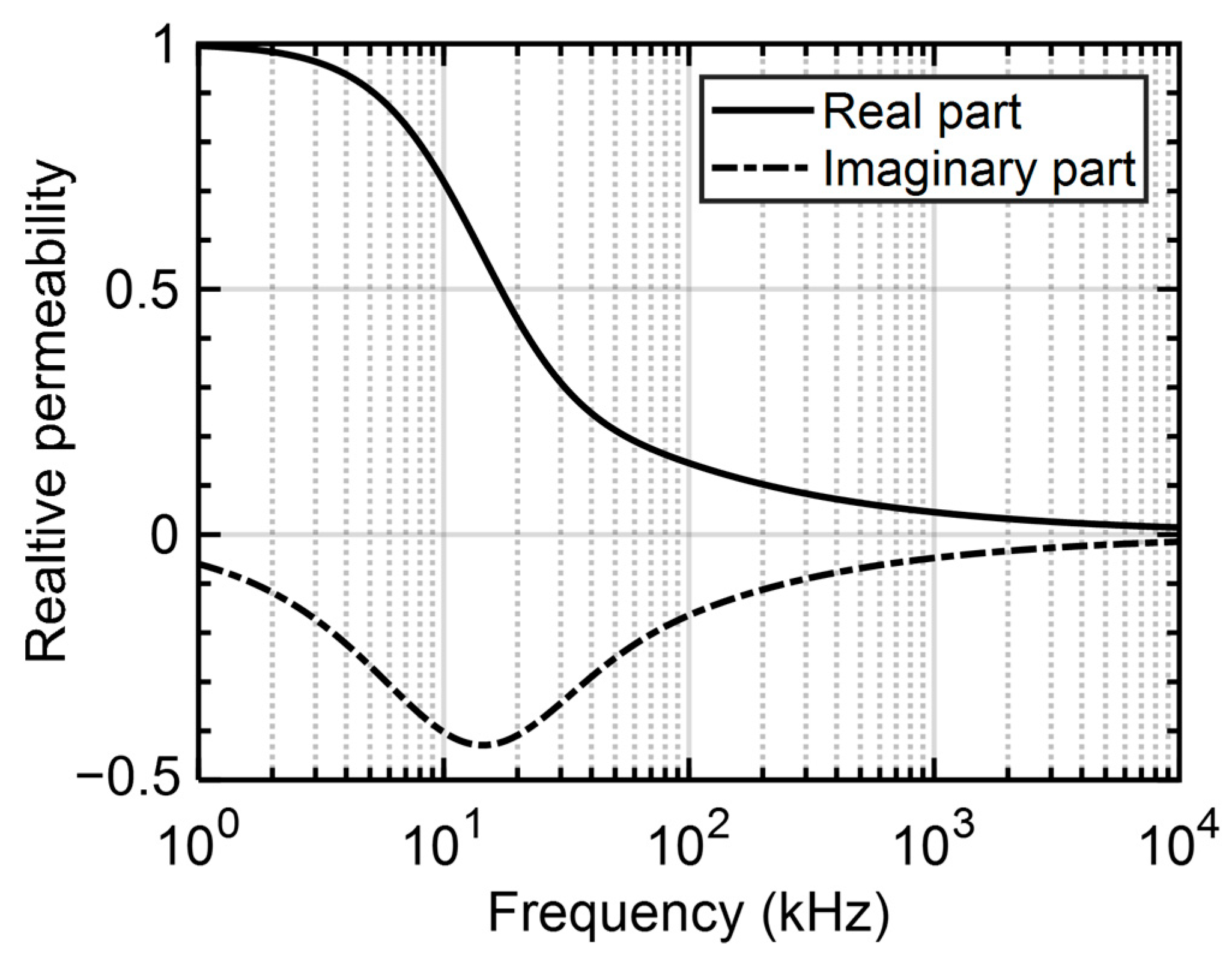
3.1. Complex Permeability of a Solid Round Wire
3.2. Complex Permeability of a Litz-Wire
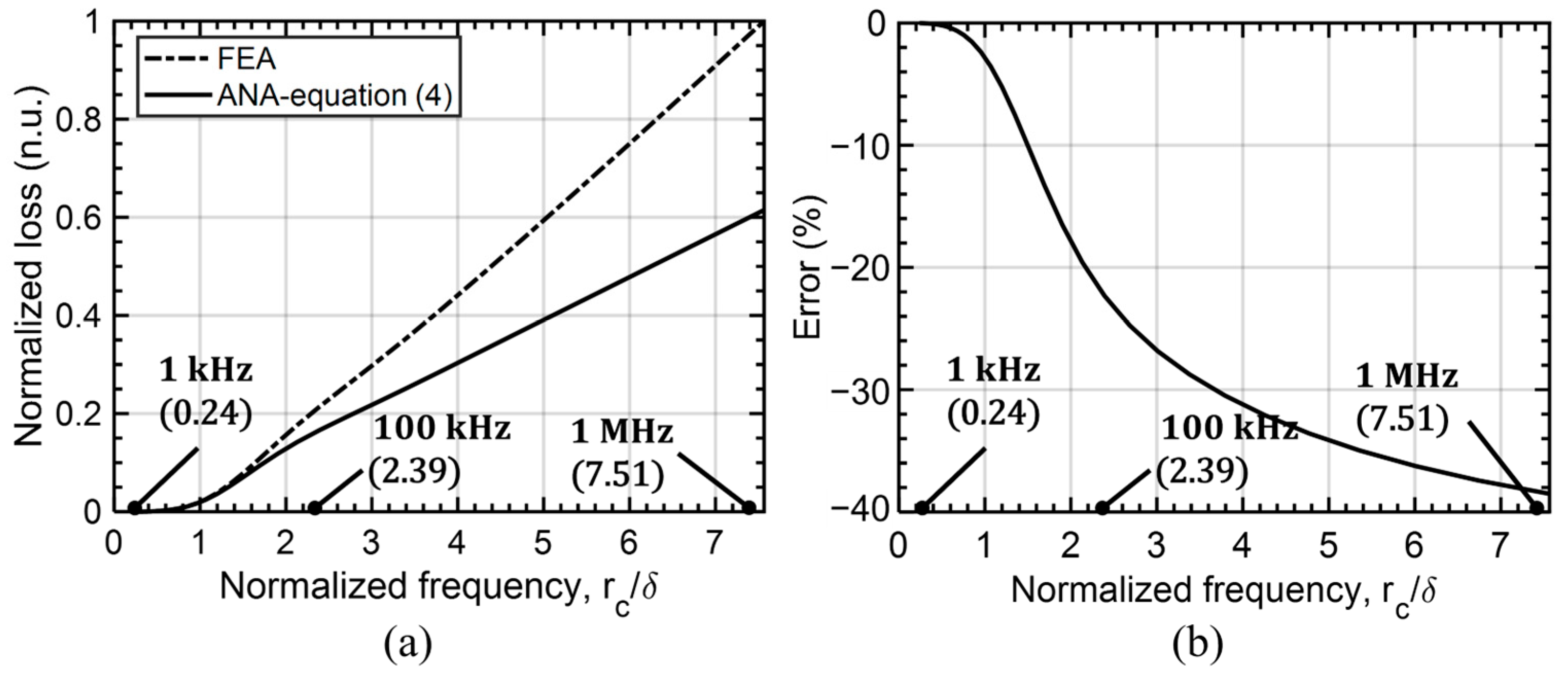
4. Iterative Calculation Approach for Higher-Frequency AC-Resistance Calculation
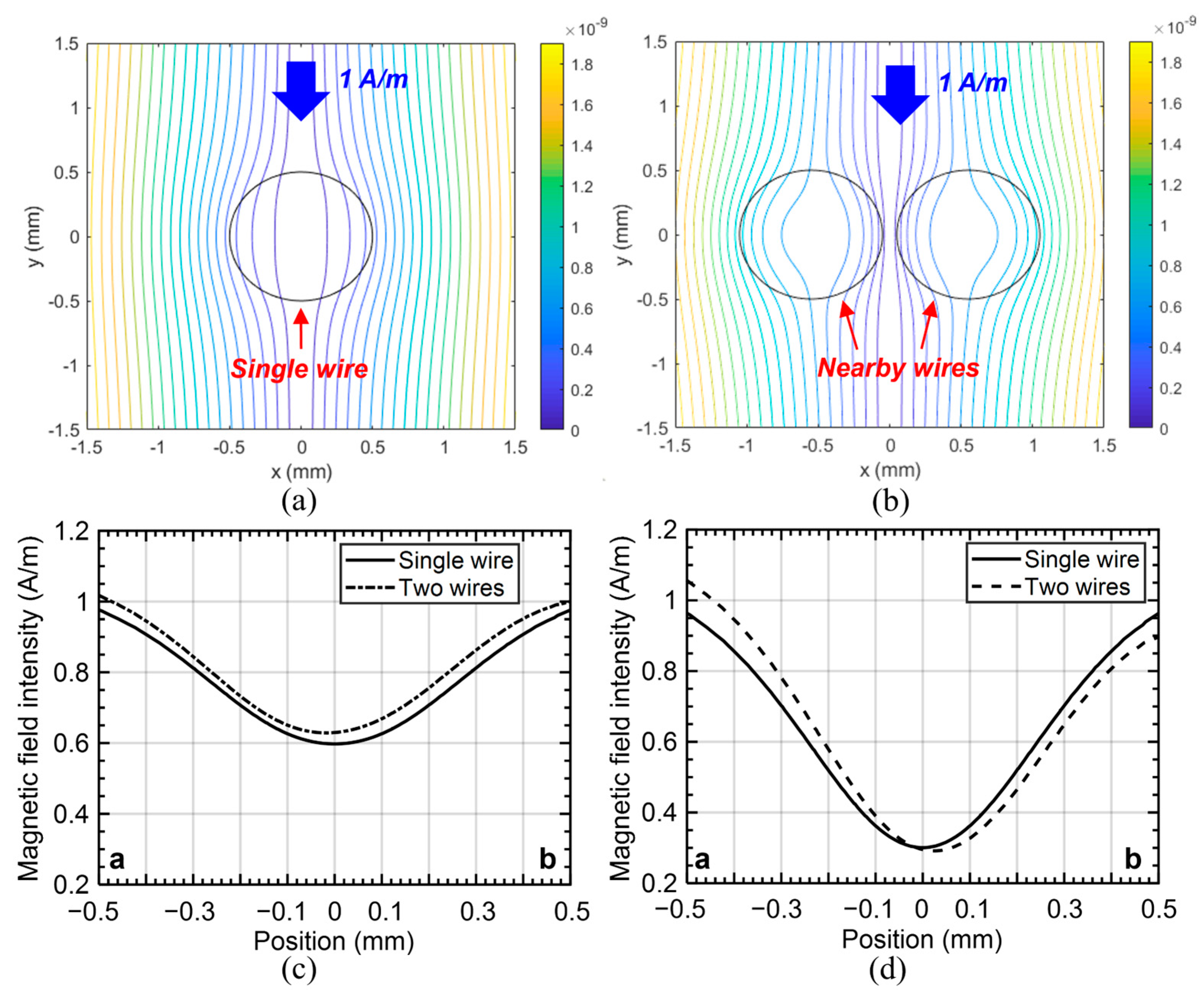
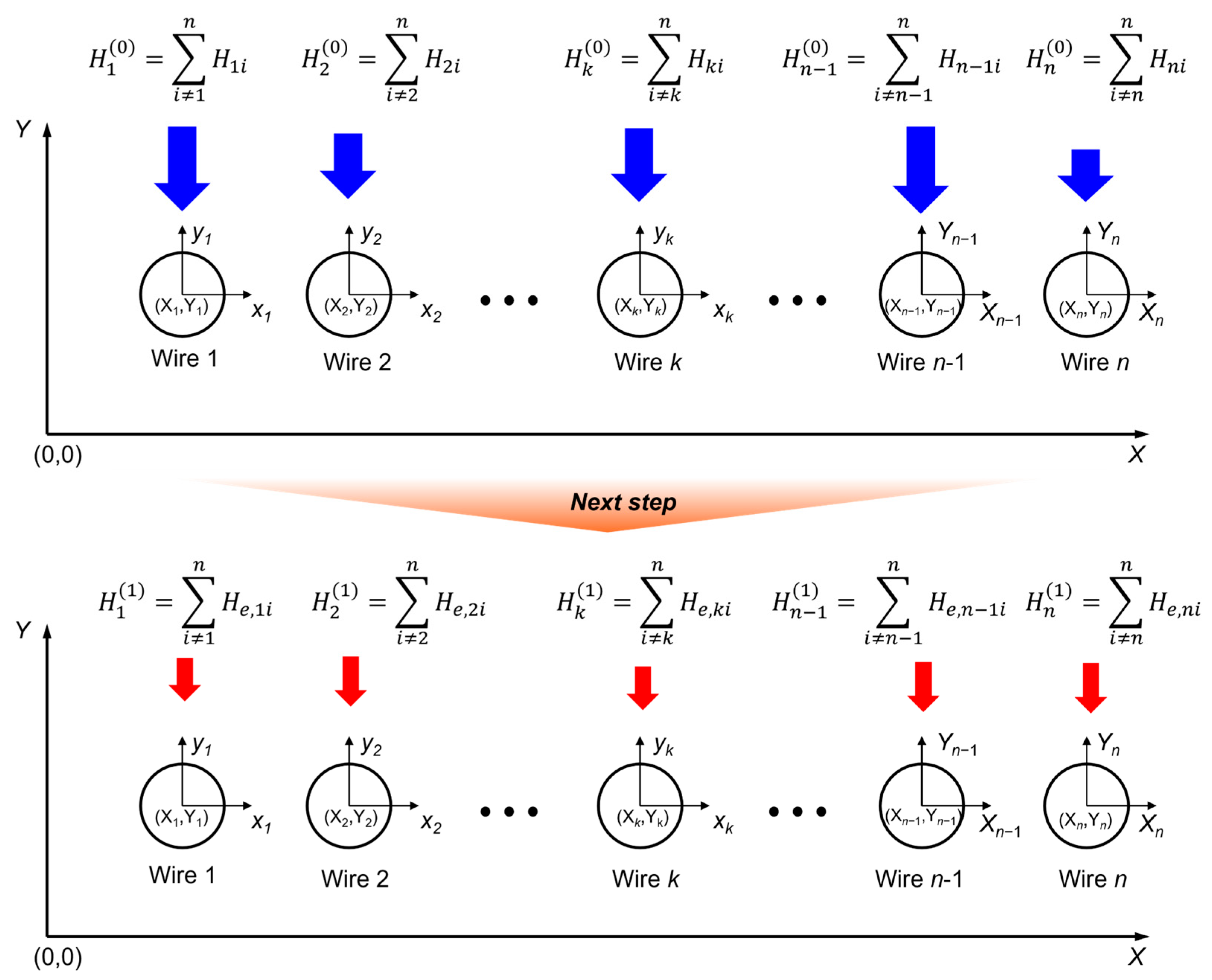
4.1. The Effect of the Magnetic Field Induced by Eddy Currents
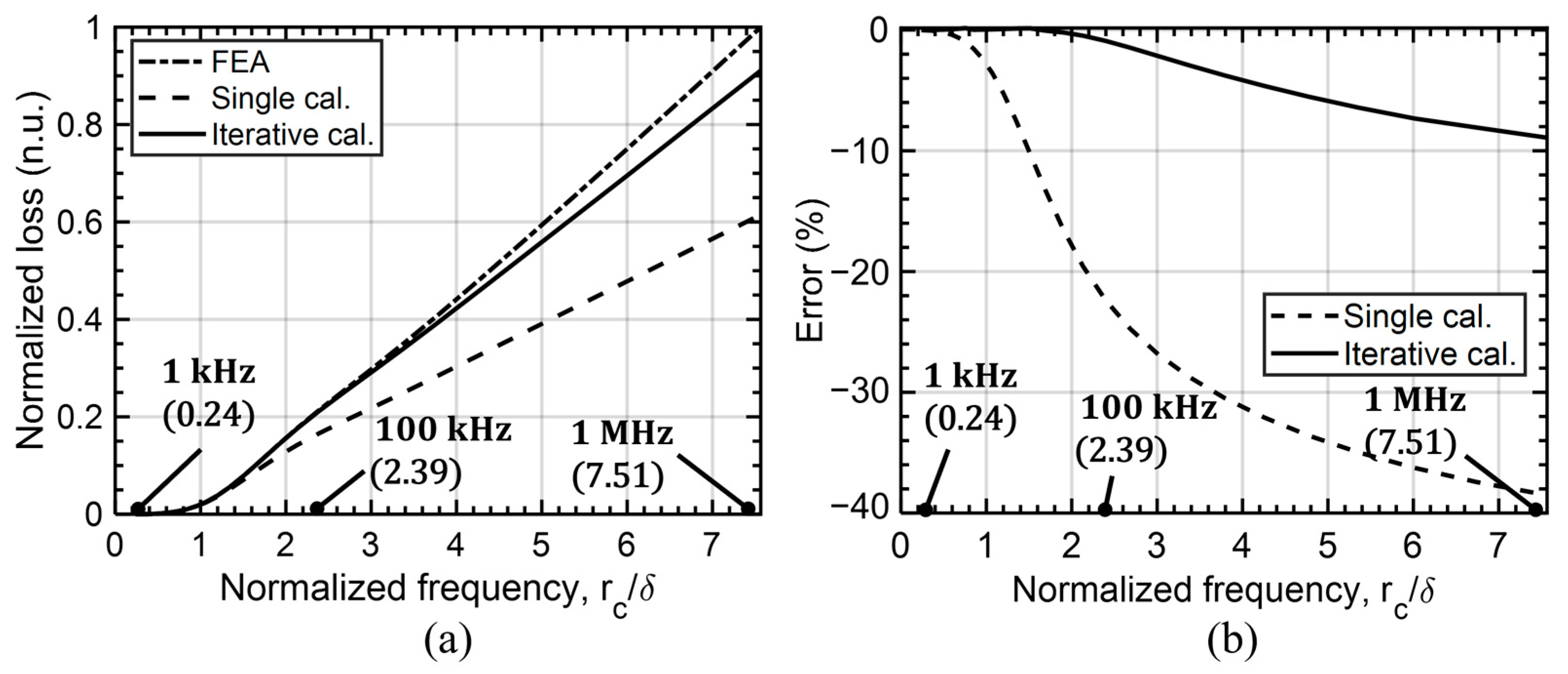
4.2. Iterative Calculation Approach
4.3. AC-Resistance Calculation for a Toroidal Inductor Winding
5. Simulation and Measurement
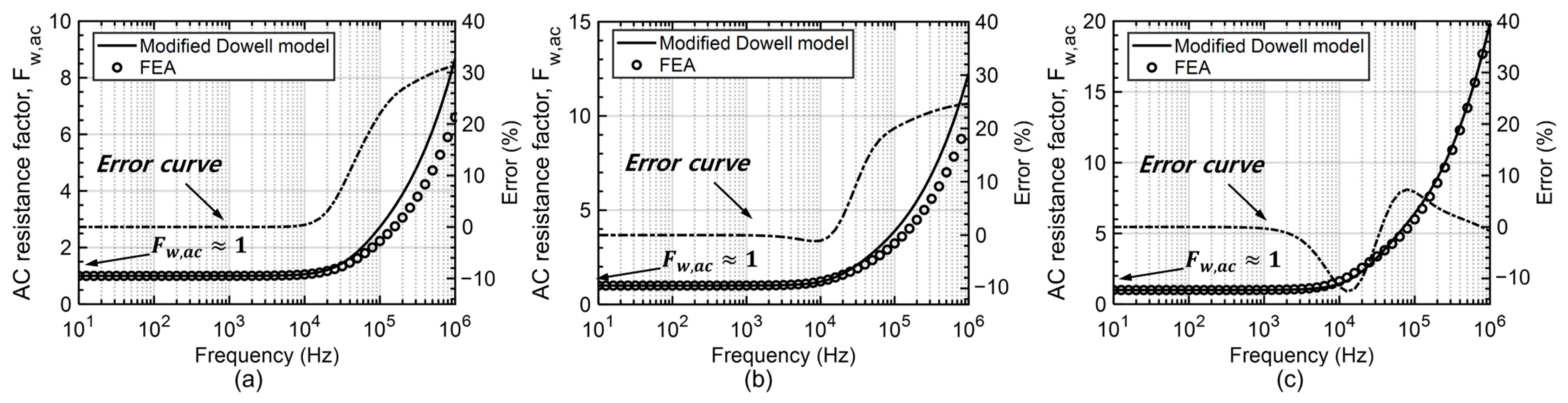
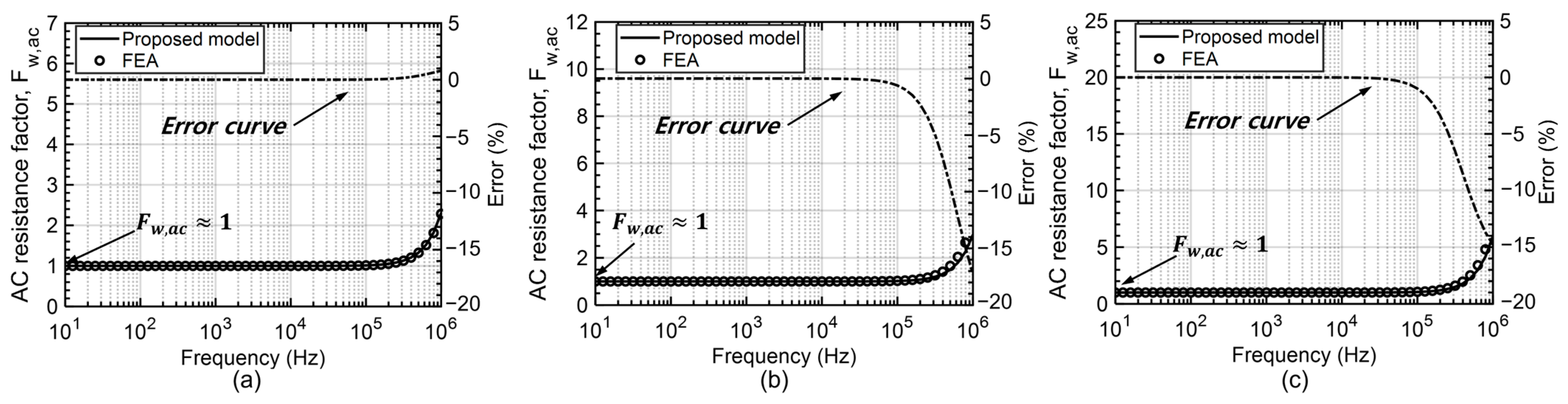
5.1. Calculation Results
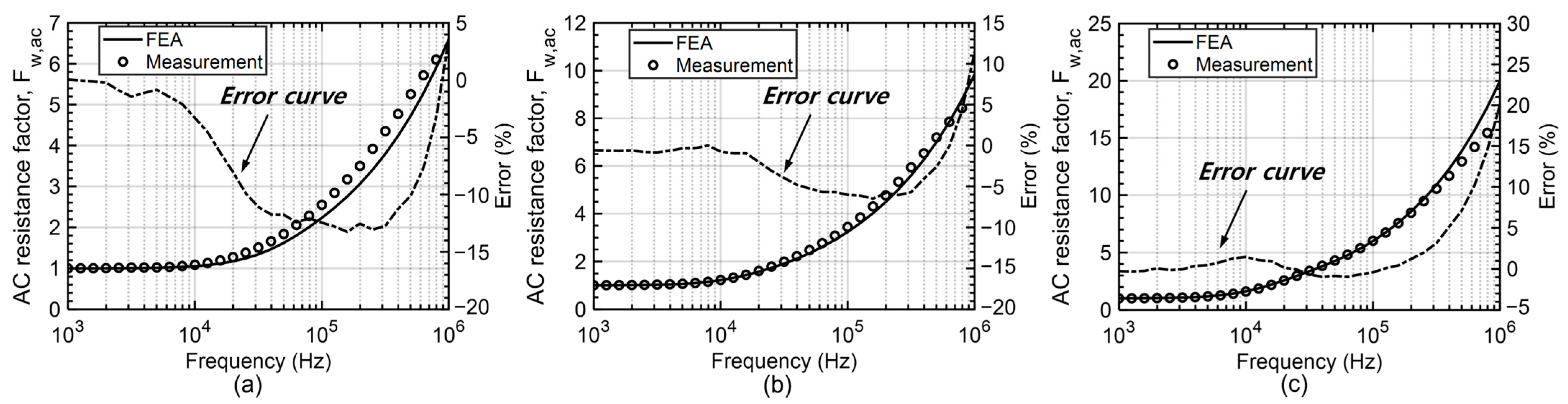
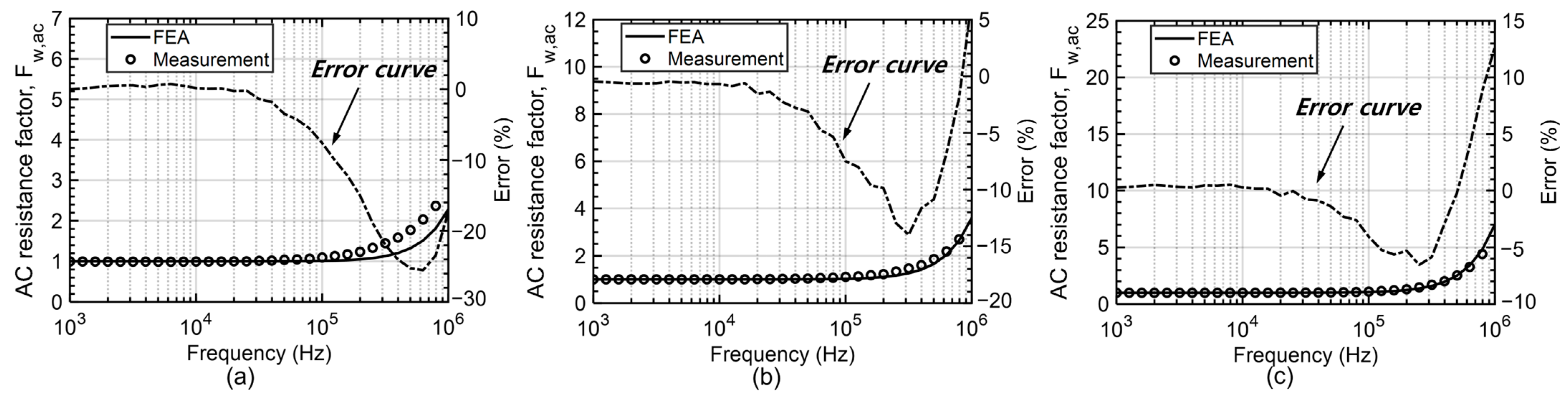
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iannaccone, G.; Sbrana, C.; Morelli, I.; Strangio, S. Power Electronics Based on Wide-Bandgap Semiconductors: Opportunities and Challenges. IEEE Access 2021, 9, 139446–139456. [Google Scholar] [CrossRef]
- Morya, A.K.; Gardner, M.C.; Anvari, B.; Liu, L.; Yepes, A.G.; Doval-Gandoy, J.; Toliyat, H.A. Wide Bandgap Devices in AC Electric Drives: Opportunities and Challenges. IEEE Trans. Transp. Electrif. 2019, 5, 3–20. [Google Scholar] [CrossRef]
- Kumar, A.; Moradpour, M.; Losito, M.; Franke, W.-T.; Ramasamy, S.; Baccoli, R.; Gatto, G. Wide Band Gap Devices and Their Application in Power Electronics. Energies 2022, 15, 9172. [Google Scholar] [CrossRef]
- Spang, M.; Albach, M. Optimized Winding Layout for Minimized Proximity Losses in Coils with Rod Cores. IEEE Trans. Magn. 2008, 44, 1815–1821. [Google Scholar] [CrossRef]
- Nan, X.; Sullivan, C.R. An Equivalent Complex Permeability Model for Litz-Wire Windings. IEEE Trans. Ind. Appl. 2009, 45, 854–860. [Google Scholar] [CrossRef]
- Gyselinck, J.; Dular, P. Frequency-domain homogenization of bundles of wires in 2-D magnetodynamic FE calculations. IEEE Trans. Magn. 2005, 41, 1416–1419. [Google Scholar] [CrossRef]
- Niyomsatian, K.; Gyselinck, J.; Sabariego, R.V. New closed-form proximity-effect complex permeability expression for characterizing litz-wire windings. In Proceedings of the Tenth International Conference on Computational Electromagnetics (CEM), Edinburgh, UK, 19–20 June 2019; pp. 1–2. [Google Scholar]
- Igarashi, H. Semi-Analytical Approach for Finite-Element Analysis of Multi-Turn Coil Considering Skin and Proximity Effects. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Otomo, Y.; Igarashi, H.; Sano, H.; Yamada, T. Analysis of Litz Wire Losses Using Homogenization-Based FEM. IEEE Trans. Magn. 2021, 57, 7402409. [Google Scholar] [CrossRef]
- Podoltsev, A.D.; Abeywickrama, K.G.N.B.; Serdyuk, Y.V.; Gubanski, S.M. Multiscale Computations of Parameters of Power Transformer Windings at High Frequencies. Part I: Small-Scale Level. IEEE Trans. Magn. 2007, 43, 3991–3998. [Google Scholar] [CrossRef]
- Etemadrezaei, M.; Lukic, S.M. Coated-Strand Litz Wire for Multi-Megahertz Frequency Applications. IEEE Trans. Magn. 2016, 52, 6301511. [Google Scholar] [CrossRef]
- Roßkopf, A.; Bär, E.; Joffe, C.; Bonse, C. Calculation of Power Losses in Litz Wire Systems by Coupling FEM and PEEC Method. IEEE Trans. Power Electron. 2016, 31, 6442–6449. [Google Scholar] [CrossRef]
- Taran, N.; Ionel, D.M.; Rallabandi, V.; Heins, G.; Patterson, D. An Overview of Methods and a New Three-Dimensional FEA and Analytical Hybrid Technique for Calculating AC Winding Losses in PM Machines. IEEE Trans. Ind. Appl. 2021, 57, 352–362. [Google Scholar] [CrossRef]
- Volpe, G.; Popescu, M.; Marignetti, F.; Goss, J. AC Winding Losses in Automotive Traction E-Machines: A New Hybrid Calculation Method. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 2115–2119. [Google Scholar]
- Acero, J.; Alonso, R.; Burdio, J.M.; Barragan, L.A.; Puyal, D. Frequency-dependent resistance in Litz-wire planar windings for domestic induction heating appliances. IEEE Trans. Power Electron. 2016, 21, 856–866. [Google Scholar] [CrossRef]
- Jabłoński, P.; Szczegielniak, T.; Kusiak, D.; Piątek, Z. Analytical–Numerical Solution for the Skin and Proximity Effects in Two Parallel Round Conductors. Energies 2019, 12, 3584. [Google Scholar] [CrossRef]
- Acero, J.; Alonso, R.; Barragan, L.A.; Burdio, J.M. Magnetic vector potential based model for eddy-current loss calculation in round-wire planar windings. IEEE Trans. Magn. 2006, 42, 2152–2158. [Google Scholar] [CrossRef]
- Cheng, K.W.E. Computation of the AC resistance of multistranded conductor inductors with multilayers for high frequency switching converters. IEEE Trans. Magn. 2000, 36, 831–834. [Google Scholar] [CrossRef]
- Geng, S.; Chu, M.; Wang, W.; Wan, P.; Peng, X.; Lu, H.; Li, P. Modelling and optimization of winding resistance for litz wire inductors. IET Power Electron. 2021, 14, 1834–1843. [Google Scholar] [CrossRef]
- Zhao, Y.; Ming, Z.; Han, B. Analytical modelling of high-frequency losses in toroidal inductors. IET Power Electron. 2023, 16, 1538–1547. [Google Scholar] [CrossRef]
- Elizondo, D.; Barrios, E.L.; Ursúa, A.; Sanchis, P. Analytical Modeling of High-Frequency Winding Loss in Round-Wire Toroidal Inductors. IEEE Trans. Power Electron. 2023, 70, 5581–5591. [Google Scholar] [CrossRef]
- Um, Y.; Park, G.S. Modeling of Frequency-Dependent Winding Losses in Solid and Litz-wire Toroidal Inductors. In Proceedings of the 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–1 December 2022; pp. 1–6. [Google Scholar]
- Foo, B.X.; Stein, A.L.F.; Sullivan, C.R. A step-by-step guide to extracting winding resistance from an impedance measurement. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 861–867. [Google Scholar]
- Um, D.Y.; Park, G.S. Resistance Variations in High-Frequency Inductors Considering Induced Fields Among Conductors. IEEE Trans. Magn. 2021, 57, 8400105. [Google Scholar] [CrossRef]
- Du, G.; Ye, W.; Zhang, Y.; Wang, L.; Pu, T. Comprehensive Analysis of Influencing Factors of AC Copper Loss for High-Speed Permanent Magnet Machine with Round Copper Wire Windings. Machines 2022, 10, 731. [Google Scholar] [CrossRef]
- Selema, A.; Ibrahim, M.N.; Sergeant, P. Mitigation of High-Frequency Eddy Current Losses in Hairpin Winding Machines. Machines 2022, 10, 328. [Google Scholar] [CrossRef]
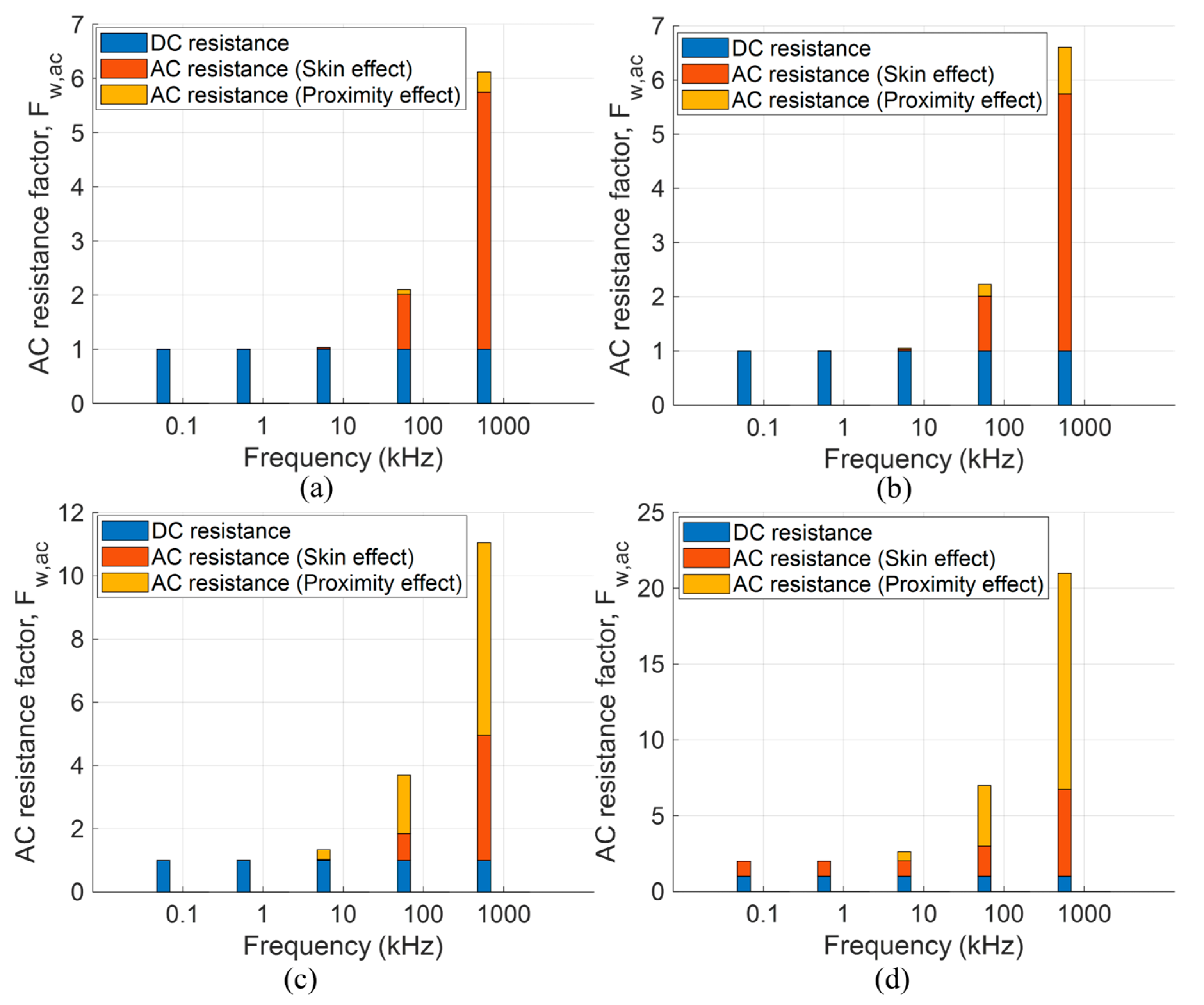


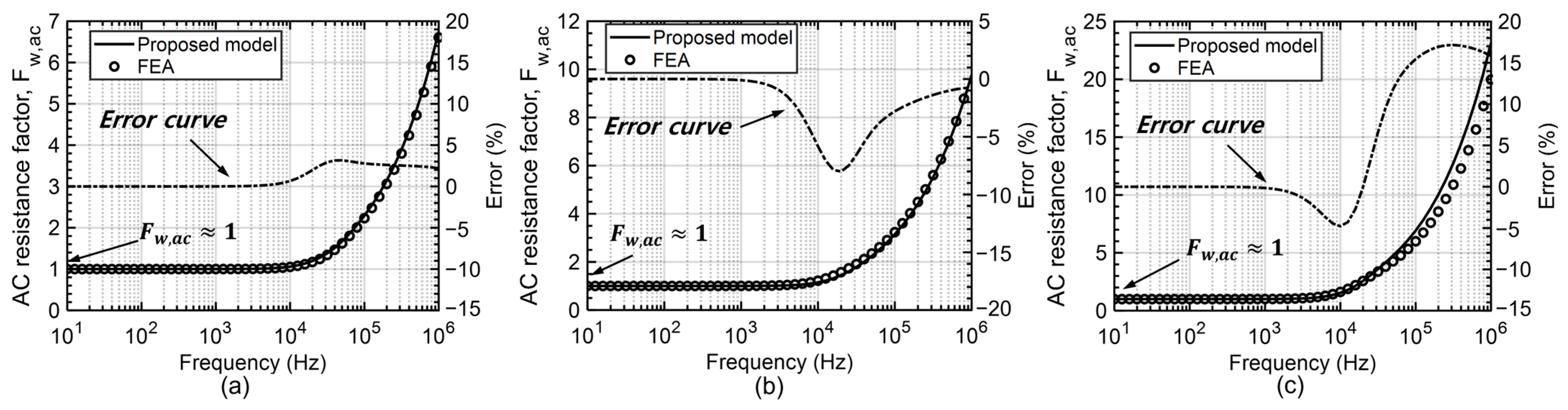

| Model | Layer | Turns | Packing Factor | Fw,ac @ 100 kHz | Fw,ac @ 1 MHz | Error | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Inner Section | Outer Section | FEA | ANA | FEA | ANA | 100 kHz | 1 MHz | |||
| Inductor #1 | 1 | 5 | 0.135 | 0.069 | 2.10 | 1.84 | 6.12 | 6.13 | −12.38% | 0.16% |
| Inductor #2 | 1 | 10 | 0.270 | 0.139 | 2.23 | 2.72 | 6.61 | 8.67 | 21.97% | 31.16% |
| Inductor #3 | 1 | 20 | 0.540 | 0.278 | 3.24 | 3.88 | 9.84 | 12.27 | 19.75% | 24.70% |
| Inductor #4 | 1 | 25 | 0.675 | 0.347 | 3.87 | 4.34 | 11.85 | 13.72 | 12.14% | 15.78% |
| Inductor #5 | 2 | 20/10 | 0.540/0.353 | 0.278/0.124 | 6.00 | 6.41 | 19.98 | 19.83 | 6.83% | −0.75% |
| Model | Wire Type | Fw,ac @ 100 kHz | Fw,ac @ 1 MHz | Error | Error | ||
|---|---|---|---|---|---|---|---|
| FEA | Proposed | FEA | Proposed | 100 kHz | 1 MHz | ||
| Inductor #1 | Solid | 2.10 | 2.08 | 6.12 | 6.12 | 1.05% | 2.00% |
| Litz | 1.01 | 1.01 | 2.17 | 2.13 | 0.04% | 1.62% | |
| Inductor #2 | Solid | 2.23 | 2.29 | 6.61 | 6.75 | −2.78% | −2.19% |
| Litz | 1.01 | 1.01 | 2.28 | 2.30 | −0.02% | −0.80% | |
| Inductor #3 | Solid | 3.24 | 3.15 | 9.84 | 9.77 | 2.80% | 0.76% |
| Litz | 1.03 | 1.02 | 3.60 | 2.98 | 0.61% | 17.30% | |
| Inductor #4 | Solid | 3.87 | 3.79 | 11.85 | 12.03 | 2.22% | −1.57% |
| Litz | 1.03 | 1.03 | 4.11 | 3.49 | 0.61% | 15.15% | |
| Inductor #5 | Solid | 6.00 | 6.92 | 19.98 | 23.15 | −15.45% | −15.83% |
| Litz | 1.06 | 1.05 | 7.01 | 5.98 | 0.99% | 14.78% | |
| Model | Wire Type | Fw,ac @ 100 kHz | Fw,ac @ 1 MHz | Error | Error | ||
|---|---|---|---|---|---|---|---|
| Proposed | Measured | Proposed | Measured | 100 kHz | 1 MHz | ||
| Inductor #2 | Solid | 2.29 | 2.55 | 6.61 | 6.37 | −10.20% | 3.77% |
| Litz | 1.01 | 1.1 | 2.28 | 2.76 | −8.18% | −17.39% | |
| Inductor #3 | Solid | 3.15 | 3.44 | 9.84 | 8.83 | −8.43% | 11.44% |
| Litz | 1.02 | 1.11 | 3.60 | 3.37 | −8.11% | 6.82% | |
| Inductor #5 | Solid | 6.92 | 6.02 | 19.98 | 16.65 | 14.95% | 20.00% |
| Litz | 1.05 | 1.11 | 7.01 | 6.22 | −5.41% | 12.70% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Um, D.-Y.; Chae, S.-A.; Park, G.-S. AC-Winding-Resistance Calculation of Toroidal Inductors with Solid-Round-Wire and Litz-Wire Winding Based on Complex Permeability Modeling. Machines 2024, 12, 228. https://doi.org/10.3390/machines12040228
Um D-Y, Chae S-A, Park G-S. AC-Winding-Resistance Calculation of Toroidal Inductors with Solid-Round-Wire and Litz-Wire Winding Based on Complex Permeability Modeling. Machines. 2024; 12(4):228. https://doi.org/10.3390/machines12040228
Chicago/Turabian StyleUm, Dae-Yong, Seung-Ahn Chae, and Gwan-Soo Park. 2024. "AC-Winding-Resistance Calculation of Toroidal Inductors with Solid-Round-Wire and Litz-Wire Winding Based on Complex Permeability Modeling" Machines 12, no. 4: 228. https://doi.org/10.3390/machines12040228
APA StyleUm, D.-Y., Chae, S.-A., & Park, G.-S. (2024). AC-Winding-Resistance Calculation of Toroidal Inductors with Solid-Round-Wire and Litz-Wire Winding Based on Complex Permeability Modeling. Machines, 12(4), 228. https://doi.org/10.3390/machines12040228






