Enhancing Gearbox Fault Diagnosis through Advanced Feature Engineering and Data Segmentation Techniques
Abstract
1. Introduction
2. Dataset and Methodologies
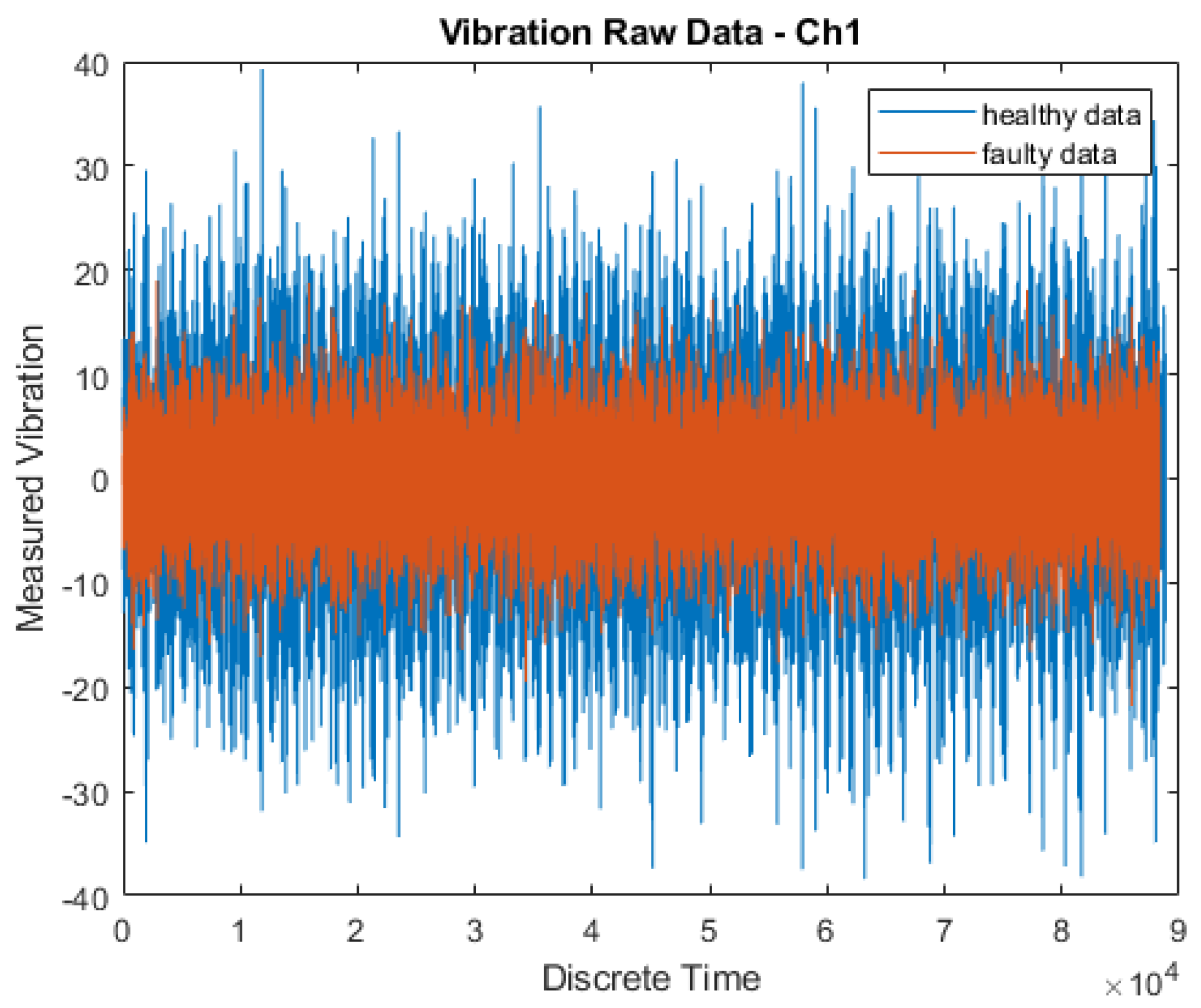
2.1. Dataset Processing
2.2. Data Segmentation
- Windowing: windowing size was 10 and the original dataset was sequenced to 10-fold;
- Bootstrapping: resampling size was 10 and the new data was resampled to 10-fold;
- Figure 4a,b describe the windowing (FNSW) and bootstrapping techniques, respectively, employed for this study. The algorithm used for this research is described in Algorithm 1.
| Algorithm 1. Calculate y = bootstrap(x,N) |
| Require: x > 0∧N ≥ 1 where x is Input data, N is bootstrap resamples Ensure: y = bootstrap(x,N) 1: if N < 1 then 2: N ⇐1 3: end if 4: if x < 1 then 5: print(Input data is insufficient) 6: end if 7: S⇐ size(x) 8: if S == 1 then 9: Out ⇐X(rand{S,N}) 10: end if |
2.3. Condition Indicators
- Root mean square (RMS) quantifies the vibration amplitude and energy of a signal in the time domain. It is computed as the square root of the average of the sum of squares of signal samples, expressed as:where x denotes the original sampled time signal, N is the number of samples, and i is the sample index.
- Standard deviation (STD) indicates the deviation from the mean value of a signal, calculated as:where xi (i = 1, …, N) is the i-th sample point of the signal x, and is the mean of the signal.
- Crest Factor (CF) represents the ratio of the maximum positive peak value of signal x to its rmsx value. It is devised to boost the presence of a small number of high-amplitude peaks, such as those caused by some types of local tooth damage. It serves to emphasize high-amplitude peaks, such as those indicating local tooth damage. A sine wave has a CF of 1.414. It is given by the following equation:where pk denotes the sample for the maximum positive peak of the signal, and x0 − pk is the value of x at pk.
- Kurtosis (K) measures the fourth-order normalized moment of a given signal x, reflecting its peakedness, i.e., the number and amplitude of peaks present in the signal. A signal comprising solely Gaussian-distributed noise yields a kurtosis value of 3. It is given by:
- Shape factor (SF) characterizes the time series distribution of a signal in the time domain:
- Skewness assesses the symmetry of the probability density function (PDF) of a time series’ amplitude. A time series with an equal number of large and small amplitude values has zero skewness, calculated as:
- Clearance factor indicates the symmetry of the PDF of a time series’ amplitude, given by:
- Impulse factor denotes the symmetry of the probability density function (PDF) of a time series’ amplitude, calculated as:
- Signal-to-noise ratio (SNR) represents the ratio of the useful signal, such as desired mechanical power or motion, to unwanted noise and vibrations generated within a gearbox during operation. It is expressed as:where P is the amplitude in dB.
- Signal-to-noise and distortion ratio (SINAD) measures signal quality in electronics, comparing the desired signal power to the combined power of noise and distortion components:where P is the amplitude in dB.
- Total harmonic distortion (THD) assesses how accurately a vibration system reproduces the output signal from a source.
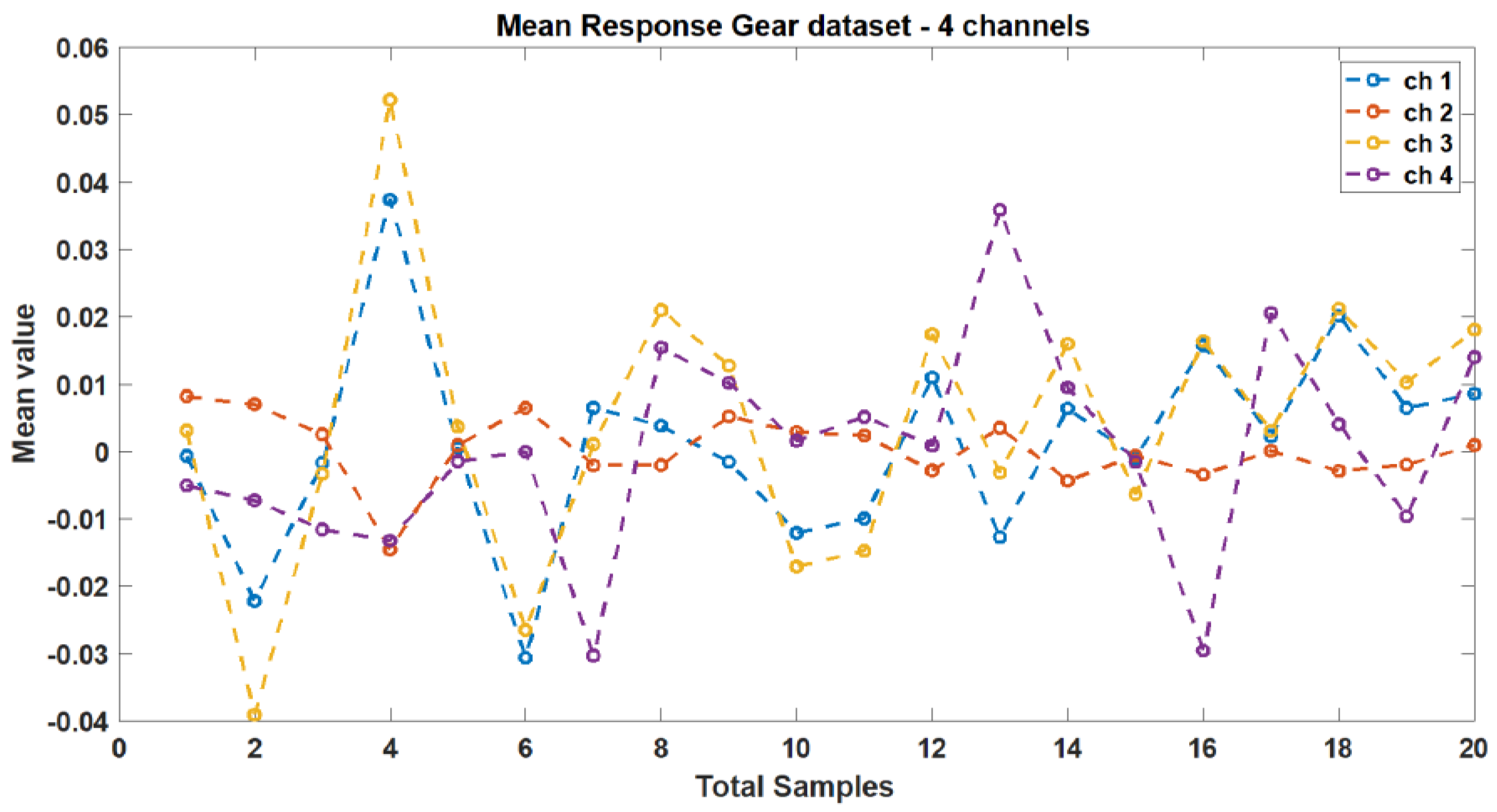
- Mean represents the average of the sum of squares of signal samples.
- Peak value denotes the maximum value of signal samples.
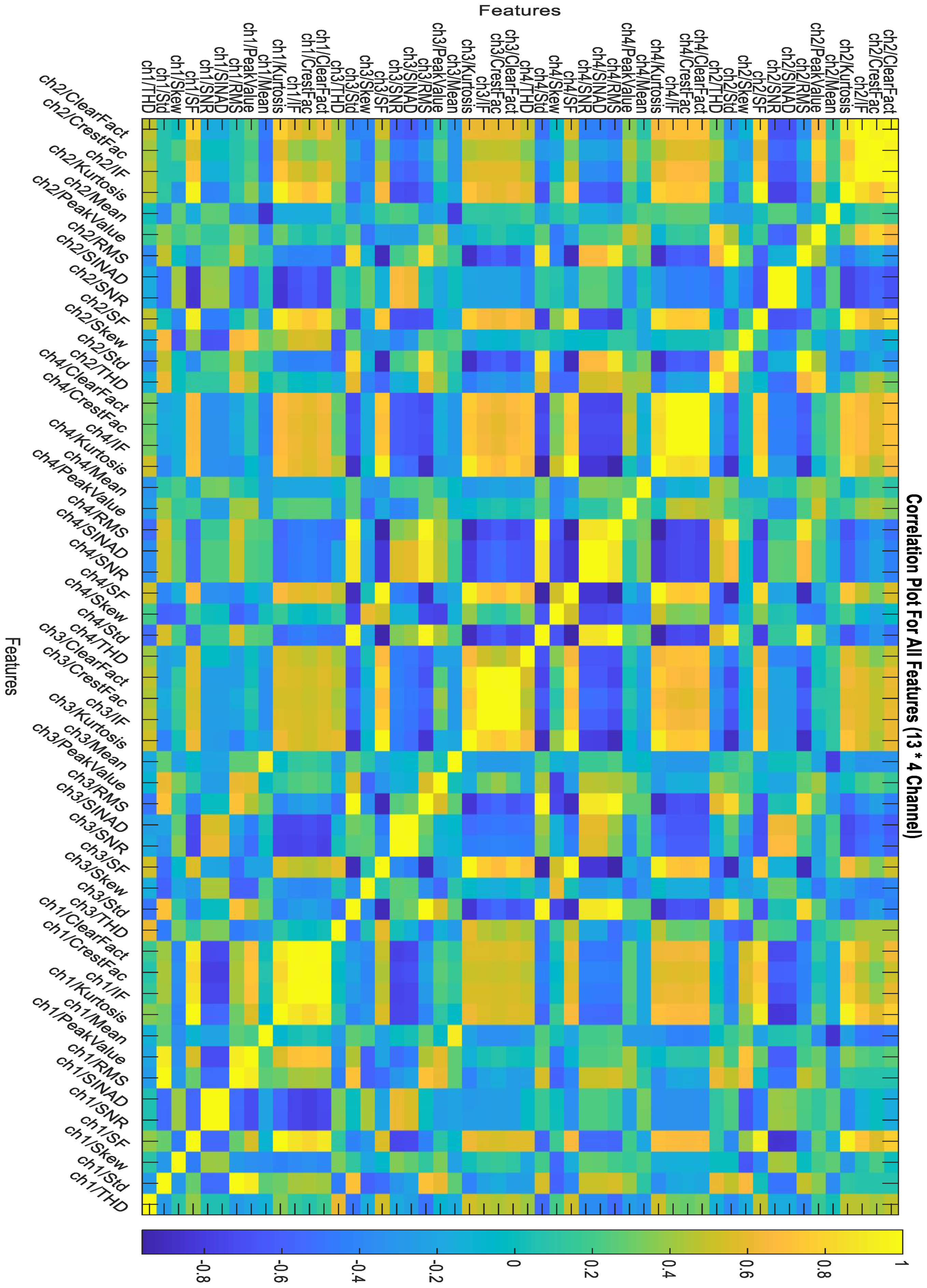
2.4. Feature Ranking and Selection
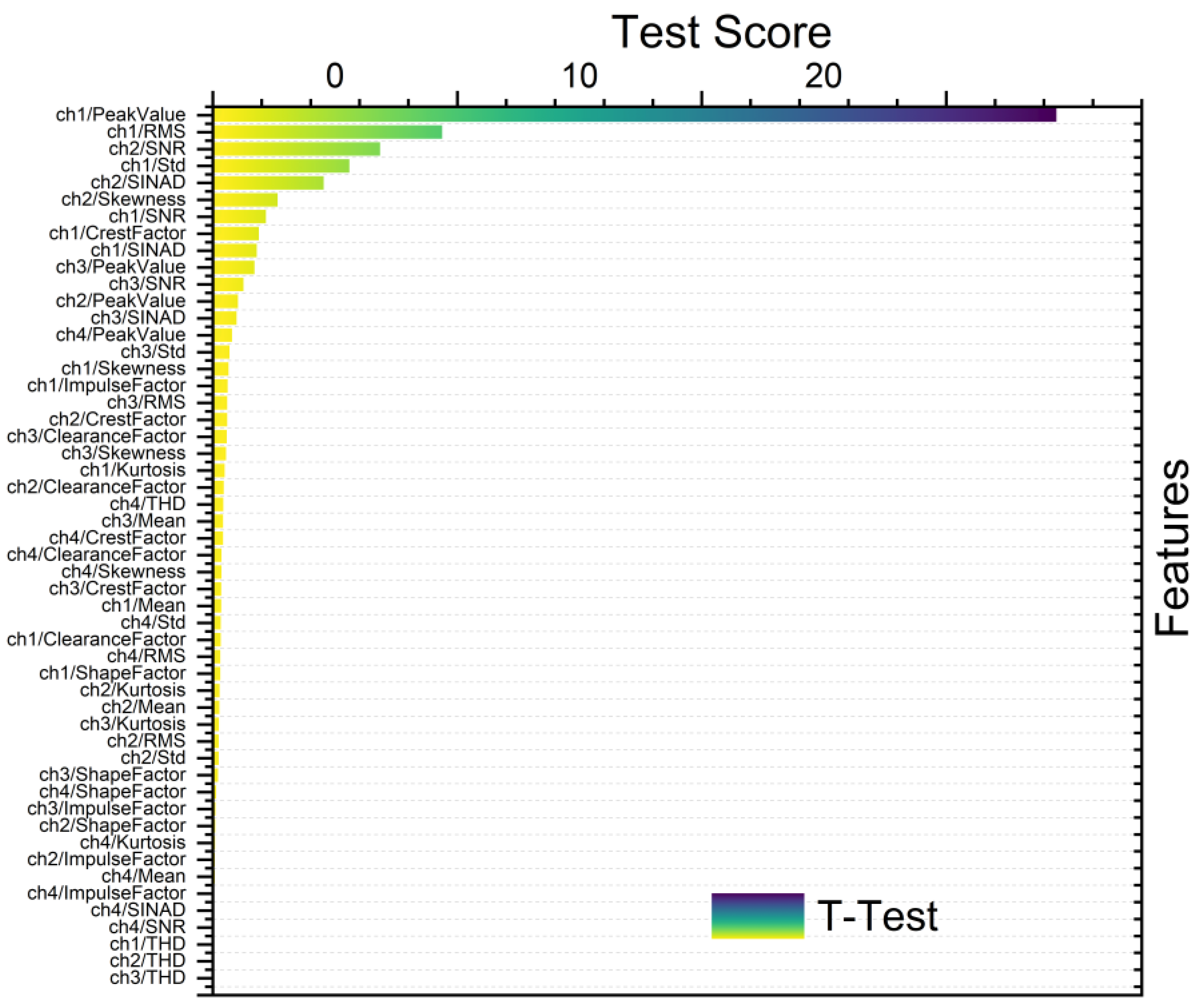
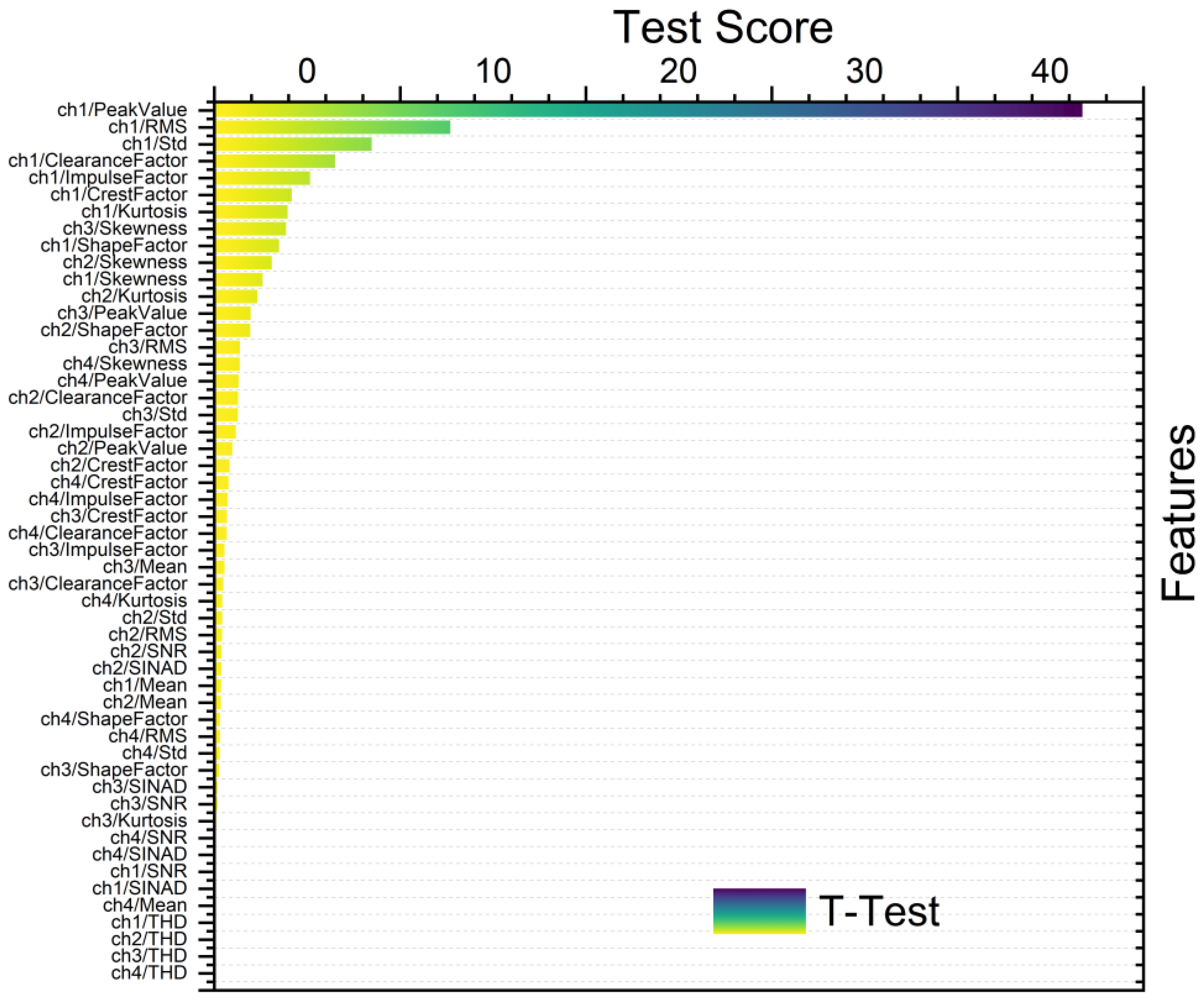
- T-test is generally employed to discern statistically significant differences between the means of two groups. Herein, it was applied in feature ranking to compare feature means across distinct classes or groups. Features exhibiting significant differences in means are identified as relevant for discrimination purposes [17].
- ROC analysis serves as a pivotal method for assessing the efficacy of classification models. Within the context of feature ranking, the ROC curve is utilized to evaluate the trade-offs between true positive rates and false positive rates at varying feature thresholds. Features characterized by a higher area under the ROC curve (AUC) are indicative of superior discriminatory power and are consequently ranked higher [18].
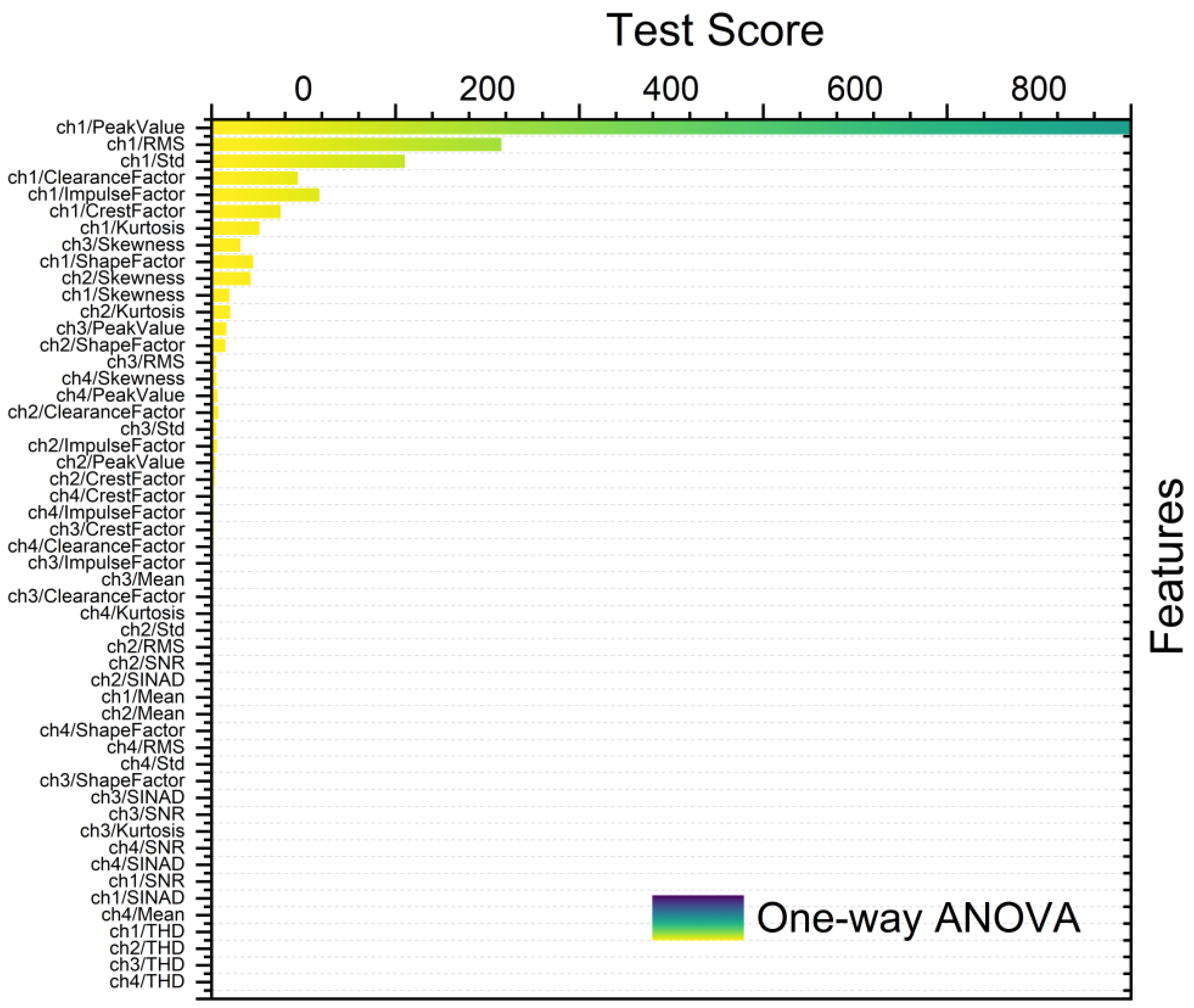
- One-way analysis of variance (ANOVA) method is used to compare means across three or more groups. Herein, one-way ANOVA served for feature ranking to ascertain the significance of variation in feature values across different classes or groups. Features demonstrating noteworthy differences in means between groups are deemed pertinent for discrimination [19].
- Monotonicity, denoting the relationship between a feature and its target variable, is evaluated using Spearman’s rank correlation coefficient. Features exhibiting monotonic relationships with the target variable are considered informative for the study’s objectives [20].
- Entropy, which serves as a measure of dataset disorder or uncertainty, plays a crucial role in feature ranking. Features characterized by higher entropy values signify greater variability and information content. To rank features based on their predictive utility, entropy-based methods such as information gain and mutual information are employed.
- Kruskal–Wallis test is a non-parametric statistical test which is utilized to compare medians across three or more groups. In feature ranking, this test is instrumental in assessing the significance of feature variations across different classes or groups. Features demonstrating significant median differences are identified as essential for discrimination [21].
- Variance-based unsupervised ranking was used to evaluate feature variability. Features exhibiting high variance values are indicative of greater diversity and are thus considered more informative for clustering or unsupervised learning tasks [22].
- Bhattacharyya distance is a metric quantifying the dissimilarity between probability distributions and is utilized to assess feature discriminative power. Larger Bhattacharyya distances between feature value distributions across classes indicate greater separability, thus highlighting the importance of features for classification purposes [23].
2.5. Machine Learning Models for Gearbox Predictive Maintenance
2.6. Performance Evaluation
- TP (true positive): an occurrence is classified as TP if at least one predicted outcome is labelled “Healthy” when the true event value is labelled “Healthy”.
- FP (false positive): an occurrence is classified as FP if at least one outcome is labelled “Faulty” when the true event value is labelled “Healthy”.
- TN (true negative): an occurrence is classified as TN if at least one outcome is labelled “Faulty” when the true event value is labelled “Faulty”.
- FN (false negative): an occurrence is classified as TP if at least one outcome is labelled with “Healthy” when the true event value is labelled “Faulty”.
3. Results and Discussion
3.1. Experimental Scenarios Based on Feature Selection and Ranking
- SCENARIO 1: Gearbox Fault Diagnosis Using Raw Data without Feature Selection
- SCENARIO 2: Gearbox Fault Diagnosis Using Raw Data with Feature Selection and without Ranking
- SCENARIO 3: Gearbox Fault Diagnosis Using Raw Data with Feature Selection and with Ranking
- SCENARIO 4: Gearbox Fault Diagnosis Using Raw Data with Feature Selection and with Ranking
3.2. Experimental Scenarios with Windowing and Bootstrapping
- SCENARIO 1: Gearbox Fault Diagnosis Using windowing with Feature Selection and with Ranking (top five features for each channel)
- SCENARIO 2: Gearbox Fault Diagnosis Using bootstrapping with Feature Selection and with Ranking (top 5 feature for each channel)
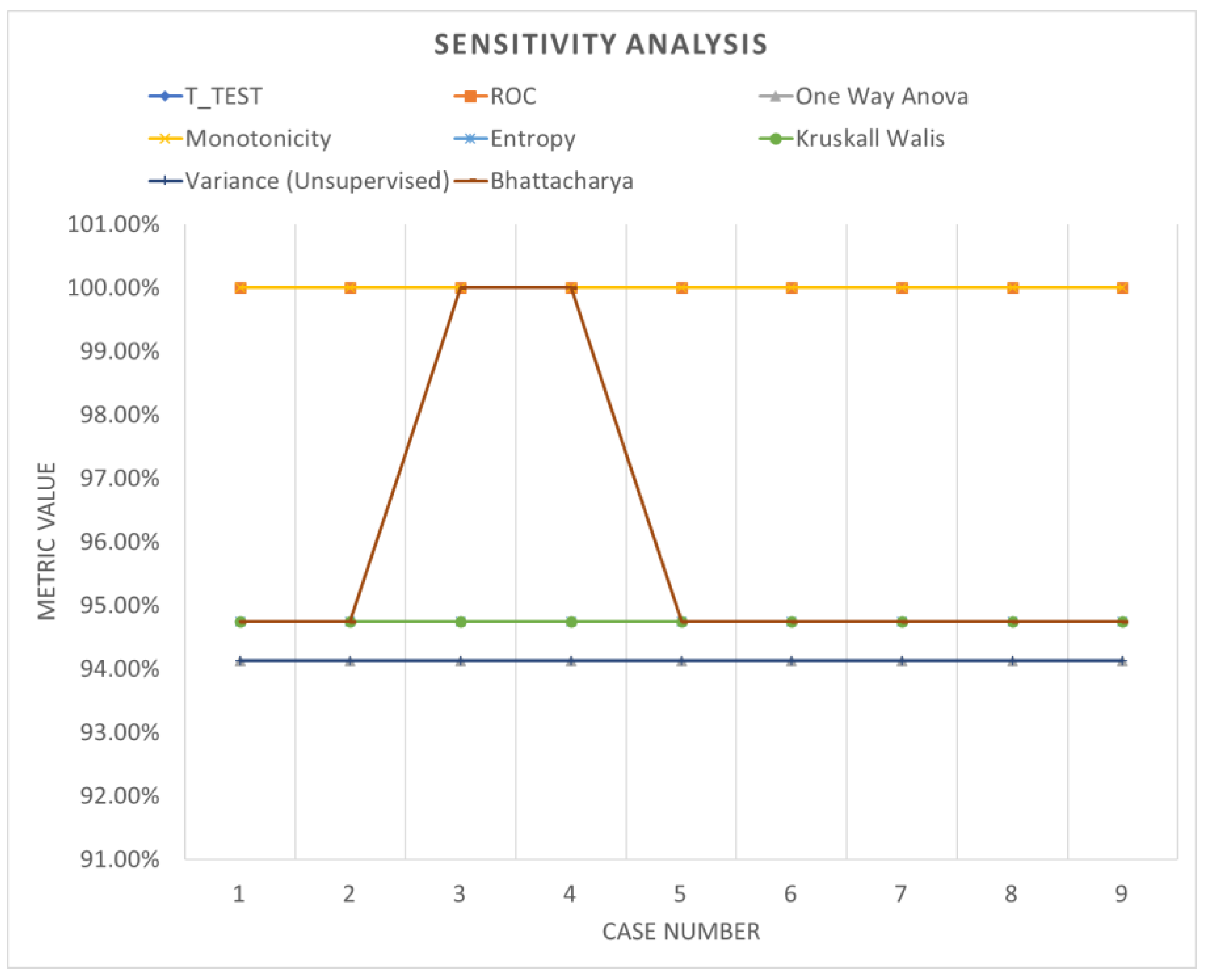
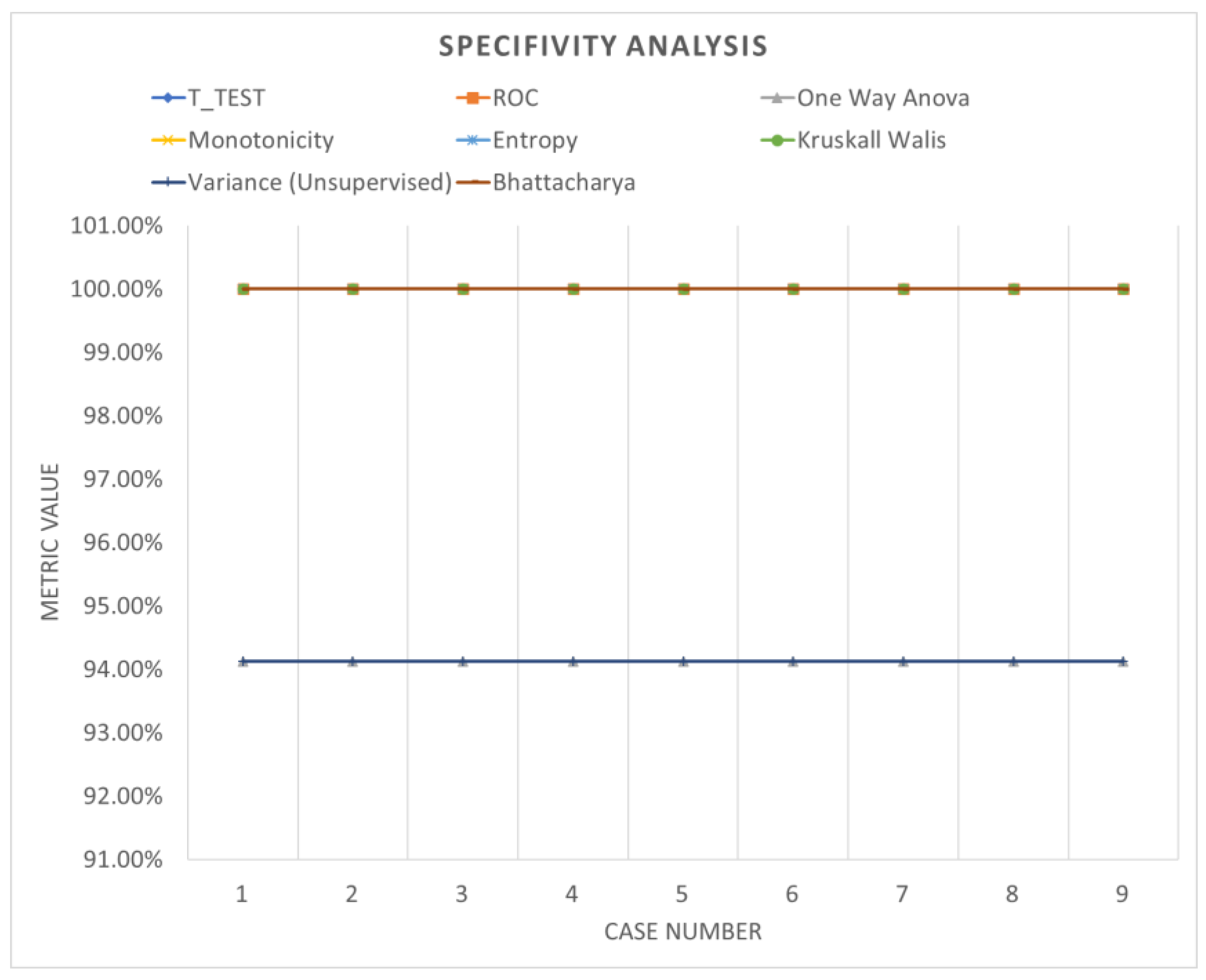
3.3. Validation of the Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Durbhaka, G.K.; Selvaraj, B.; Mittal, M.; Saba, T.; Rehman, A.; Goyal, L.M. Swarmlstm: Condition monitoring of gearbox fault diagnosis based on hybrid lstm deep neural network optimized by swarm intelligence algorithms. Comput. Mater. Contin. 2020, 66, 2041–2059. [Google Scholar]
- Malik, H.; Pandya, Y.; Parashar, A.; Sharma, R. Feature extraction using emd and classifier through artificial neural networks for gearbox fault diagnosis. Adv. Intell. Syst. Comput. 2019, 697, 309–317. [Google Scholar]
- Gu, H.; Liu, W.; Gao, Q.; Zhang, Y. A review on wind turbines gearbox fault diagnosis methods. J. Vibroeng. 2021, 23, 26–43. [Google Scholar] [CrossRef]
- Shukla, K.; Nefti-Meziani, S.; Davis, S. A heuristic approach on predictive maintenance techniques: Limitations and Scope. Adv. Mech. Eng. 2022, 14, 16878132221101009. [Google Scholar] [CrossRef]
- Li, P.; Wang, Y.; Chen, J.; Zhang, J. Machinery fault diagnosis using deep one-class classification neural network. IEEE Trans. Ind. Electron. 2018, 66, 2420–2431. [Google Scholar]
- Li, P.; Wang, J.; Chen, J. Sensor feature selection for gearbox fault diagnosis based on improved mutual information. Measurement 2020, 150, 107018. [Google Scholar]
- Kernbach, J.M.; Staartjes, V.E. Foundations of machine learning-based clinical prediction modeling: Part ii—Generalization and overfitting. In Machine Learning in Clinical Neuroscience: Foundations and Applications; Springer: Cham, Switzerland, 2022; pp. 15–21. [Google Scholar]
- Gosiewska, A.; Kozak, A.; Biecek, P. Simpler is better: Lifting interpretability performance trade-off via automated feature engineering. Decis. Support Syst. 2021, 150, 113556. [Google Scholar] [CrossRef]
- Atex, J.M.; Smith, R.D. Data segmentation techniques for improved machine learning performance. J. Artif. Intell. Res. 2018, 25, 127–145. [Google Scholar]
- Atex, J.M.; Smith, R.D.; Johnson, L. Spatial segmentation in machine learning: Methods and applications. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 234–241. [Google Scholar]
- Silhavy, P.; Silhavy, R.; Prokopova, Z. Categorical variable segmentation model for software development effort estimation. IEEE Access 2019, 7, 9618–9626. [Google Scholar] [CrossRef]
- Giordano, D.; Giobergia, F.; Pastor, E.; La Macchia, A.; Cerquitelli, T.; Baralis, E.; Mellia, M.; Tricarico, D. Data-driven strategies for predictive maintenance: Lesson learned from an automotive use case. Comput. Ind. 2022, 134, 103554. [Google Scholar] [CrossRef]
- Bersch, S.D.; Azzi, D.; Khusainov, R.; Achumba, I.E.; Ries, J. Sensor data acquisition and processing parameters for human activity classification. Sensors 2014, 14, 4239–4270. [Google Scholar] [CrossRef] [PubMed]
- Putra, I.P.E.S.; Vesilo, R. Window-size impact on detection rate of wearablesensor-based fall detection using supervised machine learning. In Proceedings of the 2017 IEEE Life Sciences Conference (LSC), Sydney, Australia, 13–15 December 2017; pp. 21–26. [Google Scholar]
- Saraiva, S.V.; de Oliveira Carvalho, F.; Santos, C.A.G.; Barreto, L.C.; de Macedo Machado Freire, P.K. Daily streamflow forecasting in sobradinho reservoir using machine learning models coupled with wavelet transform and bootstrapping. Appl. Soft Comput. 2021, 102, 107081. [Google Scholar] [CrossRef]
- Sait, A.S.; Sharaf-Eldeen, Y.I. A review of gearbox condition monitoring based on vibration analysis techniques diagnostics and prognostics. Conf. Proc. Soc. Exp. Mech. Ser. 2011, 5, 307–324. [Google Scholar]
- Wang, D.; Zhang, H.; Liu, R.; Lv, W.; Wang, D. T-test feature selection approach based on term frequency for text categorization. Pattern Recognit. Lett. 2014, 45, 1–10. [Google Scholar] [CrossRef]
- Chen, X.W.; Wasikowski, M. Fast: A roc-based feature selection metric for small samples and imbalanced data classification problems. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 124–132. [Google Scholar]
- Pawlik, P.; Kania, K.; Przysucha, B. The use of deep learning methods in diagnosing rotating machines operating in variable conditions. Energies 2021, 14, 4231. [Google Scholar] [CrossRef]
- Ompusunggu, A.P. On improving the monotonicity-based evaluation method for selecting features/health indicators for prognostics. In Proceedings of the 2020 11th International Conference on Prognostics and System Health Management (PHM-2020 Jinan), Jinan, China, 23–25 October 2020; pp. 242–246. [Google Scholar]
- Ramteke, D.S.; Parey, A.; Pachori, R.B. Automated gear fault detection of micron level wear in bevel gears using variational mode decomposition. J. Mech. Sci. Technol. 2019, 33, 5769–5777. [Google Scholar] [CrossRef]
- Ebenuwa, S.H.; Sharif, M.S.; Alazab, M.; Al-Nemrat, A. Variance ranking attributes selection techniques for binary classification problem in imbalance data. IEEE Access 2019, 7, 24649–24666. [Google Scholar] [CrossRef]
- Momenzadeh, M.; Sehhati, M.; Rabbani, H. A novel feature selection method for microarray data classification based on hidden markov model. J. Biomed. Inform. 2019, 95, 103213. [Google Scholar] [CrossRef] [PubMed]
- Ratner, B. The correlation coefficient: Its values range between 1/1, or do they. J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Mukaka, M.M. A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69. [Google Scholar]
- Mohsin, M.F.M.; Hamdan, A.R.; Bakar, A.A. The effect of normalization for real value negative selection algorithm. In Soft Computing Applications and Intelligent Systems; Noah, S.A., Abdullah, A., Arshad, H., Bakar, A.A., Othman, Z.A., Sahran, S., Omar, N., Othman, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 194–205. [Google Scholar]
- Dangut, M.D.; Skaf, Z.; Jennions, I.K. An integrated machine learning model for aircraft components rare failure prognostics with log-based dataset. ISA Trans. 2021, 113, 127–139. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.-L. Application of machine learning to a medium gaussian support vector machine in the diagnosis of motor bearing faults. Electronics 2021, 10, 2266. [Google Scholar] [CrossRef]
- Sun, L.; Liu, T.; Xie, Y.; Zhang, D.; Xia, X. Real-time power prediction approach for turbine using deep learning techniques. Energy 2021, 233, 121130. [Google Scholar] [CrossRef]
- Keartland, S.; Van Zyl, T.L. Automating predictive maintenance using oil analysis and machine learning. In Proceedings of the 2020 International AUPEC/RobMech/PRASA Conference, Cape Town, South Africa, 29–31 January 2020; pp. 1–6. [Google Scholar]
- van Dinter, R.; Tekinerdogan, B.; Catal, C. Predictive maintenance using digital twins: A systematic literature review. Inf. Softw. Technol. 2022, 151, 107008. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, H.; Wang, Y. Fault diagnosis of planetary gearbox using multi-criteria feature selection and heterogeneous ensemble learning classification. Measurement 2021, 173, 108654. [Google Scholar] [CrossRef]
- Chandrasekaran, M.; Sonawane, P.R.; Sriramya, P. Prediction of gear pitting severity by using naive bayes machine learning algorithm. In Recent Advances in Materials and Modern Manufacturing; Springer: Singapore, 2022; pp. 131–141. [Google Scholar]
- Xu, Y.; Nascimento, N.M.M.; de Sousa, P.H.F.; Nogueira, F.G.; Torrico, B.C.; Han, T.; Jia, C.; Filho, P.P.R. Multi-sensor edge computing architecture for identification of failures short-circuits in wind turbine generators. Appl. Soft Comput. 2021, 101, 107053. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hu, H. Feature convolutional networks. In Proceedings of the 13th Asian Conference on Machine Learning, Virtual, 19 November 2021; Volume 157, pp. 830–839. [Google Scholar]
- Hesabi, H.; Nourelfath, M.; Hajji, A. A deep learning predictive model for selective maintenance optimization. Reliab. Eng. Syst. Saf. 2022, 219, 108191. [Google Scholar] [CrossRef]
- KGP, K.I. Bagging and Random Forests: Reducing Bias and Variance Using Randomness by kdag iit kgp Medium. Available online: https://kdagiit.medium.com/ (accessed on 5 March 2024).
- Bechhoefer, E. High Speed Gear Dataset. Available online: https://www.kau-sdol.com/kaug (accessed on 6 December 2012).









| Layer Type/Training Settings | Units |
|---|---|
| Feature layer | 20 Features |
| FullyConnectedLayer1 | (50, 100, 500) Fully connected layer |
| BatchNormalizationLayer | Batch normalization with 100 channels |
| RELULayer | ReLU |
| FullyConnectedLayer | 2 fully connected layers |
| Softmaxlayer | Softmax |
| ClassificationOutputLayer | crossentropyex with classes “Faulty”/”Healthy” |
| Mini batchsize | 10 |
| Learning rate | 0.001 |
| Epochs | 30 |
| Prediction Model | Sub-Type | Accuracy in % |
|---|---|---|
| Decision tree | Fine tree | 58.3 |
| Medium tree | 57.8 | |
| Coarse tree | 55.3 | |
| Logistic regression 50.8 | 50.8 | |
| Naive Bayes (Gaussian) | 56.6 | |
| KNN | Fine KNN | 54.8 |
| Medium KNN | 58.1 | |
| Coarse KNN | 60.8 | |
| Cosine KNN | 56.2 | |
| Cubic KNN | 58.0 | |
| Weighted KNN | 57.4 |
| Prediction Model | Sub-Type | Accuracy (%) |
|---|---|---|
| Decision tree | Fine tree | 87.5 |
| Medium tree | 87.5 | |
| Coarse tree | 87.5 | |
| Logistic regression | 75 | |
| Naive Bayes | Gaussian | 93.8 |
| Kernel | 93.8 | |
| SVM | Linear | 37.5 |
| Quadratic | 37.5 | |
| Cubic | 37.5 | |
| Fine Gaussian | 37.5 | |
| Medium Gaussian | 37.5 | |
| Coarse Gaussian | 37.5 | |
| KNN | Fine KNN | 37.5 |
| Medium KNN | 37.5 | |
| Coarse KNN | 37.5 | |
| Cosine KNN | 37.5 | |
| Cubic KNN | 37.5 | |
| Weighted KNN | 37.5 | |
| Ensemble | Boosted trees | 37.5 |
| Bagged trees | 75 | |
| Subspace discriminant | 93.8 | |
| Subspace KNN | 75 | |
| RUSBoosted trees | 37.5 | |
| Narrow neural network | 37.5 |
| Prediction Model | Sub-Type | Accuracy (%) |
|---|---|---|
| Decision tree | Fine tree | 87.5 |
| Medium tree | 87.5 | |
| Coarse tree | 87.5 | |
| Logistic regression | 87.5 | |
| Naive Bayes | Gaussian | 100 |
| Kernel | 93.8 | |
| SVM | Linear | 43.8 |
| Quadratic | 43.8 | |
| Cubic | 43.8 | |
| Fine Gaussian | 37.5 | |
| Medium Gaussian | 43.8 | |
| Coarse Gaussian | 43.8 | |
| KNN | Fine KNN | 43.8 |
| Medium KNN | 43.8 | |
| Coarse KNN | 37.5 | |
| Cosine KNN | 43.8 | |
| Cubic KNN | 43.8 | |
| Weighted KNN | 43.8 | |
| Ensemble | Boosted trees | 37.5 |
| Bagged trees | 87.5 | |
| Subspace discriminant | 100 | |
| Subspace KNN | 75 | |
| RUSBoosted Trees | 43.8 | |
| Narrow neural network | 43.8 |
| Prediction Model | Sub-Type | Accuracy (%) |
|---|---|---|
| Decision tree | Fine tree | 87.5 |
| Medium tree | 87.5 | |
| Coarse tree | 87.5 | |
| Logistic regression | 100 | |
| Naive Bayes | Gaussian | 100 |
| Kernel | 100 | |
| SVM | Linear | 100 |
| Quadratic | 100 | |
| Cubic | 100 | |
| Fine Gaussian | 62.5 | |
| Medium Gaussian | 100 | |
| Coarse Gaussian | 87.5 | |
| KNN | Fine KNN | 100 |
| Medium KNN | 75 | |
| Coarse KNN | 37.5 | |
| Cosine KNN | 93.8 | |
| Cubic KNN | 68.8 | |
| Weighted KNN | 100 | |
| Ensemble | Boosted trees | 37.5 |
| Bagged trees | 75 | |
| Subspace discriminant | 100 | |
| Subspace KNN | 100 | |
| RUSBoosted trees | 37.5 | |
| Narrow neural network | 93.8 |
| Ranking Method | Fully Connected Layer (RELU NETWORK) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Normalization Z-Score | Normalization None | Normalization Z-Center | |||||||
| Number of Layers | |||||||||
| 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | |
| T_TEST | 96.97 | 96.97 | 96.97 | 93.94 | 93.94 | 90.91 | 93.94 | 87.88 | 93.94 |
| ROC | 100 | 100 | 100 | 100 | 93.94 | 96.97 | 96.97 | 96.97 | 100 |
| One-way ANOVA | 93.94 | 93.94 | 100 | 96.97 | 93.94 | 100 | 93.94 | 96.97 | 93.94 |
| Monotonicity | 96.97 | 96.97 | 96.97 | 75.76 | 96.97 | 96.97 | 93.94 | 93.94 | 81.82 |
| Entropy | 96.97 | 93.94 | 96.97 | 90.91 | 90.91 | 90.91 | 81.82 | 100 | 100 |
| Kruskal–Wallis | 93.94 | 96.97 | 96.97 | 96.97 | 93.94 | 93.94 | 93.94 | 90.91 | 93.94 |
| Variance (unsupervised) | 93.94 | 93.94 | 100 | 96.97 | 96.97 | 93.94 | 96.97 | 93.94 | 96.97 |
| Bhattacharya | 96.97 | 96.97 | 96.97 | 96.97 | 93.94 | 93.94 | 93.94 | 93.94 | 87.88 |
| Ranking Method | Fully Connected Layer (RELU NETWORK) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Normalization Z-Score | Normalization None | Normalization Z-Center | |||||||
| Number of Layers | |||||||||
| 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 50 | |
| T_TEST | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 |
| ROC | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| One-way ANOVA | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 |
| Monotonicity | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Entropy | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 |
| Kruskal–Wallis | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 |
| Variance (unsupervised) | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 | 93.33 |
| Bhattacharya | 96.67 | 96.67 | 100 | 100 | 96.67 | 96.67 | 96.67 | 96.67 | 96.67 |
| Ranking Method | Fully Connected Layer (RELU NETWORK) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Normalization Z-Score | Normalization None | Normalization Z-Center | |||||||
| Number of Layers | |||||||||
| 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 50 | |
| All features | 55 | 72.5 | 97.5 | 42.5 | 42.5 | 22.5 | 47.5 | 42.5 | 27.5 |
| Ranking Method | Fully Connected Layer (RELU NETWORK) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Normalization Z-Score | Normalization None | Normalization Z-Center | |||||||
| Number of Layers | |||||||||
| 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 50 | |
| TEST | 96.25 | 100 | 100 | 83.75 | 87.5 | 93.75 | 84.38 | 86.88 | 94.38 |
| Variance | 99.38 | 99.38 | 100 | 66.88 | 72.5 | 95 | 60.63 | 75 | 93.13 |
| Bhattacharya | 100 | 100 | 100 | 98.75 | 97.5 | 96.25 | 96.88 | 96.88 | 96.25 |
| Ranking Method | Fully Connected Layer (RELU NETWORK) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Normalization Z-Score | Normalization None | Normalization Z-Center | |||||||
| Number of Layers | |||||||||
| 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 50 | |
| TEST | 100 | 100 | 100 | 100 | 100 | 97.78 | 100 | 100 | 97.04 |
| Variance | 100 | 100 | 100 | 100 | 100 | 97.78 | 100 | 100 | 97.04 |
| Bhattacharya | 100 | 100 | 100 | 94.07 | 98.52 | 98.15 | 95.56 | 100 | 97.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shukla, K.; Holderbaum, W.; Theodoridis, T.; Wei, G. Enhancing Gearbox Fault Diagnosis through Advanced Feature Engineering and Data Segmentation Techniques. Machines 2024, 12, 261. https://doi.org/10.3390/machines12040261
Shukla K, Holderbaum W, Theodoridis T, Wei G. Enhancing Gearbox Fault Diagnosis through Advanced Feature Engineering and Data Segmentation Techniques. Machines. 2024; 12(4):261. https://doi.org/10.3390/machines12040261
Chicago/Turabian StyleShukla, Khyati, William Holderbaum, Theodoros Theodoridis, and Guowu Wei. 2024. "Enhancing Gearbox Fault Diagnosis through Advanced Feature Engineering and Data Segmentation Techniques" Machines 12, no. 4: 261. https://doi.org/10.3390/machines12040261
APA StyleShukla, K., Holderbaum, W., Theodoridis, T., & Wei, G. (2024). Enhancing Gearbox Fault Diagnosis through Advanced Feature Engineering and Data Segmentation Techniques. Machines, 12(4), 261. https://doi.org/10.3390/machines12040261









