Highly Self-Adaptive Path-Planning Method for Unmanned Ground Vehicle Based on Transformer Encoder Feature Extraction and Incremental Reinforcement Learning
Abstract
1. Introduction
- Firstly, the original 2D map is compressed to a 1D feature vector using an Autoencoder to lighten the computational burden of following the RL path planner. The compressed 1D feature vector can achieve a highly accurate reconstruction of the original 2D map, thus ensuring abundant and ample information is obtained while the input dimension is greatly reduced.
- Secondly, the Transformer encoder block, which has global long-range dependency analysis capability, is adopted to capture the highly intertwined correlation between UGV status at continuous instances. The results show that the Transformer encoder demonstrates better optimality than a traditional CNN or FCN thanks to its strong feature-extraction capability.
- Thirdly, incremental reinforcement learning (IRL) is adopted to improve the path planner’s generalization ability when the trained agent is deployed in totally different environments to the training environments. The results show that ICR can achieve 5× faster adaptivity than traditional transfer-learning-based fine-tuning methods.
2. Methodology
2.1. Autoencoder for Environment Representation
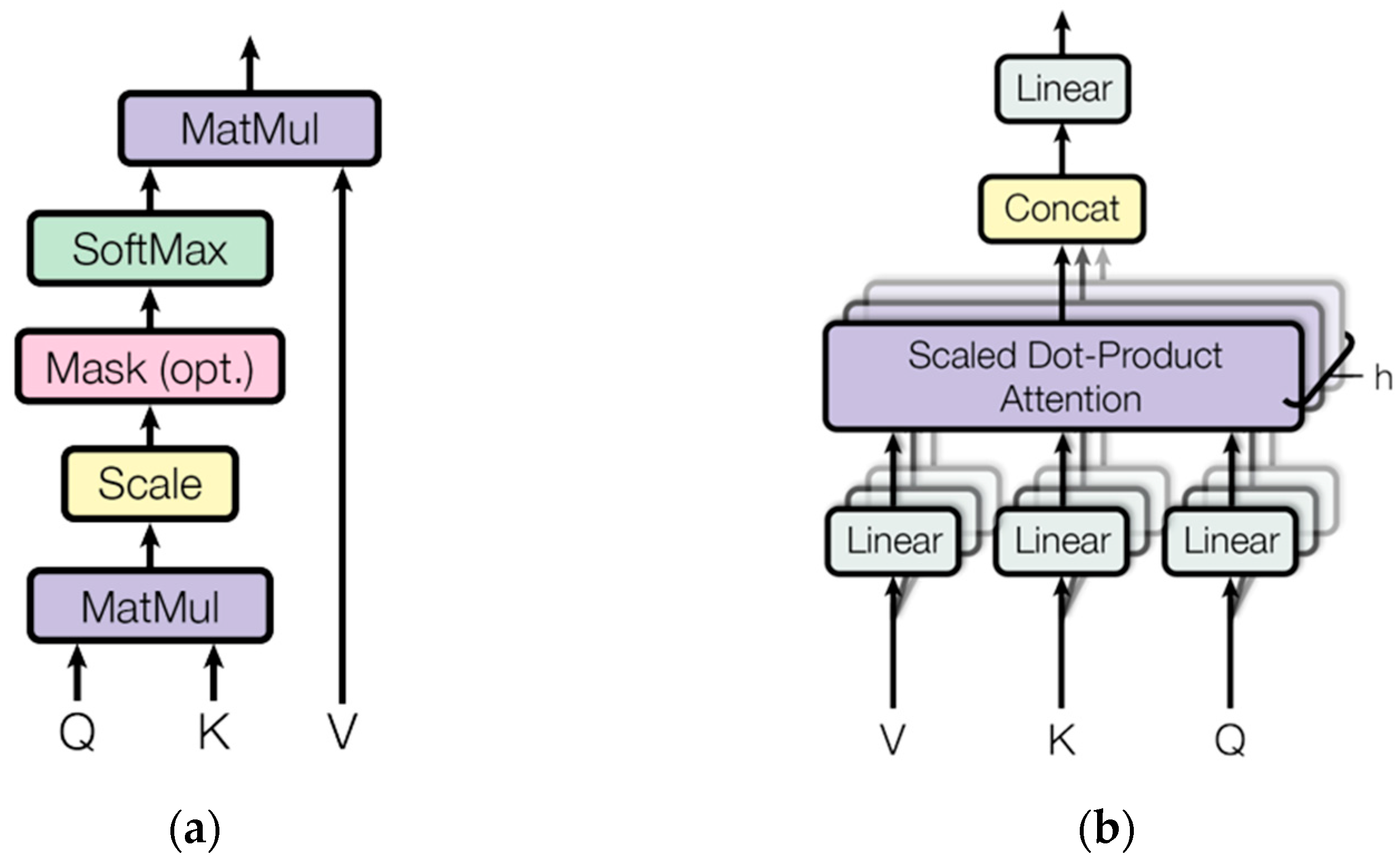
2.2. Transformer Encoder Layer
2.3. Incremental Reinforcement Learning
3. Validation
3.1. Simulation Setup
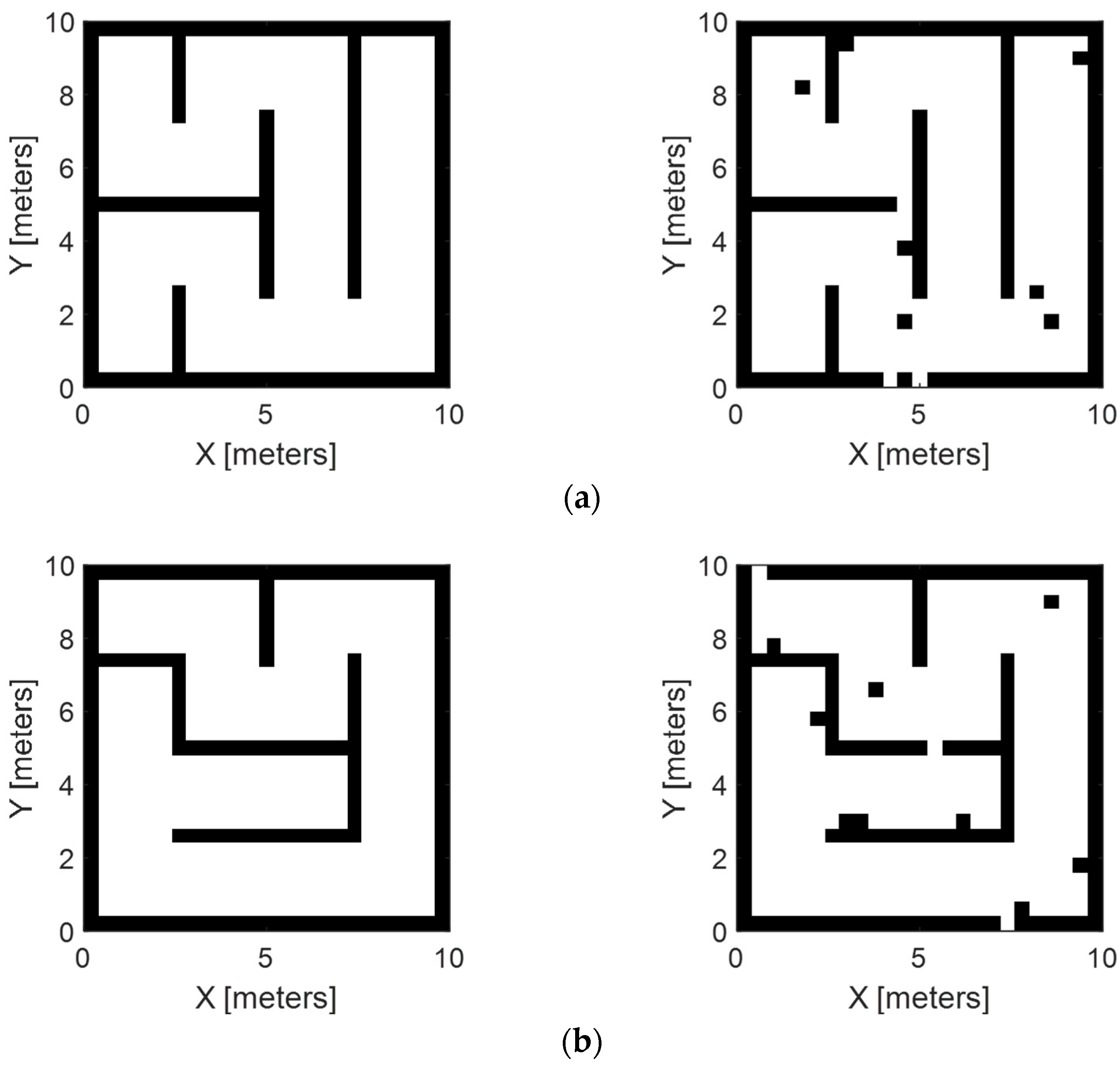
3.2. Validation of Environment Compression
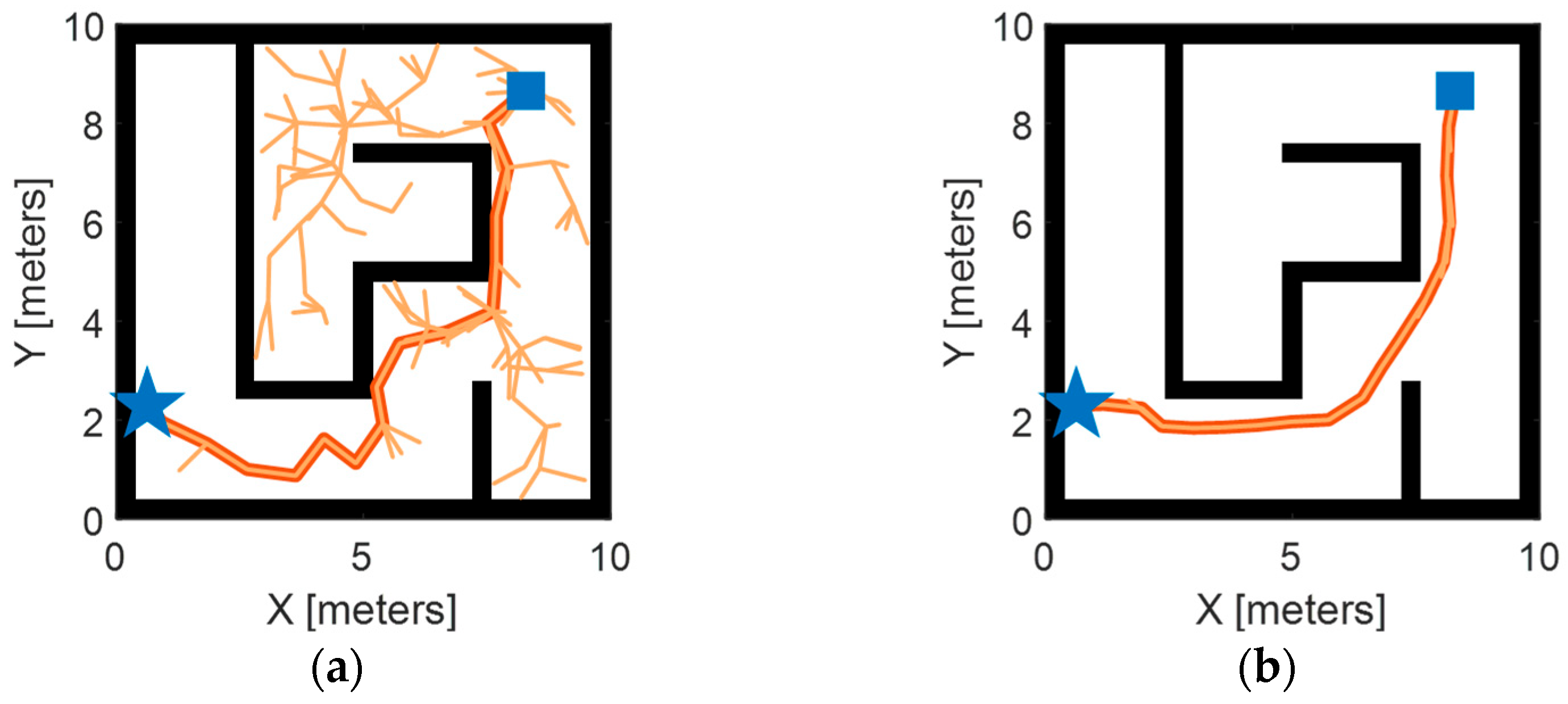
3.3. Validation of Transformer Encoder Feature Extraction
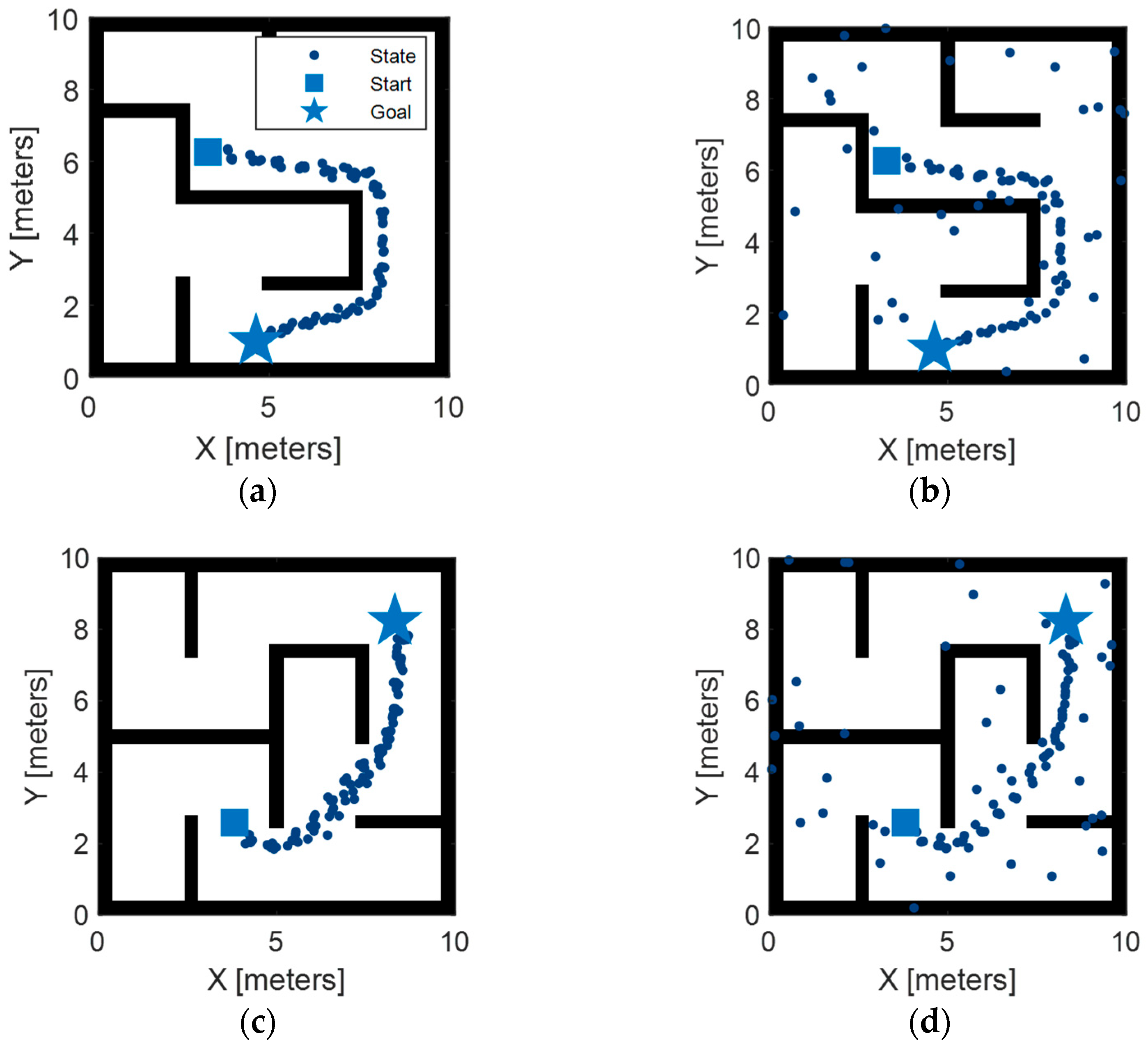
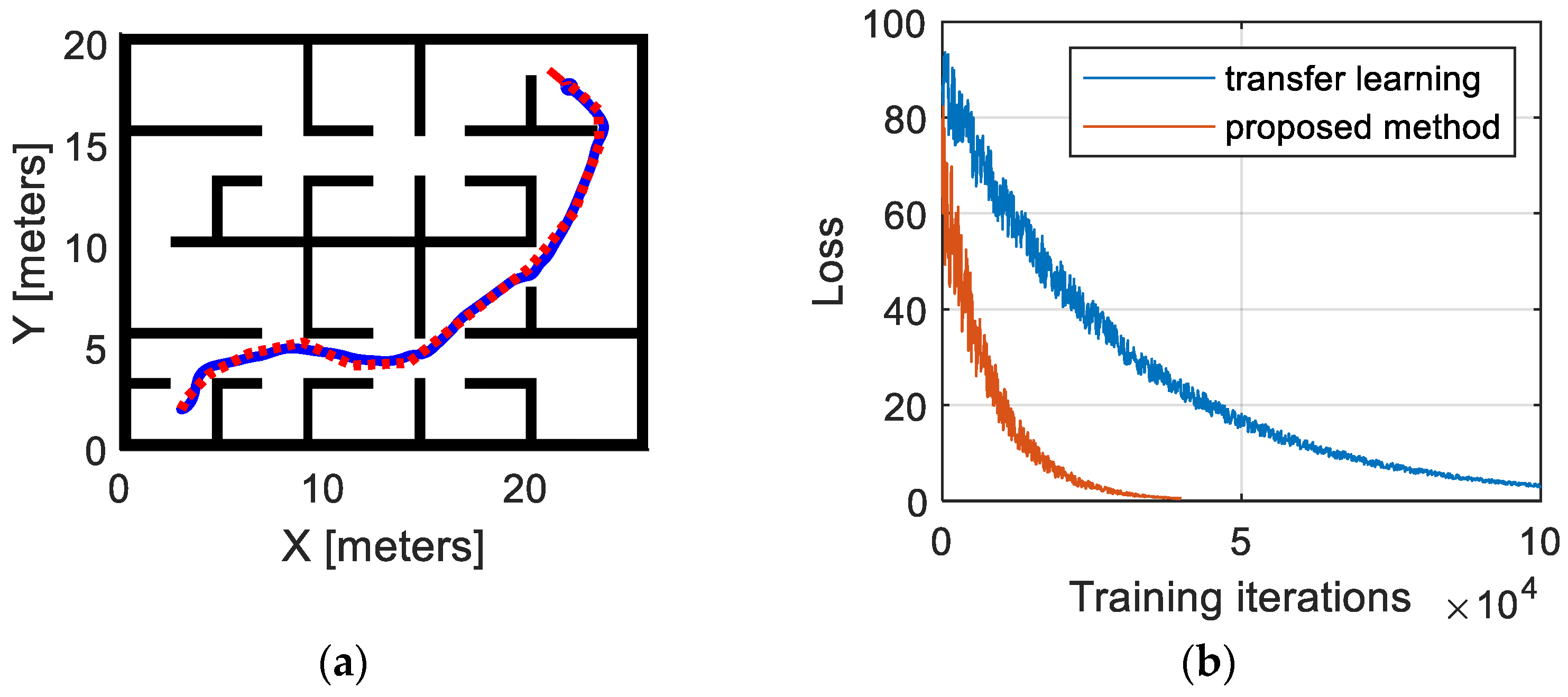
3.4. Validation of Effectiveness and Adaptability
4. Conclusions
- The utilization of an autoencoder facilitates the generation of a compressed representation of the original environment, supplying ample information for subsequent path-planning endeavors while significantly reducing the computational overhead. The MSEs between the original and reconstructed maps amount to 0.0144 and 0.0192 on the training and testing datasets, respectively.
- Comparative evaluations reveal that the Transformer encoder exhibits superior feature-extraction capabilities in contrast to commonly utilized networks such as the CNN, GRU, and LSTM. Specifically, the proposed methodology employing the Transformer encoder yields a 9.6% to 16.3% enhancement in path length and a 5.1% to 21.7% improvement in smoothness.
- The proposed methodology demonstrates superior optimality compared to uniform-sampling-based approaches and enhanced adaptability relative to traditional transfer-learning-based methodologies. Specifically, the proposed method exhibits a 14.8% reduction in path length and a 61.1% enhancement in smoothness compared to uniform-sampling-based approaches. Furthermore, leveraging incremental learning, the proposed method achieves adaptivity five times faster than traditional transfer-learning approaches.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dinelli, C.; Racette, J.; Escarcega, M.; Lotero, S.; Gordon, J.; Montoya, J.; Hassanalian, M. Configurations and applications of multi-agent hybrid drone/unmanned ground vehicle for underground environments: A review. Drones 2023, 7, 136. [Google Scholar] [CrossRef]
- Sánchez, M.; Morales, J.; Martínez, J.L. Waypoint generation in satellite images based on a cnn for outdoor ugv navigation. Machines 2023, 11, 807. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, X.; Zheng, K.; Zou, Y.; Zhou, N. Hierarchical path planner combining probabilistic roadmap and deep deterministic policy gradient for unmanned ground vehicles with non-holonomic constraints. J. Frankl. Inst. 2024, 361, 106821. [Google Scholar] [CrossRef]
- Dong, H.; Shen, J.; Yu, Z.; Lu, X.; Liu, F.; Kong, W. Low-Cost Plant-Protection Unmanned Ground Vehicle System for Variable Weeding Using Machine Vision. Sensors 2024, 24, 1287. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Liu, J.; Anavatti, S.; Garratt, M.; Abbass, H.A. Modified continuous ant colony optimisation for multiple unmanned ground vehicle path planning. Expert Syst. Appl. 2022, 196, 116605. [Google Scholar] [CrossRef]
- Jones, M.; Djahel, S.; Welsh, K. Path-planning for unmanned aerial vehicles with environment complexity considerations: A survey. ACM Comput. Surv. 2023, 55, 1–39. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; Hou, J.; Chen, L.; Hu, N. A path planning method for underground intelligent vehicles based on an improved RRT* algorithm. Electronics 2022, 11, 294. [Google Scholar] [CrossRef]
- Chen, R.; Hu, J.; Xu, W. An RRT-Dijkstra-based path planning strategy for autonomous vehicles. Appl. Sci. 2022, 12, 11982. [Google Scholar] [CrossRef]
- Wang, J.; Chi, W.; Li, C.; Wang, C.; Meng MQ, H. Neural RRT*: Learning-based optimal path planning. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1748–1758. [Google Scholar] [CrossRef]
- Chen, P.; Pei, J.; Lu, W.; Li, M. A deep reinforcement learning based method for real-time path planning and dynamic obstacle avoidance. Neurocomputing 2022, 497, 64–75. [Google Scholar] [CrossRef]
- Yu, X.; Wang, P.; Zhang, Z. Learning-based end-to-end path planning for lunar rovers with safety constraints. Sensors 2021, 21, 796. [Google Scholar] [CrossRef] [PubMed]
- Park, B.; Choi, J.; Chung, W.K. An efficient mobile robot path planning using hierarchical roadmap representation in indoor environment. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–19 May 2012; IEEE: New York, NY, USA, 2012; pp. 180–186. [Google Scholar]
- Deng, Y.; Chen, Y.; Zhang, Y.; Mahadevan, S. Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment. Appl. Soft Comput. 2012, 12, 1231–1237. [Google Scholar] [CrossRef]
- Arogundade, O.T.; Sobowale, B.; Akinwale, A.T. Prim algorithm approach to improving local access network in rural areas. Int. J. Comput. Theory Eng. 2011, 3, 413. [Google Scholar]
- Lee, W.; Choi, G.H.; Kim, T.W. Visibility graph-based path-planning algorithm with quadtree representation. Appl. Ocean. Res. 2021, 117, 102887. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Kolountzakis, M.N.; Latombe, J.C. Analysis of probabilistic roadmaps for path planning. IEEE Trans. Robot. Autom. 1998, 14, 166–171. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, X.; Yu, Y. Research on a random route-planning method based on the fusion of the A* algorithm and dynamic window method. Electronics 2022, 11, 2683. [Google Scholar] [CrossRef]
- Wu, J.; Ma, X.; Peng, T.; Wang, H. An improved timed elastic band (TEB) algorithm of autonomous ground vehicle (AGV) in complex environment. Sensors 2021, 21, 8312. [Google Scholar] [CrossRef]
- Reinhart, R.; Dang, T.; Hand, E.; Papachristos, C.; Alexis, K. Learning-based path planning for autonomous exploration of subterranean environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: New York, NY, USA, 2020; pp. 1215–1221. [Google Scholar]
- Kulathunga, G. A reinforcement learning based path planning approach in 3D environment. Procedia Comput. Sci. 2022, 212, 152–160. [Google Scholar] [CrossRef]
- Chen, G.; Pan, L.; Xu, P.; Wang, Z.; Wu, P.; Ji, J.; Chen, X. Robot navigation with map-based deep reinforcement learning. In Proceedings of the 2020 IEEE International Conference on Networking, Sensing and Control (ICNSC), Nanjing, China, 30 October–2 November 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Wang, X.; Shang, E.; Dai, B.; Nie, Y.; Miao, Q. Deep Reinforcement Learning-based Off-road Path Planning via Low-dimensional Simulation. IEEE Trans. Intell. Veh. 2023. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, X.; Zou, Y. Hierarchical path planner for unknown space exploration using reinforcement learning-based intelligent frontier selection. Expert Syst. Appl. 2023, 230, 120630. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, Z.; Yan, Y.; Yang, C.; Hu, Y. Multi-agent policy learning-based path planning for autonomous mobile robots. Eng. Appl. Artif. Intell. 2024, 129, 107631. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, W.; Rahmani, A. Multi-robot path planning using learning-based artificial bee colony algorithm. Eng. Appl. Artif. Intell. 2024, 129, 107579. [Google Scholar] [CrossRef]
- Sartori, D.; Zou, D.; Pei, L.; Yu, W. CNN-based path planning on a map. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 6–9 December 2021; IEEE: New York, NY, USA, 2021; pp. 1331–1338. [Google Scholar]
- Jin, X.; Lan, W.; Chang, X. Neural Path Planning with Multi-Scale Feature Fusion Networks. IEEE Access 2022, 10, 118176–118186. [Google Scholar] [CrossRef]
- Qureshi, A.H.; Miao, Y.; Simeonov, A.; Yip, M.C. Motion planning networks: Bridging the gap between learning-based and classical motion planners. IEEE Trans. Robot. 2020, 37, 48–66. [Google Scholar] [CrossRef]
- Bae, H.; Kim, G.; Kim, J.; Qian, D.; Lee, S. Multi-robot path planning method using reinforcement learning. Appl. Sci. 2019, 9, 3057. [Google Scholar] [CrossRef]
- Wang, M.; Zeng, B.; Wang, Q. Research on motion planning based on flocking control and reinforcement learning for multi-robot systems. Machines 2021, 9, 77. [Google Scholar] [CrossRef]
- Huang, R.; Qin, C.; Li, J.L.; Lan, X. Path planning of mobile robot in unknown dynamic continuous environment using reward-modified deep Q-network. Optim. Control. Appl. Methods 2023, 44, 1570–1587. [Google Scholar] [CrossRef]
- Akkem, Y.; Biswas, S.K.; Varanasi, A. A comprehensive review of synthetic data generation in smart farming by using variational autoencoder and generative adversarial network. Eng. Appl. Artif. Intell. 2024, 131, 107881. [Google Scholar] [CrossRef]
- Li, P.; Pei, Y.; Li, J. A comprehensive survey on design and application of autoencoder in deep learning. Appl. Soft Comput. 2023, 138, 110176. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, X.; Zou, Y.; He, J. Multi-timescale Feature Extraction from Multi-sensor Data using Deep Neural Network for Battery State-of-charge and State-of-health Co-estimation. IEEE Trans. Transp. Electrif. 2023. [Google Scholar] [CrossRef]
- Gao, H.; Yuan, H.; Wang, Z.; Ji, S. Pixel transposed convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1218–1227. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Tu, Z.; Lyu, M.R. On the diversity of multi-head attention. Neurocomputing 2021, 454, 14–24. [Google Scholar] [CrossRef]
- Cui, B.; Hu, G.; Yu, S. Deepcollaboration: Collaborative generative and discriminative models for class incremental learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 1175–1183. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Levine, S. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Fan, J.; Ou, Y.; Wang, P.; Xu, L.; Li, Z.; Zhu, H.; Zhou, Z. Markov decision process of optimal energy management for plug-in hybrid electric vehicle and its solution via policy iteration. J. Phys. Conf. Ser. 2020, 1550, 042011. [Google Scholar] [CrossRef]
- Luong, M.; Pham, C. Incremental learning for autonomous navigation of mobile robots based on deep reinforcement learning. J. Intell. Robot. Syst. 2021, 101, 1. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, A.; Li, Z.; Zhang, T.; Yuan, C.; Li, Y. From knowledge distillation to self-knowledge distillation: A unified approach with normalized loss and customized soft labels. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 17185–17194. [Google Scholar]
- Smoothness of Path—MATLAB Smoothness. Available online: https://ww2.mathworks.cn/help/nav/ref/pathmetrics.smoothness.html (accessed on 1 March 2024).
- Simon, J. Fuzzy control of self-balancing, two-wheel-driven, SLAM-based, unmanned system for agriculture 4.0 applications. Machines 2023, 11, 467. [Google Scholar] [CrossRef]


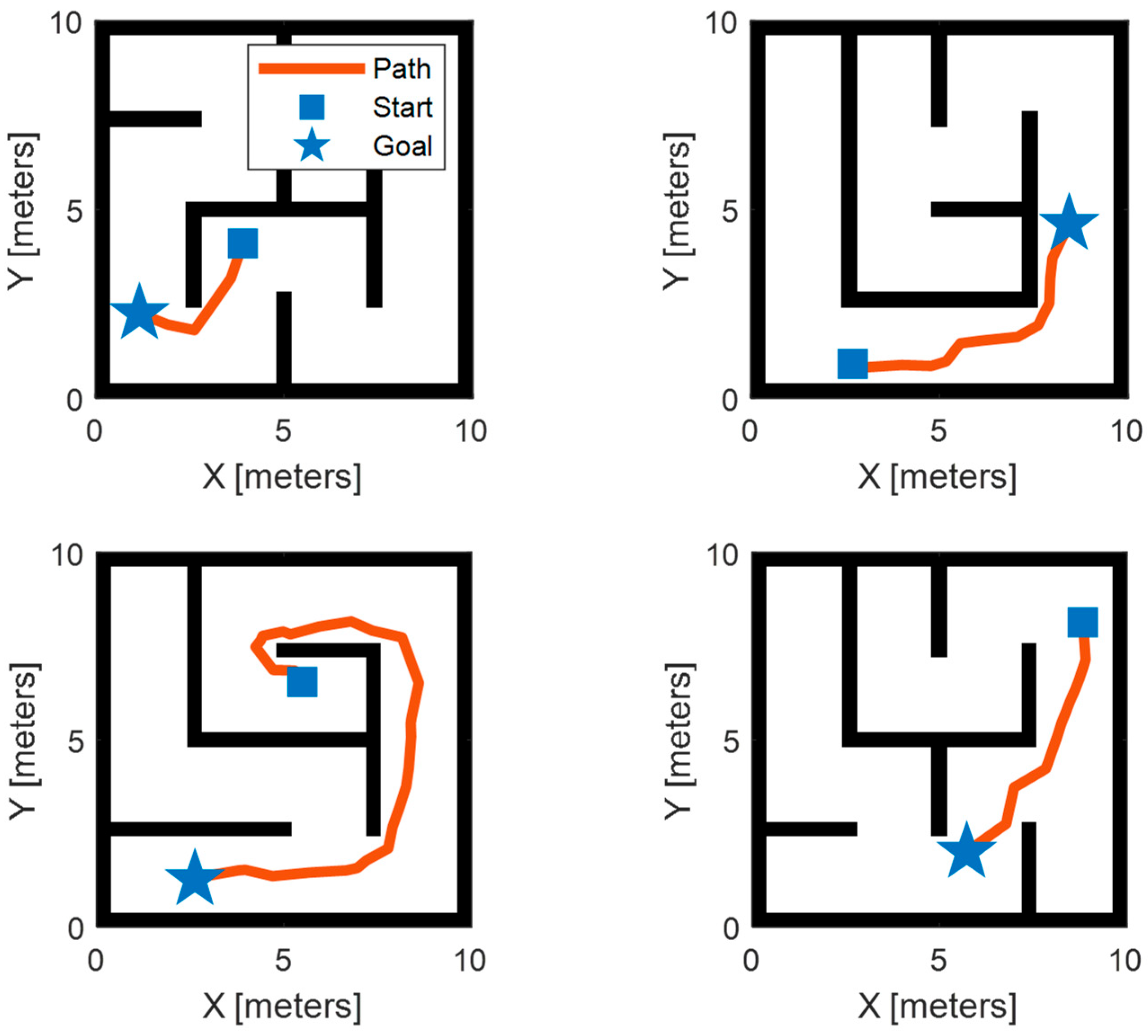


| Network Structure | Path Length | Smoothness |
|---|---|---|
| CNN | 18.96 m | 7.43 |
| GRU | 18.21 m | 6.13 |
| LSTM | 17.55 m | 7.12 |
| Transformer encoder | 15.87 m | 5.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Fan, J.; Zhou, N.; Gao, Z. Highly Self-Adaptive Path-Planning Method for Unmanned Ground Vehicle Based on Transformer Encoder Feature Extraction and Incremental Reinforcement Learning. Machines 2024, 12, 289. https://doi.org/10.3390/machines12050289
Zhang T, Fan J, Zhou N, Gao Z. Highly Self-Adaptive Path-Planning Method for Unmanned Ground Vehicle Based on Transformer Encoder Feature Extraction and Incremental Reinforcement Learning. Machines. 2024; 12(5):289. https://doi.org/10.3390/machines12050289
Chicago/Turabian StyleZhang, Tao, Jie Fan, Nana Zhou, and Zepeng Gao. 2024. "Highly Self-Adaptive Path-Planning Method for Unmanned Ground Vehicle Based on Transformer Encoder Feature Extraction and Incremental Reinforcement Learning" Machines 12, no. 5: 289. https://doi.org/10.3390/machines12050289
APA StyleZhang, T., Fan, J., Zhou, N., & Gao, Z. (2024). Highly Self-Adaptive Path-Planning Method for Unmanned Ground Vehicle Based on Transformer Encoder Feature Extraction and Incremental Reinforcement Learning. Machines, 12(5), 289. https://doi.org/10.3390/machines12050289






