Research on Vibration Characteristics of Bearingless Motorized Spindles Based on Multibody Dynamics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Finite Element Analysis of BLMS
2.2. Mathematical Model of Thermal Eccentricity Unbalanced Excitation Force
2.3. Mathematical Model of Unbalanced Magnetic Pull Due to Air Gap Inhomogeneity
2.4. Discrete Multibody Dynamics Modeling of a BLMS
3. Vibration Simulation of BLMS
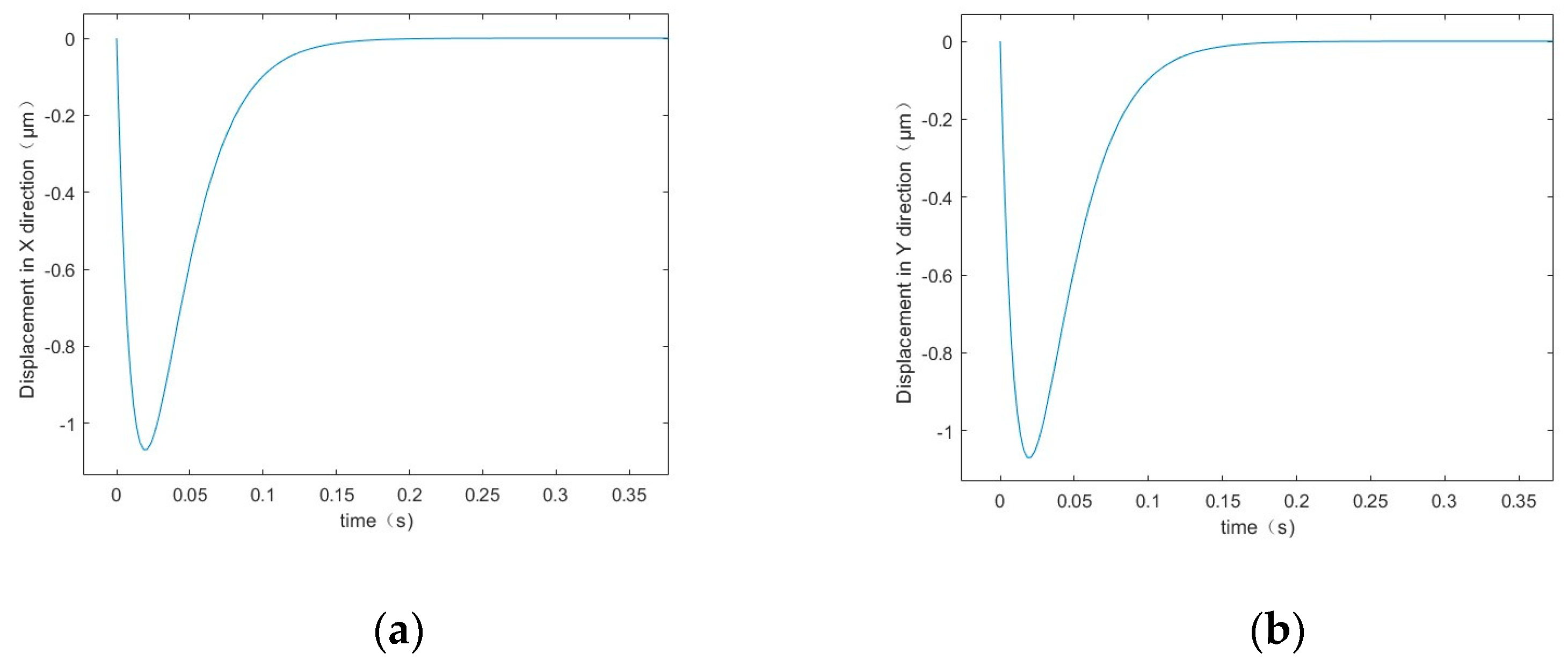
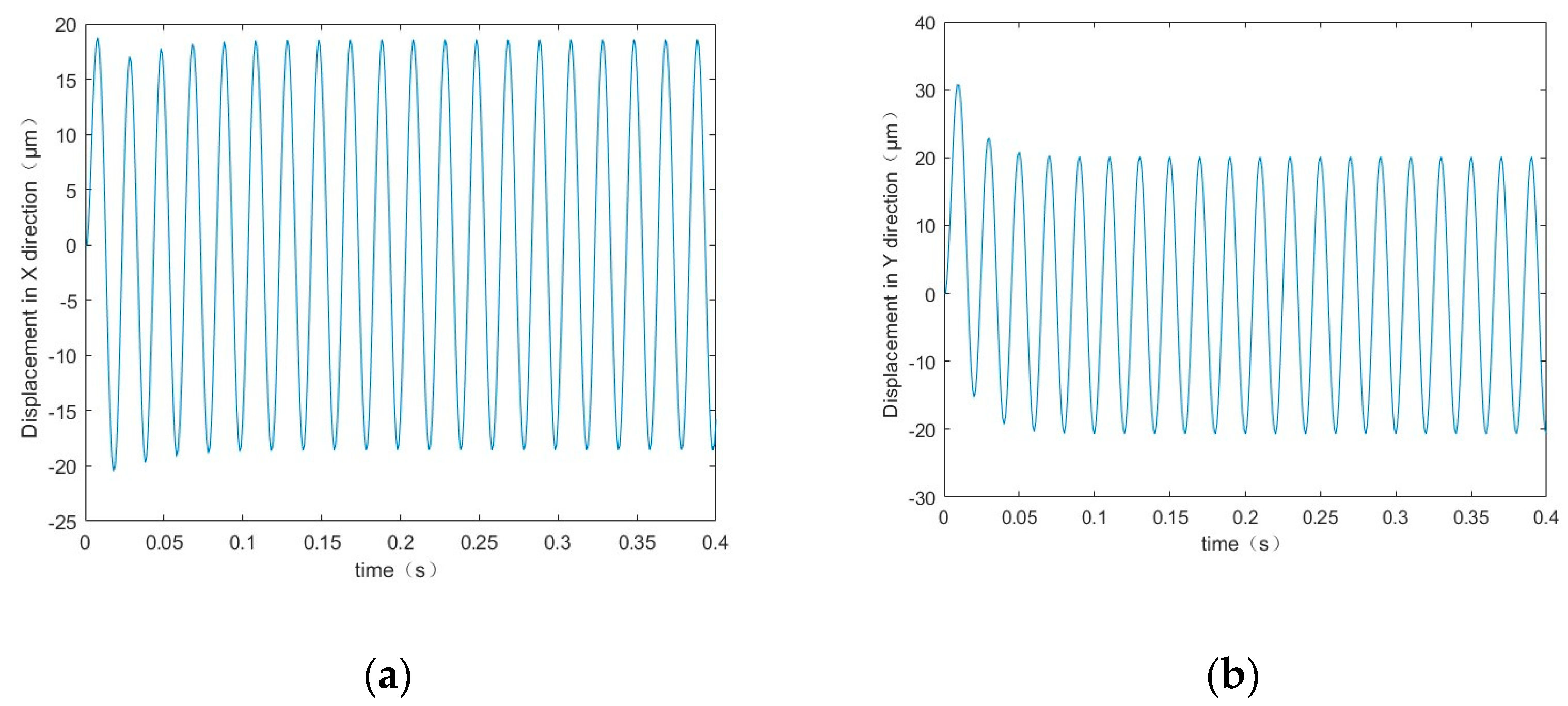
3.1. Thermal Deformation Vibration Simulation Based on Deterministic Parameters
3.2. Thermal Deformation Vibration Simulation Based on Uncertain Parameters
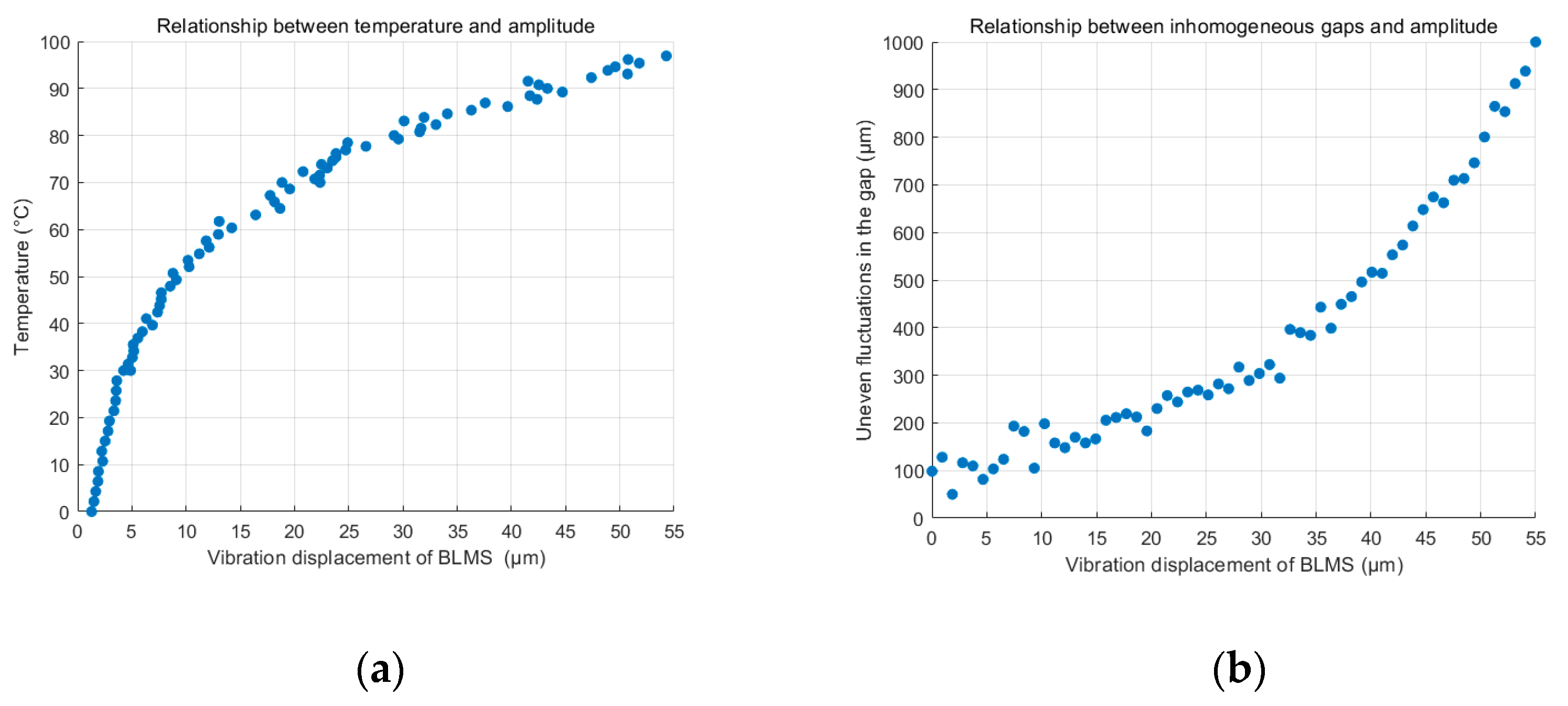
4. Results
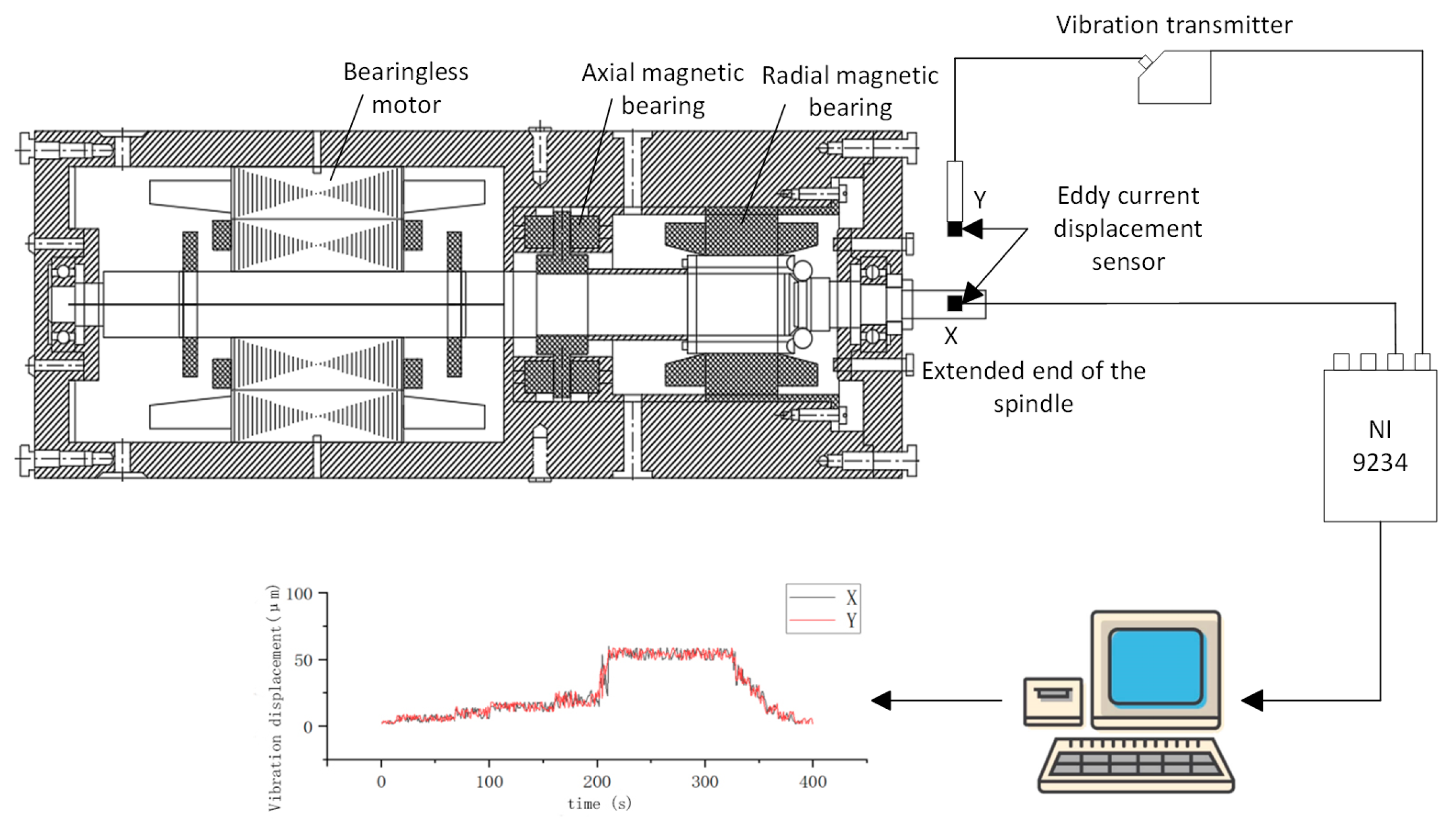
4.1. Prototype Vibration Experiment
4.2. Vibration Test Analysis
5. Discussion
- Considering the parameter uncertainties that may arise during the service life of the BLMS, this study utilized PC and LM to establish a vibration model based on multibody dynamics and time-varying parameters.
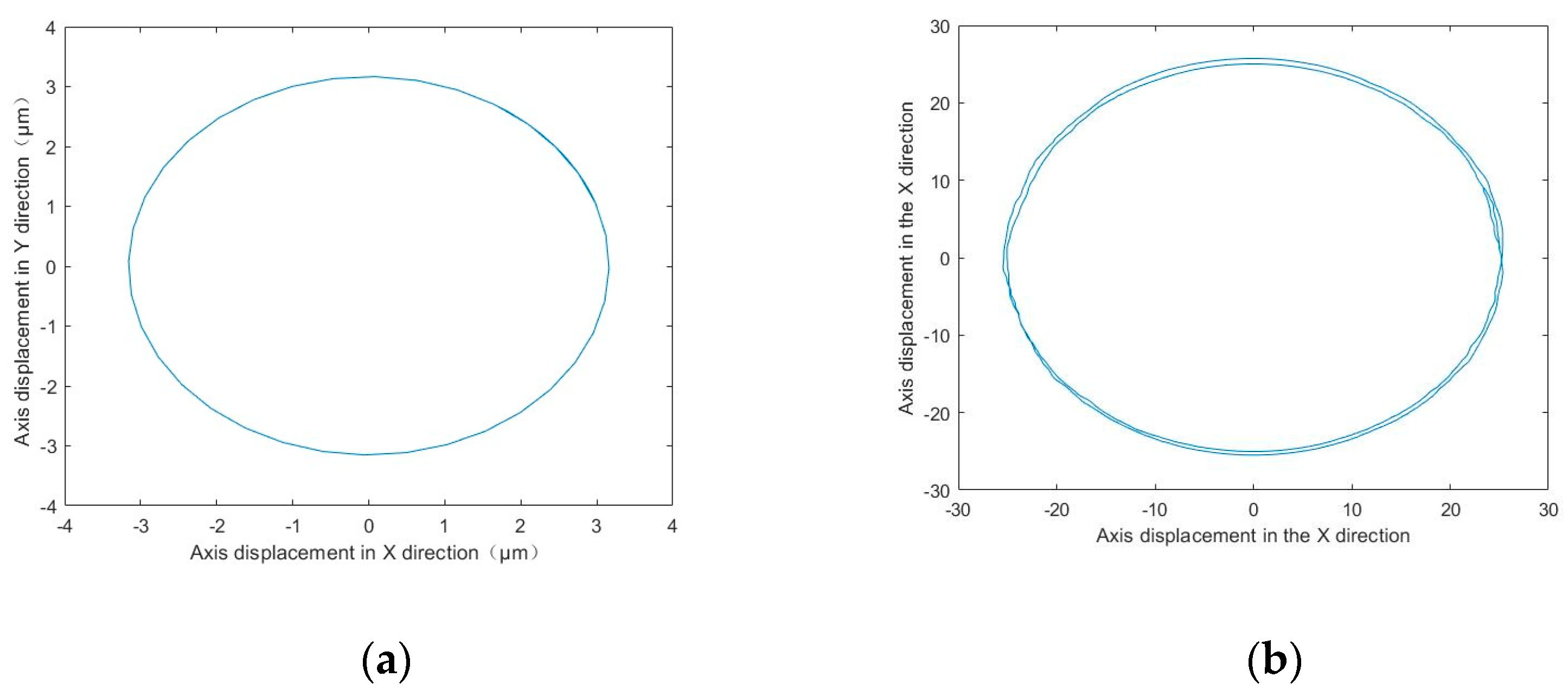
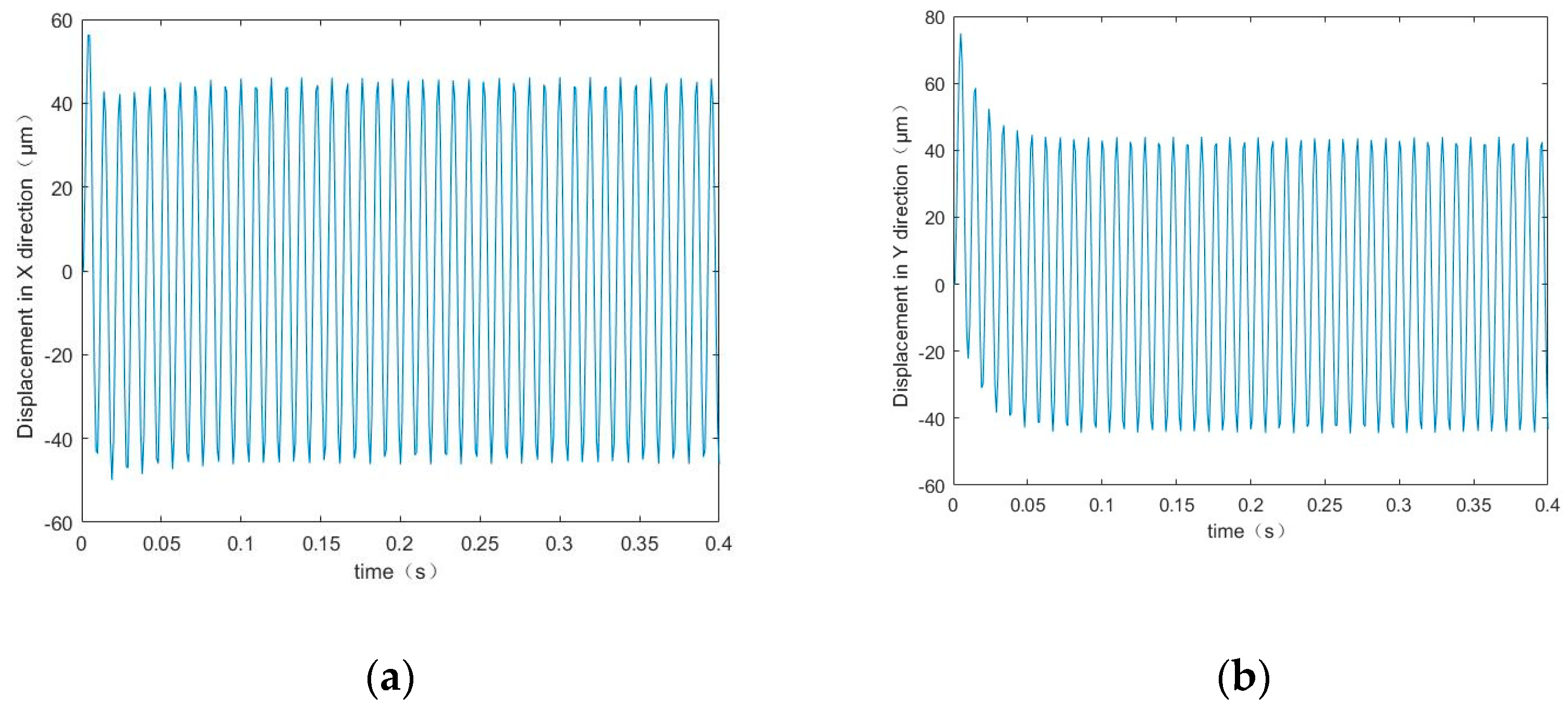
- Employing the Runge–Kutta algorithm, the motion conditions in the discrete model of the BLMS were solved. Utilizing conventional methods for simulation, the radial vibration displacement of the BLMS was estimated to be approximately 43 μm. Based on a multibody dynamic model of a BLMS with uncertain parameters, the maximum displacement of its central trajectory was calculated to be around 52 μm.
- An experimental platform was established to conduct experiments on the BLMS prototype. Vibration experiments revealed that the vibration amplitude of the BLMS increased over time, reaching a maximum displacement of approximately 55 μm. The study results indicate that the dynamic model for the BLMS, which includes uncertain parameters, is more consistent with experimental data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, Y.; Tao, X.; Li, Z.; Zhan, S.; Li, Y.; Gao, Y. A Review of Key Technologies for High-Speed Motorized Spindles of CNC Machine Tools. Machines 2022, 10, 145. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, C.; Chen, F. Progress in the Research of Reliability Technology of Machine Tools. J. Mech. Eng. 2013, 49, 130–139. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, S. Dynamic Design of a High-Speed Motorized Spindle-Bearing System. J. Mech. Des. 2010, 132, 034501. [Google Scholar] [CrossRef]
- Gerada, D.; Mebarki, A.; Brown, N.L.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-Speed Electrical Machines: Technologies, Trends, and Developments. IEEE Trans. Ind. Electron. 2014, 61, 2946–2959. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, J.; Severson, E.L. Review of Bearingless Motor Technology for Significant Power Applications. IEEE Trans. Ind. Appl. 2020, 56, 1377–1388. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, H. Decoupling Control on Outer Rotor Coreless Bearingless Permanent Magnet Synchronous Motor Using LS-SVM Generalized Inverse. Prog. Electromagn. Res. M 2022, 111, 65–76. [Google Scholar] [CrossRef]
- Knospe, C.R. Active Magnetic Bearings for Machining Applications. IFAC Proc. Vol. 2004, 37, 7–12. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, L.; Shi, T.; Liu, X. Finite Element Analysis and Dynamics Charateristic Study for High-Speed Magnetic Suspension Motorized Spindle of CNC Machine Tools. Adv. Mater. Res. 2011, 317–319, 595–599. [Google Scholar] [CrossRef]
- Li, Y.; Sheng, L.; Liu, Y.; Tian, X.; Gao, Y. Dynamic Characteristics Analysis of Permanent Magnet Grinding motorized spindle Rotor System under Eccentricity Failure and Stiffness Failure. Int. J. Dyn. Control. 2022, 10, 1349–1360. [Google Scholar] [CrossRef]
- Qiao, X.; Hu, G. Modal Analysis and Research on Joint Surface of High Speed Motorized Spindle Unit-Spindle Box. Mach. Sci. Technol. 2016, 20, 425–439. [Google Scholar] [CrossRef]
- Bai, X.; Li, J.; Gou, W. Analysis and research on vibration of high-speed motorized spindle in cutting process. J. Qinghai Univ. 2018, 36, 61–79. [Google Scholar] [CrossRef]
- Cheng, M.; Gao, F.; Li, Y. Vibration Detection and Experiment of PMSM High Speed Grinding Motorized Spindle Based on Frequency Domain Technology. Meas. Sci. Rev. 2019, 19, 109–125. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Hu, Z. Analysis of high-speed spindle unbalance vibration behavior and suppression strategy. J. Xi’an Jiao Tong Univ. 2019, 53, 24–29. [Google Scholar]
- Chen, D.; Wu, J.; Wang, L. Prediction method of rotary accuracy of motorized spindle based on vibration signal. China Sci. Technol. Sci. 2020, 50, 819–828. [Google Scholar]
- He, Y.; Chen, X.; Liu, Z.; Chen, Y. Active Vibration Control of Motorized Spindle Based on Mixed H∞/Kalman Filter Robust State Feedback Control. J. Vib. Control. 2019, 25, 1279–1293. [Google Scholar] [CrossRef]
- Bu, W.; Tu, X.; Lu, C.; Pu, Y. Adaptive Feedforward Vibration Compensation Control Strategy of Bearingless Induction Motor. Int. J. Appl. Electromagn. Mech. 2020, 63, 199–215. [Google Scholar] [CrossRef]
- Shan, W.; Chen, X. Modelling the Dynamic Performance of Motorized Spindles with Different Bearing Types. Int. J. Simul. Syst. Sci. Technol. 2016, 17, 41–47. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Z. The Fem Analysis of Dynamic Characteristics of High Speed Motorized Spindle. Comb. Mach. Tool Autom. Mach. Technol. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Kang, H.; Zhang, C.; Liu, Y. Influence of Time-varying Cutting Load on Dynamic Control Accuracy of Asynchronous Motorized Spindle. Mech. Sci. Technol. 2017, 36, 1367–1374. [Google Scholar] [CrossRef]
- Liu, J.; Lai, T.; Tie, G. Influence of thermo-mechanical coupled behaviors on milling stability of high-speed motorized spindles. Precis. Eng. 2018, 52, 94–105. [Google Scholar] [CrossRef]
- Zhang, L.; Zha, J.; Zou, C.; Chen, X.; Chen, Y. A New Method for Field Dynamic Balancing of Rigid Motorized Spindles Based on Real-Time Position Data of CNC Machine Tools. Int. J. Adv. Manuf. Technol. 2018, 102, 1181–1191. [Google Scholar] [CrossRef]
- Xu, K.; Wang, B.; Zhao, Z.; Zhao, F.; Kong, X.; Wen, B. The Influence of Rolling Bearing Parameters on the Nonlinear Dynamic Response and Cutting Stability of High-Speed Spindle Systems. Mech. Syst. Signal Process. 2020, 136, 106448. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, C.; Sun, X.; Sun, Y. An Improved Dynamic Model for Bearingless Induction Motor Considering Rotor Eccentricity and Load Change. IEEE Trans. Ind. Electron. 2022, 69, 3439–3448. [Google Scholar] [CrossRef]
- Ye, X.; Yang, Z.; Zhang, T. Modelling and Performance Analysis on a Bearingless Fixed-Pole Rotor Induction Motor. IET Electr. Power Appl. 2019, 13, 251–258. [Google Scholar] [CrossRef]
- Bossmanns, B.; Tu, J.F. A Thermal Model for High-Speed Motorized Spindles. Int. J. Mach. Tools Manuf. 1999, 39, 1345–1366. [Google Scholar] [CrossRef]
- Liu, T.; Gao, W.; Zhang, D.; Zhang, Y.; Chang, W.; Liang, C.; Tian, Y. Analytical Modeling for Thermal Errors of Motorized Spindle Unit. Int. J. Mach. Tools Manuf. 2017, 112, 53–70. [Google Scholar] [CrossRef]
- Chen, X. Thermal Properties of High-Speed Motorized Spindle and Their Effects. Jixie Gongcheng Xuebao 2013, 49, 135. [Google Scholar] [CrossRef]
- Liu, D. Finite Element Analysis of High-Speed Motorized Spindle Based on ANSYS. Open Mech. Eng. J. 2011, 5, 1–10. [Google Scholar] [CrossRef]
- Tu, X.; Bu, W.; Zeng, Q. Research on the Modelling of a Single-Winding Bearingless Permanent Magnet Brushless DC Motor. J. Phys. Conf. Ser. 2021, 1887, 012049. [Google Scholar] [CrossRef]
- Sun, Q.; Ma, C.; Xiao, S.; Niu, L.; Pu, J.; Wu, Y. Analysis of Influence of Uneven Air Gap of Hydrogenerator on Magnetic Field Strength and Rotor Magnetic Pole Stress Change. In 2020 IEEE International Conference on Energy Internet (ICEI); IEEE: Piscataway, NJ, USA, 2020; pp. 147–151. [Google Scholar] [CrossRef]
- Zhu, R.; Tong, X.; Han, Q.; He, K.; Wang, X.; Wang, X. Calculation and Analysis of Unbalanced Magnetic Pull of Rotor under Motor Air Gap Eccentricity Fault. Sustainability 2023, 15, 8537. [Google Scholar] [CrossRef]
- Xul, J.; Zheng, X.; Zhang, J.; Liu, X. Vibration Characteristics of Unbalance Response for Motorized Spindle System. Procedia Eng. 2017, 174, 331–340. [Google Scholar] [CrossRef]
- Huston, R.L. Multibody Dynamics Modeling and Analysis Methods. Appl. Mech. Rev. 1991, 44, 109–117. [Google Scholar] [CrossRef]
- Xu, C.; Jiang, S. Dynamic Analysis of a Motorized Spindle with Externally Pressurized Air Bearings. J. Vib. Acoust. 2015, 137, 041001. [Google Scholar] [CrossRef]
- Feng, H.; Jiang, S. Dynamics of a Motorized Spindle Supported on Water-Lubricated Bearings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 459–472. [Google Scholar] [CrossRef]
- Guo, D.; Chu, F.; Chen, D. The Unbalanced Magnetic Pull and Its Effects on Vibration in a Three-Phase Generator with Eccentric Rotor. J. Sound Vib. 2002, 254, 297–312. [Google Scholar] [CrossRef]
- Xu, J. Multibody Dynamics Modeling of Wind Turbines and Its Application. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Cho, S.; Jeon, K.; Kim, C.W. Vibration Analysis of Electric Motors Considering Rotating Rotor Structure Using Flexible Multibody Dynamics-Electromagnetic-Structural Vibration Coupled Analysis. J. Comput. Des. Eng. 2023, 10, 578–588. [Google Scholar] [CrossRef]
- Sheng, L.; Sun, Q.; Ye, G.; Li, W. Dynamic Analysis of Grinding motorized spindle Bearing-Rotor System under Eccentric Action. J. Adv. Mech. Des. Syst. Manuf. 2023, 17, 28. [Google Scholar] [CrossRef]
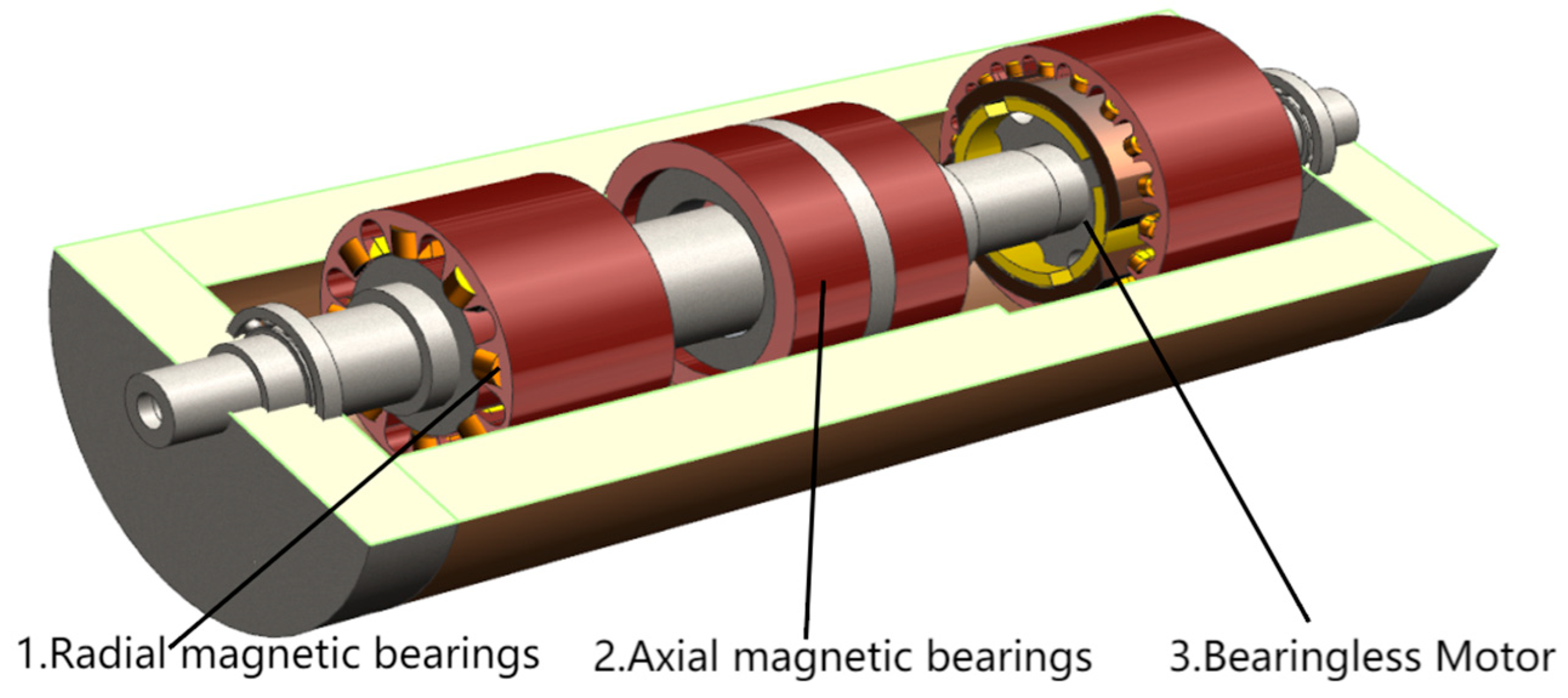

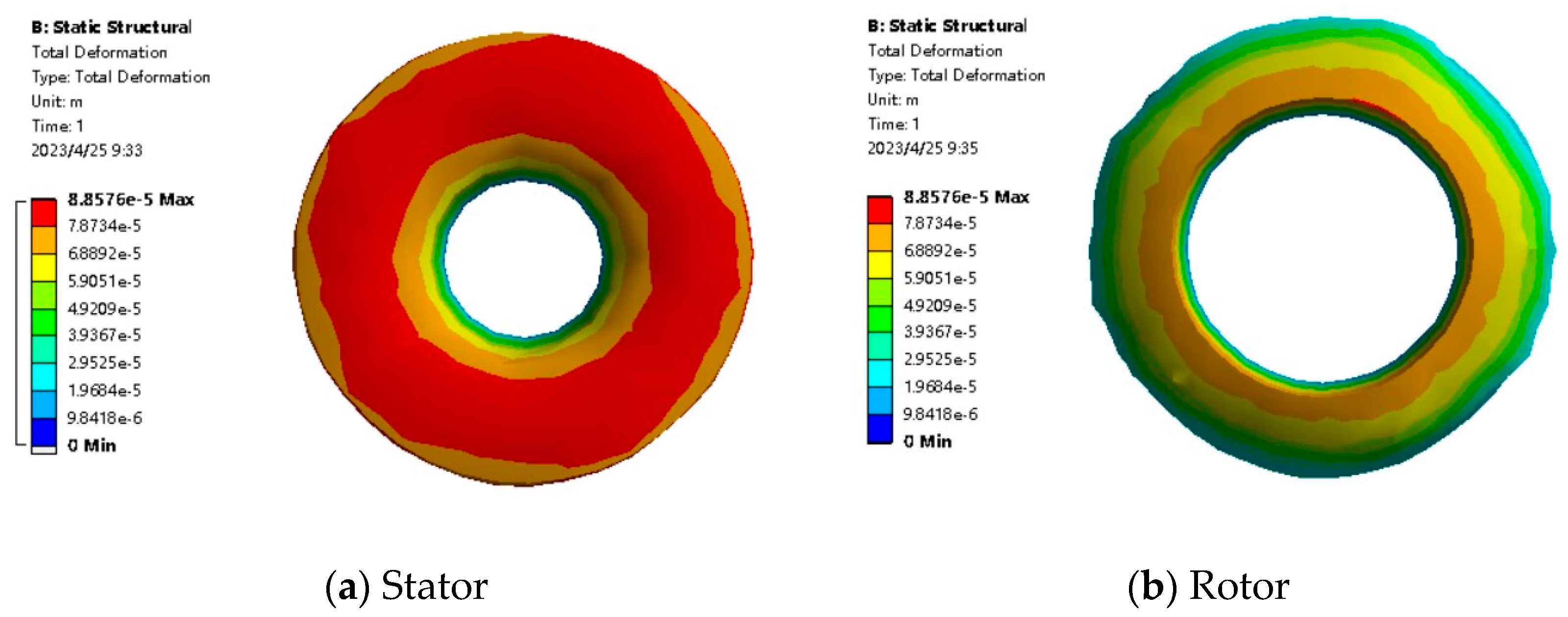

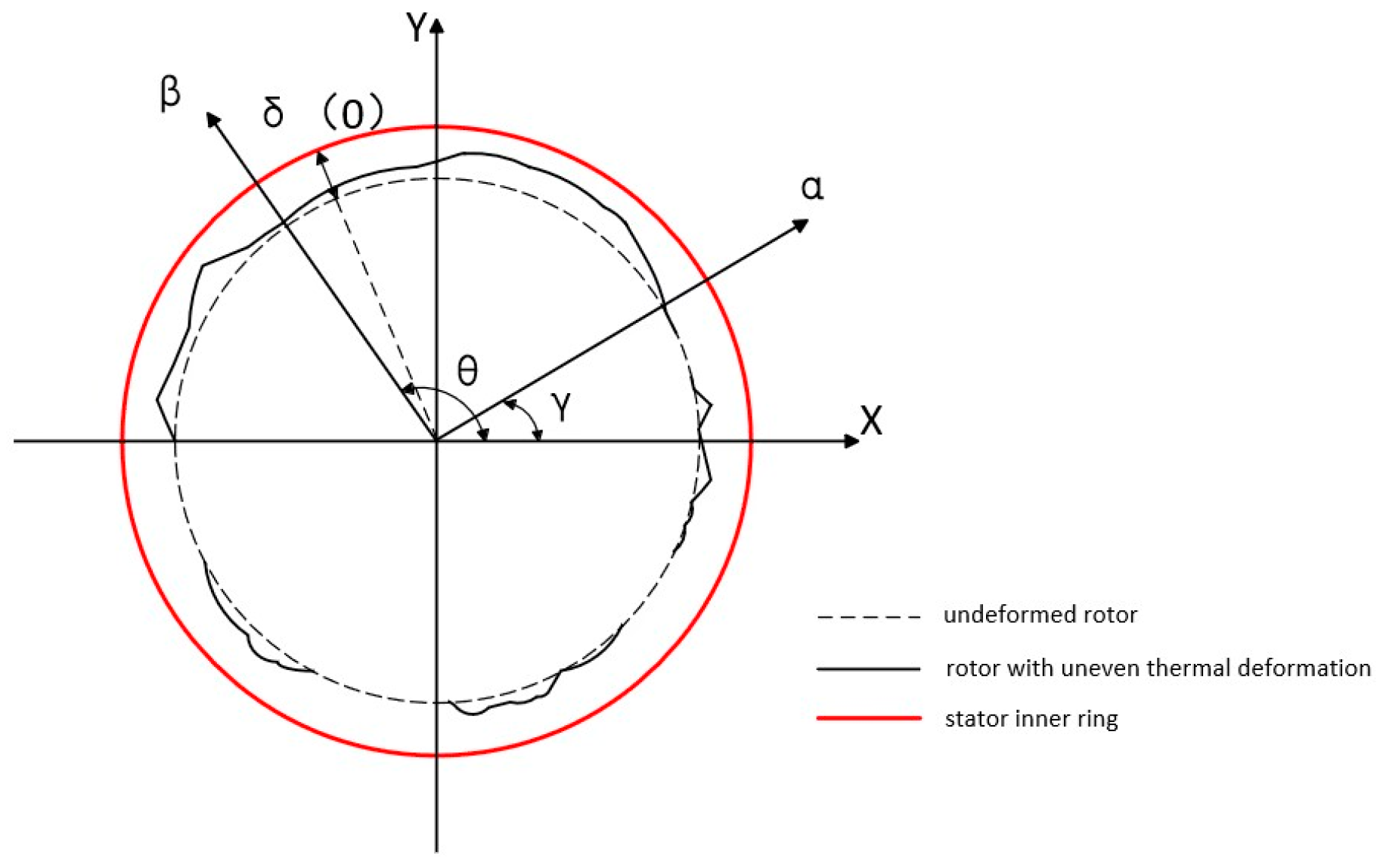
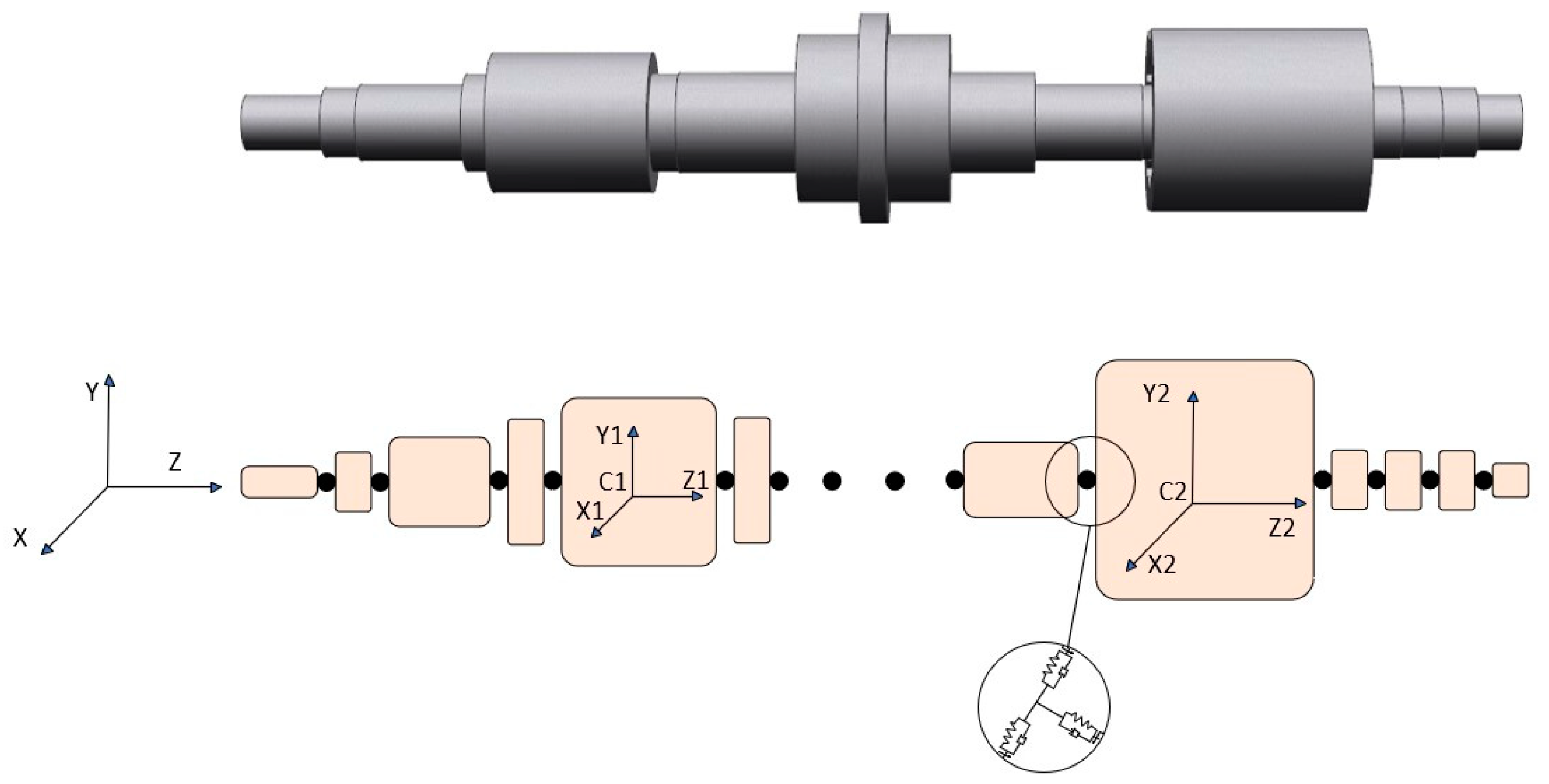





| Heat Generation Rate (kW/m3) | Numerical Value |
|---|---|
| Bearingless motor stator | 243,851 |
| Bearingless motor rotors | 226,159 |
| Radial magnetic bearing copper loss | 10,008 |
| Radial magnetic bearing iron loss | 163,516 |
| Copper loss in axial magnetic bearings | 52,135 |
| Axial magnetic bearing iron loss | 137,788 |
| Rotor wind loss | 10,623 |
| ) | Numerical Value |
|---|---|
| Bearingless motor rotor with air | 231.17 |
| Thrust magnetic bearing rotor with air | 179.84 |
| Radial magnetic bearing rotor with air | 137.81 |
| BLMS outer surface and air | 9.7 |
| Experiment Number | Activation Method | Number of Revolutions per Minute | Running Time | Peak Amplitude (μm) |
|---|---|---|---|---|
| 1 | 380 V voltage start | 3000 r/min | 400 s | X:57 Y:57 |
| 2 | 380 V voltage start | 3000 r/min | 400 s | X:56 Y:57 |
| 3 | 380 V voltage start | 3000 r/min | 400 s | X:57 Y:56 |
| 4 | 380 V voltage start | 3000 r/min | 400 s | X:56 Y:55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, J.; He, L.; Yang, J.; Liu, S. Research on Vibration Characteristics of Bearingless Motorized Spindles Based on Multibody Dynamics. Machines 2024, 12, 458. https://doi.org/10.3390/machines12070458
Meng J, He L, Yang J, Liu S. Research on Vibration Characteristics of Bearingless Motorized Spindles Based on Multibody Dynamics. Machines. 2024; 12(7):458. https://doi.org/10.3390/machines12070458
Chicago/Turabian StyleMeng, Jie, Lihong He, Jianan Yang, and Shuang Liu. 2024. "Research on Vibration Characteristics of Bearingless Motorized Spindles Based on Multibody Dynamics" Machines 12, no. 7: 458. https://doi.org/10.3390/machines12070458
APA StyleMeng, J., He, L., Yang, J., & Liu, S. (2024). Research on Vibration Characteristics of Bearingless Motorized Spindles Based on Multibody Dynamics. Machines, 12(7), 458. https://doi.org/10.3390/machines12070458





