Impact of Installation Deviations on the Dynamic Characteristics of the Shaft System for 1 Gigawatt Hydro-Generator Unit
Abstract
:1. Introduction
2. Numerical Calculation Theory of the Hydro-Generator Shaft System
2.1. Modal Analysis
2.2. Rotordynamics Analysis
3. Dynamic Characteristics Analysis and Discussions
3.1. Modal Analysis of the Shaft System without Installation Deviation
3.2. Rotordynamics Analysis of the Shaft System without Installation Deviation
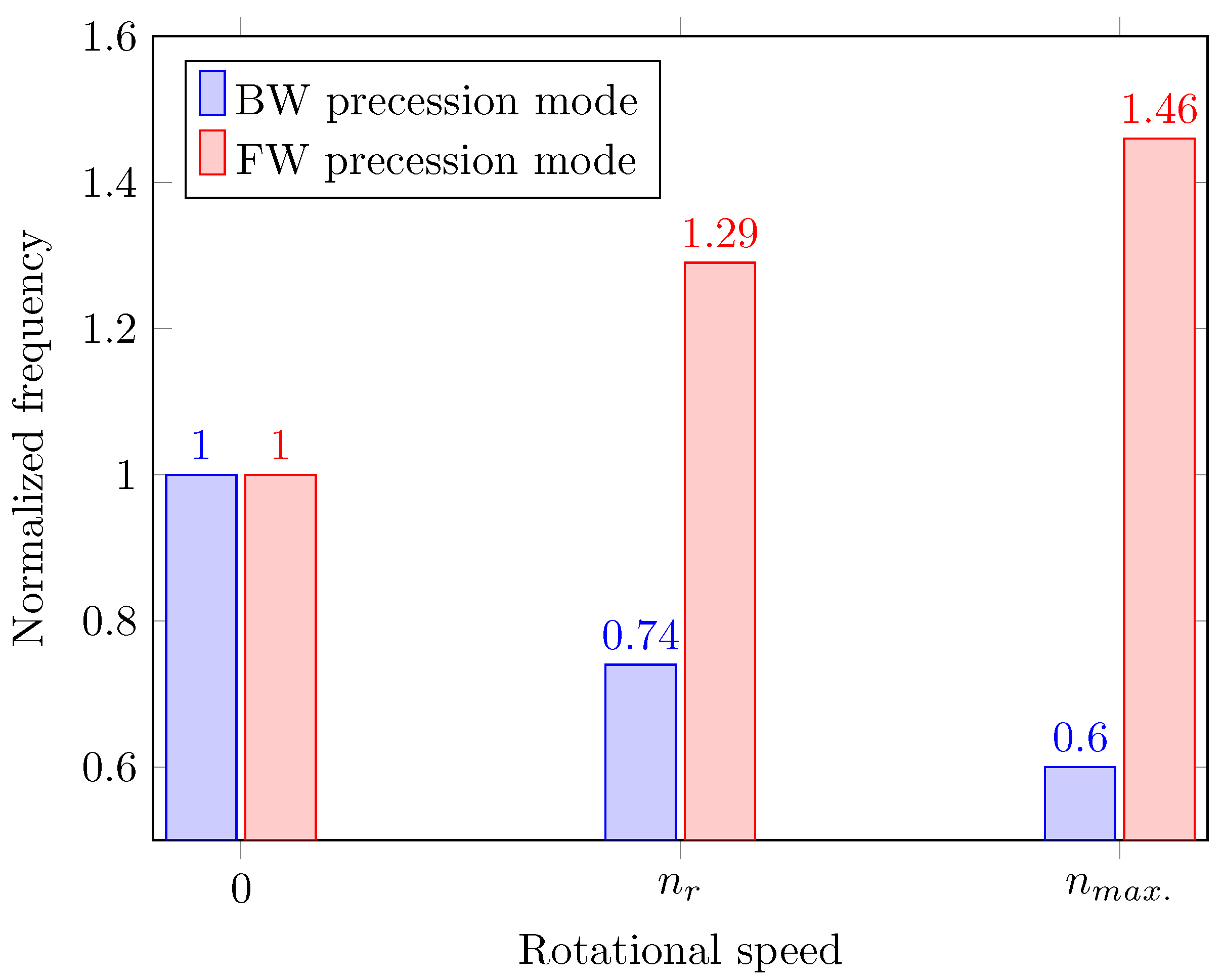
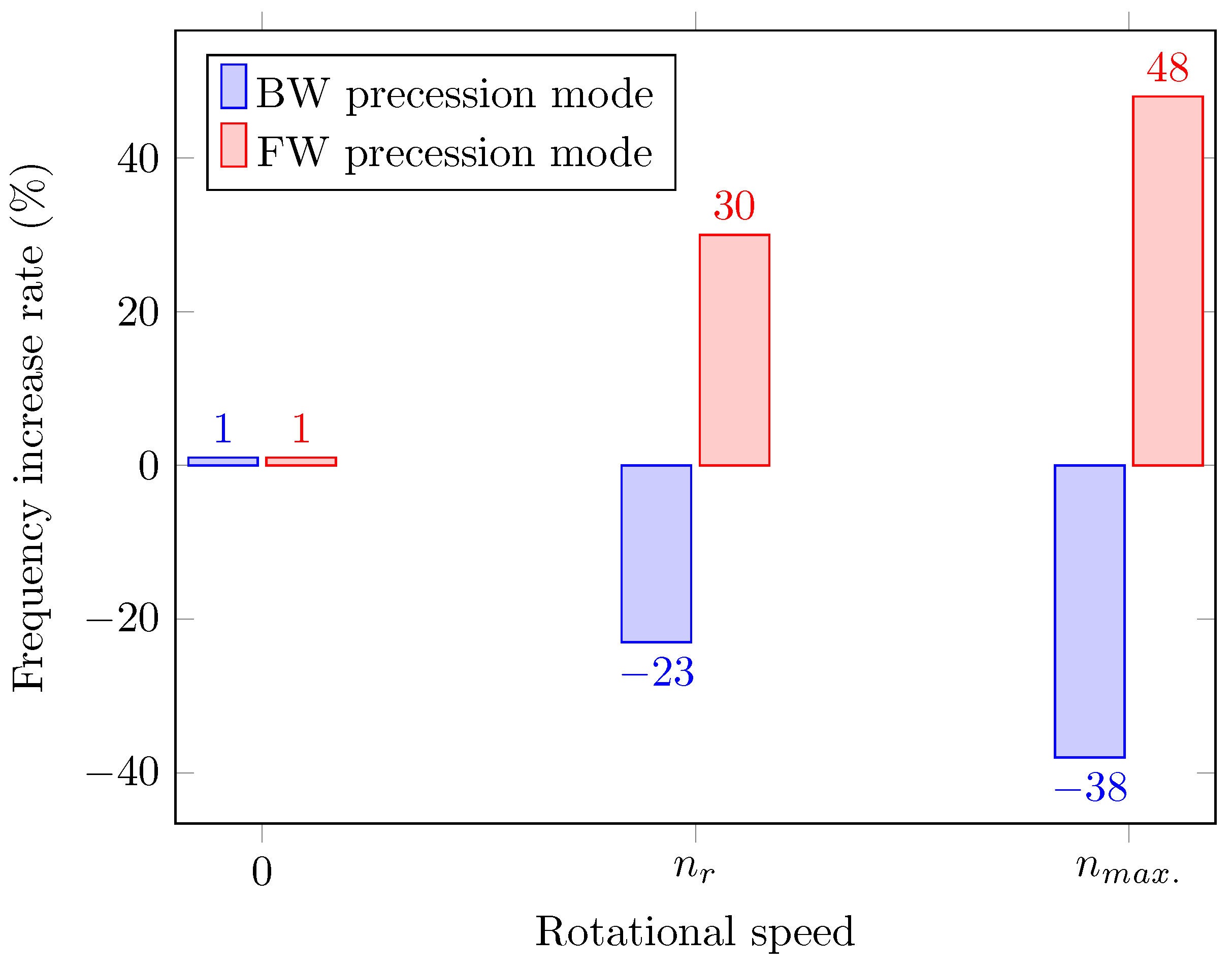
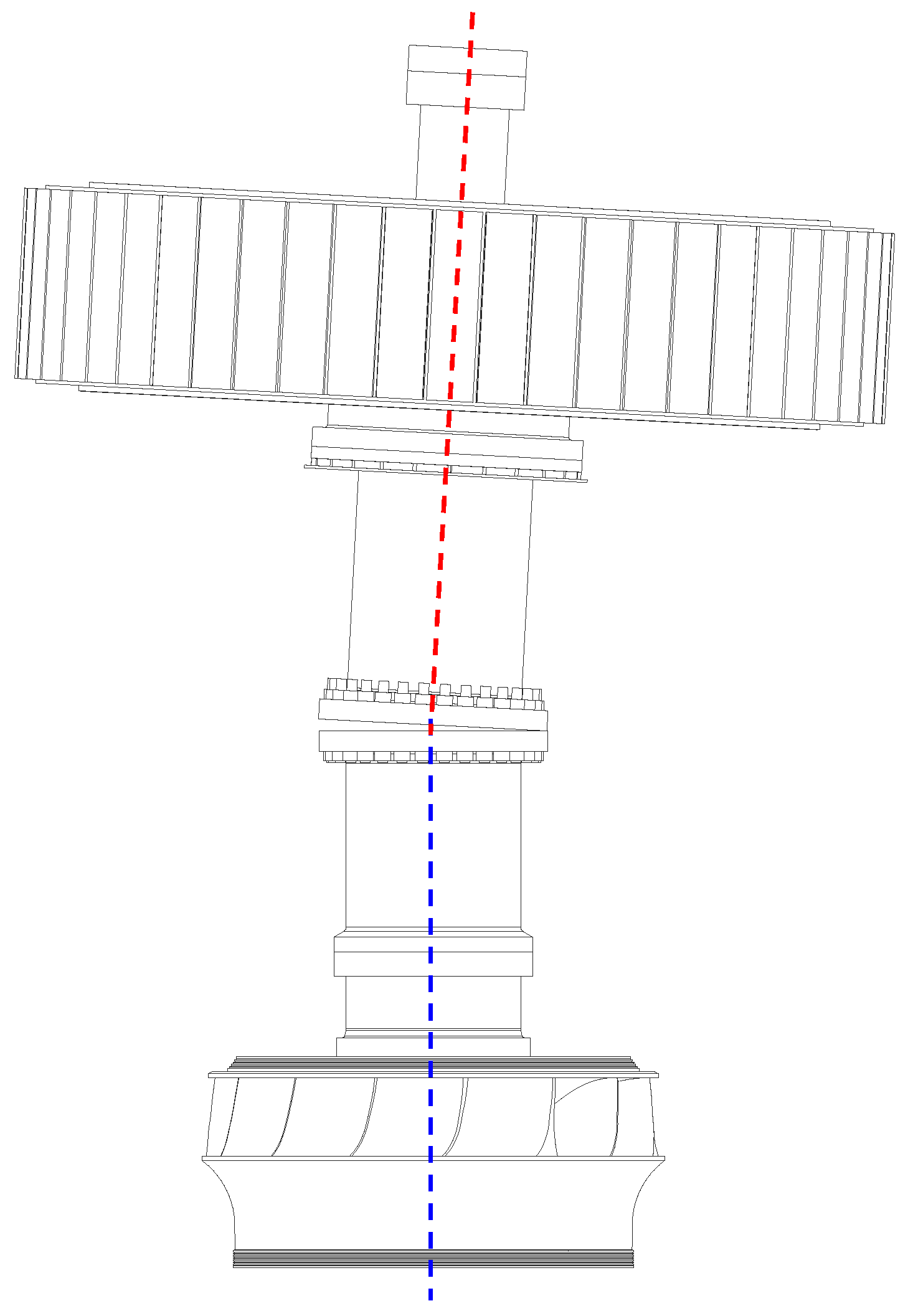
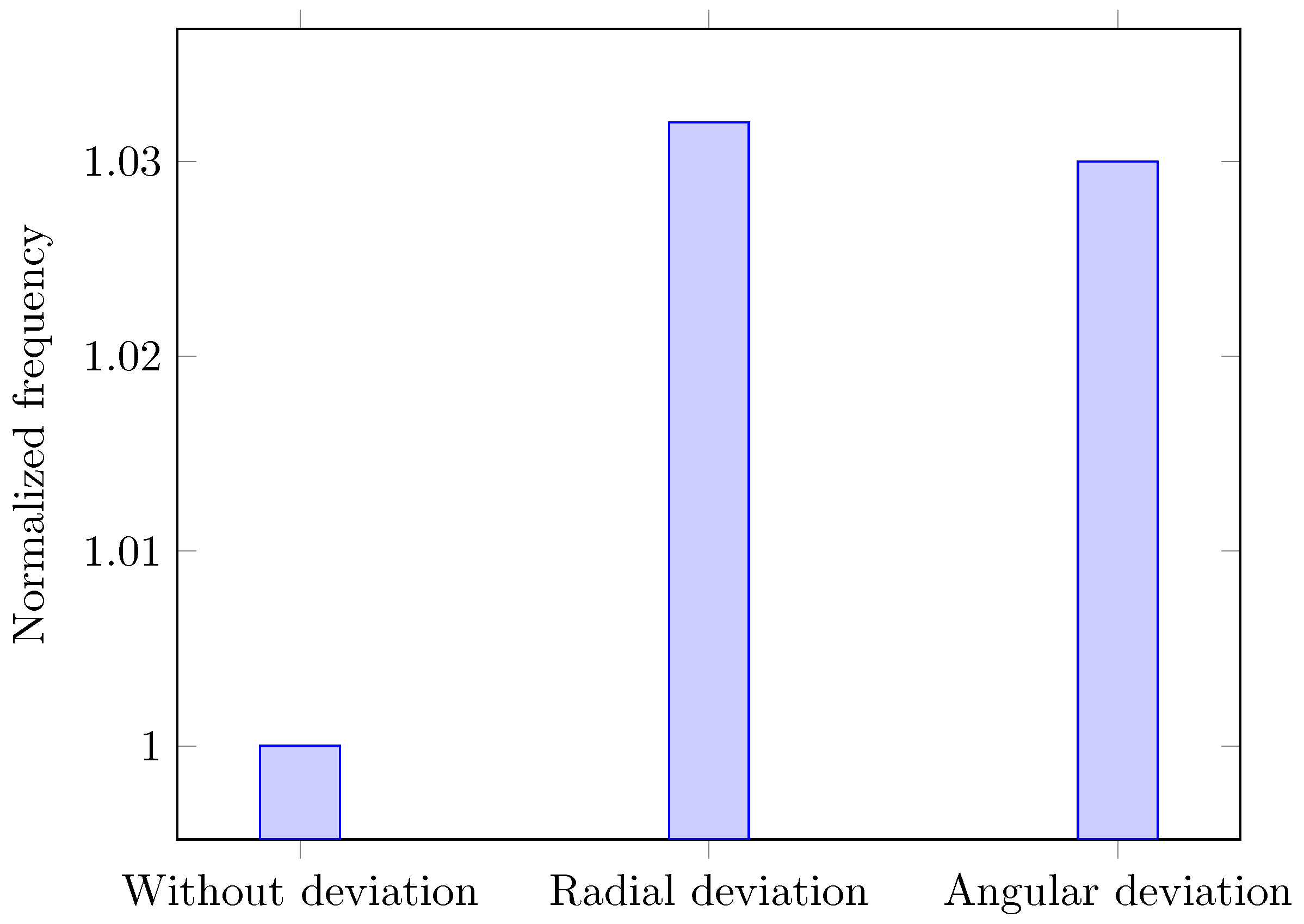
3.3. Structural Dynamic with Shaft Radial Installation Deviation
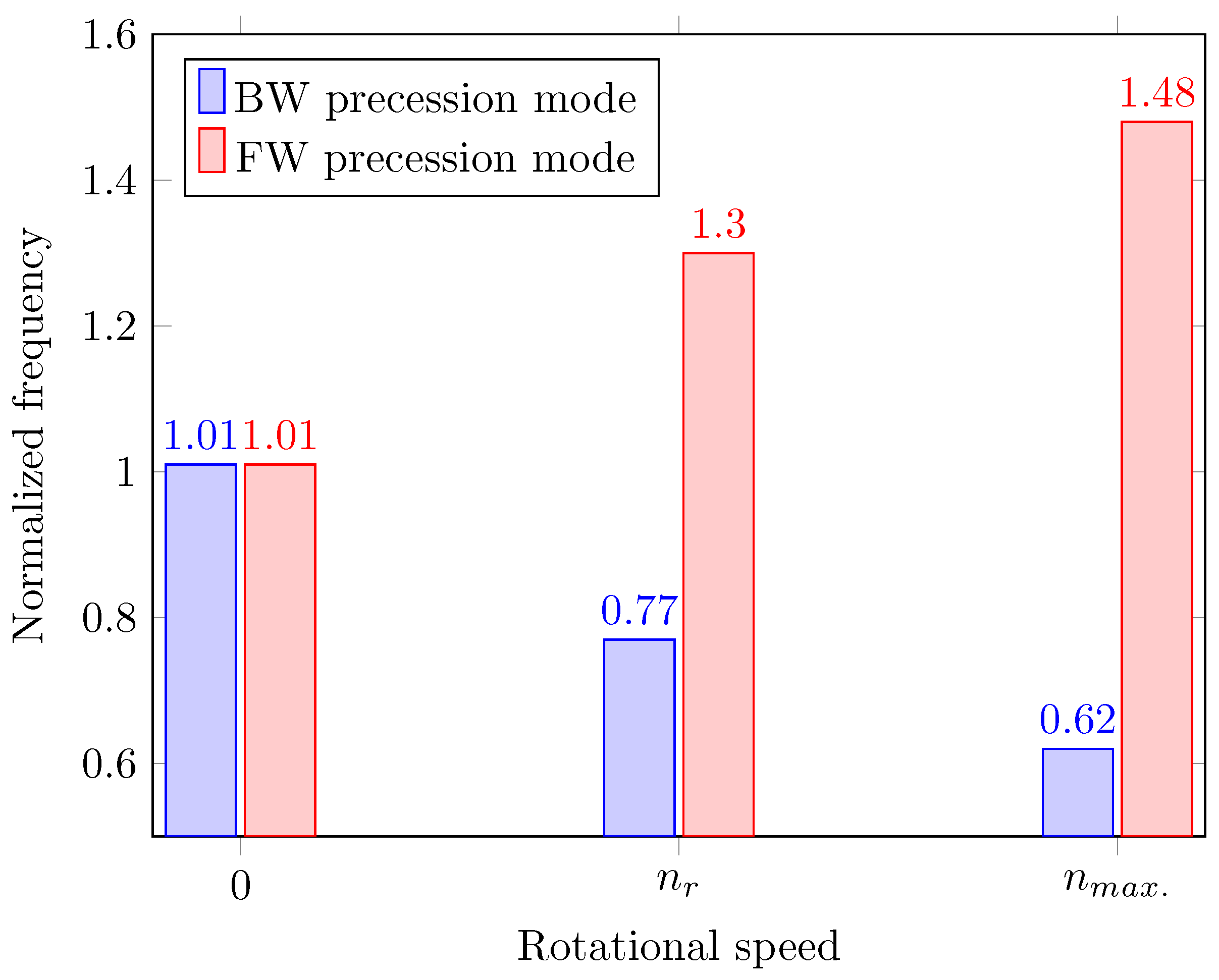
3.4. Dynamic Characteristics with Shaft Angular Installation Deviation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | three-dimensional |
| BW | backward |
| CAD | computer-aided design |
| CFD | computational fluid dynamics |
| FE | finite element |
| FEM | finite-element method |
| FIR | frequency increase rate |
| FW | forward |
| ND | nodal diameter |
| RANS | Reynolds-averaged Navier–Stokes |
| SST | shear stress transport |
| TBE | Timoshenko beam-elements |
| TMM | transfer matrix method |
References
- Almeida, R.; Shi, Q.; Gomes Selman, J.; Wu, X.; Xue, Y.; Angarita, H.; Barros, N.; Forsberg, B.; Garcia-Villacorta, R.; Hamilton, S.; et al. Reducing greenhouse gas emissions of Amazon hydropower with strategic dam planning. Nat. Commun. 2019, 10, 4281. [Google Scholar] [CrossRef] [PubMed]
- Bogaart, P. The potential for sustainable hydropower. Nat. Water 2023, 1, 22–23. [Google Scholar] [CrossRef]
- Lewis, B.J.; Cimbala, J.M.; Wouden, A.M. Major historical developments in the design of water wheels and Francis hydroturbines. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 012020. [Google Scholar] [CrossRef]
- Breeze, P. Power Generation Technologies; Elsevier Science: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Garcia, M.; Laín, S.; Orrego, S.; Barbosa, J.; Quintero, B. Hydraulic and rotor-dynamic interaction for performance evaluation on a Francis turbine. Int. J. Interact. Des. Manuf. (IJIDeM) 2016, 11, 623–632. [Google Scholar] [CrossRef]
- Shi, Y.; Zhou, J.; Lai, X.; Xu, Y.; Guo, W.; Liu, B. Stability and sensitivity analysis of the bending-torsional coupled vibration with the arcuate whirl of hydro-turbine generator unit. Mech. Syst. Signal Process. 2021, 149, 107306. [Google Scholar] [CrossRef]
- Bettig, B.P.; Han, R.P.S. Modeling the Lateral Vibration of Hydraulic Turbine-Generator Rotors. J. Vib. Acoust. 1999, 121, 322–327. [Google Scholar] [CrossRef]
- Gustavsson, R.; Aidanpää, J.O. The influence of nonlinear magnetic pull on hydropower generator rotors. J. Sound Vib. 2006, 297, 551–562. [Google Scholar] [CrossRef]
- Kahraman, G.; Osman, Ö. Mathematical modeling of vibration failure caused by balancing effect in hydraulic turbines. Mech. Based Des. Struct. Mach. 2021, 1–12. [Google Scholar]
- Lundstrom, L.; Gustavsson, R.; Aidanpää, J.O.; Dahlback, N.; Leijon, M. Influence on the stability of generator rotors due to radial and tangential magnetic pull force. Electr. Power Appl. IET 2007, 1, 1–8. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z. Computational Model for Investigating the Influence of Unbalanced Magnetic Pull on the Radial Vibration of Large Hydro-Turbine Generators. J. Vib. Acoust. 2012, 134, 051013. [Google Scholar] [CrossRef]
- Rondon, D.; Aidanpää, J.O.; Gustavsson, R. Effect of unbalancing mass placement in hydropower generators with floating rotor rim. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012094. [Google Scholar] [CrossRef]
- Cardinali, R.; Nordmann, R.; Sperber, A. Dynamic simulation of non-linear models of hydroelectric machinery. Mech. Syst. Signal Process. 1993, 7, 29–44. [Google Scholar] [CrossRef]
- Brito Junior, G.C.; Machado, R.D.; Chaves Neto, A. Using Simplified Models to Assist Fault Detection and Diagnosis in Large Hydrogenerators. Int. J. Rotating Mach. 2017, 2017, 9258456. [Google Scholar] [CrossRef]
- Boyko, A.; Popov, S.; Krajisnik, N. Investigating the Sayano-Shushenskaya Hydro Power Plant Disaster. Power 2010, 154, 48. [Google Scholar]
- Feng, F.; Chu, F. Dynamic analysis of a hydraulic turbine unit. Mech. Struct. Mach. 2001, 29, 505–531. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, J.; Fang, Y.; Wen, X.; Cao, J.; Shi, Q. Characteristic analysis of rotor dynamics of large hydraulic generating unit. Shuili Fadian Xuebao (J. Hydroelectr. Eng.) 2005, 24, 62–66. [Google Scholar]
- Albuquerque, R.B.; Barbosa, D.L. Evaluation of bending critical speeds of hydrogenerator shaft lines using the transfer matrix method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 2010–2022. [Google Scholar]
- Cao, J.; Luo, Y.; Presas, A.; Ahn, S.H.; Wang, Z.; Huang, X.; Liu, Y. Influence of rotation on the modal characteristics of a bulb turbine unit rotor. Renew. Energy 2022, 187, 887–895. [Google Scholar] [CrossRef]
- Egusquiza, E.; Valero, C.; Presas, A.; Huang, X.; Guardo, A.; Seidel, U. Analysis of the dynamic response of pump-turbine impellers. Influence of the rotor Mech. Syst. Signal Process. 2016, 68, 330–341. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Zhang, Y.; Huang, X.; Guo, T.; Zhou, L.; Wang, Z. Influence of Axial Installation Deviation on the Hydraulic Axial Force of the 1000 MW Francis Runner in the Rated Operating Condition. Energies 2023, 16, 1878. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, K.; Huang, X.; Lin, P.; Wang, Z.; Wang, W.; Zhou, L. Influence of Radial Installation Deviation on Hydraulic Thrust Characteristics of a 1000 MW Francis Turbine. Water 2023, 15, 1606. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, X.; Liu, Y.; Ma, G.; Liu, C.; Wang, Y.; Zhang, J.; Shif, Y.; Cao, J.; Wang, Z. Study on the Importance of Precise Control of Installation Deviation to the Structural Behavior of the Shaft System of a 1000 MW Hydro-generator Unit. In Proceedings of the 2022 International Conference on Environmental Science and Green Energy (ICESGE), Shenyang, China, 25–27 November 2022; pp. 192–196. [Google Scholar] [CrossRef]











| Parameter | Value | Unit |
|---|---|---|
| Rated power | 1 | GW |
| Rated head | 202 | m |
| Rated flow | 545.5 | |
| Rated rotating speed | 111.1 | rpm |
| Maximum runaway speed | 202 | rpm |
| Component | Tonne |
|---|---|
| Runner | 346.5 |
| Turbine shaft | 118 |
| Generator | 2000 |
| Generator shaft and other small parts | 216 |
| Total | 2680.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, G.; Huang, X.; Li, H.; Wang, Z.; Wang, D. Impact of Installation Deviations on the Dynamic Characteristics of the Shaft System for 1 Gigawatt Hydro-Generator Unit. Machines 2024, 12, 473. https://doi.org/10.3390/machines12070473
Song G, Huang X, Li H, Wang Z, Wang D. Impact of Installation Deviations on the Dynamic Characteristics of the Shaft System for 1 Gigawatt Hydro-Generator Unit. Machines. 2024; 12(7):473. https://doi.org/10.3390/machines12070473
Chicago/Turabian StyleSong, Gangyun, Xingxing Huang, Haijun Li, Zhengwei Wang, and Dong Wang. 2024. "Impact of Installation Deviations on the Dynamic Characteristics of the Shaft System for 1 Gigawatt Hydro-Generator Unit" Machines 12, no. 7: 473. https://doi.org/10.3390/machines12070473
APA StyleSong, G., Huang, X., Li, H., Wang, Z., & Wang, D. (2024). Impact of Installation Deviations on the Dynamic Characteristics of the Shaft System for 1 Gigawatt Hydro-Generator Unit. Machines, 12(7), 473. https://doi.org/10.3390/machines12070473









