Prediction and Dynamic Simulation Verification of Output Characteristics of Radial Piston Motors Based on Neural Networks
Abstract
:1. Introduction
2. Torque for the Radial Piston Motor
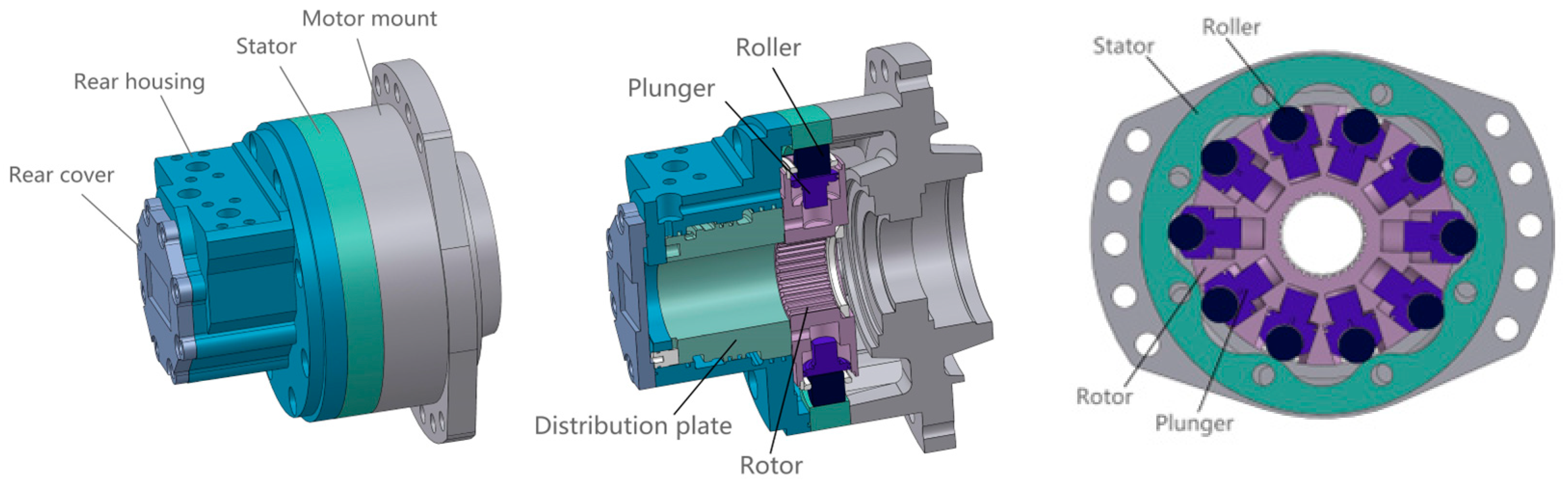
2.1. Structure of the Radial Piston Motor
2.2. Force Analysis between the Roller and the Stator Guide Rail
3. Hydraulic Motor Efficiency Testing Experiment
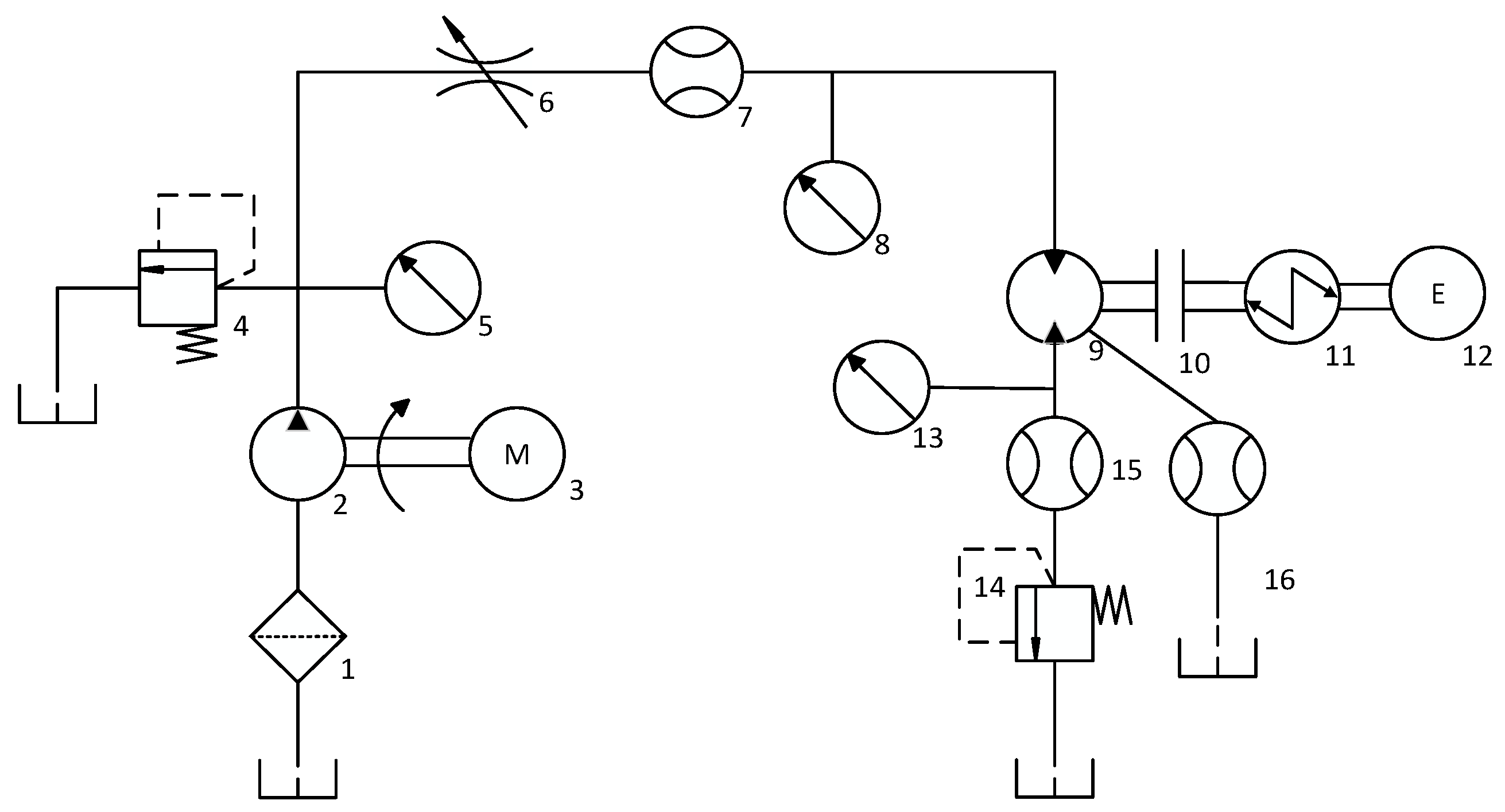
3.1. Introduction to the Experiment
3.2. Experiment Data
4. Output Characteristics Prediction
4.1. Regression Analysis
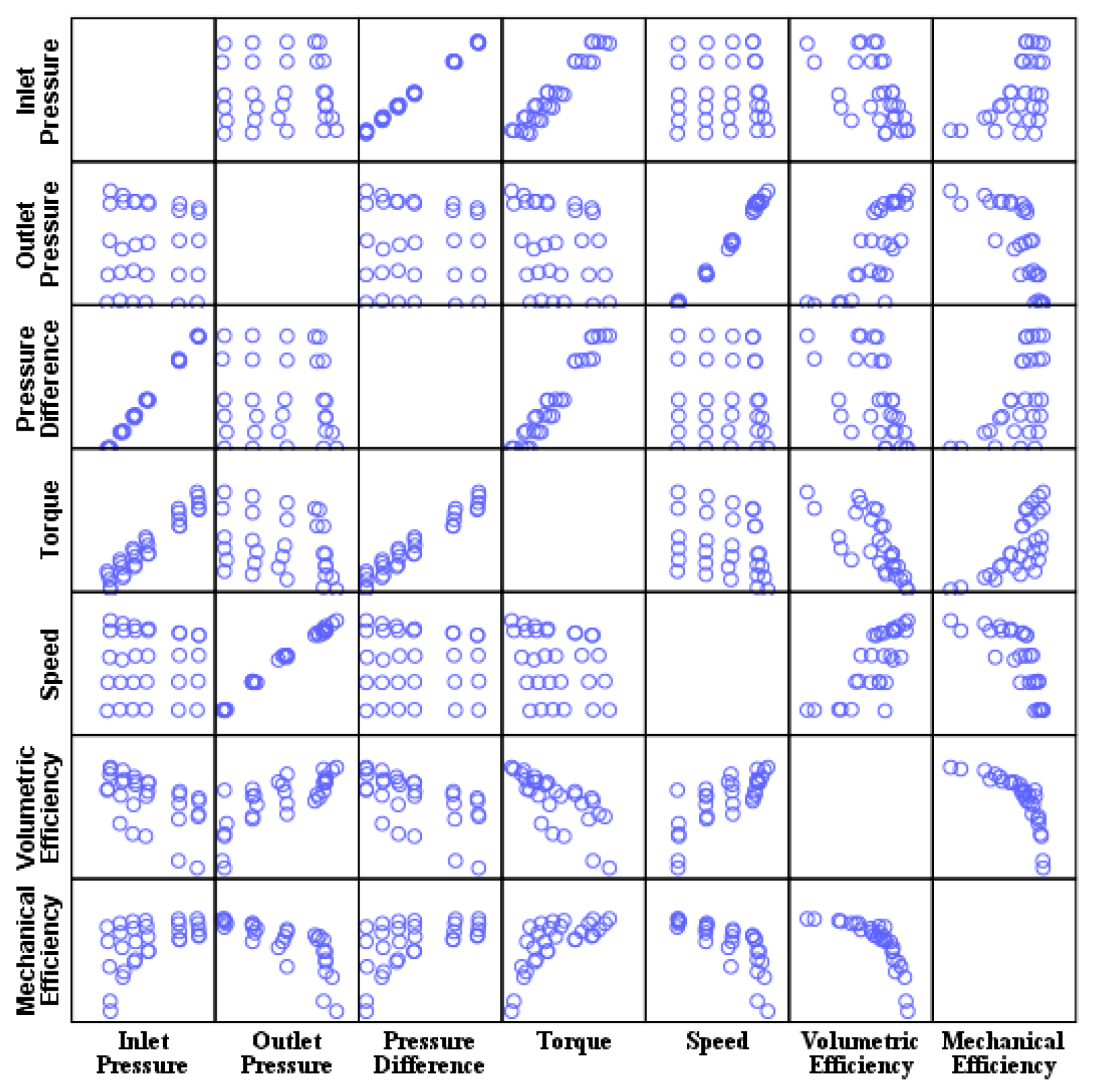
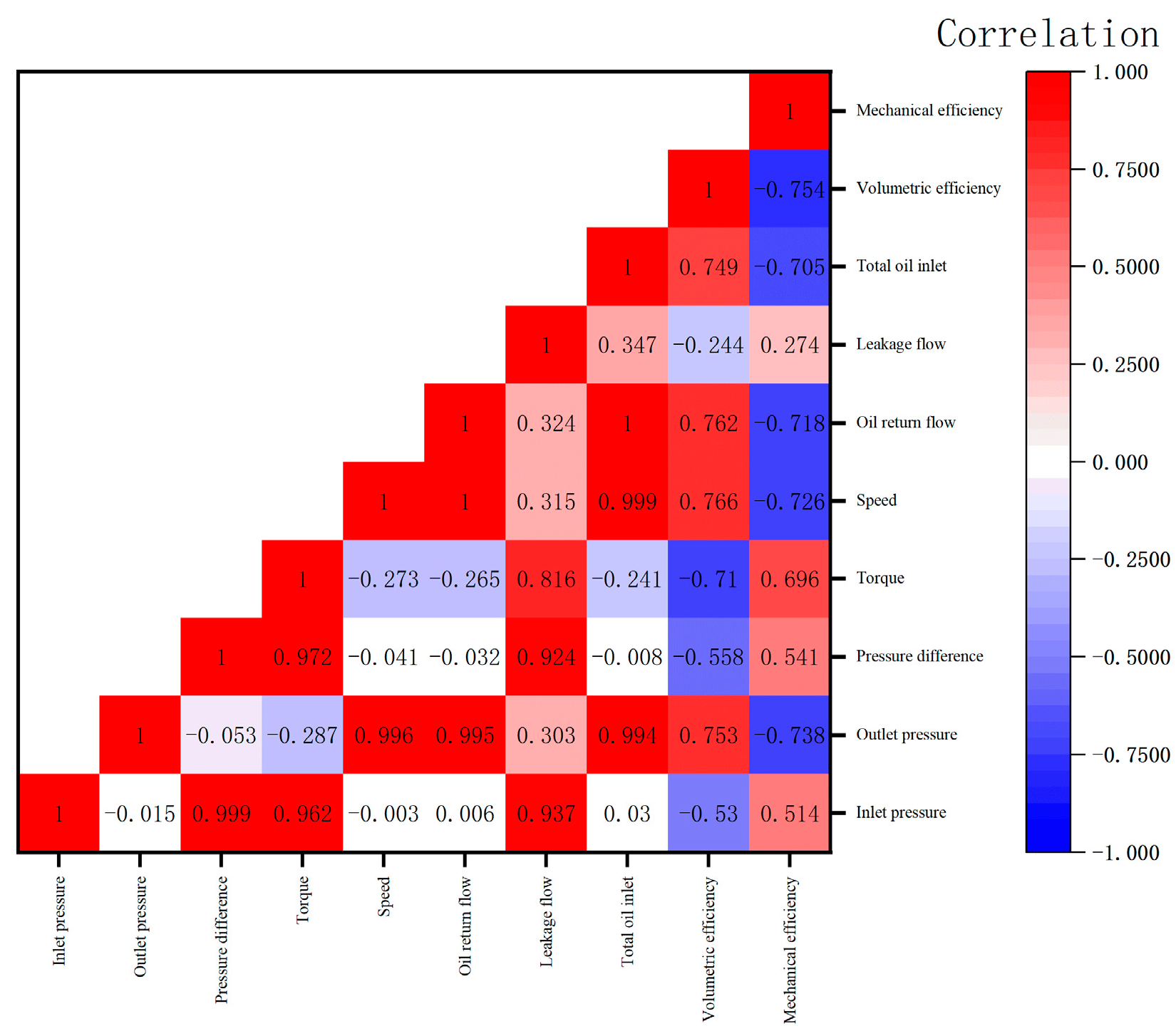
4.1.1. Correlation Analysis
4.1.2. Multiple Linear Regression
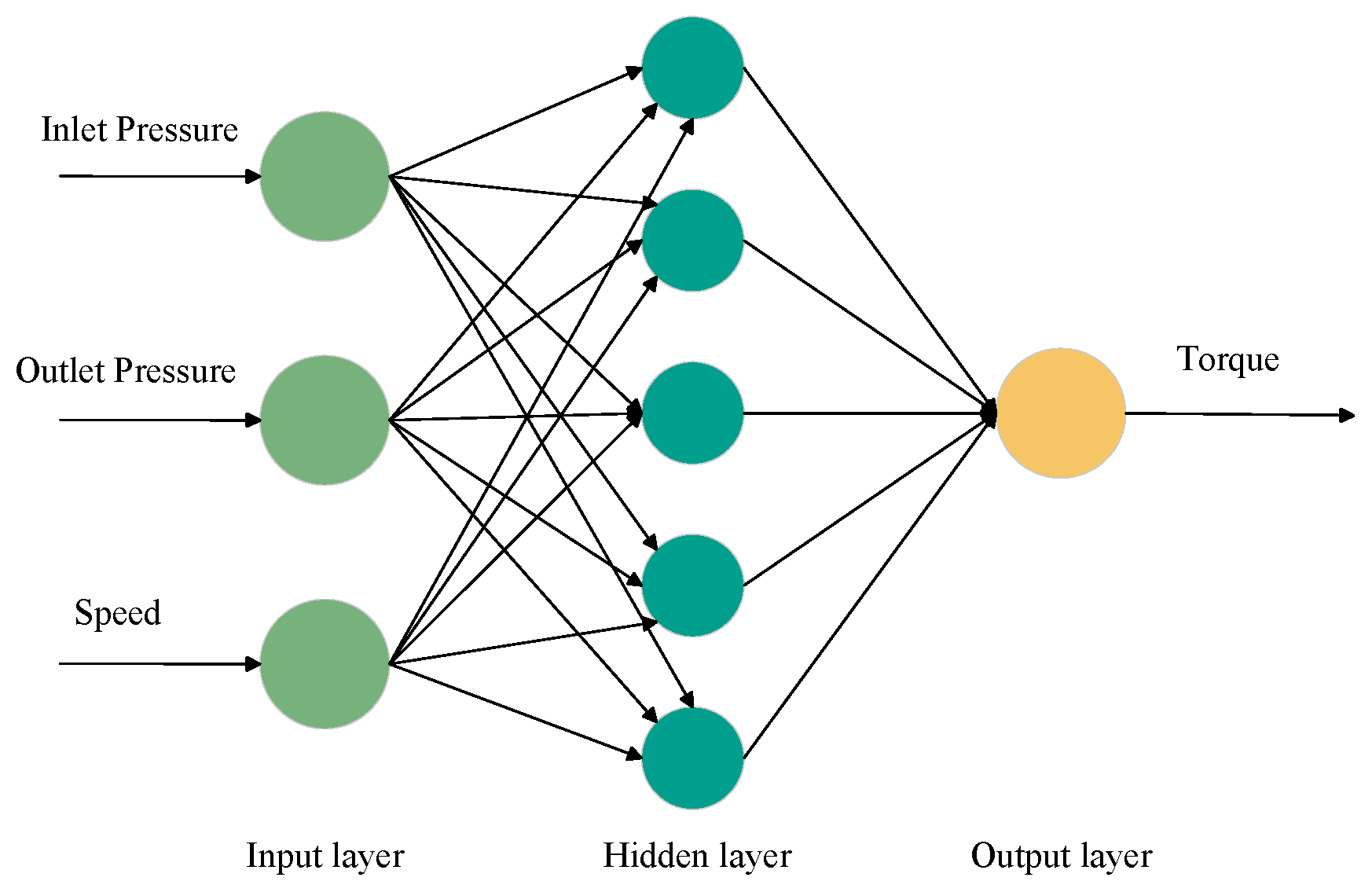
4.2. Multi-Layer Perceptron (MLP)
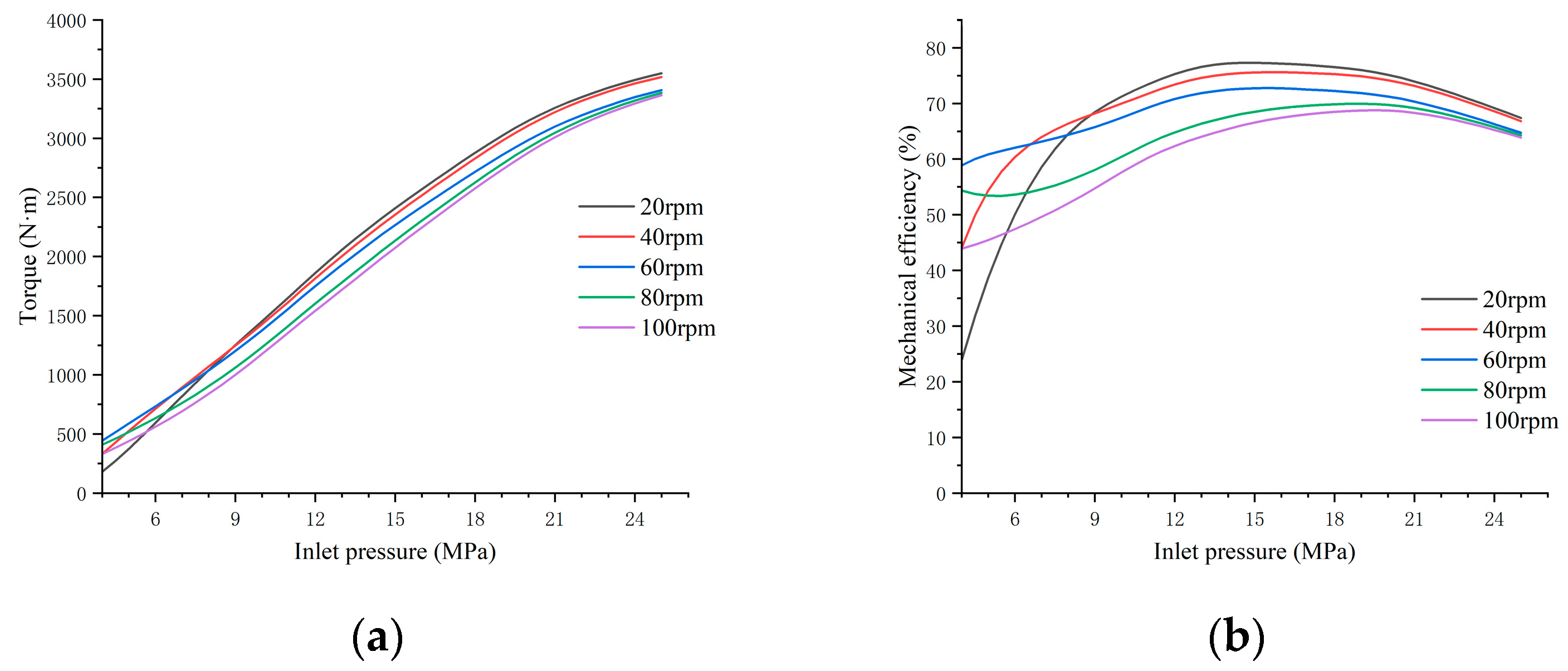
4.3. Prediction of Motor Output Characteristics
5. Dynamic Simulation
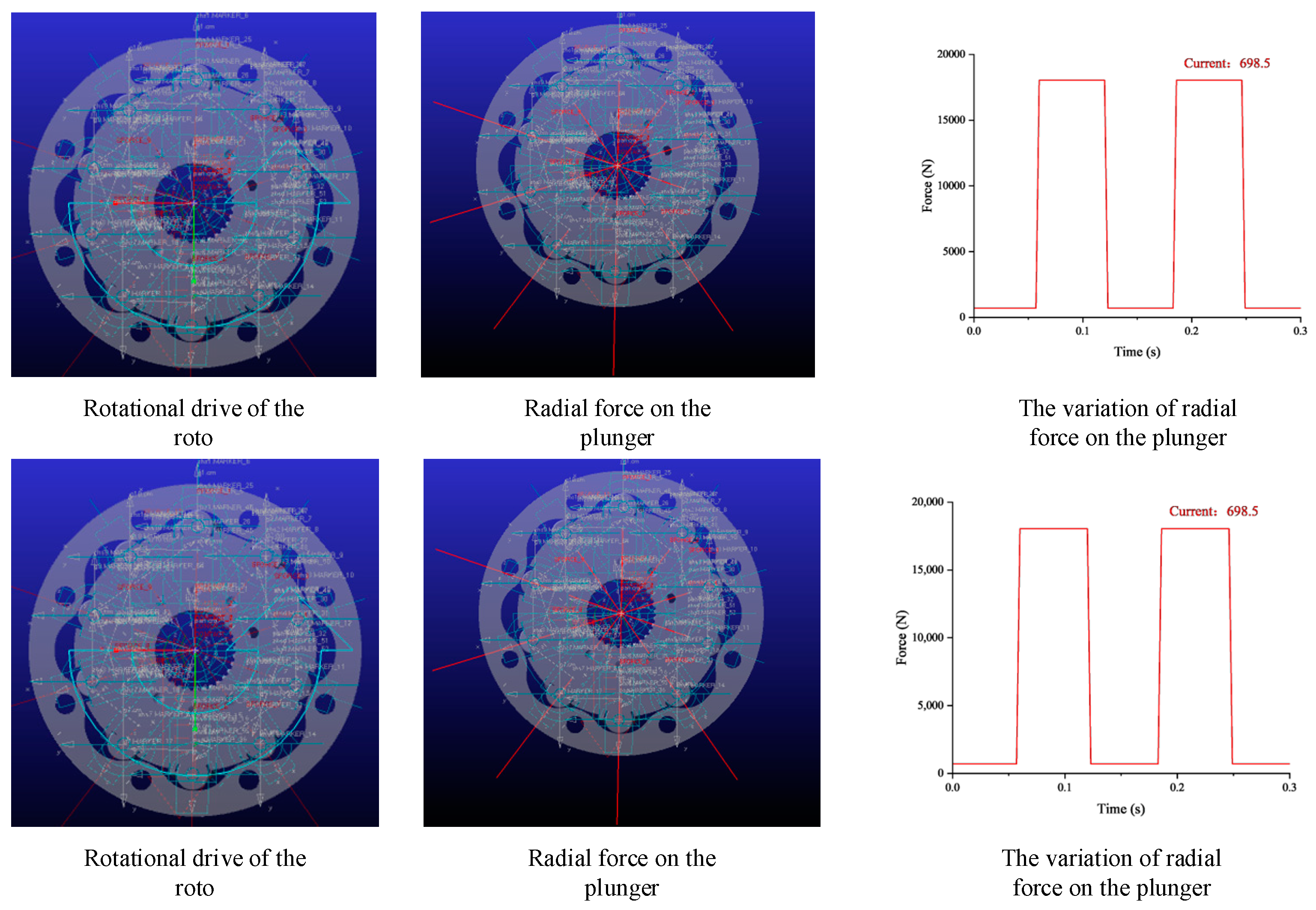
5.1. Simulation Setup
- Importing 3D Models: the model in Adams is shown in Figure 14.
- 2.
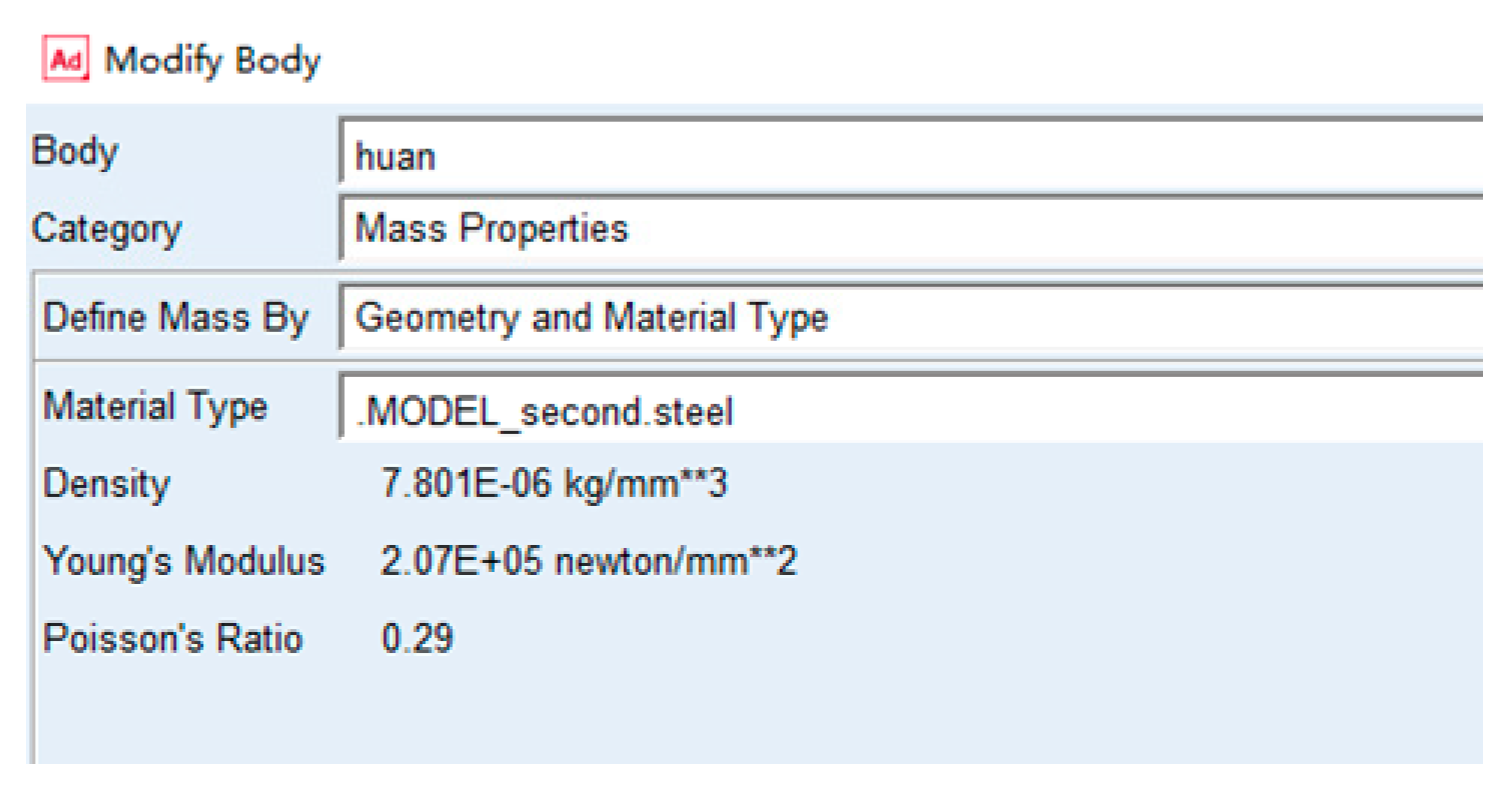
- Define Material Properties: the material setting interface in Adams is shown in Figure 15.
- 3.
- Rename the components to ensure the plunger and roller numbers correspond.
- 4.
- Create Constraint Conditions: the constraints between components are shown in Figure 16.
- 5.
- Set up the drivers and apply forces, the changes in forces and the drive are shown in Figure 17.
- 6.
- Set up the solver.
- 7.
- Run the simulation.
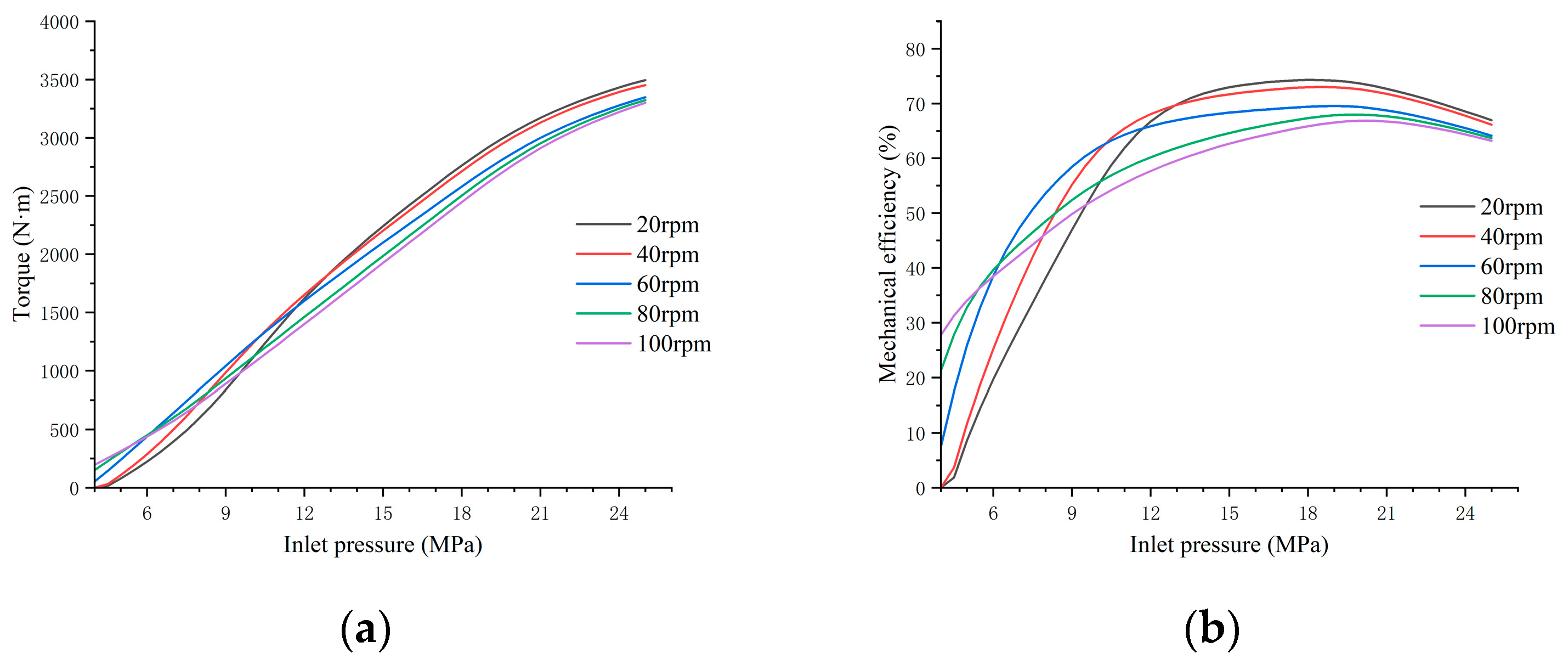
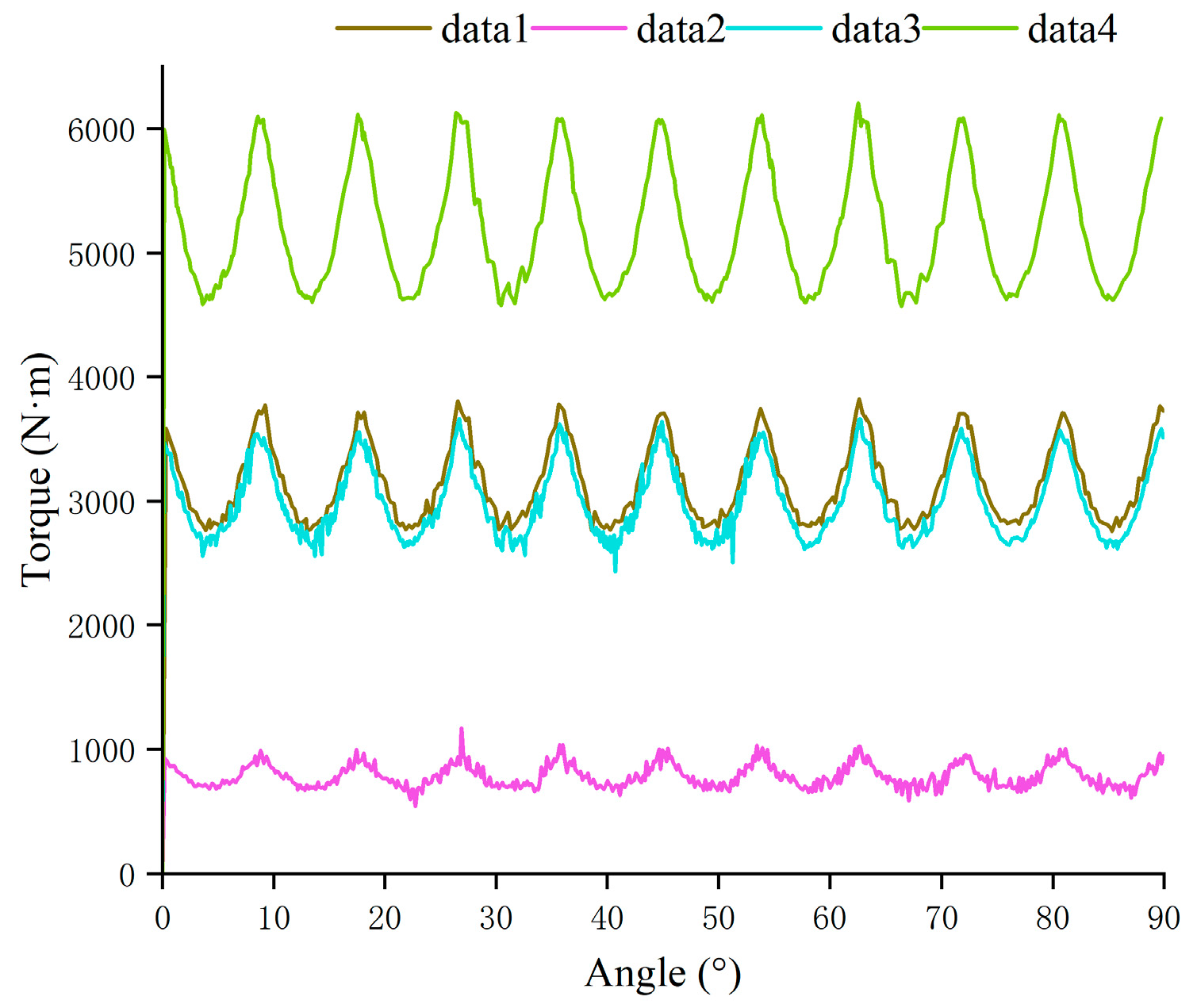
5.2. Results of Dynamic Simulation
6. Conclusions
- The neural network fits the torque information from the experimental data very well, making it suitable for predicting the torque under different operating conditions of the motor.
- The torque results from the physical experiments are consistent with those from the dynamic simulation model, indicating that using a dynamic simulation to obtain the theoretical torque of the radial piston motor is feasible. This method can provide a reference for the actual operation of the motor.
- According to the predictions of the neural network, the motor’s mechanical efficiency is stable under low-speed conditions; however, under high-speed conditions, the inlet pressure needs to be appropriately adjusted to achieve good mechanical efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Strmčnik, E.; Majdič, F.; Kalin, M. Water-lubricated behaviour of AISI 440C stainless steel and a DLC coating for an orbital hydraulic motor application. Tribol. Int. 2019, 131, 128–136. [Google Scholar] [CrossRef]
- Pettersson, U.; Jacobson, S. Textured surfaces for improved lubrication at high pressure and low sliding speed of roller/piston in hydraulic motors. Tribol. Int. 2007, 40, 355–359. [Google Scholar] [CrossRef]
- Zhang, D.; Li, Z.; Wang, L.; Kong, L.; Gao, F.; Wang, Q. Study on tribological properties of boronized and textured composite surface and its application on camshaft connecting-rod type hydraulic motor. Wear 2021, 482, 203964. [Google Scholar] [CrossRef]
- Qiu, B.; Zhao, J.; Man, J. Comparative study of materials for friction pairs in a new high water-based hydraulic motor with low speed and high pressure. Ind. Lubr. Tribol. 2019, 71, 164–172. [Google Scholar] [CrossRef]
- Lyu, F.; Zhang, J.; Zhao, S.; Li, K.; Xu, B.; Huang, W.; Xu, H.; Huang, X. Coupled evolution of piston asperity and cylinder bore contour of piston/cylinder pair in axial piston pump. Chin. J. Aeronaut. 2023, 36, 395–407. [Google Scholar] [CrossRef]
- Ceschini, L.; Marconi, A.; Martini, C.; Morri, A. Tribological behavior of components for radial piston hydraulic motors: Bench tests, failure analysis and laboratory dry sliding tests. Wear 2013, 305, 238–247. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, S.; Gao, D.; Wang, S. Distribution Performance Analysis and Experimental Research on the Port Plate Pairs of Low Speed High Torque Seawater Hydraulic Motor. Chin. J. Mech. Eng. 2019, 32, 108. [Google Scholar] [CrossRef]
- Patrosz, P. Influence of Properties of Hydraulic Fluid on Pressure Peaks in Axial Piston Pumps’ Chambers. Energies 2021, 14, 3764. [Google Scholar] [CrossRef]
- Quan, L.; Gao, H.; Guo, C.; Che, S. Assessment of the Dynamics Flow Field of Port Plate Pair of an Axial Piston Pump. Processes 2020, 8, 86. [Google Scholar] [CrossRef]
- Sliwinski, P.; Patrosz, P. Methods of Determining Pressure Drop in Internal Channels of a Hydraulic Motor. Energies 2021, 14, 5669. [Google Scholar] [CrossRef]
- Manne, V.H.B.; Vacca, A.; Merrill, K. A numerical method for evaluating the torque efficiency of hydraulic orbit motors considering deformation effects and frictional losses. Mech. Syst. Signal Process. 2021, 146, 107051. [Google Scholar] [CrossRef]
- Nie, Y.; Niu, Y.; Xing, K.; Jin, X. Hydraulic motor constant low speed characteristics measurement study. J. Phys. Conf. Ser. 2005, 2005, 012237. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, Y.; Fang, M.; Li, D.; Wu, D. Research on the torque characteristics of a seawater hydraulic axial piston motor in deep-sea environment. Ocean Eng. 2017, 146, 411–423. [Google Scholar] [CrossRef]
- Sliwinski, P. Determination of the Theoretical and Actual Working Volume of a Hydraulic Motor. Energies 2020, 13, 5933. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, Z.; Qian, X.; Wu, X.; Pang, W. Multidisciplinary Design Optimization of a Swash-Plate Axial Piston Pump. Appl. Sci. 2016, 6, 399. [Google Scholar] [CrossRef]
- Li, R.; Liu, J.; Ding, X.; Liu, Q. Study on the Influence of Flow Distribution Structure of Piston Pump on the Output of Pulsation Pump. Processes 2022, 10, 1077. [Google Scholar] [CrossRef]
- Ying, P.; Tang, H.; Chen, L.; Ren, Y.; Kumar, A. Dynamic modeling and vibration characteristics of multibody system in axial piston pump. Alex. Eng. J. 2023, 62, 523–540. [Google Scholar] [CrossRef]
- Li, R.; Liu, Q.; Cheng, Y.; Liu, J.; Sun, Q.; Zhang, Y.; Chi, Y. Analysis of the Influence of Structure and Parameters of Axial Piston Pump on Flow Pulsation. Processes 2022, 10, 2138. [Google Scholar] [CrossRef]
- Suo, X.; Jiang, Y.; Wang, W. Hydraulic axial plunger pump: Gaseous and vaporous cavitation characteristics and optimization method. Eng. Appl. Comput. Fluid Mech. 2021, 15, 712–726. [Google Scholar] [CrossRef]
- Zhang, C.; Tan, H.; Fang, Y.; Zhang, X.; Yang, Y.; Duan, Y.; Han, M.; Cui, S.; Xu, B.; Zhang, J. Deformation pre-compensated optimization design of cam ring for low pulsation hydraulic motors. J. Zhejiang Univ.-SCIENCE A 2023, 24, 130–145. [Google Scholar] [CrossRef]
- Shen, H.; Zhou, Z.; Guan, D.; Liu, Z.; Jing, L.; Zhang, C. Dynamic Contact Analysis of the Piston and Slipper Pair in Axial Piston Pump. Coatings 2020, 10, 1217. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, S.; Ye, S.; Xu, B.; Zhu, S.; Xiang, J.; Tang, H. Sound quality evaluation and prediction for the emitted noise of axial piston pumps. Appl. Acoust. 2019, 145, 27–40. [Google Scholar] [CrossRef]
- Ramchandran, G.; Agarwal, P.; Vacca, A.; Kim, K.S.; Kim, T. Modeling of radial piston machines considering elastohydro dynamic effects in both cam–piston and piston–cylinder lubricating interfaces. Meccanica 2018, 53, 2833–2860. [Google Scholar] [CrossRef]
- Nilsson, D.; Prakash, B. Investigation into the seizure of hydraulic motors. Tribol. Int. 2010, 43, 92–99. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, X.; Wei, G. Cylinder Fatigue Design of Low-Speed, High-Torque Radial Piston Motor. Coatings 2022, 12, 1192. [Google Scholar] [CrossRef]








| Serial Number | Inlet Pressure/MPa | Outlet Pressure/MPa | Pressure Difference/MPa | Speed/rpm | Torque/N·m | Mechanical Efficiency/% | Total Inflow L/min | Return Flow L/min | Volumetric Efficiency/% |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.35 | 0.31 | 4.04 | 19 | 640 | 73.69 | 26.825 | 26.3 | 95.62 |
| 2 | 6.35 | 0.32 | 6.03 | 20 | 991 | 76.45 | 29.355 | 28.8 | 91.98 |
| 3 | 8.35 | 0.31 | 8.04 | 20 | 1348 | 77.99 | 29.715 | 28.5 | 90.86 |
| 4 | 10.35 | 0.31 | 10.04 | 20 | 1697 | 78.63 | 29.8 | 28.3 | 90.60 |
| 5 | 15.4 | 0.3 | 15.1 | 19.5 | 2590 | 79.79 | 29.93 | 27.8 | 87.96 |
| 6 | 18.3 | 0.31 | 17.99 | 19.5 | 3097 | 80.08 | 30.2 | 27.5 | 87.17 |
| 7 | 4.47 | 0.44 | 4.03 | 41 | 542 | 62.56 | 57.82 | 57.1 | 95.73 |
| 8 | 6.45 | 0.45 | 6 | 41 | 895 | 69.39 | 58.24 | 57.1 | 95.04 |
| 9 | 8.47 | 0.46 | 8.01 | 41 | 1249 | 72.54 | 58.85 | 57.2 | 94.05 |
| 10 | 10.47 | 0.44 | 10.03 | 41.5 | 1598 | 74.11 | 59 | 57.2 | 94.96 |
| 11 | 15.45 | 0.44 | 15.01 | 41.5 | 2463 | 76.33 | 60.6 | 58.2 | 92.45 |
| 12 | 18.45 | 0.44 | 18.01 | 42 | 2959 | 76.43 | 61.14 | 58.2 | 92.74 |
| 13 | 4.74 | 0.6 | 4.14 | 60.5 | 383 | 43.04 | 83.9 | 83 | 97.35 |
| 14 | 6.7 | 0.56 | 6.14 | 58.5 | 764 | 57.88 | 81.83 | 80.6 | 96.51 |
| 15 | 8.78 | 0.58 | 8.2 | 61.5 | 1098 | 62.29 | 86.3 | 84.8 | 96.21 |
| 16 | 10.68 | 0.59 | 10.09 | 61.5 | 1437 | 66.25 | 86.95 | 84.85 | 95.49 |
| 17 | 15.53 | 0.6 | 14.93 | 62 | 2249 | 70.07 | 88.9 | 86.2 | 94.15 |
| 18 | 18.54 | 0.6 | 17.94 | 62 | 2769 | 71.80 | 90 | 86.7 | 93.00 |
| 19 | 4.81 | 0.77 | 4.04 | 81 | 141 | 16.24 | 111.7 | 110.5 | 97.90 |
| 20 | 6.97 | 0.78 | 6.19 | 81 | 520 | 39.08 | 113 | 111.5 | 96.77 |
| 21 | 8.75 | 0.78 | 7.97 | 81 | 832 | 48.56 | 113.23 | 111.4 | 96.57 |
| 22 | 10.7 | 0.78 | 9.92 | 81 | 1171 | 54.91 | 113.4 | 111 | 96.43 |
| 23 | 15.6 | 0.77 | 14.83 | 79 | 2037 | 63.90 | 111.7 | 108.7 | 95.48 |
| 24 | 18.55 | 0.75 | 17.8 | 77.5 | 2550 | 66.64 | 110.4 | 107.1 | 94.77 |
| 25 | 4.87 | 0.83 | 4.04 | 89 | 73 | 8.41 | 122.49 | 121.2 | 98.09 |
| 26 | 6.79 | 0.81 | 5.98 | 86.5 | 448 | 34.85 | 119.45 | 118.1 | 97.76 |
| 27 | 8.58 | 0.78 | 7.8 | 84.5 | 783 | 46.70 | 117.53 | 115.7 | 97.06 |
| 28 | 10.8 | 0.77 | 10.03 | 82.5 | 1189 | 55.15 | 115.5 | 113.1 | 96.43 |
| 29 | 15.51 | 0.74 | 14.77 | 79.5 | 2045 | 64.41 | 112.8 | 109.8 | 95.15 |
| 30 | 18.58 | 0.73 | 17.85 | 77.5 | 2588 | 67.45 | 110.8 | 107.2 | 94.43 |
| R | R2 | Adjust R2 | Standard Estimate of Error | Durbin–Watson |
|---|---|---|---|---|
| 0.898 | 0.807 | 0.785 | 8.43592 | 1.778 |
| Model Parameters | Unstandardized Coefficients | Standardized Coefficients | t | Significance | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| B | Standard Error | Beta | Tolerance | VIF | |||
| Constant | 82.052 | 7.782 | 10.544 | 0.000 | |||
| Pressure Difference | −1.602 | 2.043 | −0.436 | −0.784 | 0.440 | 0.024 | 41.549 |
| Leakage Flow | 21.431 | 12.323 | 1.021 | 1.739 | 0.094 | 0.022 | 46.371 |
| Return Flow Rate | −0.581 | 0.123 | −1.062 | −4.729 | 0.000 | 0.147 | 6.798 |
| Inlet Pressure/MPa | Outlet Pressure/MPa | Speed/rpm | Torque/N·m | Mechanical Efficiency/% | |
|---|---|---|---|---|---|
| 1 | 25 | 0.3 | 20 | 3593.5 | 67.71 |
| 2 | 4 | 0.3 | 40 | 638.7 | 80.34 |
| Data | Inlet Pressure /MPa | Outlet Pressure /MPa | Speed /rpm | Output Torque /N·m | Mechanical Efficiency/% | Theoretical Torque/N·m |
|---|---|---|---|---|---|---|
| Data 1 | 15.53 | 0.6 | 62 | 2249.0 | 70.07 | 3209.6 |
| Data 2 | 4 | 0.3 | 40 | 638.7 | 80.34 | 795.0 |
| Data 3 | 14.5 | 0.3 | 20 | 2441 | 80.02 | 3050.5 |
| Data 4 | 25 | 0.3 | 20 | 3593.5 | 67.71 | 5307.2 |
| Maximum Torque /N·m | Minimum Torque /N·m | Average Torque /N·m | |
|---|---|---|---|
| Data 1 | 3819.0 | 2759.4 | 3148.5 |
| Data 2 | 1171.4 | 540.4 | 785.4 |
| Data 3 | 3664.4 | 2434.0 | 3001.2 |
| Data 4 | 6207.3 | 4568.9 | 5224.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Xia, Z.; Tang, Y. Prediction and Dynamic Simulation Verification of Output Characteristics of Radial Piston Motors Based on Neural Networks. Machines 2024, 12, 491. https://doi.org/10.3390/machines12070491
Li C, Xia Z, Tang Y. Prediction and Dynamic Simulation Verification of Output Characteristics of Radial Piston Motors Based on Neural Networks. Machines. 2024; 12(7):491. https://doi.org/10.3390/machines12070491
Chicago/Turabian StyleLi, Chunjin, Zhengwen Xia, and Yongjie Tang. 2024. "Prediction and Dynamic Simulation Verification of Output Characteristics of Radial Piston Motors Based on Neural Networks" Machines 12, no. 7: 491. https://doi.org/10.3390/machines12070491
APA StyleLi, C., Xia, Z., & Tang, Y. (2024). Prediction and Dynamic Simulation Verification of Output Characteristics of Radial Piston Motors Based on Neural Networks. Machines, 12(7), 491. https://doi.org/10.3390/machines12070491





