Theoretical and Experimental Investigation of a Novel Wedge-Loading Planetary Traction Drive
Abstract
:1. Introduction
- The advantages of T-FRTs can be enhanced with a large speed ratio, zero spin, and a self-adaptive loading design. However, integrating these aspects into the overall design remains challenging, resulting in a few T-FRTs progressing in the prototype stage and hindering the research and development of T-FRTs;
- The development of theoretical analysis models for T-FRTs has been hindered by slow progress. Researchers usually simplify calculations by making various assumptions, such as setting the traction coefficient within T-FRTs to a constant value, which neglects the basic elastohydrodynamic lubrication (EHL) traction mechanism, or considering only isothermal EHL contact on the smooth surface, which has only a narrow range of applications. Research on the comprehensive impact of elastic deformation, loading state, surface morphology, thermal effect, and starved lubrication on the traction drive in actual working conditions is still in the early stages;
- The unique operating principles of traction drives introduce some of the most challenging kinematical and tribological problems for performance prediction [19]. The complex non-linear coupling relationship between macroscopic performance indicators and microscopic contact behavior challenges mathematical modeling and computation, and an effective solution method has not yet been developed.
- In terms of structural design, this paper proposes a new type of wedge-loading planetary traction drive (WPTD) that can achieve zero spin, large speed ratio, and self-adaptive loading;
- In terms of theoretical modeling, this paper introduces the mixed thermal EHL model into the performance analysis of traction drive for the first time. In addition, a more refined theoretical analysis model is established according to the structural characteristics of WPTD and the new loading principle. On this basis, the loading performance, transmission characteristics, and the influence of different parameters on the transmission characteristics of WPTD are analyzed;
- Regarding the solution method, regression analyses based on the results from an extensive set of simulations are performed according to the general operating conditions of the traction drive. On this basis, the fitting formulas for predicting traction contact behavior are derived, considering both hydrodynamic and surface asperity effects, and an efficient and accurate performance analysis method for all line-contact traction drives is presented. These methods significantly facilitate the design and research of subsequent traction drives.
2. Model of Traction Drive
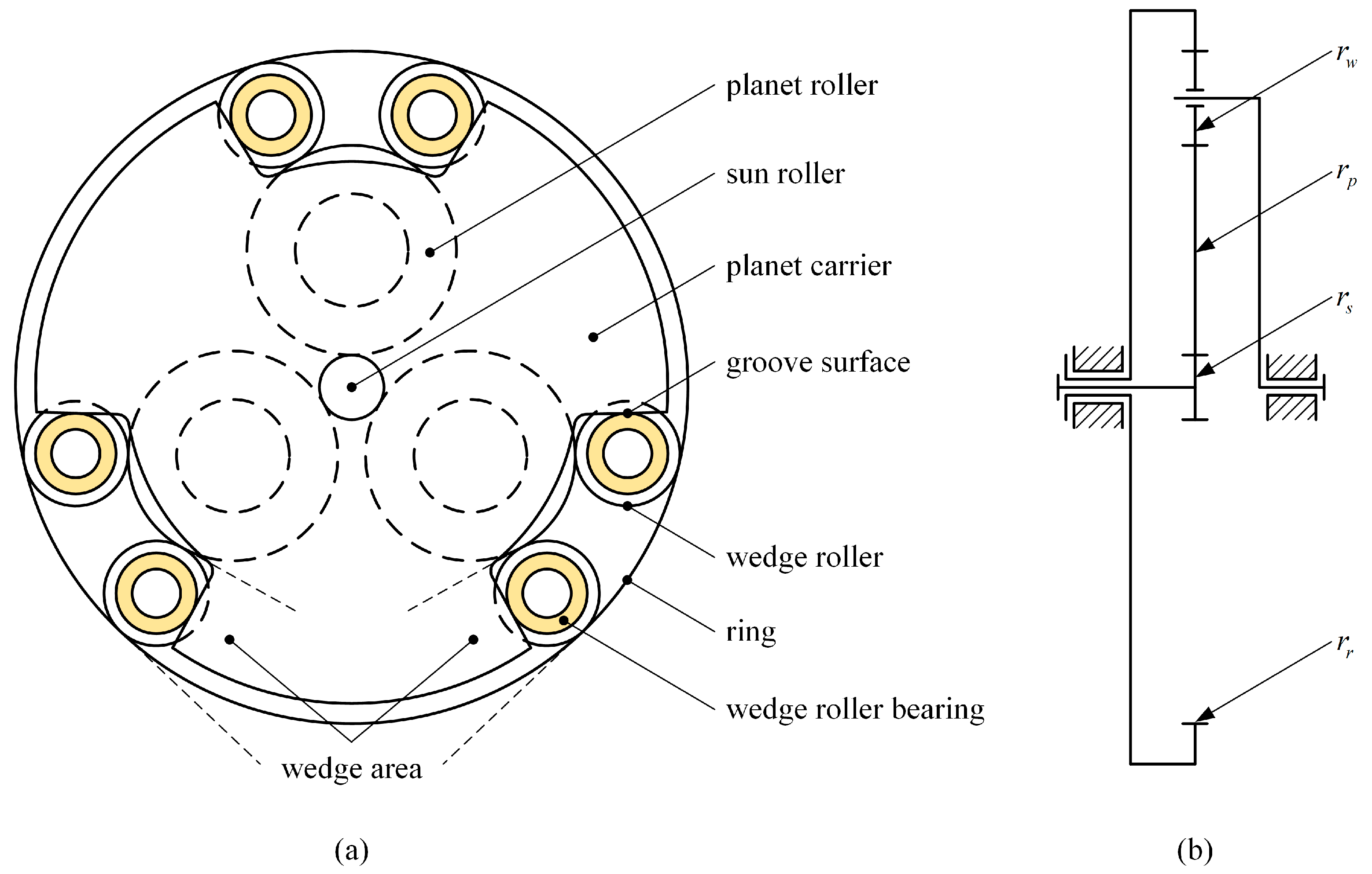
2.1. Structure and Principle
- The line contact and zero-spin design based on cylindrical rollers minimizes power loss and improves transmission efficiency and loading capacity;
- The problem of unidirectional rotation when loading with the wedge action is solved by a symmetrical arrangement of the wedge rollers. The coaxial layout of the ring and sun roller is realized, and the design range of speed ratio is expanded;
- The load acts directly on the wedge roller through the groove surface of the planet carrier, facilitating a more rapid wedging process and enhancing the dynamic response of the system through the superposition of the traction force and the contact force;
- The floating arrangement of the planet roller requires no additional support for the planet carrier, allowing greater flexibility in designing the planet carrier. Different groove surface designs are available to meet different loading characteristics and performance requirements.
| T-FRTs | Large Speed Ratio (≥15) | Zero Spin | Self-Adaptive Loading | Bidirectional Rotation | EHL Traction Mechanism |
|---|---|---|---|---|---|
| Kim et al. [9] | ✕ | ✓ | ✕ | ✓ | ✕ |
| Ai [11,12] | ✕ | ✓ | ✓ | ✓ | ✕ |
| Ai et al. [13] | ✕ | ✓ | ✓ | ✕ | ✕ |
| Yamanaka et al. [14] | ✕ | ✓ | ✓ | ✕ | ✕ |
| Flugrad et al. [15] | ✕ | ✓ | ✓ | ✕ | ✕ |
| Wang et al. [16] | ✓ | ✓ | ✓ | ✓ | ✕ |
| Jiang et al. [17,18] | ✓ | ✕ | ✓ | ✓ | ✓ |
| WPTD | ✓ | ✓ | ✓ | ✓ | ✓ |
2.2. Kinematic Analysis
2.2.1. Deformation and Displacement
2.2.2. Kinematic Quantities
2.3. Quasi-Static Response
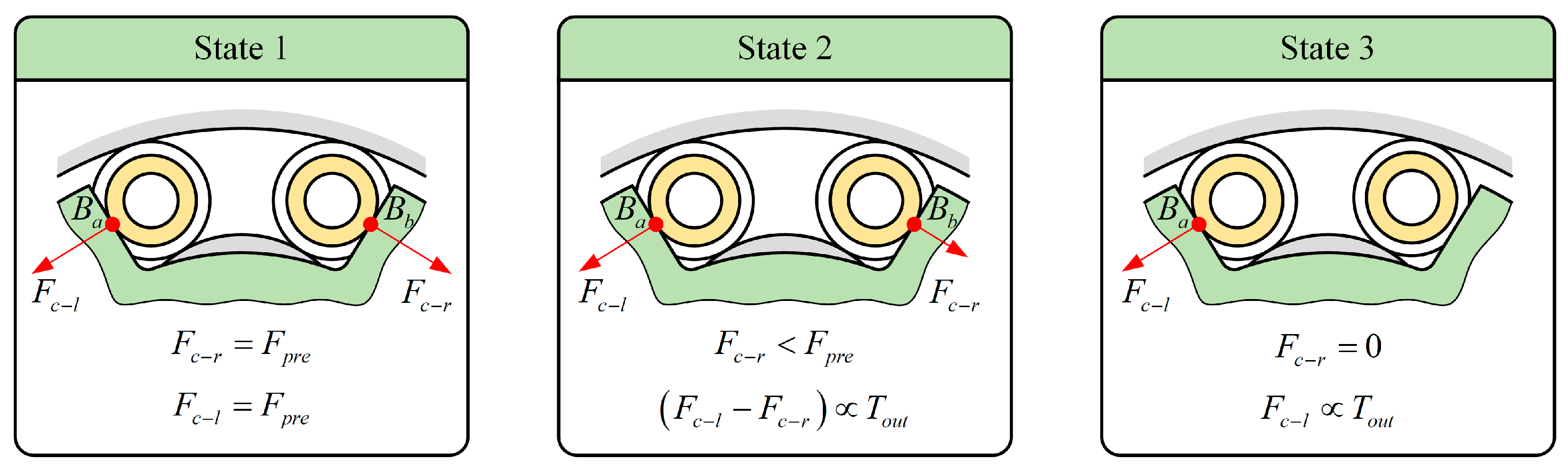
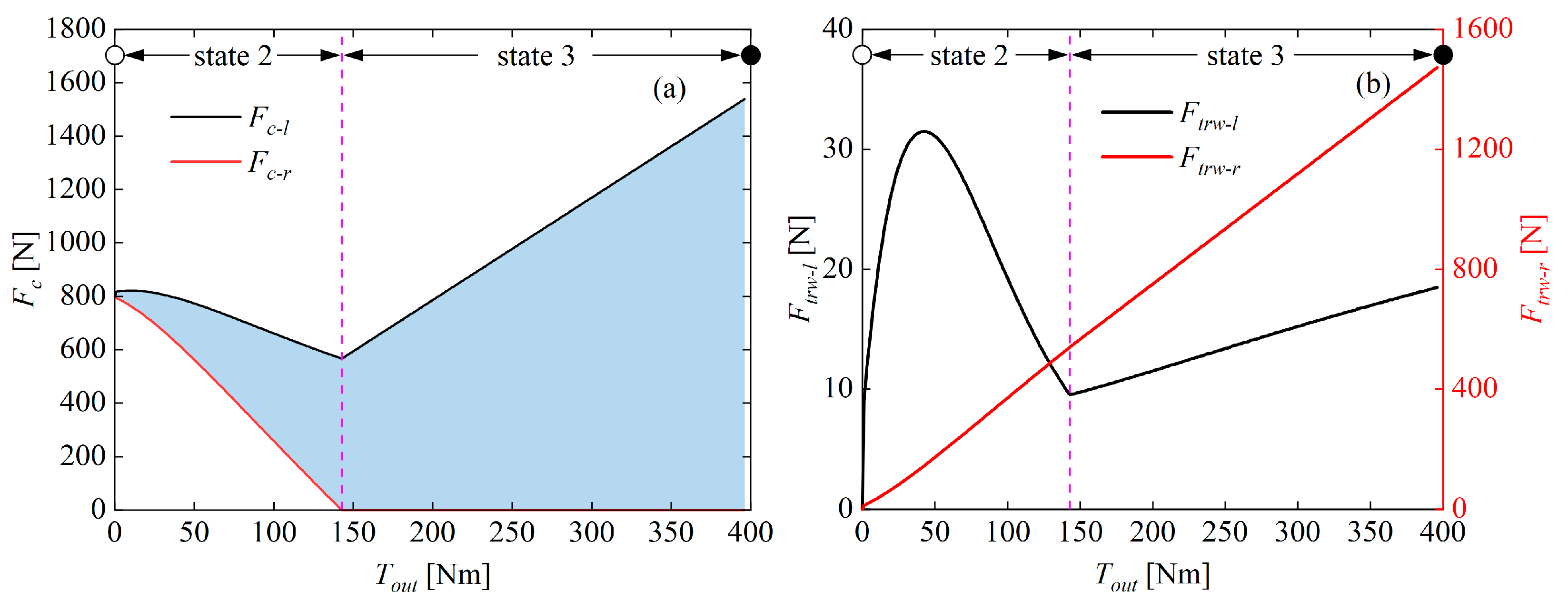
2.3.1. Loading State Analysis
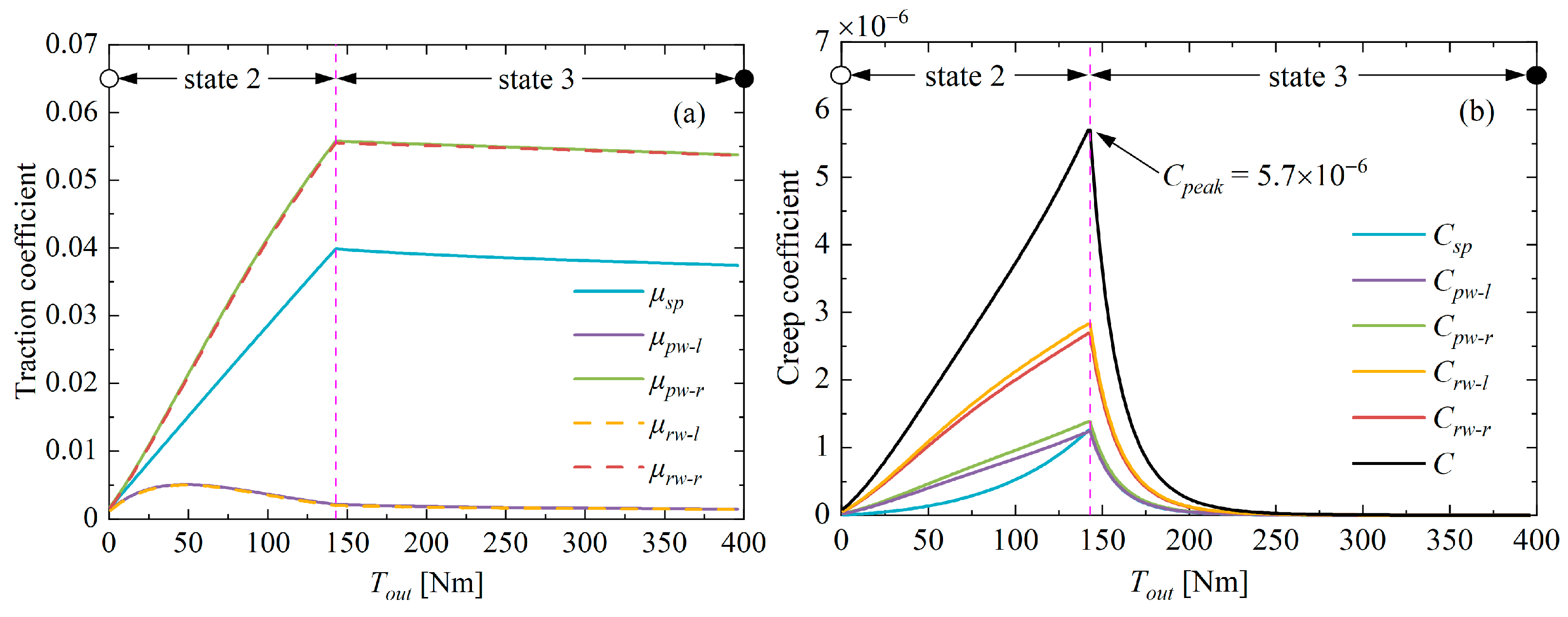
- In state 1, the centers Bl and Br of the wedge rollers without load remain in their initial positions, and the contact forces Fc-l and Fc-r are equal to the initial preload force Fpre at the contact points Ba and Bb, respectively (see Figure 4);
- In state 2, as the load gradually increases, the right wedge roller undergoes a slight displacement towards the converging end of the wedge area (in the direction away from the planet carrier groove), resulting in a gradual decrease in the contact force Fc-r. The left wedge roller precisely adjusts its position under the joint constraint of the planet roller, ring, and planet carrier to rebalance the system. Consequently, the combined contact forces on both sides of the groove surface provide the output torque Tout;
- In state 3, the load continues to increase until the point Bb loses contact, Fc-r = 0. The planet roller and wedge roller move together, consistently co-ordinating elastic deformation caused by the load. At this stage, the contact force Fc-l on the groove surface increases with the tangential load and provides the output torque Tout to the WPTD.
2.3.2. Equilibrium Equations
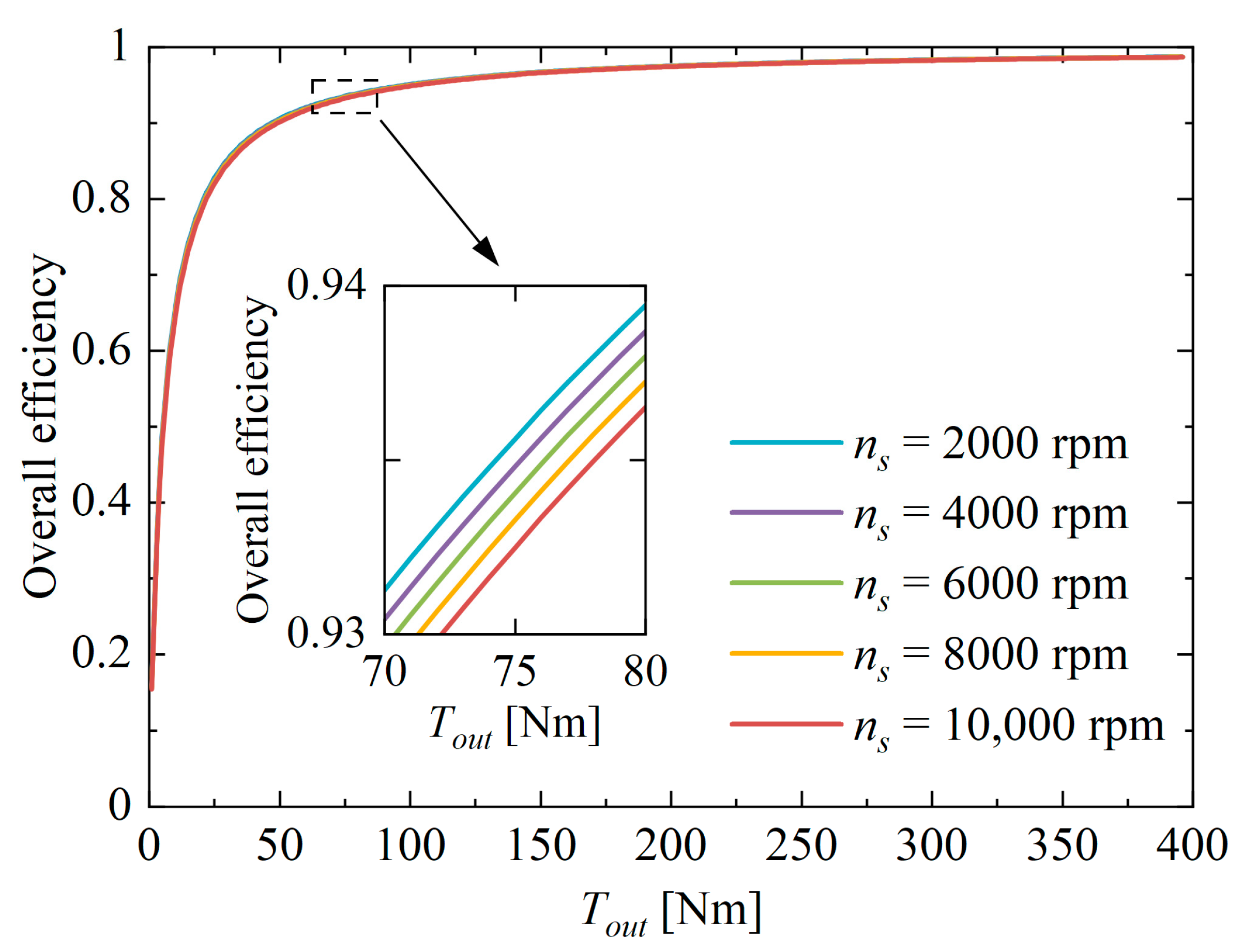
2.4. Efficiency
3. Contact Model
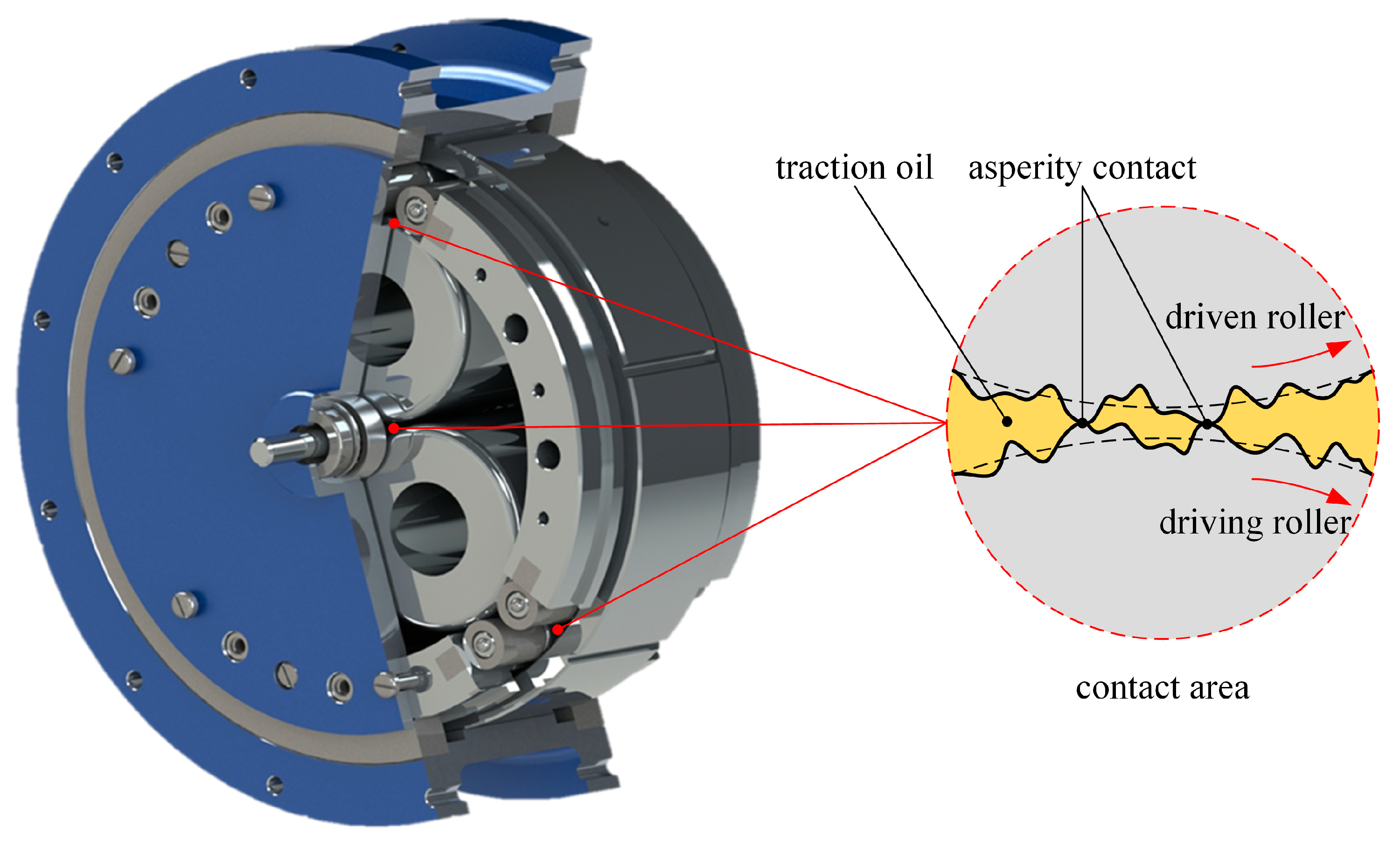
3.1. Mixed Thermal EHL
3.1.1. EHL Equations
3.1.2. Rough Surface Contact Model
3.1.3. Thermal Analysis
3.2. Traction Coefficient
3.3. Numerical Simulation and Formula Fitting
- The traction contact area is usually under high contact stresses and high shear rates which could lead to poor convergence in the numerical calculation;
- The typically large viscosity–pressure coefficient of the traction oil allows it to form a high-viscosity oil film under heavy loads but also causes the lubricant viscosity to be extremely sensitive to pressure variations, which is detrimental to the stability of numerical iterations;
- The mutual coupling of factors such as surface roughness, thermal effect, starvation, and extreme working conditions is another source of instability and significantly increases the difficulty of numerical calculations.
4. Results and Discussions
4.1. Performance Analysis
4.2. Parameter Effects
5. Experimental Verification
5.1. Test Rig Assembly
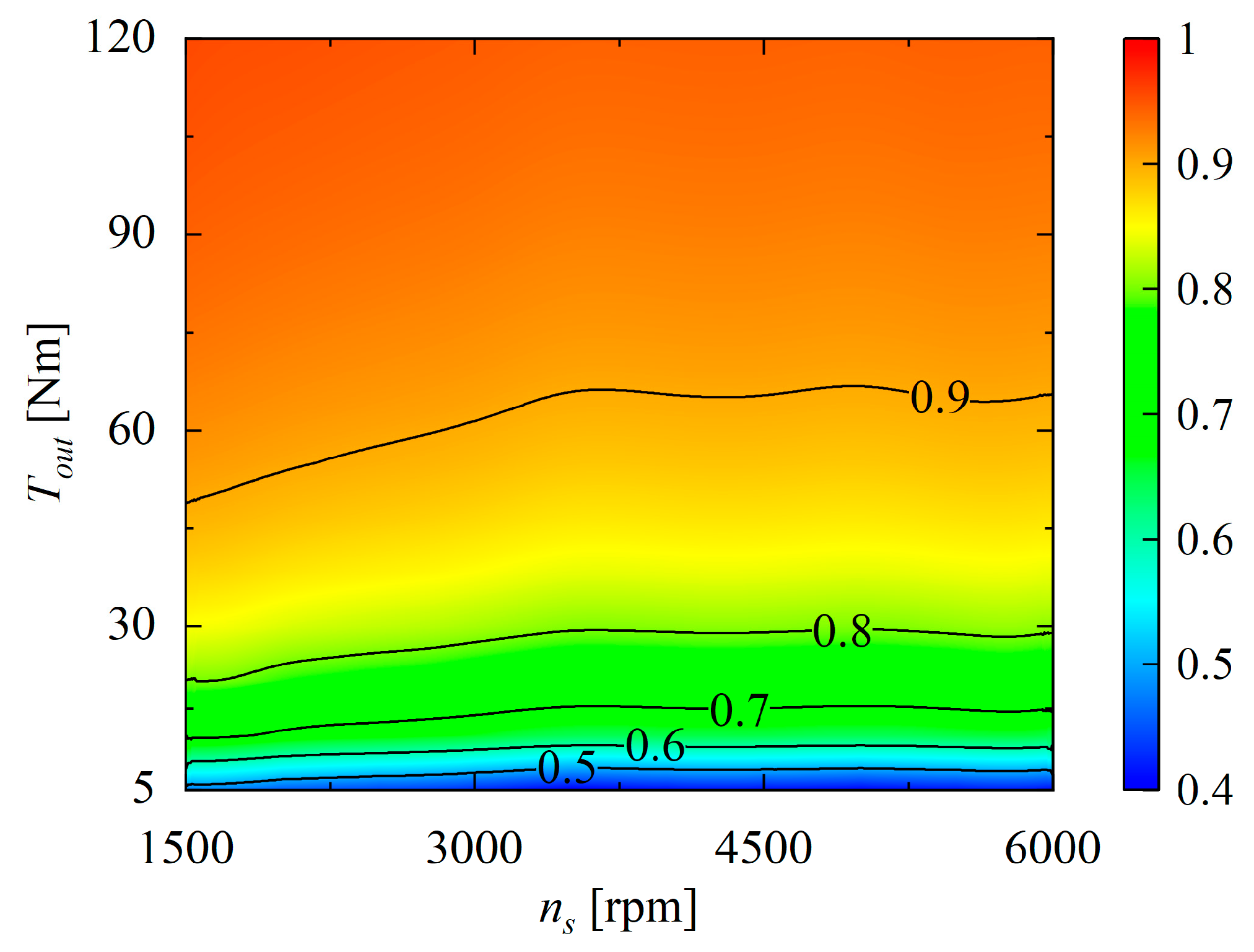
5.2. Efficiency Test
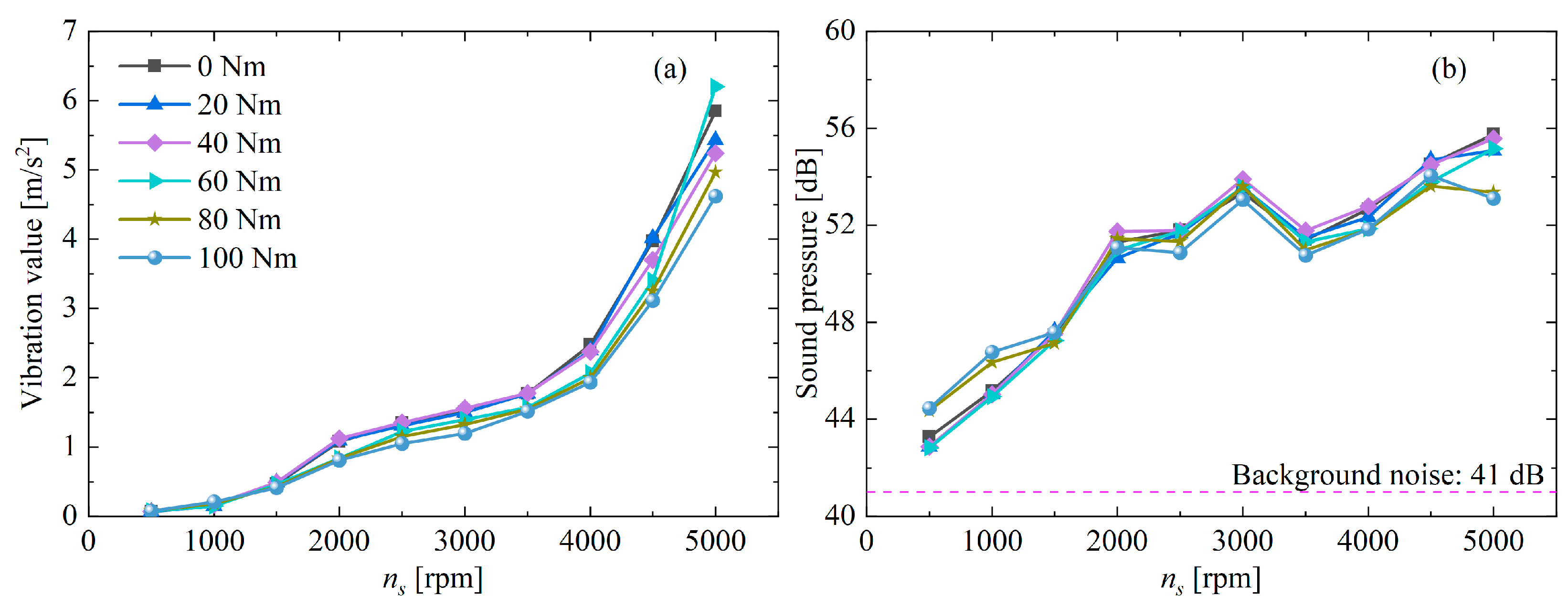
5.3. Vibration and Noise Tests
6. Conclusions
- According to the general traction drive operating conditions, the mixed thermal EHL model was adopted for the first time to analyze traction performance, and regression analyses were performed based on the results of extensive simulations. Then, the fitting formulas were derived to predict the film thickness, asperity load ratio, and traction coefficient with provision for both hydrodynamic and surface asperity effects. The results demonstrate the high prediction accuracy of the fitting formulas;
- A theoretical analysis model considering the combined effects of elastic deformation, loading state, and mixed thermal EHL was established, based on the structural characteristics of WPTD and the new loading principle, and an efficient and accurate performance-prediction method was proposed for traction drives. The theoretical analysis model can simulate the traction capacity and transmission efficiency through numerical calculation;
- The loading effect was investigated in terms of the traction coefficient, creep coefficient, and efficiency. The results showed that the proposed loading mechanism could achieve self-adaptive loading while maintaining a stable traction coefficient and avoiding slippage, reflecting its good loading effect and improved torque capacity and efficiency;
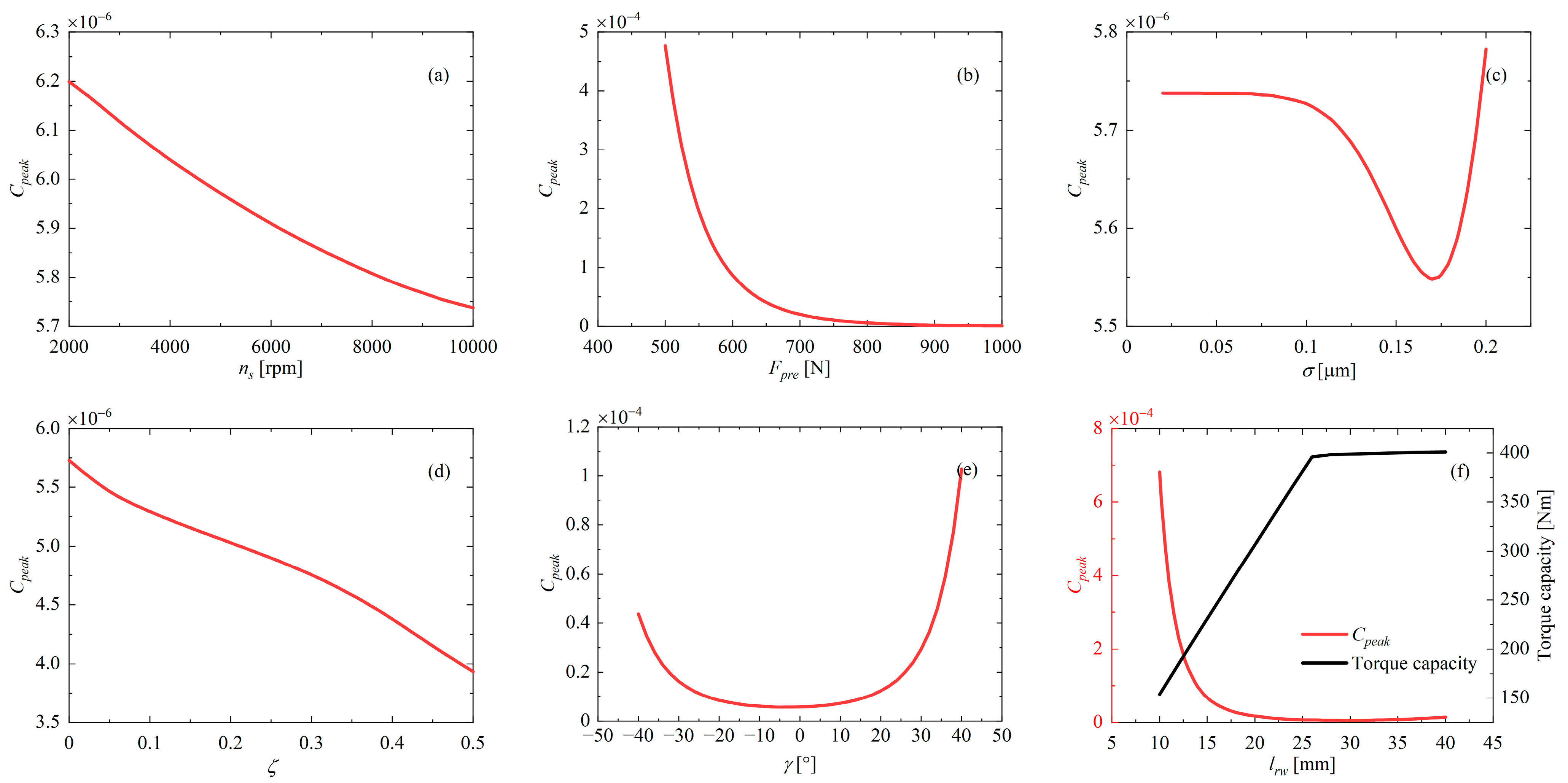
- The reasonable parameter design can improve the performance of WPTD and reduce sliding. It was confirmed that the preload force Fpre, characteristic angle γ, and contact length lrw exhibit the most significant effects on the global sliding coefficient. Therefore, these parameters deserve special attention during design to avoid transmission failure due to excessive slippage. Meanwhile, the creep coefficient variation is closely related to the loading state. These findings provide new ideas for the future design and optimization of traction drives;
- Through performance tests on the WPTD prototype, the simulation results are in reasonably good agreement with the experimental data, with the maximum efficiency error less than 9%, validating the theoretical model. The speed is found to have little effect on efficiency, while its increments can significantly increase the power density of WPTD. In addition, the test results confirm the smooth power-transfer characteristics of WPTD, with its vibration levels reduced by more than 40% compared to gear transmission. Benefiting from the zero-spin design and good loading effect, WPTD achieves a peak efficiency of 96%, and delivers superior performance in terms of high-speed potential, transmission efficiency, and vibration noise.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Definition | Unit |
| Specific heat capacity of lubricant | J/(kg·K) | |
| Global sliding coefficient | - | |
| The peak of the global sliding coefficient | - | |
| Creep coefficient in the contact area between part j and part k | - | |
| Density–temperature coefficient | K−1 | |
| Effective elasticity modulus | Pa | |
| Asperity friction coefficient | - | |
| Contact force on planet carrier groove surface | N | |
| Initial preload force | N | |
| Normal force and traction force between part j and part k | N | |
| Asperity friction force and hydrodynamic traction force | N | |
| Film thickness | m | |
| Central film thickness and minimum film thickness | m | |
| Vickers hardness | Pa | |
| Average gap between two surfaces | m | |
| Thermal conductivity of lubricant | W/(m·K) | |
| Contact length between part j and part k | m | |
| Asperity load ratio | - | |
| Limiting shear stress coefficient | - | |
| Mass of the part j | kg | |
| Input speed of sun roller | r/min | |
| Number of planet rollers | - | |
| Total pressure, asperity pressure and hydrodynamic pressure in the contact area | Pa | |
| Input power and output power | W | |
| Overall power loss | W | |
| Mass flow rate | kg/s | |
| Radius of part j | m | |
| Equivalence contact radius | m | |
| Slide-to-roll ratio | - | |
| Ideal speed ratio and actual speed ratio when the planet carrier outputs the power | - | |
| Film temperature and ambient temperature | K | |
| Bearing frictional moment | N·m | |
| Output torque | N·m | |
| Flow velocity along x and z axes | m/s | |
| Loading force per contact length | N/m | |
| Inlet and outlet position of the lubricant | m | |
| Viscosity–pressure index | - | |
| Viscosity–pressure coefficient | - | |
| , , , | The defined characteristic angles (Figure 2) | ° |
| Angular velocity of part j | rad/s | |
| Standard deviation of the surface heights | m | |
| Elastic deformation between part j and part k | m | |
| Pressure flow factor in x direction | - | |
| Limiting shear stress at atmospheric pressure | Pa | |
| Starvation degree | - | |
| Traction coefficient | - | |
| Lubricant density | kg/m3 | |
| Lubricant viscosity | pa·s | |
| Overall efficiency | - |
Appendix A
| Input | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Er (%) | Er (%) | Sim (Fit) % | Er (%) | Sim (Fit) | Er | ||||||||
| 0 | 6.1935 (6.4123) | 3.53 | 6.8173 (6.6825) | 1.98 | 54.93 (54.11) | 0.82 | 0.0666 (0.0649) | 0.0017 | |||||
| 0 | 6.1941 (6.3398) | 2.35 | 6.8182 (6.7356) | 1.21 | 54.92 (54.11) | 0.81 | 0.0665 (0.0649) | 0.0016 | |||||
| 0 | 6.1833 (6.0969) | 1.40 | 6.8090 (6.8458) | 0.54 | 55.04 (54.11) | 0.93 | 0.0672 (0.0659) | 0.0013 | |||||
| 0 | 5.1340 (5.1870) | 1.03 | 5.2761 (5.2458) | 0.57 | 26.39 (26.40) | 0.01 | 0.0319 (0.0326) | 0.0007 | |||||
| 0 | 5.1346 (5.1251) | 0.19 | 5.2765 (5.2912) | 0.28 | 26.39 (26.40) | 0.01 | 0.0701 (0.0668) | 0.0033 | |||||
| 0 | 4.9468 (4.9179) | 0.58 | 5.4409 (5.3855) | 1.02 | 26.01 (26.40) | 0.39 | 0.1016 (0.0994) | 0.0022 | |||||
| 0 | 7.1738 (7.2189) | 0.63 | 7.4272 (7.4154) | 0.16 | 9.30 (8.80) | 0.50 | 0.0843 (0.0892) | 0.0049 | |||||
| 0 | 7.1062 (7.1195) | 0.19 | 7.5906 (7.4880) | 1.35 | 9.10 (8.80) | 0.30 | 0.0963 (0.0947) | 0.0016 | |||||
| 0 | 6.6007 (6.7864) | 2.81 | 7.8411 (7.6388) | 2.58 | 8.28 (8.80) | 0.52 | 0.0991 (0.0949) | 0.0042 | |||||
| 0 | 2.2140 (2.2431) | 1.31 | 2.2771 (2.3117) | 1.52 | 18.86 (17.85) | 1.01 | 0.0262 (0.0341) | 0.0079 | |||||
| 0 | 2.2138 (2.2147) | 0.04 | 2.2777 (2.3327) | 2.41 | 18.86 (17.85) | 1.01 | 0.0856 (0.0937) | 0.0081 | |||||
| 0 | 2.0087 (2.1197) | 5.53 | 2.3666 (2.3763) | 0.41 | 18.46 (17.85) | 0.61 | 0.1001 (0.0973) | 0.0028 | |||||
| 0 | 7.2679 (7.4256) | 2.17 | 7.6284 (7.7036) | 0.99 | 8.49 (7.66) | 0.83 | 0.0375 (0.0402) | 0.0027 | |||||
| 0 | 7.2648 (7.3203) | 0.76 | 7.6493 (7.7803) | 1.71 | 8.47 (7.66) | 0.81 | 0.0880 (0.0921) | 0.0041 | |||||
| 0 | 6.8085 (6.9678) | 2.34 | 8.0417 (7.9397) | 1.27 | 7.89 (7.67) | 0.22 | 0.0983 (0.0945) | 0.0038 | |||||
| 0 | 4.4051 (4.3360) | 1.57 | 4.9242 (4.8938) | 0.62 | 0.00 (0.00) | 0.00 | 0.0733 (0.0803) | 0.0070 | |||||
| 0 | 4.3664 (4.2613) | 2.41 | 4.9848 (4.9486) | 0.73 | 0.00 (0.00) | 0.00 | 0.0927 (0.0921) | 0.0006 | |||||
| 0 | 3.8718 (4.0109) | 3.59 | 5.2739 (5.0622) | 4.01 | 0.00 (0.07) | 0.07 | 0.0974 (0.0925) | 0.0049 | |||||
| 0 | 5.1583 (5.1962) | 0.73 | 5.3989 (5.3943) | 0.09 | 8.51 (8.06) | 0.45 | 0.0689 (0.0771) | 0.0082 | |||||
| 0 | 5.1445 (5.1215) | 0.45 | 5.4526 (5.4490) | 0.07 | 8.43 (8.06) | 0.37 | 0.0925 (0.0943) | 0.0018 | |||||
| 0 | 4.7407 (4.8711) | 2.75 | 5.7895 (5.5627) | 3.92 | 7.68 (8.06) | 0.38 | 0.0990 (0.0947) | 0.0043 | |||||
| 0.19 | 2.1171 (2.2200) | 4.86 | 2.1725 (2.2505) | 3.59 | 8.48 (6.62) | 1.86 | 0.0644 (0.0532) | 0.0112 | |||||
| 0.19 | 2.1016 (2.1906) | 4.23 | 2.2017 (2.2747) | 3.32 | 8.52 (6.60) | 1.92 | 0.0916 (0.0922) | 0.0006 | |||||
| 0.19 | 1.9856 (2.0828) | 4.90 | 2.2879 (2.3153) | 1.20 | 7.97 (6.68) | 1.29 | 0.0989 (0.0943) | 0.0046 | |||||
| 0.39 | 2.1598 (2.2796) | 5.55 | 2.2099 (2.2051) | 0.22 | 1.91 (0.97) | 0.94 | 0.0033 (0.0038) | 0.0005 | |||||
| 0.39 | 2.1598 (2.2441) | 3.90 | 2.2100 (2.2282) | 0.82 | 1.91 (1.04) | 0.87 | 0.0733 (0.0618) | 0.0115 | |||||
| 0.40 | 2.0290 (2.1171) | 4.34 | 2.2674 (2.2646) | 0.12 | 1.80 (3.32) | 1.52 | 0.0974 (0.0921) | 0.0053 |
References
- Tenconi, A.; Vaschetto, S.; Vigliani, A. Electrical Machines for High-Speed Applications: Design Considerations and Tradeoffs. IEEE Trans. Ind. Electron. 2014, 61, 3022–3029. [Google Scholar] [CrossRef]
- Shen, J.; Qin, X.; Wang, Y. High-Speed Permanent Magnet Electrical Machines—Applications, Key Issues and Challenges. CES Trans. Electr. Mach. Syst. 2018, 2, 11. [Google Scholar] [CrossRef]
- Lopez, I.; Ibarra, E.; Matallana, A.; Andreu, J.; Kortabarria, I. Next generation electric drives for HEV/EV propulsion systems: Technology, trends and challenges. Renew. Sustain. Energ. Rev. 2019, 114, 109336. [Google Scholar] [CrossRef]
- Fodorean, D.; Idoumghar, L.; Brevilliers, M.; Minciunescu, P.; Irimia, C. Hybrid Differential Evolution Algorithm Employed for the Optimum Design of a High-Speed PMSM Used for EV Propulsion. IEEE Trans. Ind. Electron. 2017, 64, 9824–9833. [Google Scholar] [CrossRef]
- Wu, Z.; Li, W.; Tang, H.; Luo, S.; Zhang, L. Research on the Calculation of Rotor’s Convective Heat Transfer Coefficient of High-Speed Drive Motor for EVs Based on Multiple Scenarios. J. Electr. Eng. Technol. 2023, 18, 4245–4256. [Google Scholar] [CrossRef]
- Ouyang, T.; Huang, H.; Zhang, N.; Mo, C.; Chen, N. A model to predict tribo-dynamic performance of a spur gear pair. Tribol. Int. 2017, 116, 449–459. [Google Scholar] [CrossRef]
- Lei, Y.; Hou, L.; Fu, Y.; Hu, J.; Chen, W. Research on vibration and noise reduction of electric bus gearbox based on multi-objective optimization. Appl. Acoust. 2020, 158, 107037. [Google Scholar] [CrossRef]
- Sun, M.; Lu, C.; Liu, Z.; Sun, Y.; Chen, H.; Shen, C. Classifying, Predicting, and Reducing Strategies of the Mesh Excitations of Gear Whine Noise: A Survey. Shock. Vib. 2020, 2020, 1–20. [Google Scholar] [CrossRef]
- Kim, B.; Oh, S.; Park, S. Manufacture of elastic composite ring for planetary traction drive with silicon rubber and carbon fiber. Compos. Struct. 2004, 66, 543–546. [Google Scholar] [CrossRef]
- Itagaki, H.; Ohama, K.; Raja Rajan, A.N. Method for estimating traction curves under practical operating conditions. Tribol. Int. 2020, 149, 105639. [Google Scholar] [CrossRef]
- Ai, X. Development of zero-spin planetary traction drive transmission: Part 1—Design and principles of performance calculation. J. Tribol. 2002, 124, 386–391. [Google Scholar] [CrossRef]
- Ai, X. Development of zero-spin planetary traction drive transmission: Part 2—Performance testing and evaluation. J. Tribol. 2002, 124, 392–397. [Google Scholar] [CrossRef]
- Ai, X.; Wilmer, M.; Lawrentz, D. Development of Friction Drive Transmission. J. Tribol. 2005, 127, 857–864. [Google Scholar] [CrossRef]
- Yamanaka, M.; Sugimoto, K.; Hashimoto, R.; Inoue, K. Intelligent speed-increasing spindle using traction drive. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2011, 35, 191–196. [Google Scholar] [CrossRef]
- Flugrad, D.R.; Qamhiyah, A.Z. A self-actuating traction-drive speed reducer. J. Mech. Des. 2005, 127, 631–636. [Google Scholar] [CrossRef]
- Wang, W.; Durack, J.M.; Durack, M.J.; Zhang, J.; Zhao, P. Automotive Traction Drive Speed Reducer Efficiency Testing. Automot. Innov. 2021, 4, 81–92. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, G.; Luo, Q.; Zou, S. Asymmetric loading multi-roller planetary traction drive: Modeling and performance analysis. Mech. Mach. Theory 2022, 170, 104697. [Google Scholar] [CrossRef]
- Li, C.; Wang, G.; Jiang, Y.; Song, H. A novel traction reducer: Analysis and verification. J. Adv. Mech. Des. Syst. 2024, 18, JAMDSM0017. [Google Scholar] [CrossRef]
- Nikas, G.K. Miscalculation of film thickness, friction and contact efficiency by ignoring tangential tractions in elastohydrodynamic contacts. Tribol. Int. 2017, 110, 252–263. [Google Scholar] [CrossRef]
- De Novellis, L.; Carbone, G.; Mangialardi, L. Traction and efficiency performance of the double roller full-toroidal variator: A comparison with half- and full-toroidal drives. J. Mech. Des. 2012, 134, 071005. [Google Scholar] [CrossRef]
- Carbone, G.; Mangialardi, L.; Mantriota, G. A comparison of the performances of full and half toroidal traction drives. Mech. Mach. Theory 2004, 39, 921–942. [Google Scholar] [CrossRef]
- Johnson, K.L.; Greenwood, J.A.; Poon, S.Y. Simple Theory of Asperity Contact in Elastohydrodynamic Lubrication. Wear 1972, 19, 91–108. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. Film thickness and asperity load formulas for line-contact elastohydrodynamic lubrication with provision for surface roughness. J. Tribol. 2012, 134, 011503. [Google Scholar] [CrossRef]
- Damiens, B.; Venner, C.H.; Cann, P.M.E.; Lubrecht, A.A. Starved lubrication of elliptical EHD contacts. J. Tribol. Trans. ASME 2004, 126, 105–111. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. A study on the effect of starvation in mixed elastohydrodynamic lubrication. Tribol. Int. 2015, 85, 26–36. [Google Scholar] [CrossRef]
- Kumar, P.; Khonsari, M. Effect of Starvation on Traction and Film Thickness in Thermo-EHL Line Contacts with Shear-Thinning Lubricants. Tribol. Lett. 2008, 32, 171–177. [Google Scholar] [CrossRef]
- Ali, F.; Krupka, I.; Hartl, M. An Approximate Approach to Predict the Degree of Starvation in Ball-Disk Machine Based on the Relative Friction. Tribol. Trans. 2013, 56, 681–686. [Google Scholar] [CrossRef]
- Ali, F.; Krupka, I.; Hartl, M. Analytical and experimental investigation on friction of non-conformal point contacts under starved lubrication. Meccanica 2013, 48, 545–553. [Google Scholar] [CrossRef]
- Ebner, M.; Yilmaz, M.; Lohner, T.; Michaelis, K.; Höhn, B.R.; Stahl, K. On the effect of starved lubrication on elastohydrodynamic (EHL) line contacts. Tribol. Int. 2018, 118, 515–523. [Google Scholar] [CrossRef]
- Beheshti, A.; Aghdam, A.B.; Khonsari, M.M. Deterministic surface tractions in rough contact under stick-slip condition: Application to fretting fatigue crack initiation. Int. J. Fatigue 2013, 56, 75–85. [Google Scholar] [CrossRef]
- Pei, J.; Han, X.; Tao, Y.; Feng, S. Mixed elastohydrodynamic lubrication analysis of line contact with Non-Gaussian surface roughness. Tribol. Int. 2020, 151, 13. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B. Contact of Nominally Flat Surfaces. Proc. R. Soc. Lond. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Chang, W.R.; Etsion, I.; Bogy, D.B. An elastic-plastic model for the contact of rough surfaces. J. Tribol. Trans. ASME 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Zhao, Y.; Maietta, D.M.; Chang, L. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow. J. Tribol. Trans. ASME 2000, 122, 86–93. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. Asperity micro-contact models as applied to the deformation of rough line contact. Tribol. Int. 2012, 52, 61–74. [Google Scholar] [CrossRef]
- McCool, J.I. Relating Profile Instrument Measurements to the Functional Performance of Rough Surfaces. J. Tribol. Trans. ASME 1987, 109, 264–270. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. Theoretical and experimental investigation of traction coefficient in line-contact EHL of rough surfaces. Tribol. Int. 2014, 70, 179–189. [Google Scholar] [CrossRef]
- Kumar, P.; Khonsari, M.M. Combined effects of shear thinning and viscous heating on EHL characteristics of rolling/sliding line contacts. J. Tribol. Trans. ASME 2008, 130, 13. [Google Scholar] [CrossRef]
- Bair, S.; Winer, W.O. Rheological model for elastohydrodynamic contacts based on primary laboratory data. J. Lubr. Technol. Trans. ASME 1979, 101, 258–265. [Google Scholar] [CrossRef]
- Andersson, S.; Soderberg, A.; Bjorklund, S. Friction models for sliding dry, boundary and mixed lubricated contacts. Tribol. Int. 2007, 40, 580–587. [Google Scholar] [CrossRef]
- Popova, E.; Popov, V.L. The research works of Coulomb and Amontons and generalized laws of friction. Friction 2015, 3, 183–190. [Google Scholar] [CrossRef]
- Verbelen, F.; Druant, J.; Derammelaere, S.; Vansompel, H.; De Belie, F.; Stockman, K.; Sergeant, P. Benchmarking the permanent magnet electrical variable transmission against the half toroidal continuously variable transmission. Mech. Mach. Theory 2017, 113, 141–157. [Google Scholar] [CrossRef]
- Akehurst, S.; Parker, D.A.; Schaaf, S. CVT rolling traction drives—A review of research into their design, functionality, and modeling. J. Mech. Des. 2006, 128, 1165–1176. [Google Scholar] [CrossRef]
- Dormois, H.; Fillot, N.; Habchi, W.; Dalmaz, G.; Vergne, P.; Morales-Espejel, G.E.; Ioannides, E. A Numerical Study of Friction in Isothermal EHD Rolling-Sliding Sphere-Plane Contacts With Spinning. J. Tribol. 2010, 132, 021501. [Google Scholar] [CrossRef]
- Matsuda, K.; Goi, T.; Tanaka, K.; Imai, H.; Tanaka, H.; Sato, Y. Study on high-speed traction drive CVT for aircraft power generation—Gyroscopic effect of the thrust ball bearing on the CVT. J. Adv. Mech. Des. Syst. 2017, 11, JAMDSM0087. [Google Scholar] [CrossRef]









| Parameters | ||||||
|---|---|---|---|---|---|---|
| Min | 3.2 × 10−5 | 3 × 10−12 | 5 × 10−6 | 1.3 × 109 | 0 | 0 |
| Max | 5 × 10−4 | 7.5 × 10−11 | 1 × 10−4 | 7 × 109 | 0.2 | 0.5 |
| Parameters | Values |
|---|---|
| Lubricant viscosity at atmospheric pressure | |
| Viscosity–pressure index | |
| Pressure–viscosity coefficient | |
| Limiting shear stress at atmospheric pressure | |
| Limiting shear stress coefficient |
| Parameters | Values |
|---|---|
| Sun roller radius | |
| Planet roller radius | |
| Wedge roller radius | |
| Ring radius | |
| Number of planet rollers | |
| The defined characteristic angles | , |
| Elastic modulus | |
| Poisson ratios | |
| Ideal speed ratio | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Wang, G. Theoretical and Experimental Investigation of a Novel Wedge-Loading Planetary Traction Drive. Machines 2024, 12, 567. https://doi.org/10.3390/machines12080567
Jiang Y, Wang G. Theoretical and Experimental Investigation of a Novel Wedge-Loading Planetary Traction Drive. Machines. 2024; 12(8):567. https://doi.org/10.3390/machines12080567
Chicago/Turabian StyleJiang, Yujiang, and Guangjian Wang. 2024. "Theoretical and Experimental Investigation of a Novel Wedge-Loading Planetary Traction Drive" Machines 12, no. 8: 567. https://doi.org/10.3390/machines12080567
APA StyleJiang, Y., & Wang, G. (2024). Theoretical and Experimental Investigation of a Novel Wedge-Loading Planetary Traction Drive. Machines, 12(8), 567. https://doi.org/10.3390/machines12080567






