Steady-State Fault Propagation Characteristics and Fault Isolation in Cascade Electro-Hydraulic Control System
Abstract
:1. Introduction
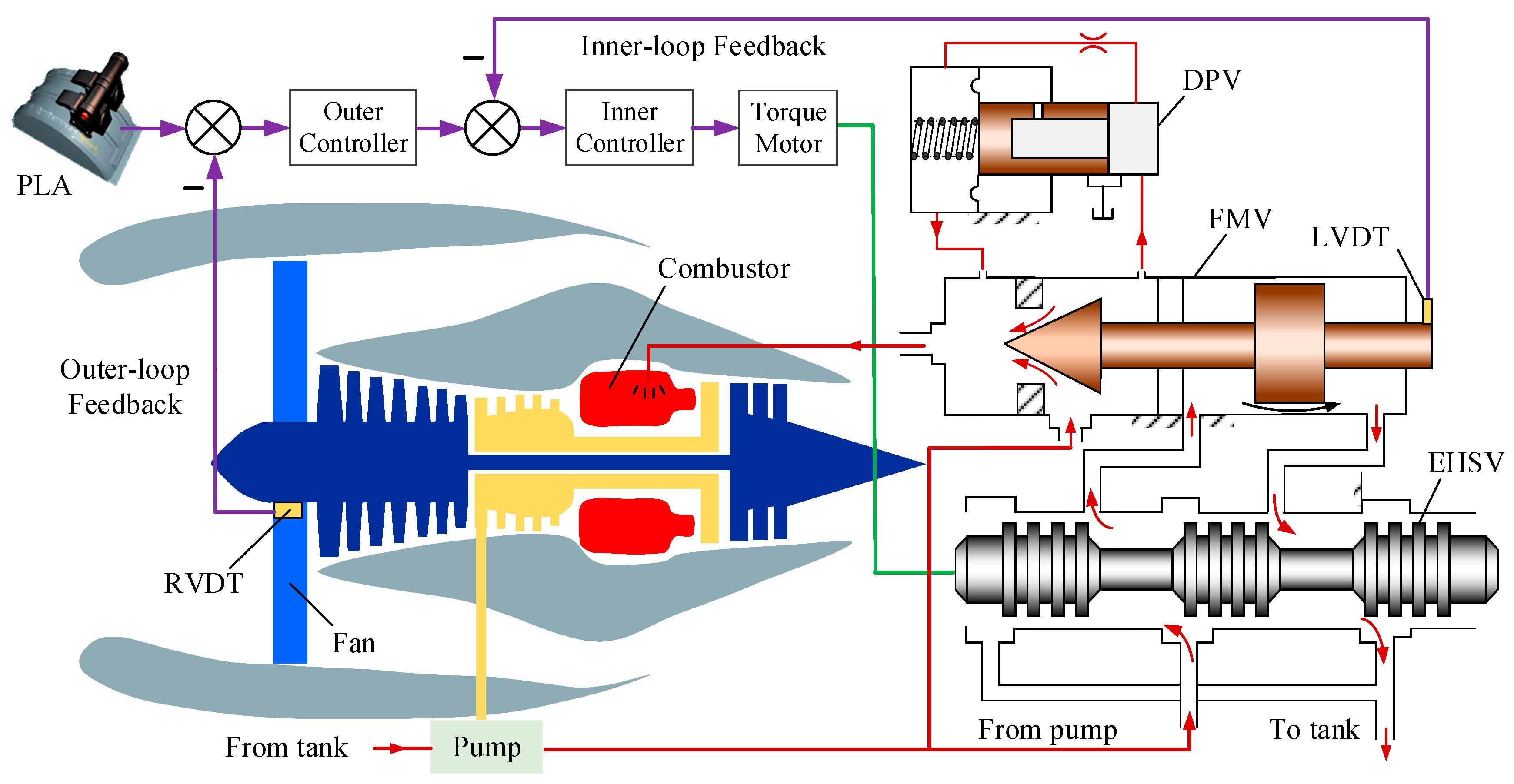
2. Cascade Electro-Hydraulic Control System of Turbofan Engine
2.1. Turbofan Engine Control System
2.2. Fault Analysis of Turbofan Engine Control System
3. Fault Diagnosis Scheme
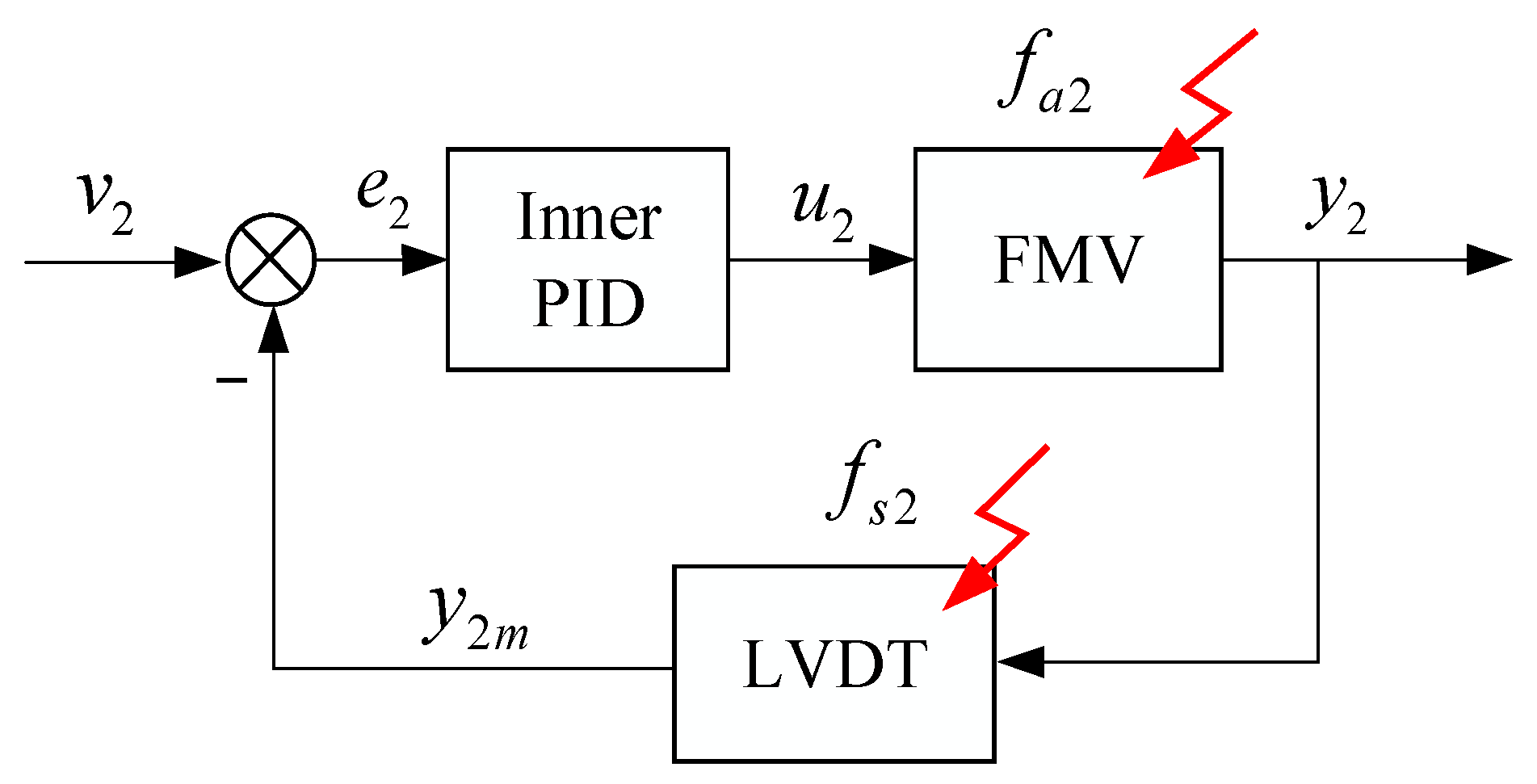
3.1. Optimal Fault Detection Filter Design for the Outer Loop System
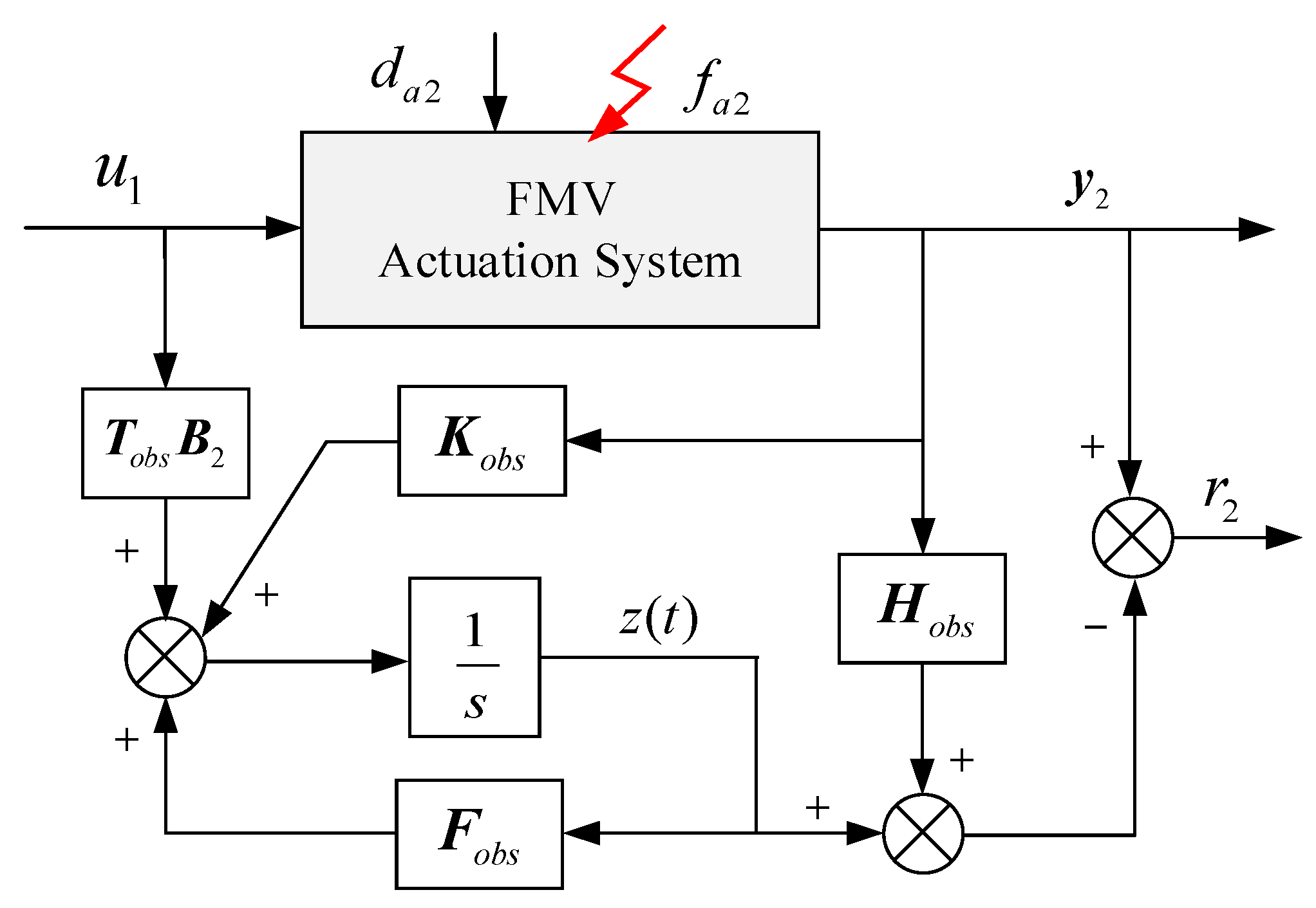
3.2. Robust Unknown Disturbance Decoupled Residual Generator for the Inner-Loop System
3.3. Steady-State Propagation Characteristics of Faults in Cascade Control Systems
3.4. Fault Isolation Scheme Based on Steady-State Fault Propagation Characteristics
4. Experiments
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ba, K.X.; Chen, C.H.; Ma, G.L.; Song, Y.H.; Wang, Y.; Yu, B.; Kong, X.D. A compensation strategy of end-effector pose precision based on the virtual constraints for serial robots with RDOFs. Fundam. Res. 2024. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.P.; Shi, J.; Wang, X. Evaluation of thermal effects on temperature-sensitive operating force of flow servo valve for fuel metering unit. Chin. J. Aeronaut. 2020, 33, 1812–1823. [Google Scholar] [CrossRef]
- Kim, D.; Park, H.J.; Kim, S.S.; Kim, D.H.; Kim, S.B.; Lee, J.; Choi, J.Y. Position control of dual redundant asymmetric tandem electro-hydrostatic actuator for aircraft based on backstepping technique. J. Aerosp. Syst. Eng. 2021, 15, 1–10. [Google Scholar]
- Zhou, T.; Zhang, L.; Han, T.; Droguett, E.L.; Mosleh, A.; Chan, F.T.S. An uncertainty-informed framework for trustworthy fault diagnosis in safety-critical applications. Reliab. Eng. Syst. Saf. 2023, 229, 108865. [Google Scholar] [CrossRef]
- Azarbani, A.; Fakharian, A.; Menhaj, M.B. On the design of an unknown input observer to fault detection, isolation, and estimation for uncertain multi-delay nonlinear systems. J. Process Control. 2023, 128, 103018. [Google Scholar] [CrossRef]
- Jyotish, N.K.; Singh, L.K.; Kumar, C.; Singh, P. Reliability and performance measurement of safety-critical systems based on petri nets: A case study of nuclear power plant. IEEE Trans. Reliab. 2023, 72, 1523–1539. [Google Scholar] [CrossRef]
- Pourtakdoust, S.H.; Mehrjardi, M.F.; Hajkarim, M.H.; Gourabi, F.N. Advanced fault detection and diagnosis in spacecraft attitude control systems: Current state and challenges. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 2679–2699. [Google Scholar] [CrossRef]
- Attouri, K.; Dhibi, K.; Mansouri, M.; Hajji, M.; Bouzrara, K.; Nounou, H. Enhanced fault diagnosis of wind energy conversion systems using ensemble learning based on sine cosine algorithm. J. Eng. Appl. Sci. 2023, 70, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.L.; Pan, Z.F.; Yuan, X.F.; Yang, C.H.; Gui, W.H. A novel deep learning-based fault diagnosis approach for chemical process with extended deep belief network. ISA Trans. 2020, 96, 457–467. [Google Scholar] [CrossRef]
- Hasan, A.; Tahavori, M.; Midtiby, H.S. Model-based fault diagnosis algorithms for robotic systems. IEEE Access 2023, 11, 2250–2258. [Google Scholar] [CrossRef]
- Abbaspour, A.; Aboutalebi, P.; Yen, K.K.; Sargolzaei, A. Neural adaptive observer-based sensor and actuator fault detection in nonlinear systems: Application in UAV. ISA Trans. 2017, 67, 317–329. [Google Scholar] [CrossRef]
- Poon, J.; Jain, P.; Konstantakopoulos, I.C.; Spanos, C.; Panda, S.K.; Sanders, S.R. Model-based fault detection and identification for switching power converters. IEEE Trans. Power Electron. 2016, 32, 1419–1430. [Google Scholar] [CrossRef]
- Jihani, N.; Kabbaj, M.N.; Benbrahim, M. Sensor fault detection and isolation for smart irrigation wireless sensor network based on parity space. Int. J. Electr. Comput. Eng. 2023, 13, 1463. [Google Scholar] [CrossRef]
- Du, Y.; Budman, H.; Duever, T.A. Integration of fault diagnosis and control based on a trade-off between fault detectability and closed loop performance. J. Process Control. 2016, 38, 42–53. [Google Scholar] [CrossRef]
- Safaeipour, H.; Forouzanfar, M.; Casavola, A. A survey and classification of incipient fault diagnosis approaches. J. Process Control. 2021, 97, 1–16. [Google Scholar] [CrossRef]
- Sun, B.W.; Wang, J.Q.; He, Z.M.; Qin, Y.R.; Wang, D.Y.; Zhou, H.Y. Fault detection for closed-loop control systems based on parity space transformation. IEEE Access 2019, 7, 75153–75165. [Google Scholar] [CrossRef]
- Kong, X.D.; Cai, B.P.; Liu, Y.H.; Zhu, H.M.; Yang, C.; Gao, C.T.; Liu, Y.Q.; Liu, Z.K.; Ji, R.J. Fault diagnosis methodology of redundant closed-loop feedback control systems: Subsea blowout preventer system as a case study. IEEE Trans. Syst. Man Cybern. Syst. 2022, 53, 1618–1629. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.D.; He, X.; Zhou, D.H. A class of observer-based fault diagnosis schemes under closed-loop control: Performance evaluation and improvement. IET Control. Theory Appl. 2017, 11, 135–141. [Google Scholar] [CrossRef]
- Sun, B.W.; Wang, J.Q.; He, Z.M.; Zhou, H.Y.; Gu, F.S. Fault identification for a closed-loop control system based on an improved deep neural network. Sensors 2019, 19, 2131. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, R.X.; Xu, M.Q. A combined model-based and intelligent method for small fault detection and isolation of actuators. IEEE Trans. Ind. Electron. 2015, 63, 2403–2413. [Google Scholar] [CrossRef]
- Grehan, J.; Ignatyev, D.; Zolotas, A. Fault detection in aircraft flight control actuators using support vector machines. Machines 2023, 11, 211. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Zhang, X.F.; Yan, T.H.; Gao, S.; Yu, Z. Data-driven fault detection of AUV rudder system: A mixture model approach. Machines 2023, 11, 551. [Google Scholar] [CrossRef]
- Jia, F.L.; Cao, F.F.; Guo, Y.Q.; He, X. Active fault diagnosis for a class of closed-loop systems via parameter estimation. J. Frankl. Inst. 2022, 359, 3979–3999. [Google Scholar] [CrossRef]
- Niemann, H.; Poulsen, N.K. Fault Detection in Closed-Loop Systems Using a Double Residual Generator. In Proceedings of the 2022 11th IFAC Symposium on Fault Detection, Supervision and Safety for Technical Processes, Pafos, Cyprus, 8–10 June 2022. [Google Scholar]
- Zhang, Y.; Wang, S.P.; Shi, J.; Yang, X.Y.; Zhang, J.R.; Wang, X. SAR performance-based fault diagnosis for electro-hydraulic control system: A novel FDI framework for closed-loop system. Chin. J. Aeronaut. 2022, 35, 381–392. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J.; Ding, H.; Zhang, H. Nonlinear cascade control of an electro-hydraulic actuator with large payload variation. Asian J. Control. 2023, 25, 101–113. [Google Scholar] [CrossRef]
- Ding, S.X. Advanced Methods for Fault Diagnosis and Fault-Tolerant Control, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 91–95. [Google Scholar]
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer: Berlin/Heidelberg, Germany, 2013; pp. 28–29. [Google Scholar]





| Fault/Disturbance | Control Input | Actual Output | Measured Output |
|---|---|---|---|
| FMV disturbance | N | N | N |
| FMV Leakage | N | N | N |
| LVDT gain bias | N | Y | N |
| Faults/Disturbance | u1 | y1 | y1m | v2 | u2 | y2 | y2m |
|---|---|---|---|---|---|---|---|
| FMV leakage | N | N | N | Y | Y | N | N |
| LVDT gain bias | N | N | N | Y | N | N | Y |
| DPV fault | N | N | N | Y | N | Y | Y |
| RVDT gain bias | Y | Y | N | Y | N | Y | Y |
| Fault Location | u1 | y1 | y1m | v2 | u2 | y2 | y2m |
|---|---|---|---|---|---|---|---|
| FMV | 0.33458 | 1.45745 | 1.45745 | −1.45745 | −0.00049 | 0.00418 | 0.00418 |
| LVDT | −0.16846 | −7.08437 | −7.08437 | 7.08437 | 0.00232 | −0.00211 | 0.49730 |
| DPV | −0.02578 | −1.73491 | −1.73491 | 1.73492 | 0.00065 | −0.83297 | −0.83297 |
| RVDT | −37.486500 | −941.745 | −36.4096 | 36.40957 | 0.01218 | −0.46858 | −0.46858 |
| Vector Angle | M1 | M2 | M3 | M4 | Isolation Results |
|---|---|---|---|---|---|
| 11.40° | 31.72° | 38.72° | 39.91° | p = 1 | |
| 65.48° | 31.46° | 45.68° | 52.52° | p = 2 | |
| 87.11° | 58.45° | 33.39° | 43.67° | p = 3 | |
| 42.10° | 54.57° | 49.93° | 34.94° | p = 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhou, R.; Meng, L.; Shi, J.; Ba, K. Steady-State Fault Propagation Characteristics and Fault Isolation in Cascade Electro-Hydraulic Control System. Machines 2024, 12, 600. https://doi.org/10.3390/machines12090600
Zhang Y, Zhou R, Meng L, Shi J, Ba K. Steady-State Fault Propagation Characteristics and Fault Isolation in Cascade Electro-Hydraulic Control System. Machines. 2024; 12(9):600. https://doi.org/10.3390/machines12090600
Chicago/Turabian StyleZhang, Yang, Rulin Zhou, Lingyu Meng, Jian Shi, and Kaixian Ba. 2024. "Steady-State Fault Propagation Characteristics and Fault Isolation in Cascade Electro-Hydraulic Control System" Machines 12, no. 9: 600. https://doi.org/10.3390/machines12090600
APA StyleZhang, Y., Zhou, R., Meng, L., Shi, J., & Ba, K. (2024). Steady-State Fault Propagation Characteristics and Fault Isolation in Cascade Electro-Hydraulic Control System. Machines, 12(9), 600. https://doi.org/10.3390/machines12090600






