A Study on the Static and Dynamic Characteristics of the Spindle System of a Spiral Bevel Gear Grinding Machine
Abstract
1. Introduction
2. Materials and Methods
2.1. Static Stiffness Model of the Spindle System
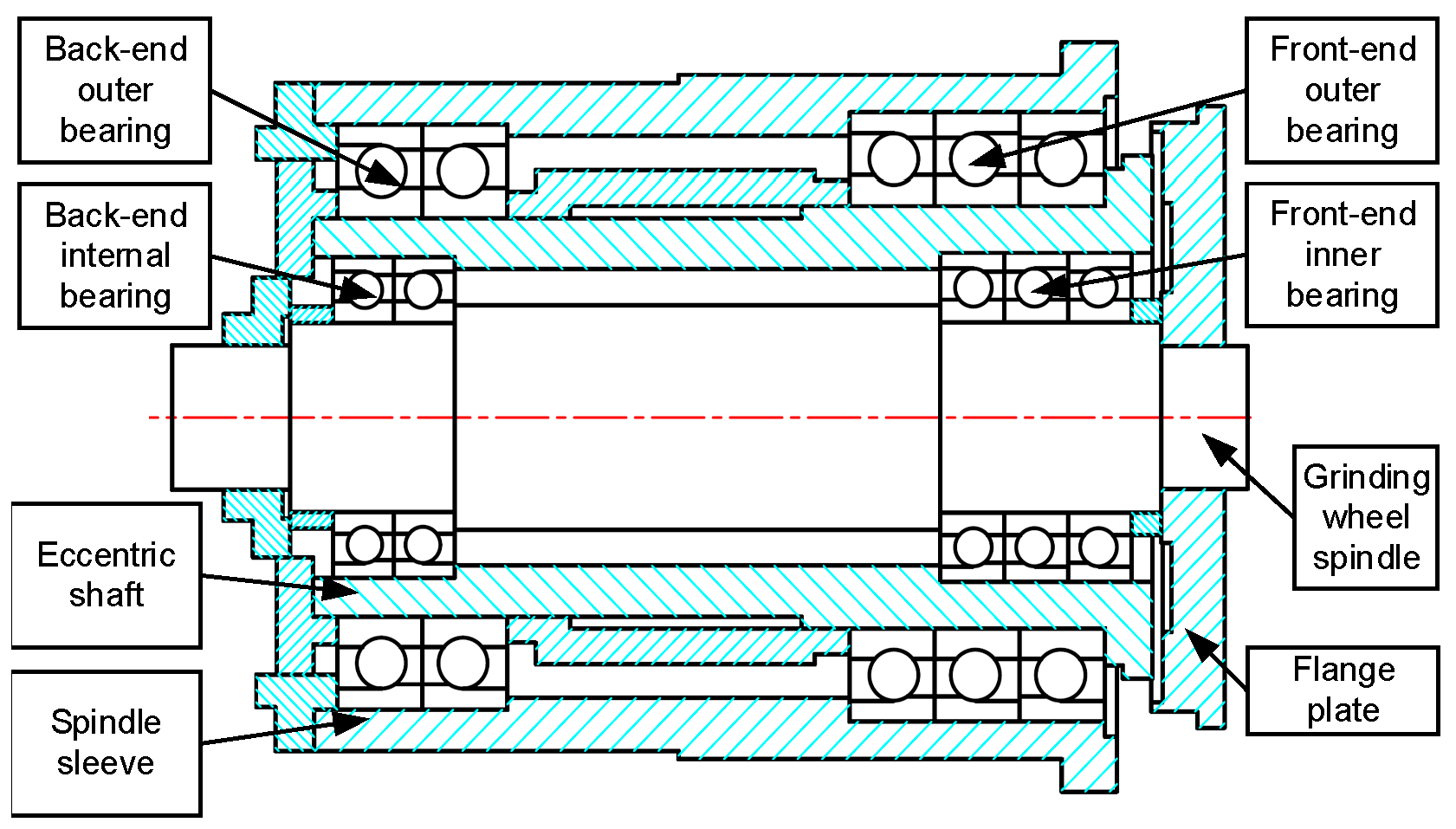
2.1.1. Analysis of the Spindle Box Structure of the Spiral Bevel Gear Grinding Machine
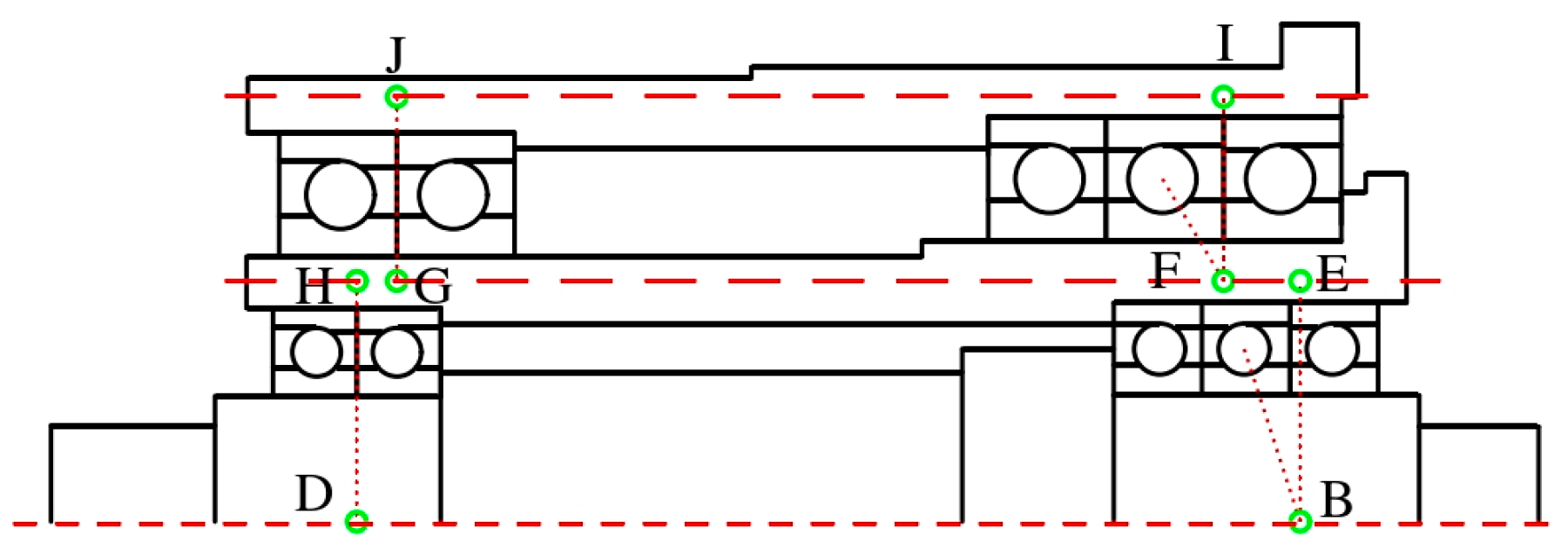
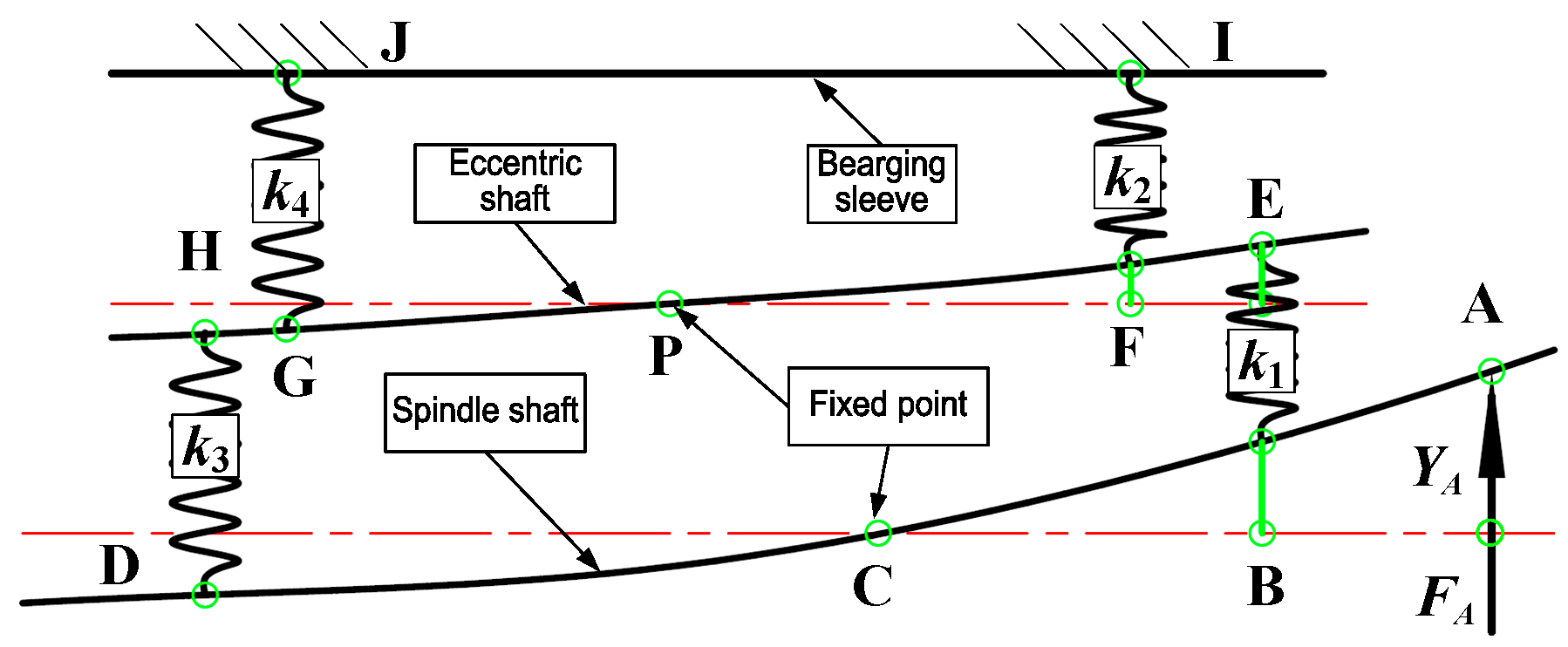
2.1.2. The Establishment of the Static Mechanics Model of the Spindle System
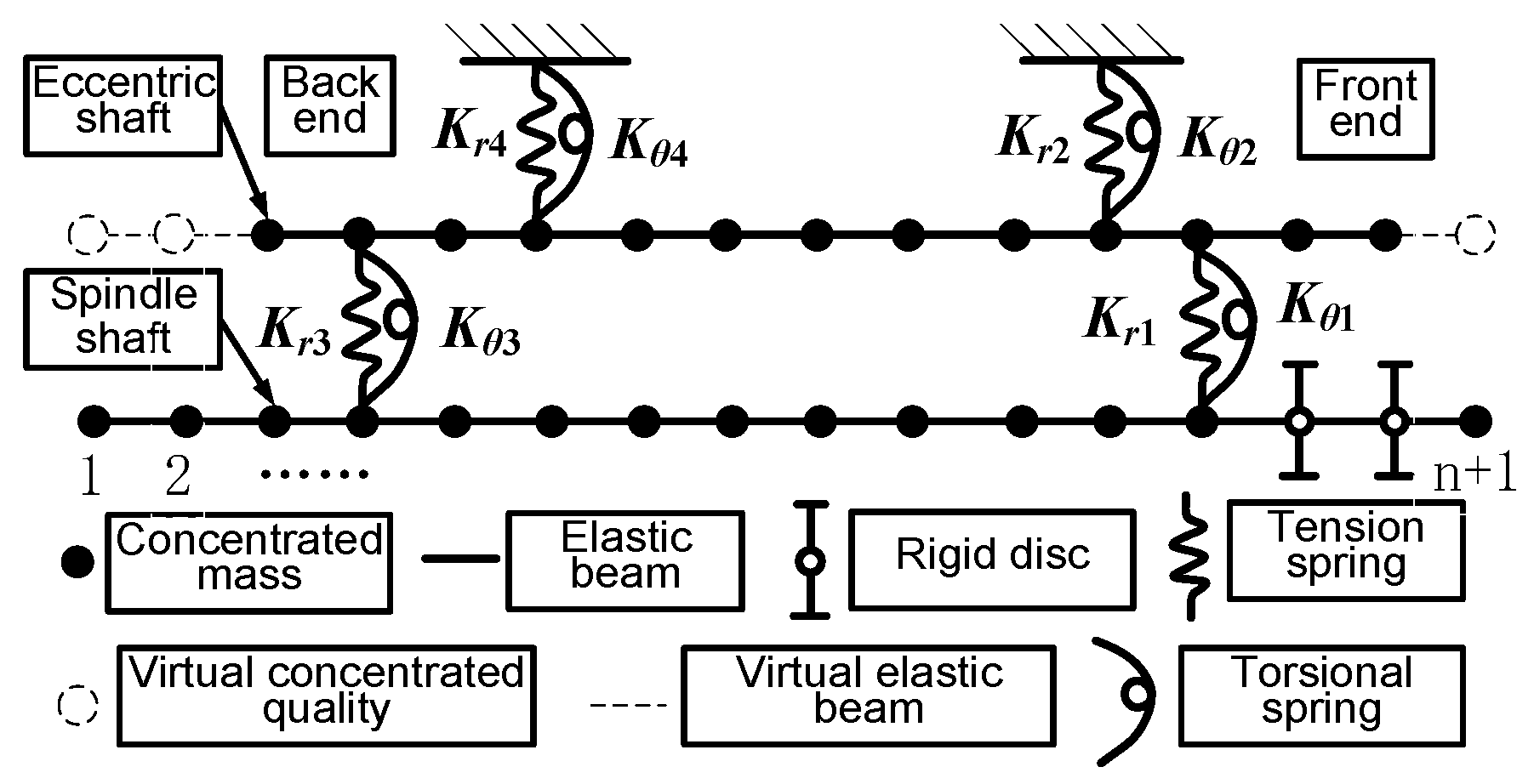
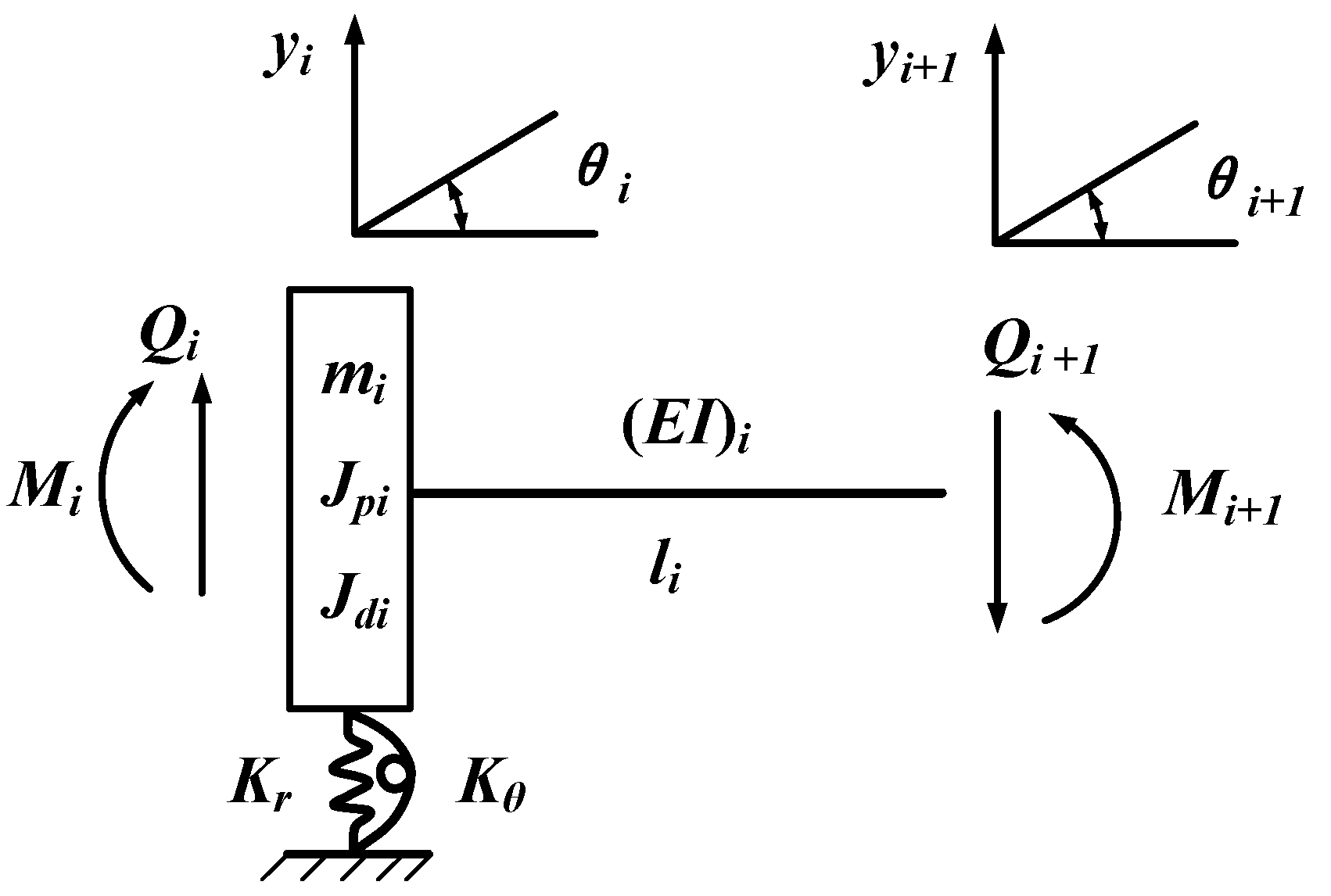
2.2. Dynamic Model of the Spindle System
2.2.1. Overall Transfer Matrix Method
2.2.2. Coupling Matrix
2.2.3. Critical Speed and Mode Shape
3. Results and Discussion
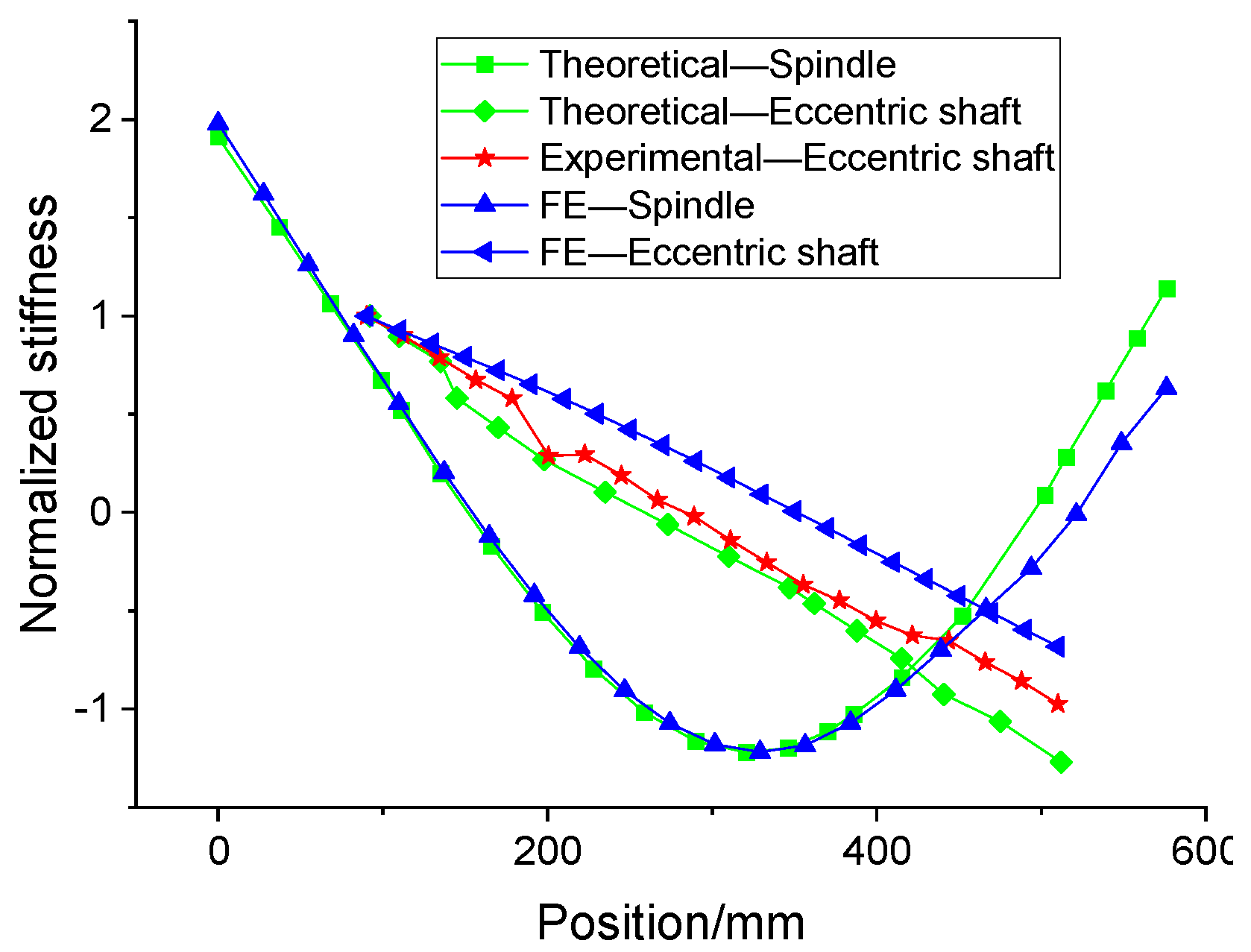
3.1. An Analysis of the Structural Parameters Affecting the Static and Dynamic Performance of the System
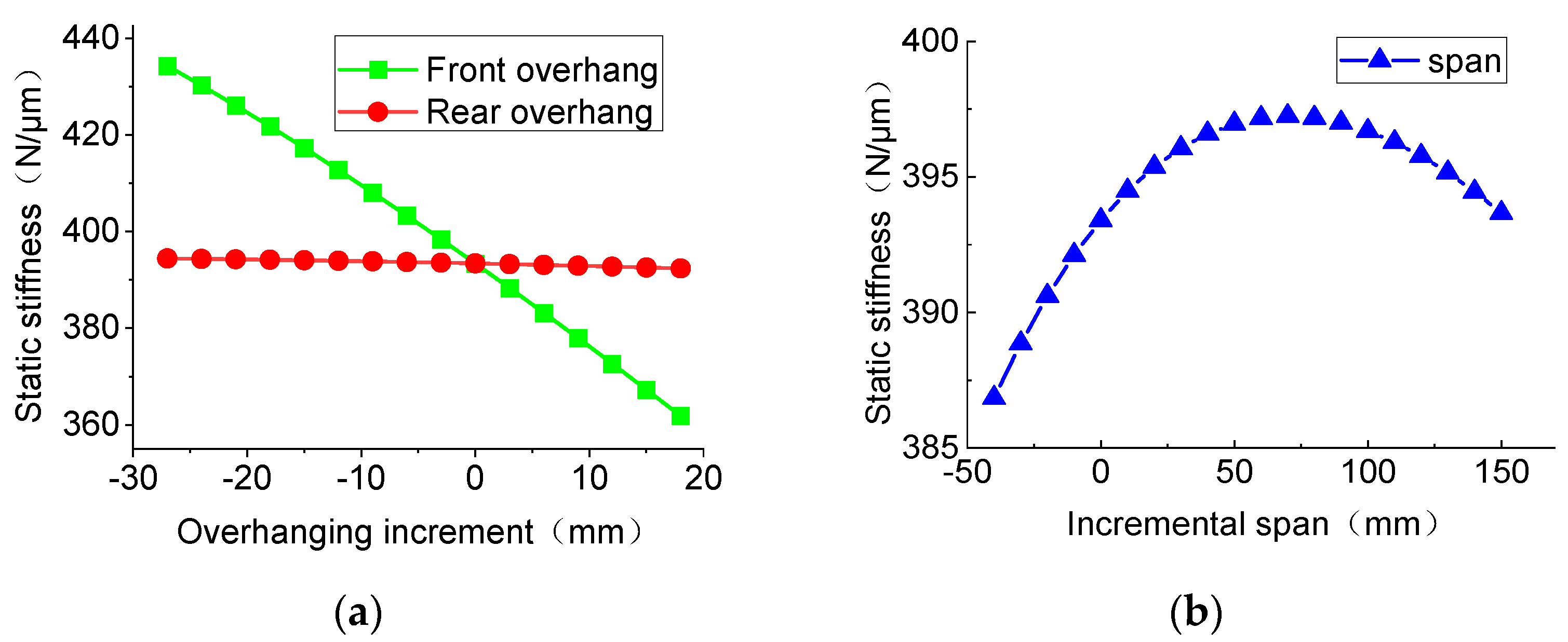
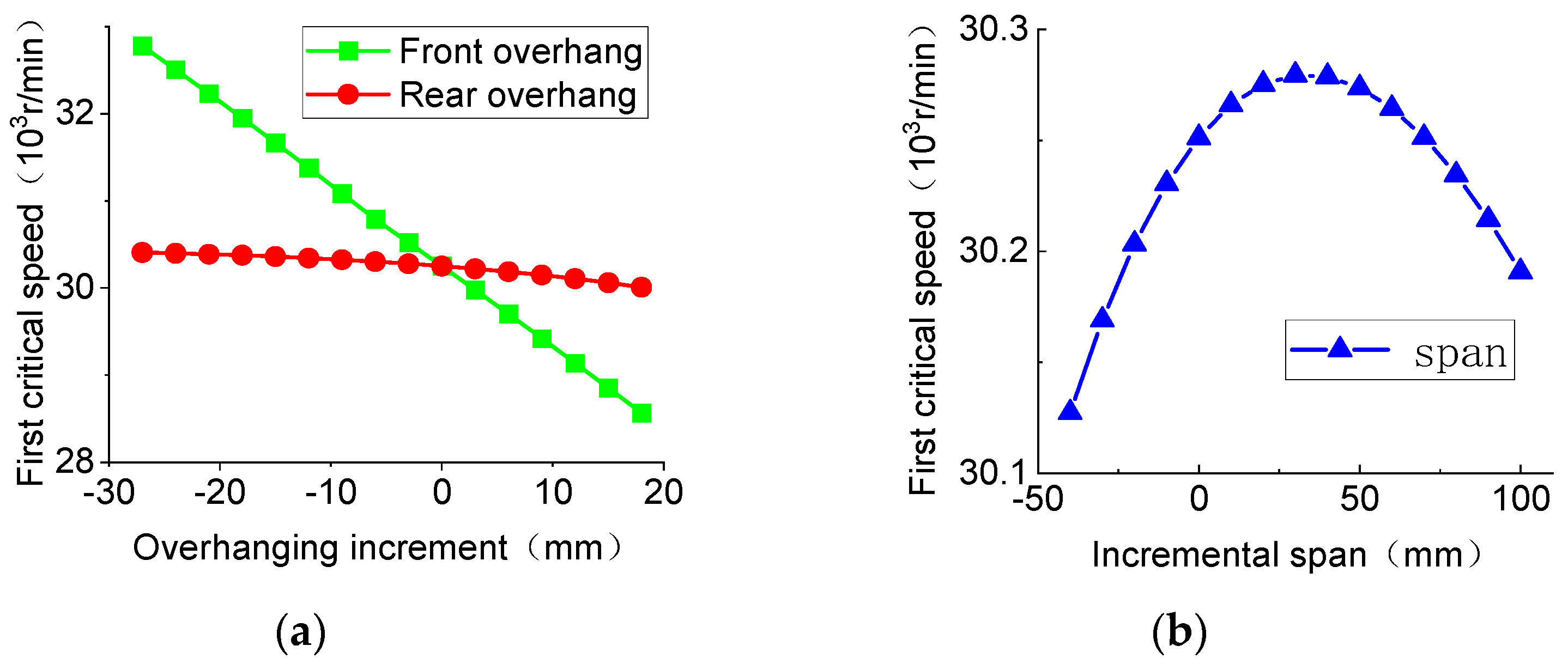
3.1.1. Overhang and Bearing Span
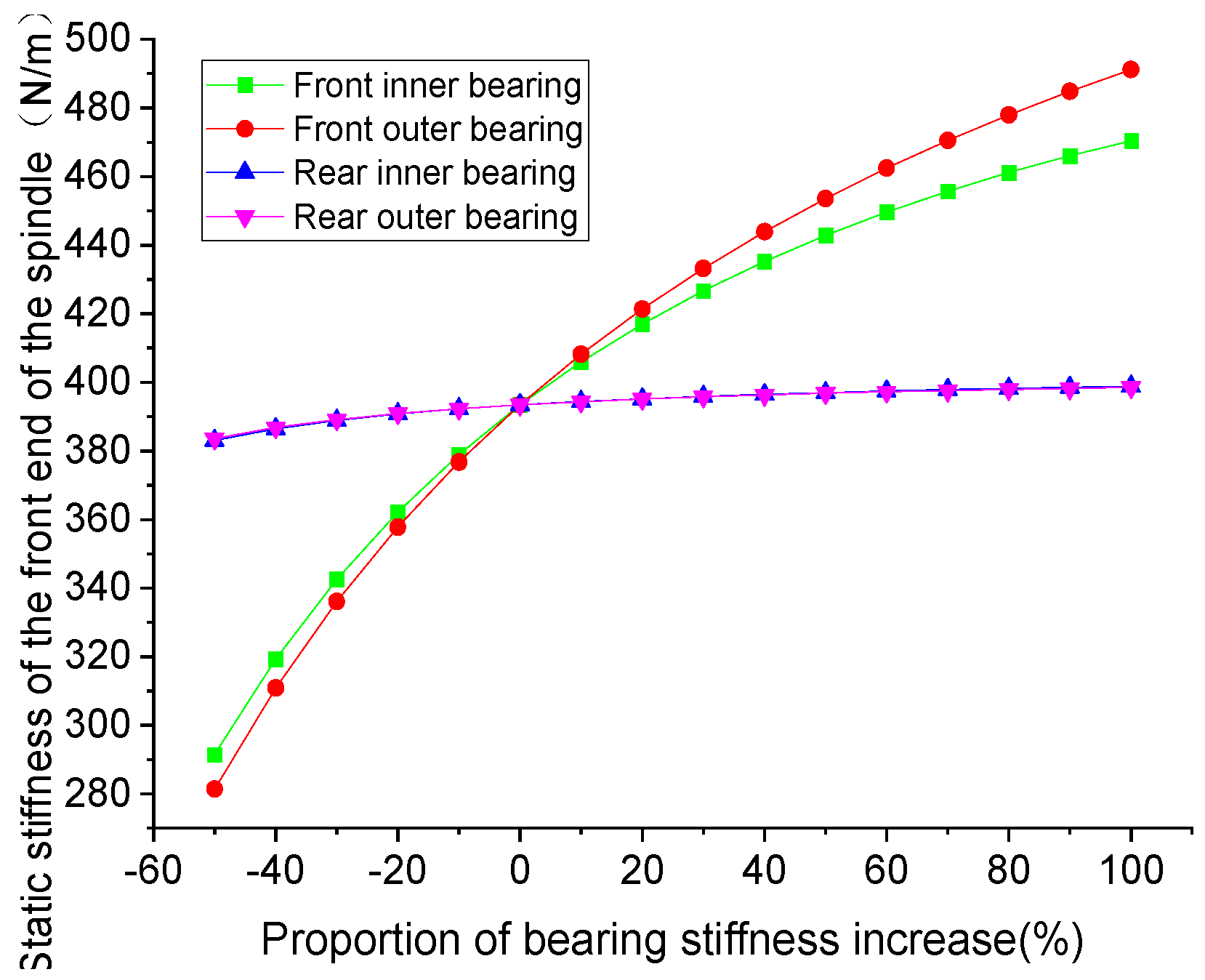
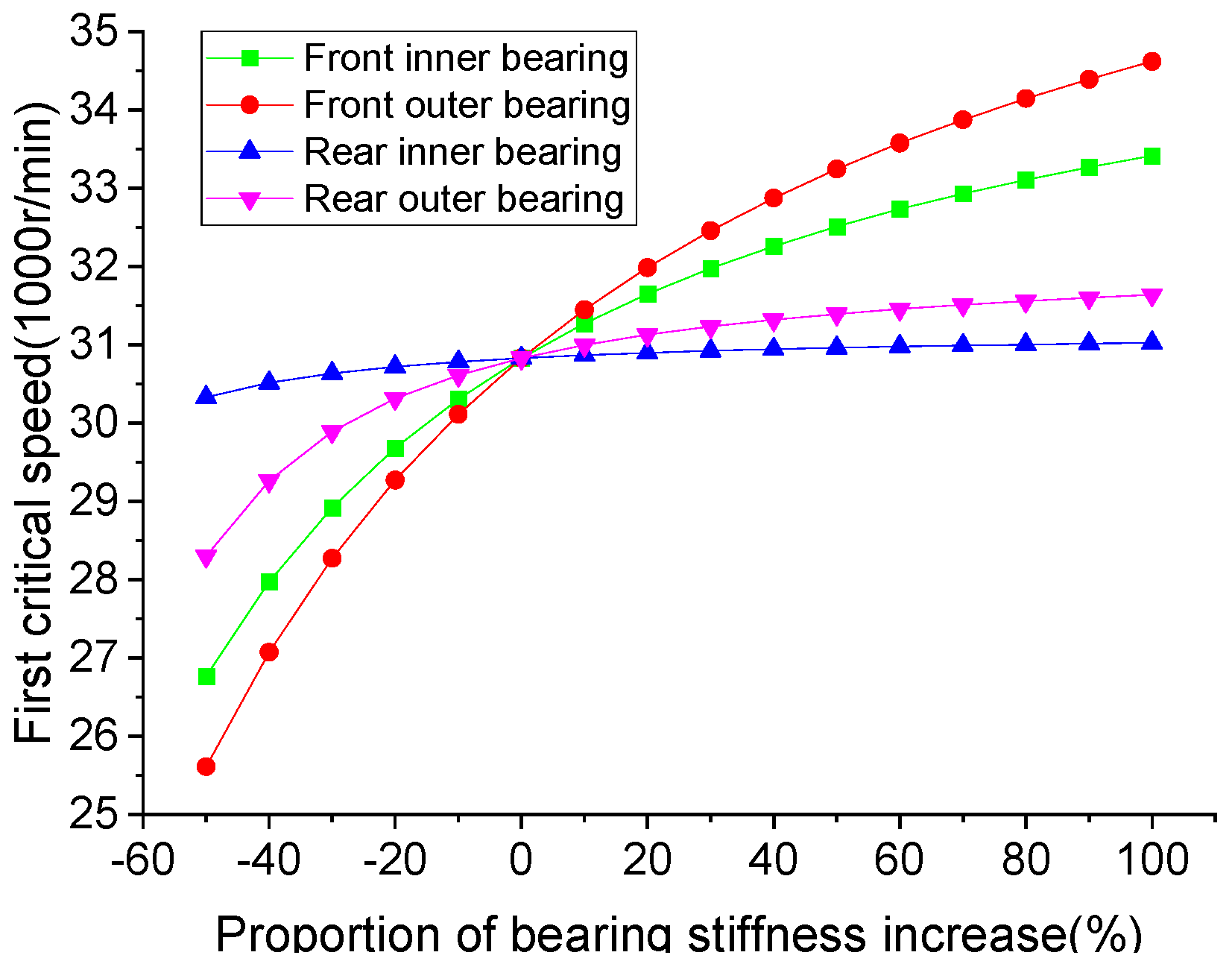
3.1.2. Bearing Stiffness
3.2. Experiments and Verification
3.2.1. Static Stiffness Measurement
3.2.2. Modal Test
3.2.3. FE Simulation Model Based on Bushing Element
3.2.4. Experimental Results and Analysis
4. Conclusions
- (1)
- Considering the static equivalent model of the triple-contact ball bearing, a static mechanics model of the double-rotor spindle system of the spiral bevel gear grinding machine is established based on Castigliano’s theorem, which can be used to calculate the static stiffness value of the spindle system. The dynamic model of the spindle–eccentric shaft system is established using the overall transfer matrix method to calculate the natural frequency, mode shape, and critical speed of the spindle system. This work fills the gap in the optimization design of the static and dynamic performance of the dual-rotor grinding machine spindle system.
- (2)
- The influence of the partial structural parameters on the static and dynamic performance of the system is analyzed. The results show that the optimal spindle bearing span for static stiffness and for first-order critical speed is different. The front overhang of the eccentric shaft has the greatest influence on the static and dynamic performance of the system. Among the four sets of bearing stiffness, the front outer bearing stiffness has the greatest influence on the static and dynamic performance of the system, while the rear inner bearing stiffness has the least influence. Therefore, the design optimization should focus on the stiffness and installation position of the front outer bearing.
- (2)
- Two sets of static mechanics experiments and modal tests are designed, and the corresponding FE simulation models are established. The comparison results show that the errors of the static stiffness and natural frequencies of the theoretical models, experiments, and FE simulation are all within 10%, and the first-order bending mode shapes are in good agreement, indicating that the theoretical models have good reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Molaie, M.; Samani, F.S.; Zippo, A.G.; Pellicano, F. Spiral Bevel Gears: Nonlinear dynamic model based on accurate static stiffness evaluation. J. Sound Vib. 2023, 544, 117395. [Google Scholar] [CrossRef]
- Chen, P.; Wang, S.; Zou, H. Efficient semi-analytic method for single tooth contact analysis of loaded spiral bevel gears. Appl. Math. Model. 2024, 129, 754–779. [Google Scholar] [CrossRef]
- Liu, Z.; Li, F.; Xu, Z.; He, Q. Semi-analytical loaded tooth contact analysis method for spiral bevel gears. Int. J. Mech. Sci. 2023, 253, 108329. [Google Scholar] [CrossRef]
- Li, C.H.; Hou, Y.L.; Du, C.; Ding, Y.C. An analysis of the electric spindle’s dynamic characteristics of high-speed grinder. J. Adv. Manuf. Syst. 2011, 10, 159–166. [Google Scholar] [CrossRef]
- Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Process. 2018, 102, 37–58. [Google Scholar] [CrossRef]
- Lin, C.-W.; Lin, Y.-K.; Chu, C.-H. Dynamic models and design of spindle-bearing systems of machine tools: A review. Int. J. Precis. Eng. Manuf. 2013, 14, 513–521. [Google Scholar] [CrossRef]
- Xi, S.; Cao, H.; Chen, X.; Niu, L. A Dynamic Modeling Approach for Spindle Bearing System Supported by Both Angular Contact Ball Bearing and Floating Displacement Bearing. J. Manuf. Sci. Eng. 2017, 140, 021014. [Google Scholar] [CrossRef]
- Xi, S.; Cao, H.; Chen, X. Dynamic modeling of spindle bearing system and vibration response investigation. Mech. Syst. Signal Process. 2019, 114, 486–511. [Google Scholar] [CrossRef]
- Hu, T.; Yin, G.; Sun, M. Model Based Research of Dynamic Performance of Shaft-Bearing System in High-Speed Field. Shock Vib. 2014, 2014, 1–12. [Google Scholar] [CrossRef][Green Version]
- Xi, S.; Cao, H.; Chen, X.; Niu, L. Dynamic modeling of machine tool spindle bearing system and model based diagnosis of bearing fault caused by collision. Procedia CIRP 2018, 77, 614–617. [Google Scholar] [CrossRef]
- Lin, S.; Jiang, S. Dynamic characteristics of motorized spindle with tandem duplex angular contact ball bearings. J. Vib. Acoust. 2019, 141, 061004. [Google Scholar] [CrossRef]
- Wu, H.; Sang, S.; An, Q. A new vibration model for a bearing-rotor system considering a bearing structure. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2011, 225, 1–11. [Google Scholar] [CrossRef]
- Jiang, S.; Lin, S. A technical note: An ultra-high-speed motorized spindle for internal grinding of small-deep hole. Int. J. Adv. Manuf. Technol. 2018, 97, 1457–1463. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, S.; Geng, K. Dynamic analysis of a high speed motorized spindle for internal grinding of slender holes. In Proceedings of the IOP Conference Series: Materials Science and Engineering, 10th International Conference on Mechatronics and Manufacturing (ICMM 2019), Bangkok, Thailand, 21–23 January 2019; p. 012013. [Google Scholar]
- Liu, J.; Lai, T.; Chen, X. Dynamics analysis of unbalanced motorized spindles supported on ball bearings. Shock Vib. 2016, 2016, 2787524. [Google Scholar] [CrossRef]
- Jiang, S.; Mao, H. Investigation of variable optimum preload for a machine tool spindle. Int. J. Mach. Tools Manuf. 2010, 50, 19–28. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, S. A modeling approach for analysis and improvement of spindle-drawbar-bearing assembly dynamics. Int. J. Mach. Tools Manuf. 2010, 50, 131–142. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, S. Dynamic design of a high-speed motorized spindle-bearing system. ASME J. Mech. Des. 2010, 132, 34501. [Google Scholar] [CrossRef]
- Li, H.; Shin, Y.C. Analysis of bearing configuration effects on high speed spindles using an integrated dynamic thermo-mechanical spindle model. Int. J. Mach. Tools Manuf. 2004, 44, 347–364. [Google Scholar] [CrossRef]
- Li, H.; Shin, Y.C. Integrated dynamic thermo-mechanical modeling of high speed spindles, part 1: Model development. J. Manuf. Sci. Eng. 2004, 126, 148–158. [Google Scholar] [CrossRef]
- Li, H.; Shin, Y.C. Integrated dynamic thermo-mechanical modeling of high speed spindles, part 2: Solution procedure and Validations. J. Manuf. Sci. Eng. 2004, 126, 159–168. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Zhang, P.; Zhou, J. Dynamics modeling and modal experimental study of high speed motorized spindle. J. Mech. Sci. Technol. 2017, 31, 1049–1056. [Google Scholar] [CrossRef]
- Xu, K.; Wang, B.; Zhao, Z.; Zhao, F.; Kong, X.; Wen, B. The influence of rolling bearing parameters on the nonlinear dynamic response and cutting stability of high-speed spindle systems. Mech. Syst. Signal Process. 2020, 136, 106448. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, F.L. Analysis on high-speed spindle online dynamic balancing regulation characteristics. Appl. Mech. Mater. 2017, 868, 207–211. [Google Scholar] [CrossRef]
- Hao, J.; Li, C.; Song, W.; Yao, Z.; Miao, H.; Xu, M.; Gong, X.; Lu, H.; Liu, Z. Thermal-mechanical dynamic interaction in high-speed motorized spindle considering nonlinear vibration. Int. J. Mech. Sci. 2023, 240, 107959. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Liu, M. Contact Analysis for Spiral Bevel Gear Based on Machine Parameters. In Recent Advances in Mechanisms, Transmissions and Applications: Proceedings of the Fifth MeTrApp Conference 2019; Springer: Berlin/Heidelberg, Germany, 2019; Volume 5, pp. 51–61. [Google Scholar]
- Zhiyong, W.; Weitao, D.U. Dynamics Analysis of Spindle-bearing Systems on Spiral Bevel Gear Cutting Machines. China Mech. Eng. 2019, 30, 2211–2216, 2223. [Google Scholar] [CrossRef]

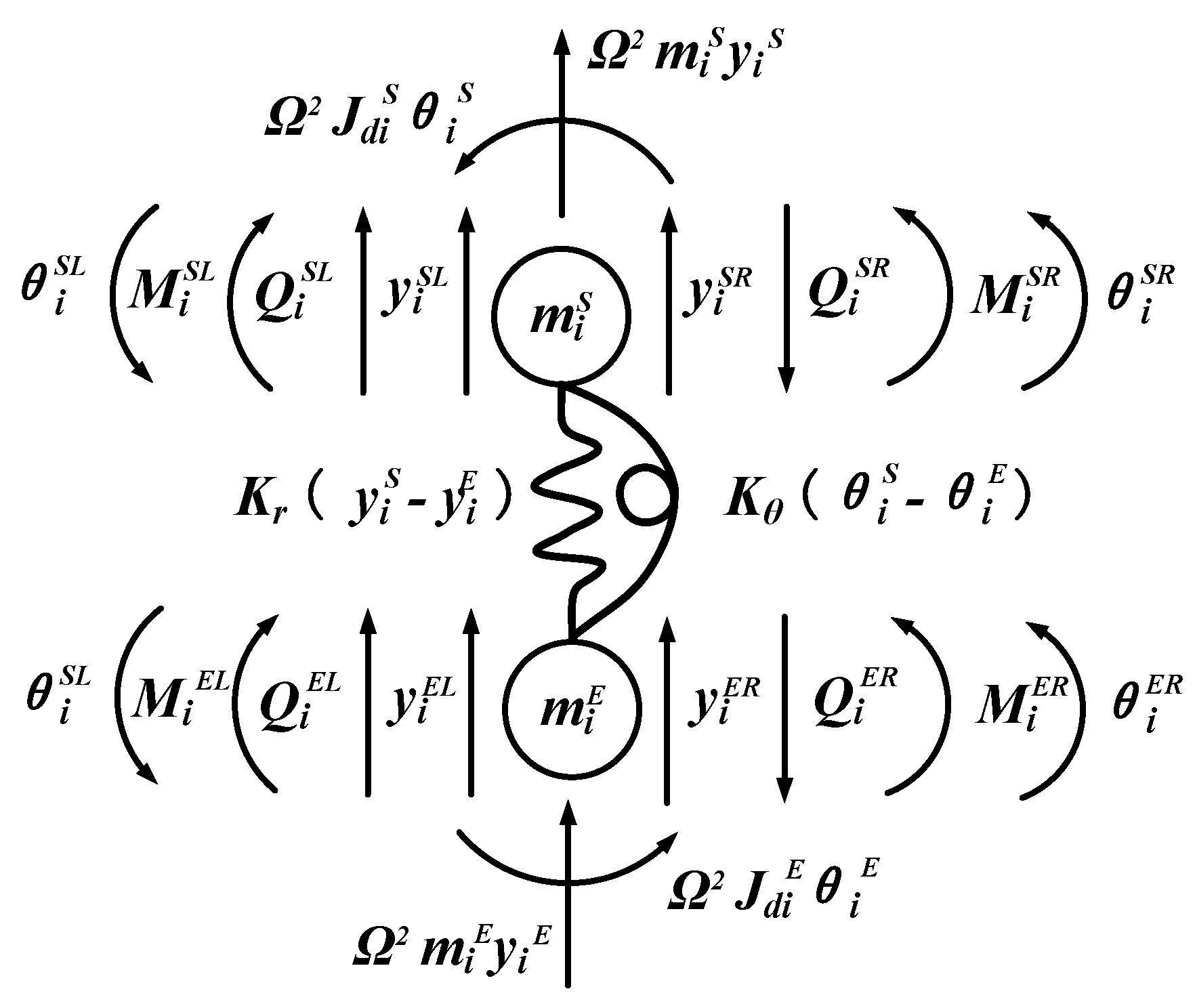
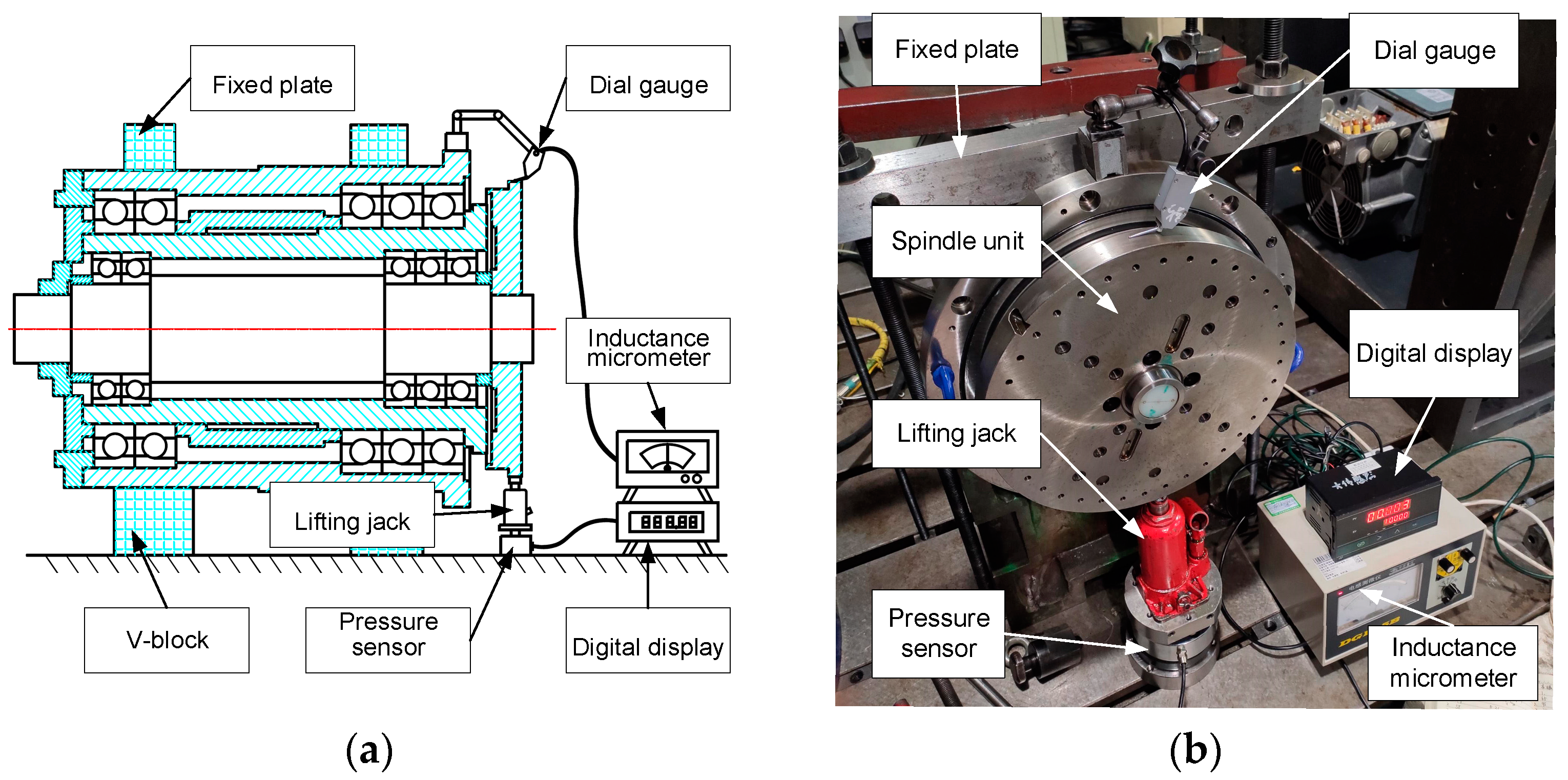
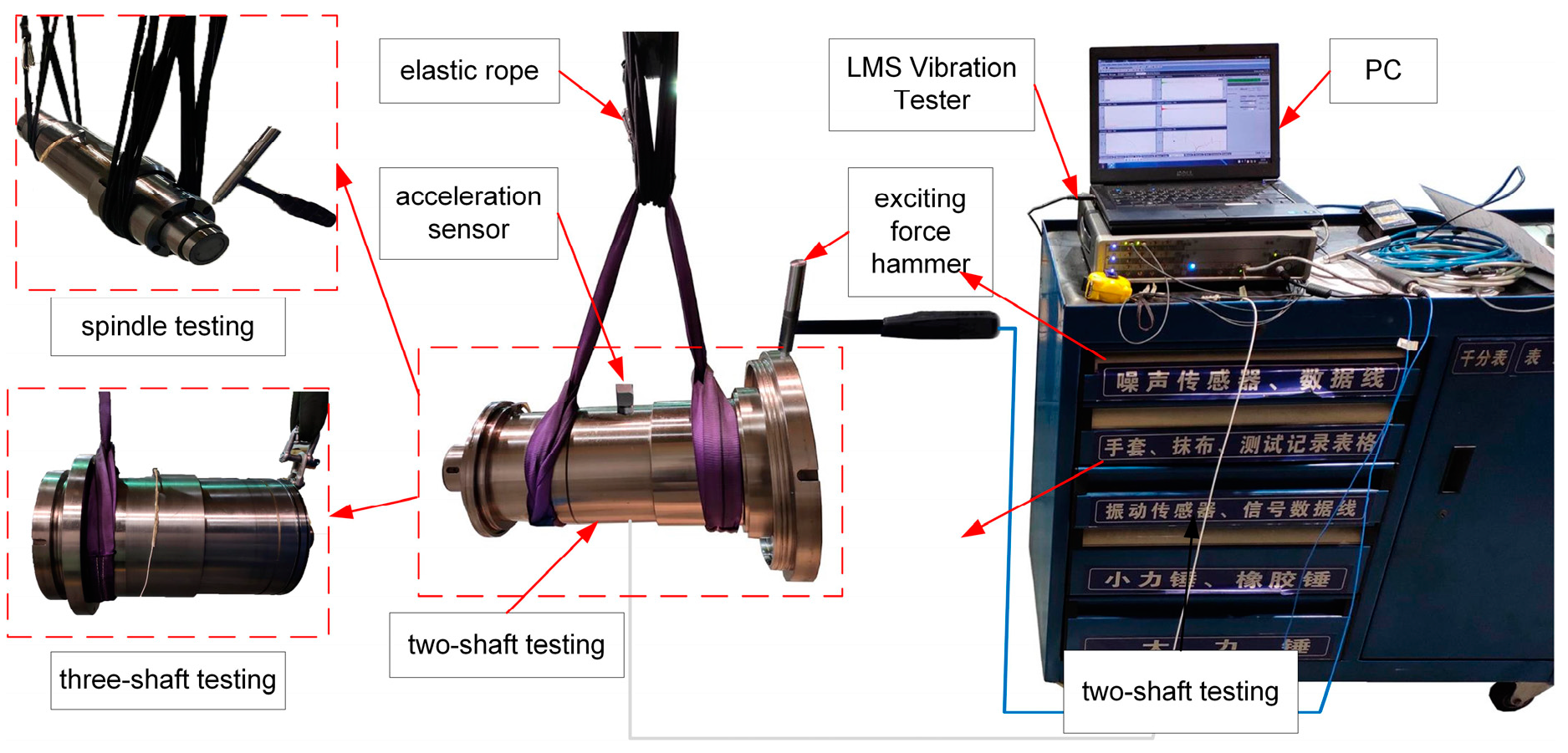
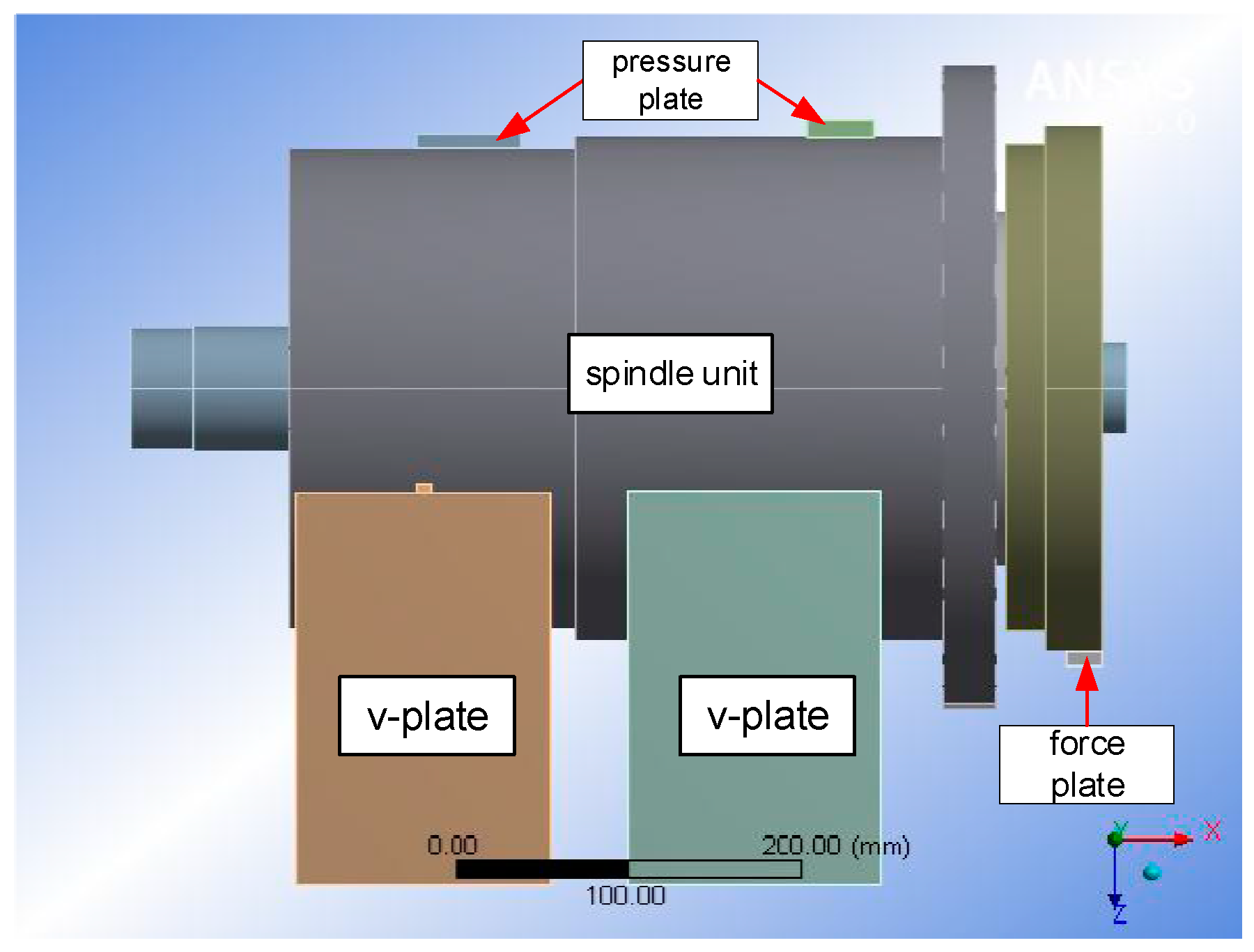

| Test Type | Theoretical Value (N/μm) | Experimental Value (N/μm) |
|---|---|---|
| Two-shaft front end (light preload) | 586.7 | 595.3 (1.44%) |
| Two-shaft front end (medium preload) | 677.9 | 696.1 (2.61%) |
| Two-shaft rear end | 287.1 | 294.6 (2.55%) |
| Three-shaft | 392.4 | 405.4 (3.21%) |
| Assembly Scheme | Experiment (Hz) | Theoretical Value (Hz) | FE (Hz) |
|---|---|---|---|
| Two-shaft First Order | 871.6 | 877.4 (0.66%) | 877.2 (0.64%) |
| Two-shaft Second Order | 1424.1 | 1333.2 (−6.38%) | 1397.8 (1.85%) |
| Three-shaft First Order | 702.9 | 716.1 (1.88%) | 687.2 (−2.23%) |
| Three-shaft Second Order | 943.6 | 880.4 (−6.70%) | 905.3 (−4.06%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Wang, J.; Huang, K.; Yu, J. A Study on the Static and Dynamic Characteristics of the Spindle System of a Spiral Bevel Gear Grinding Machine. Machines 2024, 12, 619. https://doi.org/10.3390/machines12090619
Huang S, Wang J, Huang K, Yu J. A Study on the Static and Dynamic Characteristics of the Spindle System of a Spiral Bevel Gear Grinding Machine. Machines. 2024; 12(9):619. https://doi.org/10.3390/machines12090619
Chicago/Turabian StyleHuang, Shuai, Juxin Wang, Kaifeng Huang, and Jianwu Yu. 2024. "A Study on the Static and Dynamic Characteristics of the Spindle System of a Spiral Bevel Gear Grinding Machine" Machines 12, no. 9: 619. https://doi.org/10.3390/machines12090619
APA StyleHuang, S., Wang, J., Huang, K., & Yu, J. (2024). A Study on the Static and Dynamic Characteristics of the Spindle System of a Spiral Bevel Gear Grinding Machine. Machines, 12(9), 619. https://doi.org/10.3390/machines12090619





