Design and Experimentation of the Millet Combine Harvester Header
Abstract
1. Introduction
2. Materials and Methods
2.1. Millet Mechanical Properties
2.2. Design of Key Header Components
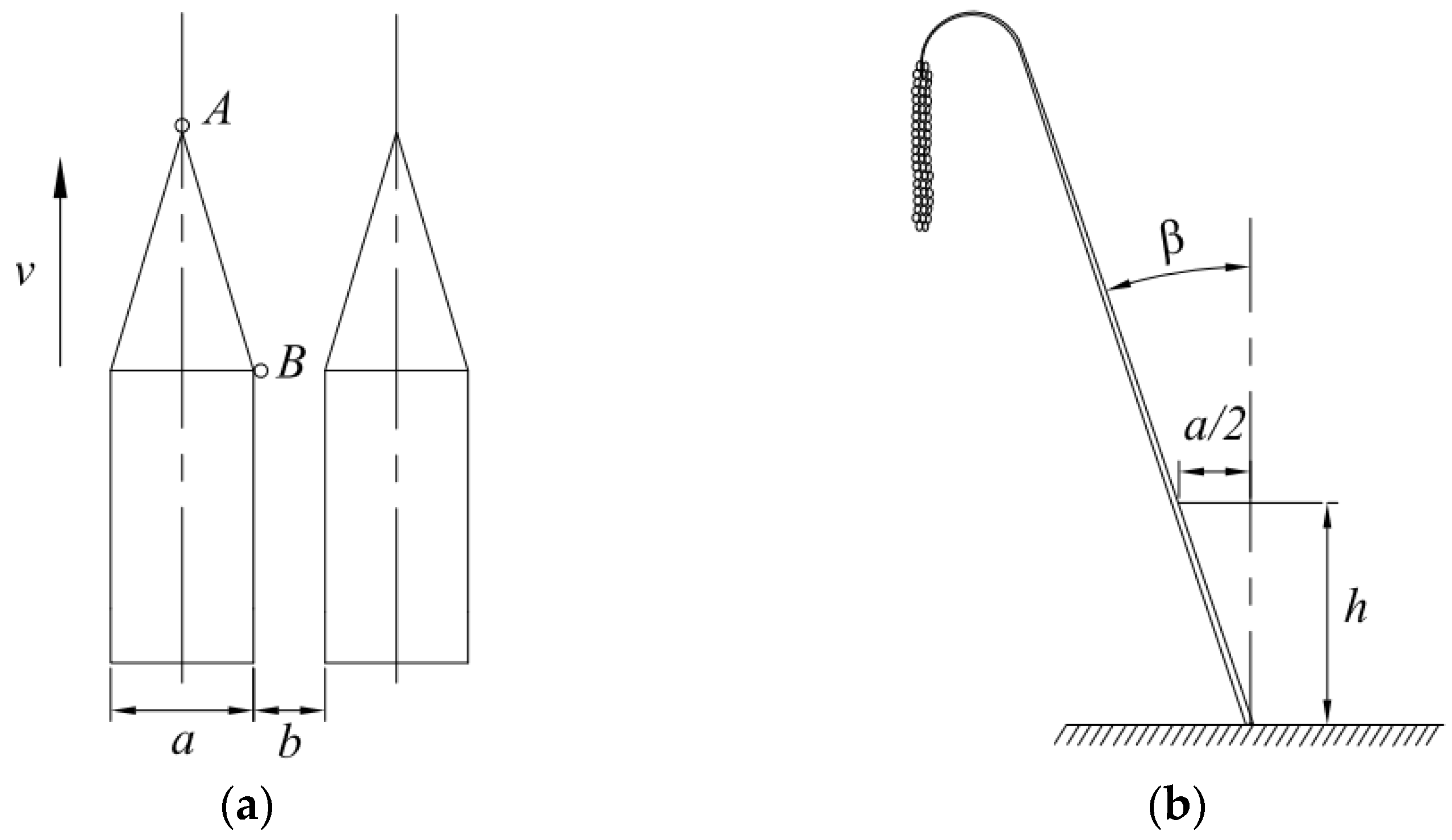
2.2.1. Design of Divider Length
2.2.2. Design of Divider Width
2.2.3. Design of Divider Angle
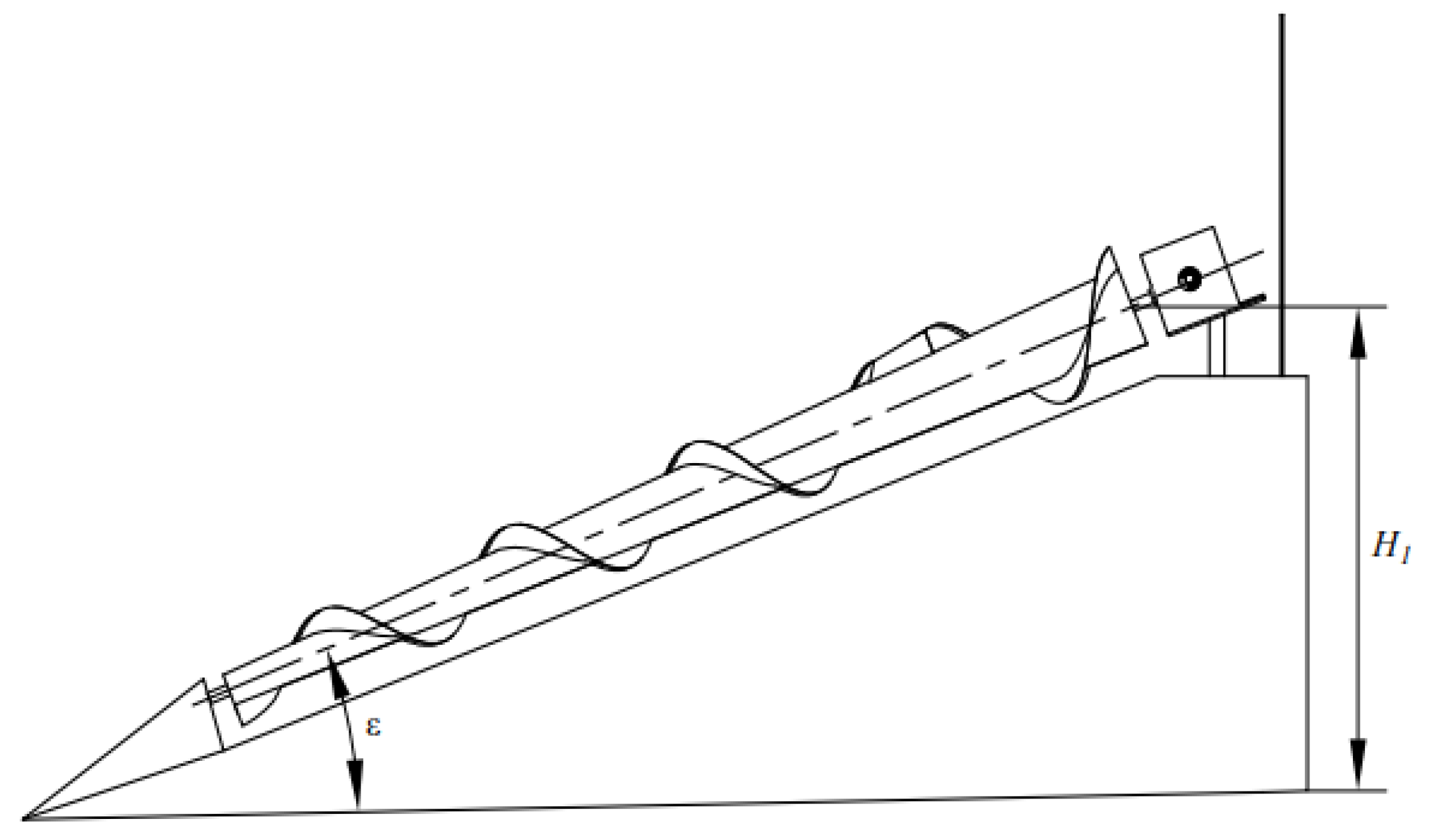
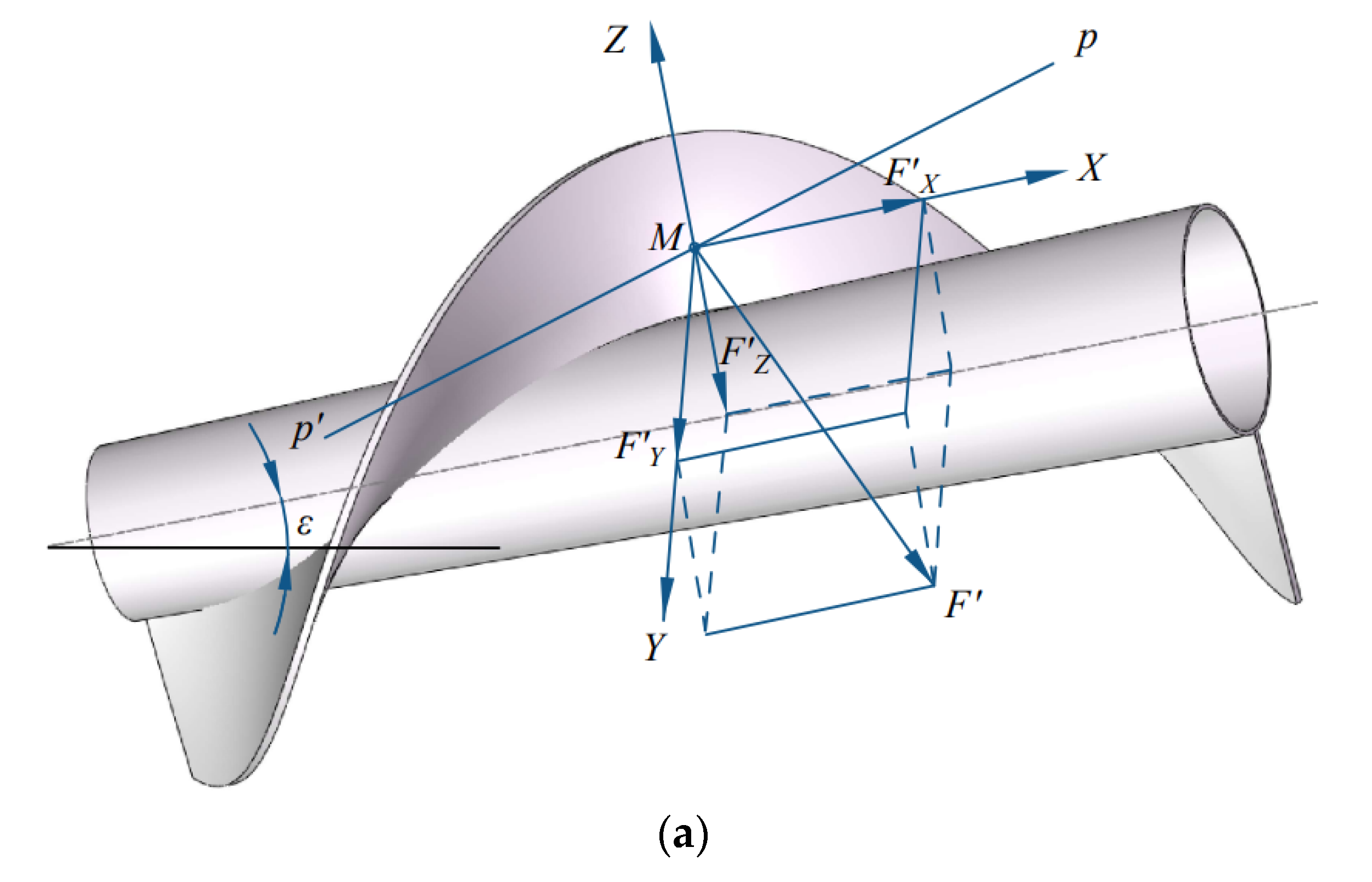
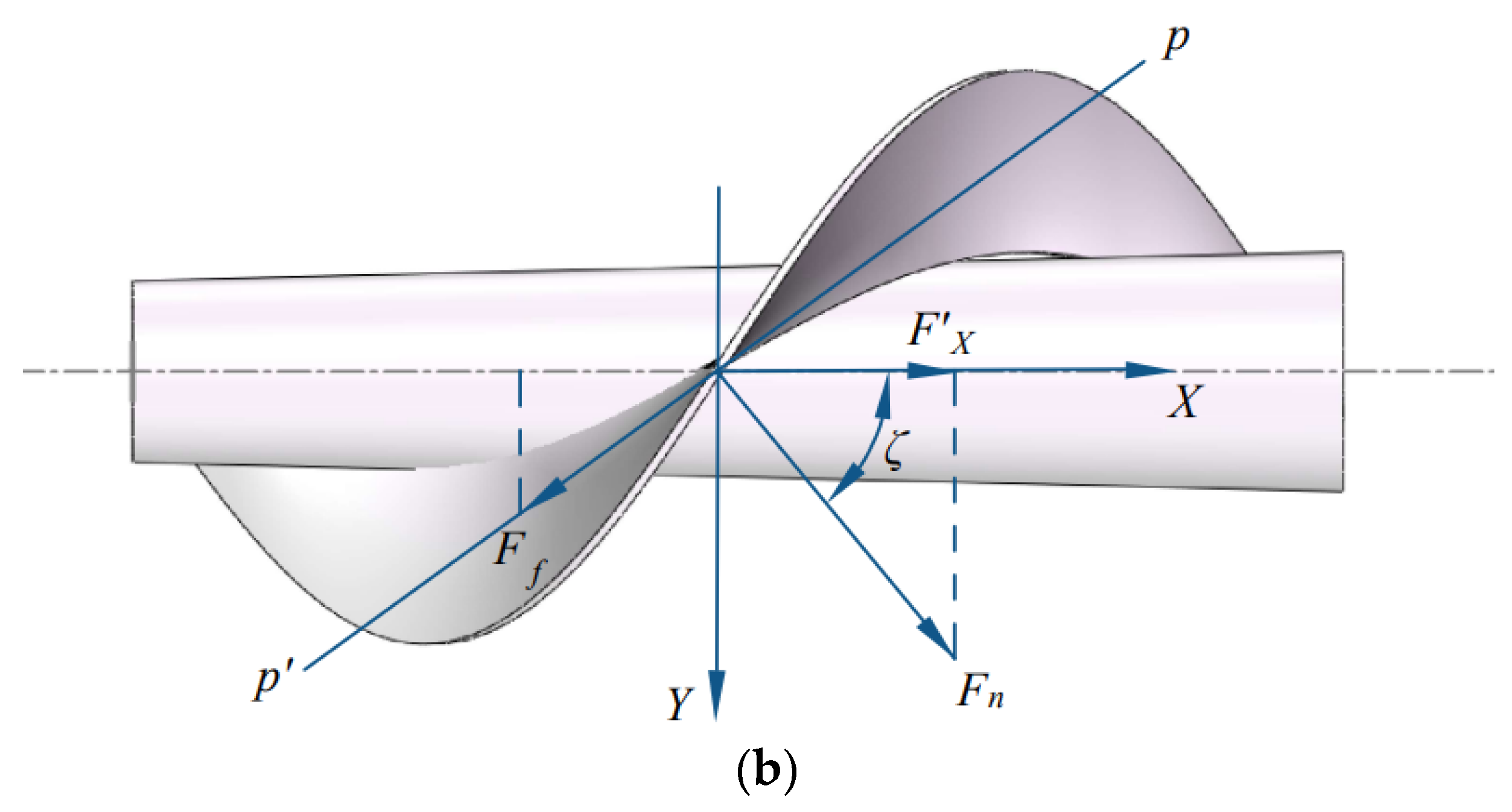
2.2.4. Parameter Design of the Grain-Lifting Cone
2.3. Overall Structure and Working Principle of the Header
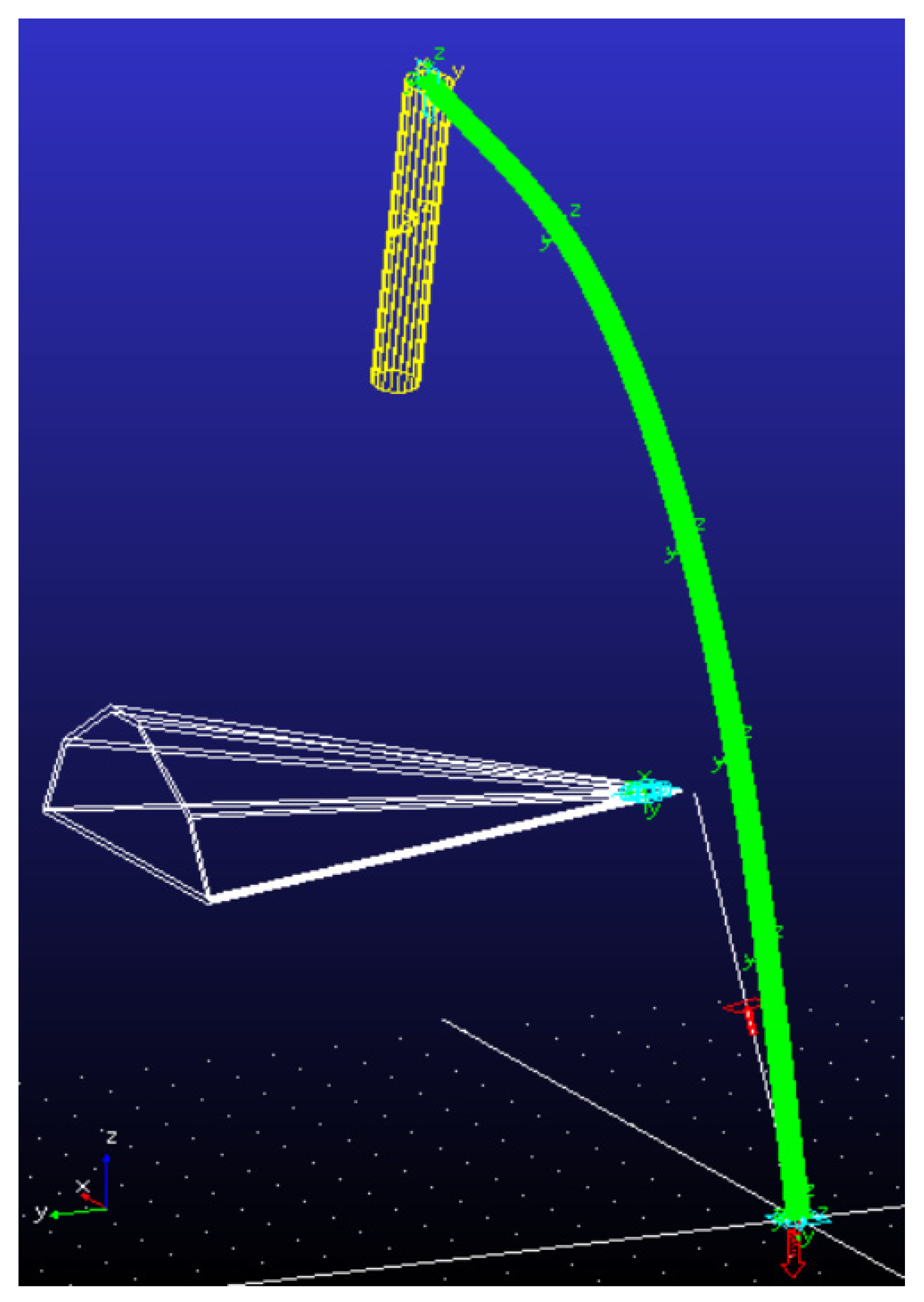
2.4. Simulation Model Establishment
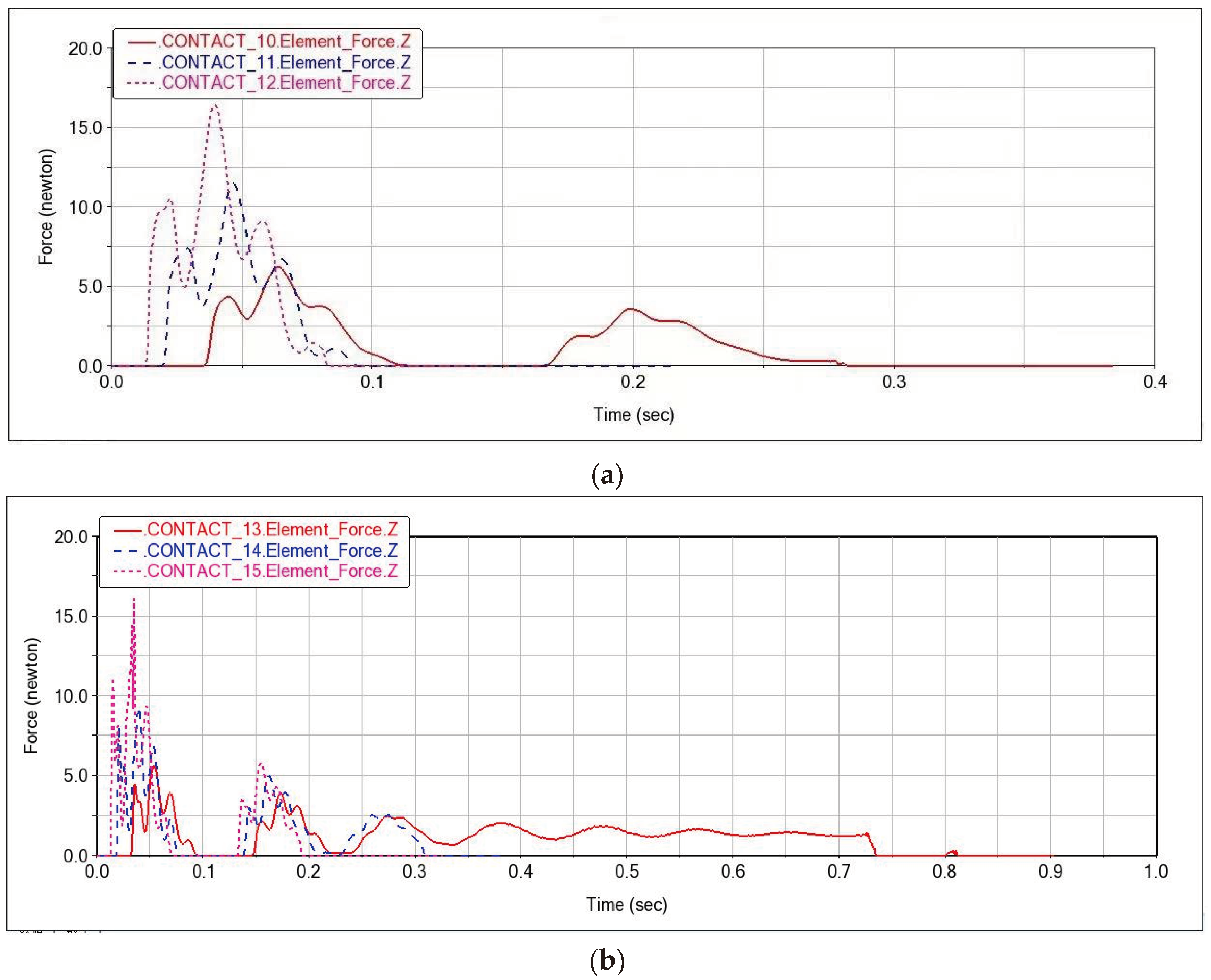
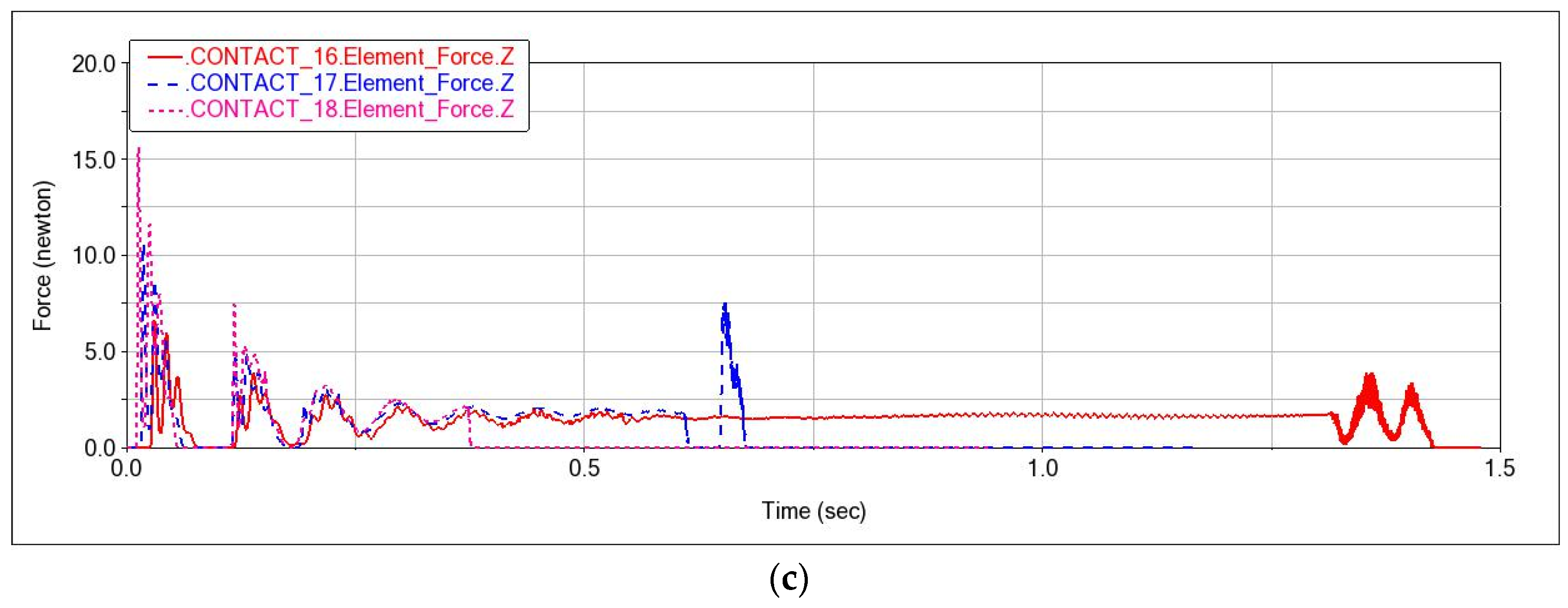
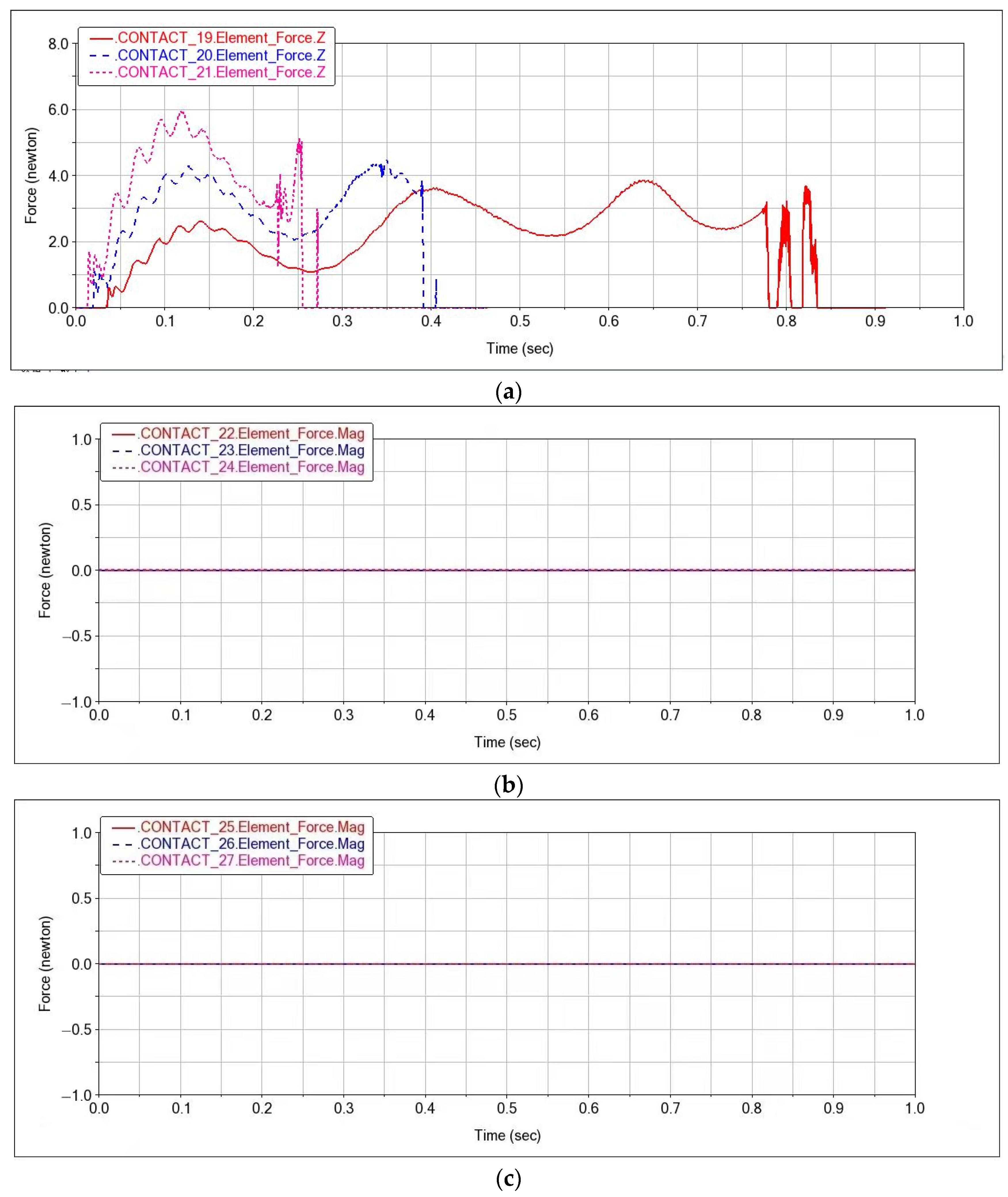
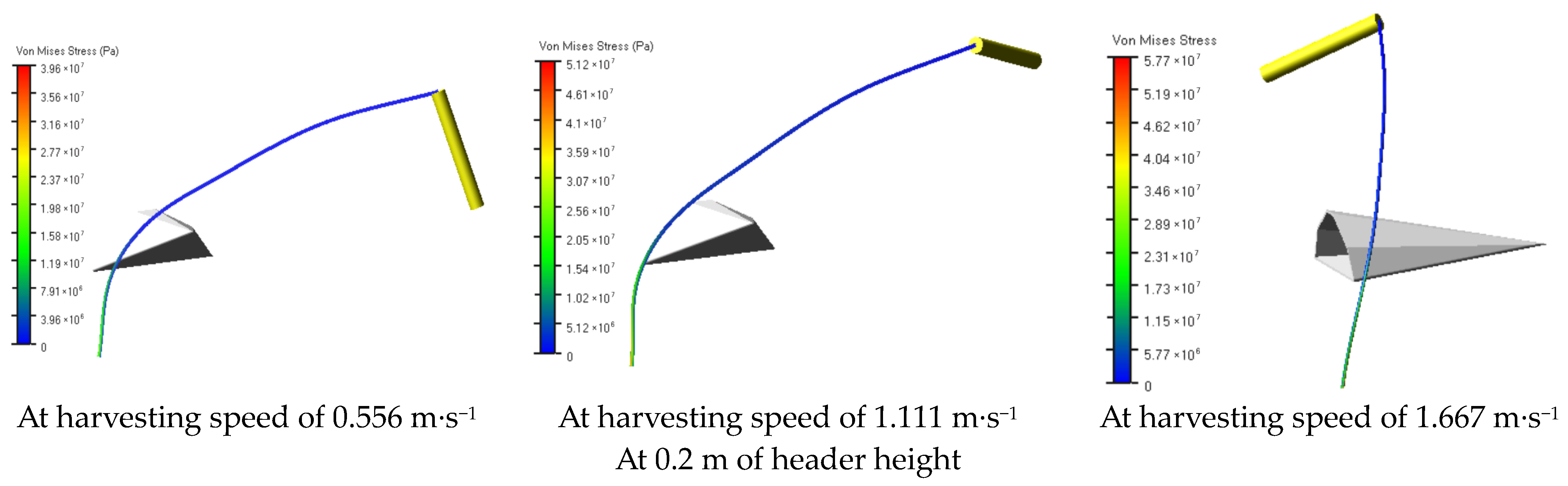
2.5. Simulated Experiments
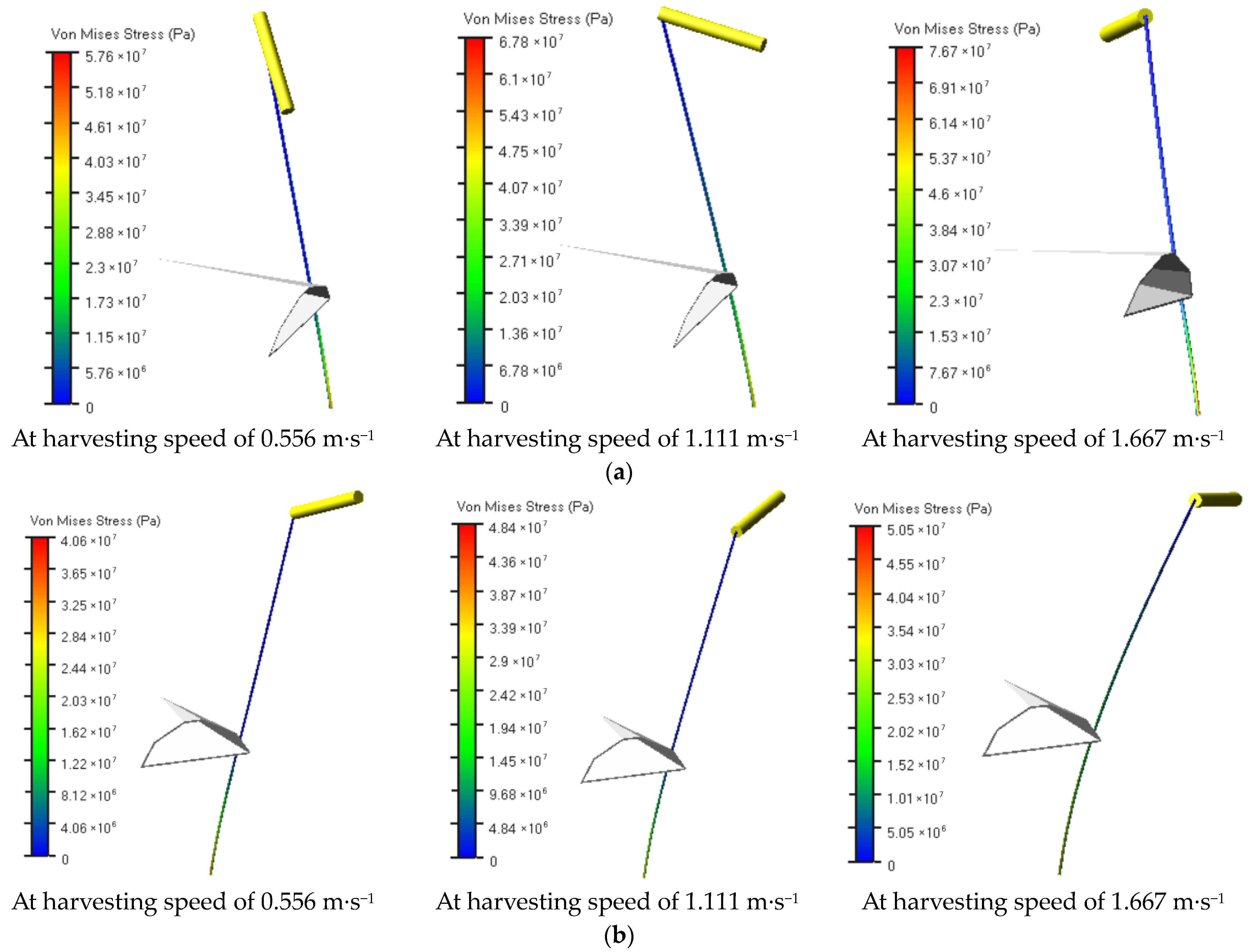
3. Results
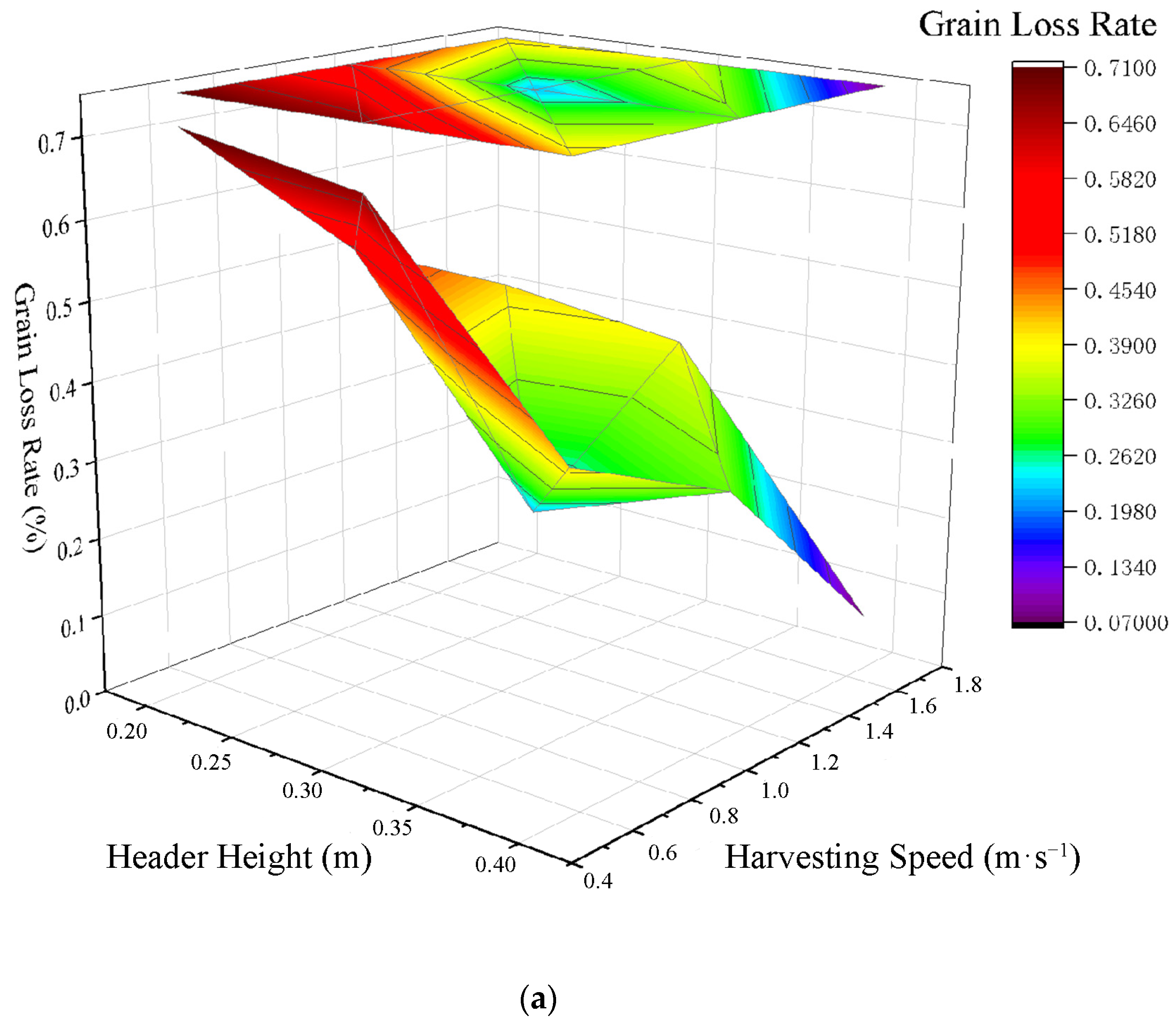
3.1. Experimental Design and Test Results
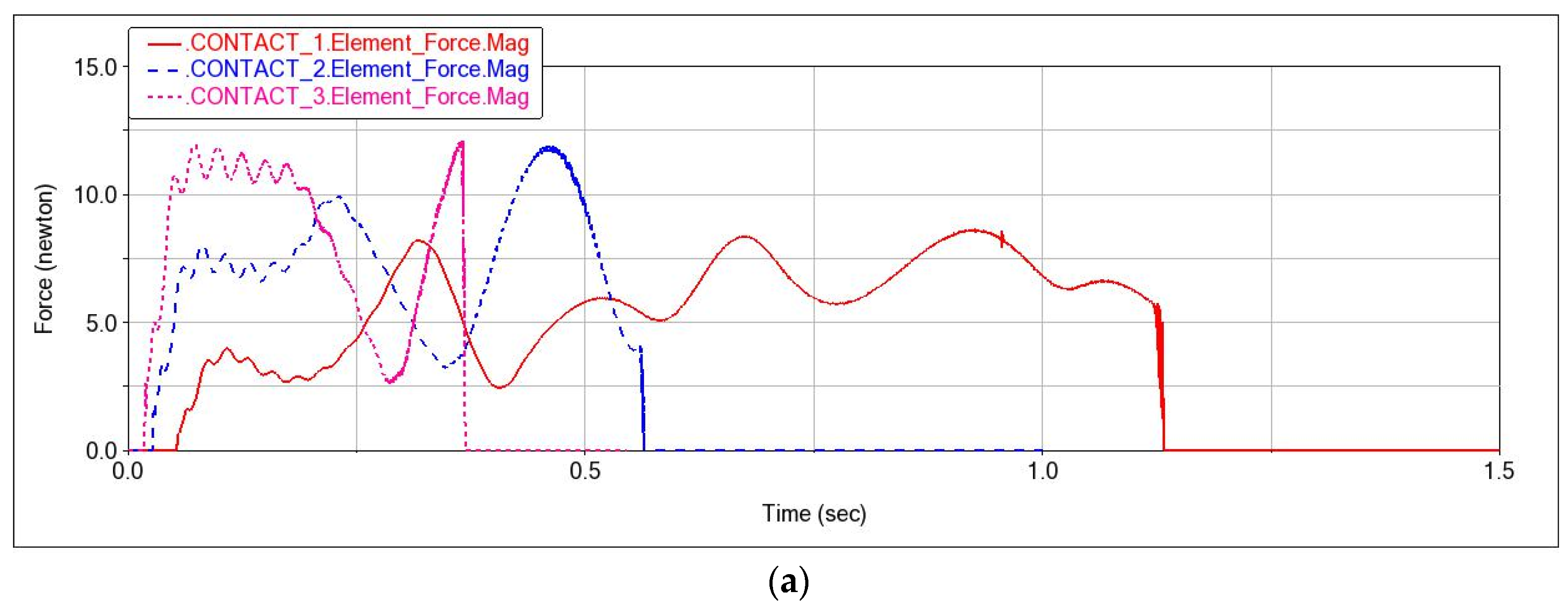
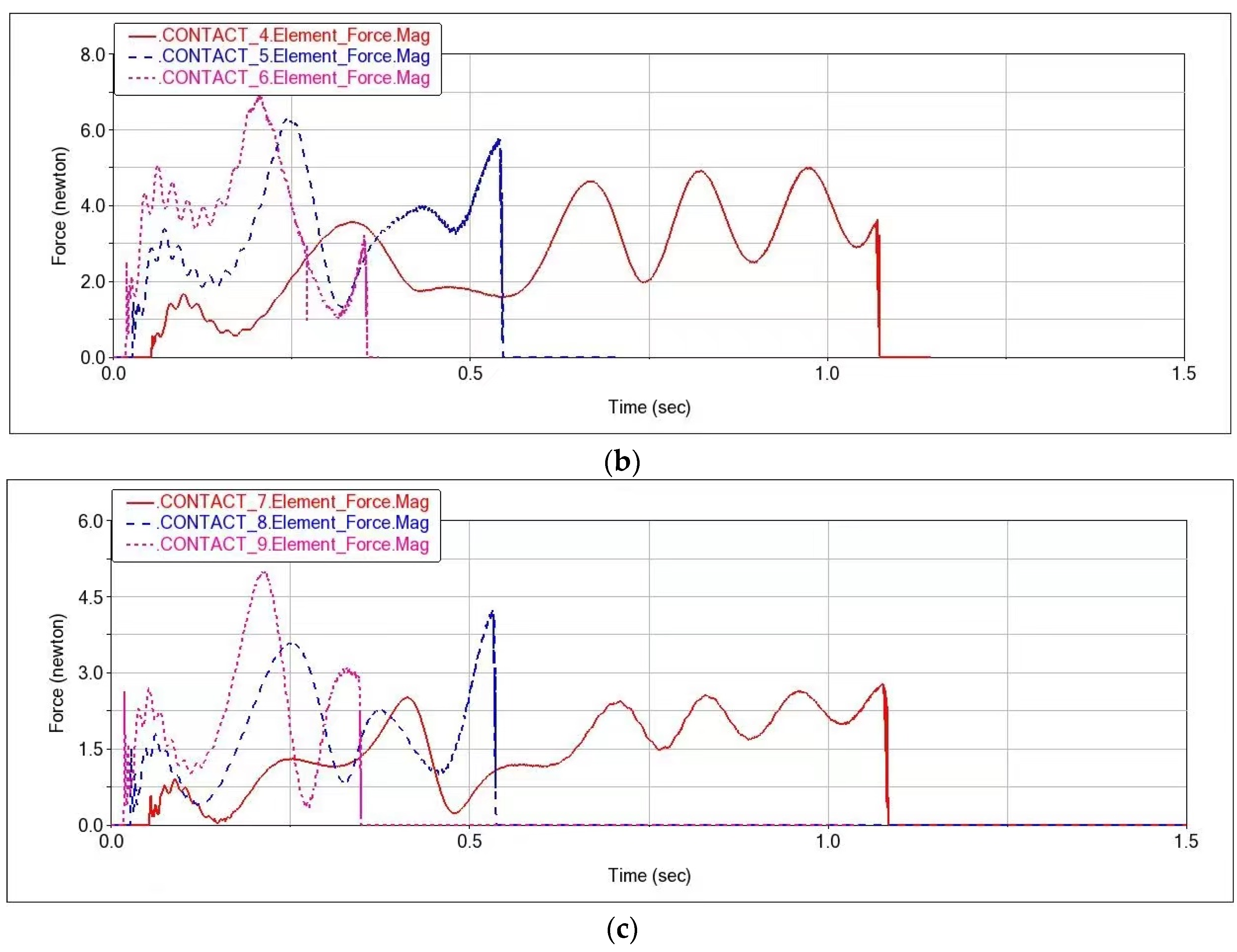
3.2. Analysis of Test Results
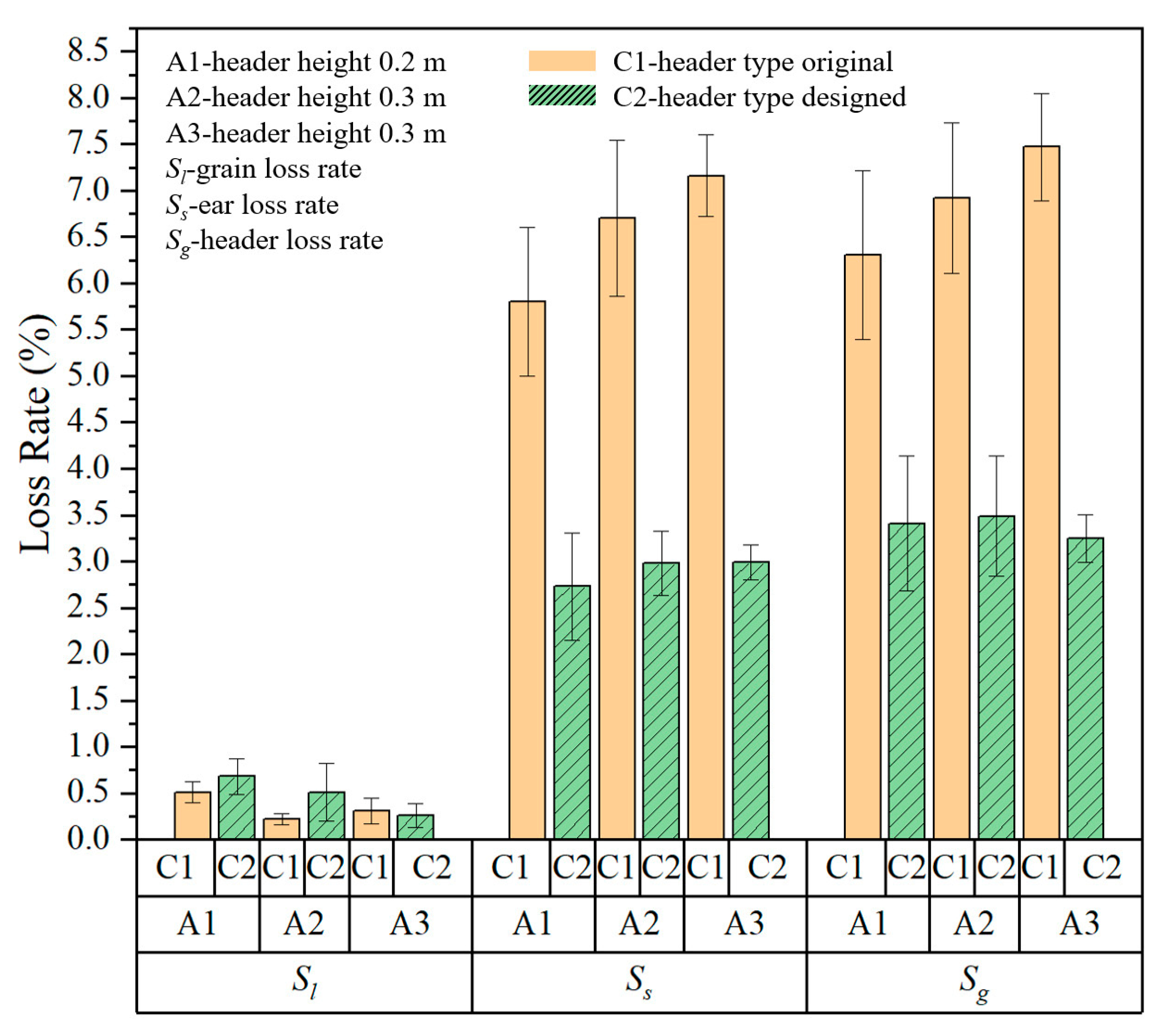
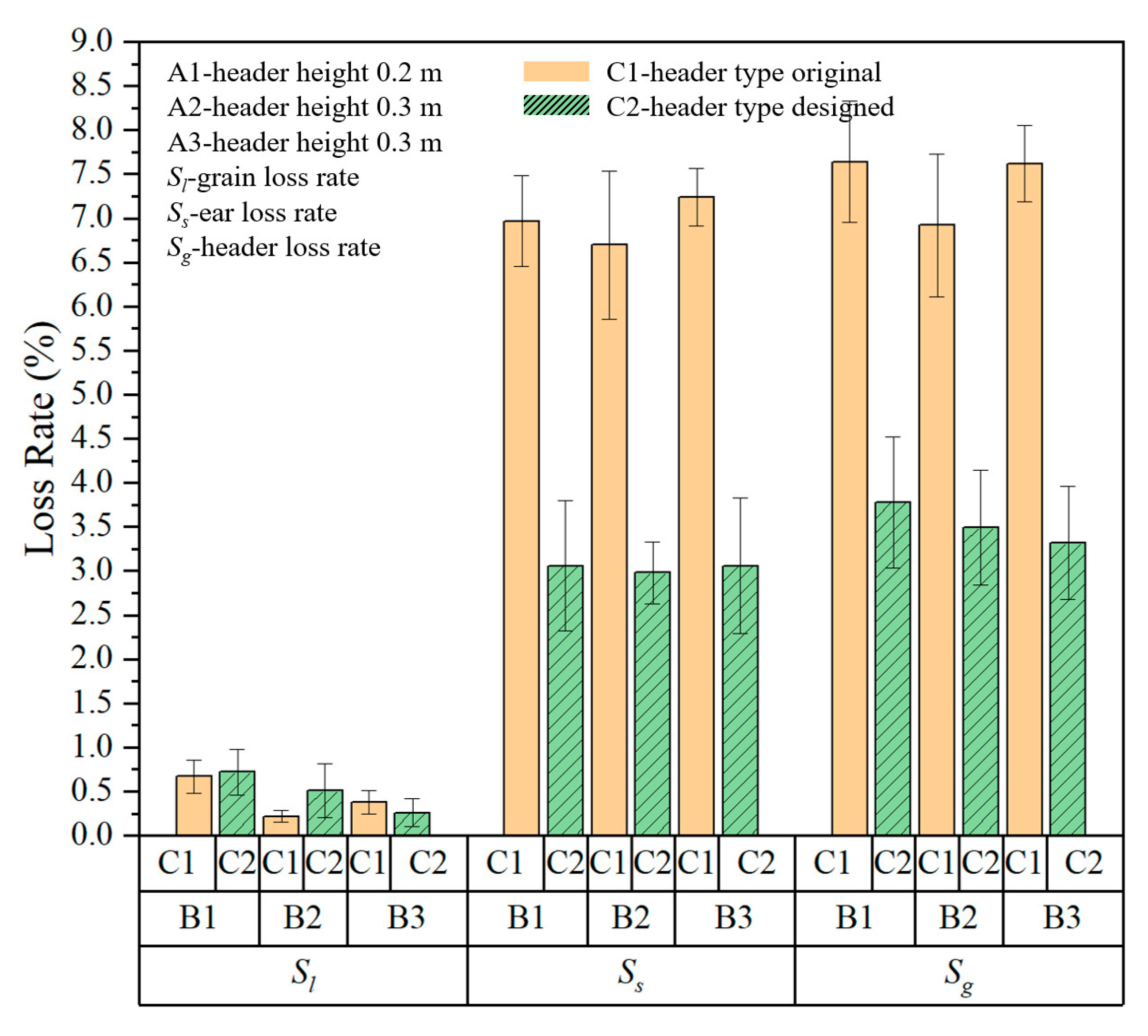
3.3. Field Experiment Results
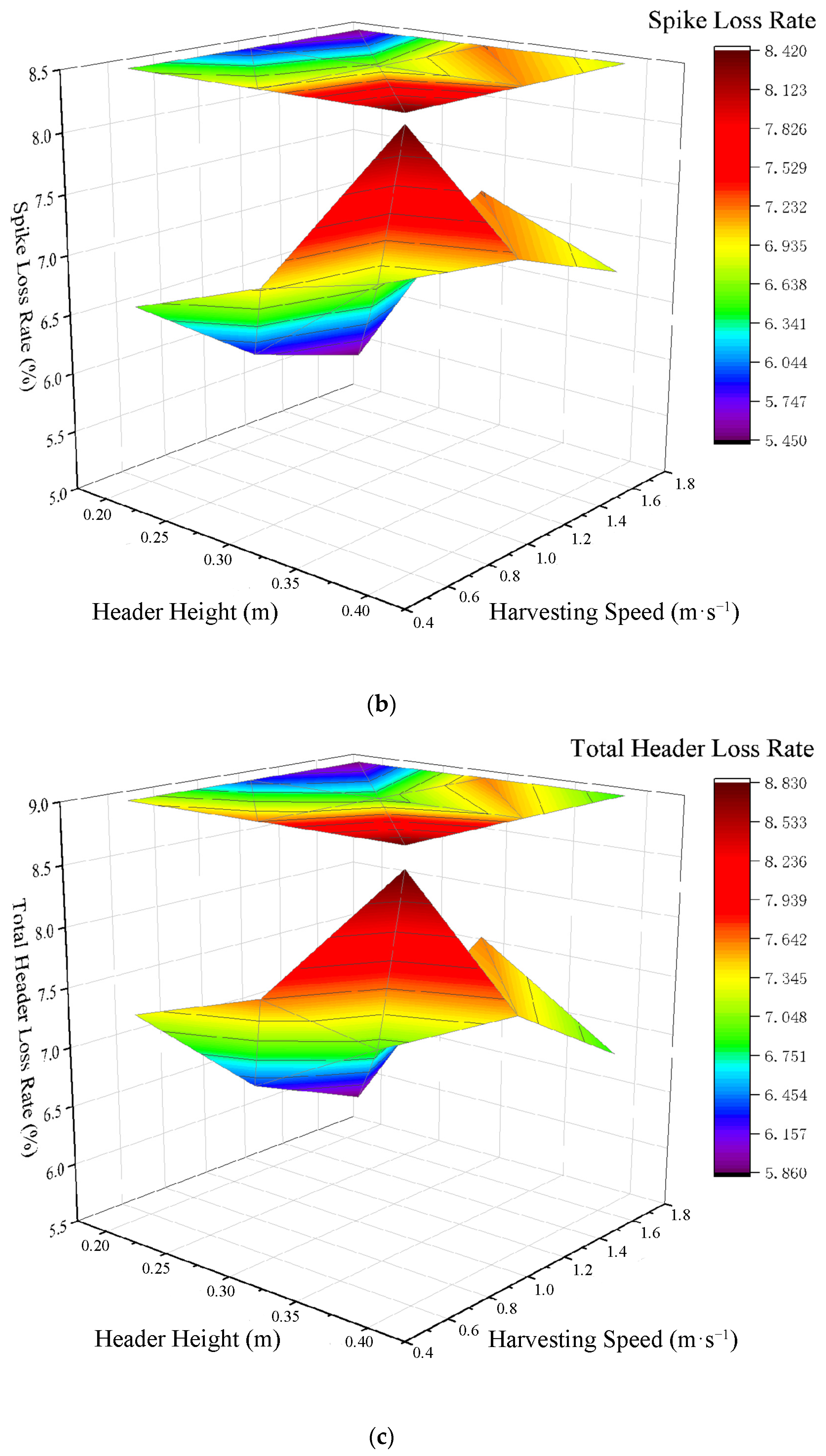
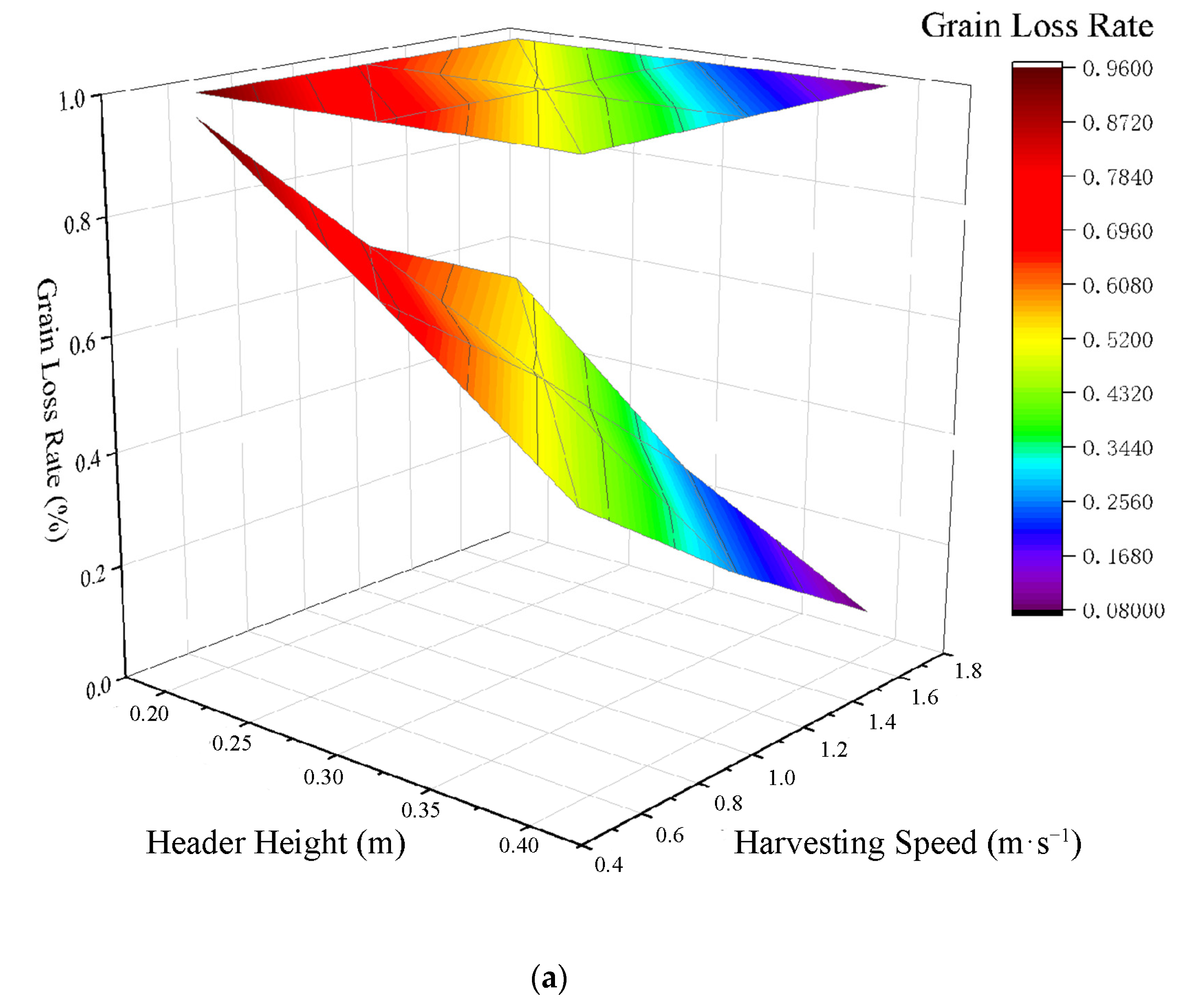
3.3.1. Effect of Header Height on Millet Harvester Header Loss Rate
3.3.2. Effect of Harvesting Speed on Millet Harvester Header Loss Rate
3.3.3. Effect of Header Type on Millet Harvester Header Loss Rate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bandyopadhyay, T.; Singh, R.K.; Ramesh, P.; Maurya, J.; Prasad, M. The Promise of Millets in the Twenty-First Century: Emphasis on Breeding, Nutrition, Food Security and Sustainability. J. Soil Sci. Plant Nutr. 2022, 23, 628–637. [Google Scholar] [CrossRef]
- Li, S.G.; Liu, F.; Liu, M.; Cheng, R.H.; Xia, E.J.; Diao, X.M. Current Status and Future Prospective of Foxtail Millet Production and Seed Industry in China. Sci. Agric. Sin. 2021, 54, 459–470. [Google Scholar]
- Wang, F.; Liu, Y.; Li, Y.; Ji, K. Research and Experiment on Variable-Diameter Threshing Drum with Movable Radial Plates for Combine Harvester. Agriculture 2023, 13, 1487. [Google Scholar] [CrossRef]
- Liang, Z.; Wada, M.E. Development of cleaning systems for combine harvesters: A review. Biosyst. Eng. 2023, 236, 79–102. [Google Scholar] [CrossRef]
- Ding, B.; Liang, Z.; Qi, Y.; Ye, Z.; Zhou, J. Improving Cleaning Performance of Rice Combine Harvesters by DEM–CFD Coupling Technology. Agriculture 2022, 12, 1457. [Google Scholar] [CrossRef]
- Luo, Y.; Wei, L.; Xu, L.; Zhang, Q.; Liu, J.; Cai, Q.; Zhang, W. Stereo-vision-based multi-crop harvesting edge detection for precise automatic steering of combine harvester. Biosyst. Eng. 2022, 215, 115–128. [Google Scholar] [CrossRef]
- Cui, Y.S.; Qin, Y.F.; Wang, H.; Jiao, Z.Y.; Wang, L.G.; Han, K.C.; Ni, G.Q. Discussion on Millet Harvest Mechanization Technology. Farm. Mach. 2020, 3, 108–110. [Google Scholar]
- Li, S.G.; Liu, F.; Zhao, W.Q.; Liu, M.; Xia, E.J.; Diao, X.M. The development history, integration models, and path selection for China’s foxtail millet seed industry. Res. Agric. Mod. 2023, 44, 32–43. [Google Scholar]
- Qiu, S.J.; Yuan, X.Y.; Zhang, Z.Q.; Zhao, Y.C.; Zhang, L. The effects of maturity period and harvesting methods on the harvesting performance of millet. J. Shanxi Agric. Univ. Nat. Sci. Ed. 2021, 41, 108–114. [Google Scholar]
- Li, L.; Zhou, L.; Hao, J.H.; Chen, C. Research on the competitiveness of agricultural modernization in the context of the 20th National Congress of the Communist Party of China—Taking Nanjing, Jiangsu as an example. J. Intell. Agric. Mech. 2023, 4, 49–56, (In Chinese and English). [Google Scholar]
- Pei, F.Q.; Yang, K.W.; Wang, M.; Tong, Y.F. Analysis of application status of intelligent manufacturing in agricultural machinery. J. Intell. Agric. Mech. 2022, 3, 7–19, (In Chinese and English). [Google Scholar]
- Qian, Z.J.; Jin, C.Q.; Liu, Z.; Yang, T.X. Development status and trends of intelligent control technology in unmanned farms. J. Intell. Agric. Mech. 2023, 4, 1–13, (In Chinese and English). [Google Scholar]
- Liang, S.N.; Jin, C.Q.; Zhang, F.F.; Kang, D.; Hu, M.J. Design and experiment of 4LZG-3.0 millet combine harvester. Trans. Chin. Soc. Agric. Eng. 2015, 31, 31–38. [Google Scholar]
- Zheng, G.Q.; Li, Y.M.; Ji, K.Z.; Liang, Z.W.; Ma, X.; Cheng, J.H. Vibration analysis and structural optimization of header frame of millet combine harvester. J. Agric. Mech. Res. 2024, 46, 41–45+53. [Google Scholar]
- Wang, R.X.; Chang, Y.P.; Li, B.; Lyu, W.Z.; Liu, J.L. Design and experiment on the key components of millet combine harvester header. J. Agric. Mech. Res. 2022, 44, 30–36. [Google Scholar]
- Li, C. Design and Experimental Study on Low-Loss Header of Millet Combine Harvester. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, May 2019. [Google Scholar]
- Zhang, X.M. The Design and Study on the Cutting Platform of Millet Combine Harvester. Master’s Thesis, Shanxi Agricultural University, Jinzhong, China, June 2017. [Google Scholar]
- Zhang, M.; Jin, M.; Wang, G.; Liang, S.N.; Wu, C.Y. Design and Test of Double Crank Planar Five-bar Reel in Rape Windrower. Trans. Chin. Soc. Agric. Mach. 2022, 53, 115–122. [Google Scholar]
- Chen, H.T.; Dun, G.Q. Optimization of parameters for soybean lifter based on dynamic simulation of virtual prototype. Trans. Chin. Soc. Agric. Eng. 2012, 28, 23–29. [Google Scholar]
- Gu, L.L.; Cao, W.B.; Sun, W.L.; Liu, J.D.; Tian, D.Y.; Ma, P. Motion Simulation and Design of Safflower Harvester Crop Lifter Adjustment Mechanism. J. Agric. Mech. Res. 2018, 40, 17–21. [Google Scholar]
- Guo, J.D.; Wu, D.L.; Chen, L.Q. Simulation of Maize Culm with Harvester Header Based on ADAMS. J. Agric. Mech. Res. 2016, 38, 80–85+100. [Google Scholar]
- Hu, Z.C.; Wang, H.O.; Peng, B.L.; Chen, Y.Q.; Wu, F.; Xie, H.X. Performance analysis and experiment on operation process of plant lifting device in 4HLB-2 type peanut combine harvester. Trans. Chin. Soc. Agric. Eng. 2012, 28, 26–31. [Google Scholar]
- Liu, W.; Huang, X.M.; Ma, L.N.; Zong, W.Y.; Zhu, Y.F. Design and Experiment of Special Header of Oil Sunflower Combine Harvester. Trans. Chin. Soc. Agric. Mach. 2020, 51, 83–88+135. [Google Scholar]
- Shu, C.X.; Cao, S.C.; Liao, Y.T.; Liao, Q.X.; Wan, X.Y.; Li, Y.T. Parameter Optimization and Experiment of Forward Laying Device for Rape Windrower Based on ADAMS. Trans. Chin. Soc. Agric. Mach. 2022, 53, 11–19+38. [Google Scholar]
- Liu, W.; Zeng, S.; Chen, X. Design and Experiment of Adaptive Profiling Header Based on Multi-Body Dynamics–Discrete Element Method Coupling. Agriculture 2024, 14, 105. [Google Scholar] [CrossRef]
- Pang, J.; Li, Y.; Ji, J.; Xu, L. Vibration excitation identification and control of the cutter of a combine harvester using triaxial accelerometers and partial coherence sorting. Biosyst. Eng. 2019, 185, 25–34. [Google Scholar] [CrossRef]
- Ma, Z.; Zhu, Y.; Chen, S.; Traore, S.N.; Li, Y.; Xu, L.; Shi, M.; Zhang, Q. Field Investigation of the Static Friction Characteristics of High-Yielding Rice during Harvest. Agriculture 2022, 12, 327. [Google Scholar] [CrossRef]
- Wang, Z.X.; Wang, L.H.; Xu, N.H.; Li, Y.; Shi, J.C. Research on the control strategy of sideslip and hysteresis of intelligent harvesting robot. J. Intell. Agric. Mech. 2022, 3, 37–44, (In Chinese and English). [Google Scholar]
- Wang, Y.K. Design and Virtual Experiment Research on Key Components of Corn Harvester Plate Header. Master’s Thesis, Shandong Agricultural University, Taian, China, May 2021. [Google Scholar]
- Li, L.; Gan, Z.Y.; Li, C.B.; Li, L.L.; Liu, J.W.; Wang, H.J. Design parameter optimization method of screw conveyor for high efficiency and energy saving. Comput. Integr. Manuf. Syst. 2023, 29, 2585–2594. [Google Scholar]
- Sosa-Méndez, D.; Lugo-González, E.; Arias-Montiel, M.; García-García, R.A. ADAMS-MATLAB co-simulation for kinematics, dynamics, and control of the Stewart–Gough platform. Int. J. Adv. Robot. Syst. 2017, 4, 1729881417719824. [Google Scholar] [CrossRef]
- Li, H.B.; Xue, J.X.; Wang, B.X.; Zhang, Y.Q.; Wu, X.H.; Li, X.B.; Cui, Q.L.; Yang, Z.M. Tensile properties of foxtail millet leaf sheath, leaf and leaf collar. Trans. Chin. Soc. Agric. Eng. 2020, 36, 11–17. [Google Scholar]
- Zhang, L. The Influence of Header Parameters on the Quality of Foxtail Millet Harvest in a Grain Combine Harvester. Master’s Thesis, Shanxi Agricultural University, Taian, China, June 2021. [Google Scholar]
- Wang, G.X.; Ma, D.L.; Liu, Y.; Liu, C.S. Research progress of contact force models in the collision mechanics of multibody system. Chin. J. Theor. Appl. Mech. 2022, 54, 3239–3266. [Google Scholar]
- Du, Y.; Mao, E.; Song, Z.; Zhu, Z.; Gao, J. Simulation on Corn Plants in Harvesting Process Based on ADAMS. Trans. Chin. Soc. Agric. Mach. 2012, Z1, 106–111. [Google Scholar]
- Vishwas, J.; Anuja-Ria, J. Two-factor, Three-level Factorial Experiments for Optimizing Size of Thiol Stabilized Gold Nanoparticles (AuNPs). Microsc. Microanal. 2023, 29, 2068–2069. [Google Scholar] [CrossRef]
- Ge, Y.Y. Analysis of Variance. In Experimental Design Methods and Application of Design-Expert Software; Wang, J.F., Ed.; Harbin Institute of Technology Press: Harbin, China, 2014; pp. 36–60. ISBN 978-7-5603-4992-3. [Google Scholar]
- GB/T 8097-2008; Test Method for Harvesting Machinery Combine Harvester. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, China National Standardization Administration: Beijing, China, 2008.
- GB/T 5262-2008; Agricultural Machinery Testing Conditions-General Rules for Measuring Methods. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, China National Standardization Administration: Beijing, China, 2008.
- Tihanov, G.; Dallev, M.; Hristova, G.; Mitkov, I. Loss of grain at harvesting wheat with a combine harvester. Series A Agron. 2021, 64, 577–582. [Google Scholar]
- Modak, S.; Raheman, H. Effects of Various Machine Parameters on Cutting Performance for High-speed Cutting of Paddy Crop. J. Biosyst. Eng. 2022, 47, 181–196. [Google Scholar] [CrossRef]
- Stefanoni, W.; Latterini, F.; Malkogiannidis, V.; Salpiggidis, V.; Alexopoulou, E.; Pari, L. Mechanical Harvesting of Castor Bean (Ricinus communis L.) with a Combine Harvester Equipped with Two Different Headers: A Comparison of Working Performance. Energies 2022, 15, 2999. [Google Scholar] [CrossRef]


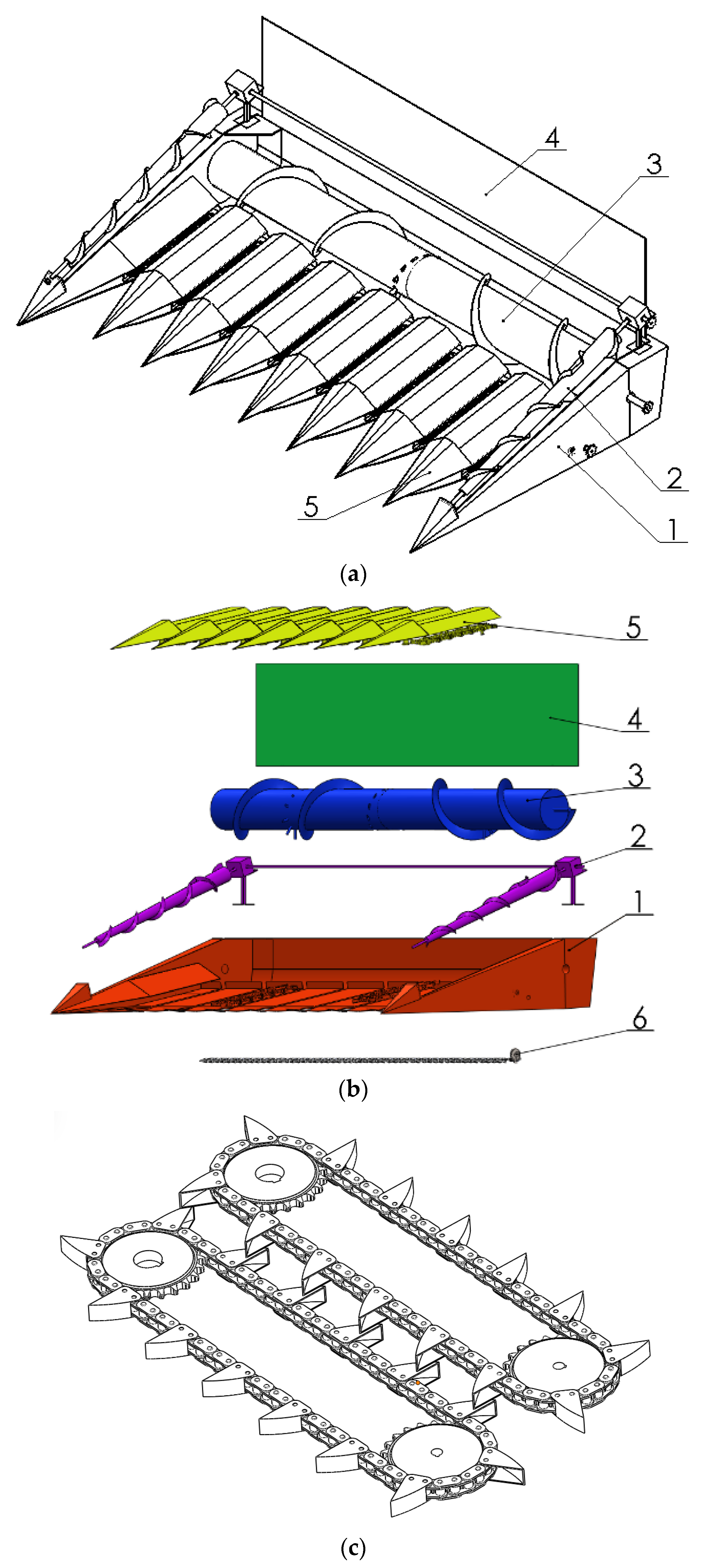





| Parameters | Mean Value | Range |
|---|---|---|
| Plant length, m | 1.50 | 1.23~1.68 |
| Stem length, m | 1.20 | 0.94~1.36 |
| Intersection height, m | 1.03 | 0.82~1.25 |
| Approximate grain density, kg∙m−3 | 42.31 | 31.92~55.18 |
| Critical bending angle of millet stems, ° | 40.51 | 29.3~62.5 |
| Friction angle between millet plants and common materials, ° | 30.88 | 19.7~52.2 |
| Central bending limit load of stems, N | 63.36 | 56.84~72.47 |
| Lower bending limit load of stems, N | 134.08 | 126.38~144.54 |
| Parameters | Parameter Values |
|---|---|
| Length of millet stalks, m | 1.23 |
| Length of millet stalk major axis, m | 0.0084 |
| Length of millet stalk minor axis, m | 0.0066 |
| Density of millet stalks, (kg∙m−3) | 480 |
| Young’s modulus of millet stalks, MPa | 8000 |
| Poisson’s ratio of millet stalks | 0.33 |
| Length of millet spikes, m | 0.271 |
| Radius of millet spikes, m | 0.0175 |
| Density of millet spikes, (kg∙m−3) | 42.3 |
| Parameter | Parameter Values |
|---|---|
| stiffness, (N·m−1) | 2.10 × 107 |
| damping, (N·s·m−1) | 0.1 |
| collision index | 5 |
| penetration depth, m | 0.0001 |
| Factor Level | Factor A Header Height, m | Factor B Harvesting Speed, (m·s−1) |
|---|---|---|
| 1 | 0.2 | 0.556 |
| 2 | 0.3 | 1.111 |
| 3 | 0.4 | 1.667 |
| Number | Experimental Factors | Experimental Indicators | |||
|---|---|---|---|---|---|
| Factor A Header Height, m | Factor B Harvesting Speed, (m·s−1) | The Maximum Contact Force between the Divider and Non-Lodged Millet Plant, N | The Maximum Z-Axis Contact Force for Moderately Lodged Millet Plant, N | The Maximum Z-Axis Contact Force for Severely Lodged Millet Plant, N | |
| 1 | 0.2 | 0.556 | 8.63 | 6.22 | 3.88 |
| 2 | 0.2 | 1.111 | 11.89 | 11.48 | 4.46 |
| 3 | 0.2 | 1.667 | 12.15 | 16.46 | 5.94 |
| 4 | 0.3 | 0.556 | 5.01 | 5.59 | 0 |
| 5 | 0.3 | 1.111 | 6.29 | 9.28 | 0 |
| 6 | 0.3 | 1.667 | 6.92 | 16.09 | 0 |
| 7 | 0.4 | 0.556 | 2.78 | 6.62 | 0 |
| 8 | 0.4 | 1.111 | 4.23 | 10.63 | 0 |
| 9 | 0.4 | 1.667 | 5.01 | 15.62 | 0 |
| Sources of Variance | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Pr > F | |
|---|---|---|---|---|---|---|
| The maximum contact force between the divider and non-lodged millet plant | Model | 85.67 | 4 | 21.42 | 64.18 | 0.0007 |
| A | 74.85 | 2 | 37.43 | 112.15 | 0.0003 | |
| B | 10.82 | 2 | 5.41 | 16.21 | 0.0121 | |
| Error | 1.33 | 4 | 0.33 | |||
| Sum | 87.00 | 8 | ||||
| The maximum Z-axis contact force for moderately lodged millet plant | Model | 149.95 | 4 | 37.49 | 92.14 | 0.0003 |
| A | 1.73 | 2 | 0.86 | 2.12 | 0.2352 | |
| B | 148.22 | 2 | 74.11 | 182.16 | 0.0001 | |
| Error | 1.63 | 4 | 0.41 | |||
| Sum | 151.58 | 8 | ||||
| The maximum Z-axis contact force for severely lodged millet plant | Model | 46.07 | 4 | 11.52 | 30.62 | 0.0029 |
| A | 45.32 | 2 | 22.66 | 60.24 | 0.0010 | |
| B | 0.75 | 2 | 0.38 | 1.00 | 0.4444 | |
| Error | 1.50 | 4 | 0.38 | |||
| Sum | 47.57 | 8 |
| Treatment | A1 | A2 | A3 | B1 | B2 | B3 | C1 | C2 |
|---|---|---|---|---|---|---|---|---|
| Value | 0.2 m | 0.3 m | 0.4 m | 0.556 m·s−1 | 1.111 m·s−1 | 1.667 m·s−1 | Single-chain header | Double-chain header |
| Number | Header Height, m | Harvesting Speed (m·s−1) | Header Type | Grain Loss Rate Sl, % | Spike Loss Rate Ss, % | Total Header Loss Rate Sg, % |
|---|---|---|---|---|---|---|
| 1 | A1 | B1 | C1 | 0.71 ± 0.22 ab | 6.55 ± 0.93 bc | 7.26 ± 1.13 ab |
| 2 | A1 | B1 | C2 | 0.96 ± 0.23 a | 2.35 ± 0.25 d | 3.31 ± 0.48 c |
| 3 | A1 | B2 | C1 | 0.51 ± 0.11 bcd | 5.80 ± 0.80 bc | 6.31 ± 0.91 b |
| 4 | A1 | B2 | C2 | 0.68 ± 0.19 ab | 2.73 ± 0.58 d | 3.41 ± 0.73 c |
| 5 | A1 | B3 | C1 | 0.41 ± 0.11 bcde | 5.45 ± 1.17 c | 5.86 ± 1.22 b |
| 6 | A1 | B3 | C2 | 0.55 ± 0.21 bcd | 2.57 ± 0.43 d | 3.12 ± 0.62 c |
| 7 | A2 | B1 | C1 | 0.67 ± 0.19 abc | 6.97 ± 0.51 abc | 7.64 ± 0.69 ab |
| 8 | A2 | B1 | C2 | 0.72 ± 0.26 ab | 3.06 ± 0.74 d | 3.78 ± 0.74 c |
| 9 | A2 | B2 | C1 | 0.22 ± 0.06 de | 6.70 ± 0.84 bc | 6.92 ± 0.81 b |
| 10 | A2 | B2 | C2 | 0.51 ± 0.31 bcd | 2.98 ± 0.35 d | 3.49 ± 0.65 c |
| 11 | A2 | B3 | C1 | 0.38 ± 0.13 bcde | 7.24 ± 0.33 ab | 7.62 ± 0.43 ab |
| 12 | A2 | B3 | C2 | 0.26 ± 0.16 cde | 3.06 ± 0.78 d | 3.32 ± 0.64 c |
| 13 | A3 | B1 | C1 | 0.41 ± 0.10 bcde | 8.42 ± 0.56 a | 8.83 ± 0.65 a |
| 14 | A3 | B1 | C2 | 0.47 ± 0.22 bcde | 3.70 ± 0.34 d | 4.17 ± 0.12 c |
| 15 | A3 | B2 | C1 | 0.31 ± 0.11 bcde | 7.16 ± 0.44 ab | 7.47 ± 0.55 ab |
| 16 | A3 | B2 | C2 | 0.26 ± 0.13 cde | 2.99 ± 0.19 d | 3.25 ± 0.26 c |
| 17 | A3 | B3 | C1 | 0.07 ± 0.03 e | 6.77 ± 1.43 bc | 6.84 ± 1.45 b |
| 18 | A3 | B3 | C2 | 0.08 ± 0.05 e | 3.42 ± 0.77 d | 3.50 ± 0.81 c |
| Source of Variation | Sum of Squares | Degrees of Freedom | Mean Square | F Value | Pr > F | |
|---|---|---|---|---|---|---|
| Grain loss rate Sl | Model | 0.86 | 5 | 0.17 | 22.19 | <0.0001 |
| A | 0.41 | 2 | 0.21 | 26.51 | <0.0001 | |
| B | 0.41 | 2 | 0.21 | 26.68 | <0.0001 | |
| C | 0.036 | 1 | 0.036 | 4.59 | 0.0534 | |
| Error | 0.093 | 12 | 0.007 | |||
| Sum | 0.95 | 17 | ||||
| Spike loss rate Ss | Model | 69.96 | 5 | 13.99 | 74.89 | <0.0001 |
| A | 4.22 | 2 | 2.11 | 11.29 | 0.0017 | |
| B | 0.76 | 2 | 0.38 | 2.04 | 0.1729 | |
| C | 64.98 | 1 | 64.98 | 347.78 | <0.0001 | |
| Error | 2.24 | 12 | 0.19 | |||
| Sum | 72.20 | 17 | ||||
| Total header loss rate Sg | Model | 66.24 | 5 | 13.25 | 65.02 | <0.0001 |
| A | 2.05 | 2 | 1.02 | 5.02 | 0.0260 | |
| B | 2.21 | 2 | 1.11 | 5.43 | 0.0209 | |
| C | 61.98 | 1 | 61.98 | 304.17 | <0.0001 | |
| Error | 2.45 | 12 | 0.20 | |||
| Sum | 68.68 | 17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, S.; Li, K.; Hu, Y.; Pan, B.; Wang, Z.; Yuan, X.; Cui, Q.; Tang, Z. Design and Experimentation of the Millet Combine Harvester Header. Machines 2024, 12, 636. https://doi.org/10.3390/machines12090636
Qiu S, Li K, Hu Y, Pan B, Wang Z, Yuan X, Cui Q, Tang Z. Design and Experimentation of the Millet Combine Harvester Header. Machines. 2024; 12(9):636. https://doi.org/10.3390/machines12090636
Chicago/Turabian StyleQiu, Shujin, Kai Li, Yifan Hu, Ben Pan, Zeze Wang, Xiangyang Yuan, Qingliang Cui, and Zhong Tang. 2024. "Design and Experimentation of the Millet Combine Harvester Header" Machines 12, no. 9: 636. https://doi.org/10.3390/machines12090636
APA StyleQiu, S., Li, K., Hu, Y., Pan, B., Wang, Z., Yuan, X., Cui, Q., & Tang, Z. (2024). Design and Experimentation of the Millet Combine Harvester Header. Machines, 12(9), 636. https://doi.org/10.3390/machines12090636






