Analytical Modeling and Experimental Validation of the Coefficient of Friction in AlSi10Mg-SiC Composites
Abstract
:1. Introduction
2. Materials and Methods
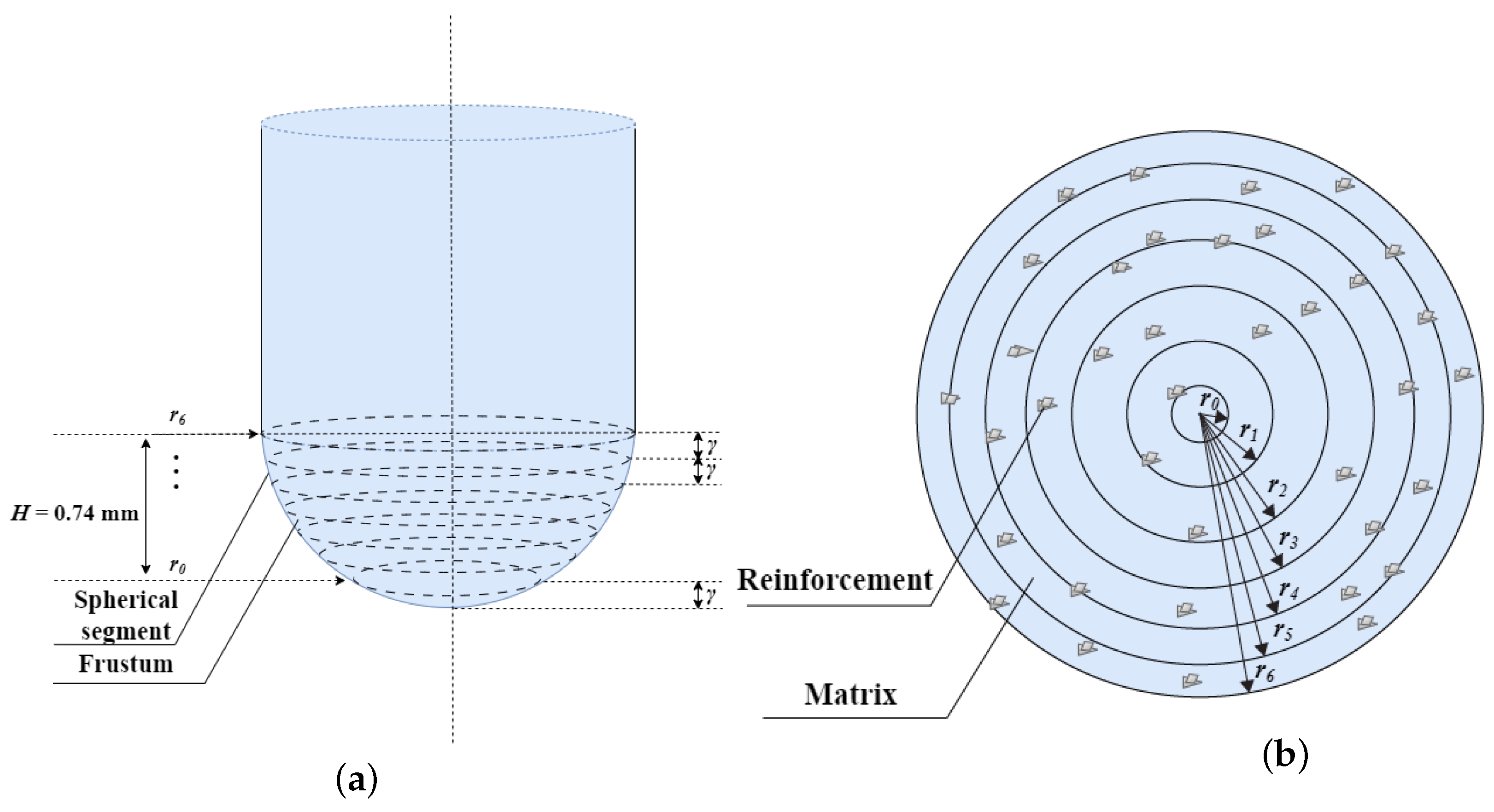
2.1. Fabrication of Composite Materials
2.2. Characterization Methods
3. Results and Discussion
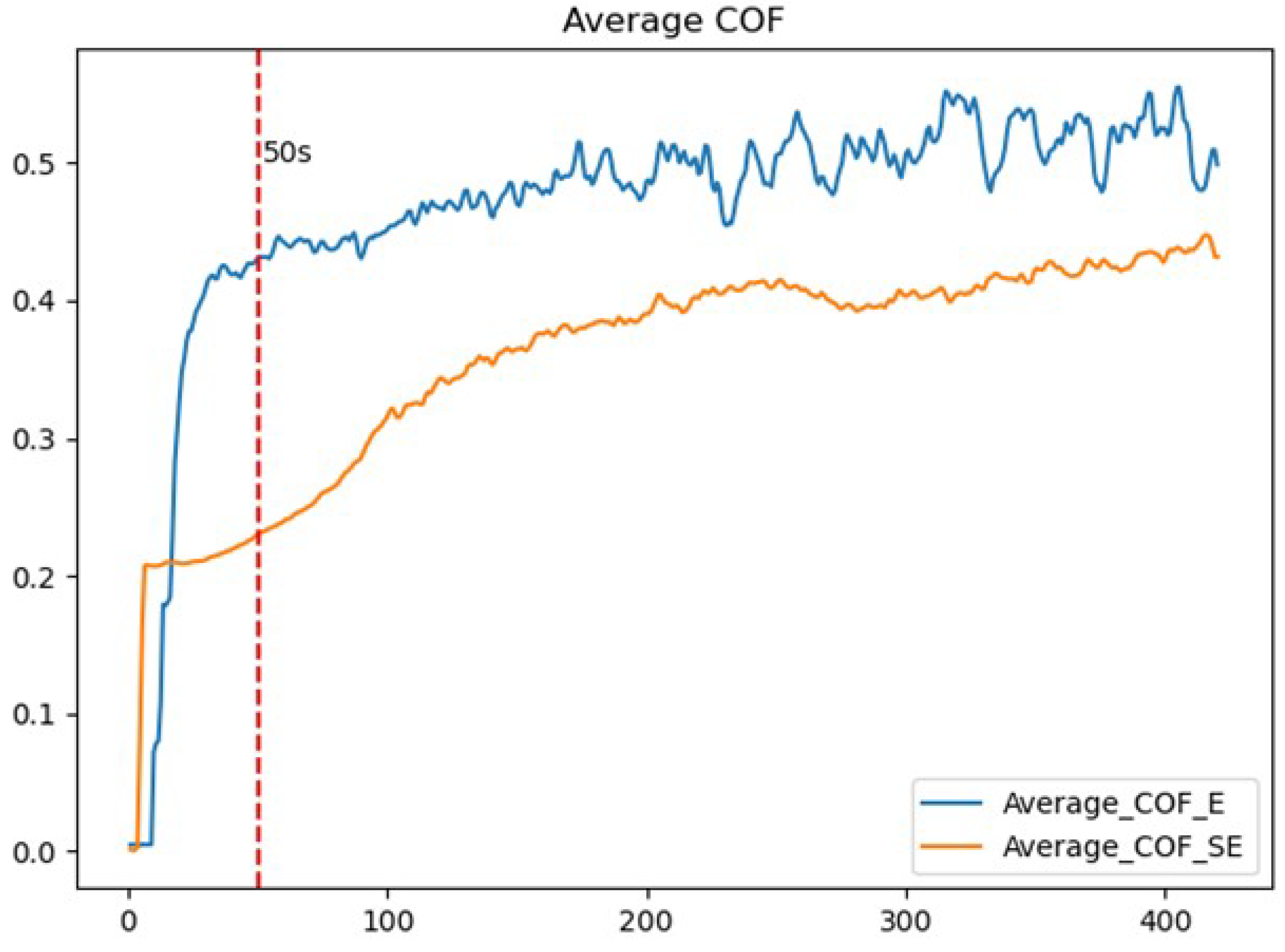
3.1. Experimental Results
3.2. Mechanism of the Friction Coefficient Oscillation
3.3. Analytical Approximation of Coefficient of Friction Evolution
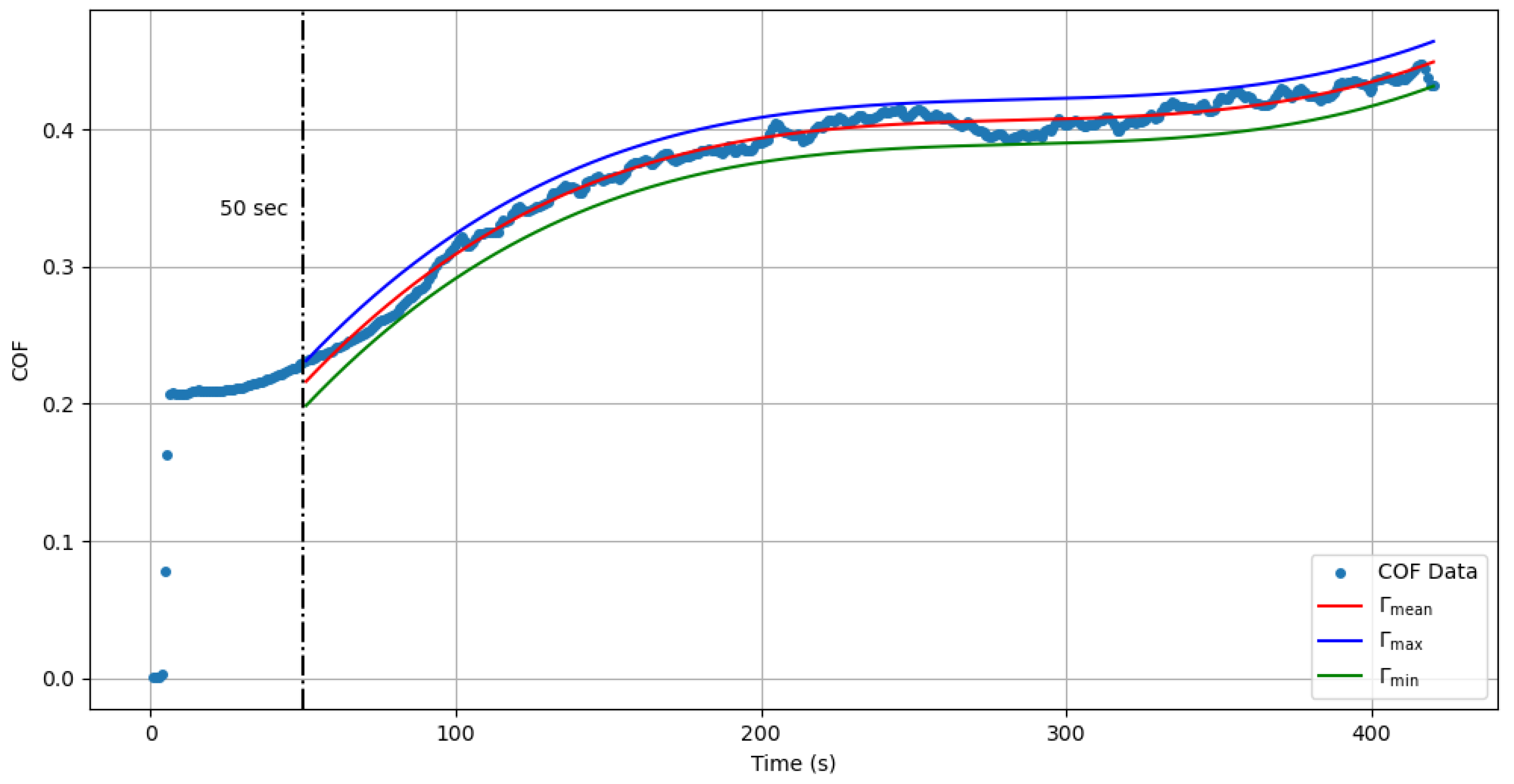
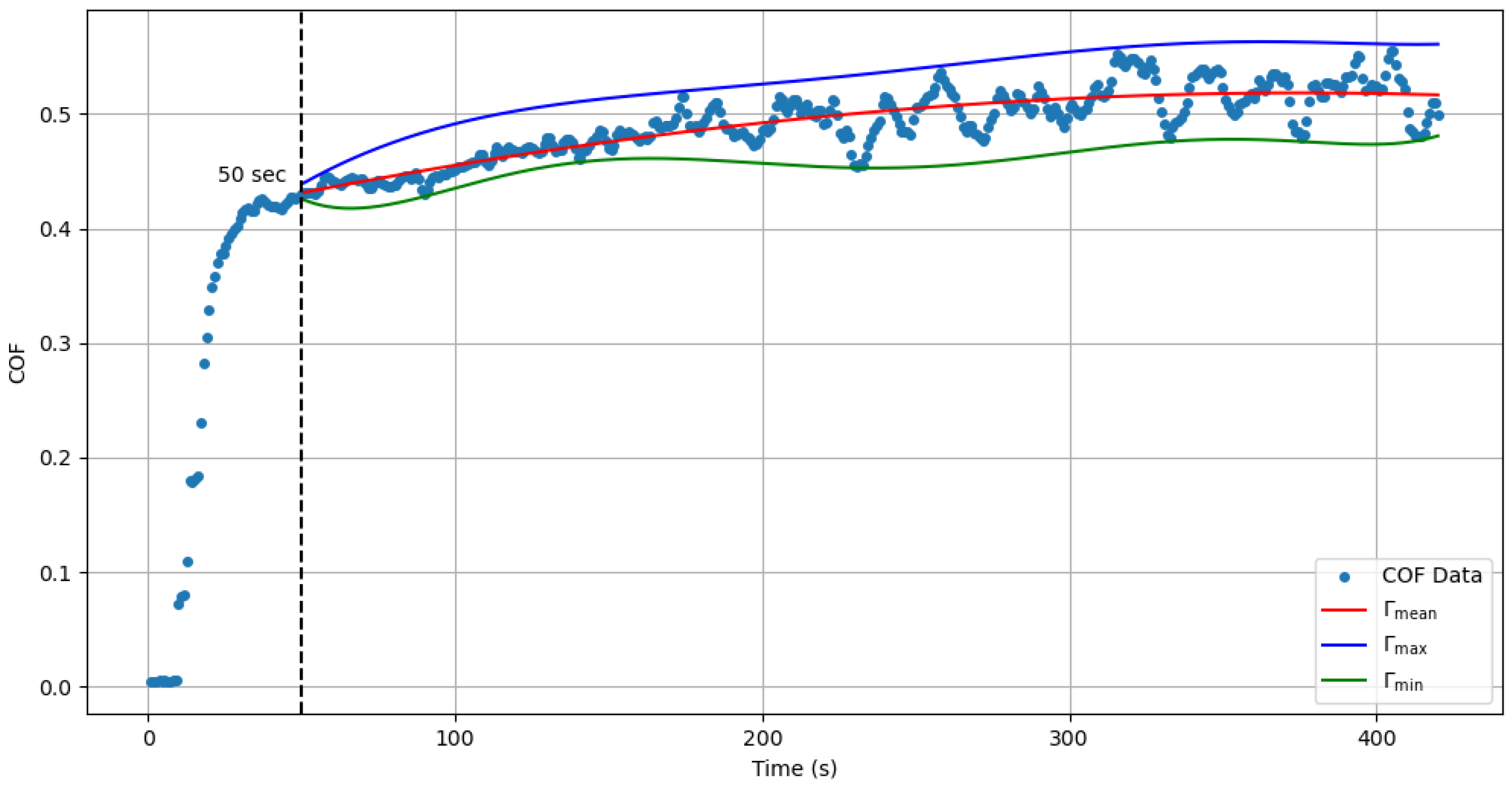
3.4. Polynomial Approximations of the Evolution Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, A.; Kumar, M. Mechanical and Dry Sliding Wear Behaviour of B4C and Rice Husk Ash Reinfroced Al 7075 Alloy Hybrid Composite for Armors Application by Using Taguchi Techniques. Mater. Today Proc. 2020, 27, 2617–2625. [Google Scholar] [CrossRef]
- Arunkumar, S.; Ashokkumar, R.; Sundaram, M.S.; SukethKanna, K.M.; Vigneshwara, S. Optimization of Wear Behaviour of Al7075 Hybrid Metal Matrix Composites Using Taguchi Approach. Mater. Today Proc. 2020, 33, 570–577. [Google Scholar] [CrossRef]
- Aydin, F. The Investigation of the Effect of Particle Size on Wear Performance of AA7075/Al2O3 Composites Using Statistical Analysis and Different Machine Learning Methods. Adv. Powder Technol. 2021, 32, 445–463. [Google Scholar] [CrossRef]
- Alizadeh, A.; Khayami, A.; Karamouz, M.; Hajizamani, M. Mechanical Properties and Wear Behavior of Al5083 Matrix Composites Reinforced with High Amounts of SiC Particles Fabricated by Combined Stir Casting and Squeeze Casting; A Comparative Study. Ceram. Int. 2022, 48, 179–189. [Google Scholar] [CrossRef]
- Kolev, M. Friction Coefficient Data and Prediction Using Decision Tree Model for Open-Cell AlSi10Mg-SiC Composites under Dry-Sliding Condition; Mendeley Data, V1, 6 June 2023. [CrossRef]
- Maleki, K.; Alizadeh, A.; Hajizamani, M. Compressive Strength and Wear Properties of SiC/Al6061 Composites Reinforced with High Contents of SiC Fabricated by Pressure-Assisted Infiltration. Ceram. Int. 2021, 47, 2406–2413. [Google Scholar] [CrossRef]
- Popov, V.L. Contact Mechanics and Friction: Physical Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 9783662530801. [Google Scholar]
- Abdelbary, A.; Chang, L. 4-Friction and Wear. In Principles of Engineering Tribology; Abdelbary, A., Chang, L., Eds.; Academic Press: Cambridge, MA, USA, 2023; pp. 127–206. ISBN 9780323991155. [Google Scholar]
- Kumar Yadav, R.; Hasan, Z.; Husain Ansari, A. Investigation of Mechanical and Wear Behavior of Al Based SiC Reinforce Metal Matrix Composite. Mater. Today Proc. 2020, 21, 1537–1543. [Google Scholar] [CrossRef]
- Kumar, B.; Joshi, A.; Mer, K.K.S.; Prasad, L.; Pathak, M.K.; Saxena, K.K. The Impact of Centrifugal Casting Processing Parameters on the Wear Behaviour of Al Alloy/Al2O3 Functionally Graded Materials. Mater. Today Proc. 2022, 62, 2780–2786. [Google Scholar] [CrossRef]
- Kolev, M. Svm_friction: A Python Based Software for Calculating, Data Analysis and Modeling the Coefficient of Friction of Aluminum Metal Matrix Composites Using Support Vector Regression. Softw. Impacts 2023, 17, 100561. [Google Scholar] [CrossRef]
- Hasan, M.S.; Kordijazi, A.; Rohatgi, P.K.; Nosonovsky, M. Application of Triboinformatics Approach in Tribological Studies of Aluminum Alloys and Aluminum-Graphite Metal Matrix Composites. In Metal-Matrix Composites; The minerals, metals & materials series; Springer International Publishing: Cham, Switzerland, 2022; pp. 41–51. ISBN 9783030925666. [Google Scholar]
- Santhosh, N.; Praveena, B.A.; Jain, R.; Abul Hasan, M.; Islam, S.; Amir Khan, M.; Razak, A. Daniyal Analysis of Friction and Wear of Aluminium AA 5083/WC Composites for Building Applications Using Advanced Machine Learning Models. Ain Shams Eng. J. 2023, 14, 102090. [Google Scholar] [CrossRef]
- Rabinowicz, E. The Intrinsic Variables Affecting the Stick-Slip Process. Proc. Phys. Soc. 1958, 71, 668. [Google Scholar] [CrossRef]
- Amer, T.S.; Shaker, M.O.; Dahab, H.A. Analysis of the Stick-Slip Behavior of Coupled Oscillators with Dry Friction. J. Low Freq. Noise Vib. Act. Control 2023, 42, 1251–1275. [Google Scholar] [CrossRef]
- Wang, S.; Hong, L.; Jiang, J. Analytical Prediction on Stick-Slip Whirling Oscillations Induced by Dry Friction between a Rotating Imbalanced Rotor and a Flexibly Supported Stator. J. Sound Vib. 2021, 511, 116333. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Forced Vibrations with Combined Coulomb and Viscous Friction. J. Fluids Eng. 1931, 53, 107–115. [Google Scholar] [CrossRef]
- Shaw, S.W. On the Dynamic Response of a System with Dry Friction. J. Sound Vib. 1986, 108, 305–325. [Google Scholar] [CrossRef]
- Bensoussan, A.; Brouste, A.; Cartiaux, F.B.; Mathey, C.; Mertz, L. Mathematical Formulation of a Dynamical System with Dry Friction Subjected to External Forces. Physica D 2021, 421, 132859. [Google Scholar] [CrossRef]
- Kolev, M.; Drenchev, L.; Petkov, V. Fabrication, Experimental Investigation and Prediction of Wear Behavior of Open-Cell AlSi10Mg-SiC Composite Materials. Metals 2023, 13, 814. [Google Scholar] [CrossRef]
- Zhang, C.; Liao, W.; Shan, Z.; Song, W.; Dong, X. Squeeze Casting of 4032 Aluminum Alloy and the Synergetic Enhancement of Strength and Ductility via Al-Ti-Nb-B Grain Refiner. Mater. Sci. Eng. A 2024, 896, 146233. [Google Scholar] [CrossRef]
- Pazhani, A.; Venkatraman, M.; Anthony Xavior, M.; Moganraj, A.; Batako, A.; Paulsamy, J.; Jayaseelan, J.; Anbalagan, A.; Shanthi Bavan, J. Synthesis and Characterisation of Graphene-Reinforced AA 2014 MMC Using Squeeze Casting Method for Lightweight Aerospace Structural Applications. Mater. Des. 2023, 230, 111990. [Google Scholar] [CrossRef]
- Menezes, P.L.; Nosonovsky, M.; Ingole, S.P.; Kailas, S.V.; Lovell, M.R. Tribology for Scientists and Engineers: From Basics to Advanced Concepts; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- De Pellegrin, D.V.; Stachowiak, G.W. Evaluating the role of particle distribution and shape in two-body abrasion by statistical simulation. Tribol. Int. 2004, 37, 255–270. [Google Scholar] [CrossRef]
| Time [s] | [60; 120] | [120; 180] | [180; 240] | [240; 300] | [300; 360] | [360; 420] |
| [] | [] | [] | [] | [] | [] |
| [] | [] | [] | [] | [] | [] | |
| [1.026; 1.443] | [1.443; 1.758] | [1.758; 2.019] | [2.019; 2.244] | [2.244; 2.445] | [2.445; 2.625] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iftikhar, S.; Kolev, M.; Kolev, D. Analytical Modeling and Experimental Validation of the Coefficient of Friction in AlSi10Mg-SiC Composites. Machines 2024, 12, 638. https://doi.org/10.3390/machines12090638
Iftikhar S, Kolev M, Kolev D. Analytical Modeling and Experimental Validation of the Coefficient of Friction in AlSi10Mg-SiC Composites. Machines. 2024; 12(9):638. https://doi.org/10.3390/machines12090638
Chicago/Turabian StyleIftikhar, Saba, Mihail Kolev, and Dimitar Kolev. 2024. "Analytical Modeling and Experimental Validation of the Coefficient of Friction in AlSi10Mg-SiC Composites" Machines 12, no. 9: 638. https://doi.org/10.3390/machines12090638
APA StyleIftikhar, S., Kolev, M., & Kolev, D. (2024). Analytical Modeling and Experimental Validation of the Coefficient of Friction in AlSi10Mg-SiC Composites. Machines, 12(9), 638. https://doi.org/10.3390/machines12090638







