Geometric Modeling and Error Propagation Analysis of an Over-Constrained Spindle Head with Kinematic Interactions

Abstract

This study presents a comprehensive geometric modeling and error propagation analysis for a 3-degrees-of-freedom spindle head, focusing on an over-constrained parallel mechanism. Four geometric error models are established for the over-constrained spindle head, each considering different combinations of constraint wrenches. A set of sensitivity indices is formulated to evaluate the effectiveness of these models. Comparative sensitivity analysis suggests that a model incorporating all constraint wrenches is suitable for error propagation analysis. Two error propagation indices are introduced to quantify the impact of the geometric source errors on the position and orientation of an individual limb structure. The coupled error propagation indices account for the kinematic interactions among limb structures, allowing for a detailed analysis of the spindle head’s terminal accuracy. The relative deviations of error propagation indices are utilized to assess the quantitative impact of kinematic interactions on the geometric errors of an individual limb structure. Furthermore, this study analyzes the cumulative effects of kinematic errors from three limb structures to reflect the influence of kinematic interactions on the terminal accuracy of the spindle head. The findings indicate that geometric errors of the limbs in such an over-constrained spindle head are mutually compensatory, reducing linear and angular errors and enhancing the spindle head’s terminal accuracy.

1. Introduction

The over-constrained parallel mechanism is a type of closed-loop mechanism with linearly dependent constraint forces/torques [1]. The over-constrained nature of such parallel mechanisms endows them with compact structure, excellent stiffness, and dynamic performance [2,3,4]. Moreover, compared to non-over-constrained parallel mechanisms with the same mobility, over-constrained parallel mechanisms often have fewer kinematic joints, resulting in fewer sources of geometric errors and potentially achieving superior kinematic accuracy [5,6]. Taking the over-constrained Exechon parallel mechanism as an example, it realizes three-degrees-of-freedom motion, including one translation and two rotations, through 13 equivalent single-degree-of-freedom joints [7,8]. This mechanism has been successfully integrated as a key spindle head with modules and guide rails and applied to high-performance milling or drilling processes for complex aerospace structural components such as aircraft wall panels, floors, and skins [9,10].

However, there are two sides to every coin. While the over-constrained nature allows parallel mechanisms to achieve compact structures and minimize sources of geometric errors, thereby enhancing their potential motion accuracy to a certain extent, ensuring strict linear correlation among the over-constrained forces/torques is essential for achieving the desired kinematic performance [11]. This requirement not only imposes stringent demands on the manufacturing and assembly precision of the components of over-constrained parallel mechanisms but also renders these mechanisms highly sensitive to perturbations from geometric errors of the components [12,13], to some extent restricting their kinematic accuracy. From the perspective of improving the kinematic accuracy of over-constrained parallel mechanisms, it is crucial to fully consider the interactive effects of the over-constrained forces/torques on the motion performance of the mechanism and establish appropriate geometric error models and conduct proper kinematic error assessments. This is also one of the key foundations for the practical application of over-constrained parallel mechanisms.

There are various methods for the geometric error modeling of parallel mechanisms, including Denavit–Hartenberg (D-H) parameterized matrices [14], the product of exponential (POE) formula [15,16], the screw method [17,18], and others. Ni et al. established an error model of a 1T2R parallel mechanism, improving the error compensation effect by improving the properties of the error identification matrix [19]. Luo et al. proposed an error model of DiaRoM-II with a dimensionless error mapping matrix [20]. Mei et al. analyzed the constraint and drive wrench of a five-axis parallel machining robot to establish its error model, realizing the error identification and compensation [21]. Chen et al. used the POE method to establish the error model of the limbs; then, they were rewritten into the form of a full rank matrix to obtain an error model of the manipulator [22]. However, none of these geometric error modeling methods can comprehensively and efficiently adapt to the diverse types of parallel mechanisms. Therefore, researchers need to adapt these methods effectively based on the structural characteristics of the specific parallel mechanism under study. These error modeling methods are mainly completed by eliminating passive error through projection after establishing an error model for the limbs [23]. For the redundant mechanism, a redundant wrench and a constraint wrench are introduced, resulting in nonlinear deformation of the mechanism. Non-redundant constraints are simply expressed by a full rank matrix [24,25]. Moreover, Shen et al. proposed a Markov data-based approach to address the long-standing challenge of modeling complex tensegrity systems, which could provide significant help in robots with tensegrity structures [26]. Furthermore, for over-constrained parallel mechanisms, the difficulty in geometric error modeling lies not only in selecting suitable modeling methods but also in fully considering the linearly dependent constraint forces/torques.

Based on geometric error modeling, the key to conducting kinematic error assessment lies in constructing concise and physically meaningful performance indicators for kinematic errors. Volume errors are often used to evaluate the distribution of terminal errors in the workspace. Stiffness is a key parameter which affects accuracy. Ye et al. estimated the deformation errors based on the robot stiffness model and defined a contour error based machining performance index [27]. Chen et al. proposed a normal stiffness performance index to evaluate the stiffness performance and optimized tool feed direction [28]. Sensitivity indices are widely used to reveal the influence of source errors on the terminal error [29]. Based on the error model of a new five-degrees-of-freedom parallel robot, Luo et al. identified important and secondary source errors through sensitivity analysis [30]. Wu et al. conducted sensitivity analysis on a novel grinding device using the Monte Carlo method based on the Sobol sequence [31]. Li et al. established a low-error-sensitivity workspace index based on sensitivity analysis to evaluate the error characteristics of parallel mechanisms [32]. Dexterity is also an index used to measure the accuracy of a robot. Shi et al. analyzed the dexterity for the 4UPS-RRR parallel ankle rehabilitation mechanism through the establishment of its Jacobian matrix [33]. Wang et al. analyzed the working space and dexterity of the robot and discovered the optimal length distributions for two-segment and three-segment continuum robots [34]. Nabavi et al. used dexterity, kinetic energy, and a new modified workspace index for optimal determination of the remaining parameters [35]. Overall, the existing kinematic error performance indicators are mostly constructed using the geometric error propagation matrix and its eigenvalues and often only focus on the kinematic performance at the mechanism level, neglecting the geometric error propagation characteristics between the limb structures. In other words, for over-constrained parallel mechanisms with complex linearly dependent constraint forces/torques between limbs, how to consider not only the mechanical system level but also the limb structural level in constructing suitable performance indices for kinematic error is still a challenge that needs to be addressed.

With the above-mentioned problem in mind, the present study will take an over-constrained spindle head as an example on which carry out the geometric modeling and error propagation analysis. For this purpose, the rest of this paper is organized as follows: Section 2 establishes the four forms of geometric error modeling with the various combination of the constraint wrenches. A set of sensitivity indices are formulated to evaluate four types of geometric error models. In Section 3, a set of error propagation indices and coupled error propagation indices are proposed to analyze the error propagation at both the limb structural level and the mechanical system level, respectively. Then, the influence pattern of the kinematic interactions between the limbs on the terminal accuracy can be revealed, and some suggestions for structural design are proposed to enhance the terminal accuracy of the spindle head. Finally, some conclusions and remarks are presented in Section 4.

2. Geometric Error Modeling and Comparison of Individual Limbs

The design process of spindle head mainly includes three steps: structure and dimension design, accuracy synthesis, and kinematic calibration of prototype. Among them, geometric error modeling plays an important role. It can reflect the mapping relationship between source errors and terminal error, not only providing important theoretical support for tolerance design and assembly of parts but also providing an important basis for kinematic calibration.

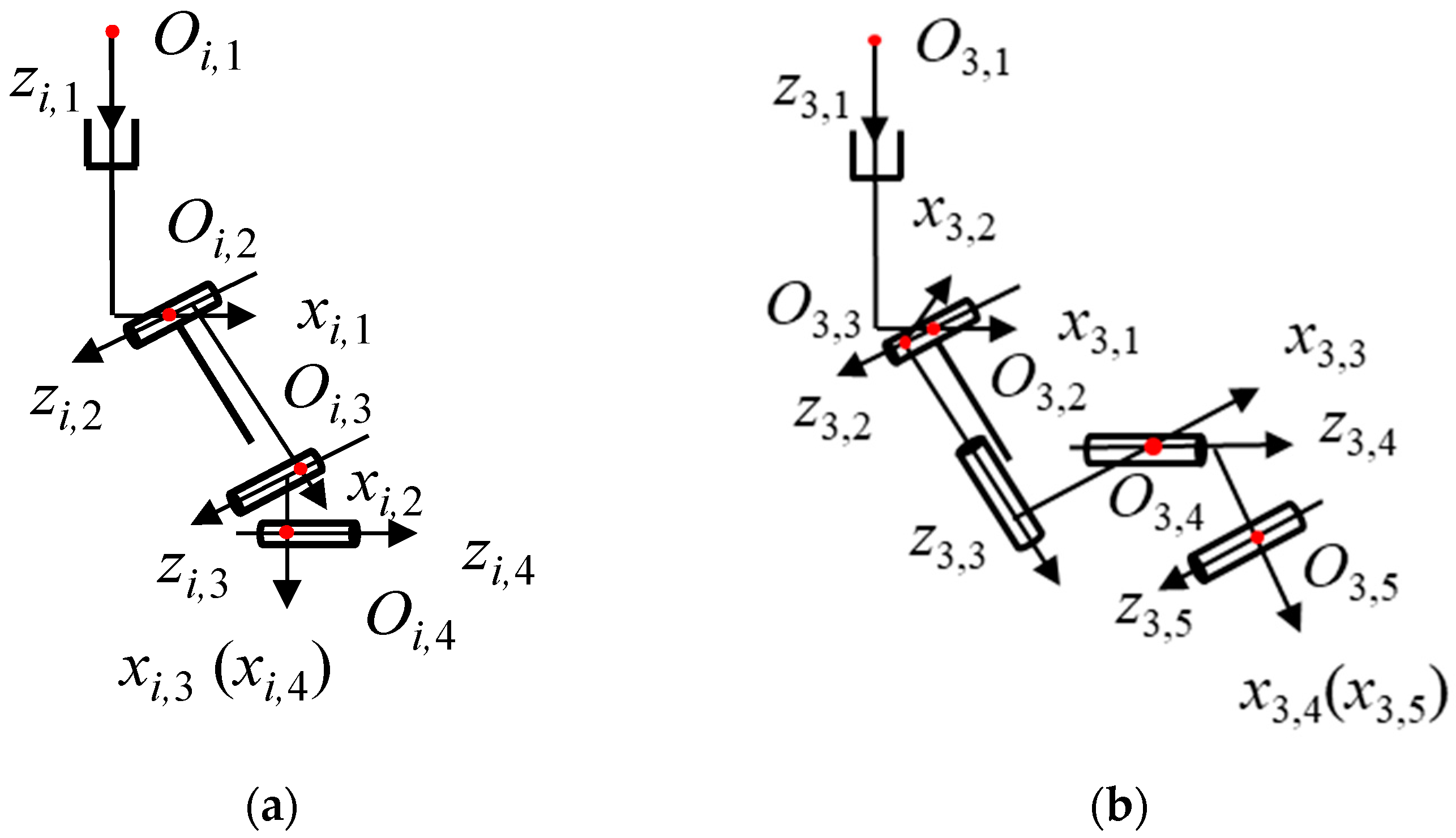
2.1. Structure Description and Coordinates Settings

In this section, a 3-degrees-of-freedom (DOF) spindle head is taken as an example to demonstrate the geometric error modeling process. The prototype model and schematic diagram of the spindle head are shown in Figure 1.

As can be seen from Figure 1, the 3-DOF spindle head is with the topological architecture of 2PRU-1PRS (“R”, “U”, “S”, and “P” represent revolute joint, universal joint, spherical joint, and actuated prismatic joint, respectively). To be specific, the spindle head mainly consists of two PRU limbs, a PRS limb, a moving platform, and a fixed base. Limb 1 and limb 2 are two symmetrically distributed PRU limbs; limb 3 is a PRS limb. A_i and B_i (i = 1, 2, 3) represent the intersections of the ith limb connected to the fixed base and the moving platform, respectively. M_i is the geometric center of a revolute joint in the ith limb. With these structural arrangements, the spindle head can perform three-axis synchronization motions and then be integrated into a hybrid kinematic machining center for multi-axis high-speed machining of components with complex geometries. To determine the physical spindle head setup, the following parameters are defined: the length of $\overline{O{A}_i}$ is called the radius of the stationary platform (r_a); the length of $\overline{M_i{B}_i}$ is called the length of the connecting rod (a); and the length of $\overline{O{B}_i}$ is called the radius of the moving platform (r_b). The dimension parameters of spindle head are shown in

Table 1. The physical setup of the 3-DOF spindle head.

Parameters	Value	Parameters	Value
ra	0.250 m	qf	0–0.5 m
a	0.315 m	Rf	0–60°
rb	0.178 m	Uf	65–145°
Sf	65–145°

.

For derivation facility, the following frames are defined. The fixed coordinate system $O-xyz$ is attached to the fixed base with $O$ at the center of A₁A₂, in which the z axis is perpendicular to the ΔA₁A₂A₃, the $x$ axis is coincident with the vector of $\overline{O{A}_3}$, and the y axis is decided by the right-hand rule. The reference coordinate system $O^{\prime }-uvw$ is attached to the moving platform with $O^{\prime }$ at the center of $B_1{B}_2$, in which the w axis is perpendicular to the plane of $\Delta B_1{B}_2{B}_3$, the u axis is coincident with the vector of $\overline{O^{\prime }{B}_3}$, the v axis is decided by the right-hand rule. Moreover, the local coordinate systems of individual limbs are depicted in Figure 2. Herein, $O_{i,j}-x_{i,j}{y}_{i,j}{z}_{i,j}$ is defined as the local coordinate system for the jth joint in the ith limb. $z_{i,j}$ is along with the jth joint axis; $x_{i,j}$ coincides with the common normal of $z_{i,j}$ and $z_{i,j+1}$; $O_{i,1}$ overlaps with $A_i$; $O_{i,j}(j>1)$ is the intersection of $z_{i,j}$ and $x_{i,j-1}$; and the axis $y_{i,j}$ can be defined by the right hand rule. Meanwhile, the frame $O-xyz$ is considered as the local coordinate system of 0th joint, and the frame $O^{\prime }-uvw$ is considered as the last local coordinate system for each limb.

2.2. Error Modeling of Individual Limbs

According to the structure of the spindle head, a “U” joint or an “S” joint can be equivalent into two or three orthogonally arranged single-DOF joints. Thus, considering such a joint structure, the source errors of the jth joint in the ith limb can be expressed as follows:

$${\delta }_{i,j}=[\delta x_{i,j}\delta y_{i,j} \delta z_{i,j} \delta {\psi }_{i,j}\delta {\theta }_{i,j}\delta {\phi }_{i,j}]\{\begin{array}{l}j=1~5 (i=1,2)\hfill \\ j=1–6 (i=3)\hfill \end{array},$$

(1)

where $\delta x_{i,j}$,$\delta y_{i,j}$, and $\delta z_{i,j}$ represent the position source errors in the frame $O_{i,j-1}-x_{i,j-1}{y}_{i,j-1}{z}_{i,j-1}$;$\delta {\psi }_{i,j}$, $\delta {\theta }_{i,j}$, and $\delta {\phi }_{i,j}$ represent the orientation source errors in the frame $O_{i,j-1}-x_{i,j-1}{y}_{i,j-1}{z}_{i,j-1}$.

To simplify the error modeling, redundant source errors in a limb structure can be merged. To be specific, when the (j − 1)th joint is a prismatic joint, $\delta z_{i,j}$ can be merged into $\delta {\omega }_{i,j-1}$; when the (j − 1)th joint is a revolute joint, $\delta {\phi }_{i,j}$ can be merged into $\delta {\omega }_{i,j-1}$; when the (j − 1)th joint is not the last joint, $\delta y_{i,j}$ is not included in the transformation. Moreover, if the (j − 1)th joint is not a prismatic joint and the motion axes of the (j − 1)th joint intersect with the jth joint, $\delta {\theta }_{i,j}$ cannot be included in the transformation. Following the elimination process, depicted as Figure 3, the simplified source errors of the three limbs can be obtained and expressed as follows.

$$\{\begin{array}{l}{\delta }_{i,1}=[\delta x_{i,1} \delta y_{i,1} \delta z_{i,1} \delta {\psi }_{i,1} \delta {\theta }_{i,1} \delta {\phi }_{i,1}]\hfill \\ {\delta }_{i,2}=[\delta x_{i,2} 0 0 \delta {\psi }_{i,2} \delta {\theta }_{i,2} \delta {\phi }_{i,2}]\hfill \\ {\delta }_{i,3}=[\delta x_{i,3} 0 \delta z_{i,3} \delta {\psi }_{i,3} \delta {\theta }_{i,3} 0]\hfill \\ {\delta }_{i,4}=[\delta x_{i,4} 0 \delta z_{i,4} \delta {\psi }_{i,4} 0 0]\hfill \\ {\delta }_{i,5}=[\delta x_{i,5} \delta y_{i,5} \delta z_{i,5} \delta {\psi }_{i,5} \delta {\theta }_{i,5} 0 ]\hfill \end{array}(i=1,2)$$

(2)

$$\{\begin{array}{l}{\delta }_{3,1}=[\delta x_{3,1} \delta y_{3,1} \delta z_{3,1} \delta {\psi }_{3,1} \delta {\theta }_{3,1} \delta {\phi }_{3,1}]\hfill \\ {\delta }_{3,2}=[\delta x_{3,2} 0 0 \delta {\psi }_{3,2} \delta {\theta }_{3,2} \delta {\phi }_{3,2}]\hfill \\ {\delta }_{3,3}=[\delta x_{3,3} 0\delta z_{3,3} \delta {\psi }_{3,3} 0 0]\hfill \\ {\delta }_{3,4}=[\delta x_{3,4} 0 \delta z_{3,4} \delta {\psi }_{3,4} 0 0]\hfill \\ {\delta }_{3,5}=[\delta x_{3,5} 0 \delta z_{3,5} \delta {\psi }_{3,5} 0,0]\\ {\delta }_{3,6}=[\delta x_{3,6} \delta y_{3,6} \delta z_{3,6} \delta {\psi }_{3,6} \delta {\theta }_{3,6} 0]\hfill \end{array}$$

(3)

As shown in Equations (2) and (3), the final geometric source errors of the spindle head can be reduced to 68 items, as listed in

Table 2. Geometric source errors after eliminating redundant items.

Order (nth)	Source Error	Order (nth)	Source Error	Order (nth)	Source Error	Order (nth)	Source Error	Order (nth)	Source Error
1	$\delta x_{1,1}$	15	$\delta x_{1,4}$	29	$\delta x_{2,2}$	43	$\delta {\psi }_{2,5}$	57	$\delta {\psi }_{3,3}$
2	$\delta y_{1,1}$	16	$\delta z_{1,4}$	30	$\delta {\psi }_{2,2}$	44	$\delta {\theta }_{2,5}$	58	$\delta x_{3,4}$
3	$\delta z_{1,1}$	17	$\delta {\psi }_{1,4}$	31	$\delta {\theta }_{2,2}$	45	$\delta x_{3,1}$	59	$\delta z_{3,4}$
4	$\delta {\psi }_{1,1}$	18	$\delta x_{1,5}$	32	$\delta {\phi }_{2,2}$	46	$\delta y_{3,1}$	60	$\delta {\psi }_{3,4}$
5	$\delta {\theta }_{1,1}$	19	$\delta y_{1,5}$	33	$\delta x_{2,3}$	47	$\delta z_{3,1}$	61	$\delta x_{3,5}$
6	$\delta {\phi }_{1,1}$	20	$\delta z_{1,5}$	34	$\delta z_{2,3}$	48	$\delta {\psi }_{3,1}$	62	$\delta z_{3,5}$
7	$\delta x_{1,2}$	21	$\delta {\psi }_{1,5}$	35	$\delta {\psi }_{2,3}$	49	$\delta {\theta }_{3,1}$	63	$\delta {\psi }_{3,5}$
8	$\delta {\psi }_{1,2}$	22	$\delta {\theta }_{1,5}$	36	$\delta {\theta }_{2,3}$	50	$\delta {\phi }_{3,1}$	64	$\delta x_{3,6}$
9	$\delta {\theta }_{1,2}$	23	$\delta x_{2,1}$	37	$\delta x_{2,4}$	51	$\delta x_{3,2}$	65	$\delta y_{3,6}$
10	$\delta {\phi }_{1,2}$	24	$\delta y_{2,1}$	38	$\delta z_{2,4}$	52	$\delta {\psi }_{3,2}$	66	$\delta z_{3,6}$
11	$\delta x_{1,3}$	25	$\delta z_{2,1}$	39	$\delta {\psi }_{2,4}$	53	$\delta {\theta }_{3,2}$	67	$\delta {\psi }_{3,6}$
12	$\delta z_{1,3}$	26	$\delta {\psi }_{2,1}$	40	$\delta x_{2,5}$	54	$\delta {\phi }_{3,2}$	68	$\delta {\theta }_{3,6}$
13	$\delta {\psi }_{1,3}$	27	$\delta {\theta }_{2,1}$	41	$\delta y_{2,5}$	55	$\delta x_{3,3}$
14	$\delta {\theta }_{1,3}$	28	$\delta {\phi }_{2,1}$	42	$\delta z_{2,5}$	56	$\delta z_{3,3}$

.

Based on the screw theory, the twist system of an individual limb, such as the PRU limb, can be expressed as follows:

$$\{\begin{array}{l}{\mathsf{\$}}_{i,1}=[{\mathbf{0}}_{3\times 1};{\mathit{s}}_{i,1}]\hfill \\ {\mathsf{\$}}_{i,2}=[{\mathit{s}}_{i,2};{\mathit{r}}_{i,2}\times {\mathit{s}}_{i,2}]\hfill \\ {\mathsf{\$}}_{i,3}=[{\mathit{s}}_{i,3};{\mathit{r}}_{i,3}\times {\mathit{s}}_{i,3}]\hfill \\ {\mathsf{\$}}_{i,4}=[{\mathit{s}}_{i,4};{\mathit{r}}_{i,4}\times {\mathit{s}}_{i,4}]\hfill \end{array}(i=1, 2),$$

(4)

where ${\mathit{s}}_{i,j}$ (i = 1, 2; j = 1, 2, 3, 4) represents an unit vector of the jth equivalent joint in the ith limb; r_i,j denotes one of the position vector of A_i, M_i, and B_i measured in the frame $O^{\prime }-uvw$.

Similarly, the twist system of an individual PRS limb can be expressed as follows:

$$\{\begin{array}{l}{\mathsf{\$}}_{3,1}=[{\mathbf{0}}_{3\times 1};{\mathit{s}}_{3,1}]\hfill \\ {\mathsf{\$}}_{3,2}=[{\mathit{s}}_{3,2};{\mathit{r}}_{3,2}\times {\mathit{s}}_{3,2}]\hfill \\ {\mathsf{\$}}_{3,3}=[{\mathit{s}}_{3,3};{\mathit{r}}_{3,3}\times {\mathit{s}}_{3,3}]\hfill \\ {\mathsf{\$}}_{3,4}=[{\mathit{s}}_{3,4};{\mathit{r}}_{3,4}\times {\mathit{s}}_{3,4}]\hfill \\ {\mathsf{\$}}_{3,5}=[{\mathit{s}}_{3,5};{\mathit{r}}_{3,5}\times {\mathit{s}}_{3,5}]\hfill \end{array},$$

(5)

where ${\mathit{s}}_{3,j}$ (j = 1, 2, 3, 4, 5) represents an unit vector of the jth equivalent joint in limb 3; and r_3,j denotes one of the position vector of A₃, M₃ and B₃ measured in the frame $O^{\prime }-uvw$.

After introducing the geometric source errors, such as the position error and orientation error between the coordinate systems and the joints, the geometric error model of an individual limb can be established as follows:

$$\begin{gathered} {\mathsf{\$}}_{e,i}={\displaystyle \sum _{j=1}^n\delta {\omega }_{i,j}}{\mathsf{\$}}_{i,j}+{\mathsf{\$}}_{\mathrm{G},i}\hspace{1em}\hspace{1em}n=\{\begin{array}{l}4,i=1,2\hfill \\ 5,i=3\hfill \end{array}, \\ {\mathsf{\$}}_{\mathrm{G},i}={\displaystyle \sum _{j=1}^{m}A{d}_{i,j-1}^{O^{\prime }}{P}_{i,j}{\delta }_{i,j}}\hspace{1em}\hspace{1em}m=\{\begin{array}{l}5,i=1, 2\hfill \\ 6,i=3\hfill \end{array}, \end{gathered}$$

(6)

where ${\mathsf{\$}}_{\mathrm{e},i}$ is the error twist of the ith limb measured in the frame $O^{\prime }-uvw$; $\delta {\omega }_{i,j}$ denotes the source error caused by joint motion; ${\delta }_{i,j}$ denotes the source errors caused by geometrical error between joints; and $A{d}_{j-1,i}^{O^{\prime }}$ and $P_{i,j}$ represent the adjoint transformation matrix and the position transformation matrix between the frame $O_{i,j-1}-x_{i,j-1}{y}_{i,j-1}{z}_{i,j-1}$ and the frame $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$, respectively, which can be further formulated as follows:

$$\begin{gathered} A{d}_{i,j-1}^{O^{\prime }}=\left[\begin{array}{cc}{T}_{i,j-1}^{O^{\prime }}& ({\mathit{r}}_{i,j-1}^{O^{\prime }}\times )T_{i,j-1}^{O^{\prime }}\\ {\mathbf{0}}_{3\times 3}& T_{i,j-1}^{O^{\prime }}\end{array}\right], \\ {P}_{i,j}=\left[\begin{array}{cc}{I}_3& ({\mathit{r}}_{i,j}^{j-1}\times )\\ {\mathbf{0}}_{3\times 3}& I_3\end{array}\right], \end{gathered}$$

(7)

where $T_{i,j-1}^{O^{\prime }}$ represents the rotational transformation matrix between the frame $O_{j-1,i}-x_{j-1,i}{y}_{j-1,i}{z}_{j-1,i}$ and the frame $O^{\prime }-uvw$; $r_{i,j-1}^{O^{\prime }}$ represents the position vector from $O_{j-1}$ to $O^{\prime }-uvw$; $r_{i,j}^{j-1}$ denotes the position vector from $O_{i,j}$ to $O_{i,j-1}-x_{i,j-1}{y}_{i,j-1}{z}_{i,j-1}$; $(r_{i,j}^{j-1}\times )$ and $(r_{i,j-1}^{O^{\prime }}\times )$ represent the skew-symmetric matrix of $r_{i,j}^{j-1}$ and $r_{i,j-1}^{O^{\prime }}$, respectively; and $I_3$ is a $3\times 3$ identity matrix.

2.3. Error Modeling of the Spindle Head

According to the twist systems formulated in Equations (4) and (5), the constraint wrenches of the PRU limbs (limb 1 and limb 2) and the PRS limb (limb 3) can be expressed as follows:

$$\{\begin{array}{l}{\mathsf{\$}}_{wc,i,1}=[{\mathbf{0}}_{3\times 1};{\mathit{s}}_{1,3}\times {\mathit{s}}_{1,4}]\hfill \\ {\mathsf{\$}}_{wc,i,2}=[{\mathit{s}}_{1,2};{\mathit{r}}_{1,3}\times {\mathit{s}}_{1,2}]\hfill \end{array}(i=1, 2),$$

(8)

$${\mathsf{\$}}_{wc,3,1}=[{\mathit{s}}_{3,2};r_{3,3}\times {\mathit{s}}_{3,2}],$$

(9)

where ${\mathsf{\$}}_{wc,i,j}$ denotes the jth constraint wrench in the ith limb, and there are two couples of linearly dependent screws as ${\mathsf{\$}}_{wc,1,1}$, ${\mathsf{\$}}_{wc,2,1}$ and ${\mathsf{\$}}_{wc,1,2}$, ${\mathsf{\$}}_{wc,2,2}$. This indicates that the 3-DOF spindle head possesses two overconstraints; herein, ${\mathsf{\$}}_{wc,i,1}(i=1,2)$ represents the even quantity along the common vertical line of two rotation axes of the universal joint; ${\mathsf{\$}}_{wc,i,2}(i=1,2)$ represents the wrench along the unit vector ${\mathit{s}}_{1,2}$ which passes through point B_i; and ${\mathsf{\$}}_{wc,3,2}$ represents the wrench along the unit vector ${\mathit{s}}_{3,2}$ which passes through point B₃.

By locking the actuated prismatic joint in each limb structure, the actuation wrenches of the PRU limbs and the PRS limb can be expressed as follows:

$${\mathsf{\$}}_{wa,i}=[p_i;r_{i,3}\times p_i](i=1,2,3),$$

(10)

where ${\mathsf{\$}}_{wa,i}$ denotes the actuation wrench in the ith limb which represents the wrench along the unit vector $p_i$ which passes through point B_i; $p_i$ represents the unit vector of the vector $\overline{M_i{B}_i}$.

Taking the inner product on both sides of Equation (6) with the constraint wrench ${\mathsf{\$}}_{wc,i,j}$, one may obtain the following:

$${\mathsf{\$}}_{wc,i,j}^{\mathrm{T}}{\mathsf{\$}}_e=E_{ce,i,j}{\epsilon }_i.$$

(11)

Herein,

$$\begin{array}{l}{E}_{ce,i,j}=\left[\begin{array}{cc}{E}_{ce,i,j}^a& E_{ce,i,j}^b\end{array}\right]\\ E_{ce,i,j}^a=\left[\begin{array}{cccc}{\mathsf{\$}}_{wc,i,j}^{\mathrm{T}}A{d}_{i,O}^{O^{\prime }}{P}_{i,1}& {\mathsf{\$}}_{wc,i,j}^{\mathrm{T}}A{d}_{i,1}^{O^{\prime }}{P}_{i,2}& {\mathsf{\$}}_{wc,i,j}^{\mathrm{T}}A{d}_{i,2}^{O^{\prime }}{P}_{i,3}& {\mathsf{\$}}_{wc,i,j}^{\mathrm{T}}A{d}_{i,3}^{O^{\prime }}{P}_{i,4}\end{array}\right] (i=1,2,3)\\ E_{ce,i,j}^b=\{\begin{array}{l}\left[{\mathsf{\$}}_{wc,i,j}^{\mathrm{T}}A{d}_{O^{\prime }}{P}_{i,4}^{O^{\prime }}\right]\hfill \\ \left[\begin{array}{cc}{\mathsf{\$}}_{wc,i,j}^{\mathrm{T}}A{d}_{i,5}^{O^{\prime }}{P}_{i,5}& {\mathsf{\$}}_{wc,i,j}^{T}A{d}_{O^{\prime }}{P}_{i,5}^{O^{\prime }}\end{array}\right]\hfill \end{array}\begin{array}{l}(i=1,2)\hfill \\ (i=3)\hfill \end{array}\\ A{d}_{O^{\prime }}=\left[\begin{array}{cc}T& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& T\end{array}\right]\\ {\epsilon }_i=\{\begin{array}{l}\left[\begin{array}{ccccc}{\delta }_{i,1}& {\delta }_{i,2}& {\delta }_{i,3}& {\delta }_{i,4}& {\delta }_{i,5}\end{array}\right]\hfill \\ \left[\begin{array}{cccccc}{\delta }_{i,1}& {\delta }_{i,2}& {\delta }_{i,3}& {\delta }_{i,4}& {\delta }_{i,5}& {\delta }_{i,6}\end{array}\right]\hfill \end{array}\begin{array}{l}(i=1,2)\hfill \\ (i=3)\hfill \end{array}\end{array}$$

where $E_{ce,i,j}$ represents the error projection matrix on constrained wrench ${\mathsf{\$}}_{wc,i,j}$; ${\epsilon }_i$ represents the source errors in the ith limb; and $T$ represents the transformation matrix of the frame $O^{\prime }-uvw$ accuracy the frame $O-xyz$.

Similarly, taking the inner product on both sides of Equation (6) with the actuation wrench ${\mathsf{\$}}_{wa,i}$, one may obtaining the following:

$${\mathsf{\$}}_{wa,i}^{\mathrm{T}}{\mathsf{\$}}_e=\delta {\omega }_{i,1}+E_{ae,i}{\epsilon }_i.$$

(12)

Herein,

$$\begin{array}{l}{E}_{ae,i}=\left[\begin{array}{cc}{E}_{ae,i}^a& E_{ae,i}^b\end{array}\right]\\ E_{ae,i}^a=\left[\begin{array}{cccc}{\mathsf{\$}}_{wa,i}^{\mathrm{T}}A{d}_{i,O}^{O^{\prime }}{P}_{i,1}& {\mathsf{\$}}_{wa,i}^{\mathrm{T}}A{d}_{i,1}^{O^{\prime }}{P}_{i,2}& {\mathsf{\$}}_{wa,i}^{\mathrm{T}}A{d}_{i,2}^{O^{\prime }}{P}_{i,3}& {\mathsf{\$}}_{wa,i}^{\mathrm{T}}A{d}_{i,3}^{O^{\prime }}{P}_{i,4}\end{array}\right](i=1,2,3)\\ E_{ae,i}^b=\{\begin{array}{l}\left[{\mathsf{\$}}_{wa,i}^{\mathrm{T}}A{d}_{O^{\prime }}{P}_{i,4}^{O^{\prime }}\right]\hfill \\ \left[\begin{array}{cc}{\mathsf{\$}}_{wa,i}^{\mathrm{T}}A{d}_{i,4}^{O^{\prime }}{P}_{i,5}& {\mathsf{\$}}_{wa,i}^{T}A{d}_{O^{\prime }}{P}_{i,5}^{O^{\prime }}\end{array}\right]\hfill \end{array}\begin{array}{l}(i=1,2)\hfill \\ (i=3)\hfill \end{array}\end{array}$$

where $E_{ae,i,j}$ represents the error projection matrix on actuated wrench ${\mathsf{\$}}_{wa,i,j}$. By assembling Equations (10) and (11) and reconfiguring them into matrix form, the geometric error model of the spindle head can be obtained and expressed as follows:

$$J_e{\mathsf{\$}}_e={\delta }_{\omega }+E_e\epsilon .$$

(13)

Herein,

$$\begin{array}{l}{\delta }_{\omega }={\left[\begin{array}{cccc}\delta {\omega }_{1,1}& \delta {\omega }_{2,1}& \delta {\omega }_{3,1}& {\mathbf{0}}_{1\times 3}\end{array}\right]}^{\mathrm{T}},\\ \epsilon ={\left[\begin{array}{ccc}{\epsilon }_1& {\epsilon }_2& {\epsilon }_3\end{array}\right]}^{\mathrm{T}},\\ J_e=[\begin{array}{cc}{J}_{ae}& J_{ce}\end{array}],\\ J_{ae}=diag\left[\begin{array}{ccc}{J}_{ae,1}& J_{ae,2}& J_{ae,3}\end{array}\right],\\ E_e={\left[\begin{array}{cc}{E}_{ae}& E_{ce}\end{array}\right]}^{\mathrm{T}},\\ E_{ae}=diag\left[\begin{array}{ccc}{E}_{ae,1}& E_{ae,2}& E_{ae,3}\end{array}\right],\end{array}$$

where ${\mathsf{\$}}_e$ denotes the error twist of the moving platform; ${\delta }_{\omega }$ represents the zero offsets along the prismatic joint axes; ε denotes the source errors, including all three limbs; $J_e$ and $E_e$ denote the wrench matrix and source error projection matrix, respectively; $J_{ae}$ and $E_{ae}$ represent the actuation wrench matrix and source error projection matrix in the driven direction, respectively; and $J_{ce}$ and $E_{ce}$ represent the constraint wrench matrix and source error projection matrix in the restrained direction, respectively.

As the terminal error of the spindle head is coupled by the kinematic errors of all three limb structures, the constraint wrench matrix $J_{ce}$ should at least contain three constraint wrenches, each from limb 1, 2, and 3. Moreover, limb 1 and limb 2 have two linearly dependent wrenches, as described in Equation (7). Thus, $J_{ce}$ and the corresponding source error projection matrix $E_{ce}$ have four selectable forms for the geometric error model of the spindle head.

As shown in

Table 3. $E_{ce}$ in different models.

Error Models	${\mathit{J}}_{\mathit{c}\mathit{e}}$	${\mathit{E}}_{\mathit{c}\mathit{e}}$
Model 1	$diag{\left[\begin{array}{ccc}{\mathsf{\$}}_{wc,1,1}^{\mathrm{T}}& {\mathsf{\$}}_{wc,2,1}^{\mathrm{T}}& {\mathsf{\$}}_{wc,3,1}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$	$diag\left[\begin{array}{ccc}{E}_{ce,1,1}& E_{ce,2,1}& E_{ce,3,1}\end{array}\right]$
Model 2	$diag{\left[\begin{array}{ccc}{\mathsf{\$}}_{wc,1,2}^{\mathrm{T}}& {\mathsf{\$}}_{wc,2,1}^{\mathrm{T}}& {\mathsf{\$}}_{wc,3,1}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$	$diag\left[\begin{array}{ccc}{E}_{ce,1,2}& E_{ce,2,1}& E_{ce,3,1}\end{array}\right]$
Model 3	$diag{\left[\begin{array}{ccc}{\mathsf{\$}}_{wc,1,1}^{\mathrm{T}}& {\mathsf{\$}}_{wc,2,2}^{\mathrm{T}}& {\mathsf{\$}}_{wc,3,1}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$	$diag\left[\begin{array}{ccc}{E}_{ce,1,1}& E_{ce,2,2}& E_{ce,3,1}\end{array}\right]$
Model 4	${\left[\begin{array}{ccccc}{\mathsf{\$}}_{wc,1,1}^{\mathrm{T}}& {\mathsf{\$}}_{wc,1,2}^{\mathrm{T}}& {\mathsf{\$}}_{wc,2,1}^{\mathrm{T}}& {\mathsf{\$}}_{wc,2,2}^{\mathrm{T}}& {\mathsf{\$}}_{wc,3}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$	$\left[\begin{array}{ccc}{E}_{ce,1,1}& & \\ E_{ce,1,2}& & \\ & E_{ce,2,1}& \\ & E_{ce,2,2}& \\ & & E_{ce,3}\end{array}\right]$

, the four forms of the constraint wrench matrix $J_{ce}$ and the source error projection matrix $E_{ce}$ are given in detail. Correspondingly, there are four forms for the geometric error model of the over-constrained spindle head, named as models 1, 2, 3, and 4 for clarity. It should be noted that model 4 includes all five constraint wrenches. In this case, the geometric error model of the spindle head needs to be rewritten as follows:

$$\begin{array}{l}{\mathsf{\$}}_e=J_{e,i}^{+}{\delta }_{\omega }+J_{e,i}^{+}{E}_e^i\epsilon \\ {\delta }_{\omega }={\left[\begin{array}{cccc}\delta {\omega }_{1,1}& \delta {\omega }_{2,1}& \delta {\omega }_{3,1}& {\mathbf{0}}_{1\times 5}\end{array}\right]}^{\mathrm{T}},\end{array}$$

(14)

where $J_e^{+}$ represents the generalized inverse matrix of the Jacobian matrix $J_e$; and  denotes the error coefficient matrix for the spindle head.

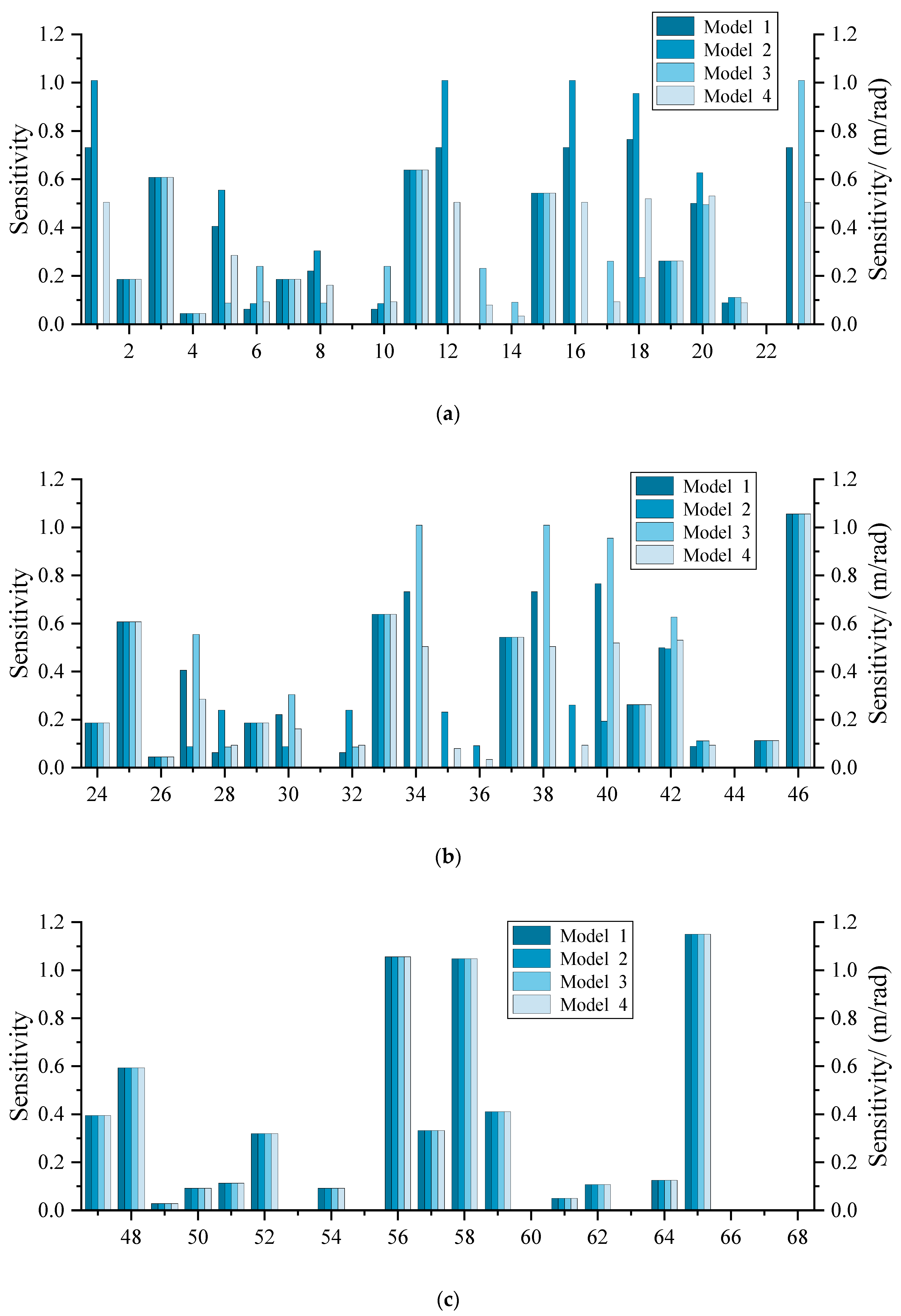
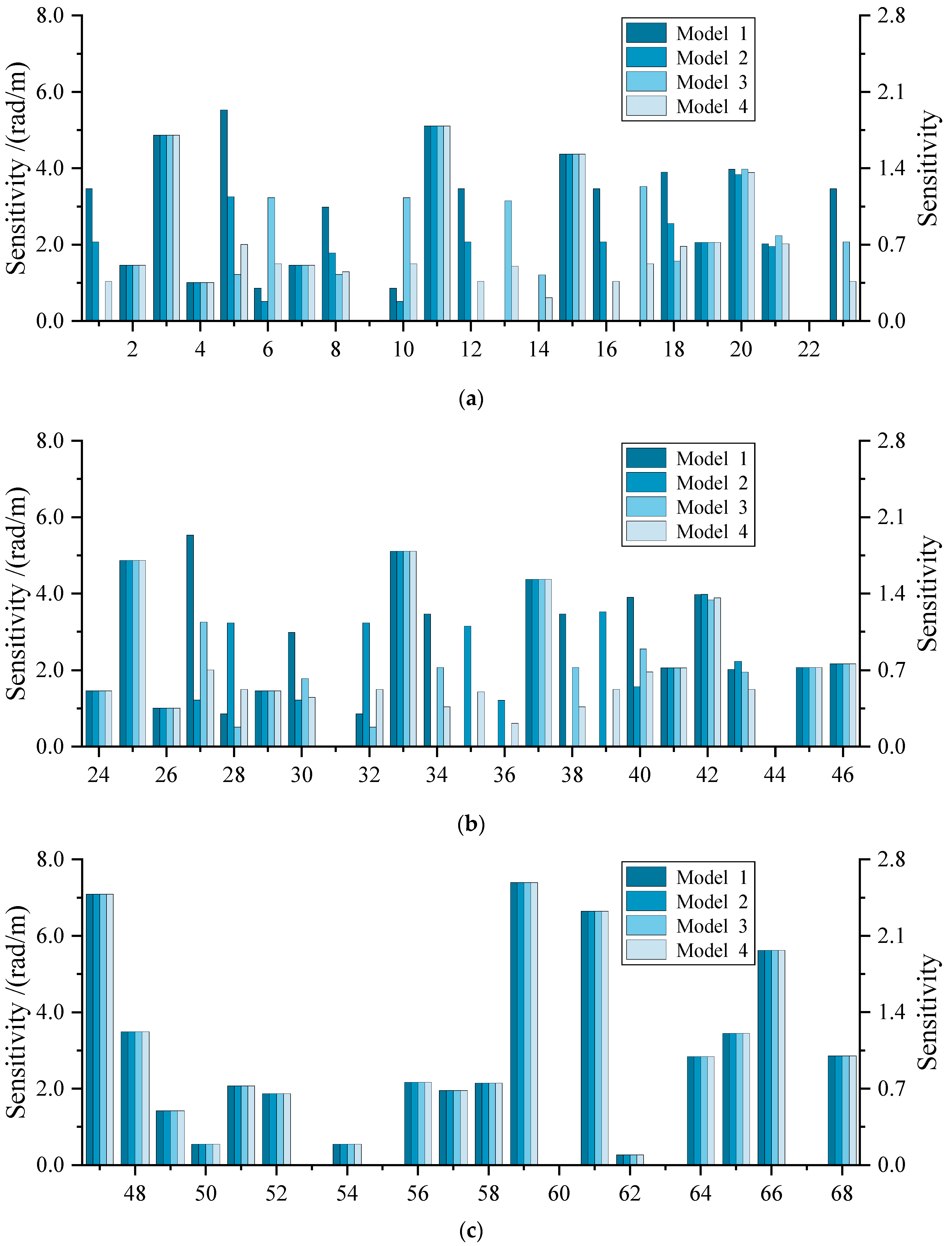
2.4. Comparative Sensitivity Analysis

To evaluate the effectiveness of the proposed four types of geometric error models comparatively, a set of sensitivity indices is formulated through the error coefficient matrix of the spindle head. Herein, for the nth geometric source error, the sensitivity coefficients of the terminal position error and orientation error are defined as follows:

$$\{\begin{array}{c}{\mu }_r^{(n)}=\sqrt{{\displaystyle \sum _{i=1}^3{\widehat{J}}_{\epsilon ,i,n}^2}}\\ {\mu }_{\theta }^{(n)}=\sqrt{{\displaystyle \sum _{i=4}^6{\widehat{J}}_{\epsilon ,i,n}^2}}\end{array},$$

(15)

where ${\widehat{J}}_{\mathsf{\epsilon },i,n}$ denotes the element at the ith row and the nth column of the error coefficient matrix ${\widehat{J}}_{\mathsf{\epsilon }}$.

With the above-defined sensitivity coefficients, the volumetric sensitivity indices of the terminal position error and orientation error aroused from the nth geometric source error throughout the spindle head’s workspace can be formulated as follows:

$$\{\begin{array}{c}{\eta }_r^{(n)}={\displaystyle \frac{{\displaystyle {\int }_V{\mu }_r^{(n)}dV}}{V}}\\ {\eta }_{\theta }^{(n)}={\displaystyle \frac{{\displaystyle {\int }_V{\mu }_{\theta }^{(n)}dV}}{V}}\end{array},$$

(16)

where V denotes the spindle head’s reachable workspace, which can be identified through a “sliced partition” searching algorithm proposed in our previous publication.

By adopting the above volumetric sensitivity indices, the sensitivities of a total of 68 geometric source errors regarding the terminal position error and orientation error of the spindle head can be computed, as demonstrated in Figure 4 and Figure 5. To facilitate expression, each depicted figure employs two vertical axes with different physical units to accommodate the dimensional differences between sensitivity indicators of the position source errors and orientation source errors.

As shown in Figure 4 and Figure 5, different geometric source errors often exhibit varying sensitivities, with some showing zero sensitivity indices. This phenomenon demonstrates that different source errors of the spindle head have varying impacts on its terminal position error and orientation error, and some geometric source errors do not propagate kinematic error effects to the moving platform (such source errors can be disregarded during tolerance design to enhance efficiency). A comparison between Figure 4 and Figure 5 reveals that sensitivity indices for source errors $\delta z_{1,1}$, $\delta x_{1,3}$, $\delta x_{1,4}$, etc., calculated using the proposed four geometric error models, are consistent. This suggests that these models adequately reflect the sensitivity indices of geometric source errors regarding terminal position/orientation error to a certain extent. However, for source errors $\delta {\theta }_{1,1}$, $\delta {\psi }_{1,2}$, $\delta {\phi }_{1,2}$, etc., there are differences in sensitivity values obtained from the geometric error models of model 1, model 2, model 3, and model 4, as shown in

Table 4. Identifiability of the source errors in different geometric error models.

Source Errors	Model 1	Model 2	Model 3	Model 4	Source Errors	Model 1	Model 2	Model 3	Model 4
$\delta x_{1,1}$	√	√	×	√	$\delta x_{2,1}$	√	×	√	√
$\delta {\theta }_{1,1}$	√	√	√	√	$\delta {\theta }_{2,1}$	√	√	√	√
$\delta {\phi }_{1,1}$	√	√	√	√	$\delta {\phi }_{2,1}$	√	√	√	√
$\delta {\psi }_{1,2}$	√	√	√	√	$\delta {\psi }_{2,2}$	√	√	√	√
$\delta {\phi }_{1,2}$	√	√	√	√	$\delta {\phi }_{2,2}$	√	√	√	√
$\delta z_{1,3}$	√	√	×	√	$\delta z_{2,3}$	√	×	√	√
$\delta {\psi }_{1,3}$	×	×	√	√	$\delta {\psi }_{2,3}$	×	√	×	√
$\delta {\theta }_{1,3}$	×	×	√	√	$\delta {\theta }_{2,3}$	×	√	×	√
$\delta z_{1,4}$	√	√	×	√	$\delta z_{2,4}$	√	×	√	√
$\delta {\psi }_{1,4}$	×	×	√	√	$\delta {\psi }_{2,4}$	×	√	×	√
$\delta x_{1,5}$	√	√	√	√	$\delta x_{2,5}$	√	√	√	√
$\delta z_{1,5}$	√	√	√	√	$\delta z_{2,5}$	√	√	√	√
$\delta {\psi }_{1,5}$	√	√	√	√	$\delta {\psi }_{2,5}$	√	√	√	√

.

From Table 4, it can be observed that model 1 fails to identify sensitivity indices for source errors $\delta {\psi }_{1,3}$, $\delta {\theta }_{1,3}$, $\delta {\psi }_{1,4}$, etc.; model 2 fails for source errors $\delta x_{2,1}$, $\delta z_{2,3}$, $\delta z_{2,4}$, etc.; and model 3 fails for source errors $\delta x_{1,1}$, $\delta z_{1,3}$, $\delta {\psi }_{2,3}$, etc. Meanwhile, model 4 successfully identifies sensitivity indices for all geometric source errors of the spindle head. This indicates that model 4 can effectively reflect the influence of geometric source errors on the terminal position/orientation error of the spindle head, thereby providing more rational guidance for source error identification. As a result, the geometric model considering all constraint wrenches of limb structures can be adopted as the basis of the error propagation intensity analysis and the tolerance design of such over-constrained mechanical systems.

The summary of this chapter is as follows: Several error models are established, and the optimal model is selected by comparing their different sensitivity coefficients. First, the structure and dimension parameters are described, and the relevant values of dimension parameters are determined based on existing research. Subsequently, error models of the limbs are established, and the passive joint errors are eliminated by taking the inner product with a driven wrench and constraint wrench. Finally, they are sorted into the different error models of the parallel mechanism, and the optimal error model is selected by comparing the sensitivity coefficients.

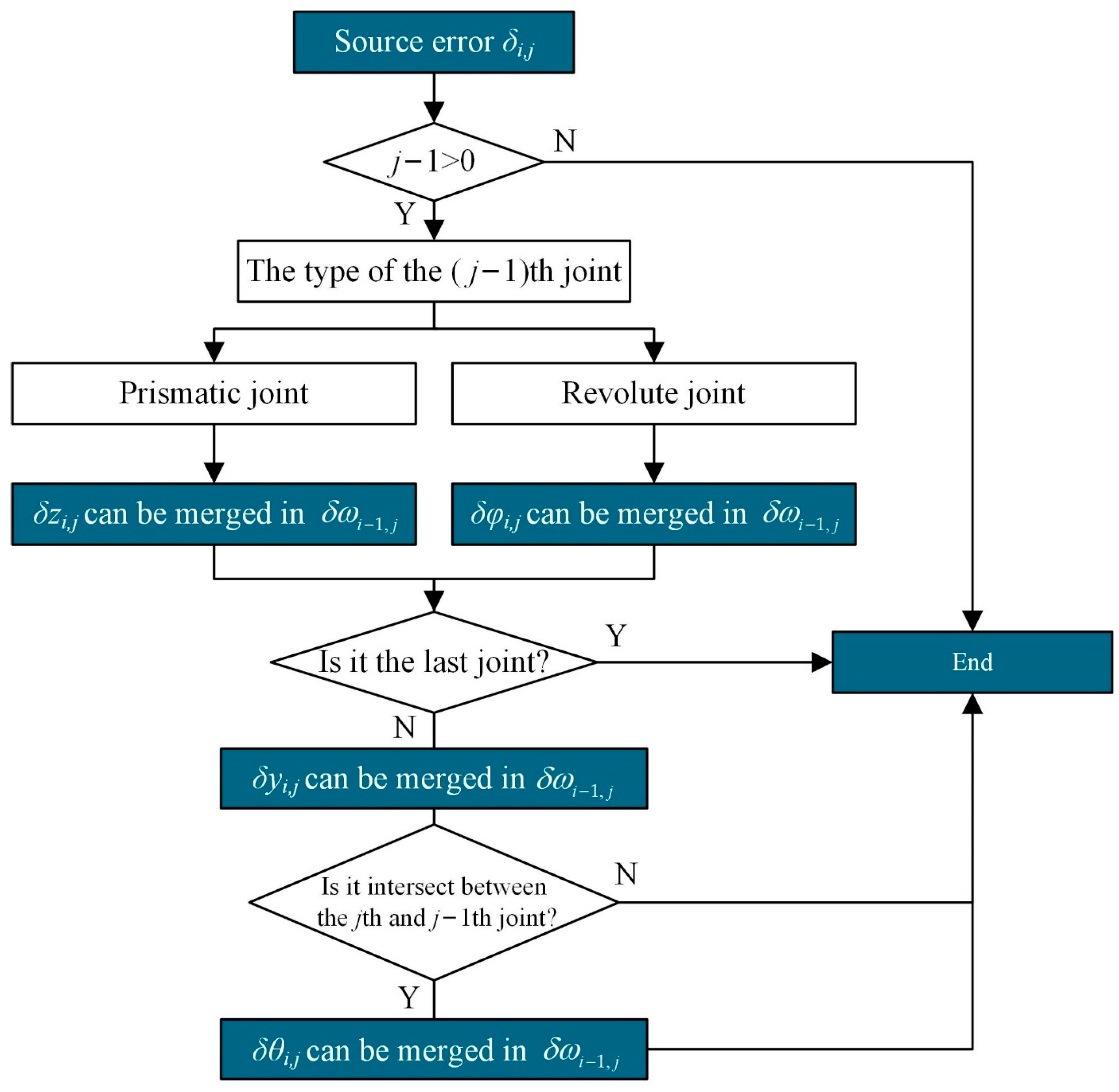
3. Error Propagation Analysis with Kinematic Interactions

In this section, a set of error propagation indices and coupled error propagation indices is proposed to analyze the error propagation at the limb structural level and the mechanical system level, respectively, revealing the influence pattern of the kinematic interactions between the limbs on the terminal accuracy of the over-constrained spindle head.

3.1. Error Propagation Index

Based on the geometric error modeling, a set of error propagation indices is proposed to describe the perturbation effects of the geometric source errors on the position and the orientation of the individual limb structure quantitatively, which is formulated as follows:

$$\{\begin{array}{c}{\sigma }_{T,i}=\sqrt{{\displaystyle \sum _{j=1}^3{\mathsf{\$}}_{e,i,j}^2}}\\ {\sigma }_{R,i}=\sqrt{{\displaystyle \sum _{j=4}^6{\mathsf{\$}}_{e,i,j}^2}}\end{array},$$

(17)

where ${\mathsf{\$}}_{e,i,j}$ represents the jth row of the error twist ${\mathsf{\$}}_{e,i}$ of the ith limb measured in the frame $O^{\prime }-uvw$; and ${\sigma }_{T,i}$ and ${\sigma }_{R,i}$ denote the linear error propagation index and the angular error propagation index of the ith individual limb structure, respectively.

From the above definitions, it can be found that the error propagation index quantitatively describes how much the perturbation of geometric errors affect the kinematic accuracy of the individual limb structure (without the kinematic interactions among limb structures). In such a way, a larger value of the error propagation index means a “stronger” geometric error propagation ability, indicating that more attention should be paid to the corresponding design tolerance when designing such a limb structure of the spindle head.

Considering the kinematic interactions among limb structures of the over-constrained spindle head, one may define the coupled error propagation index for the ith limb in the spindle head as follows:

$$\{\begin{array}{c}{\tilde{\sigma }}_{T,i}=\sqrt{{\displaystyle \sum _{j=1}^3{\widehat{\mathsf{\$}}}_{e,i,j}^2}}\\ {\tilde{\sigma }}_{R,i}=\sqrt{{\displaystyle \sum _{j=4}^6{\widehat{\mathsf{\$}}}_{e,i,j}^2}}\end{array},$$

(18)

where ${\widehat{\mathsf{\$}}}_{e,i,j}$ represents the jth row and the ith column of the error twist ${\mathsf{\$}}_e$ of the platform of the spindle head in which source errors only adopted in the ith limb; and ${\tilde{\sigma }}_{T,i}$ and ${\tilde{\sigma }}_{R,i}$ denote the coupled linear error propagation index and the coupled angular error propagation index of the ith individual limb structure in the over-constrained spindle head, respectively.

From the above Equation (18), it is evident that the coupled error propagation index quantitatively describes the perturbation to the terminal accuracy of the spindle head caused by the geometric errors of an individual limb structure (with the kinematic interactions among limb structures). In other words, a larger coupled error propagation index indicates a greater influence of the corresponding limb on the terminal accuracy of the spindle head, necessitating more attention during tolerance design and structural optimization stages.

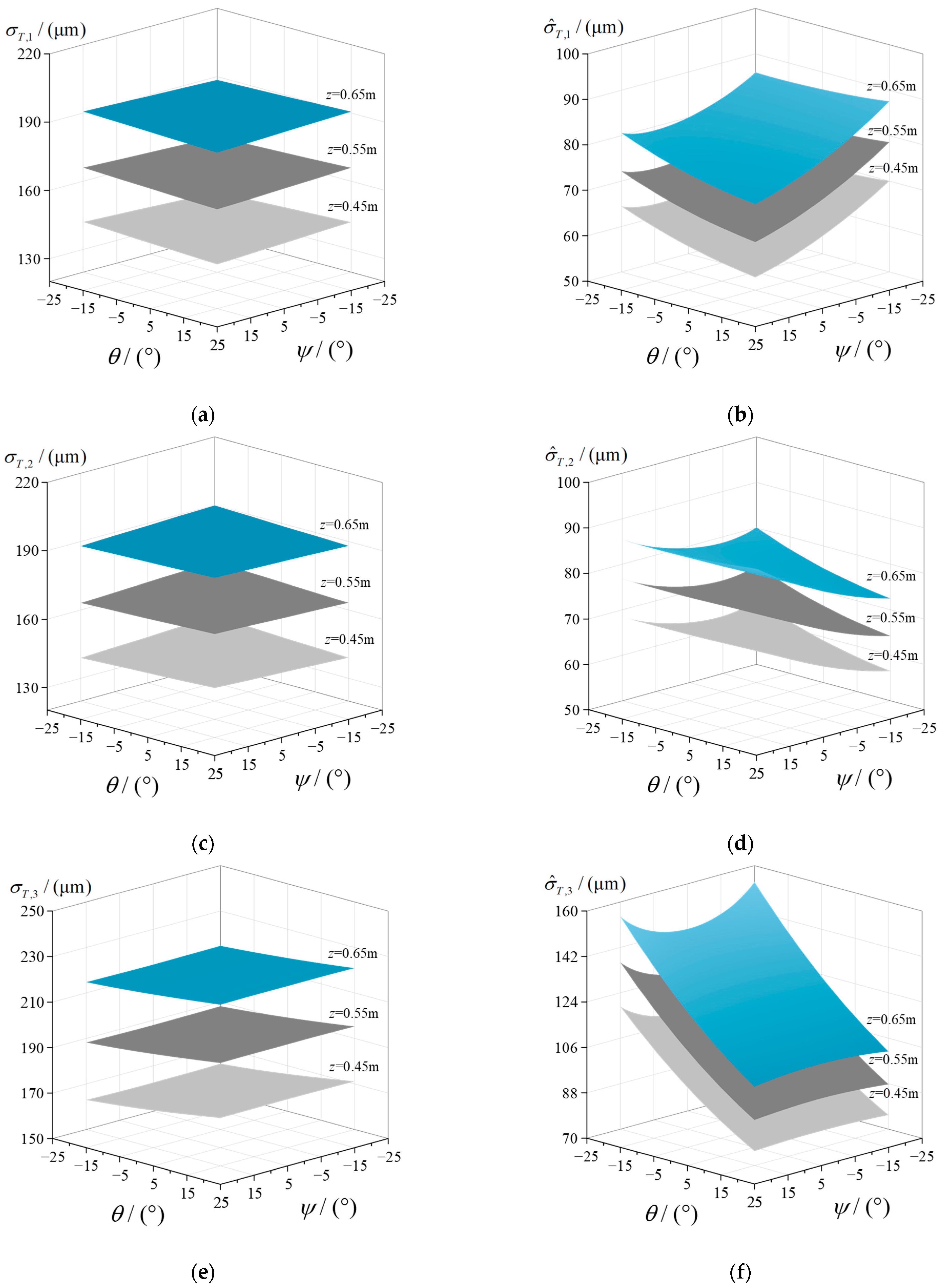
3.2. Error Propagation Analysis for Individual Limb

Without the loss of generality, the initial tolerances of the limb assemblages of the spindle head are given in

Table 5. Tolerances of the PRU limbs (i = 1,2).

Error	Tolerance	Error	Tolerance	Error	Tolerance	Error	Tolerance
$\delta x_{i,1}$	130 μm	$\delta x_{i,2}$	62 μm	$\delta {\psi }_{i,3}$	0.056°	$\delta x_{i,5}$	114 μm
$\delta y_{i,1}$	87 μm	$\delta {\psi }_{i,2}$	0.014°	$\delta {\theta }_{i,3}$	0.056°	$\delta y_{i,5}$	43 μm
$\delta z_{i,1}$	36 μm	$\delta {\theta }_{i,2}$	0.014°	$\delta {\phi }_{i,3}$	0.025°	$\delta z_{i,5}$	27 μm
$\delta {\psi }_{i,1}$	0.064°	$\delta {\phi }_{i,2}$	0.010°	$\delta x_{i,4}$	48 μm	$\delta {\psi }_{i,5}$	0.034°
$\delta {\theta }_{i,1}$	0.085°	$\delta x_{i,3}$	14 μm	$\delta z_{i,4}$	28 μm	$\delta {\theta }_{i,5}$	0.006°
$\delta {\phi }_{i,1}$	0.032°	$\delta z_{i,3}$	74 μm	$\delta {\psi }_{i,4}$	0.0138°	$\delta {\phi }_{i,5}$	0.080°

,

Table 6. Tolerances of the PRS limbs.

Error	Tolerance	Error	Tolerance	Error	Tolerance	Error	Tolerance
$\delta x_{3,1}$	142 μm	$\delta {\psi }_{3,2}$	0.014°	$\delta z_{3,4}$	46 μm	$\delta z_{3,6}$	27 μm
$\delta y_{3,1}$	93 μm	$\delta {\theta }_{3,2}$	0.014°	$\delta {\psi }_{3,4}$	0.016°	$\delta {\psi }_{3,6}$	0.031°
$\delta z_{3,1}$	41 μm	$\delta {\phi }_{3,2}$	0.010°	$\delta x_{3,5}$	65 μm	$\delta {\theta }_{3,6}$	0.005°
$\delta {\psi }_{3,1}$	0.075°	$\delta x_{3,3}$	63 μm	$\delta z_{3,5}$	36 μm	$\delta {\phi }_{3,6}$	0.037°
$\delta {\theta }_{3,1}$	0.091°	$\delta z_{3,3}$	14 μm	$\delta {\psi }_{3,5}$	0.014°
$\delta {\phi }_{3,1}$	0.037°	$\delta {\psi }_{3,3}$	0.068°	$\delta x_{3,6}$	63 μm
$\delta x_{3,2}$	62 μm	$\delta x_{3,4}$	32 μm	$\delta y_{3,6}$	25 μm

and

Table 7. Tolerances of the error of joint motion.

Error	Tolerance	Error	Tolerance	Error	Tolerance	Error	Tolerance
$\delta {\omega }_{1,1}$	67 μm	$\delta {\omega }_{2,1}$	67 μm	$\delta {\omega }_{3,1}$	69 μm	$\delta {\omega }_{3,5}$	0.039°
$\delta {\omega }_{1,2}$	0.036°	$\delta {\omega }_{2,2}$	0.036°	$\delta {\omega }_{3,2}$	0.036°
$\delta {\omega }_{1,3}$	0.041°	$\delta {\omega }_{2,3}$	0.041°	$\delta {\omega }_{3,3}$	0.046°
$\delta {\omega }_{1,4}$	0.035°	$\delta {\omega }_{2,4}$	0.035°	$\delta {\omega }_{3,4}$	0.037°

based on engineering experience. For batch production of the components in the spindle head, the geometric source errors are random variables which are characterized by normal distributions. The value of a position or orientation source error can be generated from a normal distribution with a mean value of zero and a standard deviation of 1/6 corresponding tolerances, listed in Table 5, Table 6 and Table 7. Thereafter, Monte Carlo simulations of the geometric errors of the spindle head are carried out in the allowed tolerance zones. The variations of the linear/angular error propagation index and the coupled linear/angular error propagation index for three limb structures of the spindle head are illustrated in Figure 6 and Figure 7, respectively. The number of samples is set as 10⁵.

Figure 6a,c,e shows the variations of the linear error propagation index of the three limb structures. It can be seen that the linear error propagation indices of all three limbs increase with the increase in the position coordinate z and are less impacted by the orientation coordinates ψ and θ of the spindle head’s platform. Figure 6b,d,f shows the variations of the coupled linear error propagation index of the three limb structures. It is obvious that the coupled linear error propagation indices of the three limbs are mainly impacted by the orientation coordinates ψ and θ, rather than the coordinate z.

Furthermore, in Figure 6, the coupled linear error distributions of limb 1 and limb 2 are mirrored with respect to the plane of ψ = 0, and the coupled linear error distribution of limb 3 is symmetric with respect to the plane of ψ = 0. The observed phenomena indicate that regardless of whether kinematic interactions among limb structures are considered, the linear error propagation index and the coupled linear error propagation index for the three limbs are pose-dependent. For instance, limb 1 has a greater impact on the terminal linear error at larger absolute values of the orientation coordinate ψ, while limb 3 has a more significant influence at larger absolute values of orientation coordinate θ. Therefore, incorporating the error propagation performance at different configurations into the trajectory planning process of the spindle head can help enhance its terminal accuracy.

Figure 7a,c,e show the variations of the angular error propagation index of the three limb structures. It can be seen that the position and orientation coordinates z, ψ, and θ do not affect the angular error propagation indices of the three limbs. Figure 7b,d,f show the variations of the coupled angular error propagation index of three limb structures. It can be seen that the coupled angular error propagation indices of three limbs increase with the increasing of the position coordinate z, while the orientation coordinates ψ and θ have different effects on these indices and have more significant influence than the coordinate z. Similar to the linear error distributions described in Figure 6, the coupled angular error distributions of limb 1 and limb 2 are mirrored with respect to the plane of ψ = 0, and the coupled angular error distribution of limb 3 is symmetric with respect to the plane of ψ = 0. As a result, the angular error propagation index and the coupled angular error propagation index for the three limbs are pose-dependent too. From the perspective of kinematic enhancement, the over-constrained spindle head has better terminal accuracy when the orientation is near the home position with ψ = 0 and θ = 0.

With the error propagation effects of limbs in mind, the relative deviations of ${\sigma }_{T,i}$/${\sigma }_{R,i}$ and ${\widehat{\sigma }}_{T,i}$/${\widehat{\sigma }}_{R,i}$ (i = 1, 2, 3) are employed to describe quantitatively the extent to which the geometric errors of the ith limb structure is affected by the kinematic interactions of the other limbs, as expressed in the following:

$$\{\begin{array}{c}{\eta }_{T,i}={\displaystyle \frac{{\sigma }_{T,i}-{\widehat{\sigma }}_{T,i}}{{\sigma }_{T,i}}}\times 100\%\\ {\eta }_{R,i}={\displaystyle \frac{{\sigma }_{R,i}-{\widehat{\sigma }}_{R,i}}{{\sigma }_{R,i}}}\times 100\%\end{array}(i=1,2,3).$$

(19)

In Equation (19), ${\eta }_{T,i}$ and ${\eta }_{R,i}$ represent the relative changes in the linear and angular errors of the ith limb before and after considering the kinematic interactions of the limb structures, respectively, which measure the magnitude of the kinematic error coupling at the limb structural level. Both ${\eta }_{T,i}$ and ${\eta }_{R,i}$ are positive values, indicating that the ith limb is experiencing error compensation due to the kinematic interactions of the other limbs, and vice versa. Moreover, the larger the values of ${\eta }_{T,i}$ and ${\eta }_{R,i}$, the more pronounced the compensatory effect of the other limb structures on the ith limb. For clarity, the average and maximum values of ${\eta }_{T,i}$ and ${\eta }_{R,i}$ within the spindle’s workspace are presented in

Table 8. Linear/angular error of the ith limb before and after considering the kinematic interactions of other limbs.

Index		Limb 1		Limb 2		Limb 3
		Average	Maximum	Average	Maximum	Average	Maximum
Linear error indices	${\sigma }_{T,i}$ (μm)	169.0	194.7	168.5	194.1	195.8	225.0
	${\widehat{\sigma }}_{T,i}$ (μm)	73.4	89.6	73.1	89.0	111.2	157.8
	${\eta }_{T,i}$	56.6%	54.0%	56.6%	54.1%	43.2%	29.9%
Linear error indices	${\sigma }_{R,i}$ (°)	8.21 × 10−3	8.23 × 10−3	8.21 × 10−3	8.22 × 10−3	8.34 × 10−3	8.35 × 10−3
	${\widehat{\sigma }}_{R,i}$ (°)	4.66 × 10−3	5.83 × 10−3	4.66 × 10−3	5.82 × 10−3	5.32 × 10−3	7.54 × 10−3
	${\eta }_{R,i}$	43.2%	29.2%	43.2%	29.2%	36.2%	9.7%

.

Table 8 shows that both the average and maximum values of ${\eta }_{T,i}$ and ${\eta }_{R,i}$ are positive, with ${\eta }_{T,1}$ and ${\eta }_{R,1}$ and ${\eta }_{T,2}$ and ${\eta }_{R,2}$ being equal, respectively. This observation suggests that the linear and angular errors of the ith limb structure are subject to varying degrees of compensation from the other limbs. Additionally, due to the identical structure and symmetrical arrangement of limb 1 and limb 2, their compensatory effects from the other limbs are also consistent. Furthermore, the comparison reveals that ${\eta }_{T,1}$/${\eta }_{T,2}$ and ${\eta }_{R,1}$/${\eta }_{R,2}$ are both greater than ${\eta }_{T,3}$ and ${\eta }_{R,3}$, indicating that the geometric error compensation experienced by limb 1 and limb 2 is greater than that experienced by limb 3. Therefore, it is necessary to pay closer attention to the structural design and component selection of limb 3 during the design phase to ensure that it possesses equivalent motion accuracy to the other limbs, thus not compromising the overall motion performance of the over-constrained spindle head.

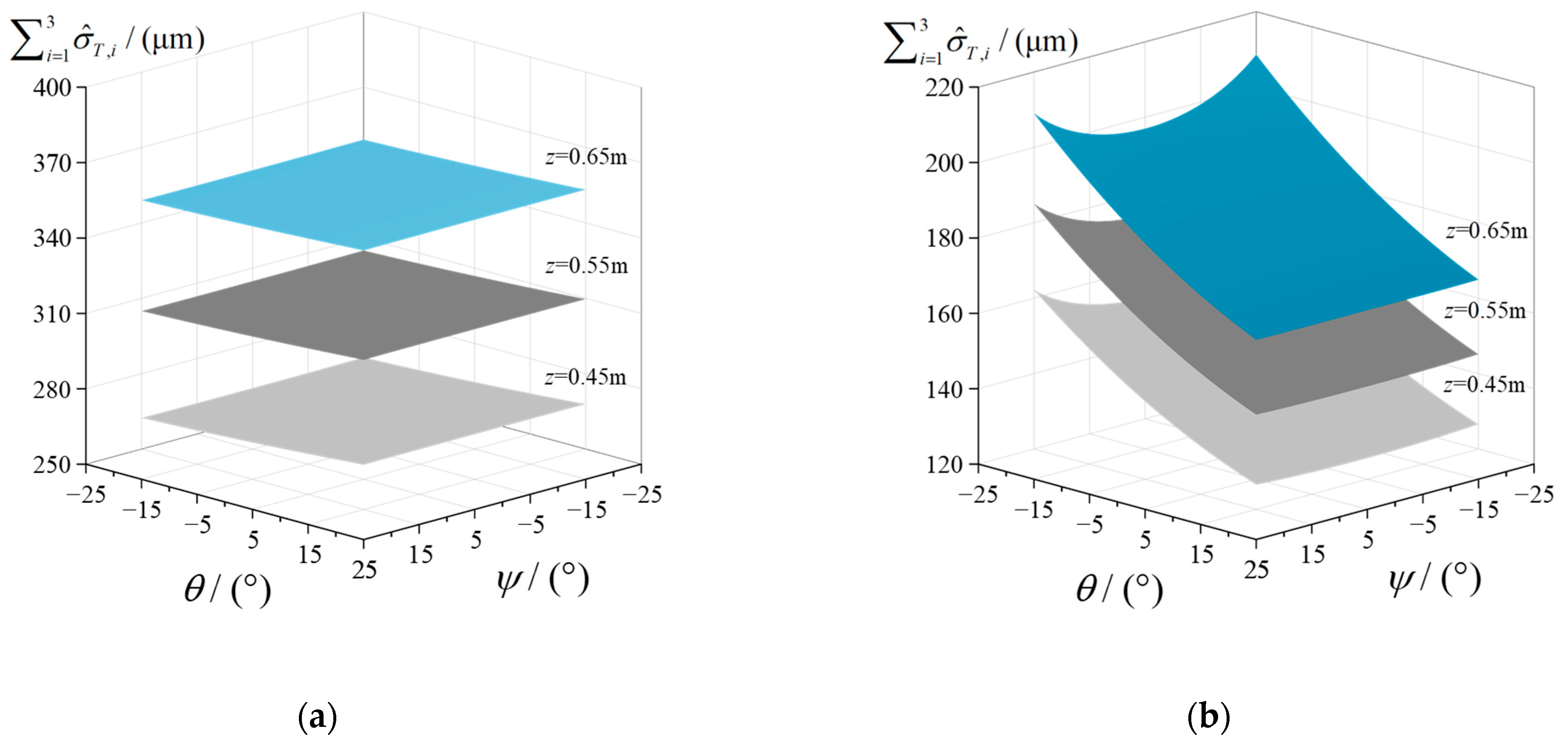
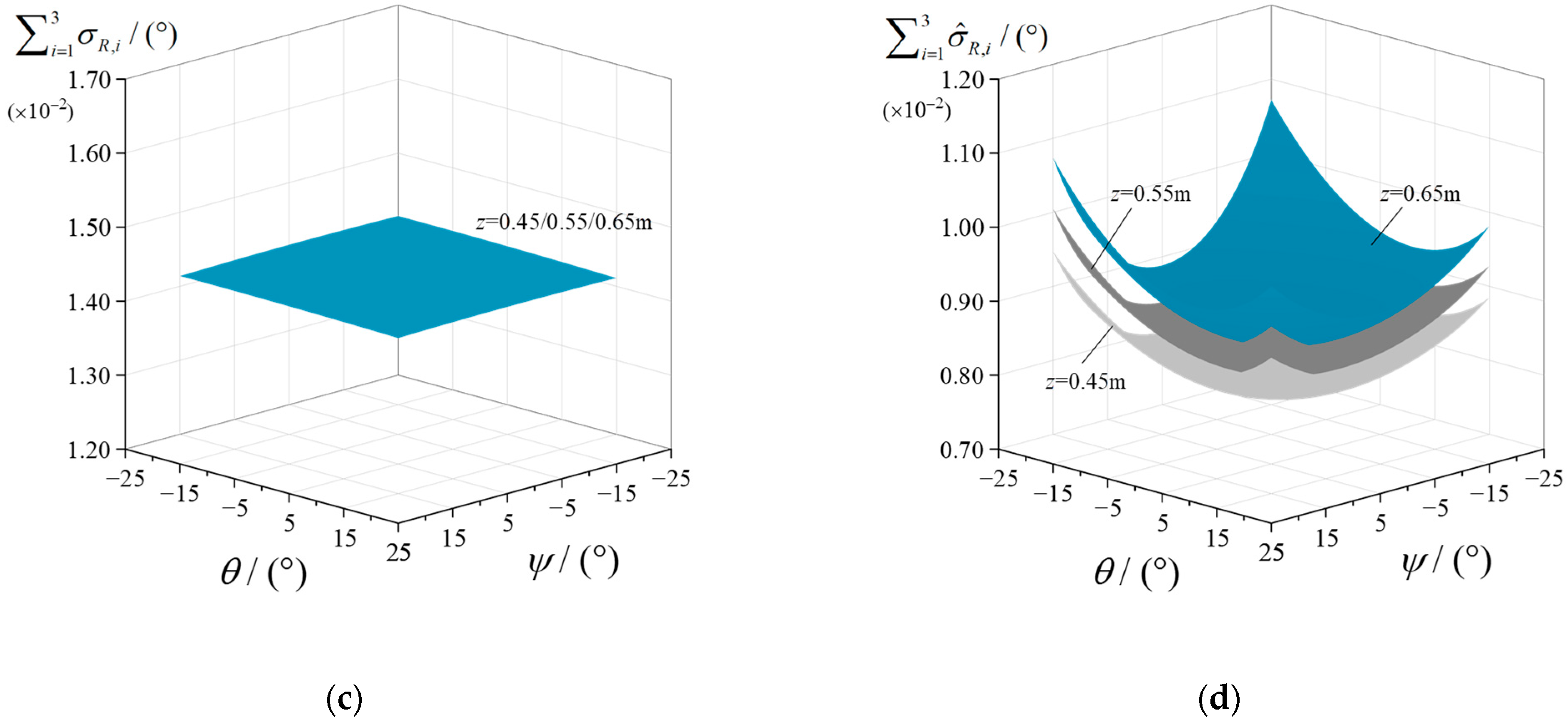
3.3. Error Propagation Analysis for Terminal Platform

The terminal error of the spindle head stems from the cumulative effects of the kinematic errors of the three limb structures. Consequently, ${\displaystyle {\sum }_{i=1}^3{\sigma }_{T,i}}$/${\displaystyle {\sum }_{i=1}^3{\sigma }_{R,i}}$ and ${\displaystyle {\sum }_{i=1}^3{\widehat{\sigma }}_{T,i}}$/${\displaystyle {\sum }_{i=1}^3{\widehat{\sigma }}_{R,i}}$ can represent the terminal linear/angular errors of the spindle head without and with considering the kinematic interactions of the three limbs, respectively, as depicted in Figure 8.

Figure 8a,c illustrate the distributions of linear and angular errors at the spindle head’s terminal, respectively, when the kinematic interactions of the three limbs are not considered. It is evident from the figures that the terminal linear error is significantly influenced by the position coordinate z, while the angular error is unaffected by both z and the orientation coordinates ψ and θ. In contrast, Figure 8b,d show the distributions of linear and angular errors at the spindle head’s terminal when the kinematic interactions of the three limbs are taken into account. Both linear error and angular error at the spindle head’s terminal are significantly influenced by both the position coordinate z and the orientation coordinates ψ and θ, demonstrating clear position dependence. To reflect the impact of the kinematic interactions of limbs on the terminal accuracy of the spindle head intuitively, it is convenient to take the relative deviations of ${\displaystyle {\sum }_{i=1}^3{\sigma }_{T,i}}$/${\displaystyle {\sum }_{i=1}^3{\sigma }_{R,i}}$ and ${\displaystyle {\sum }_{i=1}^3{\widehat{\sigma }}_{T,i}}$/${\displaystyle {\sum }_{i=1}^3{\widehat{\sigma }}_{R,i}}$, as expressed in the following:

$$\{\begin{array}{c}{\eta }_T={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^3{\sigma }_{T,i}}-{\displaystyle {\sum }_{i=1}^3{\widehat{\sigma }}_{T,i}}}{{\displaystyle {\sum }_{i=1}^3{\sigma }_{T,i}}}}\times 100\%\\ {\eta }_R={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^3{\sigma }_{R,i}}-{\displaystyle {\sum }_{i=1}^3{\widehat{\sigma }}_{R,i}}}{{\displaystyle {\sum }_{i=1}^3{\sigma }_{R,i}}}}\times 100\%\end{array}.$$

(20)

In Equation (20), ${\eta }_T$ and ${\eta }_R$ denote the relative changes in the terminal linear error and the terminal angular error of the spindle head before and after considering the kinematic interactions of limbs, respectively, which quantify the magnitude of the kinematic error coupling at the level of mechanical system. Both ${\eta }_T$ and ${\eta }_R$ being positive indicates mutual compensation between the limb structures, whereas negative values suggest otherwise. Furthermore, the greater the values of ${\eta }_T$ and ${\eta }_R$, the more pronounced the mutual compensation between the limb structures. For clarity, the average and maximum of ${\eta }_T$ and ${\eta }_R$ within the spindle head’s reachable workspace are provided in

Table 9. Terminal error of the spindle head before and after considering the kinematic interactions of limbs.

End Index		Average	Maximum
Linear error indices	${\displaystyle {\sum }_{i=1}^3{\sigma }_{T,i}}$ (μm)	313.6	359.2
	${\displaystyle {\sum }_{i=1}^3{\widehat{\sigma }}_{T,i}}$ (μm)	163.9	213.0
	${\eta }_T$	47.7%	40.7%
Angular error indices	${\displaystyle {\sum }_{i=1}^3{\sigma }_{R,i}}$ (°)	1.43 × 10−2	1.44 × 10−2
	${\displaystyle {\sum }_{i=1}^3{\widehat{\sigma }}_{R,i}}$ (°)	8.68 × 10−3	1.09 × 10−2
	${\eta }_R$	39.3%	24.3%

.

Table 9 reveals that both the average and maximum values of ${\eta }_T$ and ${\eta }_R$ are positive, with the average value of ${\eta }_T$ reaching up to 47.7%. This phenomenon once again indicates that there is a mutual compensation relationship between the geometric errors of the limbs in such an over-constrained spindle head, and such interactive compensation significantly reduces the moving platform’s linear error, enhancing the terminal accuracy of the spindle head.

4. Conclusions

(1)

Four geometric error models considering different combinations of constraint wrenches are established for the over-constrained spindle head. A set of sensitivity indices is formulated to evaluate the effectiveness of these models. Comparative sensitivity analysis suggests that among the three error models considered without all constraints, there are six source errors that cannot be identified. A model incorporating all constraint wrenches can effectively reflect the influence of all geometric source errors on the terminal position/orientation error of the spindle head and is suitable for error propagation intensity analysis of such an over-constrained mechanical system.

(2)

The proposed error propagation indices quantitatively describe how much the perturbation of geometric errors affect the kinematic accuracy of the individual limb structure. The coupled error propagation indices quantitatively describe the perturbation to the terminal accuracy of the spindle head caused by the geometric errors of an individual limb structure. These two kinds of performance indices can be adopted to analyze the error propagation at the limb structural level and the mechanical system level of the spindle head, respectively.

(3)

Further error propagation analysis results show that the error propagation indices for the three limbs are pose-dependent, and the kinematic errors of a limb structure are subject to varying degrees of compensation from the other limbs. The average of linear error indices of limb 1 and limb 2 are reduced by 56.6%; the average of linear error indices of limb 3 are reduced by 43.2%. Moreover, there is a mutual compensation relationship between the geometric errors of the limbs in such an over-constrained spindle head. By taking the mixing mechanism as an example, the results show that the average linear error is reduced by 47.7%. Such interactive compensation significantly reduces the moving platform’s linear error, enhancing the terminal accuracy of the spindle head.