Cyber-Physical Scheduling System for Multiobjective Scheduling Optimization of a Suspension Chain Workshop Using the Improved Non-Dominated Sorting Genetic Algorithm II
Abstract
1. Introduction
2. Research Background
2.1. Cyber-Physical System and Digital Twins
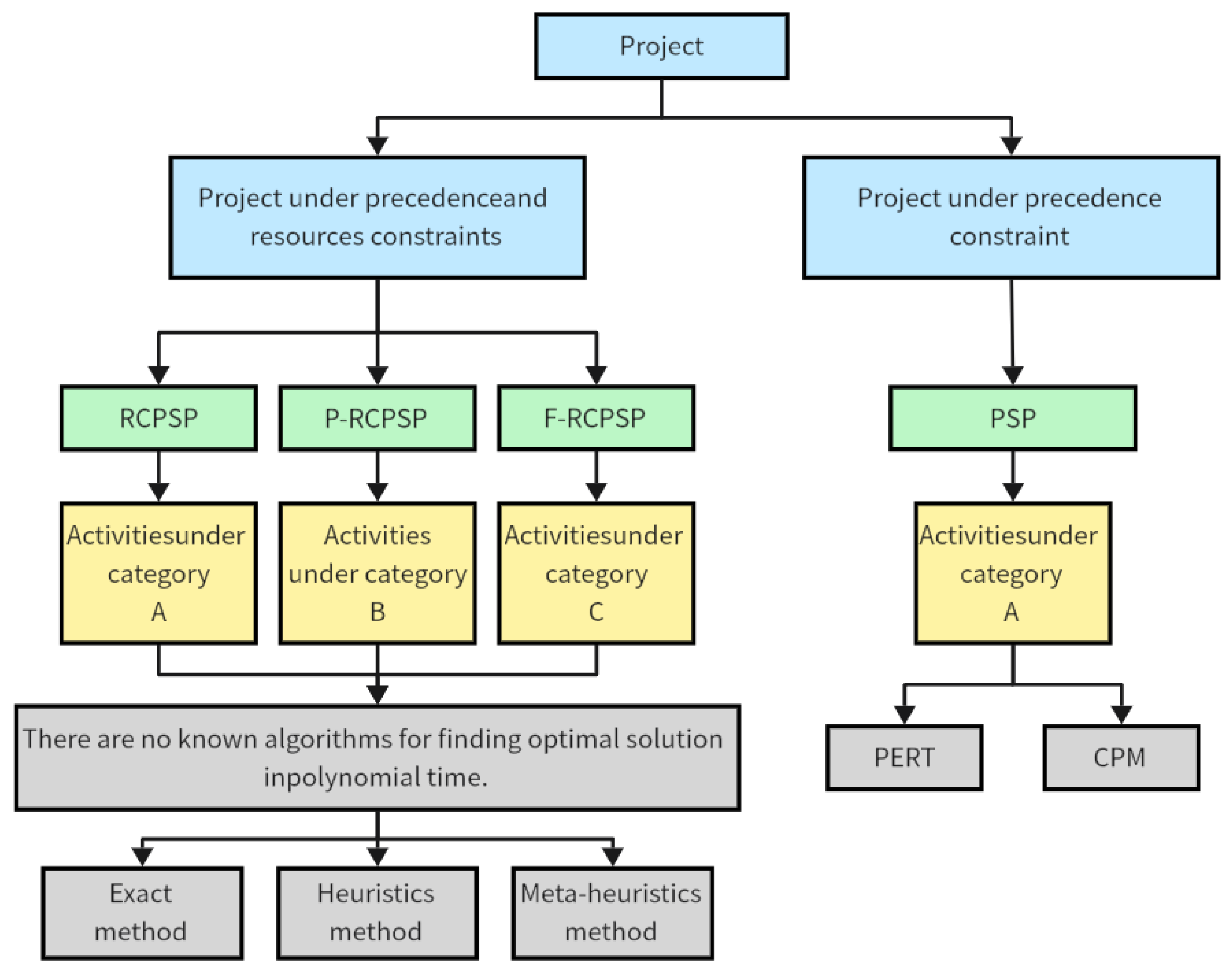
2.2. Multiobjective Scheduling Problem
2.3. Multiconstraint Scheduling Problem
2.4. About Simulation and Modeling
3. Model Establishment
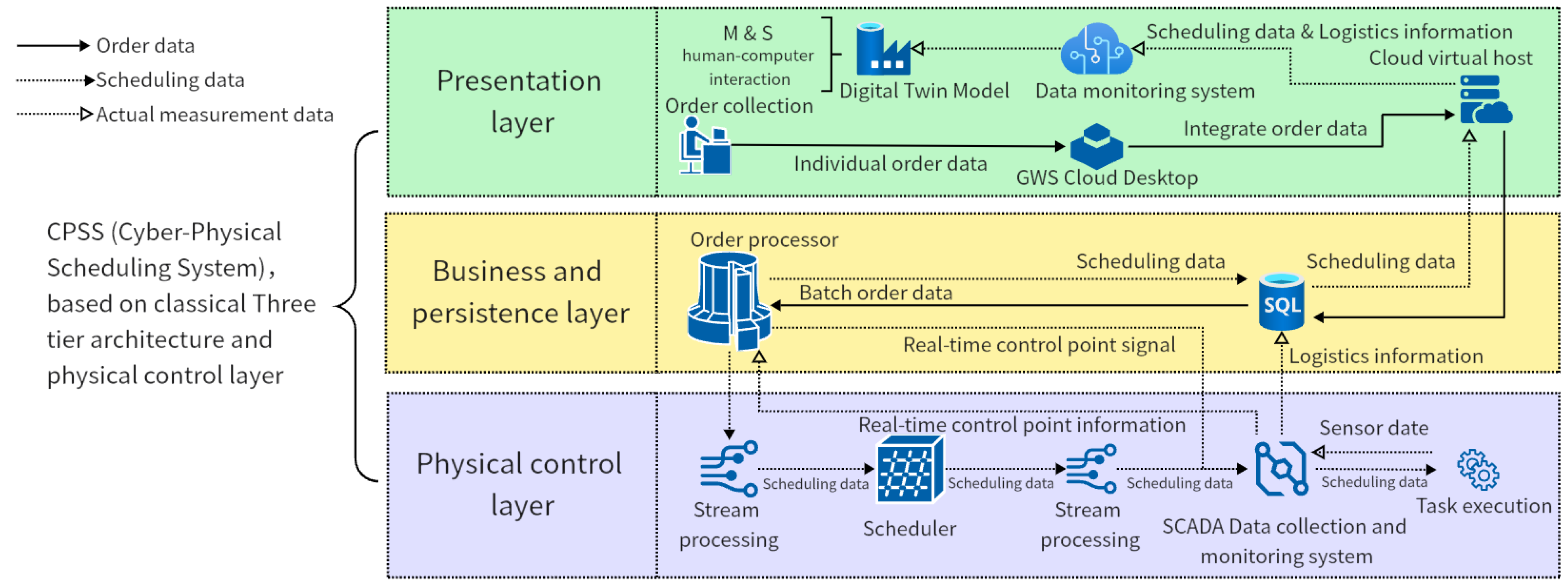
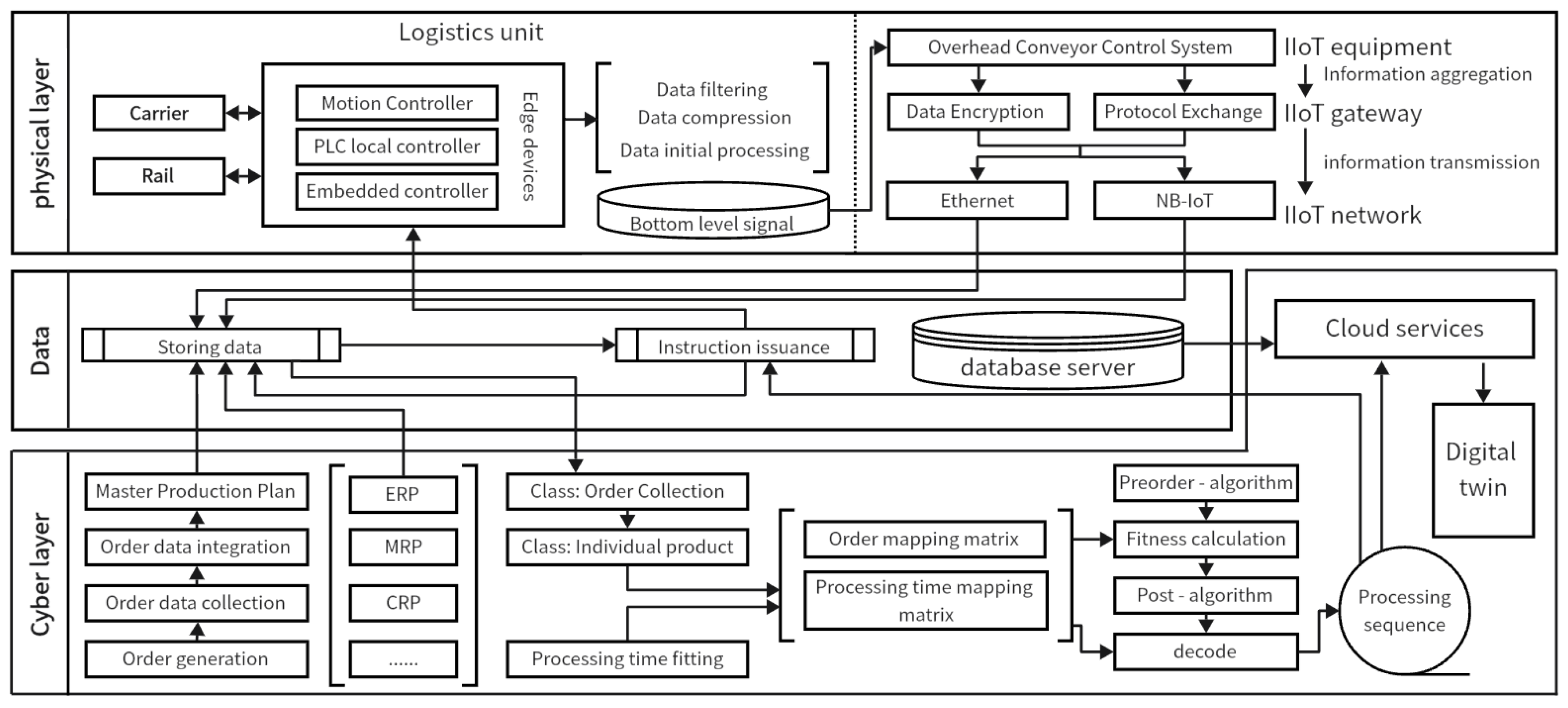
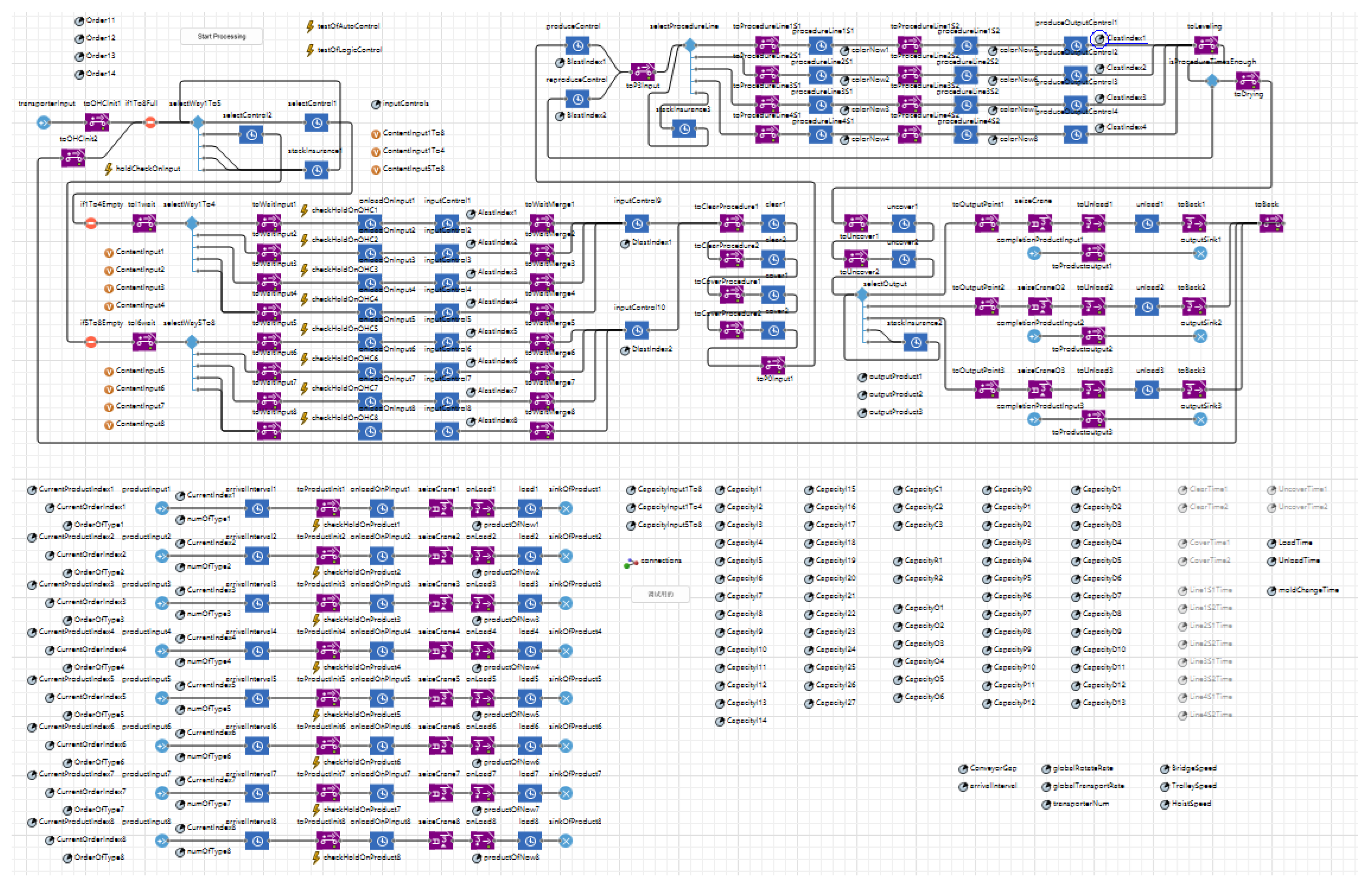
3.1. Design of Cyber-Physical Scheduling Systems
3.2. Practical Application Context
- First, the mathematical model is constructed, which will be used for the design and improvement of the algorithm.
- Next, the discrete system simulation model is constructed to verify the algorithm’s results through simulation.
- Finally, the logical control model is constructed. These models, derived from the discrete system simulation model, will guide the operation of the suspension–chain–transportation system.
4. Algorithm Model Establishment
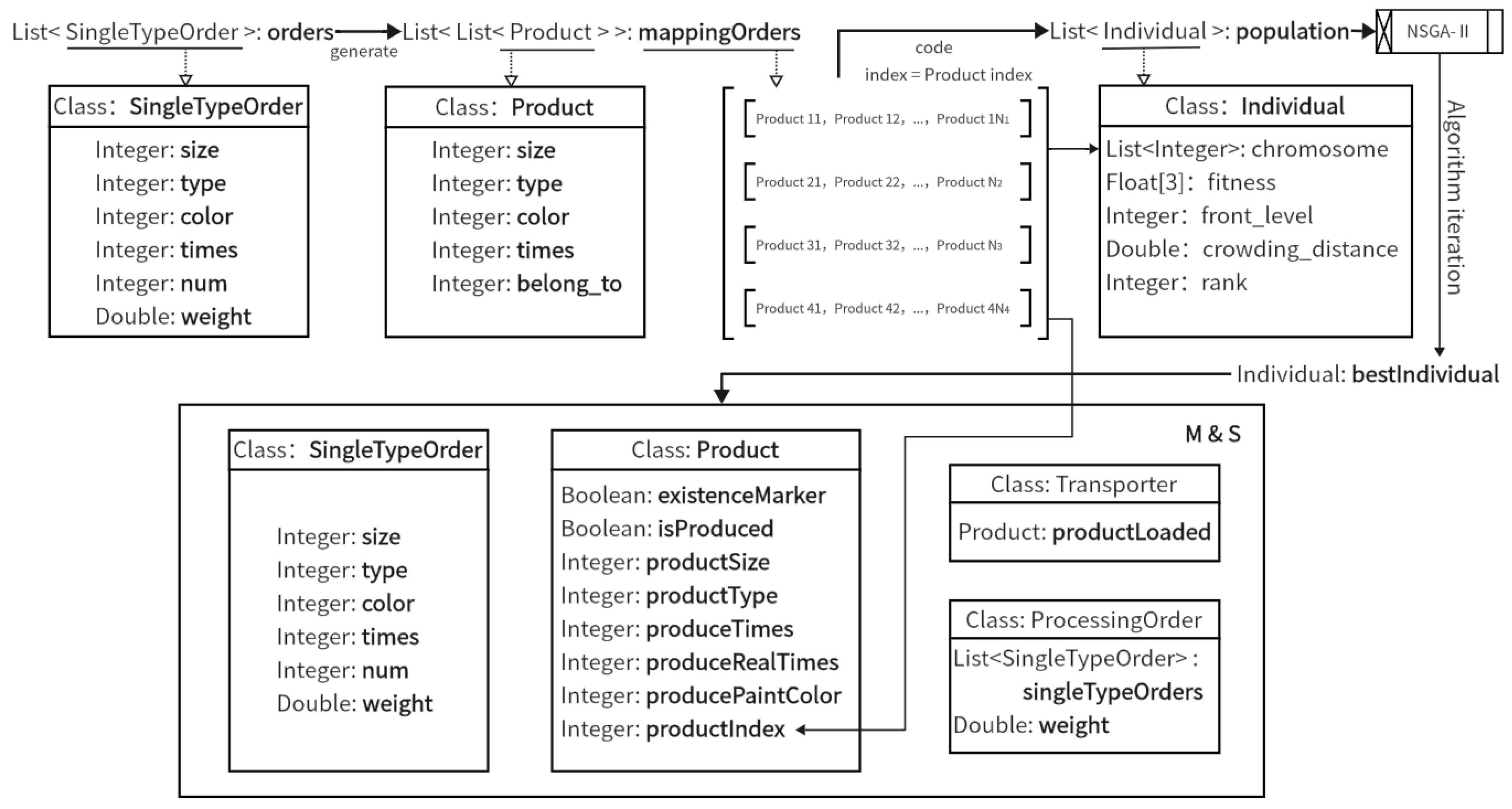
4.1. Symbol Definitions
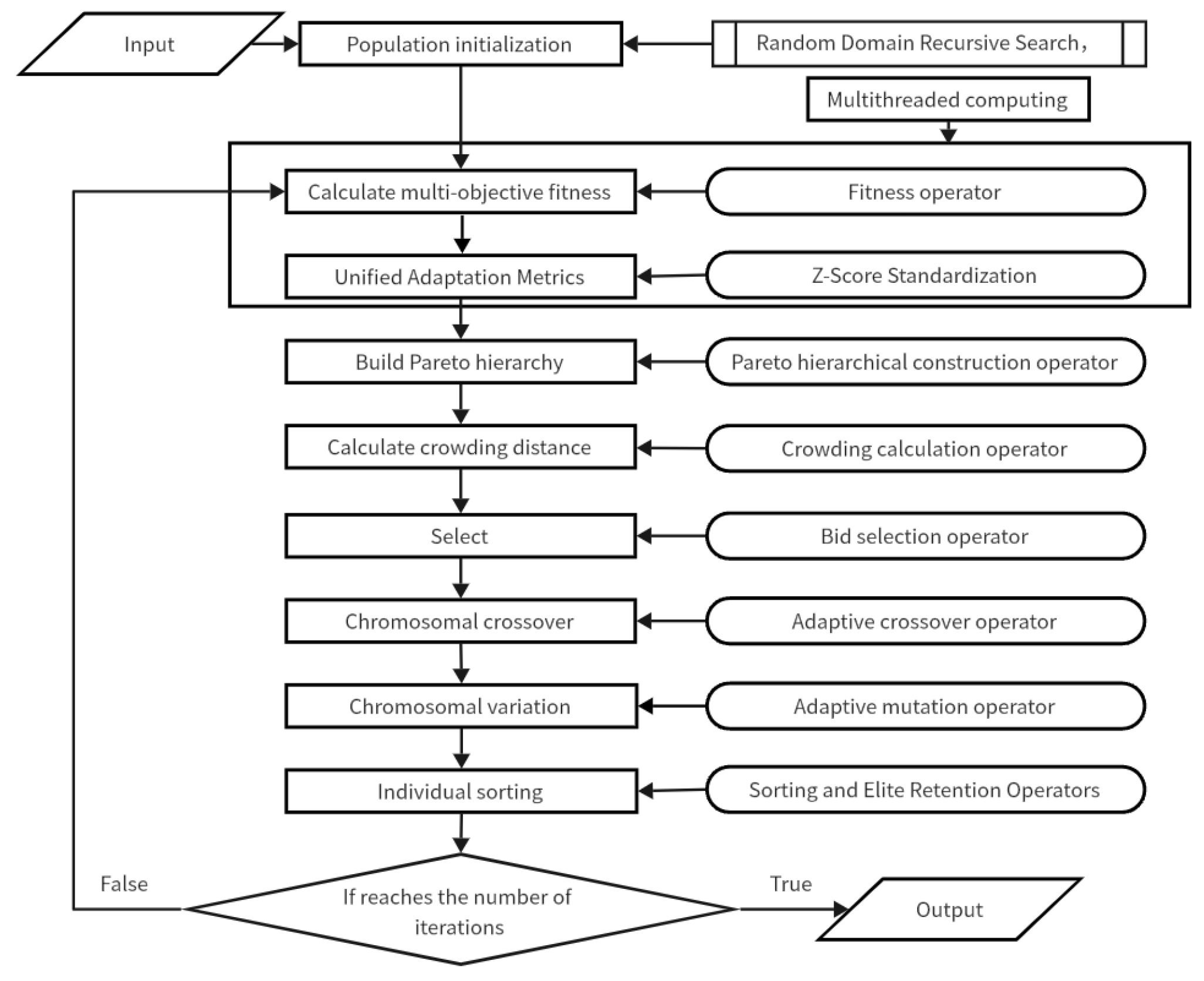
4.2. Algorithm Framework Selection
4.3. Encoding
4.4. Constraints
- Within the same production line, no two operations on any workpiece should occur consecutively more than once.
- Across all production lines, there should be no excessive distance between any two consecutive operations on any workpiece.
4.5. Objective Function
- Maximize the product of the weight and the last output time of each order i, summed over all orders n:where represents the weight of order i, and denotes the output time of the last workpiece of order i.
- Minimize the number of tool changeovers across all production lines m, where is the total time spent on tool changes per production line:Here, represents the total tool change time for production line j.
4.6. Operator Design
4.6.1. Population Initialization
| Algorithm 1 InsertGens |
| Require: , , , Ensure: , ,
|
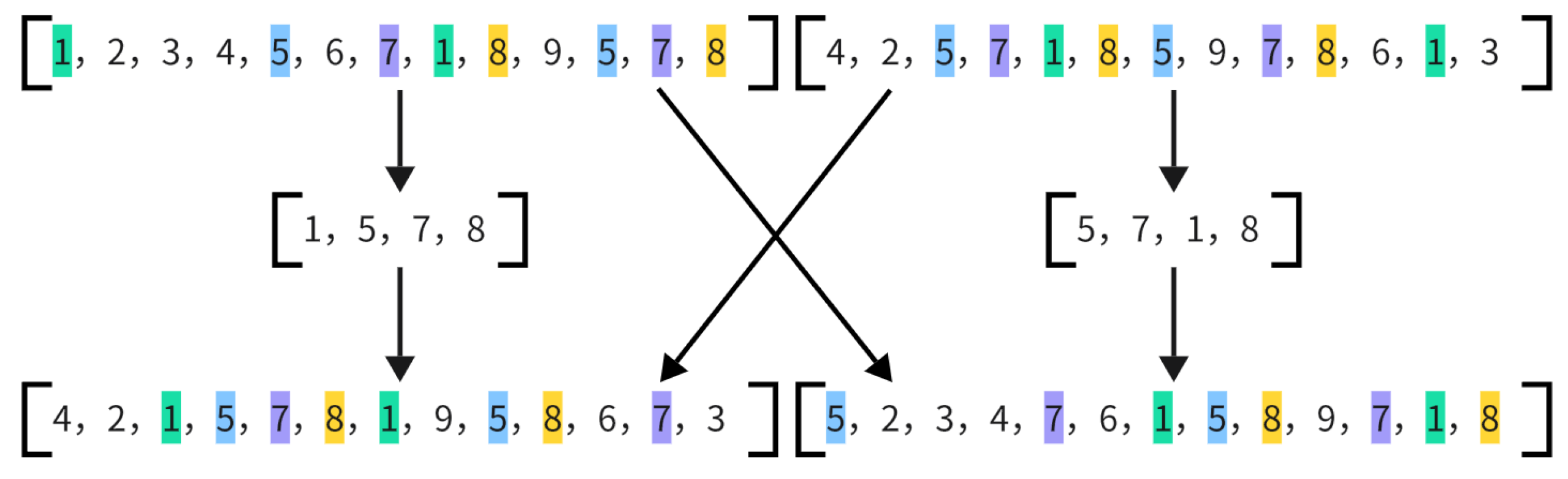
4.6.2. Crossover
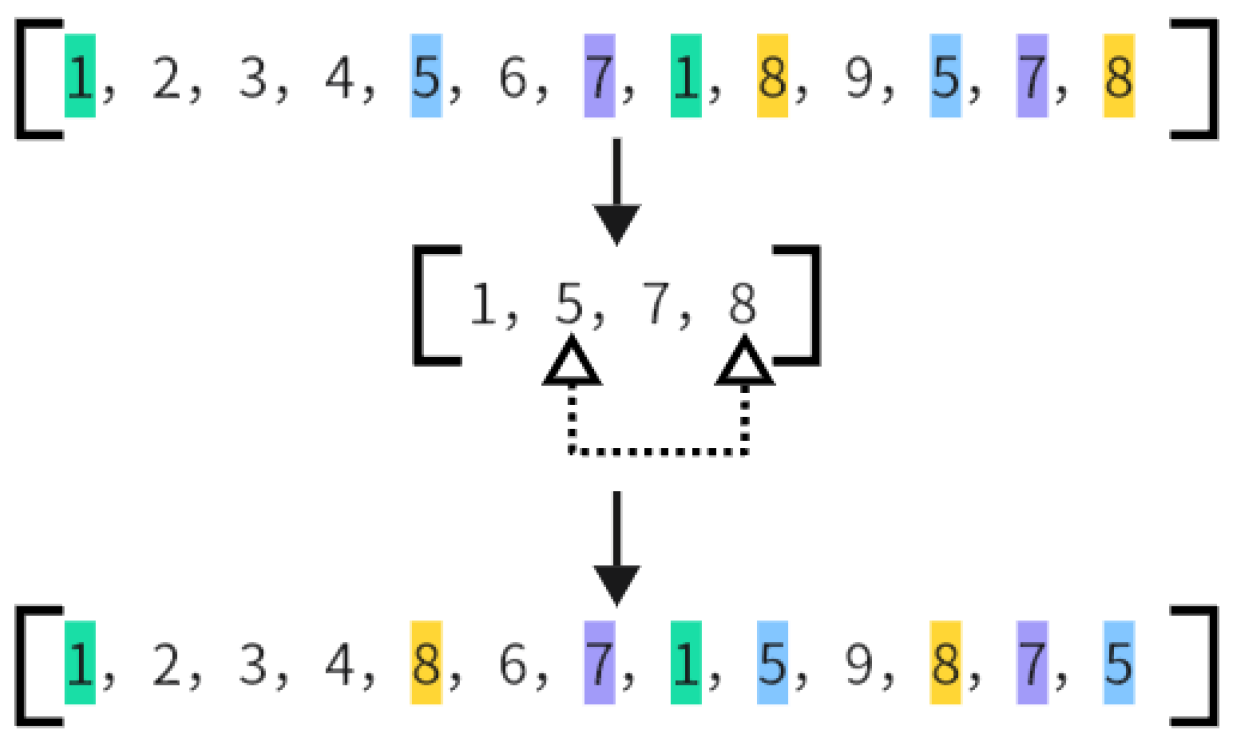
4.6.3. Mutation
4.7. Fitting of Processing Time
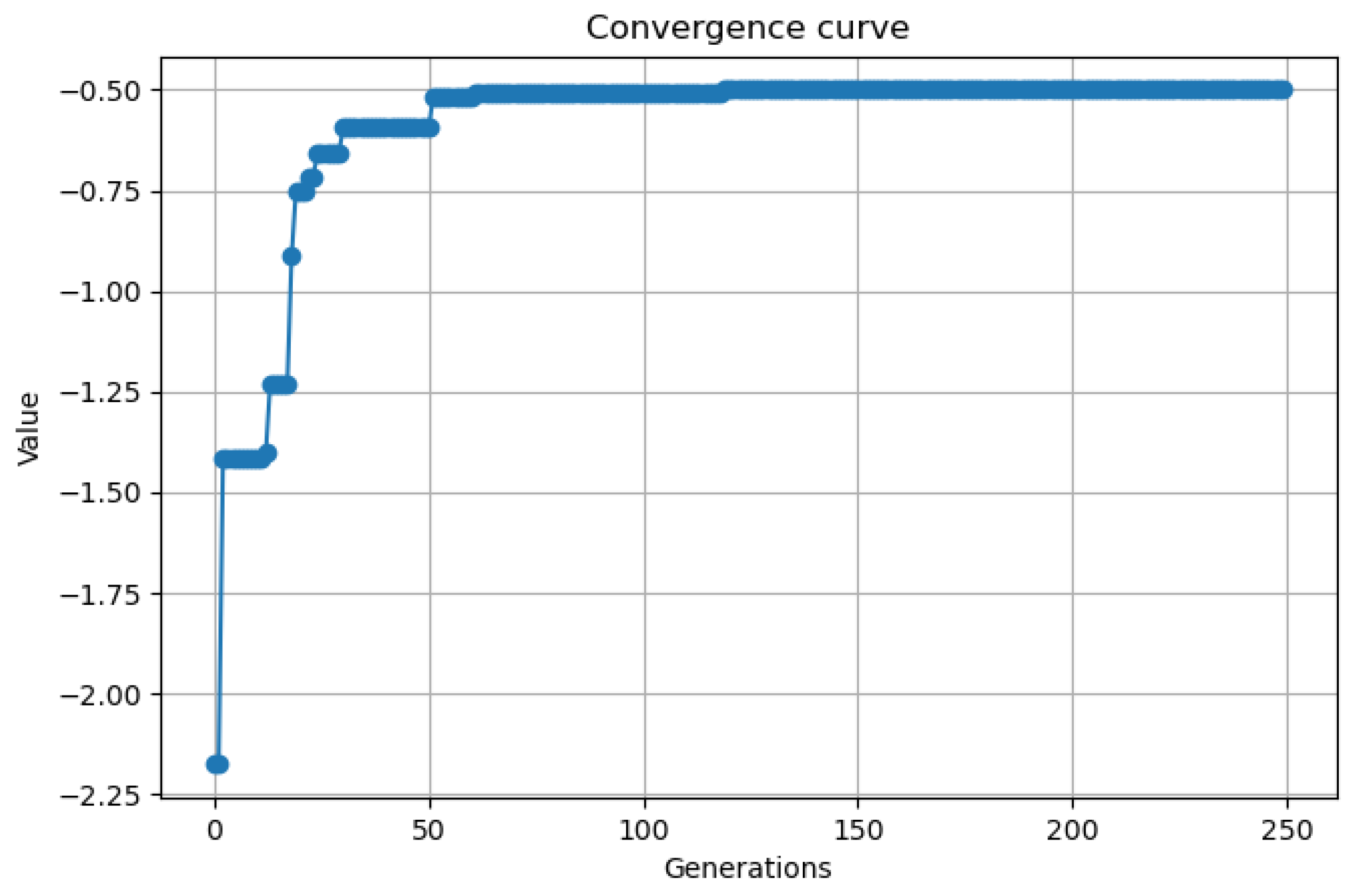
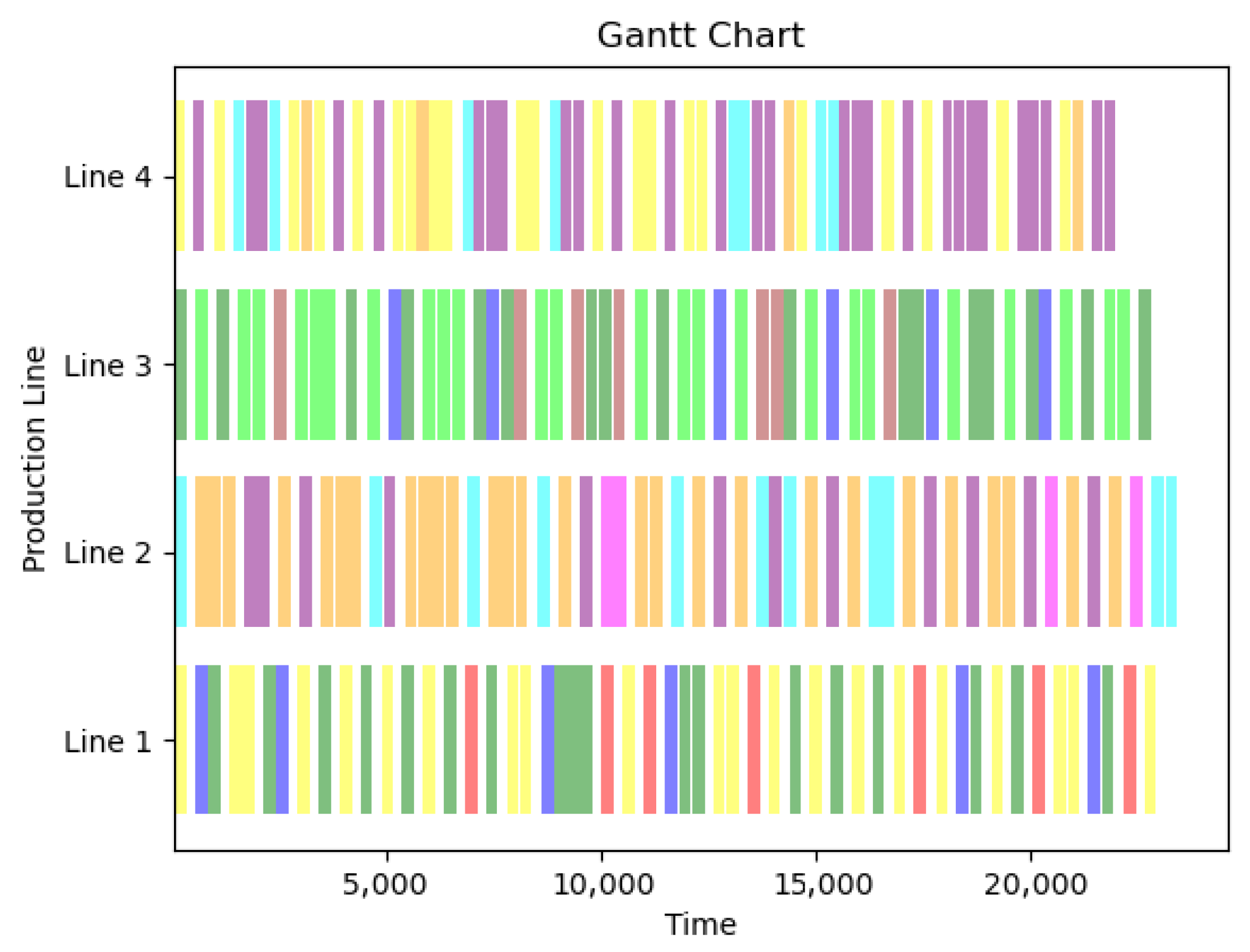
4.8. Algorithm Convergence Results
5. Simulation Model Establishment
5.1. Simulation Fidelity
5.1.1. Randomly Repeated Experiments
5.1.2. Module Decoupling
5.1.3. Constraints and Assumptions
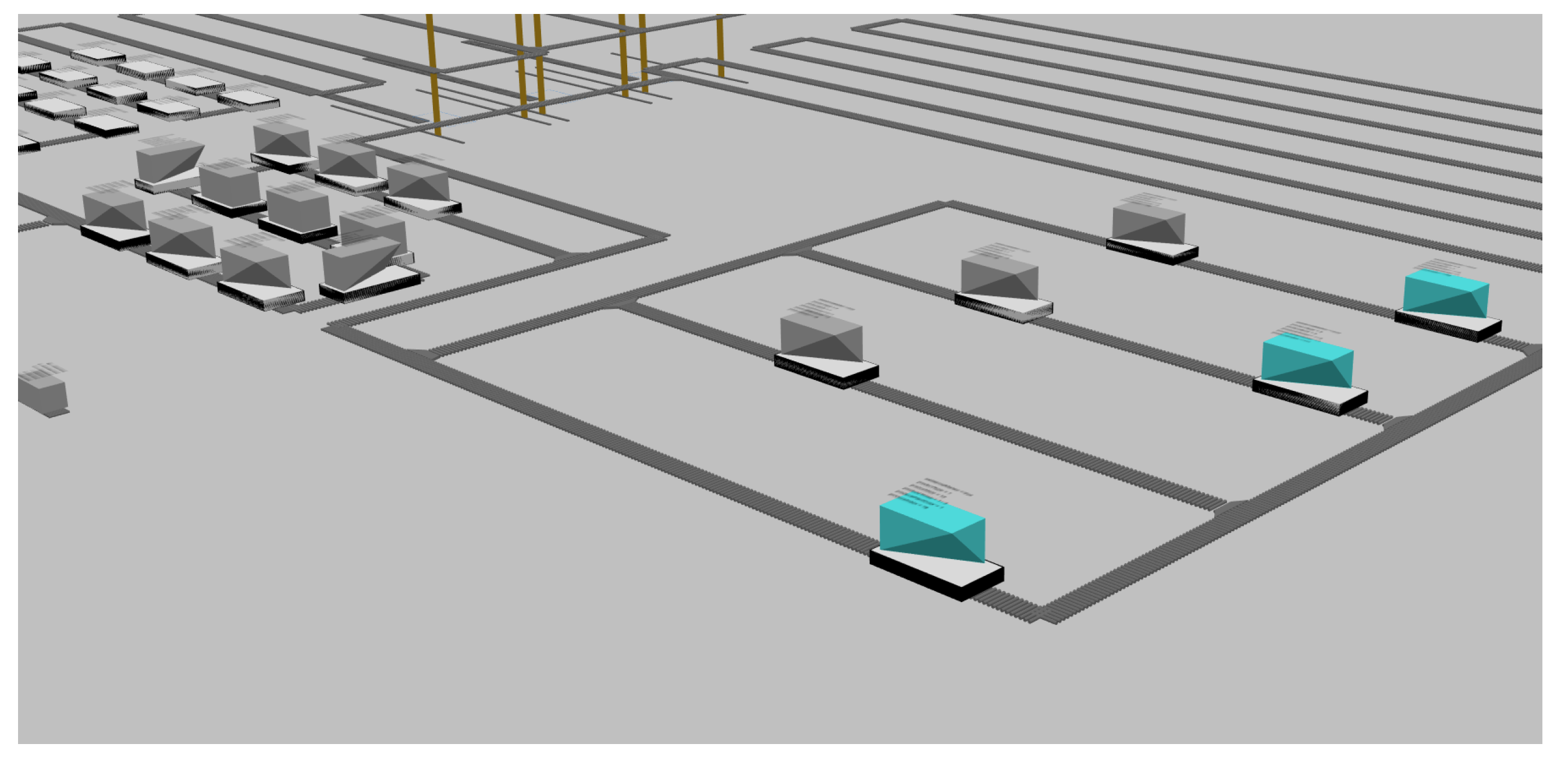
- The suspension chain is replaced with a roller conveyor line, and turntables are employed at corners instead. Since their performance and parameters are identical and Anylogic does not have a pre-packaged suspension chain model, substituting with an existing roller conveyor line ensures equivalent effectiveness while considerably simplifying the workload.
- The tray’s speed during operation is constant, and the acceleration of the tray on the conveyor belt is neglected. In production, trays move slowly; therefore, strict speed requirements are not necessary. Additionally, due to the significant acceleration of workpieces during movement, neglecting tray acceleration increases model stability.
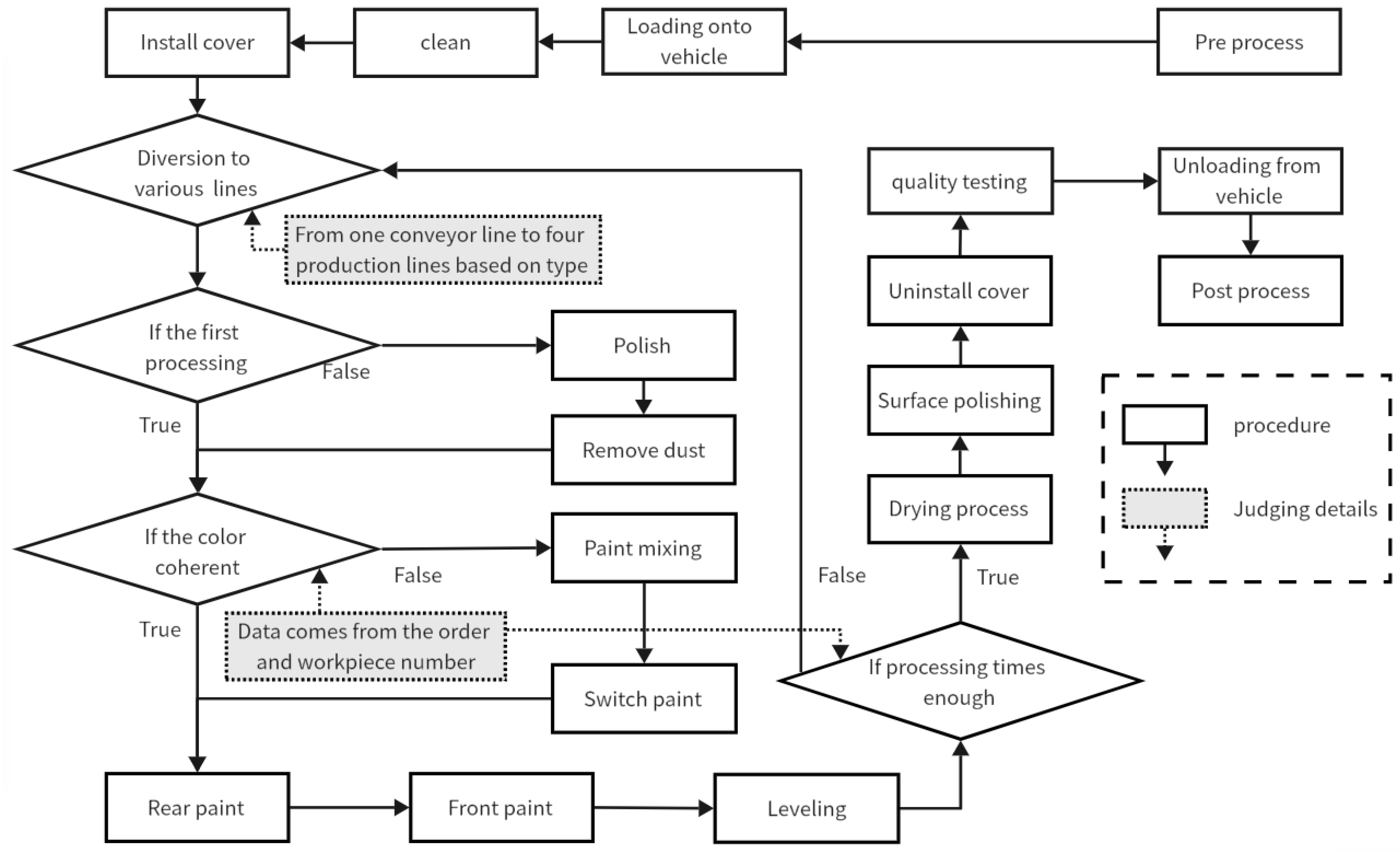
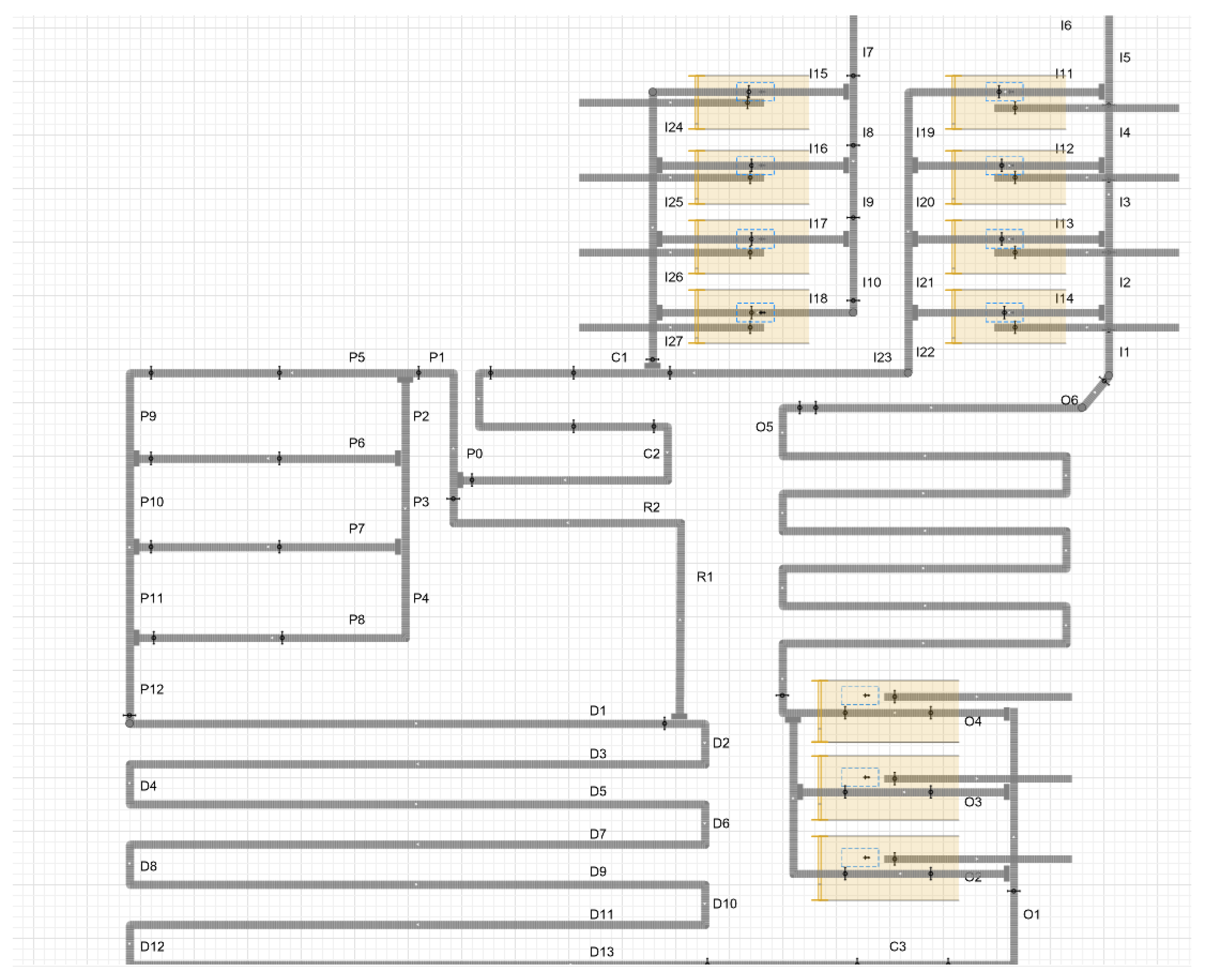
5.2. The Logic Control Scheme
- Output sequence from loading ports 1–4 to I22.
- Output sequence from loading ports 5–8 to I27.
- Output sequence from two loading-port convergence nodes into mainline C1.
- Output sequence from four processing lines to P12.
- Output sequence from the initial processing and repeat processing workpieces into main processing line P1.
6. Joint Simulation
6.1. Simulation Parameters
6.2. Experimental Design
6.3. Simulation Result
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dafflon, B.; Moalla, N.; Ouzrout, Y. The challenges, approaches, and used techniques of CPS for manufacturing in Industry 4.0: A literature review. Int. J. Adv. Manuf. Technol. 2021, 113, 2395–2412. [Google Scholar] [CrossRef]
- Zamfirescu, C.B.; Pirvu, B.C.; Schlick, J.; Zuehlke, D. Preliminary Insights for an Anthropocentric Cyber-Physical Reference Architecture of the Smart Factory. Stud. Inform. Control 2013, 22, 269–278. [Google Scholar] [CrossRef]
- Hermann, M.; Pentek, T.; Otto, B. Design Principles for Industry 4.0 Scenarios. 2015. Available online: http://www.snom.mb.tu-dortmund.de/cms/de/forschung/Arbeitsberichte/Design-Principles-for-Industrie-4_0-Scenarios.pdf (accessed on 11 May 2016).
- Dai, K.; Zhu, Z.; Tang, Y.; Shen, G.; Li, X.; Sa, Y. Position synchronization tracking of multi-axis drive system using hierarchical sliding mode control. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–16. [Google Scholar] [CrossRef]
- Strobel, J.; Sumpf, J.; Bartsch, R.; Golder, M. Real-time measuring and monitoring of relevant parameters in Complex chain conveyor systems. innoTRAC J. 2020, 1, 64–73. [Google Scholar] [CrossRef]
- Kulkarni, A.J.; Kulkarni, T.M.; Mahadik, O.J.; Mahindrakar, P.V. Design of continuous loading vertical chain conveyor. Int. J. Adv. Res. Ideas Innov. Technol. 2018, 4, 465–469. [Google Scholar]
- Issa, S.; Tu, Y. A survey in the resource-constrained project and multi-project scheduling problems. J. Proj. Manag. 2020, 5, 117–138. [Google Scholar] [CrossRef]
- Guo, K.; Li, J.; Niu, M. Multi-agent interests service composition optimization in cloud manufacturing environment. IEEE Access 2023, 11, 53760–53771. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, P. Bi-level optimization of shared manufacturing service composition based on improved NSGA-II. PLoS ONE 2024, 19, e0303968. [Google Scholar] [CrossRef]
- Jing, W.; Zhang, Y.; Chen, Y.; Zhang, H.; Huang, W. Cloud-edge collaboration composition and scheduling for flexible manufacturing service with a multi-population co-evolutionary algorithm. Robot.-Comput.-Integr. Manuf. 2024, 90, 102814. [Google Scholar] [CrossRef]
- Sha, L.; Gopalakrishnan, S.; Liu, X.; Wang, Q. Cyber-physical systems: A new frontier. In Proceedings of the 2008 IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing (sutc 2008), Taichung, Taiwan, 11–13 June 2008; pp. 1–9. [Google Scholar]
- Wang, F.Y. The Emergence of Intelligent Enterprises: From CPS to CPSS. IEEE Intell. Syst. 2010, 25, 85–88. [Google Scholar] [CrossRef]
- Lee, J.; Kundu, P. Integrated cyber-physical systems and industrial metaverse for remote manufacturing. Manuf. Lett. 2022, 34, 12–15. [Google Scholar] [CrossRef]
- Monostori, L.; Kádár, B.; Bauernhansl, T.; Kondoh, S.; Kumara, S.; Reinhart, G.; Sauer, O.; Schuh, G.; Sihn, W.; Ueda, K. Cyber-physical systems in manufacturing. CIRP Ann. 2016, 65, 621–641. [Google Scholar] [CrossRef]
- Kao, H.A.; Jin, W.; Siegel, D.; Lee, J. A Cyber Physical Interface for Automation Systems—Methodology and Examples. Machines 2015, 3, 93–106. [Google Scholar] [CrossRef]
- Cinar, E.; Kalay, S.; Saricicek, I. A Predictive Maintenance System Design and Implementation for Intelligent Manufacturing. Machines 2022, 10, 1006. [Google Scholar] [CrossRef]
- Fu, T.; Liu, S.; Li, P. Digital twin-driven smelting process management method for converter steelmaking. J. Intell. Manuf. 2024, 1–17. [Google Scholar] [CrossRef]
- Hoffmann, M.W.; Malakuti, S.; Grüner, S.; Finster, S.; Gebhardt, J.; Tan, R.; Schindler, T.; Gamer, T. Developing industrial cps: A multi-disciplinary challenge. Sensors 2021, 21, 1991. [Google Scholar] [CrossRef]
- Yaacoub, J.P.A.; Salman, O.; Noura, H.N.; Kaaniche, N.; Chehab, A.; Malli, M. Cyber-physical systems security: Limitations, issues and future trends. Microprocess. Microsyst. 2020, 77, 103201. [Google Scholar] [CrossRef] [PubMed]
- Tantawy, A.; Abdelwahed, S.; Erradi, A.; Shaban, K. Model-based risk assessment for cyber physical systems security. Comput. Secur. 2020, 96, 101864. [Google Scholar] [CrossRef]
- Bernardi, S.; Gentile, U.; Marrone, S.; Merseguer, J.; Nardone, R. Security modelling and formal verification of survivability properties: Application to cyber–physical systems. J. Syst. Softw. 2021, 171, 110746. [Google Scholar] [CrossRef]
- Yu, Z.; Gao, H.; Cong, X.; Wu, N.; Song, H.H. A Survey on Cyber–Physical Systems Security. IEEE Internet Things J. 2023, 10, 21670–21686. [Google Scholar] [CrossRef]
- Lei, D. Multi-objective production scheduling: A survey. Int. J. Adv. Manuf. Technol. 2009, 43, 926–938. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Zhang, J.; Yang, M.; Wu, W. Multi-objective evolutionary algorithm-enabled multi-stage collaborative scheduling for automotive production. Comput. Ind. Eng. 2024, 191, 110151. [Google Scholar] [CrossRef]
- Yahui, W.; Ling, S.; Cai, Z.; Liuqiang, F.; Xiangjie, J. NSGA-II algorithm and application for multi-objective flexible workshop scheduling. J. Algorithms Comput. Technol. 2020, 14, 1748302620942467. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Ahmed, A.N.; Kisi, O.; El-Shafie, A. Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey Wolf optimization (GWO) algorithm. J. Hydrol. 2020, 582, 124435. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, H.; Tang, D. An improved hybrid particle swarm optimization for multi-objective flexible job-shop scheduling problem. Kybernetes 2020, 49, 2873–2892. [Google Scholar] [CrossRef]
- Ding, H.; Gu, X. Improved particle swarm optimization algorithm based novel encoding and decoding schemes for flexible job shop scheduling problem. Comput. Oper. Res. 2020, 121, 104951. [Google Scholar] [CrossRef]
- Bo, L.; Chen, G.; Tao, N. An improved bacterial foraging optimization for multi-objective flexible job-shop scheduling problem. J. Eur. Syst. Autom. 2018, 51, 323. [Google Scholar]
- Liang, X.; Du, Z. Genetic algorithm with simulated annealing for resolving job shop scheduling problem. In Proceedings of the 2020 IEEE 8th International Conference on Computer Science and Network Technology (ICCSNT), Dalian, China, 20–22 November 2020; pp. 64–68. [Google Scholar]
- Han, N.; Li, F.; Chen, S.; Zhang, K.; Feng, J. Research on Optimal Scheduling of Home Energy Management System Based on NSGA III Multi-Objective Optimization Algorithm. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 585, p. 012008. [Google Scholar]
- Ma, Y.; Yu, L.; Zhang, G.; Lu, Z.; Wu, J. Source-load uncertainty-based multi-objective multi-energy complementary optimal scheduling. Renew. Energy 2023, 219, 119483. [Google Scholar] [CrossRef]
- Fu, T.; Li, P.; Liu, S. An imbalanced small sample slab defect recognition method based on image generation. J. Manuf. Process. 2024, 118, 376–388. [Google Scholar] [CrossRef]
- Bao, L.; Zheng, M.; Zhou, Q.; Gao, P.; Xu, Y.; Jiang, H. Multi-objective optimization of partition temperature of steel sheet by NSGA-II using response surface methodology. Case Stud. Therm. Eng. 2022, 31, 101818. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, F.; Ji, X.; Li, H.; Zhou, J. A Pareto-based discrete particle swarm optimization for parallel casting workshop scheduling problem with fuzzy processing time. Knowl.-Based Syst. 2022, 256, 109872. [Google Scholar] [CrossRef]
- Li, S.; Zhang, M.; Wang, N.; Cao, R.; Zhang, Z.; Ji, Y.; Li, H.; Wang, H. Intelligent scheduling method for multi-machine cooperative operation based on NSGA-III and improved ant colony algorithm. Comput. Electron. Agric. 2023, 204, 107532. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. Multiobjective optimization and multiple constraint handling with evolutionary algorithms. I. A unified formulation. IEEE Trans. Syst. Man Cybern.-Part A Syst. Humans 1998, 28, 26–37. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Coello, C.A.C. Constraint-handling in nature-inspired numerical optimization: Past, present and future. Swarm Evol. Comput. 2011, 1, 173–194. [Google Scholar] [CrossRef]
- Ming, M.; Trivedi, A.; Wang, R.; Srinivasan, D.; Zhang, T. A dual-population-based evolutionary algorithm for constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2021, 25, 739–753. [Google Scholar] [CrossRef]
- Qin, H.; Fan, P.; Tang, H.; Huang, P.; Fang, B.; Pan, S. An effective hybrid discrete grey wolf optimizer for the casting production scheduling problem with multi-objective and multi-constraint. Comput. Ind. Eng. 2019, 128, 458–476. [Google Scholar] [CrossRef]
- Novara, F.M.; Novas, J.M.; Henning, G.P. A novel constraint programming model for large-scale scheduling problems in multiproduct multistage batch plants: Limited resources and campaign-based operation. Comput. Chem. Eng. 2016, 93, 101–117. [Google Scholar] [CrossRef]
- Kui, C.; Li, B. Research on FJSP of improved particle swarm optimization algorithm considering transportation time. J. Syst. Simul. 2021, 33, 845–853. [Google Scholar]
- Peng, C.; Li, Z.; Zhong, H.; Li, X.; Lin, A.; Liao, Y. Research on Multi-Objective Scheduling Algorithm of Job Shop Considering Limited Storage and Transportation Capacity. IEEE Access 2023, 11, 94252–94280. [Google Scholar] [CrossRef]
- Dan, Y.; Liu, G.; Fu, Y. Optimized flowshop scheduling for precast production considering process connection and blocking. Autom. Constr. 2021, 125, 103575. [Google Scholar] [CrossRef]
- Akbar, M.; Irohara, T. NSGA-II variants for solving a social-conscious dual resource-constrained scheduling problem. Expert Syst. Appl. 2020, 162, 113754. [Google Scholar] [CrossRef]
- Garcia Marquez Basaldua, J.C. Cyber-Physical Production Systems and Their Practical Integration and Application with Simio Software. Master’s Thesis, University of Texas at El Paso, El Paso, TX, USA, 2023. [Google Scholar]
- Balci, O. Verification, validation, and accreditation. In Proceedings of the 1998 Winter Simulation Conference. Proceedings (cat. no. 98ch36274), Washington, DC, USA, 13–16 December 1998; Volume 1, pp. 41–48. [Google Scholar]
- IEEE 1730.2™-2022; IEEE Recommended Practice for Verification, Validation and Acceptance/Accreditation of a Distributed Simulation: An Overlay to the Distributed Simulation Engineering and Execution Process. The Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 2022.
- SISO-GUIDE-001.2-2013; Guide for Generic Methodology for Verification and Validation (GMVV) to Support Acceptance of Models, Simulations, and Data, GM-VV Volume 2: Implementation Guide. Simulation Interoperability Standards Organization, Inc.: Orlando, FL, USA, 2013.
- Wang, Y.; Li, J.; Hongbo, S.; Li, Y.; Akhtar, F.; Imran, A. A survey on VV&A of large-scale simulations. Int. J. Crowd Sci. 2019, 3, 63–86. [Google Scholar]
- Yuan, M.; Li, Y.; Zhang, L.; Pei, F. Research on intelligent workshop resource scheduling method based on improved NSGA-II algorithm. Robot.-Comput.-Integr. Manuf. 2021, 71, 102141. [Google Scholar] [CrossRef]
- Shi, S.; Xiong, H. Solving the multi-objective job shop scheduling problems with overtime consideration by an enhanced NSGA-II. Comput. Ind. Eng. 2024, 190, 110001. [Google Scholar] [CrossRef]
- Tamssaouet, K.; Dauzère-Pérès, S.; Knopp, S.; Bitar, A.; Yugma, C. Multiobjective optimization for complex flexible job-shop scheduling problems. Eur. J. Oper. Res. 2022, 296, 87–100. [Google Scholar] [CrossRef]
- Cheng, Y.; Xie, Z.; Xin, Y.; Chen, K.; Zarei, R. Flexible job shop scheduling method for optimizing mold resource setup time. IEEE Access 2024, 12, 33486–33503. [Google Scholar] [CrossRef]
- Calzarossa, M.C.; Della Vedova, M.L.; Massari, L.; Nebbione, G.; Tessera, D. Multi-objective optimization of deadline and budget-aware workflow scheduling in uncertain clouds. IEEE Access 2021, 9, 89891–89905. [Google Scholar] [CrossRef]
- Amiri, M.F.; Behnamian, J. Multi-objective green flowshop scheduling problem under uncertainty: Estimation of distribution algorithm. J. Clean. Prod. 2020, 251, 119734. [Google Scholar] [CrossRef]
- Yao, S.; Jiang, Z.; Li, N.; Zhang, H.; Geng, N. A multi-objective dynamic scheduling approach using multiple attribute decision making in semiconductor manufacturing. Int. J. Prod. Econ. 2011, 130, 125–133. [Google Scholar] [CrossRef]

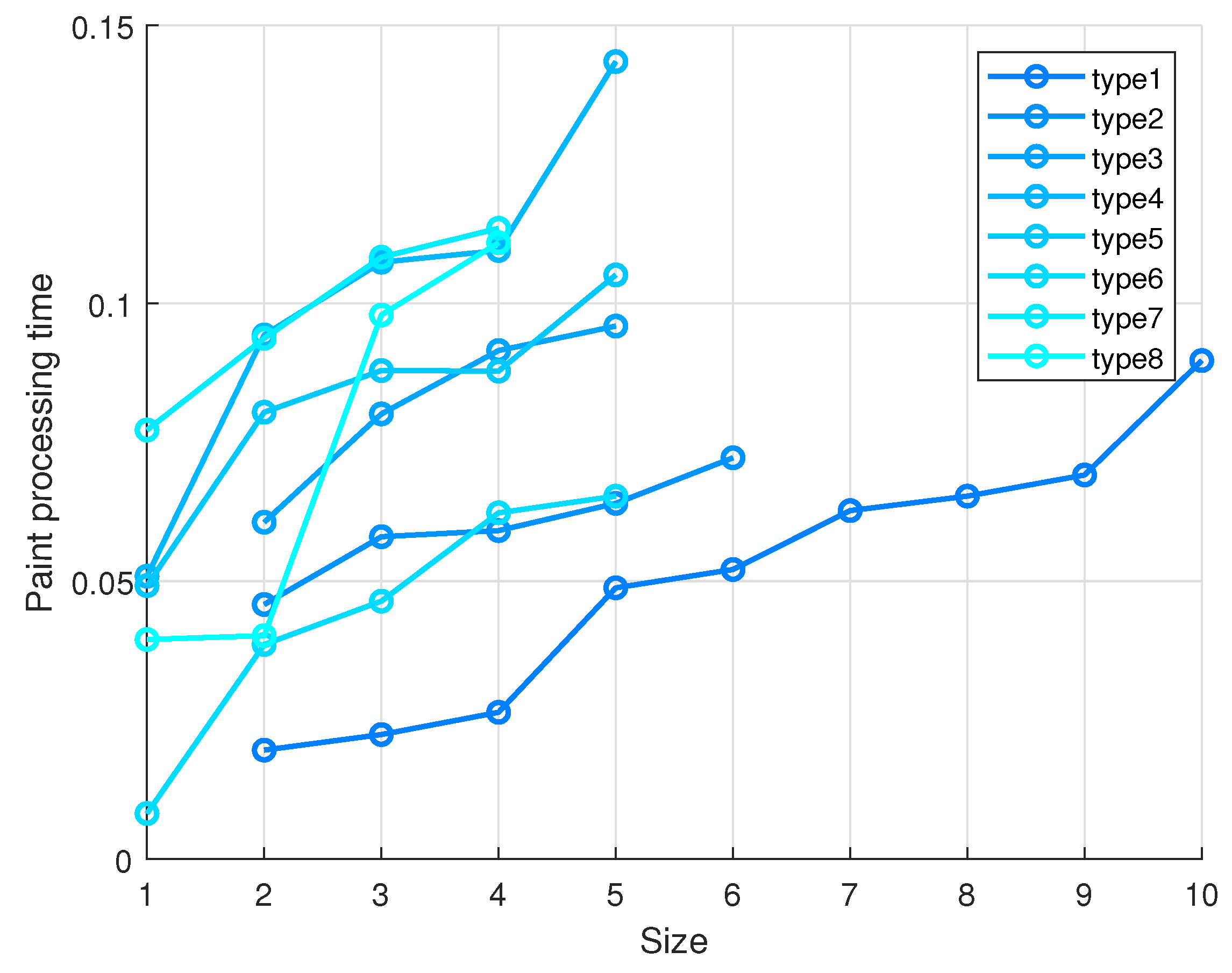
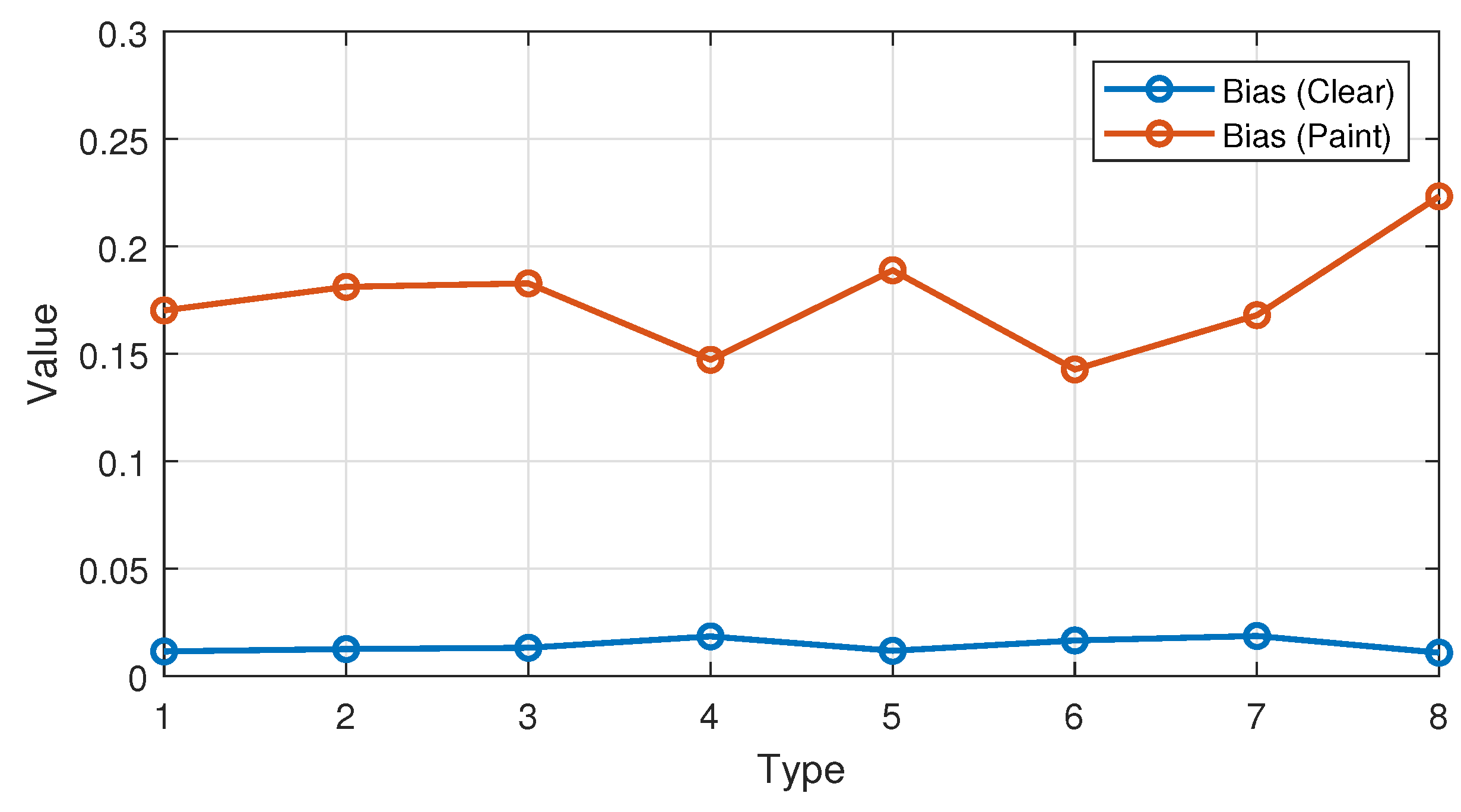
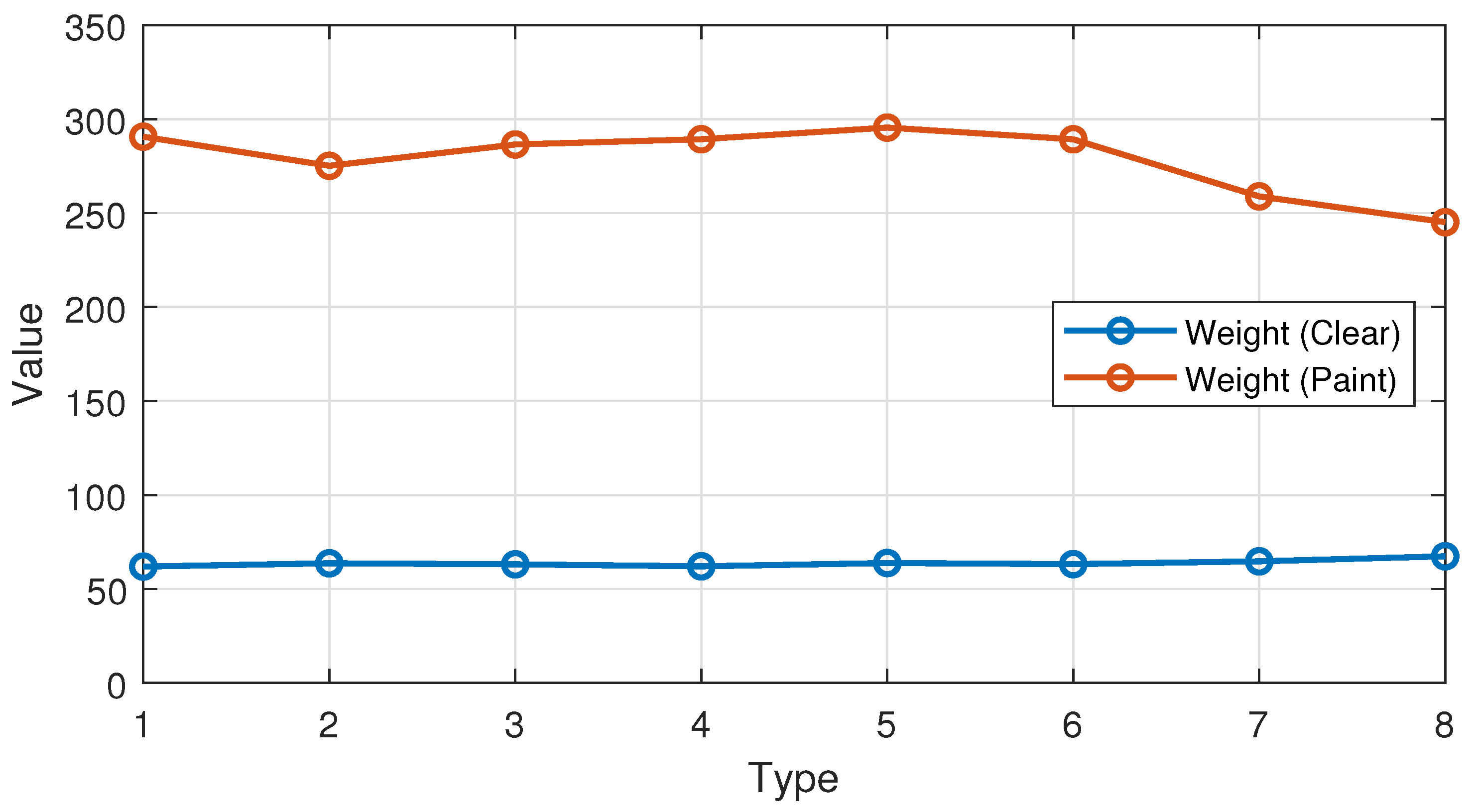
| Name | Definition Range | Meaning |
|---|---|---|
| If workpiece be loaded | ||
| Allow Carriers Loading | ||
| - | If the total input sufficient | |
| - | Activate Algorithm Logic |
| Name | Definition Range | Data Type | Meaning |
|---|---|---|---|
| int | Current Input Lane with Carriages | ||
| - | int | All Input Lanes with Carriages | |
| - | int | First, Four Inputs with Carriages | |
| - | int | Last Four Inputs with Carriages | |
| int | Number of Changeovers per Station | ||
| double | Output Time for Each Order | ||
| double | Importance Index for Each Order |
| Name | Definition Range | Data Type | Meaning |
|---|---|---|---|
| int | Input Section Capacity | ||
| int | Output Section Capacity | ||
| int | Cleaning and Masking Section Capacity | ||
| int | Processing Section Capacity | ||
| int | Multiple Processing Section Capacity | ||
| int | Drying Section Capacity | ||
| - | double | Safety Distance | |
| - | List<double> | Interval of Workpiece Arrivals | |
| - | double | Conveyor Speed | |
| - | int | Number of Carriers | |
| − | Cleaning Processing Time | ||
| − | Time of (un)Loading Masking | ||
| − | Time of Spray Coating | ||
| double | Workpiece Loading Time | ||
| double | Workpiece Unloading Time | ||
| - | double | Changeover Time | |
| - | int | Number of Orders | |
| - | int | Number of Workpieces | |
| int | Input Section Current Inventory | ||
| int | Output Section Current Inventory | ||
| int | Cleaning and Masking Section Current Inventory | ||
| int | Processing Section Current Inventory | ||
| int | Multiple Processing Section Current Inventory | ||
| int | Drying Section Current Inventory |
| Order | Color | Size | Type | Times | Num | Weight |
|---|---|---|---|---|---|---|
| 1 | 3 | 8 | 1 | 1 | 6 | 0.60 |
| 2 | 1 | 10 | 1 | 2 | 3 | 0.65 |
| 3 | 1 | 5 | 2 | 2 | 9 | 2.90 |
| 4 | 2 | 6 | 2 | 2 | 11 | 0.68 |
| 5 | 3 | 4 | 3 | 2 | 14 | 0.53 |
| 6 | 1 | 3 | 3 | 1 | 11 | 0.07 |
| 7 | 1 | 3 | 4 | 2 | 6 | 1.70 |
| 8 | 2 | 1 | 4 | 1 | 3 | 0.22 |
| 9 | 3 | 1 | 5 | 1 | 6 | 1.80 |
| 10 | 1 | 3 | 5 | 2 | 12 | 0.01 |
| 11 | 3 | 1 | 6 | 2 | 3 | 0.47 |
| 12 | 3 | 3 | 6 | 2 | 9 | 0.48 |
| 13 | 1 | 1 | 7 | 2 | 11 | 1.55 |
| 14 | 1 | 3 | 7 | 1 | 3 | 0.48 |
| 15 | 3 | 1 | 8 | 2 | 14 | 1.24 |
| 16 | 3 | 1 | 8 | 2 | 4 | 0.43 |
| Number of Experiments | Weighted Fitness |
|---|---|
| 1 | −0.5000 |
| 2 | −0.4999 |
| 3 | −0.5000 |
| 4 | −0.4687 |
| 5 | −0.4999 |
| 6 | −0.5000 |
| 7 | −0.5000 |
| 8 | −0.2490 |
| 9 | −0.4892 |
| 10 | −0.4460 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Hu, J.; Lu, J.; Zhang, W. Cyber-Physical Scheduling System for Multiobjective Scheduling Optimization of a Suspension Chain Workshop Using the Improved Non-Dominated Sorting Genetic Algorithm II. Machines 2024, 12, 666. https://doi.org/10.3390/machines12090666
Zhao W, Hu J, Lu J, Zhang W. Cyber-Physical Scheduling System for Multiobjective Scheduling Optimization of a Suspension Chain Workshop Using the Improved Non-Dominated Sorting Genetic Algorithm II. Machines. 2024; 12(9):666. https://doi.org/10.3390/machines12090666
Chicago/Turabian StyleZhao, Wenbin, Junhan Hu, Jiansha Lu, and Wenzhu Zhang. 2024. "Cyber-Physical Scheduling System for Multiobjective Scheduling Optimization of a Suspension Chain Workshop Using the Improved Non-Dominated Sorting Genetic Algorithm II" Machines 12, no. 9: 666. https://doi.org/10.3390/machines12090666
APA StyleZhao, W., Hu, J., Lu, J., & Zhang, W. (2024). Cyber-Physical Scheduling System for Multiobjective Scheduling Optimization of a Suspension Chain Workshop Using the Improved Non-Dominated Sorting Genetic Algorithm II. Machines, 12(9), 666. https://doi.org/10.3390/machines12090666





