Dynamics and Failure Analysis on Rigid–Flexible Coupling Structure to Bucket Wheel Stacker Reclaimer
Abstract
:1. Introduction
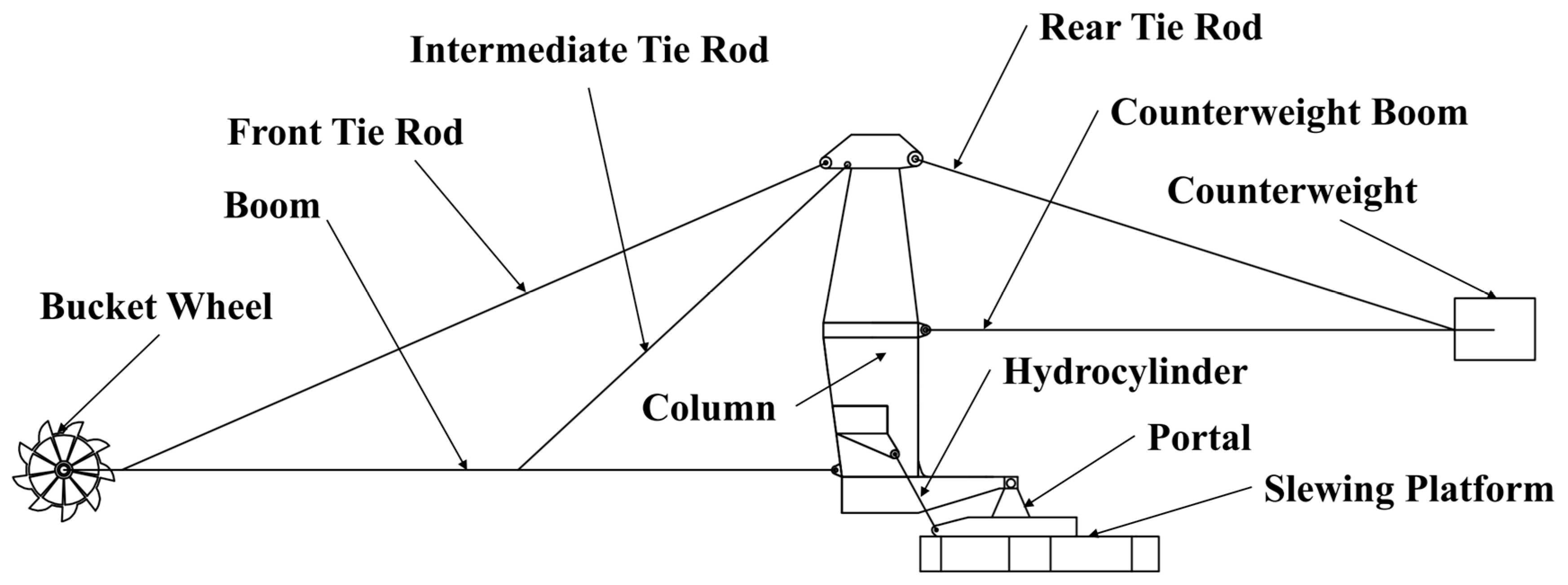
2. Bucket Wheel Stacker Reclaimer
2.1. Introduction of Bucket Wheel Stacker Reclaimer
2.2. Modeling of Bucket Wheel Stacker and Reclaimer
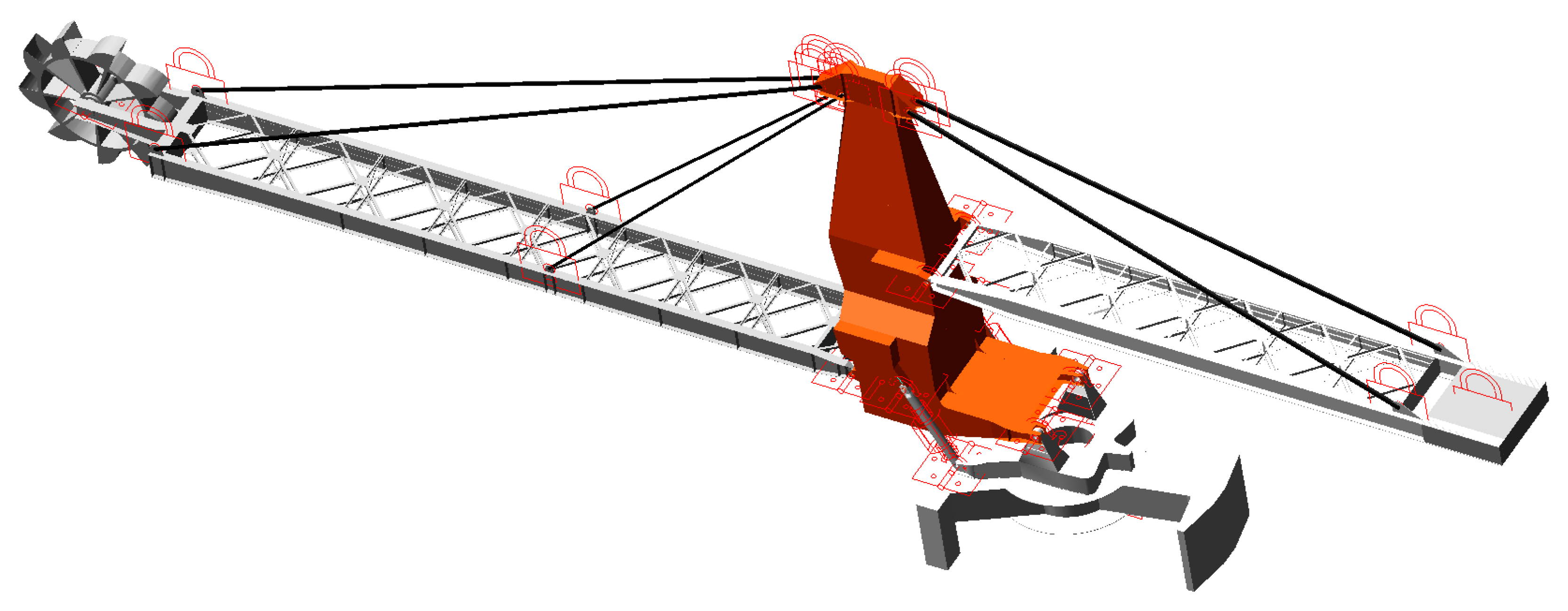
2.2.1. Establishment of Rigid Body Model
2.2.2. Establishment of Flexible Body
2.2.3. Establishment of Rigid–Flexible Coupling Model
3. Dynamics Analysis
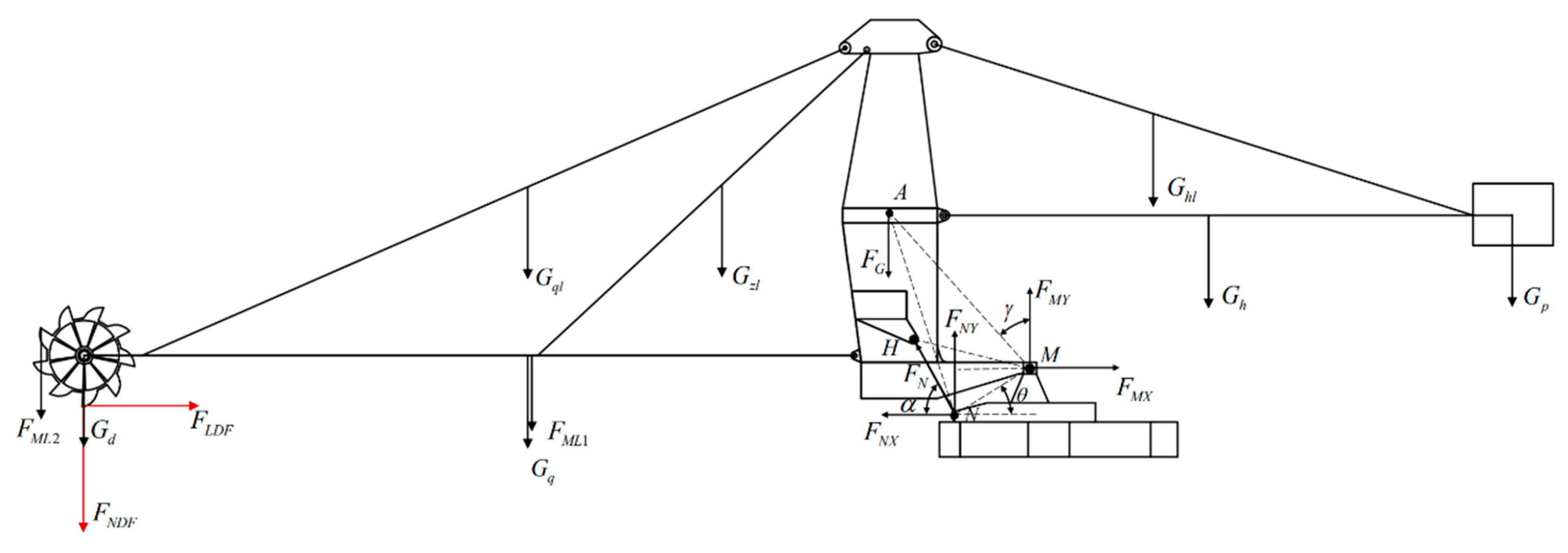
3.1. Column Force Analysis
3.2. Load Calculation
3.2.1. Dead Load DL
3.2.2. Material Load ML
3.2.3. Incrustation Load ICL
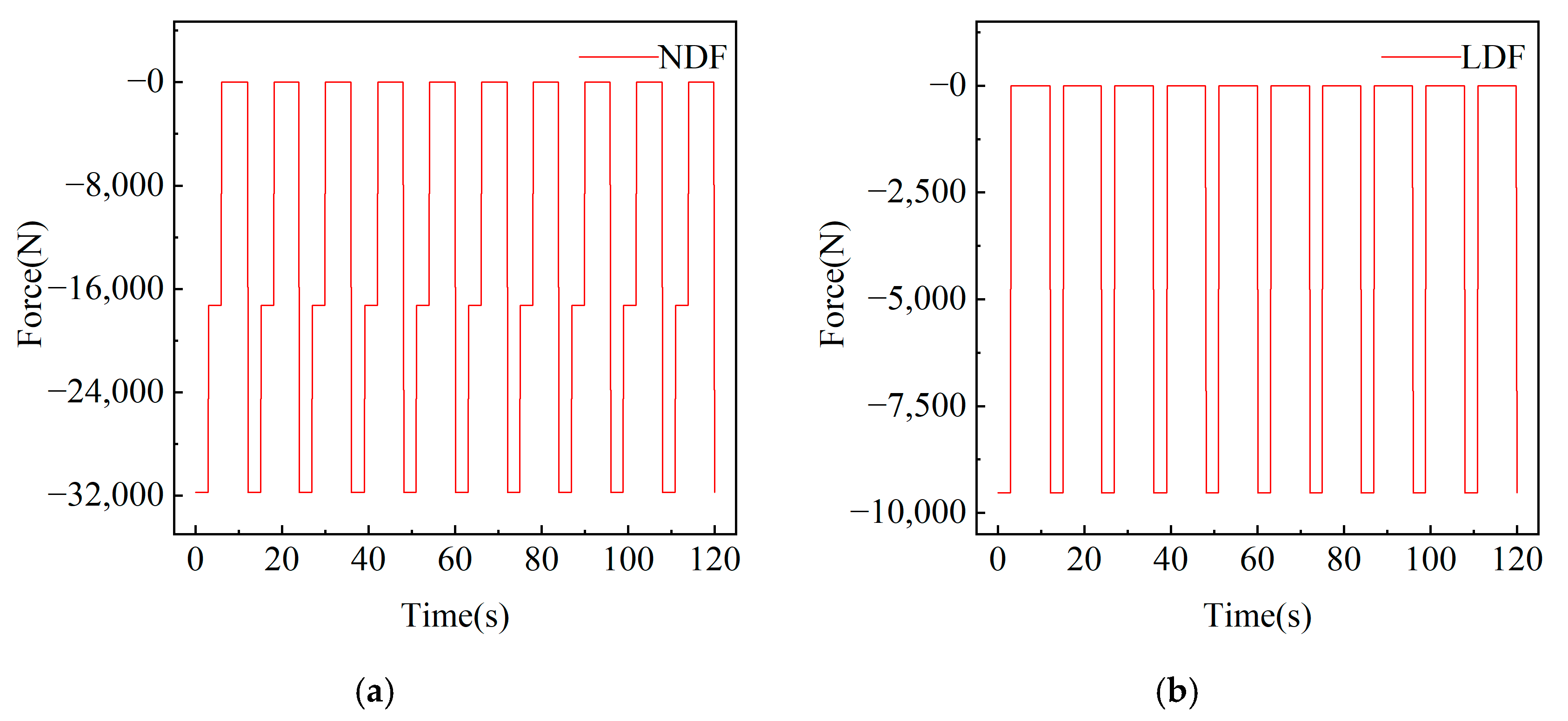
3.2.4. Excavator Force
3.2.5. Digging Force Excitation Frequency Calculation
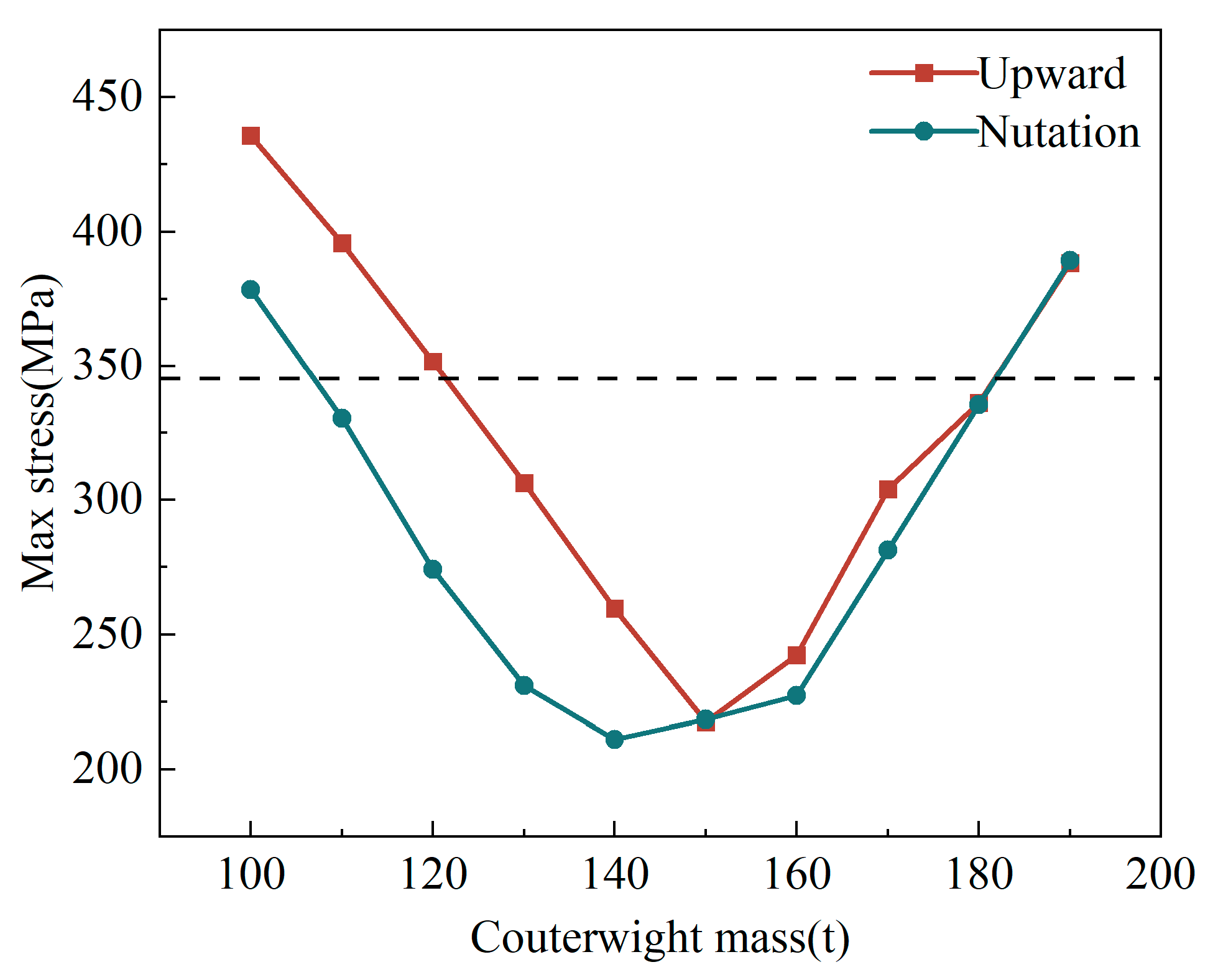
3.3. Parameter Settings
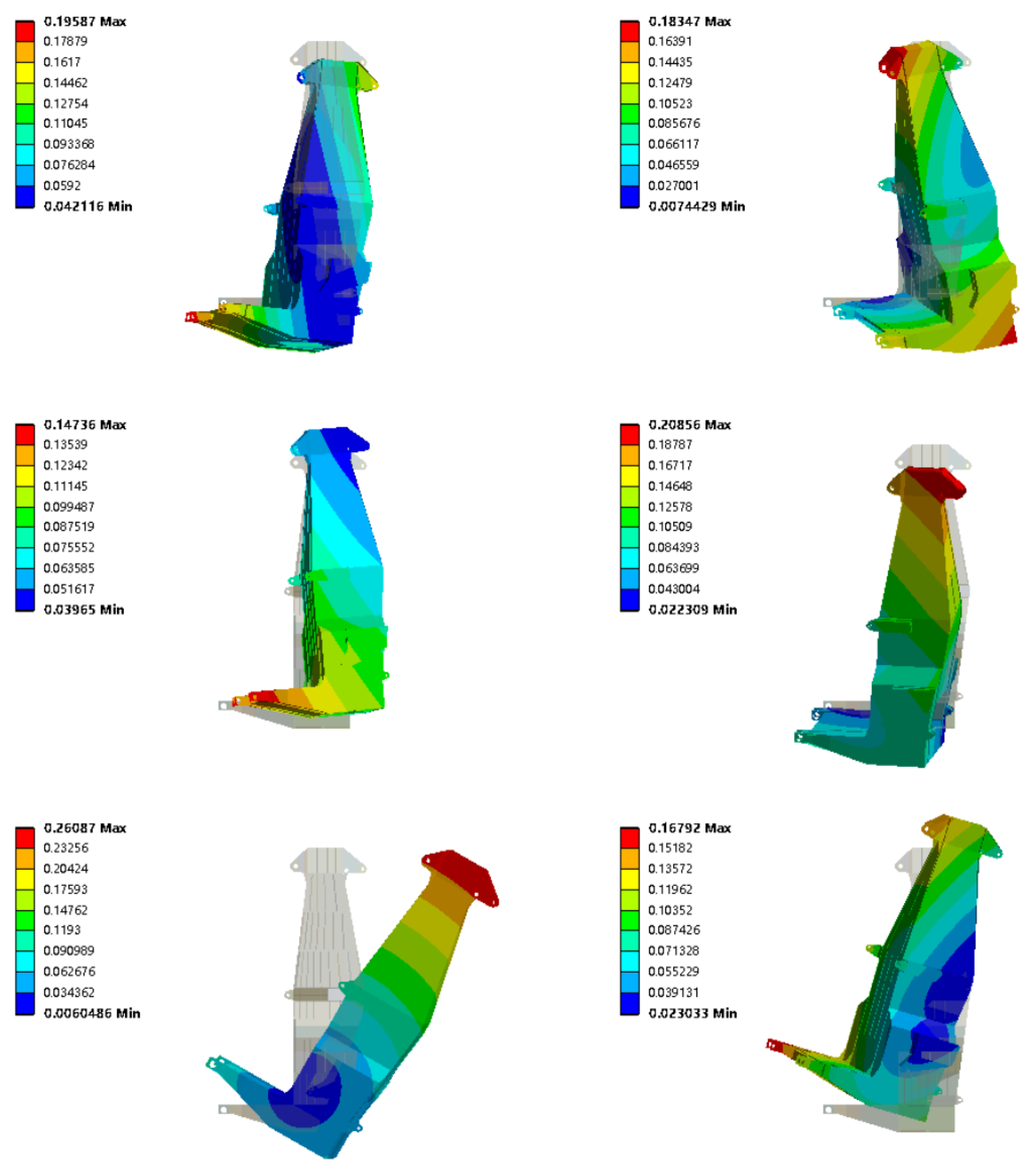
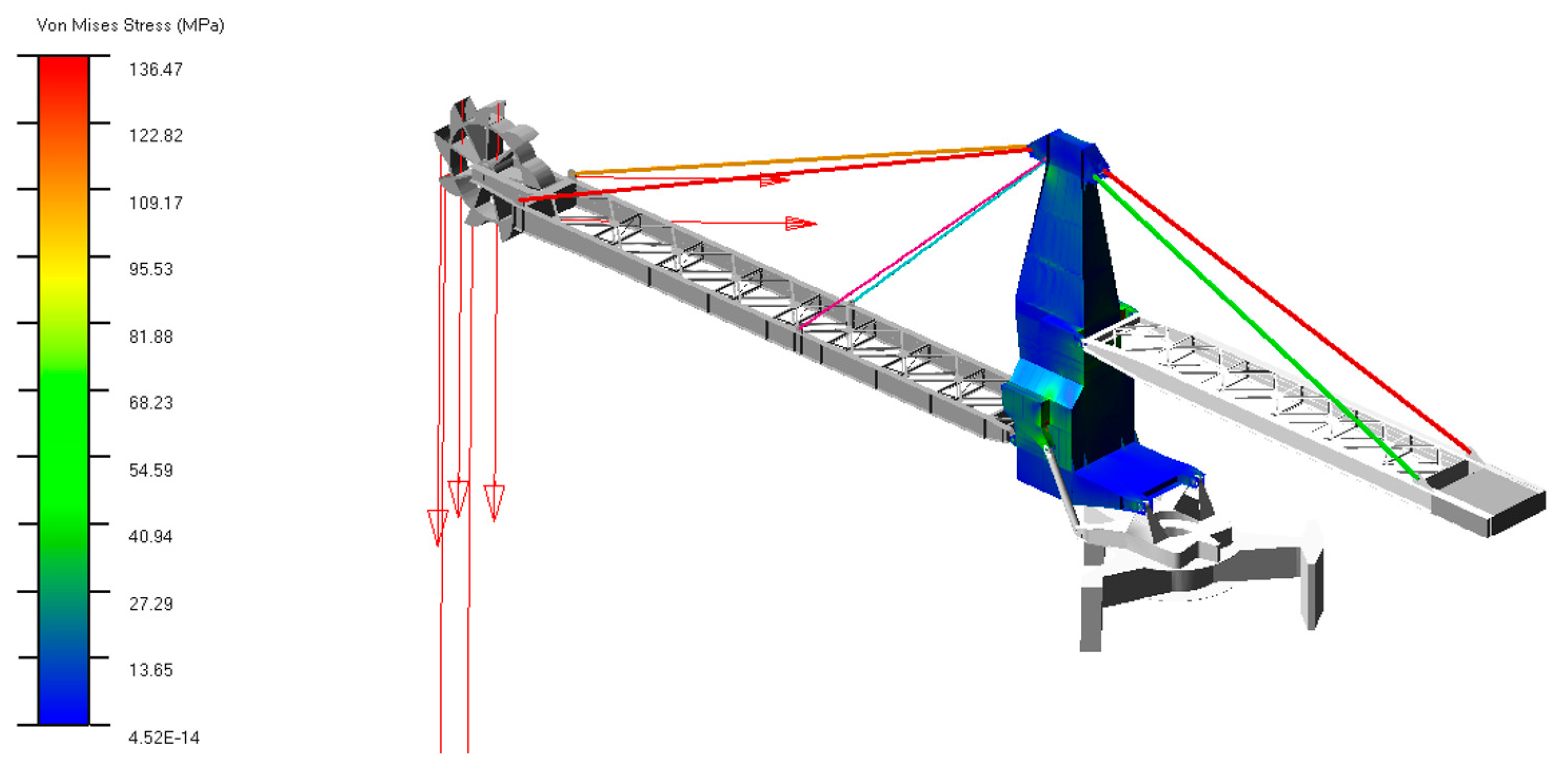
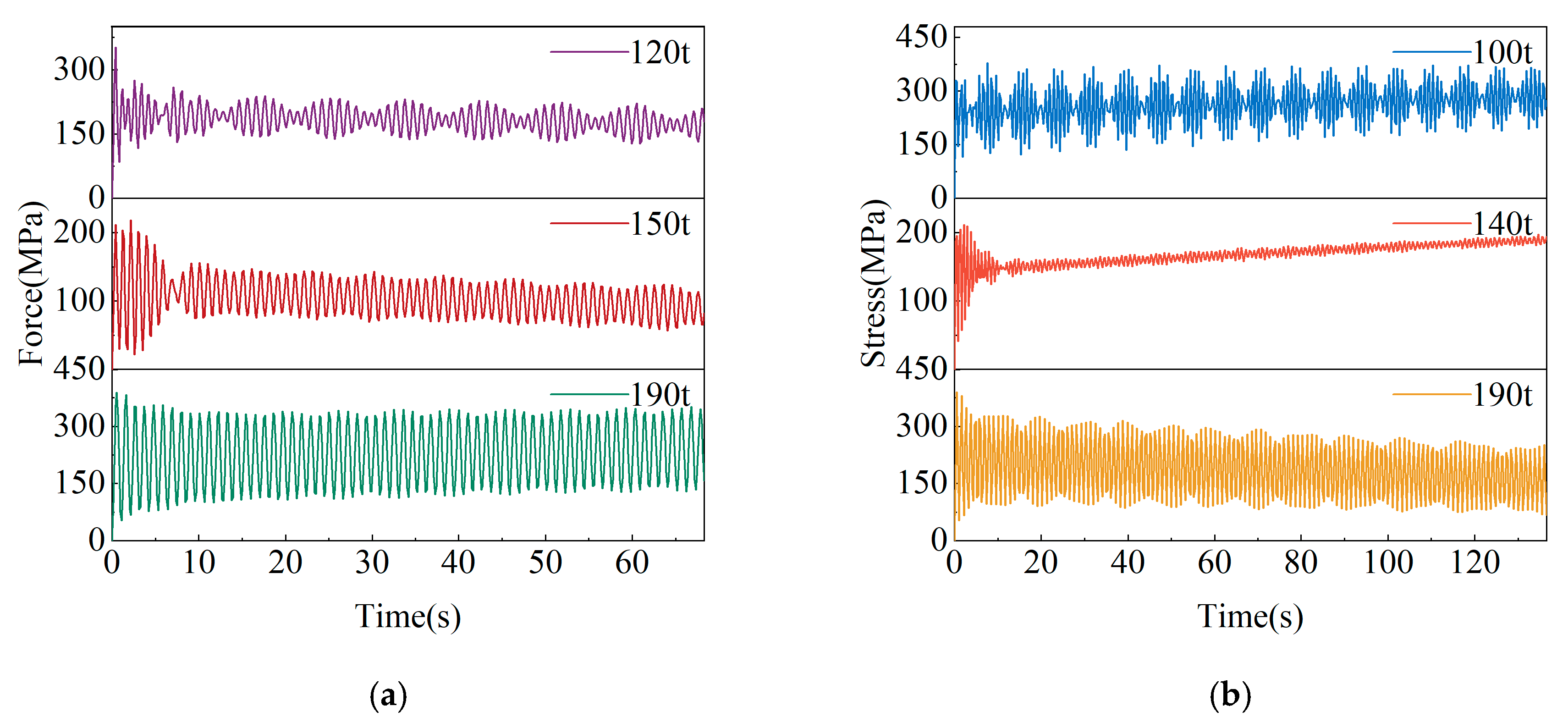
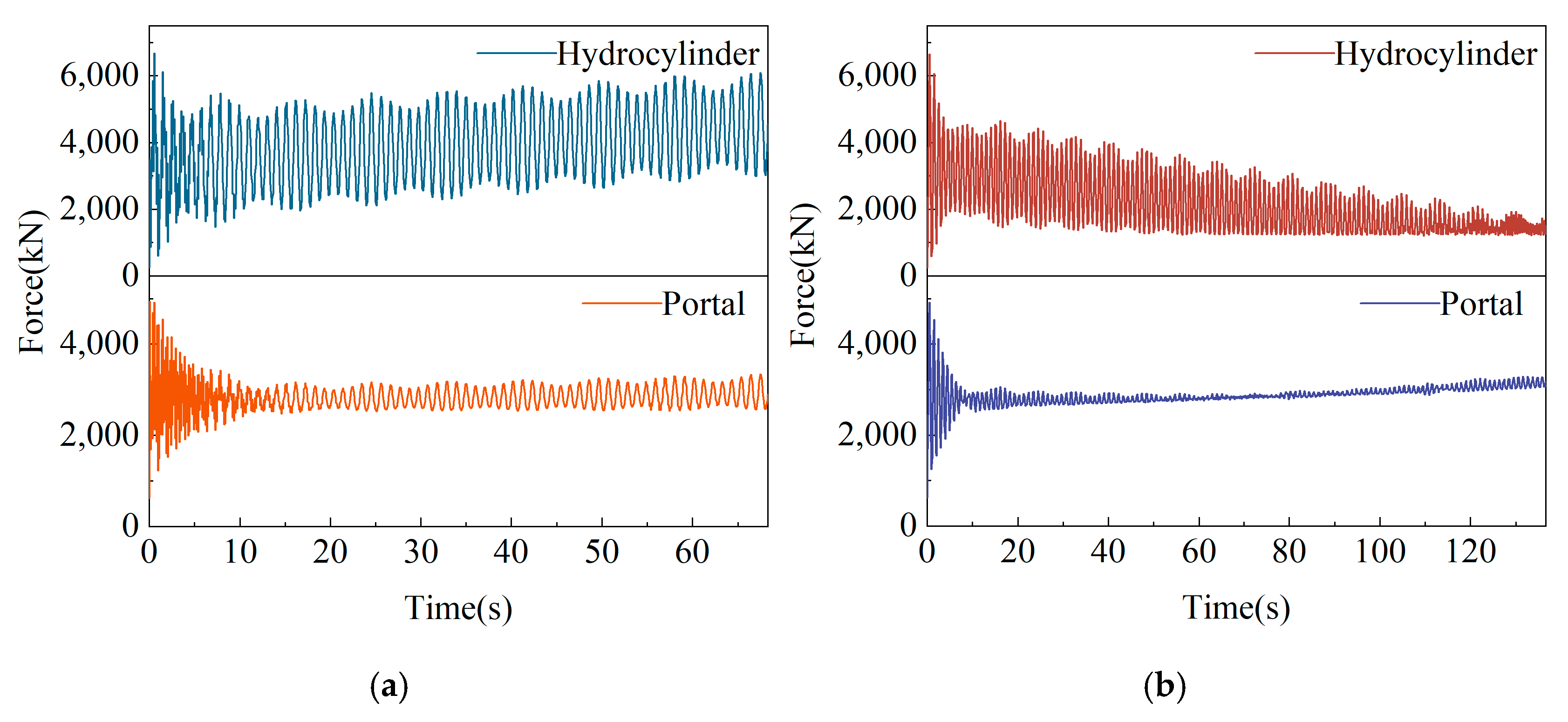
3.4. Analysis Results of Working Conditions
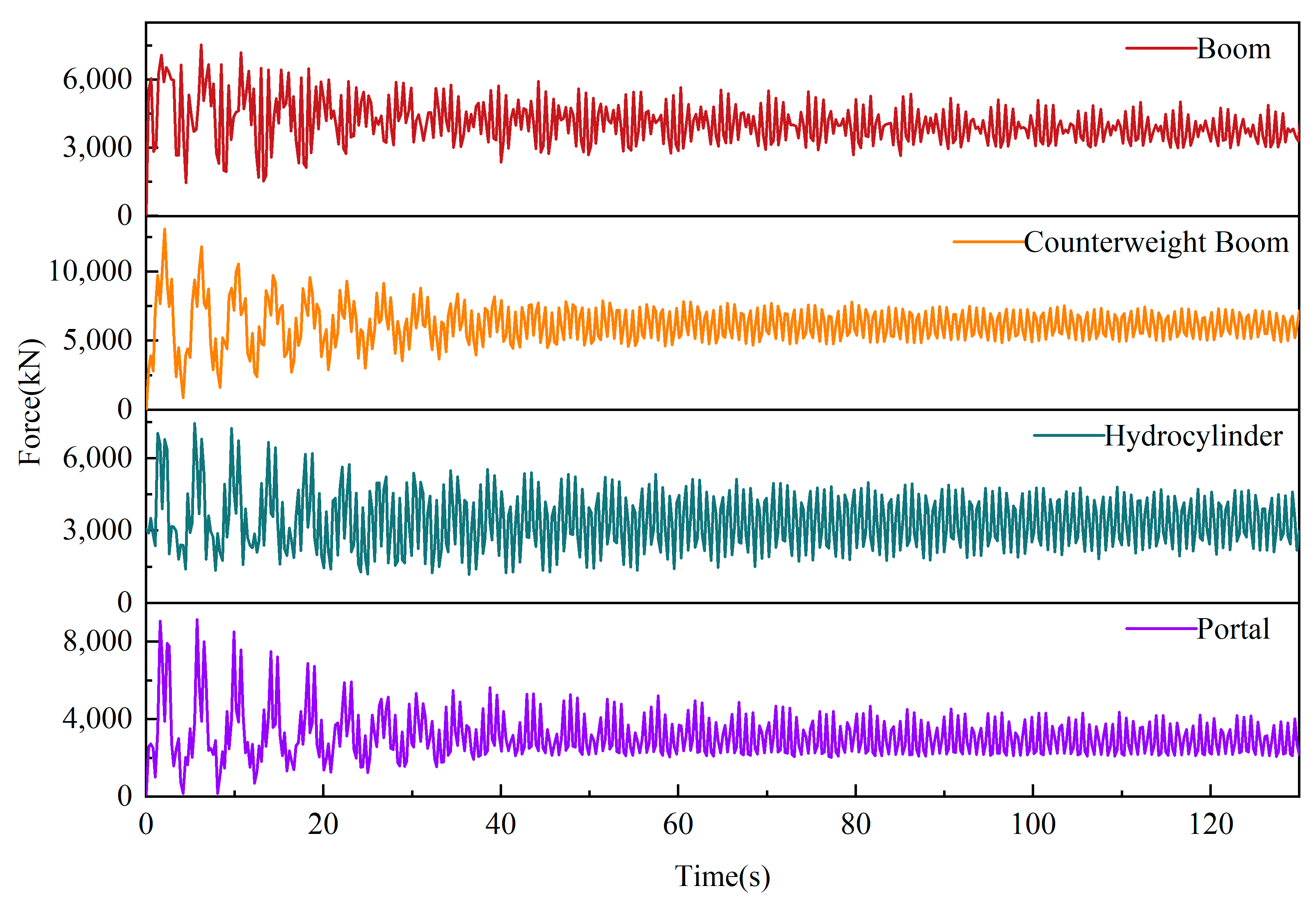
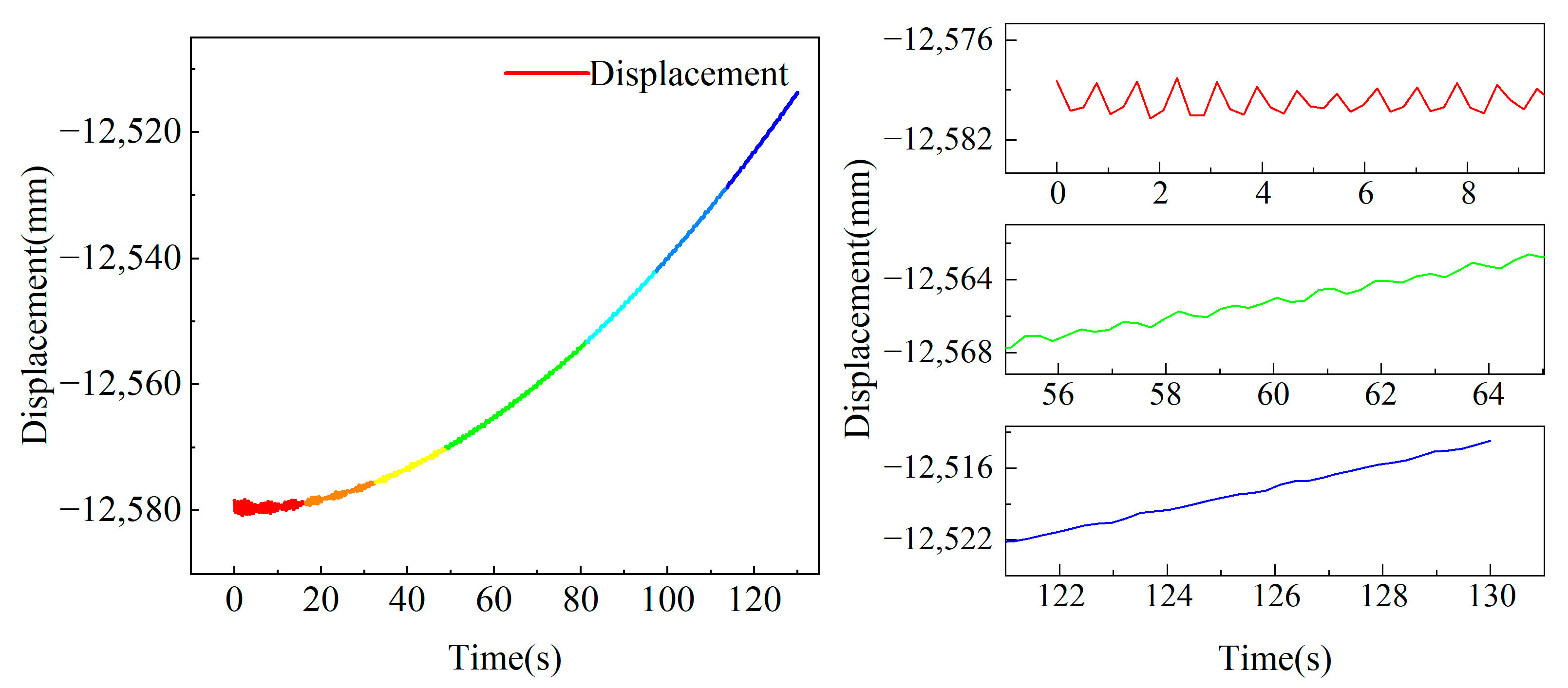
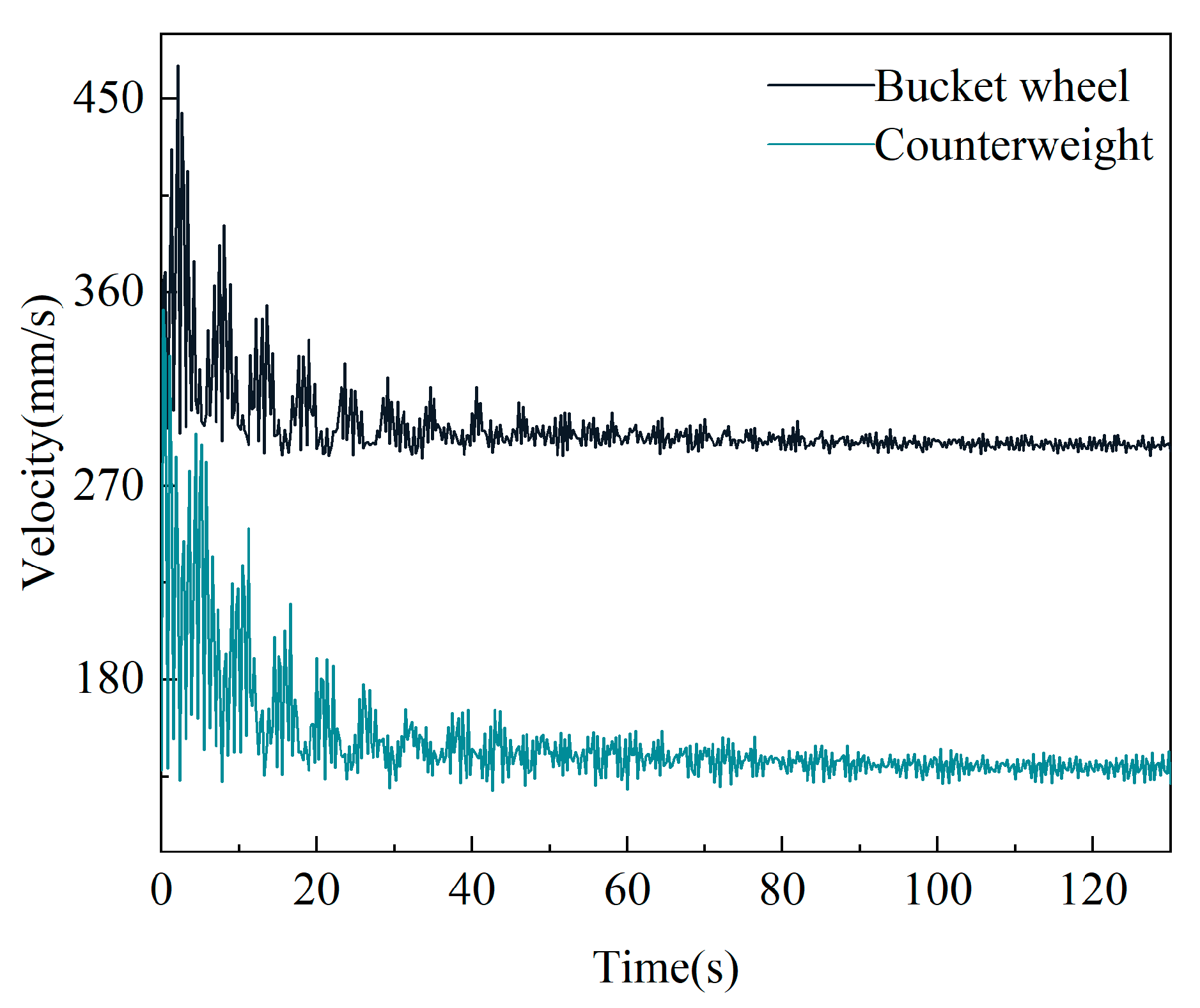
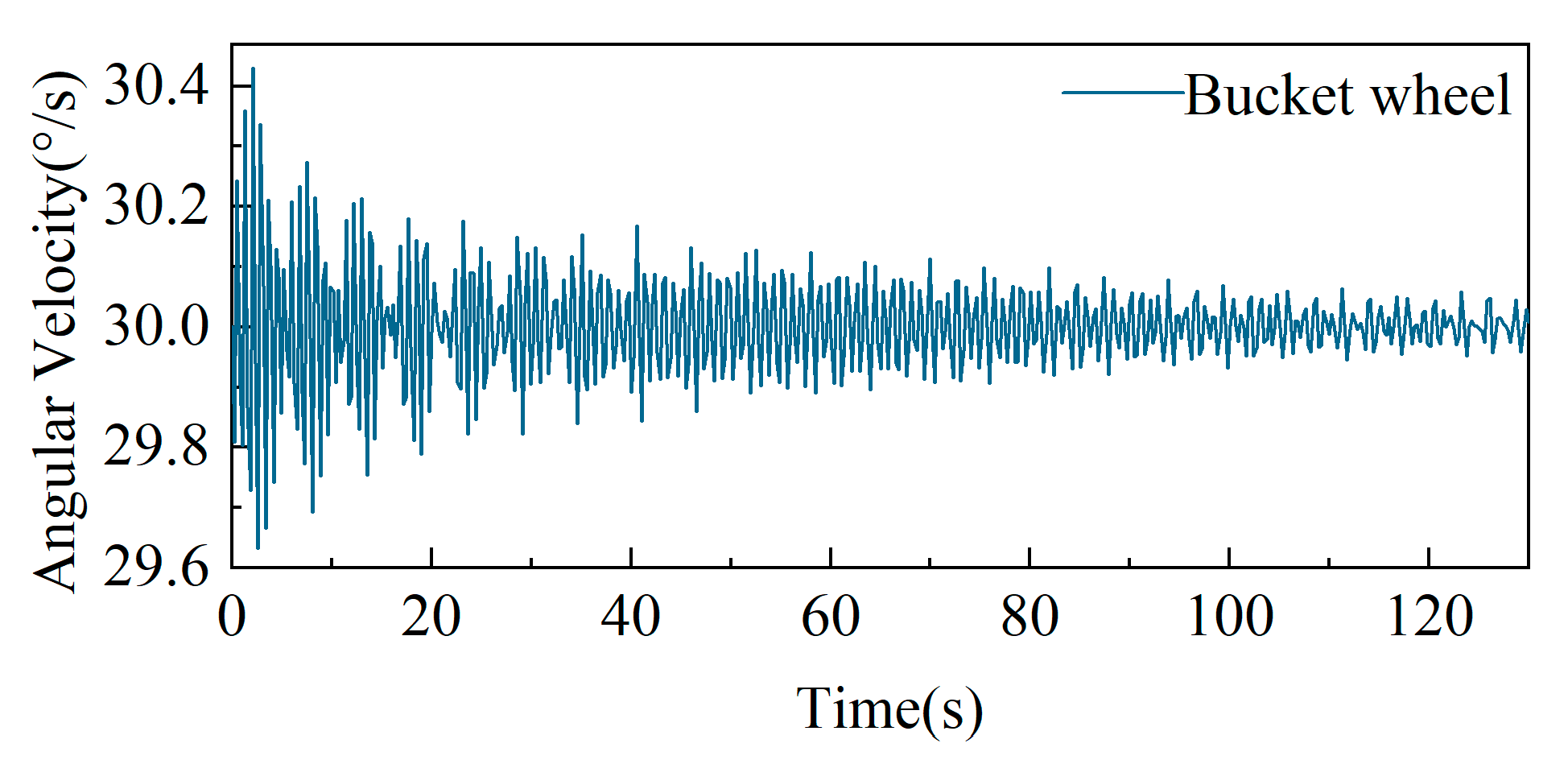
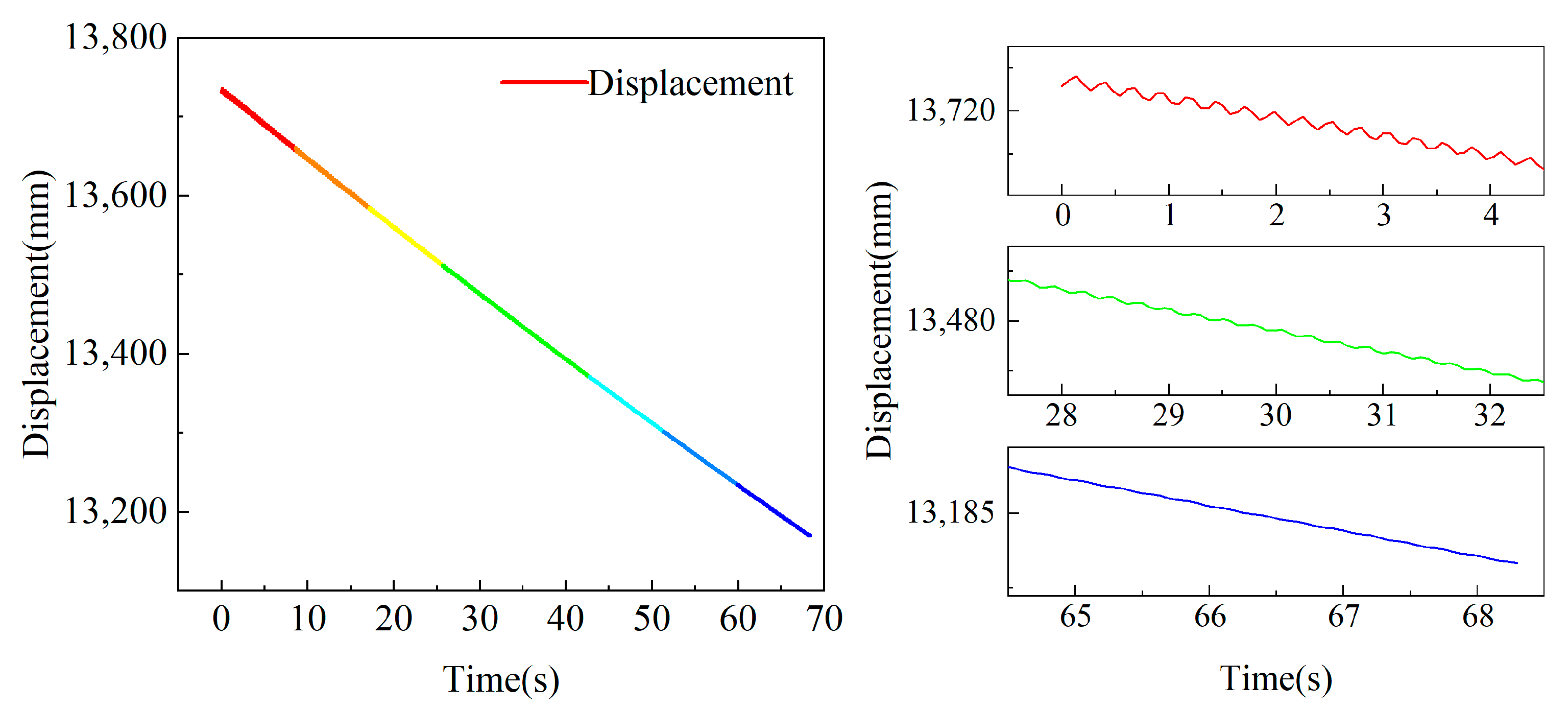
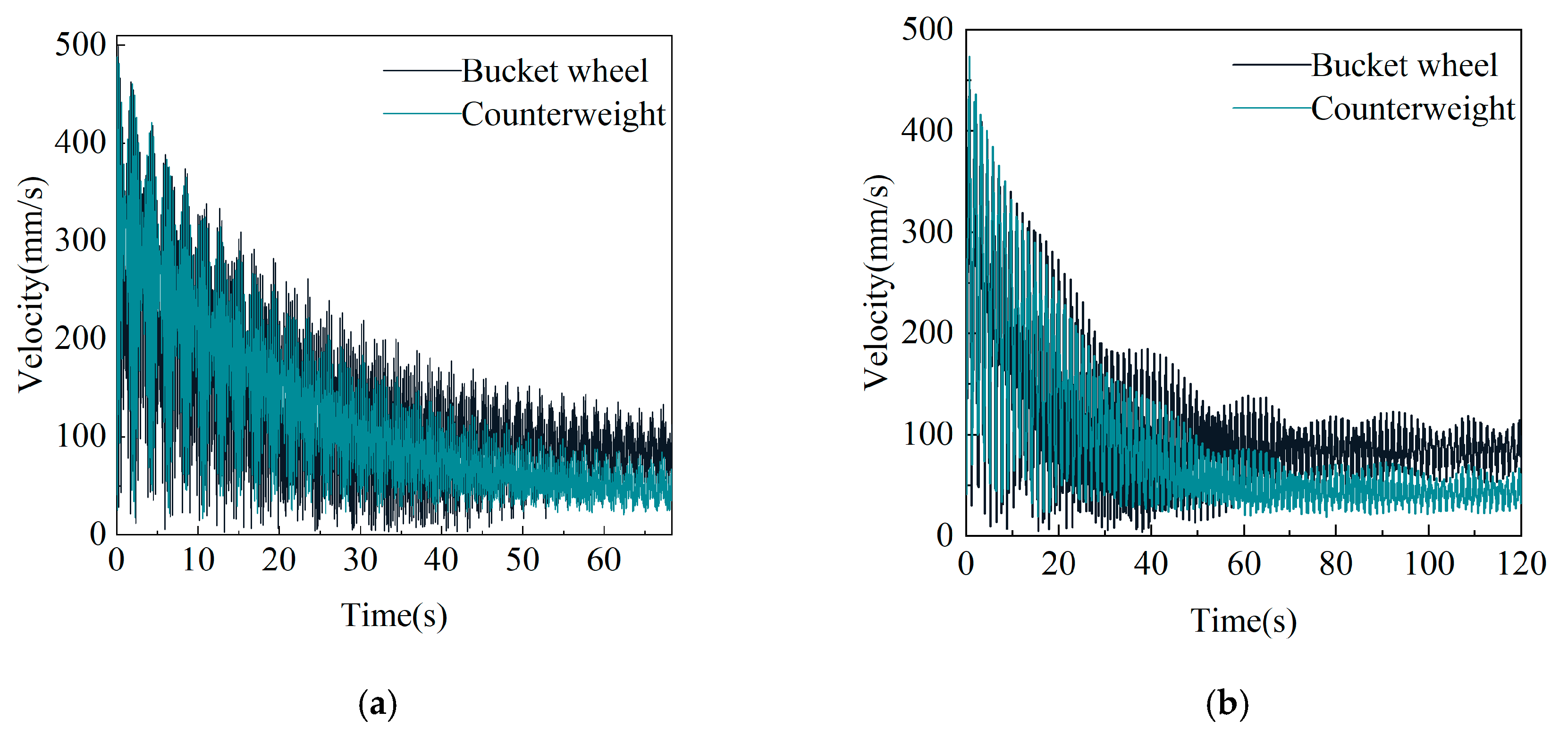
3.4.1. Full-Load Rotary Reclaiming
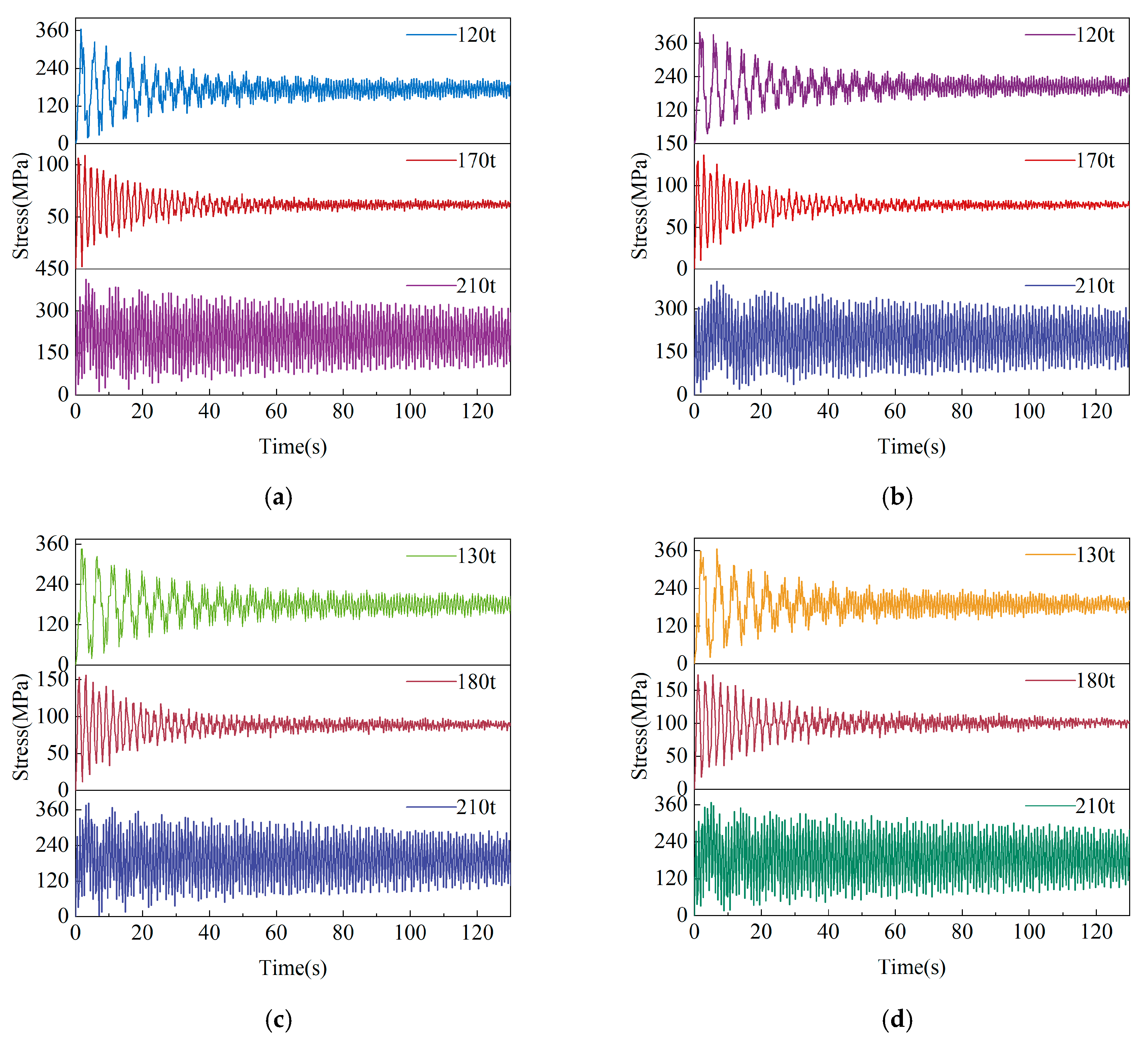
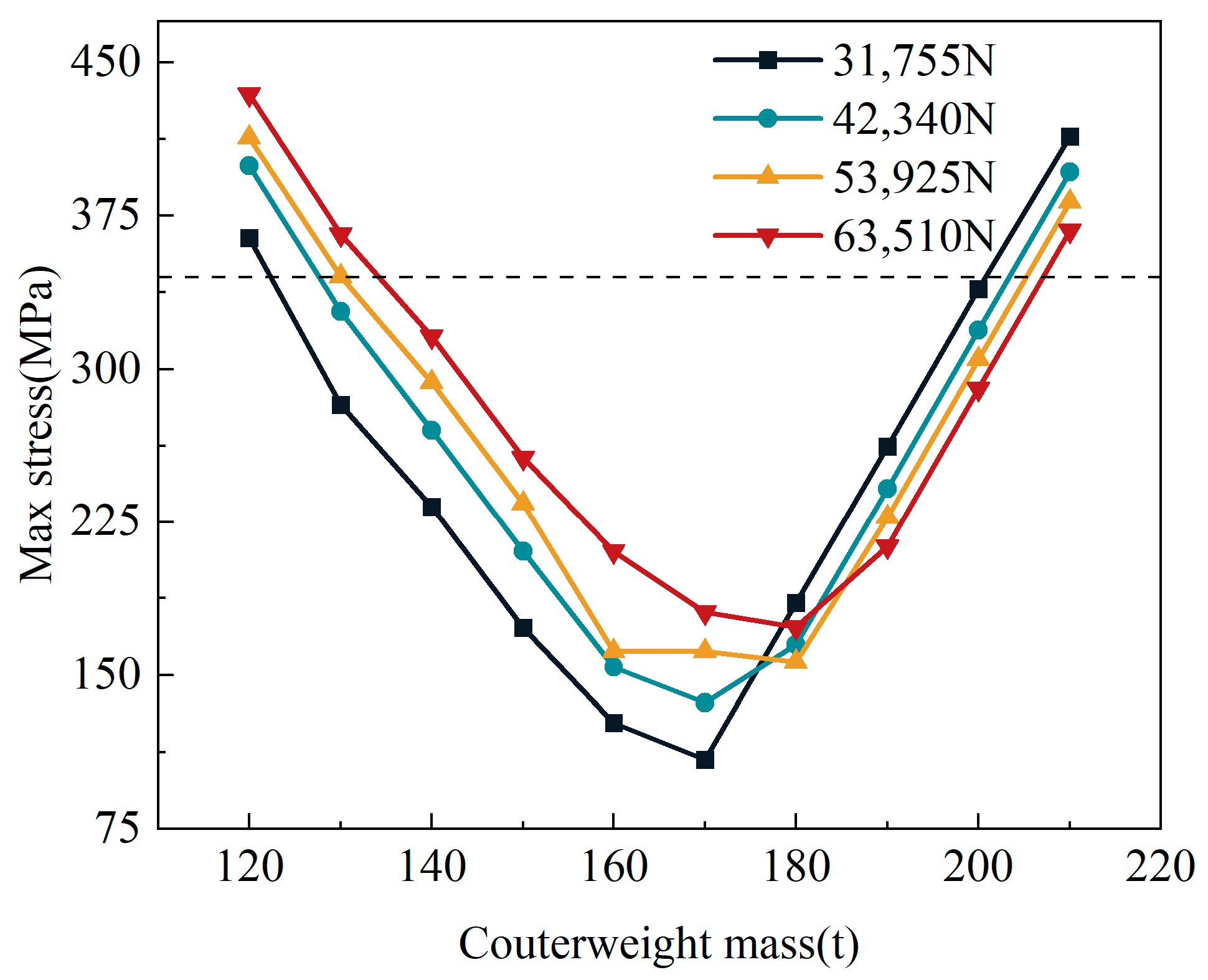
3.4.2. Resonance Risk Analysis
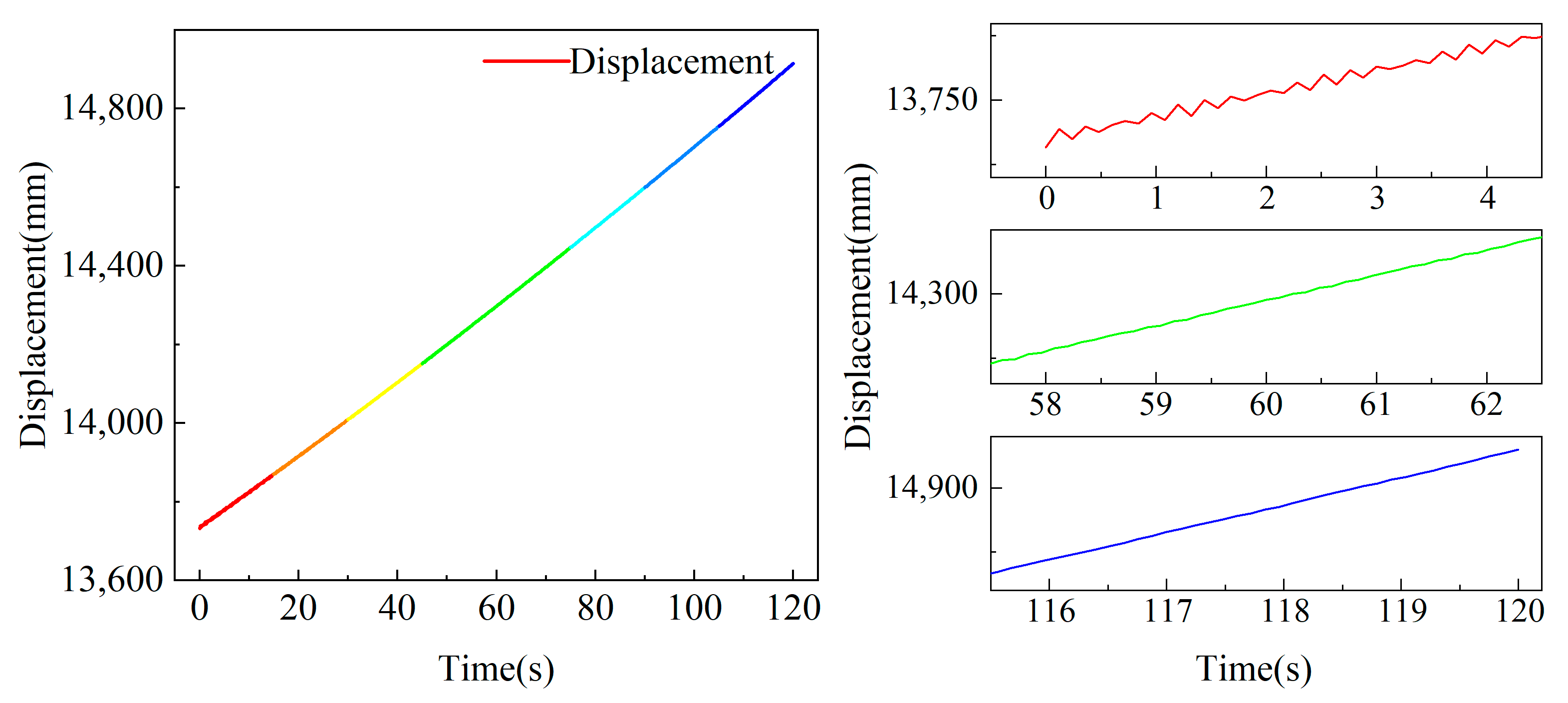
3.4.3. No-Load Pitch
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, J.; Zhang, W.P.; Zou, D.Q. Development and validation of a rigid-flexible coupled dynamic valve-train model. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2012, 226, 94–111. [Google Scholar] [CrossRef]
- Liu, Z.F.; Ye, P.; Guo, X.W.; Guo, Y. Rigid-flexible coupling dynamic analysis on a mass attached to a rotating flexible rod. Appl. Math. Model. 2014, 38, 4985–4994. [Google Scholar] [CrossRef]
- Gu, J.P.; Qin, Y.X.; Xia, Y.Y.; Jiao, Q.Q.; Gao, H.B.; Zhang, Y.Y.; Zhang, H. Research on Dynamic Characteristics of Composite Towering Structure. Int. J. Appl. Mech. 2021, 13, 2150096. [Google Scholar] [CrossRef]
- He, X.H.; Gai, Y.B.; Wu, T. Simulation of train-bridge interaction under wind loads: A rigid-flexible coupling approach. Int. J. Rail Transp. 2018, 6, 274–282. [Google Scholar] [CrossRef]
- Xin, Y.; Dong, R.; Lv, S. Dynamic Simulation Analysis of Truck Crane Based on ADAMS. Recent Pat. Mech. Eng. 2023, 16, 94–111. [Google Scholar] [CrossRef]
- Cao, X.; Yang, Y.; Wang, W.; Gu, Z. Rigid-Flexible Coupling Dynamic Modeling of a Tower Crane with Long Flexible Boom. In Proceedings of the International Conference on Mechanical Design, ICMD 2017, Beijing, China, 13–15 October 2017; Springer: Singapore, 2018; Volume 55, pp. 39–57. [Google Scholar]
- Wang, B.Y.; Liu, Z.Y.; Zheng, P.F. Rigid-flexible coupling dynamic modeling and analysis of dumbbell-shaped spacecraft. Aerosp. Sci. Technol. 2022, 126, 107641. [Google Scholar] [CrossRef]
- He, B.; Tang, W.; Cao, J.T. Virtual prototyping-based multibody systems dynamics analysis of offshore crane. Int. J. Adv. Manuf. Technol. 2014, 75, 161–180. [Google Scholar] [CrossRef]
- Lai, Q.H.; Yu, Q.X.; Dong, J.Y. Dynamic analysis of rotary tiller gearbox based on EDEM, ADAMS and ANSYS. J. Intell. Fuzzy Syst. 2019, 36, 1153–1160. [Google Scholar] [CrossRef]
- Ren, H.W.; Zhang, D.S.; Gong, S.X.; Zhou, K.; Xi, C.Y.; He, M.; Li, T.J. Dynamic impact experiment and response characteristics analysis for 1:2 reduced-scale model of hydraulic support. Int. J. Min. Sci. Technol. 2021, 31, 347–356. [Google Scholar] [CrossRef]
- Xu, D.-L.; Dai, C.; Zhang, H.-C. Dynamic simulation and connector’s effect on the response characteristics of multi-modular floating structure using ADAMS. Zhendong Gongcheng Xuebao/J. Vib. Eng. 2018, 31, 456–467. [Google Scholar]
- Chatterjee, A.; Das, D. A Review of Bucket Wheel Reclaimer Failure Through Mechanical Test and Metallographic Analysis. J. Fail. Anal. Prev. 2014, 12, 402–407. [Google Scholar] [CrossRef]
- Araujo, L.S.; De Almeida, L.H.; Batista, E.M.; Landesmann, A. Failure of a bucket-wheel stacker reclaimer: Metallographic and structural analyses. J. Fail. Anal. Prev. 2012, 226, 94–111. [Google Scholar] [CrossRef]
- Guo, Z.; Zhu, X.; Wang, M. Optimization of safety valve block of the pitch mechanism of bucket wheel stacker reclaimer. In Proceedings of the 4th International Conference on Mechanical, Electric and Industrial Engineering, MEIE 2021, Kunming, China, 22–24 May 2021; Volume 1983. [Google Scholar]
- Yao, J.; Qiu, X.M.; Zhou, Z.P.; Fu, Y.Q.; Xing, F.; Zhao, E.F. Buckling failure analysis of all-terrain crane telescopic boom section. Eng. Fail. Anal. 2015, 57, 105–117. [Google Scholar] [CrossRef]
- Shen, J.H.; Dai, Z.L.; Xiang, L.; Wang, G.X. Stiffness analysis of rotary elastic joint for a flexible bucket wheel reclaimer via theoretical, numerical and experimental methods. Powder Technol. 2024, 432, 119119. [Google Scholar] [CrossRef]
- Yang, Q.L.; Qu, F.Z.; Yu, Z.Y.; Xie, Z.Y. Stress and stability analysis of slewing motion for crawler crane mounted on flexible ground. Eng. Fail. Anal. 2019, 105, 817–827. [Google Scholar] [CrossRef]
- Gao, H.B.; Qin, Y.X.; Wang, L.H. A Semi-Analytical Solution for the Stress Field and Stress Intensity Factor of Hole-Edge Cracks Using Improved Muskhelishvili Method. Int. J. Appl. Mech. 2024, 16, 2450044. [Google Scholar] [CrossRef]
- Hameed, A.; Zubair, O.; Shams, T.A.; Mehmood, Z.; Javed, A. Failure analysis of a broken support strut of an aircraft landing gear. Eng. Fail. Anal. 2020, 117, 104847. [Google Scholar] [CrossRef]
- Klinger, C. Failures of cranes due to wind induced vibrations. Eng. Fail. Anal. 2014, 43, 198–220. [Google Scholar] [CrossRef]
- ISO 5049:1994; Mobile Equipment for Continuous Handling of Bulk Materials—Safety Code. International Organization for Standardization: Geneva, Switzerland, 1994.
- ANSI/ASA S2.62-2009; Criteria for Evaluating Flexible Rotor Balance. Acoustical Society of America: New York, NY, USA, 2009.
| Component1 | Component2 | Constraint | Degree of Freedom |
|---|---|---|---|
| Boom | Column | Revolute | 1 |
| Counterweight Boom | Column | Revolute | 1 |
| Tie Rod | Column | Fixed | 0 |
| Portal | Column | Revolute | 1 |
| Hydraulic Cylinder | Column | Revolute | 1 |
| Bucket Wheel | Boom | Revolute | 1 |
| Counterweight | Counterweight Boom | Fixed | 0 |
| Portal | Hydraulic Cylinder | Revolute | 1 |
| Cylinder Barrel | Piston Rod | Translation | 1 |
| Boom | Tie Rod | Fixed | 0 |
| Counterweight Boom | Tie Rod | Fixed | 0 |
| Portal | Slewing Platform | Revolute | 1 |
| Ground | Slewing Platform | Fixed | 0 |
| Components | Boom | Counterweight Boom | Front Tie Rod | Intermediate Tie Rod | Rear Tie Rod | Bucket Wheel X | Bucket Wheel Y | Counterweight |
|---|---|---|---|---|---|---|---|---|
| L/mm | 21,250 | 16,700 | 22,436 | 21,870 | 16,531 | 42,500 | 7480 | 30,500 |
| Name | Unit | Meaning |
|---|---|---|
| N | The digging resistance of the bucket wheel when digging materials | |
| N | The lateral digging resistance of the bucket wheel when digging materials | |
| N | The force generated by the material load on the conveyor belt | |
| N | The force generated by the material load in the bucket wheel | |
| N | Gravity of the boom | |
| N | Gravity of the counterweight boom | |
| N | Gravity of the front tie rod | |
| N | Gravity of the intermediate tie rod | |
| N | Gravity of the rear tie rod | |
| N | Gravity of the bucket wheel | |
| N | Gravity of the counterweight | |
| mm | The moment arm of the boom | |
| mm | The moment arm of the counterweight boom | |
| mm | The moment arm of the front tie rod | |
| mm | The moment arm of the intermediate tie rod | |
| mm | The moment arm of the rear tie rod | |
| mm | The moment arm of the bucket wheel in the horizontal direction | |
| mm | The moment arm of the bucket wheel in the vertical direction | |
| mm | The moment arm of the counterweight |
| Components | Boom | Counterweight Boom | Front Tie Rod | Intermediate Tie Rod | Rear Tie Rod | Bucket Wheel | Balanced Weight |
|---|---|---|---|---|---|---|---|
| Mass/t | 67 | 32 | 7.5 | 4 | 14 | 41.03 | 170 |
| Material Type | Particle Size (mm) | |||
|---|---|---|---|---|
| Sand | 0.5–9 | 50–200 | 31,755 | 9526.5 |
| Limestone | 0–150 | 150–250 | 42,340 | 12,702 |
| Lignite | 0–300 | 50–250 | 53,925 | 16,177.5 |
| Coal | 0–300 | 100–400 | 63,510 | 19,053 |
| Counterweight (t) | First-Order Mode Frequency (Hz) | |
|---|---|---|
| 120 | 1.439766 | 0.520917982505 |
| 130 | 1.391040 | 0.539164941339 |
| 140 | 1.339650 | 0.559847721420 |
| 150 | 1.289182 | 0.581764250509 |
| 160 | 1.241412 | 0.604150757363 |
| 170 | 1.197047 | 0.626541814983 |
| 180 | 1.156178 | 0.648689042691 |
| 190 | 1.118632 | 0.670461778315 |
| 200 | 1.084134 | 0.691796401552 |
| 210 | 1.052383 | 0.712668296618 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Qin, Y.; Chen, L. Dynamics and Failure Analysis on Rigid–Flexible Coupling Structure to Bucket Wheel Stacker Reclaimer. Machines 2025, 13, 209. https://doi.org/10.3390/machines13030209
Wang X, Qin Y, Chen L. Dynamics and Failure Analysis on Rigid–Flexible Coupling Structure to Bucket Wheel Stacker Reclaimer. Machines. 2025; 13(3):209. https://doi.org/10.3390/machines13030209
Chicago/Turabian StyleWang, Xiaozhen, Yixiao Qin, and Lin Chen. 2025. "Dynamics and Failure Analysis on Rigid–Flexible Coupling Structure to Bucket Wheel Stacker Reclaimer" Machines 13, no. 3: 209. https://doi.org/10.3390/machines13030209
APA StyleWang, X., Qin, Y., & Chen, L. (2025). Dynamics and Failure Analysis on Rigid–Flexible Coupling Structure to Bucket Wheel Stacker Reclaimer. Machines, 13(3), 209. https://doi.org/10.3390/machines13030209





