Analysis of Rotor Lamination Sleeve Loss in High-Speed Permanent Magnet Synchronous Motor
Abstract
:1. Introduction
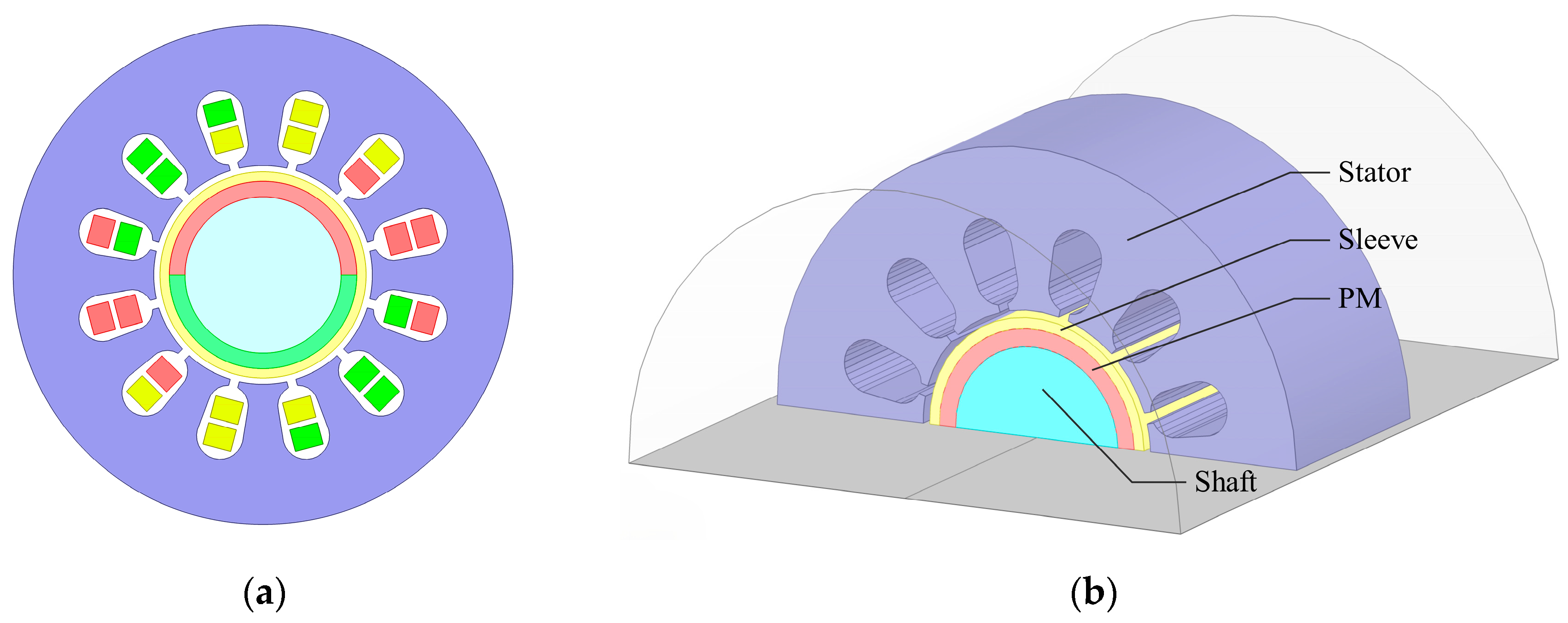
2. Structure and Parameters of HSPMSM
3. Analysis and Calculation of Rotor Eddy Current
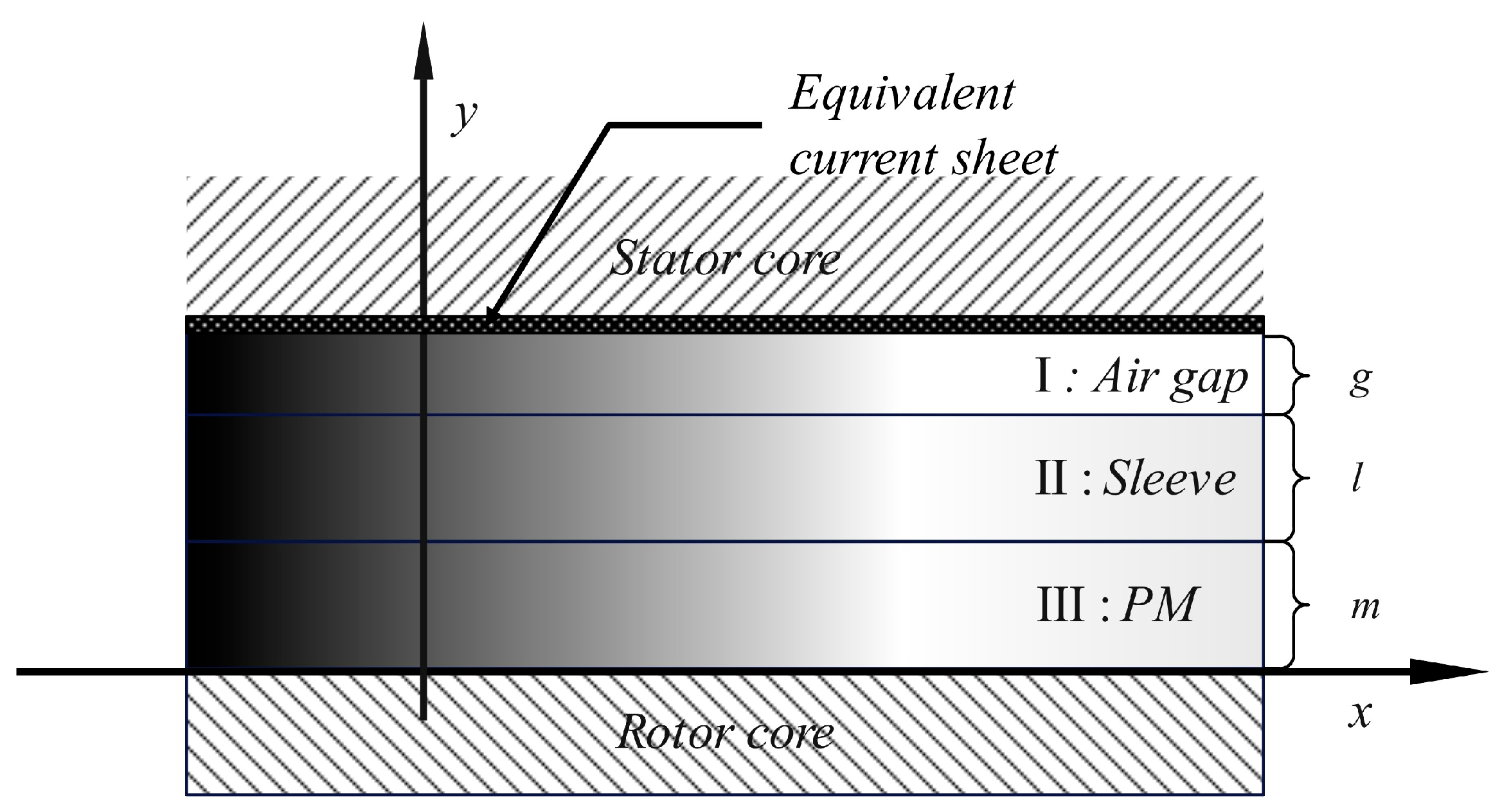
3.1. Simplification of the Analytical Computational Model
- The relative permeability and bulk conductivity of the permanent magnet and the sleeve were considered constant and isotropic.
- The stator winding current was represented by an equivalent current sheet model within the slots.
- The relative permeability of the stator core was assumed to approach infinity, while its bulk conductivity approached zero.
- The sleeve, permanent magnet, and air gap computation domains were regarded as semi-infinite planes.
- The stator slot shape was simplified, with a uniform current distribution within the slots.
- The effect of the slot opening on the air gap flux density waveform was neglected.
- End effects were ignored, and only the axial eddy current distribution was considered.
3.2. Establishment of Analytical Model of Rotor Eddy Current Loss
- Air gap domain
- Laminated core domain
- Permanent magnet domain
- Boundary condition configuration
- Global boundary at the retaining sleeve
4. Finite Element Simulation
4.1. Model of Lamination Structure Sleeve for Permanent Magnet Motor
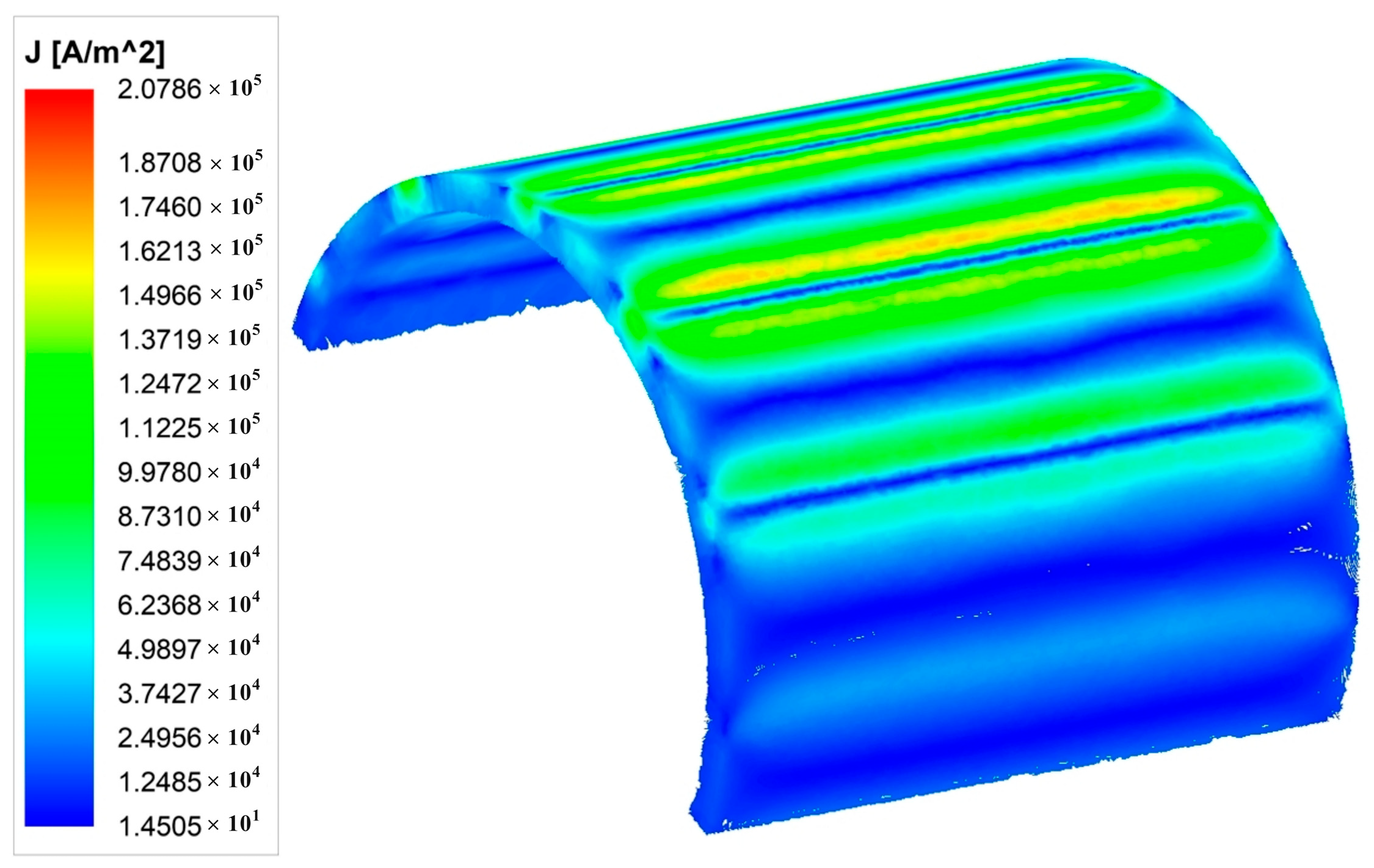
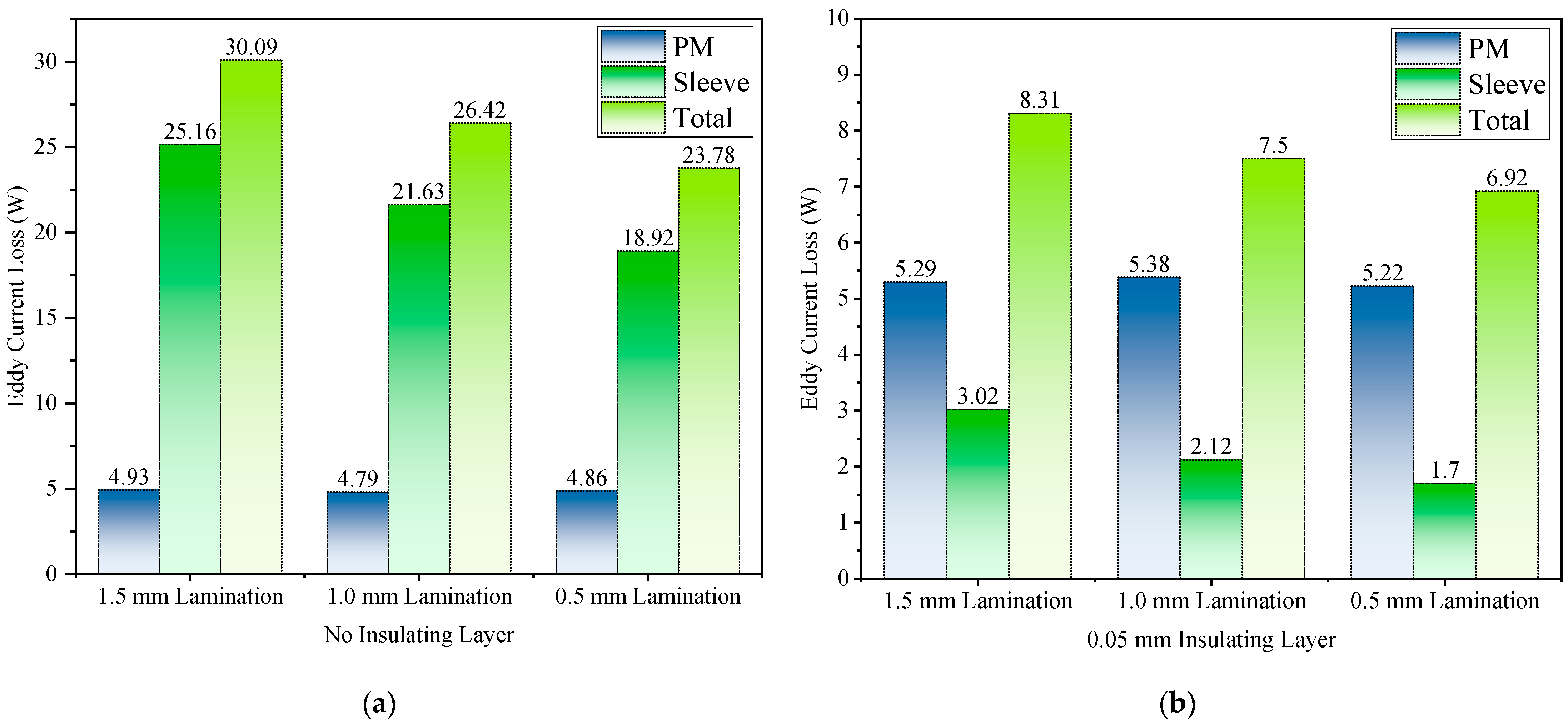
4.2. Finite Element Simulation Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.; Xu, Z.; Wang, H.; Liu, W. Research on Magnetic-Fluid-Thermal-Stress Multi-Field Bidirectional Coupling of High Speed Permanent Magnet Synchronous Motors. Case Stud. Therm. Eng. 2024, 54, 104012. [Google Scholar] [CrossRef]
- Gerada, D.; Mebarki, A.; Brown, N.L.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-Speed Electrical Machines: Technologies, Trends, and Developments. IEEE Trans. Ind. Electron. 2014, 61, 2946–2959. [Google Scholar] [CrossRef]
- Tong, W.; Sun, R.; Zhang, C.; Wu, S.; Tang, R. Loss and Thermal Analysis of a High-Speed Surface-Mounted PMSM With Amorphous Metal Stator Core and Titanium Alloy Rotor Sleeve. IEEE Trans. Magn. 2019, 55, 8102104. [Google Scholar] [CrossRef]
- Cheng, X.; Xu, W.; Du, G.; Zeng, G.; Zhu, J. Novel Rotors with Low Eddy Current Loss for High Speed Permanent Magnet Machines. Trans. Electr. Mach. Syst. 2019, 3, 187–194. [Google Scholar] [CrossRef]
- Du, G.; Wang, L.; Zhou, Q.; Pu, T.; Hu, C.; Tong, J.; Huang, N.; Xu, W. Influence of Rotor Sleeve on Multiphysics Performance for HSPMSM. IEEE Trans. Ind. Applicat. 2023, 59, 1626–1638. [Google Scholar] [CrossRef]
- Pan, B.; Tao, D.; Ge, B.; Wang, L.; Hou, P. Analysis of Eddy Current Loss of 120-kW High-Speed Permanent Magnet Synchronous Motor. Machines 2022, 10, 346. [Google Scholar] [CrossRef]
- Niu, S.; Ho, S.L.; Fu, W.N.; Zhu, J. Eddy Current Reduction in High-Speed Machines and Eddy Current Loss Analysis With Multislice Time-Stepping Finite-Element Method. IEEE Trans. Magn. 2012, 48, 1007–1010. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Gerada, C. Rotor Eddy Current Loss and Multiphysics Fields Analysis for a High-Speed Permanent Magnet Machine. IEEE Trans. Ind. Electron. 2021, 68, 5100–5111. [Google Scholar] [CrossRef]
- Tong, W.; Hou, M.; Sun, L.; Wu, S. Analysis and Experimental Verification of Segmented Rotor Structure on Rotor Eddy Current Loss of High-Speed Surface-Mounted Permanent Magnet Machine. In Proceedings of the 2021 IEEE International Magnetic Conference (INTERMAG), Lyon, France, 26–30 April 2021; pp. 1–5. [Google Scholar]
- Sitnikov, M.A.; Martin, F.; Belahcen, A. Fast and Accurate Methodologies for the Eddy Current Losses Analysis in Axially Laminated Rotor of Synchronous Reluctance Machines under Different Loads. IET Electr. Power Appl. 2024, 18, 995–1004. [Google Scholar] [CrossRef]
- Lee, S.-H.; Song, S.-W.; Jeong, M.-J.; Kim, W.-H.; Jung, D.-H. A Novel Sleeve Design to Reduce the Eddy Current Loss of High-Speed Electrical Machines. Machines 2023, 11, 756. [Google Scholar] [CrossRef]
- Ge, B.; Yang, Z.; Dong, C.; Liu, J.; Xu, Y. Electromagnetic Property Analysis and Rotor Eddy Current Loss Optimization of Low Temperature and High Speed Permanent Magnet Motor Materials. In Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10 May 2024; pp. 83–88. [Google Scholar]
- Ding, M.; Fang, H.; Qu, R. Reduction of Rotor Loss in High-Speed Electrical Machines With a Novel Composite Sleeve. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5 November 2023; pp. 78–81. [Google Scholar]
- Cui, Z.; Le, Y.; Wang, K.; Wang, H.; Zheng, S. A Low Rotor Eddy Current Loss Design Approach to HSPMSM for Small-Scale Magnetically Suspended Turbomolecular Pump. IEEE Trans. Ind. Electron. 2024, 1–11. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Ding, H.; Guo, Y.; Sun, Y. Influence of Retaining Sleeve Conductivity and Thickness on Rotor Eddy Current Loss in High-Speed Permanent Magnet Motors. In Proceedings of the 2024 Third International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Dubai, United Arab Emirates, 22 November 2024; pp. 1–7. [Google Scholar]
- Zhang, W.; Xu, Y.; Xin, F. Comparative Research of Yokeless and Segmented Armature Axial Flux Motors with Surface-Mounted and Tangential Permanent Magnet Rotor. In Proceedings of the 2024 IEEE 21st Biennial Conference on Electromagnetic Field Computation (CEFC), Jeju, Republic of Korea, 2 June 2024; pp. 1–2. [Google Scholar]
- Ciriani, C.; Khan, H.A.; Mansour, K.; Olivo, M.; Tessarolo, A. Simple and Accurate Computation of Rotor Eddy-Current Losses in Surface-Mounted Permanent Magnet Machines Accounting for Magnet Circumferential Segmentation. IEEE Access 2024, 12, 36810–36824. [Google Scholar] [CrossRef]
- De La Barriere, O.; Hlioui, S.; Ben Ahmed, H.; Gabsi, M. An Analytical Model for the Computation of No-Load Eddy-Current Losses in the Rotor of a Permanent Magnet Synchronous Machine. IEEE Trans. Magn. 2016, 52, 8103813. [Google Scholar] [CrossRef]





| Properties | Value | Properties | Value |
|---|---|---|---|
| Rated power (kW) | 10 | Stator outer diameter (mm) | 160 |
| Rated speed (rpm) | 30,000 | Stator inter diameter (mm) | 70 |
| Rated voltage (V) | 380 | Core length (mm) | 60 |
| Pole number | 2 | Air gap thickness (mm) | 2 |
| Stator slots | 12 | Sleeve thickness (mm) | 3 |
| Phase number | 3 | PM thickness (mm) | 5 |
| PM material | NdFe35 | Frequency (Hz) | 500 |
| Name | TC4 Ti | Carbon Fibre | NdFe35 | |
|---|---|---|---|---|
| Tangential | Radial | |||
| Density (kg/m3) | 4430 | 1650 | 7400 | |
| Relative permeability | 1 | 1 | 1 | 1.058 |
| Bulk conductivity (105 S/m) | 5.6 | 0.3 | 0.01 | 6.95 |
| Poisson ratio | 0.34 | 0.3 | 0.015 | 0.24 |
| Yield/tensile stress (MPa) | 825 | 1960 | −100 | 75 |
| Finite Element | Analytical | |
|---|---|---|
| No Lamination | 41.64 W | 45.78 W |
| Lamination | 1.82 W | 2.42 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Liang, S.; Wang, F.; Tian, J.; Chen, K.; Liu, S. Analysis of Rotor Lamination Sleeve Loss in High-Speed Permanent Magnet Synchronous Motor. Machines 2025, 13, 236. https://doi.org/10.3390/machines13030236
Tian Y, Liang S, Wang F, Tian J, Chen K, Liu S. Analysis of Rotor Lamination Sleeve Loss in High-Speed Permanent Magnet Synchronous Motor. Machines. 2025; 13(3):236. https://doi.org/10.3390/machines13030236
Chicago/Turabian StyleTian, Yiming, Shiqiang Liang, Fukang Wang, Jiahao Tian, Kai Chen, and Shi Liu. 2025. "Analysis of Rotor Lamination Sleeve Loss in High-Speed Permanent Magnet Synchronous Motor" Machines 13, no. 3: 236. https://doi.org/10.3390/machines13030236
APA StyleTian, Y., Liang, S., Wang, F., Tian, J., Chen, K., & Liu, S. (2025). Analysis of Rotor Lamination Sleeve Loss in High-Speed Permanent Magnet Synchronous Motor. Machines, 13(3), 236. https://doi.org/10.3390/machines13030236







