Cage Strength Analysis and Improvement of High-Speed Deep Groove Ball Bearings
Abstract
:1. Introduction
2. Rigid-Flexible Coupling Dynamic Model of Deep Groove Ball Bearings
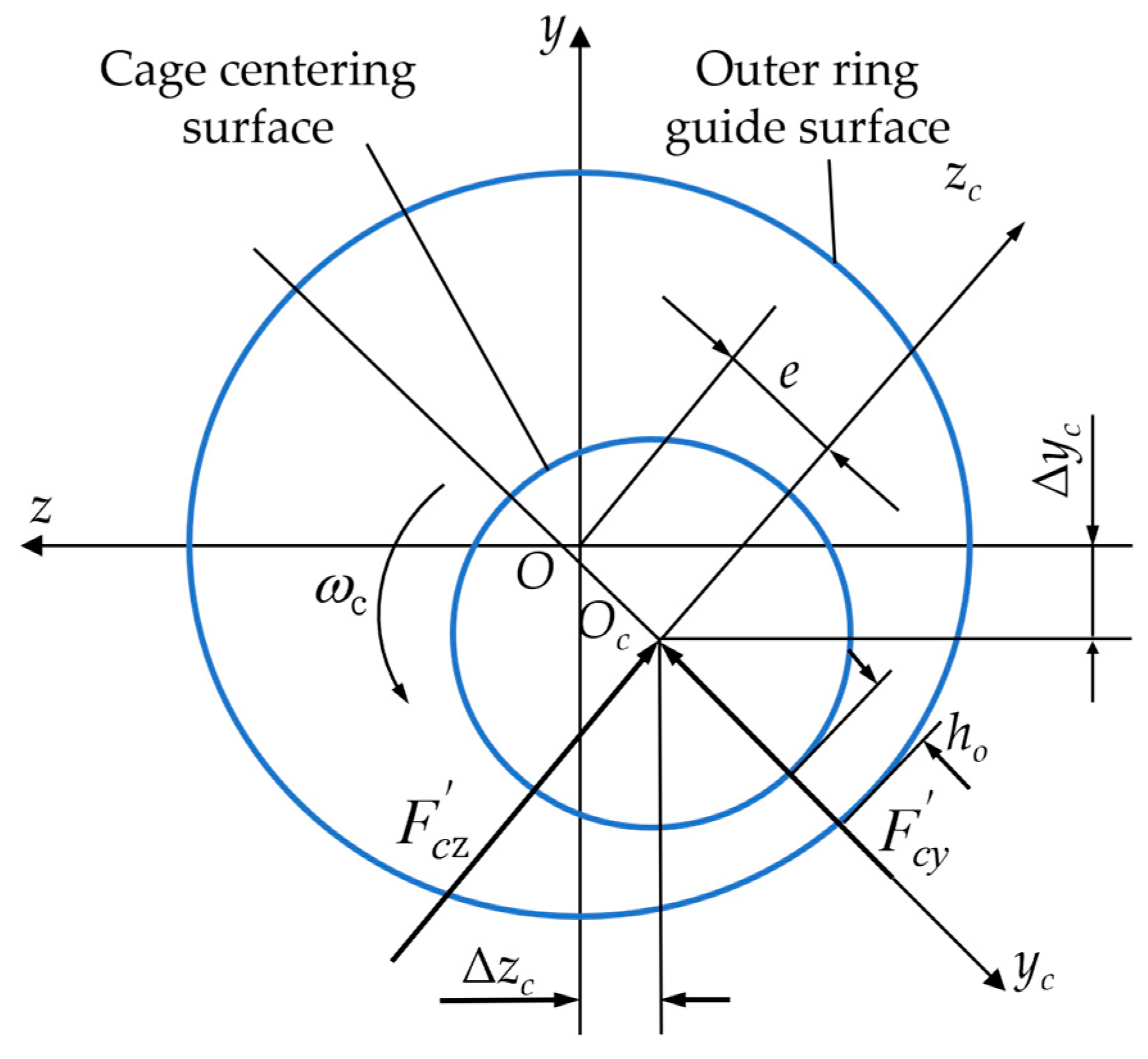
2.1. Cage Centrifugal Force
2.2. Temperature
- (1)
- Cage thermal expansion
- (2)
- The impact of lubrication performance
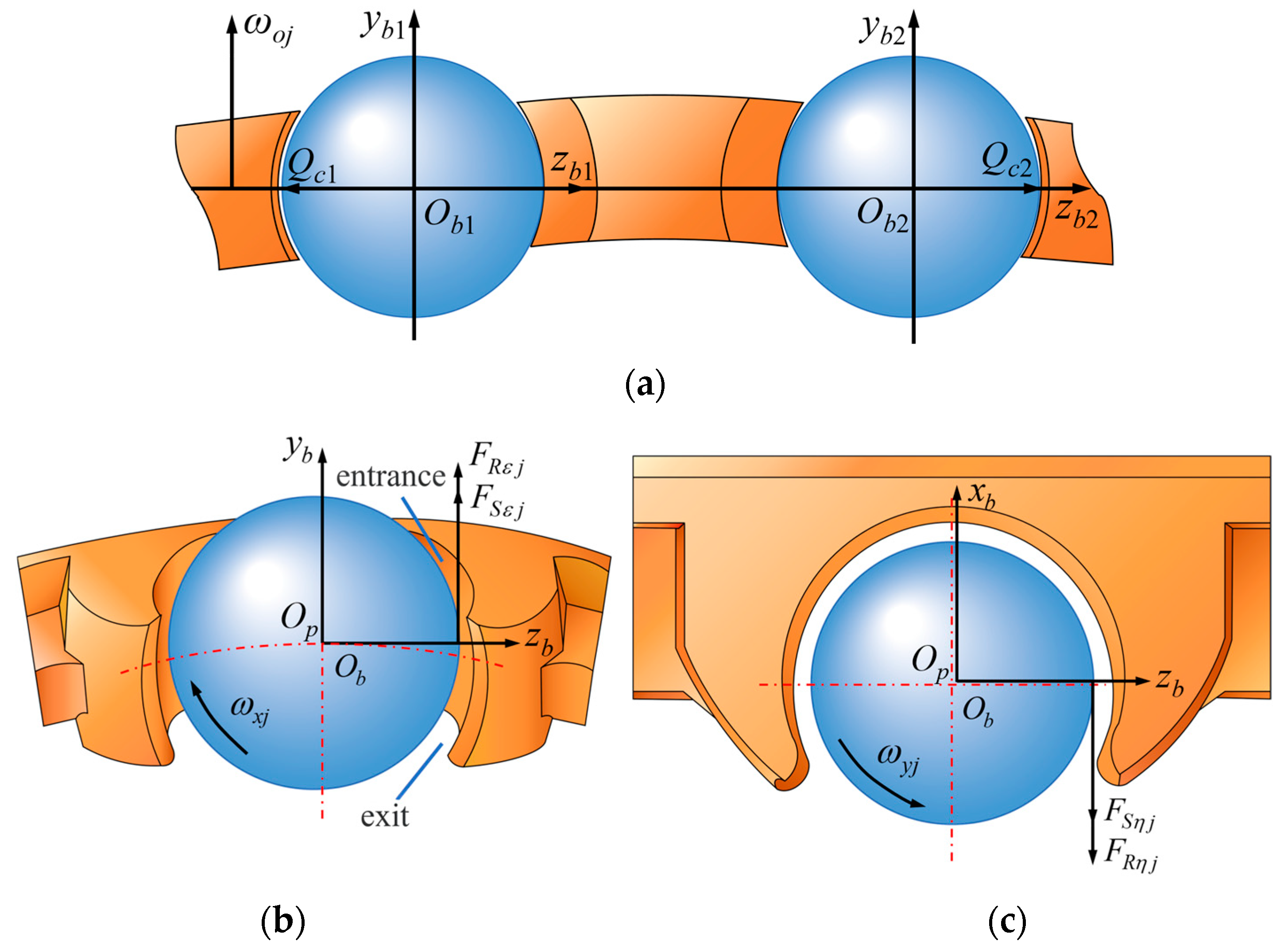
2.3. Interaction Between Ball Bearing Components
- (1)
- Normal force between pocket and steel ball
- (2)
- Tangential force between pocket and steel ball
- (3)
- The interaction between the cage and the guiding ring
2.4. Cage Flexible Body Dynamics Differential Equation
- (1)
- The inertial coordinate system {O; X, Y, Z} is fixed in space, with its origin coinciding with the bearing center. The X-axis is aligned with the bearing axis, and the YOZ plane passes through the bearing center while remaining parallel to the bearing radial plane.
- (2)
- The inner ring coordinate system, denoted as {oi; xi, yi, zi}, is defined such that its origin coincides with the centroid of the inner ring. The xi-axis is aligned with the rotational axis of the inner ring, while the yioizi plane passes through the centroid and aligns with the radial plane of the inner ring.
- (3)
- The cage coordinate system, denoted as {oc; xc, yc, zc}, has its origin coinciding with the center of the cage pocket’s center plane. The xc axis is aligned with the cage’s rotational axis, while the yc and zc plane intersects the center of the cage pocket’s center plane and aligns with the cage’s radial plane.
- (4)
- The coordinate system of the j-th cage pocket center, denoted as {opj; xpj, ypj, zpj}, has its origin, opj, coinciding with the center of the cage pocket. In this system, the ypj axis is aligned along the radial direction of the cage, while the zpj axis is oriented along the circumferential direction of the cage. The xpj axis is defined according to the right-hand rule, derived from the ypj and zpj axes. This coordinate system, {opj; xpj, ypj, zpj }, is fixed at the center of the j-th cage pocket and moves in conjunction with the cage. Each cage pocket possesses its own distinct local coordinate system.
- (5)
- The coordinate system {obj; xbj, ybj, zbj} for the center of the j-th ball is defined such that its origin, obj, coincides with the center of the ball. In this system, the ybj axis is aligned with the radial direction of the bearing, while the zbj axis is oriented along the circumferential direction of the bearing. The xbj axis is determined using the right-hand rule based on the orientation of ybj and zbj. This coordinate system { obj; xbj, ybj, zbj} is fixed at the center of the j-th ball and moves in conjunction with the ball, meaning that each ball possesses its own local coordinate system.
3. Model Solving Process
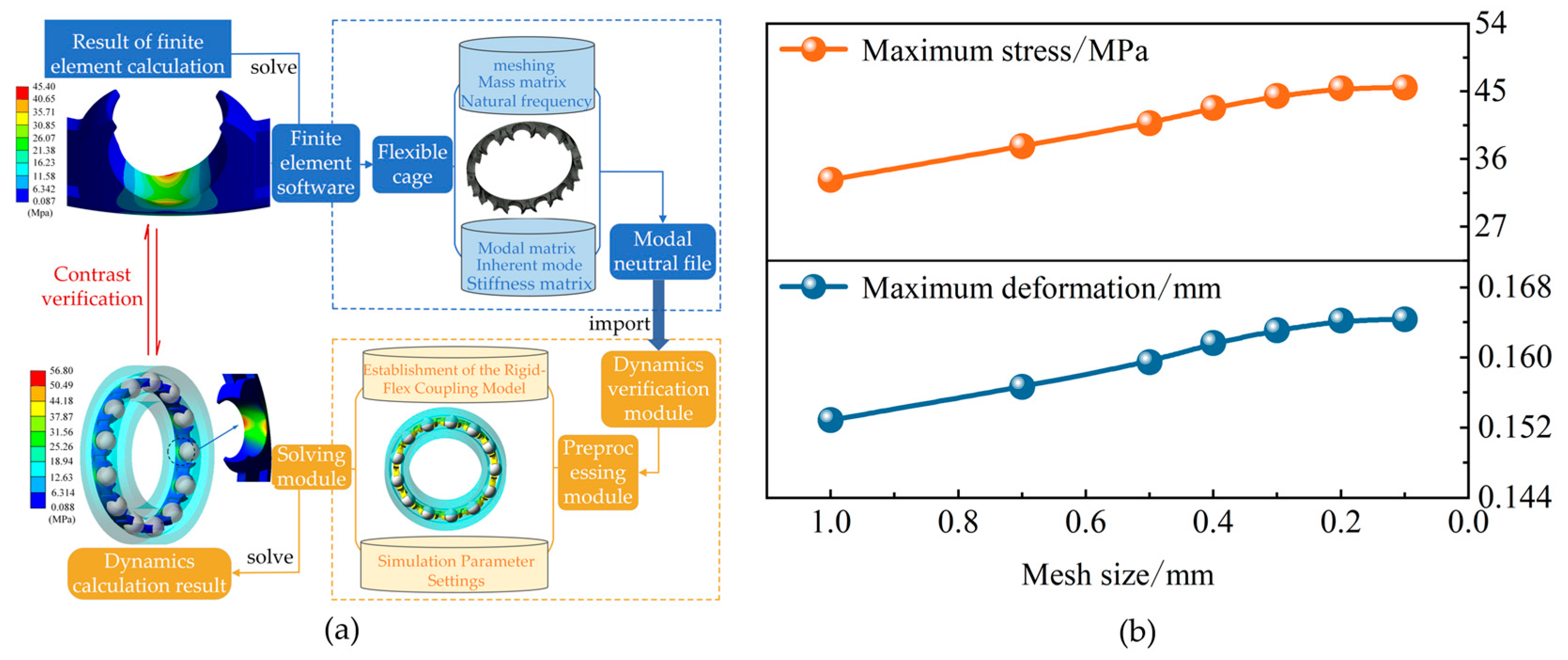
3.1. Modeling and Calculation of Flexible Cage
- (1)
- Firstly, the cage is pre-processed, and then the modal matrix, mass matrix, stiffness matrix, natural frequency, and natural mode of the flexible cage are outputted into a modal neutral file, referred to as the MNF file.
- (2)
- To begin the process, load the Adams/Auto Flex module and import the modal neutral file into Adams/View. Subsequently, create the flexible body and establish the rigid–flexible coupling model. Next, connect the flexible cage with other bearing components using dummy bodies. At this stage, it is essential to restrict the radial translation and the axial and circumferential rotations of the inner ring while permitting other degrees of freedom. Finally, establish constraint forces among the various components of the bearing.
- (3)
- Thirdly, the simulation time is set to 0.5 s, with a step size of 20,000. Additionally, the post-processing panel is established using macro commands within the program. relevant calculation results are extracted during the Adams post-processing stage, and grid-independent calculations are conducted. As illustrated in Figure 7b, the optimal grid size is 0.2 mm.
- (4)
- In the Adams post-processing, the equivalent stress and equivalent strain values at various nodes are obtained. The maximum equivalent stress and the stress contour plots are combined to identify the locations of weak strength in the cage. Meanwhile, perform verification calculations on the cage strength utilizing finite element software to analyze the impact of steel ball collisions on the retainer’s strength.
3.2. Analysis of the Inherent Vibration Characteristics of Flexible Cage
4. Cage Dynamic Contact Simulation
4.1. Working Condition Parameters
- (1)
- External load
- (2)
- Steady state speed
- (3)
- Acceleration and deceleration
- (4)
- Temperature
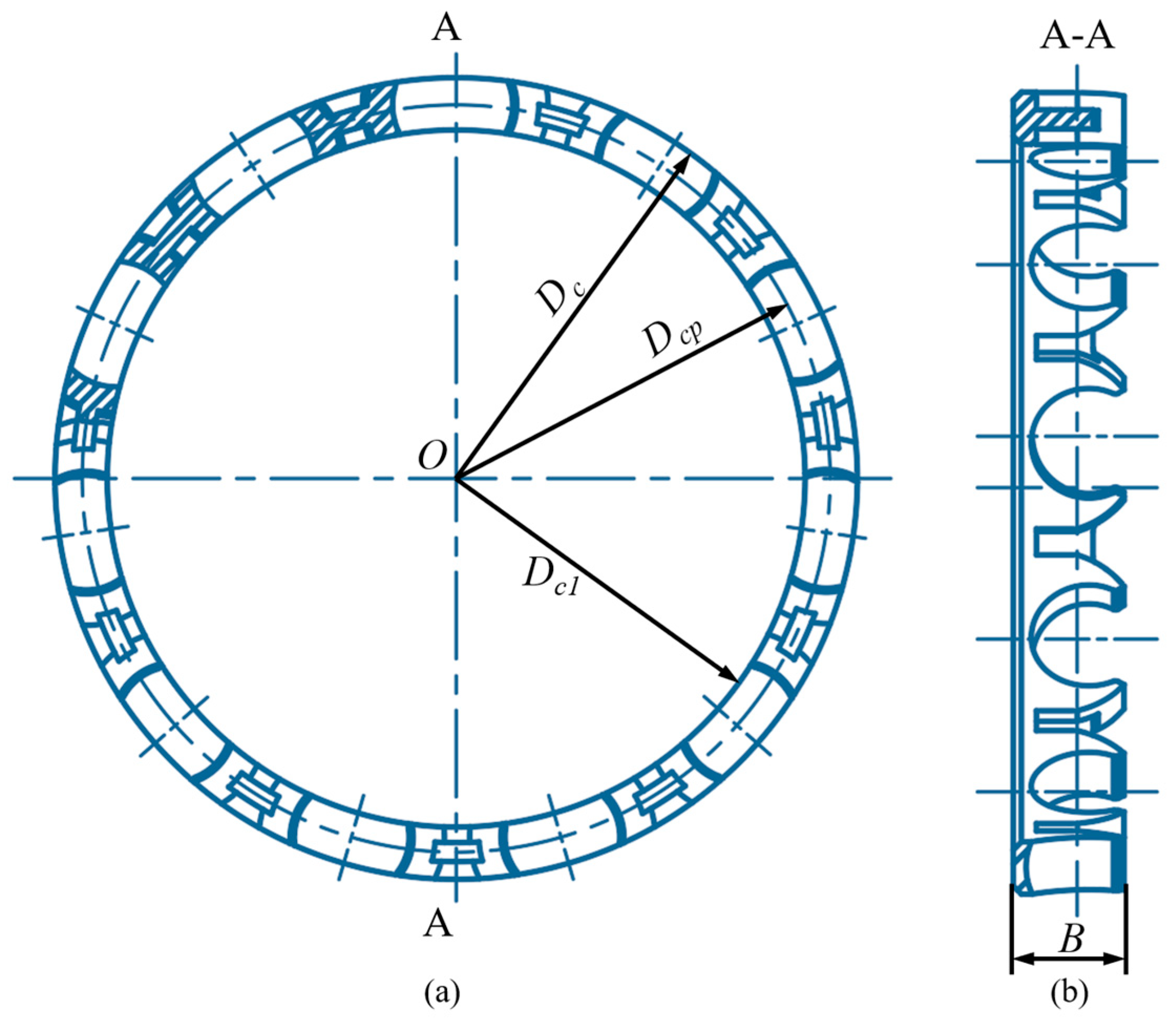
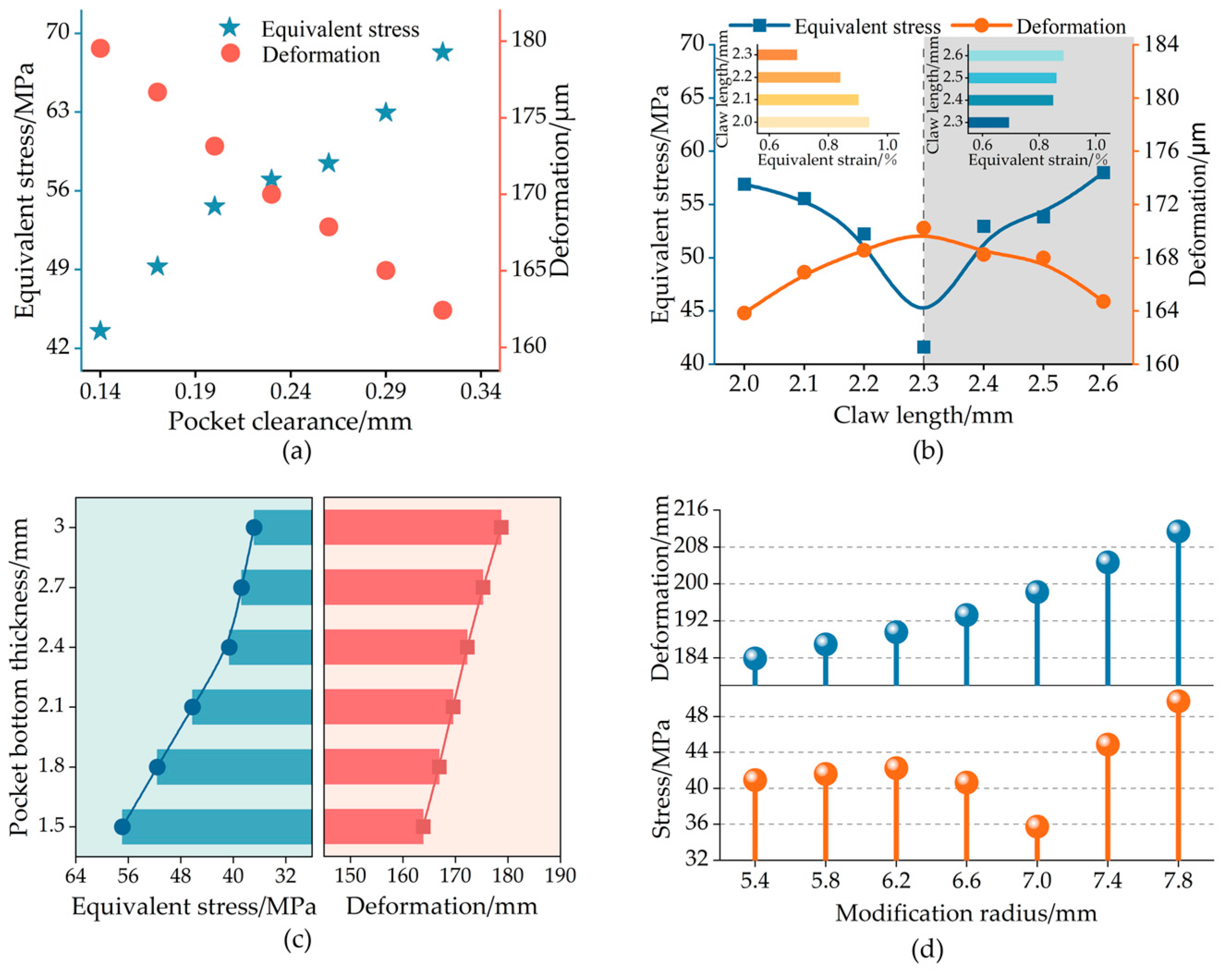
4.2. Cage Structural Parameters
- (1)
- Pocket clearance
- (2)
- Claw length
- (3)
- Pocket bottom thickness
4.3. Cage Strength Design Direction
- (1)
- Design direction
- (2)
- Improve the strength of the pockets bottom
- (3)
- Reduce the influence of centrifugal force
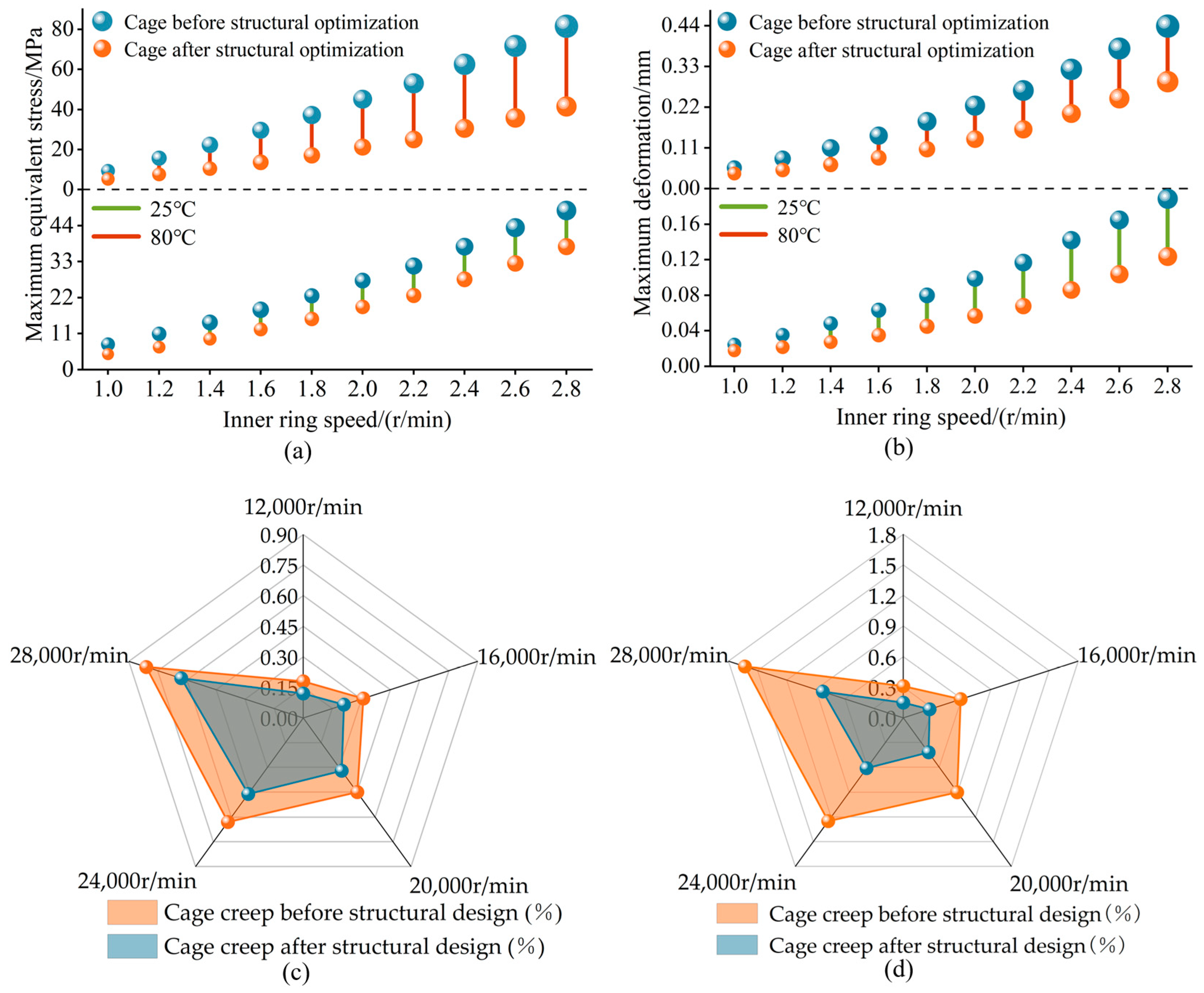
4.4. Structural Verification
5. Conclusions
- (1)
- The rotational speed is the primary factor influencing the sensitivity of cage strength. For every increase of 2000 r/min in the rotational speed, the stress and deformation of the cage increase by 15% to 20%. The acceleration mainly affects the cage stress amplitude, while it has little effect on cage strength. As the rotational speed increases, the sensitivity of cage strength to temperature obviously intensifies. The equivalent stress and radial deformation of the cage are elevated by 5%~16% at 80 °C, compared to 25 °C;
- (2)
- As the length of the claw increases, the stress initially decreases before rising again, while the deformation first increases and subsequently decreases. In contrast, as the modification radius increases, the stress exhibits a similar pattern of initial decrease followed by an increase, whereas the deformation consistently increases. Furthermore, an increase in the pocket thickness leads to a gradual decrease in stress, an increase in deformation. Conversely, an increase in the pocket gap results in an increase in stress and a decrease in deformation;
- (3)
- With a pocket clearance of 0.23 mm, a claw length of 2.3 mm, a bottom thickness of 2.4 mm, and a shaping radius of 7.0 mm, the strength of the cage was evaluated both before and after the improvements. The improved cage demonstrates a maximum reduction in equivalent stress of 22% to 34% at 25 °C, along with a maximum reduction in deformation of 33% to 39% in the radial direction, when compared to the pre-improvement cage. At 80 °C, the maximum equivalent stress is reduced by 50% to 55%, and the maximum deformation in the radial direction is reduced by 35% to 41%. The results indicated that the enhanced cage exhibited superior strength.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DGBB(s) | Deep Groove Ball Bearing(s) |
References
- He, F.; Xie, G.X.; Luo, J. Electrical bearing failures in electric vehicles. Friction 2020, 8, 4–28. [Google Scholar] [CrossRef]
- Qu, Y.F.; Mao, H.S. Key technologies and development trends of new energy vehicle electric drive systems. Era. Car. 2023, 15, 80–82. (In Chinese) [Google Scholar]
- Wang, P.F. Vibration characteristics of rotor-bearing system with angular misalignment and cage fracture: Simulation and experiment. Mech. Syst. Signal. Process. 2023, 182, 109545. [Google Scholar] [CrossRef]
- Chen, M.H. (63/22/C3) Bearing cage fracture failure analysis. Harbin. Bear. 2022, 43, 4. (In Chinese) [Google Scholar]
- Wang, M.; Yan, K. Dynamic performance analysis of ball bearings with multi-factor coupling excitation. Precis. Eng. 2024, 89, 70–90. [Google Scholar] [CrossRef]
- Thibault, N. Dynamic model of a deep grooves ball bearing dedicated to the study of instantaneous angular speed of rotating assemblies. Tribol. Int. 2022, 174, 107753. [Google Scholar] [CrossRef]
- Gillet, S. Cyclic creep strain rate criterion for short-fibre reinforced thermoplastics: Validation of creep and fatigue performance across a wide range of load ratios. Int. J. Fatigue 2024, 183, 108257. [Google Scholar] [CrossRef]
- Chen, Q.X. Structural Design and Dynamic Analysis of High-Speed Bearing Cage for Electric Drive of New Energy Vehicles. Master’s Thesis, Hunan University of Technology, Zhuzhou, China, 2023. (In Chinese). [Google Scholar]
- Li, T. Design and Performance Analysis of Key Components of Deep Groove Ball Bearings for High-Speed Motors for New Energy Vehicles. Master’s Thesis, Soochow University, Suzhou, China, 2020. (In Chinese). [Google Scholar]
- Ma, S.J. New bearing model with flexible cage and study of dynamic behavior under variable-speed. Mech. Syst. Signal. Process. 2024, 208, 111045. [Google Scholar] [CrossRef]
- Wang, M.K. Dynamic modeling and properties analysis for ball bearing driven by structure flexible deformations. Tribol. Int. 2023, 179, 108163. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, X.L.; He, Y. Influence of appearance and working condition parameters on dynamic performance of bearing flexible cage. Flight Control Detect. 2021, 4, 7. [Google Scholar]
- Zhao, D.T.; Hong, J. Dynamic interaction between the rolling element and cage of rolling bearing considering cage flexibility and clearance. Mech. Mach. Theory 2022, 174, 104905. [Google Scholar] [CrossRef]
- Liu, Y.Q. Skidding dynamic performance of rolling bearing with cage flexibility under accelerating conditions. Mech. Syst. Signal. Process. 2021, 150, 107257. [Google Scholar] [CrossRef]
- Sadeghi, F. A Discrete Element Approach for Modeling Cage Flexibility in Ball Bearing Dynamics Simulations. J. Tribol. 2009, 131, 021102. [Google Scholar]
- Ashtekar, A. A New Approach for Including Cage Flexibility in Dynamic Bearing Models by Using Combined Explicit Finite and Discrete Element Methods. J. Tribol. 2012, 134, 041502. [Google Scholar] [CrossRef]
- Wang, M.K. Transient collision behavior and cage instable whirling mechanism in ball bearings: Modeling approach and properties investigation. Tribol. Int. 2023, 185, 108497. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, J.Q. Theoretical and Experimental Approaches for Flexible Cage Dynamic Characteristics of Four-Point Contact Ball Bearing Considering Multi-Point Contact Behaviors. Mech. Syst. Signal Process. 2025, 223, 111929. [Google Scholar] [CrossRef]
- Yao, T.Q. Multibody dynamics simulation of thin-walled four-point contact ball bearing with interactions of balls, ring raceways and crown-type cage. Multibody Syst. Dyn. 2020, 48, 337–372. [Google Scholar] [CrossRef]
- Li, N. Research on Dynamic Modeling and Vibration Characterization of Integrated Bearings. Appl. Sci. 2024, 15, 98. [Google Scholar]
- Gao, S. Ultra-high-speed hybrid ceramic triboelectric bearing with real-time dynamic instability monitoring. Nano. Energy 2022, 103, 107759. [Google Scholar] [CrossRef]
- Cui, Y.C. Failure Inducement Factor Analysis and Optimal Design Method of Ball Bearing Cage for Aviation Motor. Machines 2024, 12, 466. [Google Scholar] [CrossRef]
- Yang, F. Study on the vibration characteristics of angular contact ball bearing cage under rolling-sliding compound motion. Meas. Sci. Technol. 2024, 35, 125125. [Google Scholar] [CrossRef]
- Cui, L. A new fatigue damage accumulation rating life model of ball bearings under vibration load. Ind. Lubr. Tribol. 2020, 72, 1205–1215. [Google Scholar] [CrossRef]
- Zhang, X.C. Characteristics and Mechanism of Surface Damage of Hybrid Ceramic Ball Bearings for High-Precision Machine Tool. Eng. Failure Anal. 2022, 142, 106784. [Google Scholar] [CrossRef]
- Fang, B.; Zhang, J.H. Analytical Determination of the Optimal Clearance for the Fatigue Life of Ball Bearing Under Different Load Conditions. J. Tribol. 2022, 144, 10. [Google Scholar] [CrossRef]
- Zeng, G. Study on the mass imbalance macro-micro friction and wear characteristics of high-speed angular contact ball bearing cages. Tribol. Int. 2025, 204, 110491. [Google Scholar] [CrossRef]
- Alarifi, I.M. A performance evaluation study of 3d printed nylon/glass fiber and nylon/carbon fiber composite materials. J. Mater. Res. Technol. 2022, 21, 884–892. [Google Scholar] [CrossRef]
- Gangben, C.S.R.; Huang, Z.Q.; Luo, J.W. Design and Calculation of Ball Bearing; China Machine Press: Beijing, China, 2003; pp. 171–175. [Google Scholar]
- Deng, S.E. Flexible body dynamics analysis of high-speed angular contact ball bearing cage. J. Ordnance. Ind. 2011, 32, 625–631. (In Chinese) [Google Scholar]
- Wang, G.X.; Niu, Z.P. Improved Craig–Bampton Method Implemented into Durability Analysis of Flexible Multibody Systems. Actuators 2023, 12, 65. [Google Scholar] [CrossRef]
- Benjamin, B. Interface reduction technique for Enhanced Craig-Bampton method. Mech. Syst. Signal. Process. 2024, 208, 111074. [Google Scholar]
- Jia, X.F. Research on vibration characteristics of high-speed ball bearing crown cage. Vib. Shock 2022, 41, 16–30. (In Chinese) [Google Scholar]



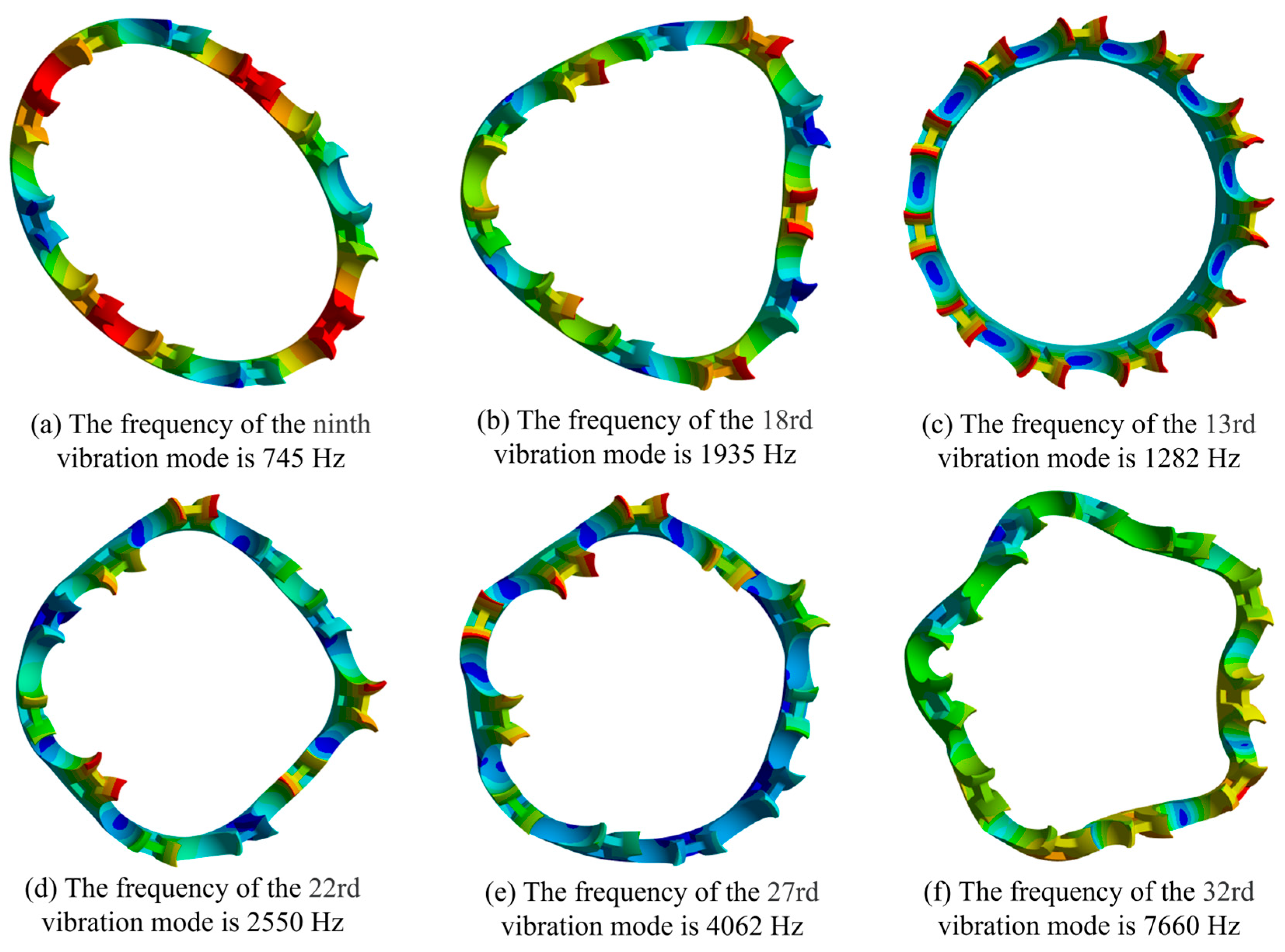
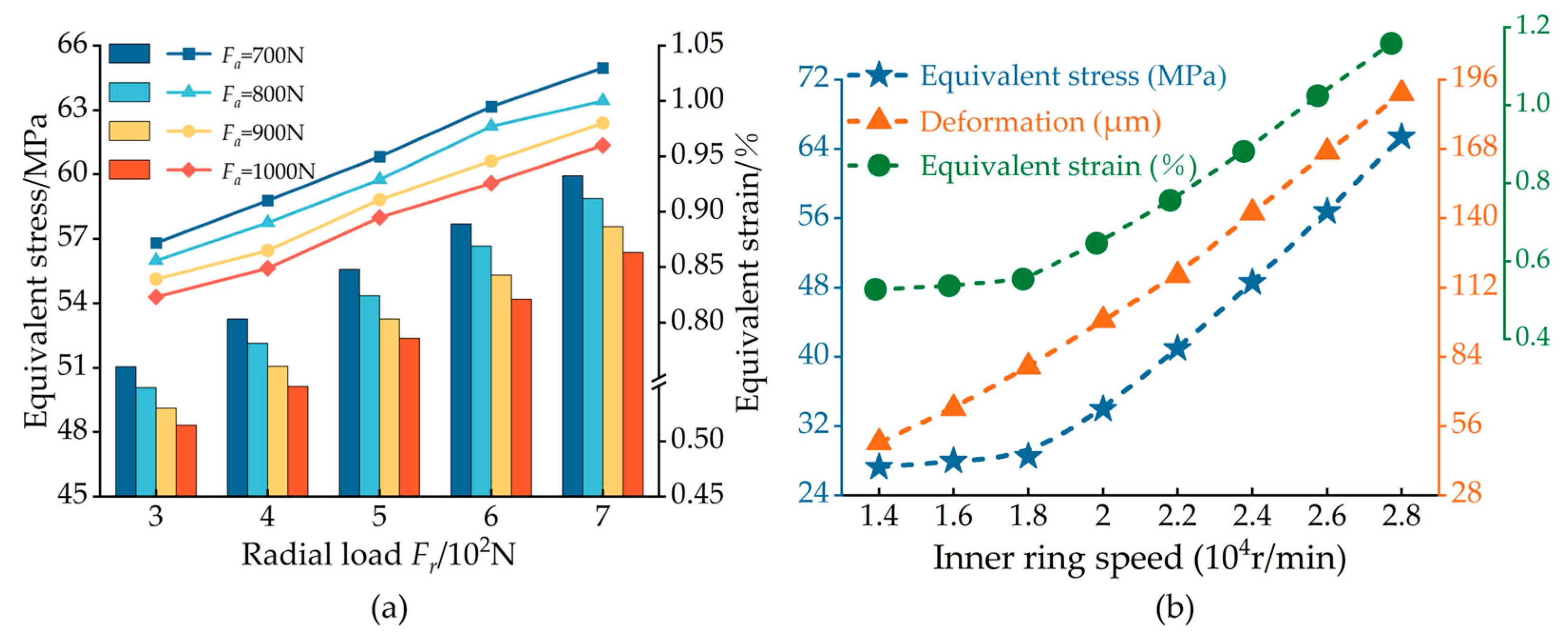
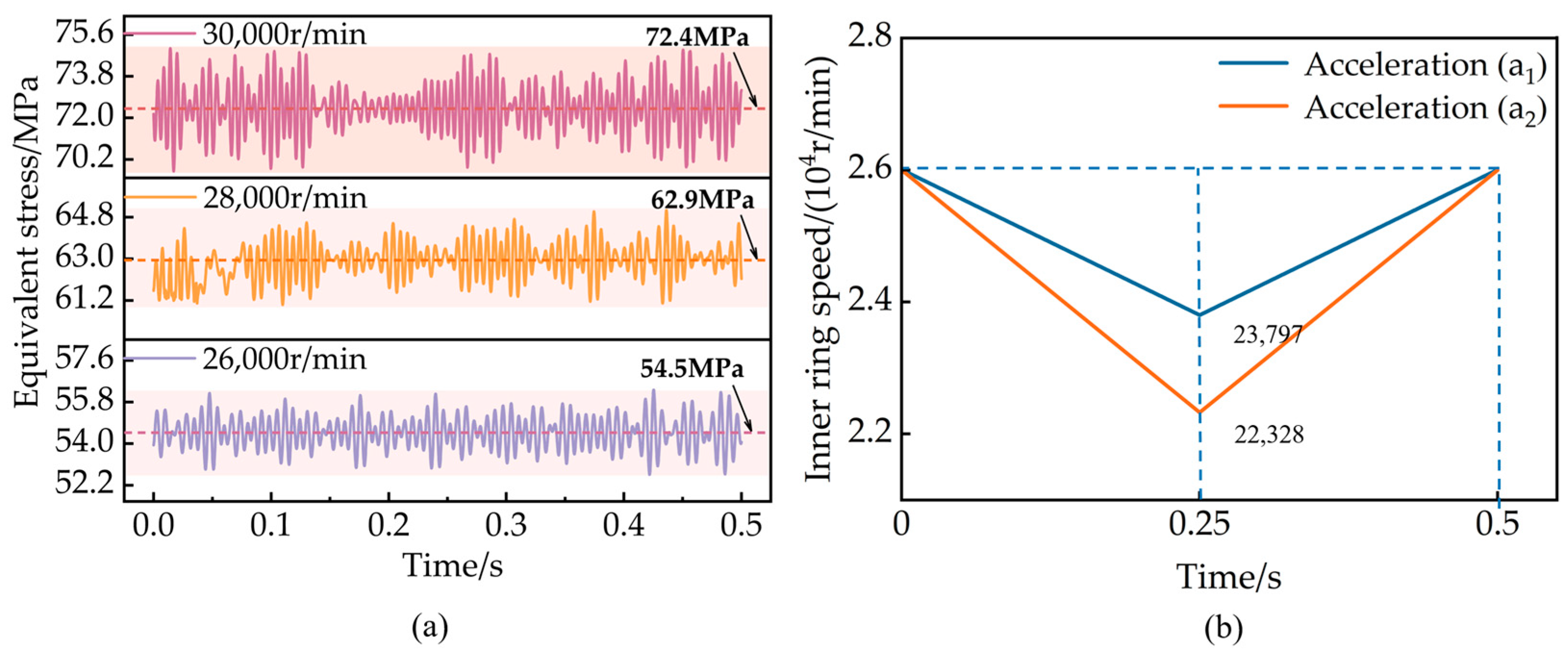
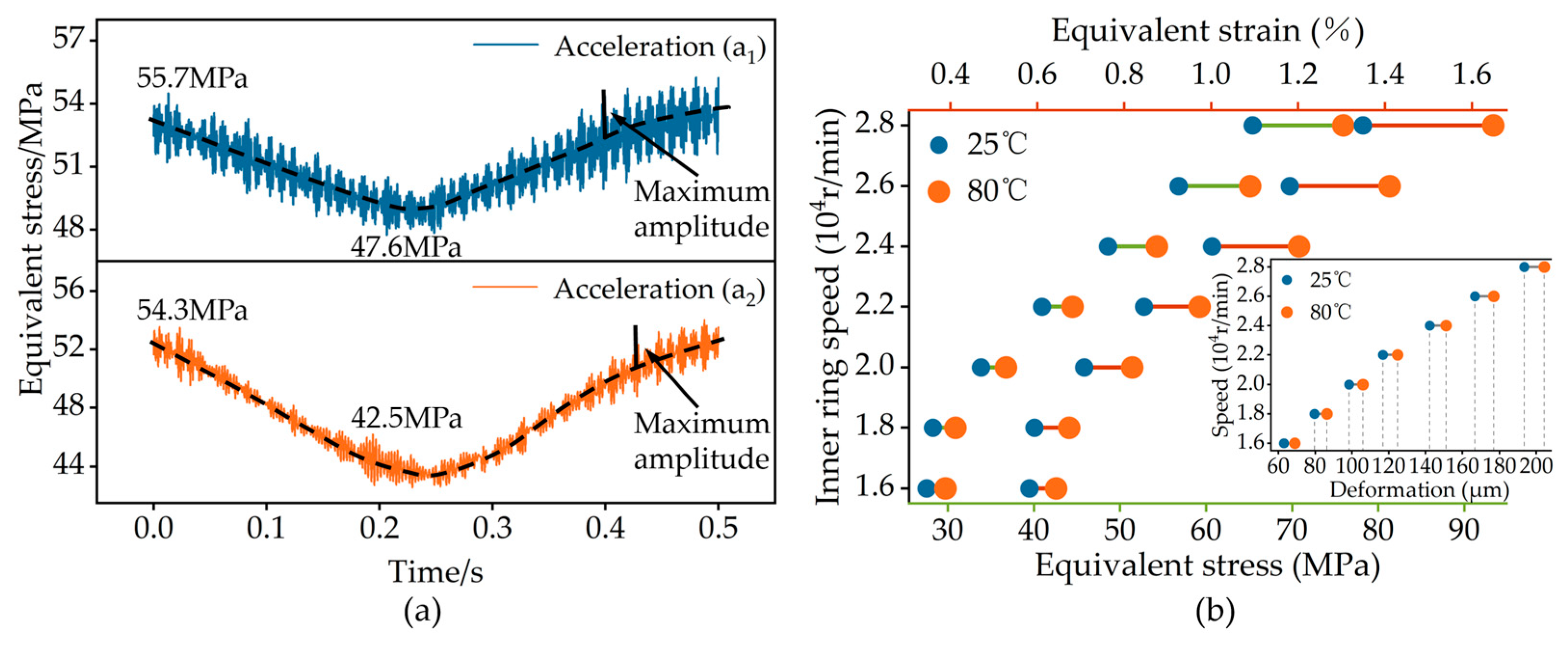


| Parameters | Value | Parameters | Value |
|---|---|---|---|
| bearing outer diameter/mm | 72.0 | inner diameter of cage/mm | 11.0 |
| bearing inner diameter/mm | 37.1 | outer diameter of cage/mm | 51.4 |
| bearing width/mm | 19.0 | the way the cage is guided | outer guide |
| number of steel balls | 11 | lubrication mode | oil lubrication |
| materials of steel balls and rings | GCr15 | materials for the cage | PA46 + GF30 |
| density of steel balls and rings/(kg·m−3) | 7810 | density of cage/(kg·m−3) | 1410 |
| elastic modulus of steel balls and rings/GPa | 208 | elastic modulus of cage/GPa | 6 |
| Poisson’s ratio of steel ball and rings | 0.30 | Poisson’s ratio of cage | 0.42 |
| temperature/℃ | 25, 80 | axial load (Fx)/N | 550 |
| the speed of outer ring/(r/min) | 0 | radial load (Fy)/N | 850 |
| the speed of inner ring/(r/min) | 26,000 | the speed of cage/(r/min) | 11,107 |
| acceleration a1/(r/min2) | 8812 | acceleration a2/(r/min2) | 14,688 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Du, S.; Tian, H.; Huang, L. Cage Strength Analysis and Improvement of High-Speed Deep Groove Ball Bearings. Machines 2025, 13, 241. https://doi.org/10.3390/machines13030241
Zhang W, Du S, Tian H, Huang L. Cage Strength Analysis and Improvement of High-Speed Deep Groove Ball Bearings. Machines. 2025; 13(3):241. https://doi.org/10.3390/machines13030241
Chicago/Turabian StyleZhang, Wenhu, Shengjie Du, Heng Tian, and Li Huang. 2025. "Cage Strength Analysis and Improvement of High-Speed Deep Groove Ball Bearings" Machines 13, no. 3: 241. https://doi.org/10.3390/machines13030241
APA StyleZhang, W., Du, S., Tian, H., & Huang, L. (2025). Cage Strength Analysis and Improvement of High-Speed Deep Groove Ball Bearings. Machines, 13(3), 241. https://doi.org/10.3390/machines13030241




