Review of Agricultural Machinery Seat Semi-Active Suspension Systems for Ride Comfort
Abstract
1. Introduction
2. Research Status of Agricultural Machinery Seat Suspension Systems
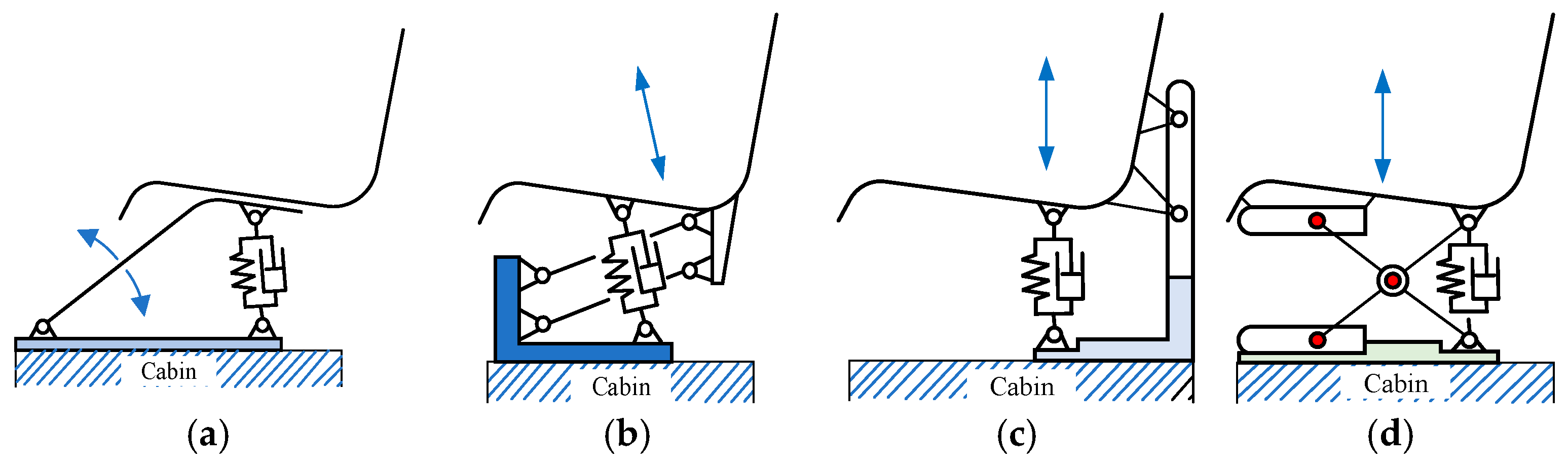
2.1. Basic Structure and Classification of Seat Suspension Systems
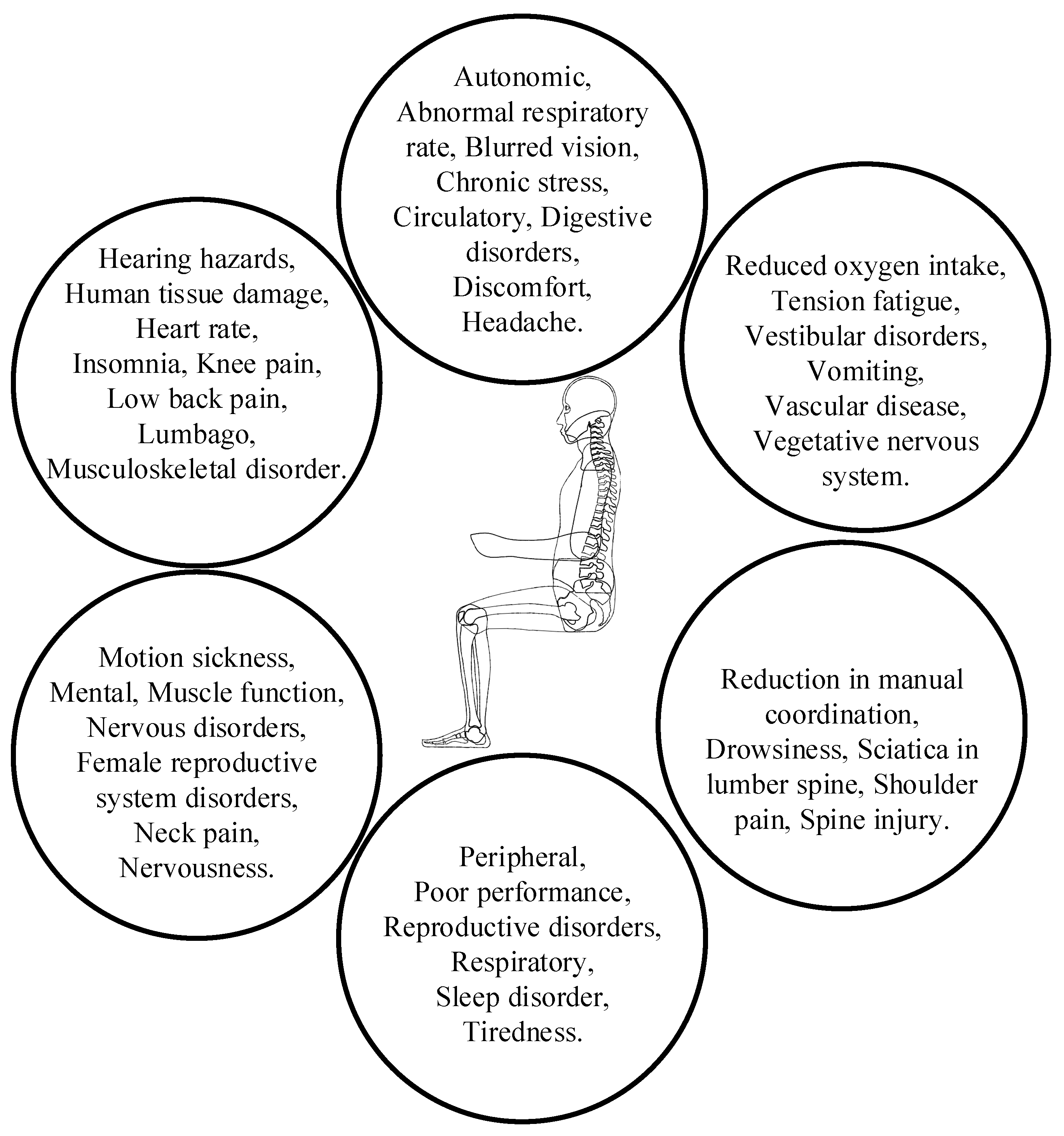
2.2. Evaluation Indicators for Ride Comfort of Seat Suspension System
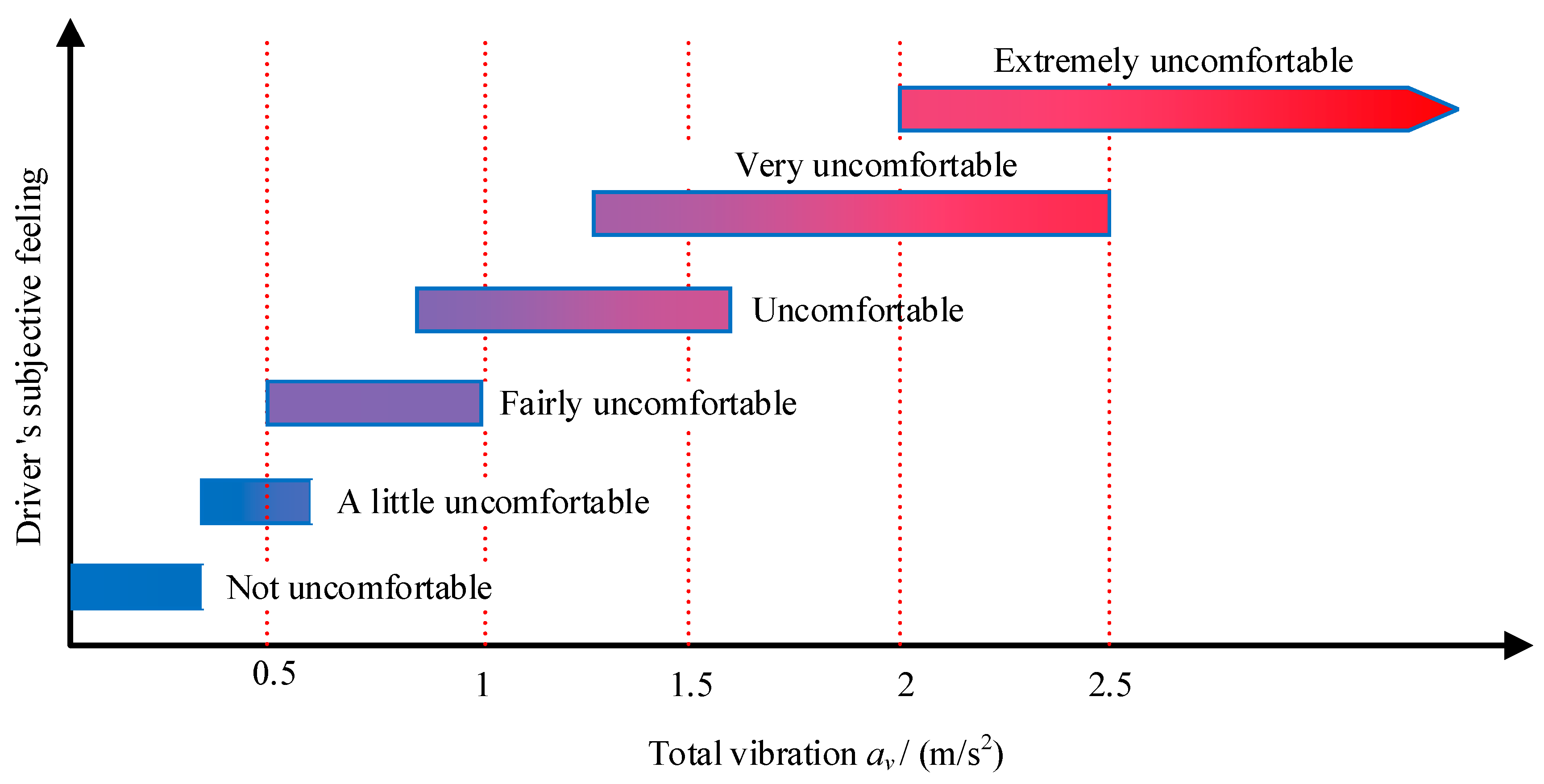
2.2.1. Ride Comfort Analysis
- Acceleration Power Spectral Density
- 2.
- Meister Chart
- 3.
- Comfort Level
- (1)
- Basic Evaluation Method
- (2)
- Auxiliary Evaluation Method
- 4.
- Seat Effective Amplitude Transmissibility (SEAT) Values
2.2.2. Suspension System Constraint Analysis
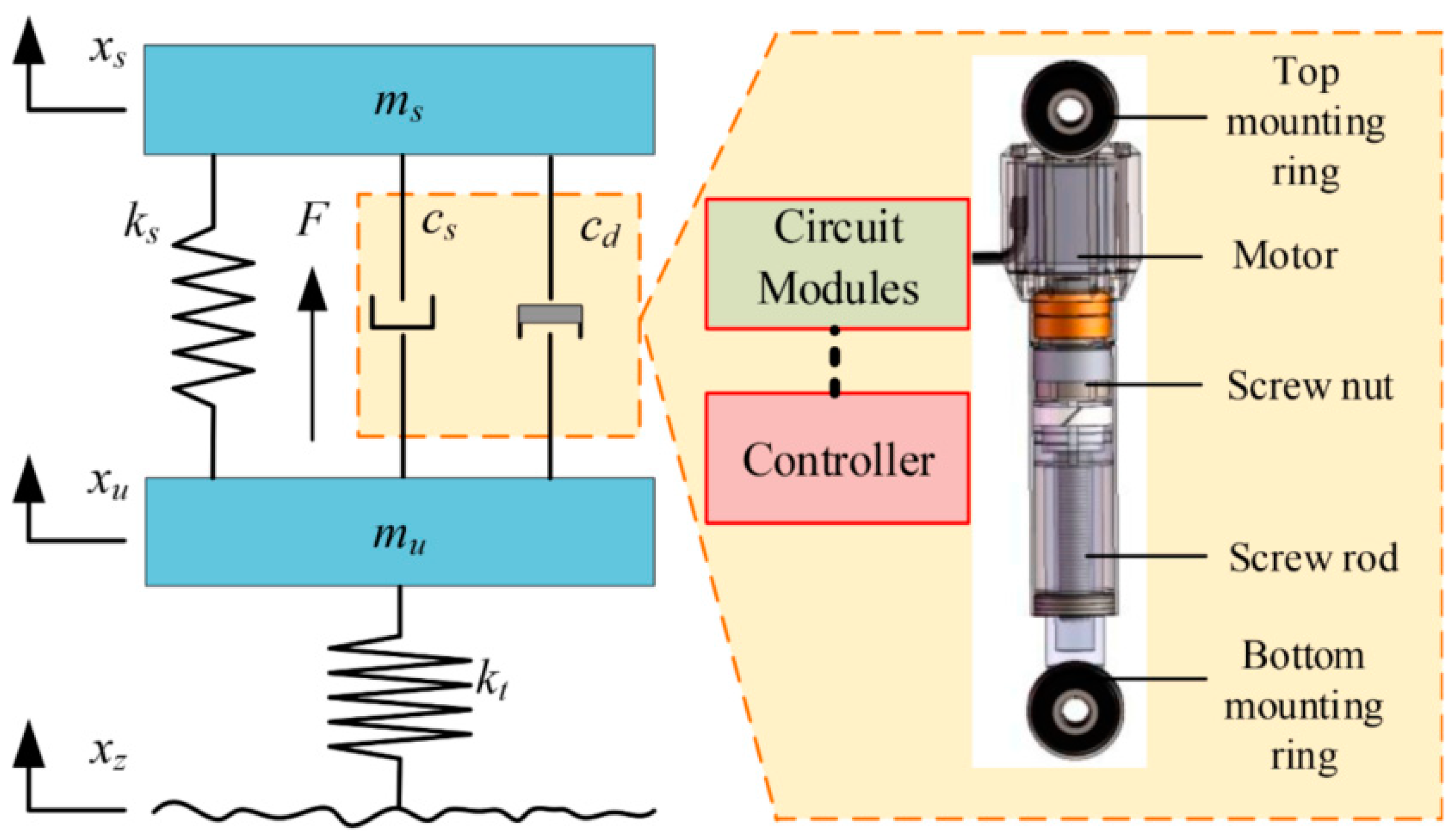
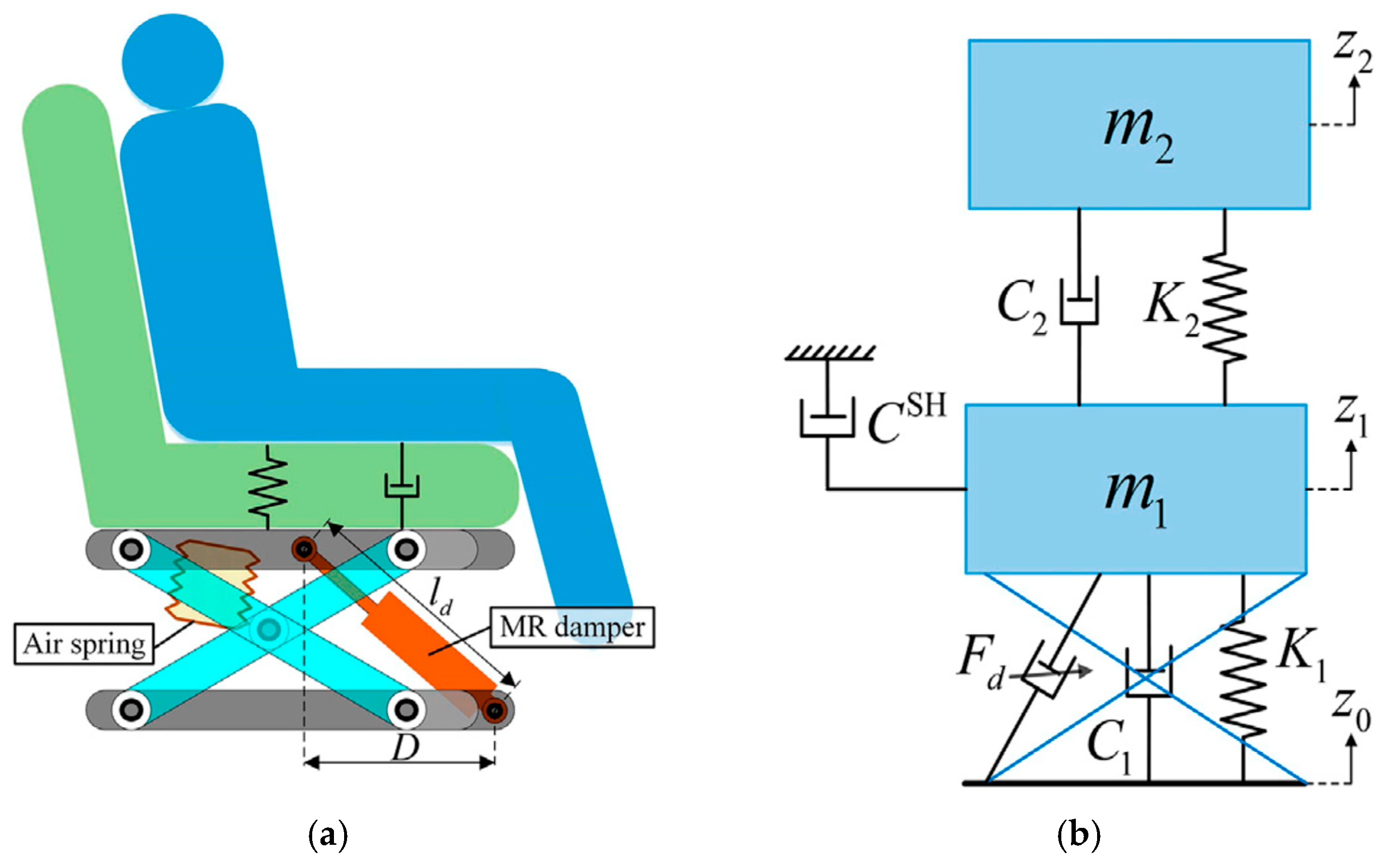
2.3. Seat Semi-Active Suspension System
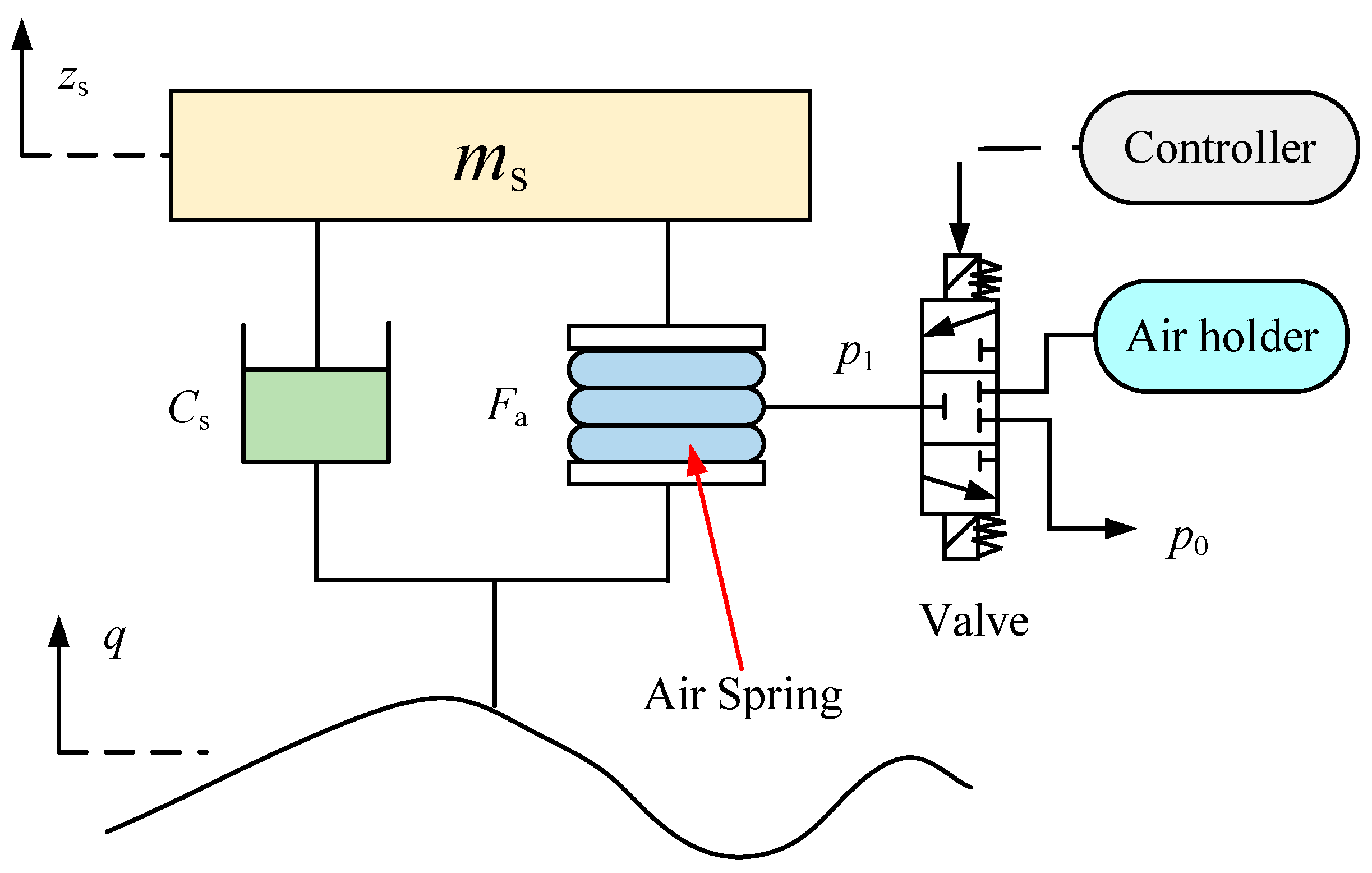
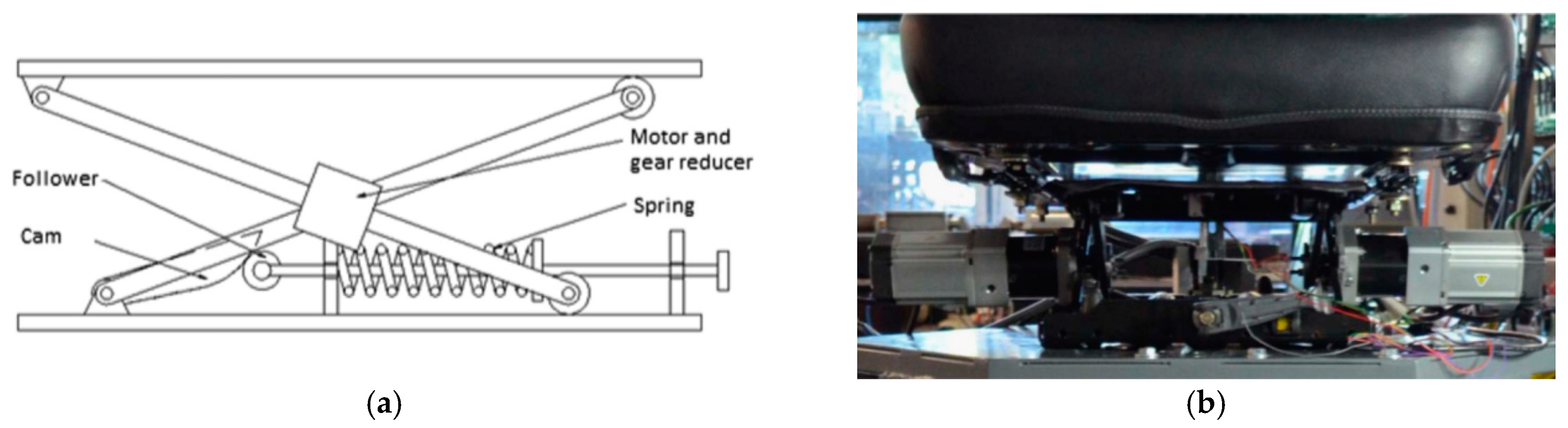
2.3.1. Variable-Stiffness Semi-Active Suspension System
2.3.2. Variable-Damping Semi-Active Suspension System
- Servo/Solenoid Valve Damper
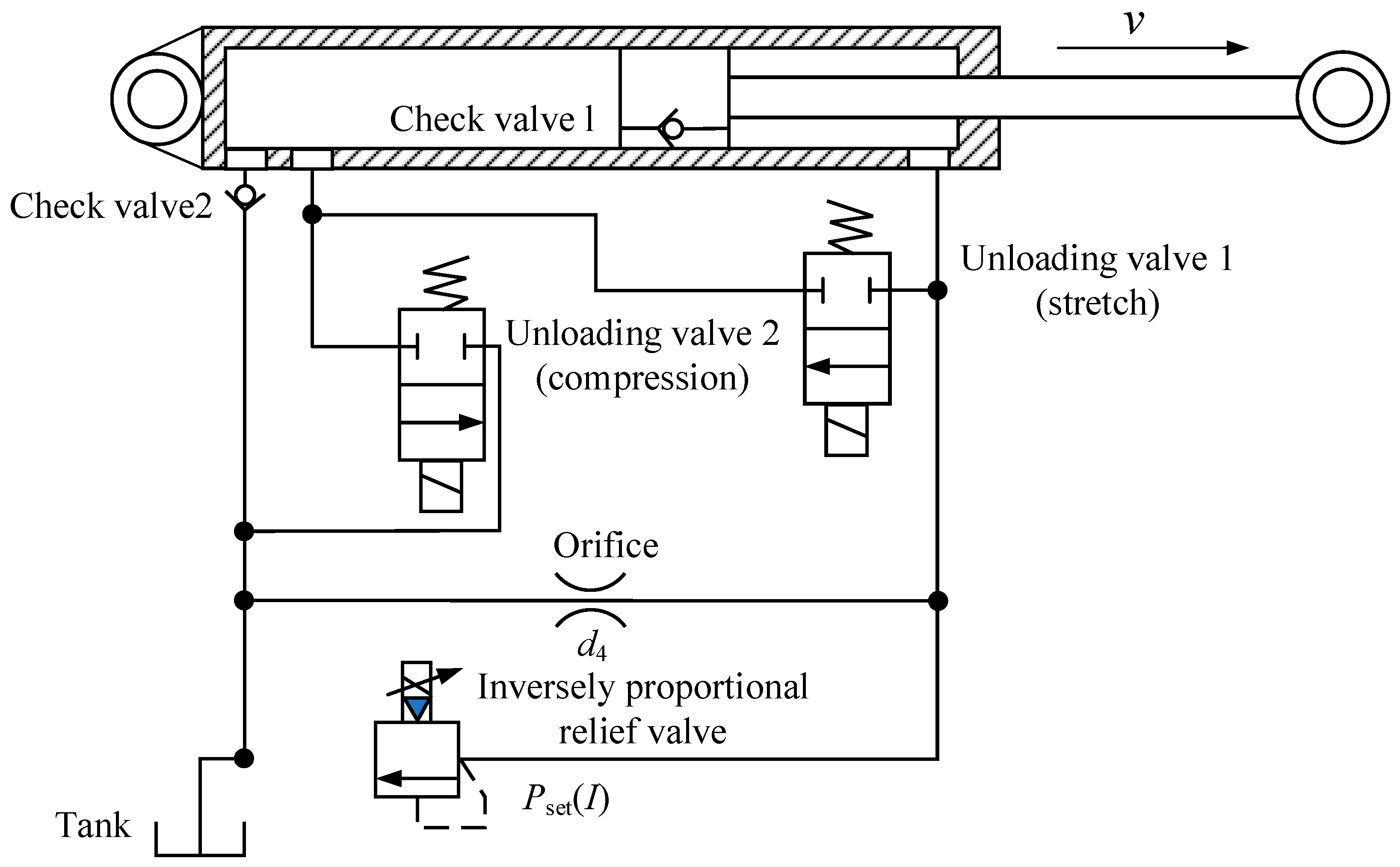
- 2.
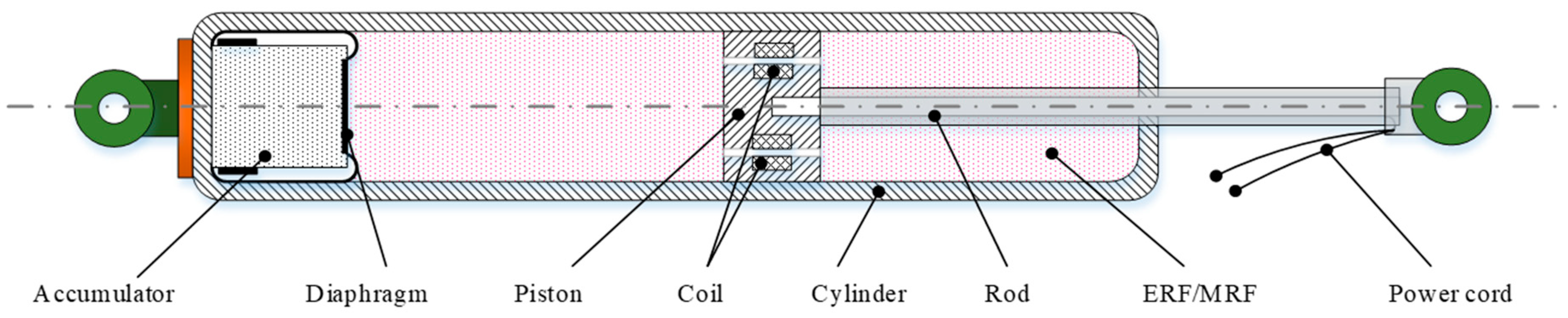
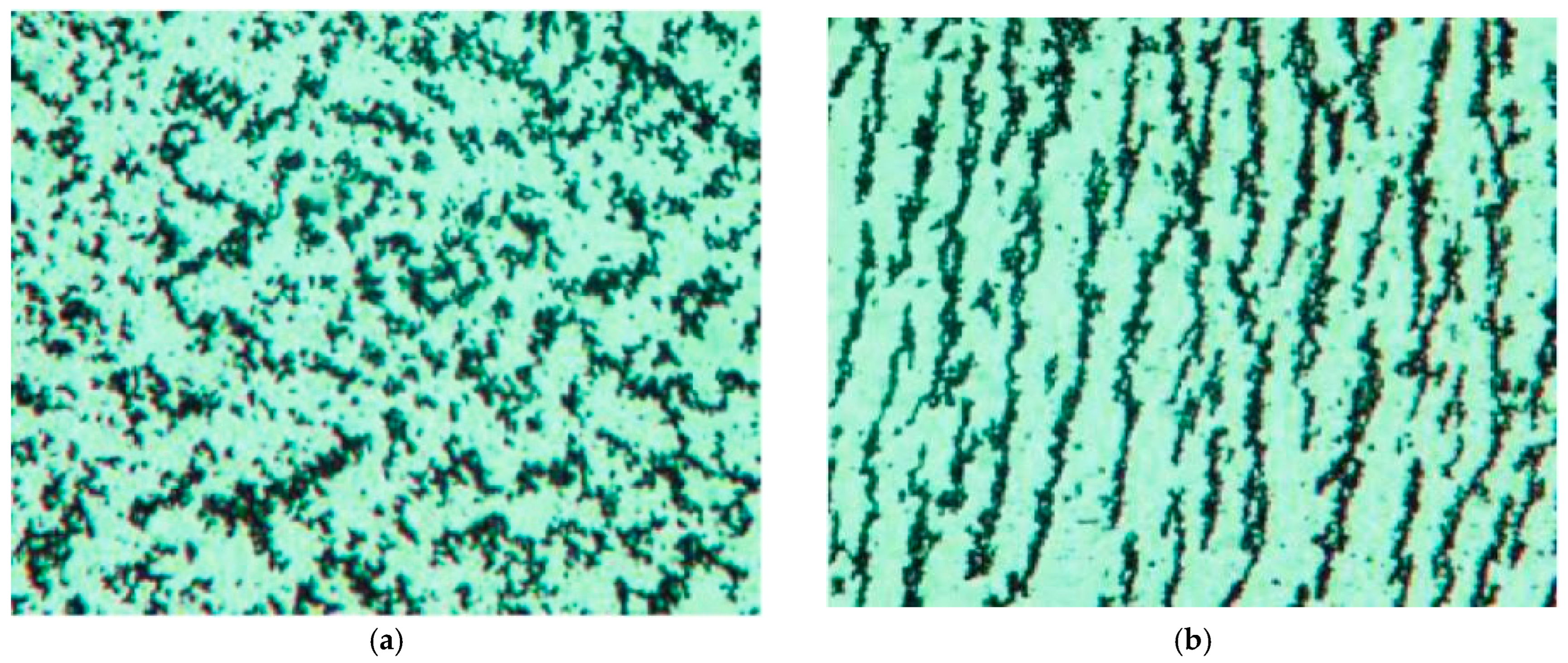
- Electrorheological (ER)/Magnetorheological (MR) Dampers
- 3.
- Electromagnetic Damper
2.4. Active Seat Suspension System
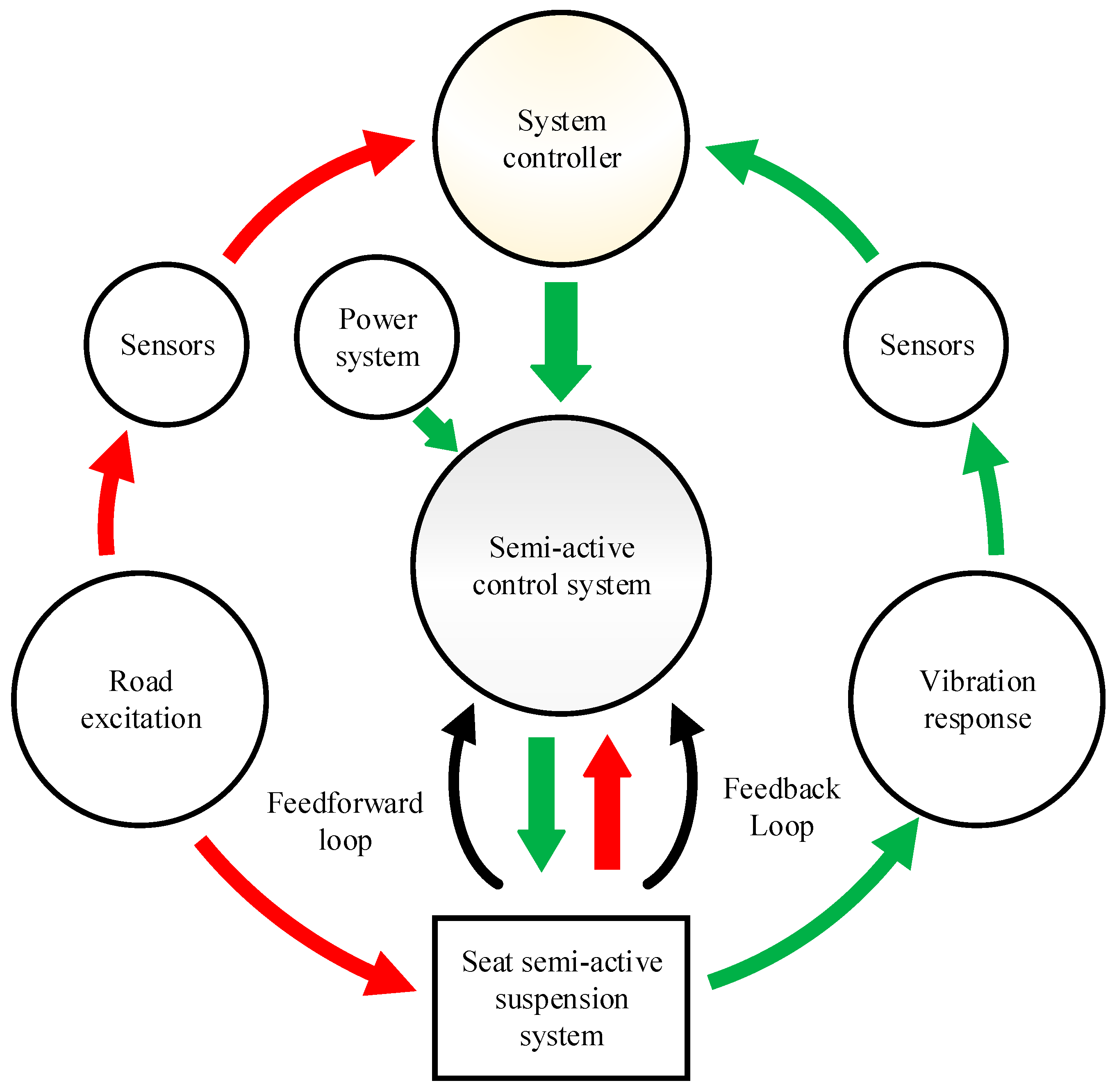
3. Research Status of Seat Semi-Active Suspension System Control Technology
3.1. Single Control Method
3.1.1. Skyhook Control
3.1.2. PID Control
3.1.3. Sliding Mode Control
3.1.4. Fuzzy Control
3.2. Composite Control Method
3.2.1. Fuzzy–PID Control
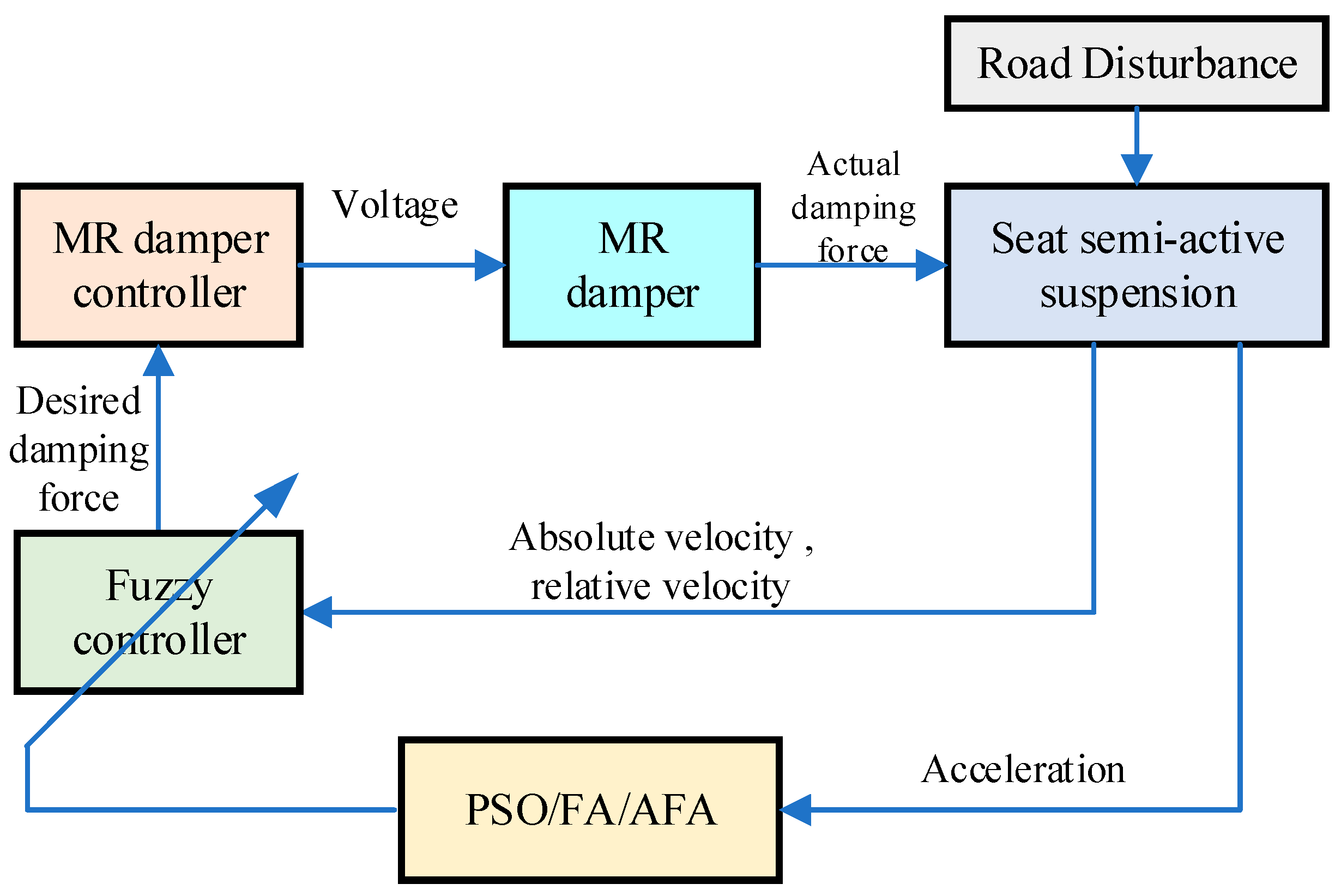
3.2.2. Integrated Intelligent Algorithm Composite Control
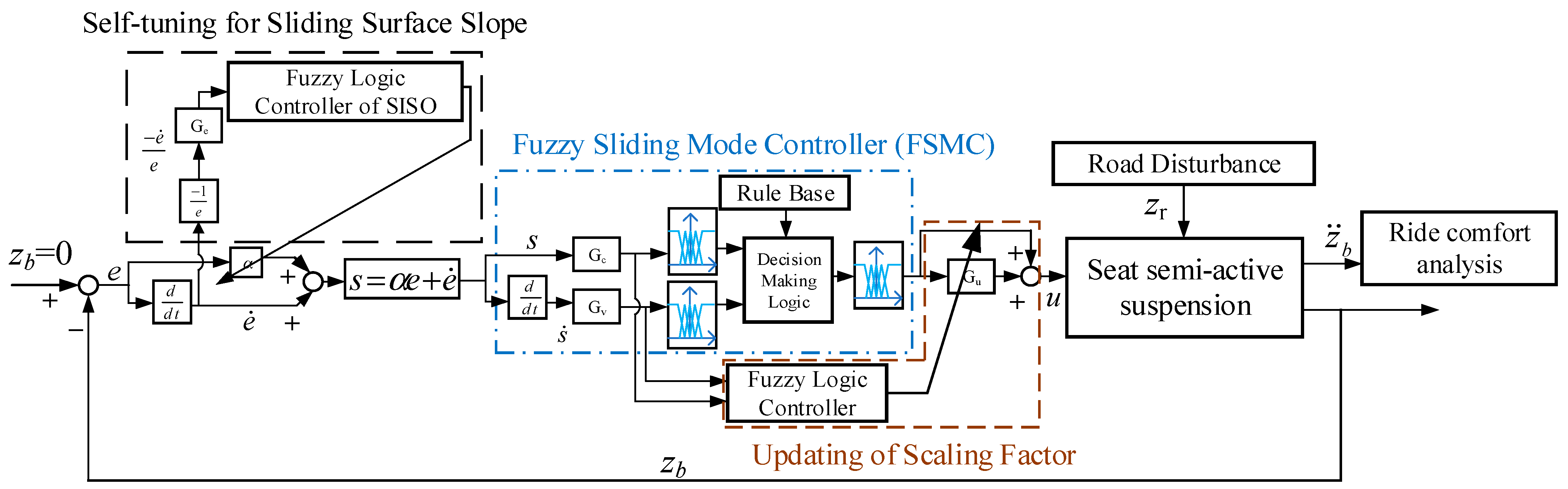
3.2.3. Fuzzy Sliding Mode Control
4. Key Technical Challenges of Agricultural Machinery Seat Semi-Active Suspension System
4.1. Spatial Layout and Dynamic Performance Optimization Design of Seat Suspension
4.1.1. Flexible Design of Overall Layout
- Coordination between spatial structure and ergonomics: optimize the structural design of the suspension system based on ergonomics, ensuring that the seat layout fits the driver’s height, visibility, and operating habits, reducing fatigue during long hours of operation.
- Matching of seat and human body’s center of mass: properly position the seat to ensure a dynamic balance between the human body’s center of mass and the seat suspension system, improving overall vehicle stability and reducing vibration transmission caused by imbalances.
- Pairing of elastic and damping components: scientifically configure the elastic and damping components of the suspension system to optimize suspension performance, thereby minimizing the transmission of mechanical vibrations and ensuring driver comfort in complex working environments.
4.1.2. Dynamic Performance Optimization Design
- Nonlinear behavior of dynamic stiffness and damping
- 2.
- Frequency adaptability and resonance avoidance
- 3.
- Working condition adaptability and real-time adjustment capability
- Nonlinear dynamic modeling
- 2.
- Multi-objective optimization
- 3.
- Adaptive control strategy
- 4.
- Simulation and experimental verification
4.2. Complexity and Uncertainty of Working Environment
- Load Fluctuations and Uneven Load Distribution
- 2.
- Climate and Environmental Conditions
- 3.
- Working Speed and Timing
- 4.
- Working Obstacles and Sudden Events
4.3. Real-Time Performance and Robustness of Control Algorithms
- Real-Time Issues in Control Algorithms
- 2.
- Robustness Issues in Control Algorithms
4.4. Specific Issues and Improvement Measures
- External Disturbances and System Errors
- 2.
- Environmental and Load Variations
- 3.
- Uncertainties in Suspension Components
- 4.
- Nonlinearity and Complexity
5. Conclusions and Outlook
5.1. Conclusions
5.2. Outlook
- In-Depth Application of Composite Control Methods
- 2.
- Integration of Variable Stiffness and Damping Elements
- 3.
- Synergistic Optimization of Composite Control and Intelligent Damping Elements
- 4.
- Development of Intelligent and Personalized Vibration Damping
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Coyte, J.L.; Stirling, D.; Du, H.; Ros, M. Seated whole-body vibration analysis, technologies, and modeling: A survey. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 725–739. [Google Scholar] [CrossRef]
- Hilal, Y.Y.; Al-rajabo, S.A.J.; Dahham, G.A. The effects of vibrating wings subsoiler plow on driver’s seat of agricultural tractors and mechanization performance. Soil Tillage Res. 2021, 205, 104806. [Google Scholar] [CrossRef]
- Guruguntla, V.; Lal, M. Multi-body modelling and ride comfort analysis of a seated occupant under whole-body vibration. J. Vib. Control 2022, 29, 3078–3095. [Google Scholar] [CrossRef]
- Bhuiyan, M.H.U.; Fard, M.; Robinson, S.R. Effects of whole-body vibration on driver drowsiness: A review. J. Saf. Res. 2022, 81, 175–189. [Google Scholar] [CrossRef]
- Sun, L.; Shang, T.; Chen, H.; Wang, Z.; Wang, C.; Luo, F. Development of a model for the optimization of the main factors influencing a 162kW wheeled tractor driver’s whole body vibration. J. Low Freq. Noise Vib. Act. Control 2023, 43, 156–169. [Google Scholar] [CrossRef]
- Pan-Zagorski, W.; Johnson, P.W.; Pereny, M.; Kim, J.H. Automotive seat comfort and vibration performance evaluation in dynamic settings. Appl. Sci. 2022, 12, 1043. [Google Scholar] [CrossRef]
- Kim, J.H.; Zigman, M.; Aulck, L.S.; Ibbotson, J.A.; Dennerlein, J.T.; Johnson, P.W. Whole body vibration exposures and health status among professional truck drivers: A cross-sectional analysis. Ann. Occup. Hyg. 2016, 60, 936–948. [Google Scholar] [CrossRef]
- Burstrom, L.; Nilsson, T.; Wahlstrom, J. Whole-body vibration and the risk of low back pain and sciatica: A systematic review and meta-analysis. Int. Arch. Occup. Environ. Health 2015, 88, 403–418. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Nguyen, V.; Wang, C.; Xu, S.; Li, H. Review research on isolation systems of the cab and driver’s seat in soil compactors. SAE Int. J. Veh. Dyn. Stab. NVH 2023, 7, 22. [Google Scholar] [CrossRef]
- Zhao, S.; Qu, G.; Liu, M.; Chen, X.; Gao, Z.; Xu, L. Research on tractor active seat suspension based on model predictive control. IEEE Access 2023, 11, 117078–117093. [Google Scholar] [CrossRef]
- Yang, X.; Bi, S.; Liu, Y.; Yang, Y.; Liu, C.; Qin, J. Improvement of commercial vehicle seat suspension employing a mechatronic inerter element. World Electr. Veh. J. 2024, 15, 194. [Google Scholar] [CrossRef]
- Li, H.; Zheng, X.; Dai, W.; Qiu, Y. Prediction of ride comfort of high-speed trains based on train seat–human body coupled dynamics model. Appl. Sci. 2022, 12, 12900. [Google Scholar] [CrossRef]
- Bhatia, A.; Kalsi, S.; Sehgal, A.K.; Singh, I. Comparative study of different seat cushion materials to improve the comfort of tractor seat. J. Inst. Eng. India Ser. A 2022, 103, 387–396. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, W.; Chen, X.; Xu, L.; Cao, Y. Vibration performance analysis and multi-objective optimization design of a tractor scissor seat suspension system. Agriculture 2022, 13, 48. [Google Scholar] [CrossRef]
- Barrie, A.; Govers, M.; Habegger, J.; Hassan, M.; Oliver, M. Smart whole-body vibration attenuation, cushion for heavy equipment seating: Model and simulation. J. Low Freq. Noise Vib. Act. Control 2024, 44, 230–250. [Google Scholar] [CrossRef]
- Sebesta, K.; Zacek, J.; Salva, M. Experimental Device for Testing of Semi-Active Magnetorheological Damper. MM Sci. J. 2023, 2023, 6407–6412. [Google Scholar] [CrossRef]
- Heidarian, A.; Wang, X. Review on seat suspension system technology development. Appl. Sci. 2019, 9, 2834. [Google Scholar] [CrossRef]
- Zhu, H.; Rui, X.; Yang, F.; Zhu, W.; Gu, J. Semi-active scissors-seat suspension with magneto-rheological damper. Front. Mater. 2020, 7, 591283. [Google Scholar] [CrossRef]
- Qiu, C.; Liu, X.; Shen, Y. Improvement of the Vehicle Seat Suspension System Incorporating the Mechatronic Inerter Element. World Electr. Veh. J. 2023, 14, 29. [Google Scholar] [CrossRef]
- Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Intelligent control based on a neural network for aircraft landing gear with a magnetorheological damper in different landing scenarios. Appl. Sci. 2020, 10, 5962. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, S.; Li, Z.; Hu, Z.; Li, Z. Semi-Active Suspension Control Strategy Based on Negative Stiffness Characteristics. Mathematics 2024, 12, 3346. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, G.; Yang, C.; Yu, L.; Zhu, W. NSGA-II-TLQR control of semi-active suspension system with magnetorheological damper considering response time delay. J. Vib. Eng. Technol. 2024, 12, 825–838. [Google Scholar] [CrossRef]
- Abbas, S.B.; Youn, I. Optimal Control of a Semi-Active Suspension System Collaborated by an Active Aerodynamic Surface Based on a Quarter-Car Model. Electronics 2024, 13, 3884. [Google Scholar] [CrossRef]
- Chunyu, W.; Litong, H. Study on modeling and control for a novel active suspension. Int. J. Automot. Technol. 2024, 25, 533–540. [Google Scholar] [CrossRef]
- Li, Y.; Ma, S.; Li, K.; Tong, S. Adaptive fuzzy output feedback fault-tolerant control for active suspension systems. IEEE Trans. Intell. Veh. 2024, 9, 2469–2478. [Google Scholar] [CrossRef]
- Liu, W.; Gong, M.; Chen, H.; Zhao, D. Energy-saving tracking control and experiment of nonlinear active suspension for multi-axle vehicles considering road slope. Mech. Syst. Signal Process. 2025, 226, 112328. [Google Scholar] [CrossRef]
- Samaroo, K.; Awan, A.W.; Islam, S. Semi-active suspension design for an in-wheel-motor-driven electric vehicle using a dynamic vibration-absorbing structure and pid-controlled magnetorheological damper. Machines 2025, 13, 47. [Google Scholar] [CrossRef]
- Zhang, K.; As’arry, A.; Zhu, L.; Hairuddin, A.A.; Hassan, M.K.; Md Zain, M.Z. Enhancing ride comfort of semi-active suspension through collaboration control using dung beetle optimizer optimized Fuzzy PID controller. Adv. Mech. Eng. 2025, 17, 1–14. [Google Scholar] [CrossRef]
- Ni, X.; Luo, M.; Cheng, J.; Yan, H.; Shi, K. Dual-stage transmission event-triggered sliding mode control for interval type-2 fuzzy vehicle active suspension systems under improved weighted try-once discard protocol with hybrid network attacks. Inf. Sci. 2025, 698, 121770. [Google Scholar] [CrossRef]
- Deng, M.; Sun, D.; Zhan, L.; Xu, X.; Zou, J. Advancing active suspension control with TD3-PSC: Integrating physical safety constraints into deep reinforcement learning. IEEE Access 2024, 12, 115628–115641. [Google Scholar] [CrossRef]
- Wang, C.; Cui, X.; Zhao, S.; Zhou, X.; Song, Y.; Wang, Y.; Guo, K. A deep reinforcement learning-based active suspension control algorithm considering deterministic experience tracing for autonomous vehicle. Appl. Soft Comput. 2024, 153, 111259. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Sun, C.; Pan, Q.; He, T. Improvement of vibration isolation performance of multi-mode control seat suspension system through road recognition using wavelet-LSTM approach. J. Mech. Sci. Technol. 2024, 38, 121–136. [Google Scholar] [CrossRef]
- Turan, M.K.; Erzan Topcu, E.; Karpat, F. Modelling and investigation of a driver seat suspension with negative stiffness structure. Int. J. Simul. Model. 2024, 23, 275–286. [Google Scholar] [CrossRef]
- Choi, Y.T.; Wereley, N.M.; Hiemenz, G.J. Three-Axis Vibration Isolation of a Full-Scale Magnetorheological Seat Suspension. Micromachines 2024, 15, 1417. [Google Scholar] [CrossRef]
- Cao, J.; Liu, P.; Ning, D.; Sun, S.; Liu, G. Vibration control of the seat suspension with a magnetorheological damper-based controllable inerter. J. Vib. Control 2024, 31, 92–103. [Google Scholar] [CrossRef]
- Gösele, M.; Sandner, P. Analysis of blockchain technology in the mobility sector. Forsch. Im Ingenieurwesen 2019, 83, 809–816. [Google Scholar] [CrossRef]
- Papaioannou, G.; Voutsinas, A.; Koulocheris, D. Optimal design of passenger vehicle seat with the use of negative stiffness elements. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 234, 610–629. [Google Scholar] [CrossRef]
- Li, S.; Feng, G.; Zhao, Q.; Lu, Z. Design and research of semiactive quasi-zero stiffness vibration isolation system for vehicles. Shock Vib. 2021, 2021, 5529509. [Google Scholar] [CrossRef]
- Shi, X.; Zhao, F.; Yan, Z.; Zhu, S.; Li, J.Y. High-performance vibration isolation technique using passive negative stiffness and semiactive damping. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1034–1055. [Google Scholar] [CrossRef]
- Li, X.; Li, F.; Shang, D. Dynamic Characteristics Analysis of ISD Suspension System under Different Working Conditions. Mathematics 2021, 9, 1345. [Google Scholar] [CrossRef]
- Yang, X.; Yan, L.; Shen, Y.; Liu, Y.; Liu, C. Optimal design and dynamic control of an ISD vehicle suspension based on an ADD positive real network. IEEE Access 2020, 8, 94294–94306. [Google Scholar] [CrossRef]
- Yang, X.; Yan, L.; Shen, Y.; Li, H.; Liu, Y. Dynamic performance analysis and parameters perturbation study of inerter–spring–damper suspension for heavy vehicle. J. Low Freq. Noise Vib. Act. Control 2020, 40, 1335–1350. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, J.; Du, F.; Yang, X.; Liu, Y.; Chen, L.; Folęga, P. Dynamic performance analysis of semiactive vehicle ISD suspension based on the power-driven-damper strategy. Shock Vib. 2024, 2024, 3495503. [Google Scholar] [CrossRef]
- Li, F.; Ma, P.; Zhao, Y.; Li, X.; Wen, B. Optimization design and vibration reduction performance analysis of vehicle suspension structure. J. Vib. Control 2025. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, X. A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems. Appl. Sci. 2019, 9, 3326. [Google Scholar] [CrossRef]
- Maradey Lázaro, J.G.; Esteban Villegas, H.S.; Aldana Afanador, A.F.; Cáceres Mojica, K.S. Optimal control of an active suspension system applying distributed parameter simulation test. Int. J. Automot. Mech. Eng. 2023, 20, 10359–10370. [Google Scholar] [CrossRef]
- Jiao, R.; Nguyen, V.; Le, V. Ride comfort performance of hydro pneumatic isolation for soil compactors cab in low frequency region. J. Vibroeng. 2020, 22, 1174–1186. [Google Scholar] [CrossRef]
- Nur Hazar Yavuz, A.; Yavuz, A. Investigation of vehicle-induced whole-body vibration with experimental rat models. J. Res. Pharm. 2023, 27, 2310–2329. [Google Scholar] [CrossRef]
- Amari, M.; Perrin, N. Whole-body vibration exposure in unfavourable seated postures: Apparent mass and seat-to-head transmissibility measurements in the fore-and-aft, lateral, and vertical directions. Ergonomics 2023, 66, 136–151. [Google Scholar] [CrossRef]
- Singh, A.; Samuel, S.; Dhabi, Y.K.; Singh, H. Whole-body vibration: Characterization of seat-to-head transmissibility for agricultural tractor drivers during loader operation. Smart Agric. Technol. 2023, 4, 100164. [Google Scholar] [CrossRef]
- Dumitriu, M. Effect of the asymmetry of suspension damping on the ride comfort of railway vehicles. Aust. J. Mech. Eng. 2020, 20, 1379–1391. [Google Scholar] [CrossRef]
- Kat, C.J.; Jooste, J.S.; Grant, C.C.; Becker, P.J.; Els, P.S. Cardiovascular response to whole-body vibration on an automobile seat. Ergonomics 2021, 64, 1405–1415. [Google Scholar] [CrossRef]
- Sharma, R.C.; Sharma, S.; Sharma, N.; Sharma, S.K. Linear and nonlinear analysis of ride and stability of a three-wheeled vehicle subjected to random and bump inputs using bond graph and simulink methodology. SAE Int. J. Commer. Veh. 2021, 15, 65–79. [Google Scholar] [CrossRef]
- Choi, C.; Shing, P.; Wang, S.; Huszti, E. Measuring vibration and shock in power wheelchairs for clinical application. Assist. Technol. 2025, 37, S36–S43. [Google Scholar] [CrossRef]
- Hsiao, C.-Y.; Wang, Y.-H. Evaluation of ride comfort for active suspension system based on self-tuning fuzzy sliding mode control. Int. J. Control Autom. Syst. 2022, 20, 1131–1141. [Google Scholar] [CrossRef]
- Delcor, L.; Parizet, E.; Ganivet-Ouzeneau, J.; Caillet, J. Assessment of helicopter passengers’ vibration discomfort: Proposal for improvement of the ISO 2631-1 standard. Ergonomics 2022, 65, 296–304. [Google Scholar] [CrossRef]
- Singh, A.; Samuel, S.; Singh, H.; Kumar, Y.; Prakash, C. Evaluation and analysis of whole-body vibration exposure during soil tillage operation. Safety 2021, 7, 61. [Google Scholar] [CrossRef]
- Desai, R.; Guha, A.; Seshu, P. Modelling and simulation of an integrated human-vehicle system with non-linear cushion contact force. Simul. Model. Pract. Theory 2021, 106, 102206. [Google Scholar] [CrossRef]
- Koulocheris, D.; Vossou, C. Sensitivity analysis of a driver’s lumped parameter model in the evaluation of ride comfort. Vehicles 2023, 5, 1030–1045. [Google Scholar] [CrossRef]
- Youqun, Z.; Fen, L. Vehicle System Dynamics; Science Press: Beijing, China, 2021. [Google Scholar]
- Wei, G.; Sun, S.L. Influence of rotary tiller on vibration of tractor semi-active seat. J. Mach. Manuf. Reliab. 2022, 51, 397–405. [Google Scholar] [CrossRef]
- Leileil, Z.; Hao, Z.; Yuewei, Y.; Ran, Z.; Fan, D.; Xiyu, S.; Jiahe, D. Ideal twin dynamic deflection tracking control strategy for air suspension systems. J. Xi’an Jiaotong Univ. 2025, 59, 159–171. [Google Scholar]
- Zheng, E.; Fan, Y.; Zhu, R.; Zhu, Y.; Xian, J. Prediction of the vibration characteristics for wheeled tractor with suspended driver seat including air spring and MR damper. J. Mech. Sci. Technol. 2016, 30, 4143–4156. [Google Scholar] [CrossRef]
- Zheng, E.; Cui, S.; Yang, Y.; Xue, J.; Zhu, Y.; Lin, X.; Sabbioni, E. Simulation of the vibration characteristics for agricultural wheeled tractor with implement and front axle hydropneumatic suspension. Shock Vib. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Zheng, E.; Zhong, X.; Zhu, R.; Xue, J.; Cui, S.; Gao, H.; Lin, X. Investigation into the vibration characteristics of agricultural wheeled tractor-implement system with hydro-pneumatic suspension on the front axle. Biosyst. Eng. 2019, 186, 14–33. [Google Scholar] [CrossRef]
- Jianmin, S.; Xiang, L.; Guohao, Z.; Dechen, Y. Fuzzy sliding mode control of seat-driver and hydro pneumatic suspension system based on fast power reaching law. Mod. Manuf. Eng. 2022, 4, 59–67. [Google Scholar] [CrossRef]
- Sihong, Z.; Jiasheng, W.; Minna, W. Experimental study on vibration characteristics of shear seat with air suspension with additional air chamber. J. Vib. Shock 2010, 28, 104–106. [Google Scholar] [CrossRef]
- Junjie, C.; Konghui, G.; Zhihong, Y.; Qiongyao, W.; Lei, Z. Research on unified model of vertical stiffness for convoluted air spring. J. Mech. Eng. 2022, 58, 180–187. [Google Scholar] [CrossRef]
- Soliman, A.M.A.; Kaldas, M.M.S. Semi-active suspension systems from research to mass-market—Review. J. Low Freq. Noise Vib. Act. Control 2019, 40, 1005–1023. [Google Scholar] [CrossRef]
- Wang, W.L.; Xu, G.X. Fluid formulae for damping changeability conceptual design of railway semi-active hydraulic dampers. Int. J. Non-Linear Mech. 2009, 44, 809–819. [Google Scholar] [CrossRef]
- Zoccolini, L.; Bruschi, E.; Cattaneo, S.; Quaglini, V. Current Trends in Fluid Viscous Dampers with Semi-Active and Adaptive Behavior. Appl. Sci. 2023, 13, 10358. [Google Scholar] [CrossRef]
- Yang, L.; Wang, R.; Ding, R.; Liu, W.; Zhu, Z. Investigation on the dynamic performance of a new semi-active hydro-pneumatic inerter-based suspension system with MPC control strategy. Mech. Syst. Signal Process. 2021, 154, 107569. [Google Scholar] [CrossRef]
- Graczykowski, C.; Faraj, R. Identification-Based predictive control of Semi-Active Shock-Absorbers for adaptive dynamic excitation mitigation. Meccanica 2020, 55, 2571–2597. [Google Scholar] [CrossRef]
- Weber, F.; Spensberger, S.; Obholzer, F.; Distl, J.; Braun, C. Semi-active cable damping to compensate for damping losses due to reduced cable motion close to cable anchor. Appl. Sci. 2022, 12, 1909. [Google Scholar] [CrossRef]
- Faraj, R.; Mikułowski, G.; Wiszowaty, R. Study on the state-dependent path-tracking for smart pneumatic shock-absorber. Smart Mater. Struct. 2020, 29, 115008. [Google Scholar] [CrossRef]
- Lin, X.; Chen, S.; Huang, G. A shuffled frog-leaping algorithm based mixed-sensitivity H∞ control of a seismically excited structural building using MR dampers. J. Vib. Control 2017, 24, 2832–2852. [Google Scholar] [CrossRef]
- Mester, S.; Szalai, I. Temperature and electric field dependence of the viscosity of electrorheological (ER) fluids: Warming up of an electrorheological clutch. Hung. J. Ind. Chem. 2020, 48, 59–64. [Google Scholar] [CrossRef]
- Kumar, R.; Roy, A.K.; Kumar, K. Comparative study on controllable electro-magneto rheological fluids—A brief review. J. Mol. Eng. Mater. 2023, 11, 2330002. [Google Scholar] [CrossRef]
- Chauhan, V.; Kumar, A.; Sham, R. Magnetorheological fluids: A comprehensive review. Manuf. Rev. 2024, 11, 6. [Google Scholar] [CrossRef]
- Ullah, Z.; Sermsrisuwan, T.; Pornpipatsakul, K.; Chaichaowarat, R.; Wannasuphoprasit, W. High-Transparency Linear Actuator Using an Electromagnetic Brake for Damping Modulation in Physical Human–Robot Interaction. J. Sens. Actuator Netw. 2024, 13, 65. [Google Scholar] [CrossRef]
- Chaichaowarat, R.; Nishimura, S.; Krebs, H.I. Macro-mini linear actuator using electrorheological-fluid brake for impedance modulation in physical human–robot interaction. IEEE Robot. Autom. Lett. 2022, 7, 2945–2952. [Google Scholar] [CrossRef]
- Padma, Y.; Nuthalapati, S.; Pantangi, U.S. Synthesis and rheological characterization of nano—Magnetorheological fluid using inverse spinel ferrite (NiFe2O4). Int. J. Appl. Ceram. Tec. 2022, 19, 1870–1878. [Google Scholar] [CrossRef]
- Li, S.; Qi, S.; Liu, J.; Fu, J.; Li, Y.; Bai, L.; Yu, M. Cooperativity of nanoscale magnetic zeolitic imidazolate framework in magnetorheological fluid. J. Ind. Eng. Chem. 2024, 132, 238–246. [Google Scholar] [CrossRef]
- Han, W.; Wang, S.; Rui, X.; Dong, Y.; Choi, H. Core/shell magnetite/copolymer composite nanoparticles enabling highly stable magnetorheological response. Int. J. Mech. Syst. Dyn. 2022, 2, 155–164. [Google Scholar] [CrossRef]
- Ji, D.; Luo, Y.; Ren, H.; Wei, D.; Shao, J. Numerical simulation and experimental analysis of microstructure of magnetorheological fluid. J. Nanomater. 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Chen, X.; Xu, L.; Zhang, S.; Zhao, S.; Liu, K. Parameter identification of the Bouc-Wen model for the magnetorheological damper using fireworks algorithm. J. Mech. Sci. Technol. 2022, 36, 2213–2224. [Google Scholar] [CrossRef]
- Chen, X.; Wei, W.; Xu, L.; Zhang, S.; Zhao, S. Parameter identification of Bouc-Wen model for MR damper by parameter sensitivity analysis and modified PSO algorithm. Int. J. Appl. Electrom. 2022, 69, 513–531. [Google Scholar] [CrossRef]
- Chen, X.; Song, H.; Zhao, S.; Xu, L. Ride comfort investigation of semi-active seat suspension integrated with quarter car model. Mech. Ind. 2022, 23, 18. [Google Scholar] [CrossRef]
- Jiang, M.; Rui, X.; Yang, F.; Zhu, W.; Zhu, H.; Han, W. Design and dynamic performance research of MR hydro-pneumatic spring based on multi-physics coupling model. Nonlinear Dyn. 2023, 111, 8191–8215. [Google Scholar] [CrossRef]
- Jiang, R.; Rui, X.; Zhu, W.; Yang, F.; Zhang, Y.; Gu, J. Design of multi-channel bypass magnetorheological damper with three working modes. Int. J. Mech. Mater. Des. 2021, 18, 155–167. [Google Scholar] [CrossRef]
- Jiang, M.; Rui, X.; Yang, F.; Zhu, W.; Zhang, Y. Multi-objective optimization design for a magnetorheological damper. J. Intel. Mat. Syst. Str. 2021, 33, 33–45. [Google Scholar] [CrossRef]
- Jiang, M.; Rui, X.; Zhu, W.; Yang, F.; Zhu, H.; Jiang, R. Parameter sensitivity analysis and optimum model of the magnetorheological damper’s Bouc–Wen model. J. Vib. Control 2020, 27, 2291–2302. [Google Scholar] [CrossRef]
- Jiang, R.; Rui, X.; Wang, G.; Yang, F.; Zhu, W.; Wei, M. Design and modeling of an innovative magnetorheological fluid-elastomeric damper with compact structure. J. Intel. Mat. Syst. Str. 2020, 31, 2088–2100. [Google Scholar] [CrossRef]
- Jiang, M.; Rui, X.; Zhu, W.; Yang, F.; Gu, J. Control and experimental study of 6-DOF vibration isolation platform with magnetorheological damper. Mechatronics 2022, 81, 102706. [Google Scholar] [CrossRef]
- Xiaojie, M.; Hailong, Y.; Xiaoting, R. MRD modeling and its application in seat cushioning. Noise Vib. Control 2017, 37, 58–62. Available online: https://kns.cnki.net/kcms2/article/abstract?v=52O9CKbg8L4v6P0NJ6ybhV8j7ugQZz58aKPalkBGc-olCICs5MpTrWeoWEK8IW8Tt7ZW96KcmNIyx9IMftxPHUF5qGxHbwmIFgWjJfML4ZTliYNCFuZdDS7J-BPUhuU4K2RxDRlNgH2hQJIcluq9ebWQo6VjfVXTI2XIy3mYfgPK6D1Yv4LGyWnU9UiY0ggk&uniplatform=NZKPT&language=CHS (accessed on 16 March 2025).
- Zhu, H.; Rui, X.; Yang, F.; Zhu, W.; Wei, M. An efficient parameters identification method of normalized Bouc-Wen model for MR damper. J. Sound Vib. 2019, 448, 146–158. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Nguyen, V.Q. SD-TCSs control deriving from fractional-order sliding mode and fuzzy-compensator. Int. J. Control Autom. Syst. 2022, 20, 1745–1755. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Choi, S.-B.; Kim, J.-H. Smart dampers-based vibration control—Part 1: Measurement data processing. Mech. Syst. Signal Process. 2020, 145, 106958. [Google Scholar] [CrossRef]
- Tuan, N.V.; Quynh, L.V.; Thao, V.T.P.; Duy, L.Q. Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: Results and discussion. Vibroeng. Procedia 2020, 33, 147–152. [Google Scholar] [CrossRef]
- Qin, A.; Zhang, B.; Ning, D.; Tan, B.; Du, H. A self-sensing approach for estimating suspension displacement and velocity in semi-active electromagnetic dampers. Mech. Syst. Signal Process. 2024, 208, 111049. [Google Scholar] [CrossRef]
- Theunissen, J.; Tota, A.; Gruber, P.; Dhaens, M.; Sorniotti, A. Preview-based techniques for vehicle suspension control: A state-of-the-art review. Annu. Rev. Control 2021, 51, 206–235. [Google Scholar] [CrossRef]
- Jamolov, U.; Peccini, F.; Maizza, G. Multiphysics Design of an Automotive Regenerative Eddy Current Damper. Energies 2022, 15, 5044. [Google Scholar] [CrossRef]
- Billon, K.; Zhao, G.; Collette, C.; Chesné, S. Hybrid mass damper: Theoretical and experimental power flow analysis. J. Vib. Acoust. 2022, 144, 041003. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Du, H.; Li, W.; Zhang, N. Vibration control of an energy regenerative seat suspension with variable external resistance. Mech. Syst. Signal Process. 2018, 106, 94–113. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Du, H.; Li, W.; Li, W. Control of a multiple-DOF vehicle seat suspension with roll and vertical vibration. J. Sound Vib. 2018, 435, 170–191. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Wei, L.; Zhang, B.; Du, H.; Li, W. Vibration reduction of seat suspension using observer based terminal sliding mode control with acceleration data fusion. Mechatronics 2017, 44, 71–83. [Google Scholar] [CrossRef]
- Amjadian, M.; Agrawal, A.K.; Silva, C.E.; Dyke, S.J. Experimental testing and validation of the dynamic model of a magneto-solid damper for vibration control. Mech. Syst. Signal Process. 2022, 166, 108479. [Google Scholar] [CrossRef]
- Sun, R.; Wong, W.; Cheng, L. A tunable hybrid damper with Coulomb friction and electromagnetic shunt damping. J. Sound Vib. 2022, 524, 116778. [Google Scholar] [CrossRef]
- Sun, R.; Wong, W.; Cheng, L. Bi-objective optimal design of an electromagnetic shunt damper for energy harvesting and vibration control. Mech. Syst. Signal Process. 2023, 182, 109571. [Google Scholar] [CrossRef]
- Youn, I.; Ahmad, E. Anti-Jerk Optimal Preview Control Strategy to Enhance Performance of Active and Semi-Active Suspension Systems. Electronics 2022, 11, 1657. [Google Scholar] [CrossRef]
- Kojis, P.; Šabanovič, E.; Skrickij, V. Deep neural network based data-driven virtual sensor in vehicle semi-active suspension real-time control. Transport 2022, 37, 37–50. [Google Scholar] [CrossRef]
- Xia, D.; Fu, J.; Li, W.; Han, G.; Du, X.; Luo, L.; Yu, M. Incremental proportion integration differentiation control of all-terrain vehicle magnetorheological suspension system under low-frequency disturbances. Smart Mater. Struct. 2023, 32, 075019. [Google Scholar] [CrossRef]
- Ikeda, K.; Kuroda, J.; Uchino, D.; Ogawa, K.; Endo, A.; Kato, T.; Kato, H.; Narita, T. Vibration characteristics control of resonance point in vehicle: Fundamental considerations of control system without displacement and velocity information. Vibration 2022, 6, 1–10. [Google Scholar] [CrossRef]
- Maciejewski, I.; Pecolt, S.; Błażejewski, A.; Krzyzynski, T.; Glowinski, S. Controller of Pneumatic Muscles Implemented in Active Seat Suspension. Appl. Sci. 2024, 14, 6385. [Google Scholar] [CrossRef]
- Mahto, P.R.; Mahato, A.C.; Sharma, M.; Mahata, P.; Tripathi, J.P. Various vibration harvesting techniques for rotating system: An overview. J. Vib. Eng. Technol. 2025, 13, 1–21. [Google Scholar] [CrossRef]
- Gan, Z.; Hillis, A.J.; Darling, J. Adaptive control of an active seat for occupant vibration reduction. J. Sound Vib. 2015, 349, 39–55. [Google Scholar] [CrossRef]
- Maciejewski, I.; Meyer, L.; Krzyzynski, T. The vibration damping effectiveness of an active seat suspension system and its robustness to varying mass loading. J. Sound Vib. 2010, 329, 3898–3914. [Google Scholar] [CrossRef]
- Kawana, M.; Shimogo, T. Active suspension of truck seat. Shock Vib. 1998, 5, 35–41. [Google Scholar] [CrossRef]
- Danh, L.T.; Ahn, K.K. Active pneumatic vibration isolation system using negative stiffness structures for a vehicle seat. J. Sound Vib. 2014, 333, 1245–1268. [Google Scholar] [CrossRef]
- Périsse, J.; Jezequel, L. An original feedback control with a reversible electromechanical actuator used as an active isolation system for a seat suspension. Part I: Theoretical study. Veh. Syst. Dyn. 2000, 34, 305–331. [Google Scholar] [CrossRef]
- Périsse, J.; Jezequel, L. An original feedback control with a reversible electromechanical actuator used as an active isolation system for a seat suspension. Part II: Experimental study. Veh. Syst. Dyn. 2000, 34, 381–399. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Zhang, J.; Du, H.; Li, W.; Wang, X. An active seat suspension design for vibration control of heavy-duty vehicles. J. Low Freq. Noise Vib. Act. Control 2016, 35, 264–278. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Li, H.; Du, H.; Li, W. Active control of an innovative seat suspension system with acceleration measurement based friction estimation. J. Sound Vib. 2016, 384, 28–44. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Zhang, F.; Du, H.; Li, W.; Zhang, B. Disturbance observer based Takagi-Sugeno fuzzy control for an active seat suspension. Mech. Syst. Signal Process. 2017, 93, 515–530. [Google Scholar] [CrossRef]
- Zając, K.; Kowal, J.; Konieczny, J. Skyhook Control Law Extension for Suspension with Nonlinear Spring Characteristics. Energies 2022, 15, 754. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Xiao, H.; Zhao, D.; Gao, S.; Spurgeon, S.K. Sliding mode predictive control: A survey. Annu. Rev. Control 2022, 54, 148–166. [Google Scholar] [CrossRef]
- Cai, J.; Dou, X.; Cheok, A.D.; Ding, W.; Yan, Y.; Zhang, X. Model predictive control strategies in switched reluctance motor drives—An overview. IEEE Trans. Power Electron. 2025, 40, 1669–1685. [Google Scholar] [CrossRef]
- Petrlik, M.; Baca, T.; Hert, D.; Vrba, M.; Krajnik, T.; Saska, M. A robust UAV system for operations in a constrained environment. IEEE Robot. Autom. Lett. 2020, 5, 2169–2176. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Ren, B. Energy saving quadrotor control for field inspections. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1768–1777. [Google Scholar] [CrossRef]
- Ayas, M.S.; Sahin, E. FOPID controller with fractional filter for an automatic voltage regulator. Comput. Electr. Eng. 2021, 90, 106895. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Q.; Ren, B. Wind turbine crack inspection using a quadrotor with image motion blur avoided. IEEE Robot. Autom. Lett. 2023, 8, 1069–1076. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, Z.; Gao, Z.; Zhang, W. Reinforcement learning-based fault-tolerant control for quadrotor UAVs under actuator fault. IEEE Trans. Ind. Inform. 2024, 20, 13926–13935. [Google Scholar] [CrossRef]
- Qu, C.; Cheng, L.; Gong, S.; Huang, X. Experience replay enhances excitation condition of neural-network adaptive control learning. J. Guid. Control Dyn. 2025, 48, 3. [Google Scholar] [CrossRef]
- Al-Hadithi, B.M.; Gómez, J. Fuzzy Control of Multivariable Nonlinear Systems Using T–S Fuzzy Model and Principal Component Analysis Technique. Processes 2025, 13, 217. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Y.; Li, Y.; Jia, N.; Xu, J. Applications of machine learning in real-time control systems: A review. Meas. Sci. Technol. 2024, 36, 012003. [Google Scholar] [CrossRef]
- Negash, B.A.; You, W.; Lee, J.; Lee, C.; Lee, K. Semi-active control of a nonlinear quarter-car model of hyperloop capsule vehicle with Skyhook and Mixed Skyhook-Acceleration Driven Damper controller. Adv. Mech. Eng. 2021, 13, 168781402199952. [Google Scholar] [CrossRef]
- Anaya-Martinez, M.; Lozoya-Santos, J.-d.-J.; Félix-Herrán, L.C.; Tudon-Martinez, J.-C.; Ramirez-Mendoza, R.-A.; Morales-Menendez, R. Control of Automotive Semi-Active MR Suspensions for In-Wheel Electric Vehicles. Appl. Sci. 2020, 10, 4522. [Google Scholar] [CrossRef]
- Papaioannou, G.; Koulocheris, D.; Velenis, E. Skyhook control strategy for vehicle suspensions based on the distribution of the operational conditions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2776–2790. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Yang, X.; Zhang, X.; Yang, Y. General theory of skyhook control and its application to semi-active suspension control strategy design. IEEE Access 2019, 7, 101552–101560. [Google Scholar] [CrossRef]
- Ruitao, G.; Yang, W.; Zhou, Y.; Hong, J.; Zhixiang, L.; Jian, S. Tractor driving seat suspension system research status and strategies in china: A review. IFAC-Pap. 2018, 51, 576–581. [Google Scholar] [CrossRef]
- Munyaneza, O.; Sohn, J.W. Modeling and control of hybrid MR seat damper and whole body vibration evaluation for bus drivers. J. Low Freq. Noise Vib. Act. Control 2021, 41, 659–675. [Google Scholar] [CrossRef]
- Mao, Q.; Xu, Y.; Chen, J.; Chen, J.; Georgiou, T.T. Maximization of gain/phase margins by PID control. IEEE Trans. Autom. Control 2025, 70, 34–49. [Google Scholar] [CrossRef]
- Ferhath, A.A.; Kasi, K. Dynamic modelling of a semi-active suspension system for a half-car roll model utilizing PID control techniques. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 131. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, X.; Lin, F.; Yang, Y.; Zhang, J. Novel Proportional–Integral–Derivative Control Framework on Continuous-Time Positive Systems Using Linear Programming. Mathematics 2024, 12, 617. [Google Scholar] [CrossRef]
- Russo, R.; Terzo, M. Modelling, parameter identification, and control of a shear mode magnetorheological device. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2011, 225, 549–562. [Google Scholar] [CrossRef]
- Ho, C.; Lang, Z.Q.; Sapiński, B.; Billings, S.A. Vibration isolation using nonlinear damping implemented by a feedback-controlled MR damper. Smart Mater. Struct. 2013, 22, 105010. [Google Scholar] [CrossRef]
- Manzo Hernández, J.P.; Solano Vargas, J.C.; Barrera Fernández, J.M.; Moreno Orduña, D.; Sánchez Saquín, C.H. A novel adaptive PID controller with new seesaw algorithms using alternative derivatives. Syst. Sci. Control. Eng. 2024, 12, 2363625. [Google Scholar] [CrossRef]
- Yuchen, Z.; Kunming, G.; Yanling, L.; Zonghe, G.; Chicheng, M. Setting active PID controller parameters based on orthogonal test method. J. Shandong Univ. Technol. Nat. Sci. Ed. 2022, 35, 63–68. [Google Scholar] [CrossRef]
- Sennan, S. PID based tractor semi-active suspension design and simulation. Agric. Equip. Veh. Eng. 2019, 57, 60–63. [Google Scholar] [CrossRef]
- Kumar, J.; Bhushan, G. Analysis and improvement of driver’s ride comfort by implementing optimized hybrid semi-active vibration damper with fuzzy-pid controller. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 2243–2255. [Google Scholar] [CrossRef]
- Weber, F. Robust force tracking control scheme for MR dampers. Struct. Control Health Monit. 2015, 22, 1373–1395. [Google Scholar] [CrossRef]
- Tharehalli Mata, G.; Mokenapalli, V.; Krishna, H. Performance analysis of MR damper based semi-active suspension system using optimally tuned controllers. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2871–2884. [Google Scholar] [CrossRef]
- Zhenpeng, L.; Fengrong, B.; Wang, X.; Teng, M.; Zhiwei, X. Adaptive fuzzy sliding mode control for semi-active seat suspensions. J. Vib. Shock 2021, 4, 265–271. [Google Scholar] [CrossRef]
- Soosairaj, A.S.; Kandavel, A. Ride comfort analysis of driver seat using super twisting sliding mode controlled magnetorheological suspension system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 3606–3618. [Google Scholar] [CrossRef]
- Park, D.-W.; Choi, S.-B. Moving sliding surfaces for high-order variable structure systems. Int. J. Control 2010, 72, 960–970. [Google Scholar] [CrossRef]
- Shuwei, F.; Bijuan, A.; Wei, Y.; Wenjun, Z. Semi-active sliding mode control of 3-RPS seat suspensions used in construction vehicles. Noise Vib. Control 2024, 44, 158–164. [Google Scholar]
- Zhang, H.; Wang, E.; Zhang, N.; Min, F.; Subash, R.; Su, C. Semi-active sliding mode control of vehicle suspension with magneto-rheological damper. Chin. J. Mech. Eng. 2014, 28, 63–75. [Google Scholar] [CrossRef]
- Dubey, A.; Kumar, R. Neutrosophic inventory management: A cost-effective approach. Economics 2024, 18, 20220101. [Google Scholar] [CrossRef]
- Castillo, O.; Muhuri, P.K.; Melin, P.; Pulkkinen, P. Emerging issues and applications of type-2 fuzzy sets and systems. Eng. Appl. Artif. Intel. 2020, 90, 103596. [Google Scholar] [CrossRef]
- Mendel, J.M. Explaining the performance potential of rule-based fuzzy systems as a greater sculpting of the state space. IEEE Trans. Fuzzy Syst. 2018, 26, 2362–2373. [Google Scholar] [CrossRef]
- Mendel, J.M. Non-singleton fuzzification made simpler. Inf. Sci. 2021, 559, 286–308. [Google Scholar] [CrossRef]
- Güven, Y.; Köklü, A.; Kumbasar, T. Exploring Zadeh’s general type-2 fuzzy logic systems for uncertainty quantification. IEEE Trans. Fuzzy Syst. 2025, 33, 314–324. [Google Scholar] [CrossRef]
- Tang, X.; Ning, D.; Du, H.; Li, W.; Wen, W. Takagi-Sugeno fuzzy model-based semi-active control for the seat suspension with an electrorheological damper. IEEE Access 2020, 8, 98027–98037. [Google Scholar] [CrossRef]
- Wangsheng, W.; Quanyu, Y.; Yi, J.; Ping, X. Study on control system of automobile semi-active suspension based on simulink and fuzzy algorithm. J. Anhui Sci. Technol. Univ. 2017, 31, 82–90. [Google Scholar]
- Kou, F.; Jing, Q.; Gao, Y.; Wu, J. A novel endocrine composite fuzzy control strategy of electromagnetic hybrid suspension. IEEE Access 2020, 8, 211750–211761. [Google Scholar] [CrossRef]
- Aliasghary, M.; Mohammadikia, R. A novel single-input interval type-2 fractional-order fuzzy controller for systems with parameter uncertainty. Soft Comput. 2021, 26, 4961–4977. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, D.; Wong, P.K.; Li, W.; Zhao, J. Dynamic-output-feedback based interval type-2 fuzzy control for nonlinear active suspension systems with actuator saturation and delay. Inf. Sci. 2022, 607, 1174–1194. [Google Scholar] [CrossRef]
- Jian, L.; Liangang, Z.; Cao, W.; Qian, Z.; Yang, W. Leader optimal selection method for the distributed control system of active distribution networks. CSEE J. Power Energy Syst. 2024, 10, 314–323. [Google Scholar] [CrossRef]
- Yunlang, X.; Feng, S.; Xinyi, S.; Liang, G.; Shuo, H.; Xiaofeng, Y. A composite neural network-based adaptive sliding mode control method for reluctance actuator maglev system. Neural Comput. Appl. 2023, 35, 15877–15890. [Google Scholar] [CrossRef]
- Chen, F.; Qian, C.; Jiang, Y.; Xu, Y. Hybird nonlinear control for fighter with center of gravity perturbation and aerodynamic parameter uncertainty. IEEE Access 2021, 9, 139315–139327. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, L.; Jiang, L.; Xu, Z. CMAC-PID composite control for the position control of a fully variable valve system. Int. J. Automot. Technol. 2023, 24, 681–691. [Google Scholar] [CrossRef]
- Pham, D.-B.; Nguyen, T.-v.-A.; Bui, N.-T. Composite fuzzy-based control strategy for uncertain underactuated system. IEEE Access 2024, 12, 155564–155577. [Google Scholar] [CrossRef]
- Islam, M.S.; Roy, T.K.; Bushra, I.J.; Ghosh, S.K.; Oo, A.M.T. A novel composite control approach to enhance stability in wind/PV/PEM fuel cell/hydrogen/BESS—Based DC microgrids. J. Eng. 2025, 2025, e70062. [Google Scholar] [CrossRef]
- Yang, C.; Yang, X.; Zhou, Y. Research on the performance of magnetorheological semi-active suspension with stepped by-pass valve based on fuzzy PID control. J. Magn. 2023, 28, 277–285. [Google Scholar] [CrossRef]
- Jiang, J.; Min, L.; Jing, Y.; Ding, S.; Yu, M.; Jie, W. Improving ride comfort of a soil compactor based on the NSS embedded into the seat’s semiactive suspension. Int. J. Acoust. Vib. 2023, 28, 117–129. [Google Scholar] [CrossRef]
- Do, X.P.; Van, M.; Nguyen, N.P. A novel switching adaptive control for randomly switching systems with an application to suspension systems. Eur. J. Control 2022, 65, 100635. [Google Scholar] [CrossRef]
- Hu, G.; Liu, Q.; Ding, R.; Li, G. Vibration control of semi-active suspension system with magnetorheological damper based on hyperbolic tangent model. Adv. Mech. Eng. 2017, 9, 168781401769458. [Google Scholar] [CrossRef]
- Jain, S.; Saboo, S.; Pruncu, C.I.; Unune, D.R. Performance Investigation of Integrated Model of Quarter Car Semi-Active Seat Suspension with Human Model. Appl. Sci. 2020, 10, 3185. [Google Scholar] [CrossRef]
- Mohammadikia, R.; Aliasghary, M. Design of an interval type-2 fractional order fuzzy controller for a tractor active suspension system. Comput. Electron. Agric. 2019, 167, 105049. [Google Scholar] [CrossRef]
- Sun, C.; Zhu, H. Active disturbance rejection control of bearingless permanent magnet slice motor based on RPROP neural network optimized by improved differential evolution algorithm. IEEE Trans. Power Electron. 2024, 39, 3064–3074. [Google Scholar] [CrossRef]
- Mendoza-Flores, S.; Velázquez-Villegas, F.; Cuenca-Jiménez, F. Optimization of a horizontal washing machine suspension system: Studying a 7 DOF dynamic model using a genetic algorithm through a bounding box fitness function. J. Vib. Eng. Technol. 2024, 12, 6865–6884. [Google Scholar] [CrossRef]
- Wang, G.; Kou, F. Optimization of dual-function suspension structures using particle swarm optimization approaches. Int. J. Appl. Electrom. 2024, 75, 19–37. [Google Scholar] [CrossRef]
- Guo, Q.; Yang, X.; Li, K.; Li, D. Parameters identification of magnetorheological damper based on particle swarm optimization algorithm. Eng. Appl. Artif. Intel. 2025, 143, 110016. [Google Scholar] [CrossRef]
- Yaghoubi, S.; Ghanbarzadeh, A. Modeling and optimization of car suspension system in the presence of magnetorheological damper using Simulink-PSO hybrid technique. Results Eng. 2024, 22, 102065. [Google Scholar] [CrossRef]
- Yan, L.; Chen, J.; Duan, C.; Zhao, C.; Yang, R. A Vibration Control Method Using MRASSA for 1/4 Semi-Active Suspension Systems. Electronics 2023, 12, 1778. [Google Scholar] [CrossRef]
- Liu, Y.; As’arry, A.; Ahmed, H.; Hairuddin, A.A.; Hassan, M.K.; Zakaria, M.Z.; Yang, S. Online optimal tuning of fuzzy PID controller using grey wolf optimizer for quarter car semi-active suspension system. Adv. Mech. Eng. 2024, 16, 1–14. [Google Scholar] [CrossRef]
- Malarczyk, M. Optymalizacja systemu sterowania napędami elektrycznymi oraz układu zawieszenia robota kołowo-kroczącego z wykorzystaniem algorytmu Grey Wolf Optimizer. Prz. Elektrotech. 2023, 1, 151–157. [Google Scholar] [CrossRef]
- Xu, E.; Zhao, R. Research on Displacement Sensorless Control for Bearingless Synchronous Reluctance Motor Based on the Whale Optimization Algorithm–Elman Neural Network. Actuators 2024, 13, 192. [Google Scholar] [CrossRef]
- Ab Talib, M.H.; Mat Darus, I.Z.; Mohd Samin, P.; Mohd Yatim, H.; Hadi, M.S.; Shaharuddin, N.M.R.; Mazali, I.I.; Ardani, M.I.; Mohd Yamin, A.H. Experimental evaluation of ride comfort performance for suspension system using PID and fuzzy logic controllers by advanced firefly algorithm. J. Braz. Soc. Mech. Sci. 2023, 45, 132. [Google Scholar] [CrossRef]
- Ab Talib, M.H.; Mat Darus, I.Z.; Mohd Samin, P.; Mohd Yatim, H.; Ardani, M.I.; Shaharuddin, N.M.R.; Hadi, M.S. Vibration control of semi-active suspension system using PID controller with advanced firefly algorithm and particle swarm optimization. J. Amb. Intel. Hum. Comp. 2020, 12, 1119–1137. [Google Scholar] [CrossRef]
- Ab Talib, M.H.; Mat Darus, I.Z.; Mohd Samin, P. Fuzzy logic with a novel advanced firefly algorithm and sensitivity analysis for semi-active suspension system using magneto-rheological damper. J. Amb. Intel. Hum. Comp. 2018, 10, 3263–3278. [Google Scholar] [CrossRef]
- Yong, H.; Seo, J.; Kim, J.; Kim, M.; Choi, J. Suspension control strategies using switched soft actor-critic models for real roads. IEEE Trans. Ind. Electron. 2023, 70, 824–832. [Google Scholar] [CrossRef]
- Najafi, A.; Masih-Tehrani, M.; Emami, A.; Esfahanian, M. A modern multidimensional fuzzy sliding mode controller for a series active variable geometry suspension. J. Braz. Soc. Mech. Sci. 2022, 44, 425. [Google Scholar] [CrossRef]
- Sun, C.; Xu, Z.; Deng, S.; Tong, B. Integration sliding mode control for vehicle yaw and rollover stability based on nonlinear observation. Trans. Inst. Meas. Control 2022, 44, 3039–3056. [Google Scholar] [CrossRef]
- Han, C.; Choi, S.-B.; Lee, T.-H.; An, J.-H. Vibration control of mr seat suspension using a new adaptive composite controller. Trans. Korean Soc. Noise Vib. Eng. 2018, 28, 288–295. [Google Scholar] [CrossRef]
- Shin, D.K.; Phu, D.X.; Choi, S.-M.; Choi, S.-B. An adaptive fuzzy sliding mode control of magneto-rheological seat suspension with human body model. J. Intell. Mater. Syst. Struct. 2015, 27, 925–934. [Google Scholar] [CrossRef]
- Li, I.H. Design for a fluidic muscle active suspension using parallel-type interval type-2 fuzzy sliding control to improve ride comfort. Int. J. Fuzzy Syst. 2022, 24, 1719–1734. [Google Scholar] [CrossRef]
- Spaggiari, A.; Cocconcelli, M.; Castagnetti, D.; Dragoni, E.; Rubini, R. Synthesis and optimization of an eight-bar linkage mechanism for seat suspensions. J. Braz. Soc. Mech. Sci. 2022, 44, 429. [Google Scholar] [CrossRef]
- Maciejewski, I.; Blazejewski, A.; Pecolt, S.; Krzyzynski, T. A sliding mode control strategy for active horizontal seat suspension under realistic input vibration. J. Vib. Control 2022, 29, 2539–2551. [Google Scholar] [CrossRef]
- Dimitriadis, C.I.; Kateris, D.; Xyradakis, P.; Gialama, A.; Gialamas, T. Vibration assessment of tractor operator based on vibration signals. INMATEH Agric. Eng. 2023, 71, 776–784. [Google Scholar] [CrossRef]
- Xu, J.; Li, R.; Li, Y.; Zhang, Y.; Sun, H.; Ding, X.; Ma, Y. Research on Variable-Universe Fuzzy Control Technology of an Electro-Hydraulic Hitch System. Processes 2021, 9, 1920. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, Z.; Qin, J.; Mao, E.; Mitsuoka, M.; Inoue, E.; Shin, S. Factorial significance on tractor stability under variation of terrain roughness employing the Taguchi method. Int. J. Agric. Biol. Eng. 2018, 11, 88–94. [Google Scholar] [CrossRef]
- Kim, S.W.; Kim, S.H.; Kim, S.C. A Study on determination of suspension spring coefficient of electric UTV for agricultural use through virtual simulation. Korean Inst. Smart Media 2022, 11, 75–81. [Google Scholar] [CrossRef]
- Choi, K.; Oh, J.; Kim, H.-S.; Han, H.-W.; Park, J.-H.; Lee, G.-H.; Seo, J.; Park, Y.-J. Experimental study on the dynamic characteristics of hydro-pneumatic semi-active suspensions for agricultural tractor cabins. Appl. Sci. 2020, 10, 8992. [Google Scholar] [CrossRef]
- Gomez-Gil, J.; Gomez-Gil, F.J.; Martin-de-Leon, R. The Influence of Tractor-Seat Height above the Ground on Lateral Vibrations. Sensors 2014, 14, 19713–19730. [Google Scholar] [CrossRef]
- Visconte, C.; Cavallone, P.; Carbonari, L.; Botta, A.; Quaglia, G. Design of a Mechanism with Embedded Suspension to Reconfigure the Agri_q Locomotion Layout. Robotics 2021, 10, 15. [Google Scholar] [CrossRef]
- Shaer, B.; Kenné, J.P.; Kaddissi, C.; Mintsa, H.A. Real-time hybrid control of electrohydraulic active suspension. Int. J. Robust Nonlinear Control 2017, 27, 4968–4991. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, P.; Leng, D.; Zhan, H.; Luan, G.; Ning, D.; Yu, J. Prescribed performance control-based semi-active vibration controller for seat suspension equipped with an electromagnetic damper. Vibration 2023, 6, 303–318. [Google Scholar] [CrossRef]
- Park, J.; Jang, S.; Park, M.; Park, H.; Yoon, J.; Hwang, M. SAM: Semi-active mechanism for extensible continuum manipulator and real-time hysteresis compensation control algorithm. Int. J. Med. Robot. 2024, 20, e70014. [Google Scholar] [CrossRef]
- Li, J.; Tian, D.; Zhou, J.; Duan, X.; Sheng, Z.; Zhao, D.; Cao, D. Distributed robust model predictive control for virtual coupling under structural and external uncertainty. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8751–8769. [Google Scholar] [CrossRef]
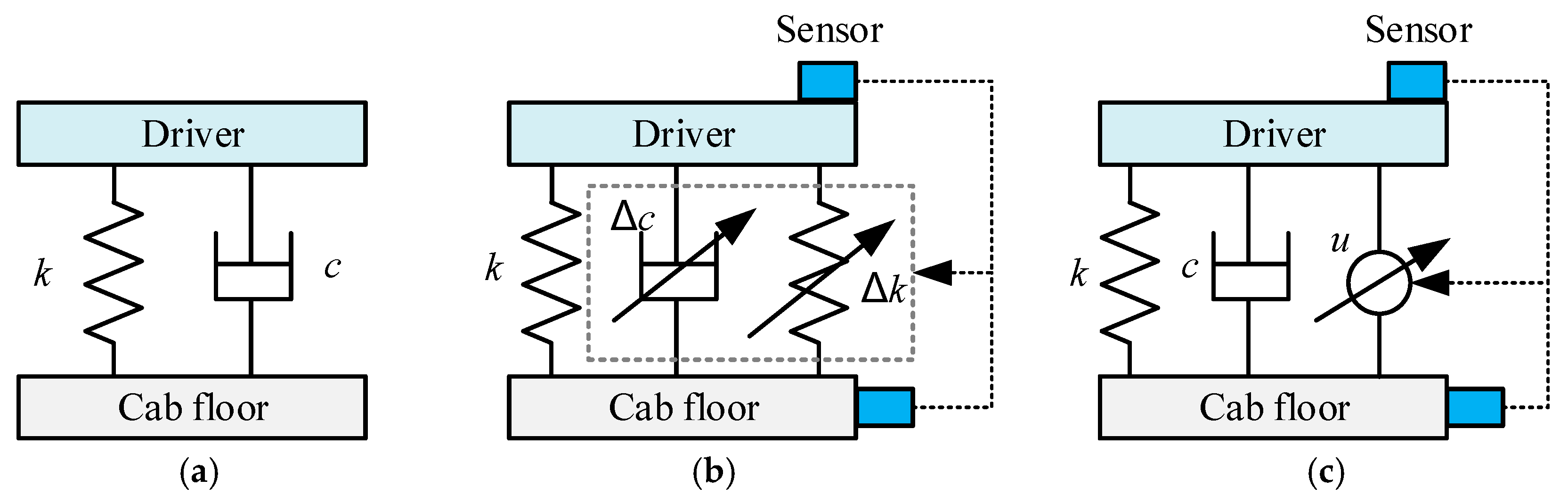

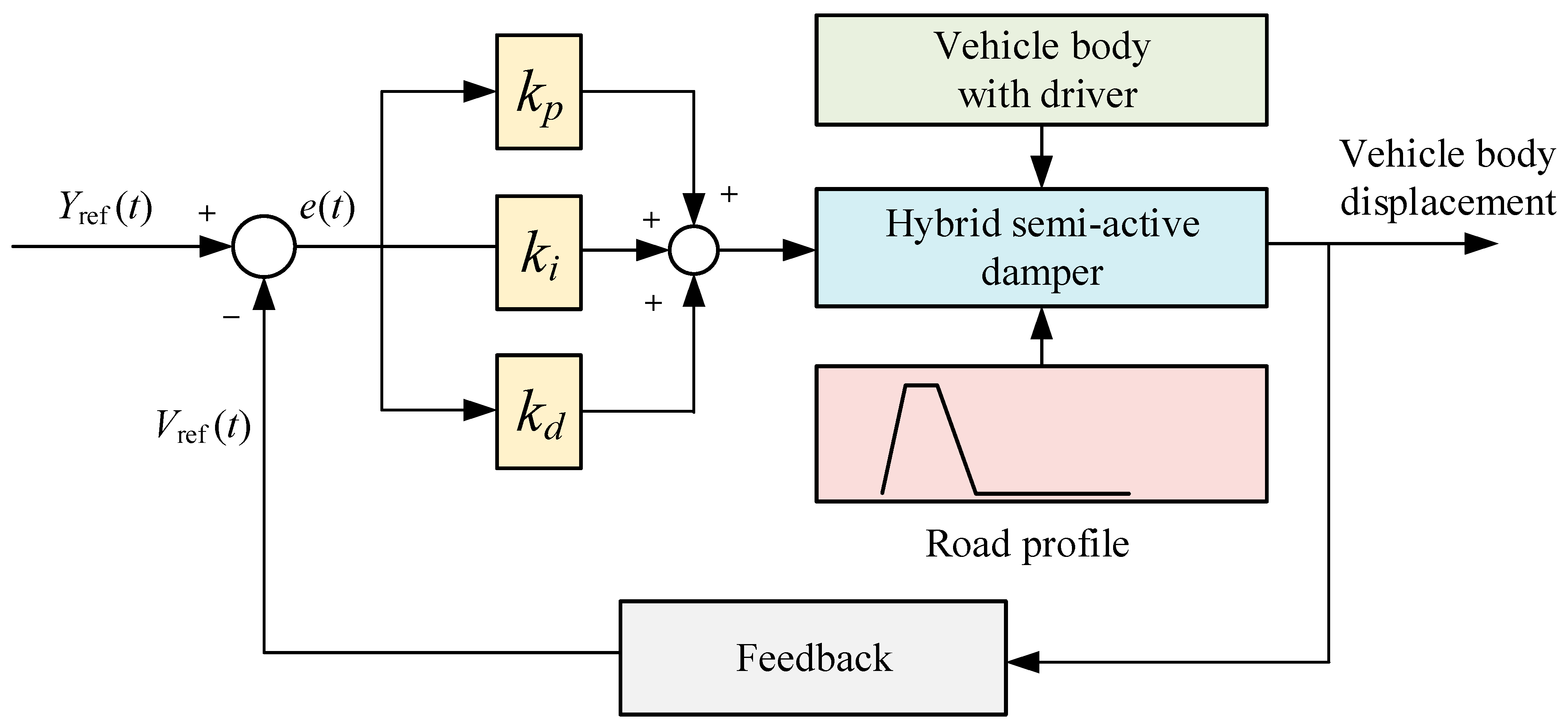
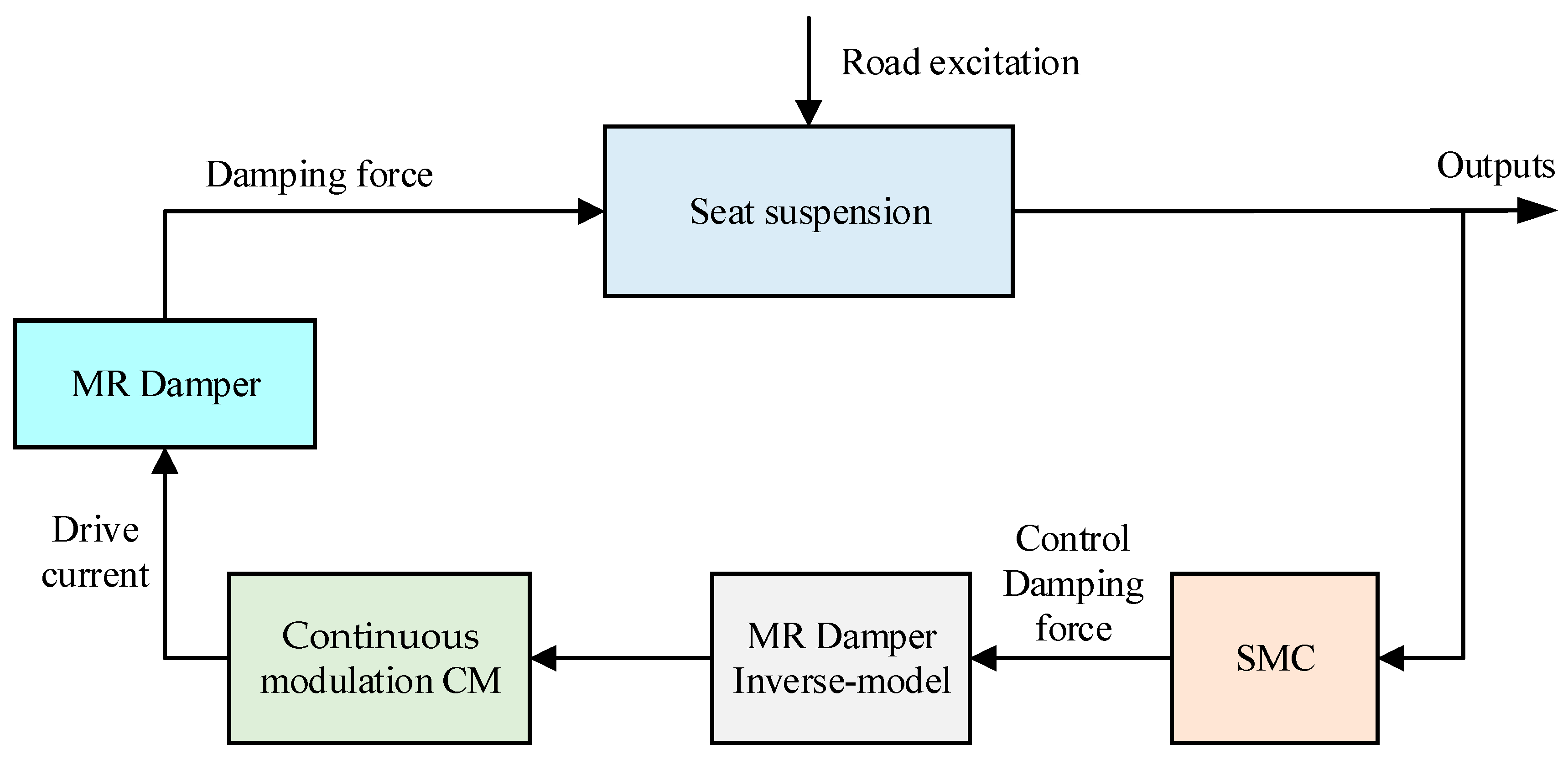
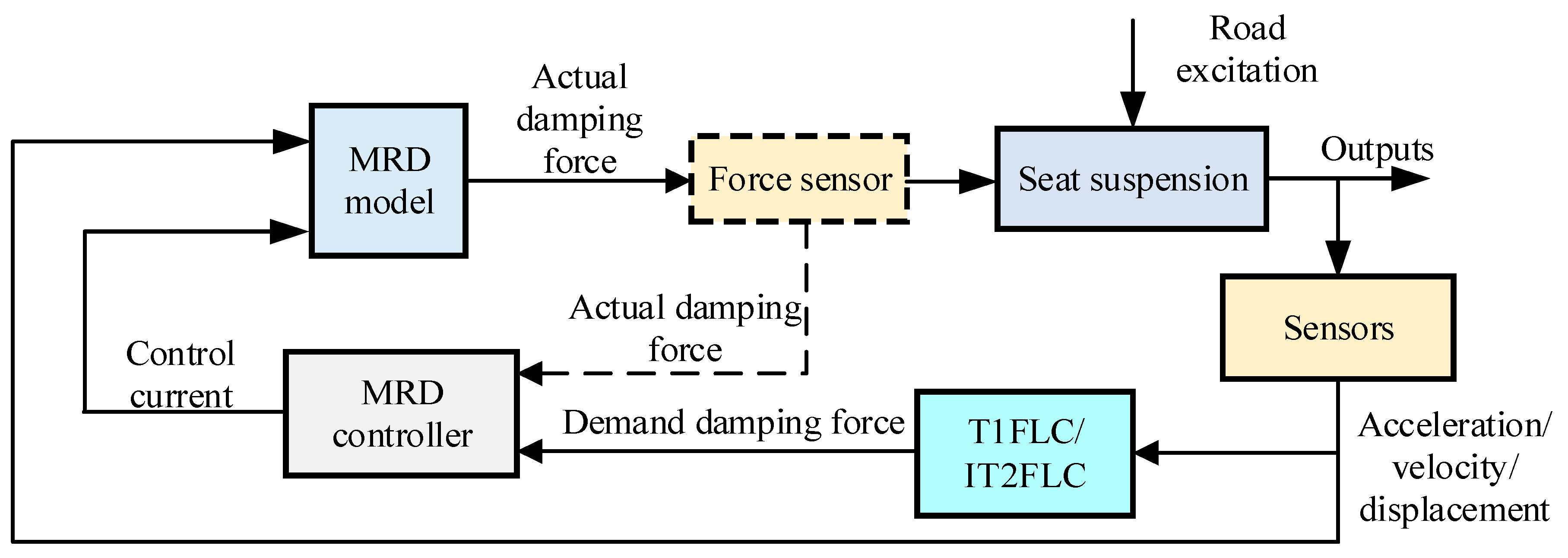
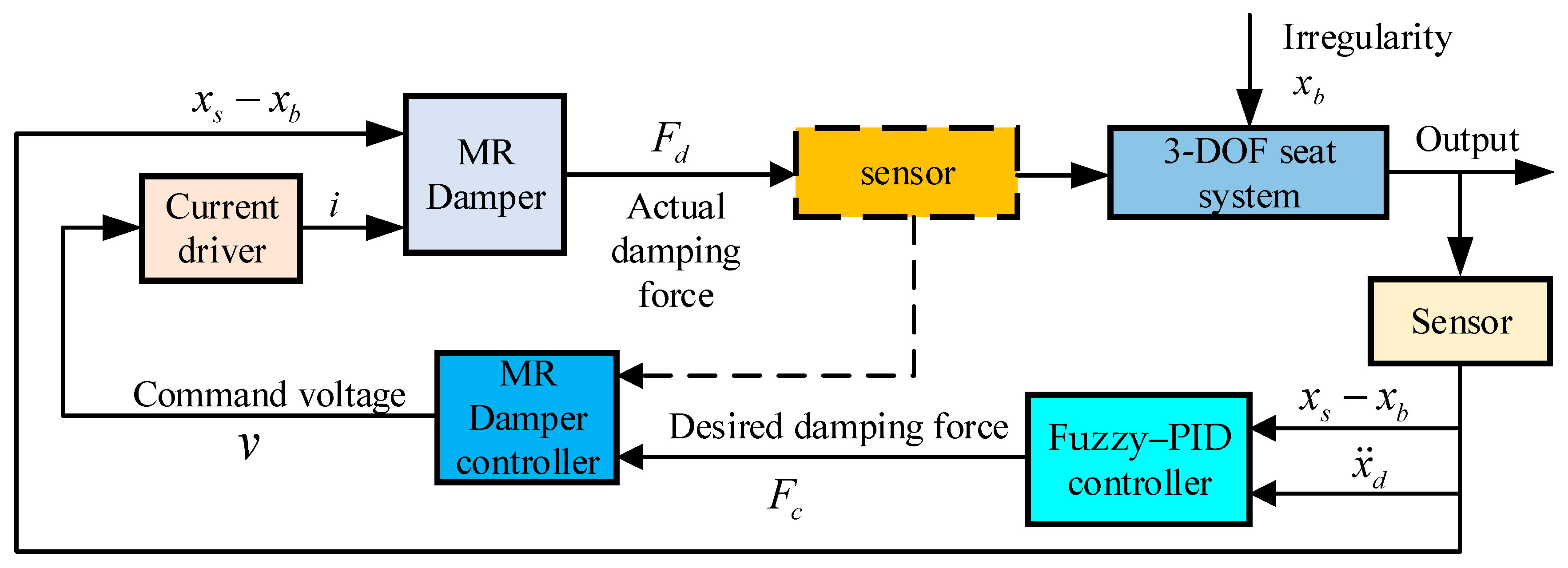
| Characteristic | System Category | ||
|---|---|---|---|
| Passive Suspension | Semi-Active Suspension | Active Suspension | |
| Regulating element | Passive dampers | Damping-adjustable shock absorber/Variable Stiffness | Actuator |
| Principle of action | Suspension k-c characteristic fixed | Damping/Stiffness continuously adjustable or step-adjustable | Adjust the force between the connectors |
| Control variable | - | c/k | u |
| Frequency response width | - | 0~40 Hz | 0~30 Hz |
| Power requirements | None | Low | High |
| Structural complexity | Simple | General | Complex |
| Cost | Low | Moderate | High |
| Characteristic | ERF | MRF |
|---|---|---|
| Maximum yield stress | 2~10 kPa | 50~100 kPa |
| Supply voltage | 2~5 kV | 2~25 V |
| Impurity sensitivity | Sensitive | Insensitive |
| Density | 1000~2000 kg/m3 | 3000~4000 kg/m3 |
| Response time | Millisecond level | Millisecond level |
| Temperature range | 10~90 °C | −50~150 °C |
| Maximal electric field | 4000 kV/m | 250 kA/m |
| Energy consumption | 1000 J/m3 | 1 × 105 J/m3 |
| Control current | 1~10 mA | 1~2 A |
| Cost | Low | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wang, Z.; Shi, H.; Jiang, N.; Zhao, S.; Qiu, Y.; Liu, Q. Review of Agricultural Machinery Seat Semi-Active Suspension Systems for Ride Comfort. Machines 2025, 13, 246. https://doi.org/10.3390/machines13030246
Chen X, Wang Z, Shi H, Jiang N, Zhao S, Qiu Y, Liu Q. Review of Agricultural Machinery Seat Semi-Active Suspension Systems for Ride Comfort. Machines. 2025; 13(3):246. https://doi.org/10.3390/machines13030246
Chicago/Turabian StyleChen, Xiaoliang, Zhelu Wang, Haoyou Shi, Nannan Jiang, Sixia Zhao, Yiqing Qiu, and Qing Liu. 2025. "Review of Agricultural Machinery Seat Semi-Active Suspension Systems for Ride Comfort" Machines 13, no. 3: 246. https://doi.org/10.3390/machines13030246
APA StyleChen, X., Wang, Z., Shi, H., Jiang, N., Zhao, S., Qiu, Y., & Liu, Q. (2025). Review of Agricultural Machinery Seat Semi-Active Suspension Systems for Ride Comfort. Machines, 13(3), 246. https://doi.org/10.3390/machines13030246





