Analysis of Electromagnetic Vibration in Permanent Magnet Motors Based on Random PWM Technology
Abstract
:1. Introduction
- (1)
- Adding filters
- (2)
- PWM control strategy
2. Analysis of Electromagnetic Force
3. Basic Principles of Random PWM Technology
4. Implementation of Random PWM Technology
4.1. Simulation Implementation
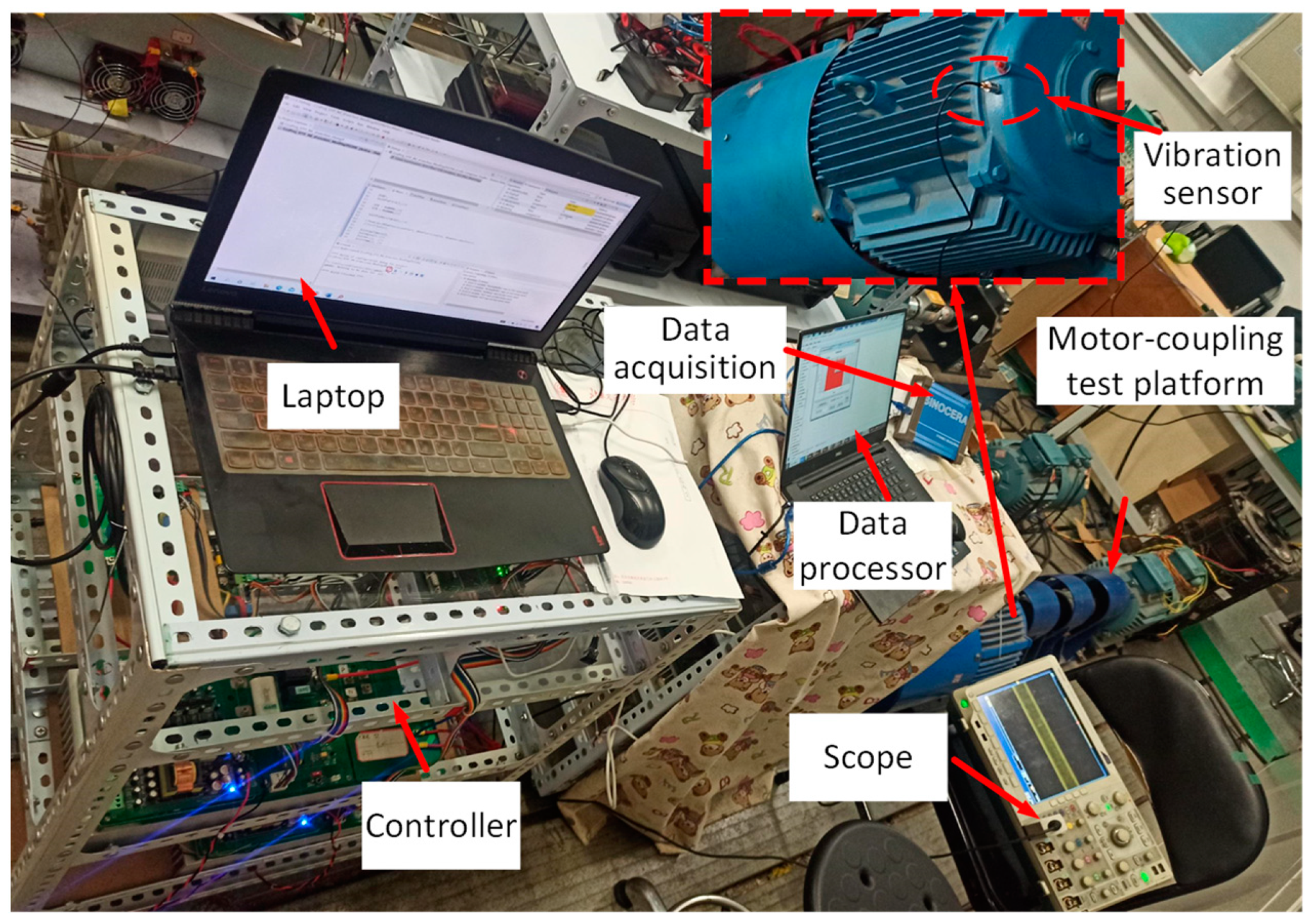
4.2. Test Validation
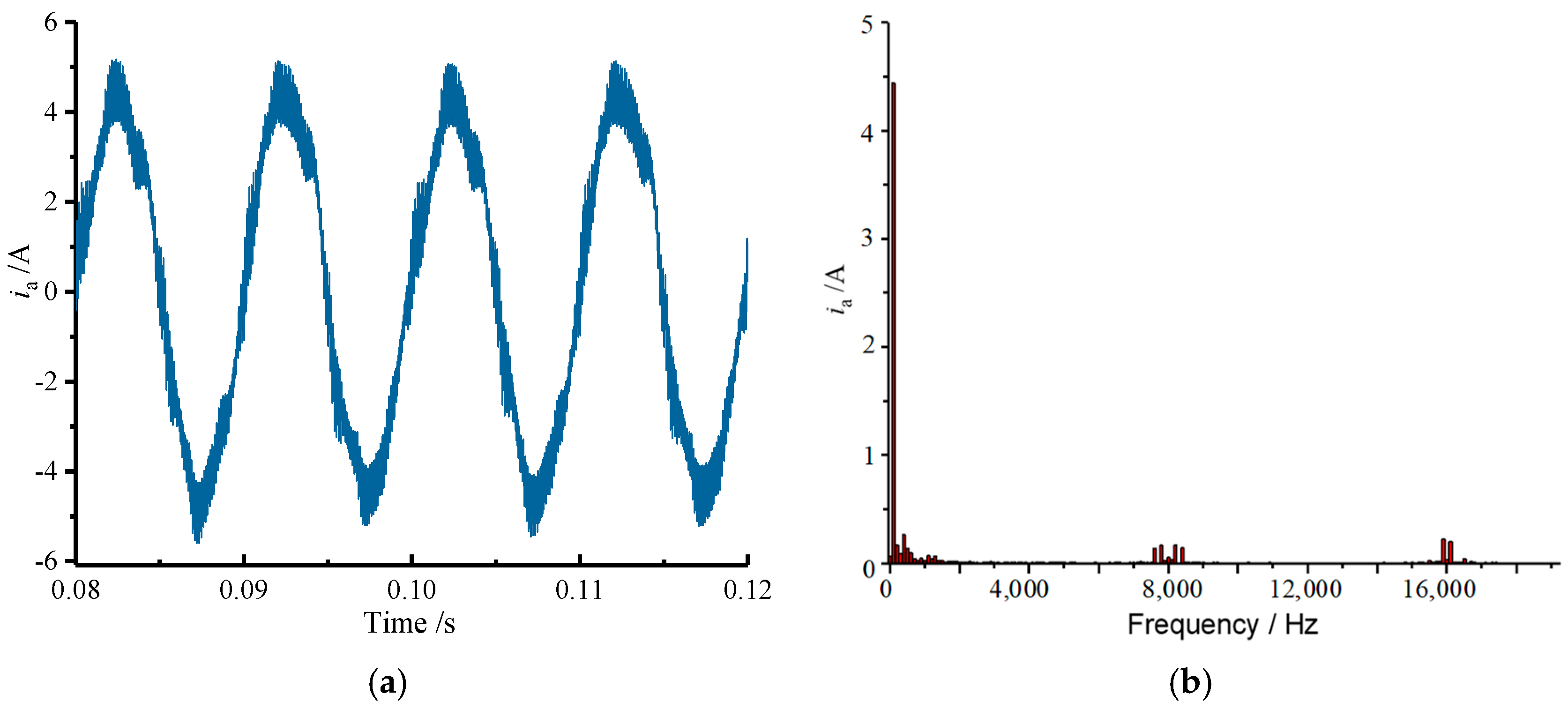
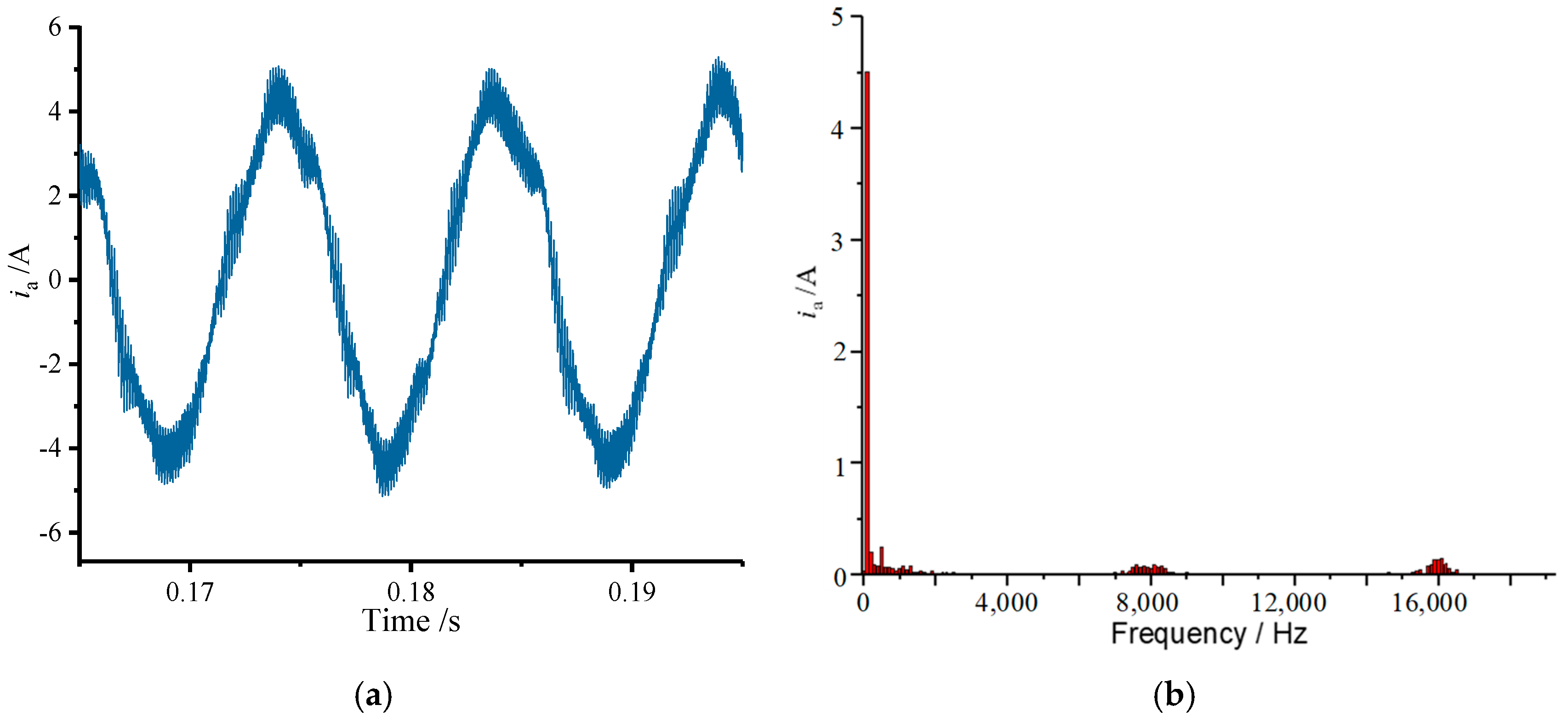
4.2.1. Current Waveforms
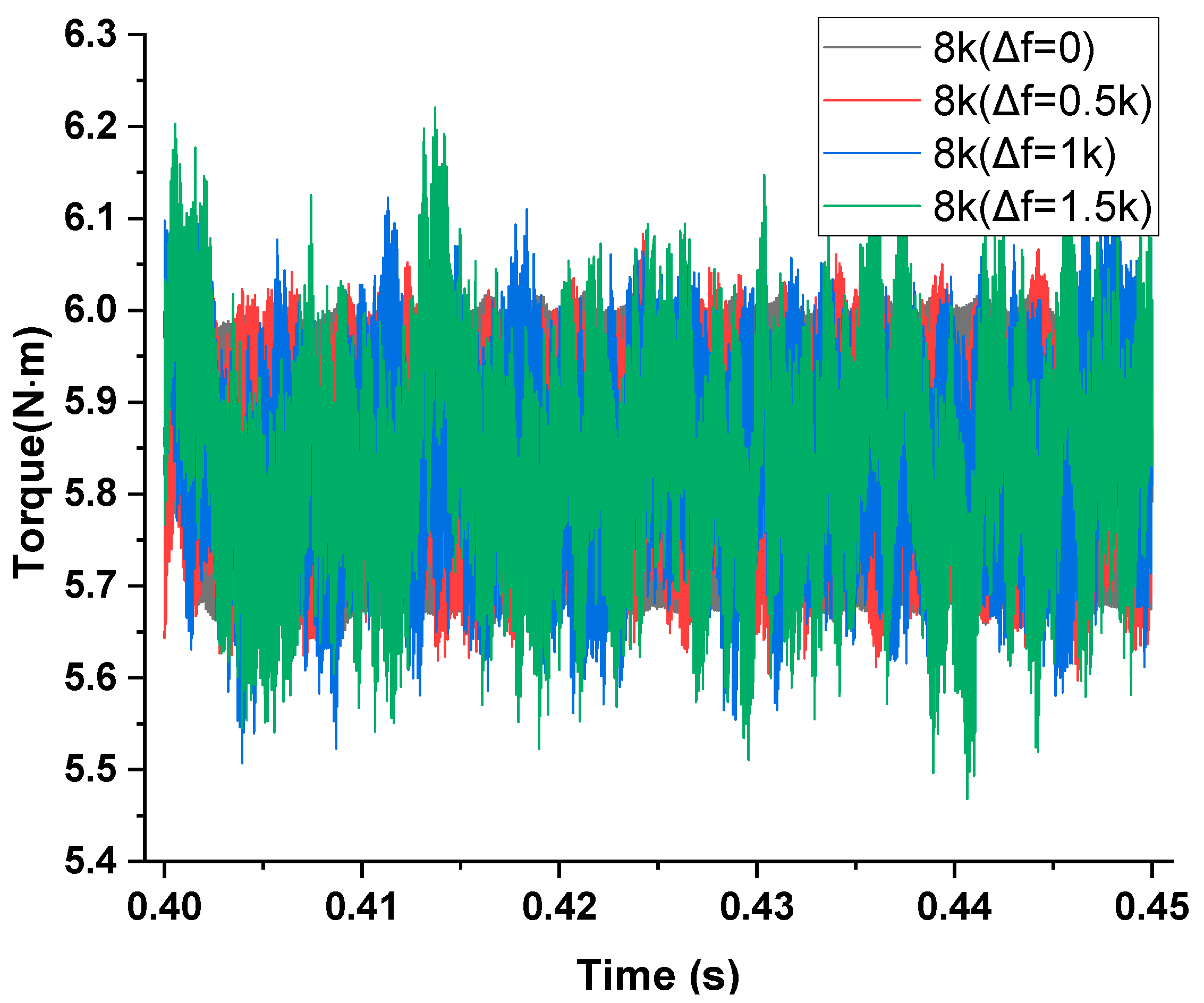
4.2.2. Electromagnetic Vibration Waveforms
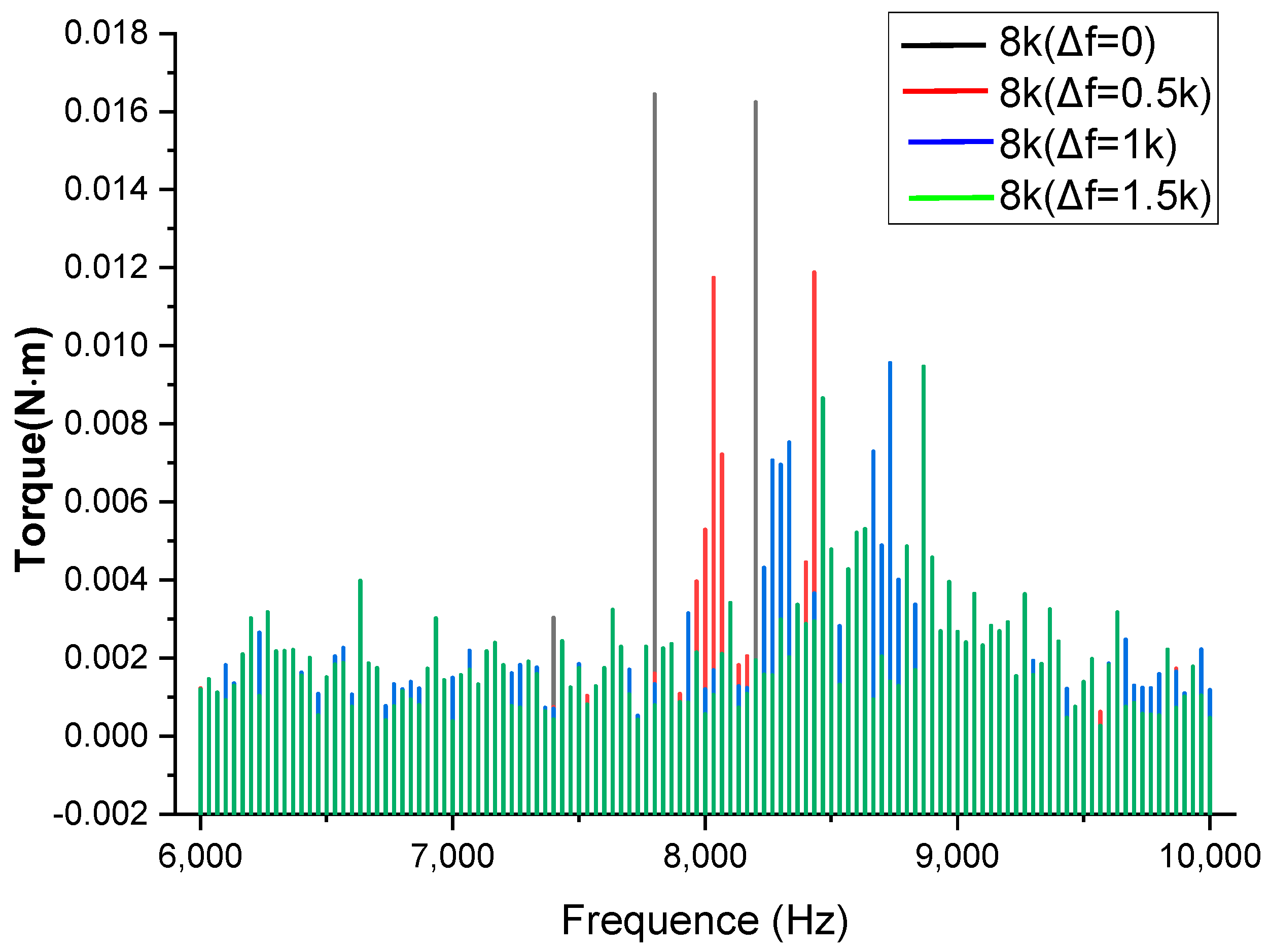
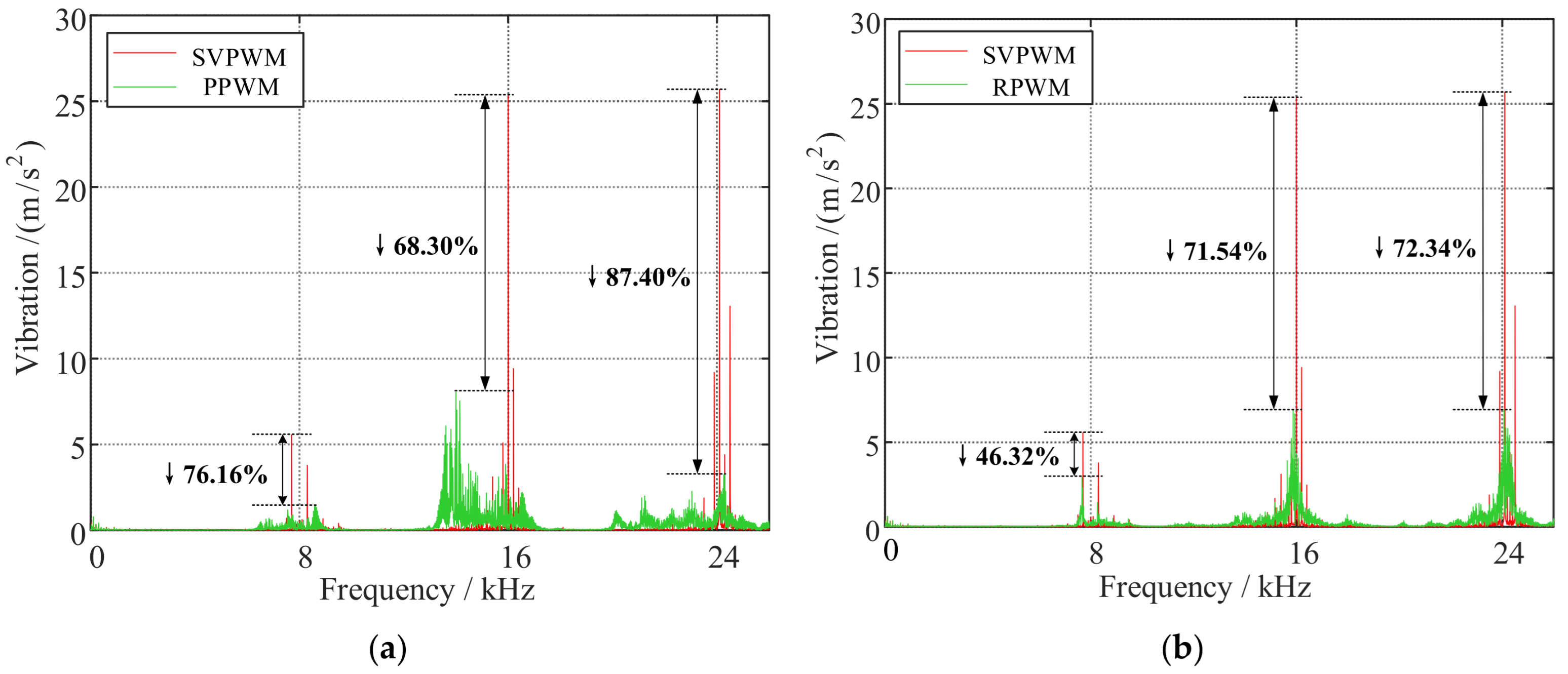
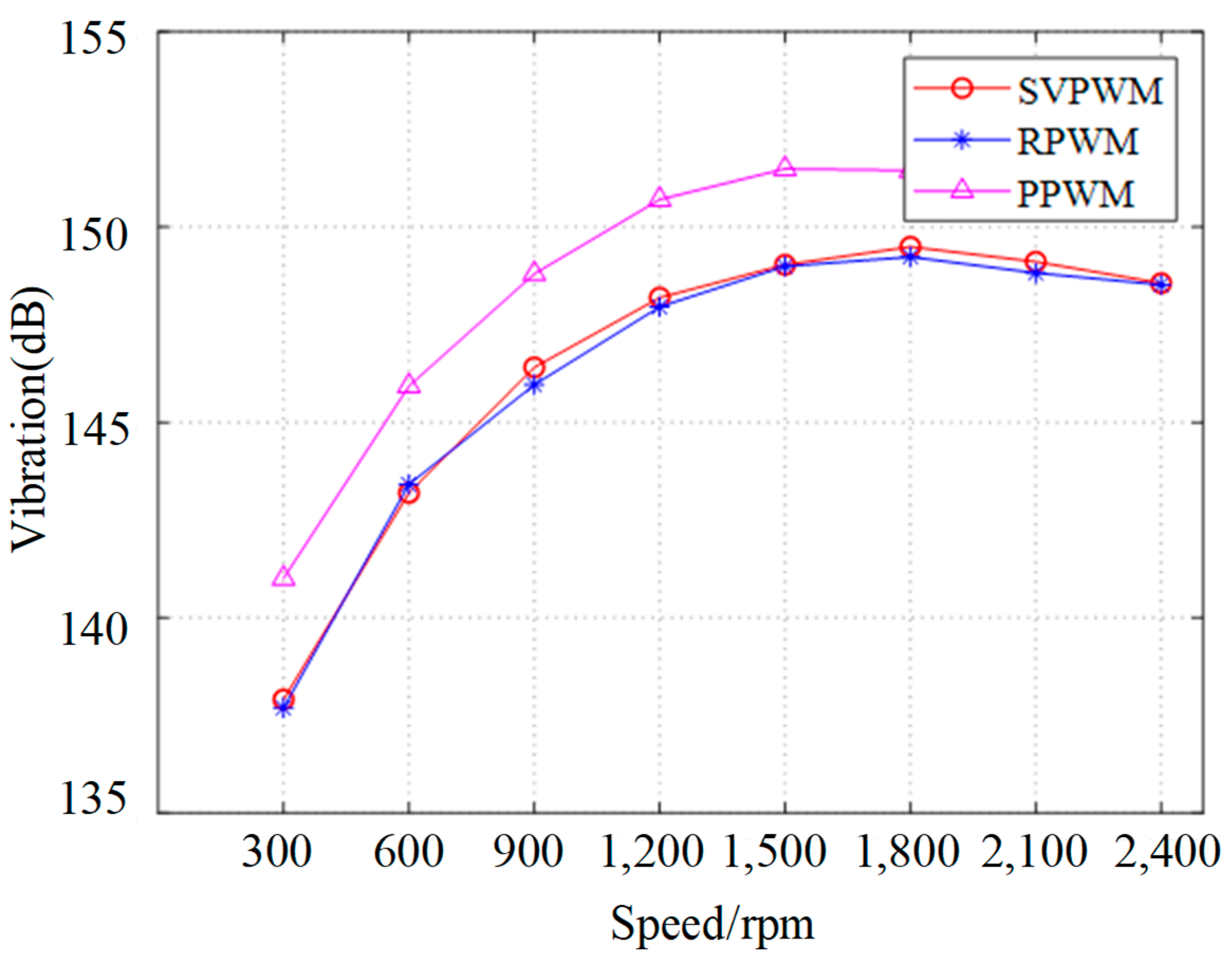
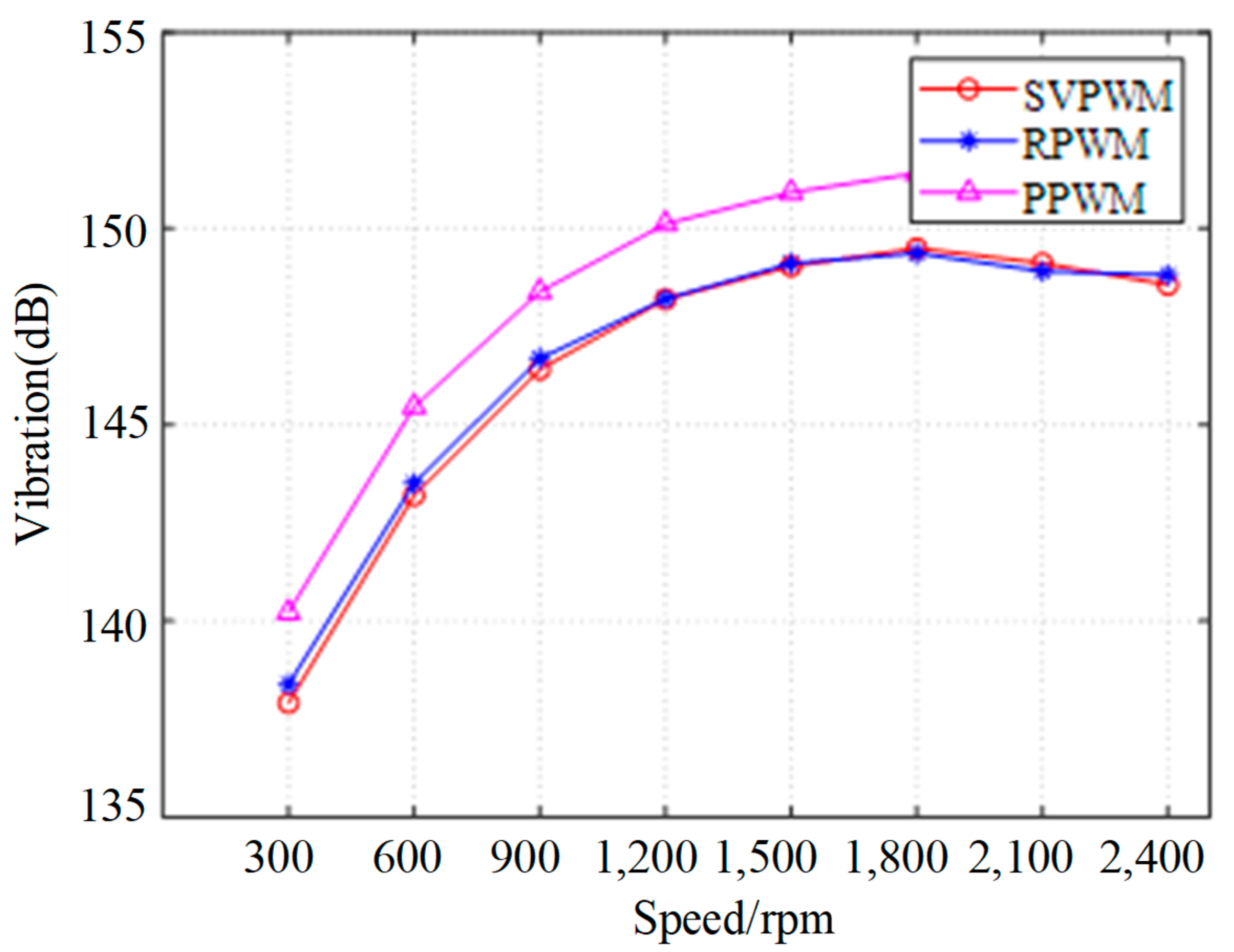
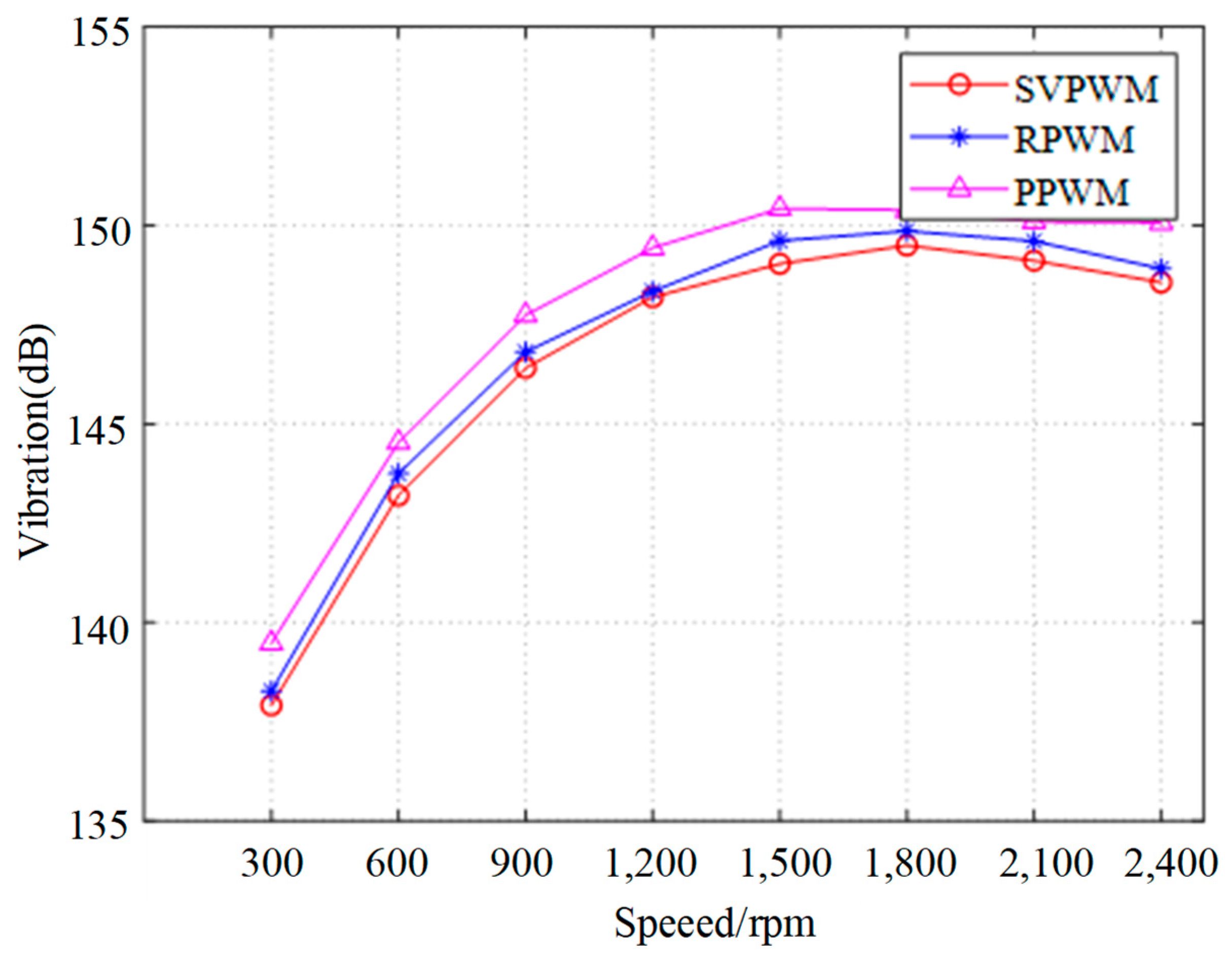
4.2.3. Comparison of Reduction Method
5. Conclusions
- (1)
- The high-frequency current harmonics generated by the rich high-frequency voltage harmonics embedded in the square wave output from the inverter are basically concentrated near the carrier frequency fc and its integer multiple frequency mfc (m ≥ 2), and these high-amplitude, narrow-bandwidth high-frequency current harmonics generate noise that is particularly sensitive to the human ear. Therefore, it is crucial to mitigate the high-frequency harmonic components of the current and the associated motor vibrations near the carrier frequency by employing a PWM modulation strategy.
- (2)
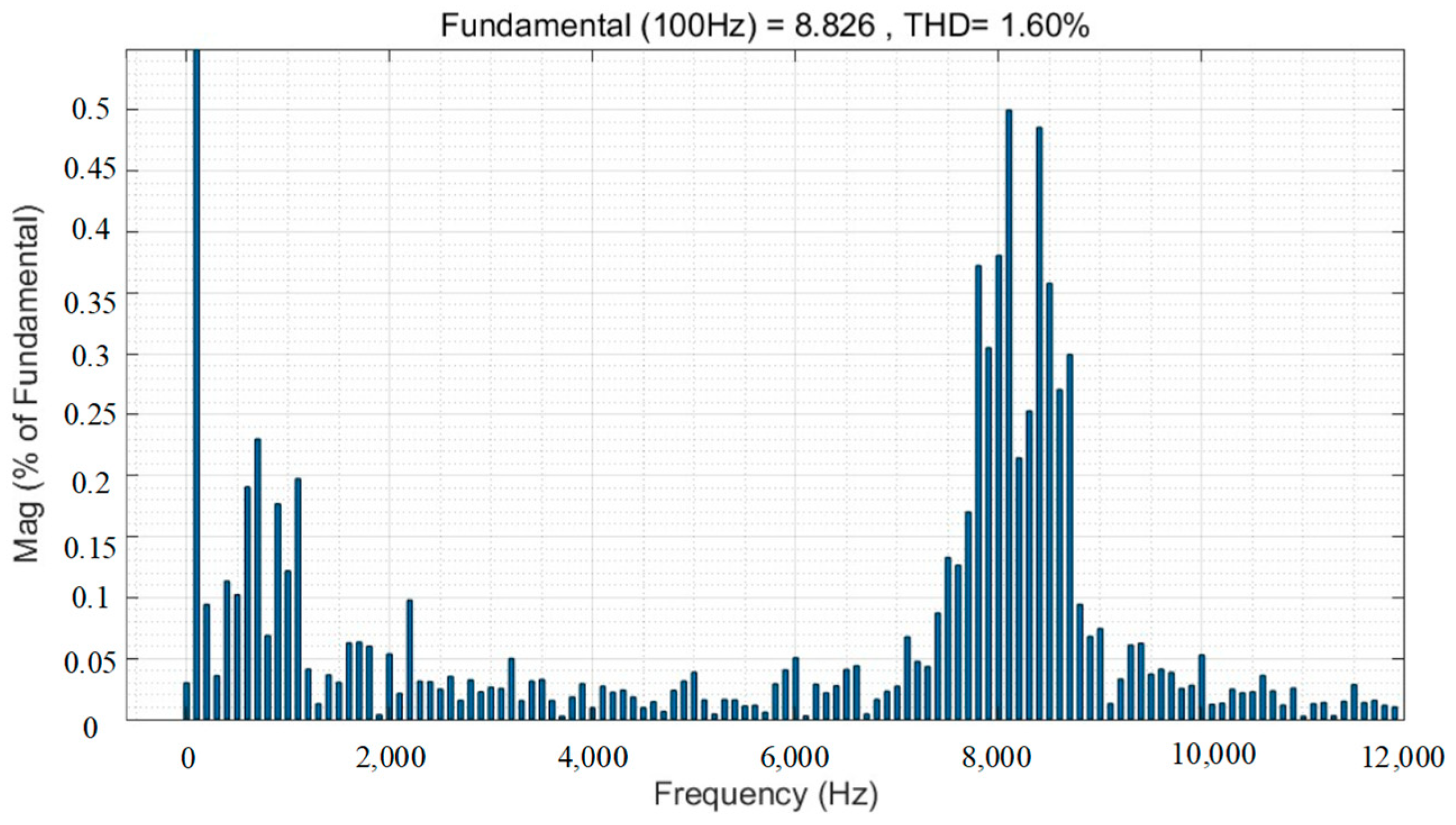
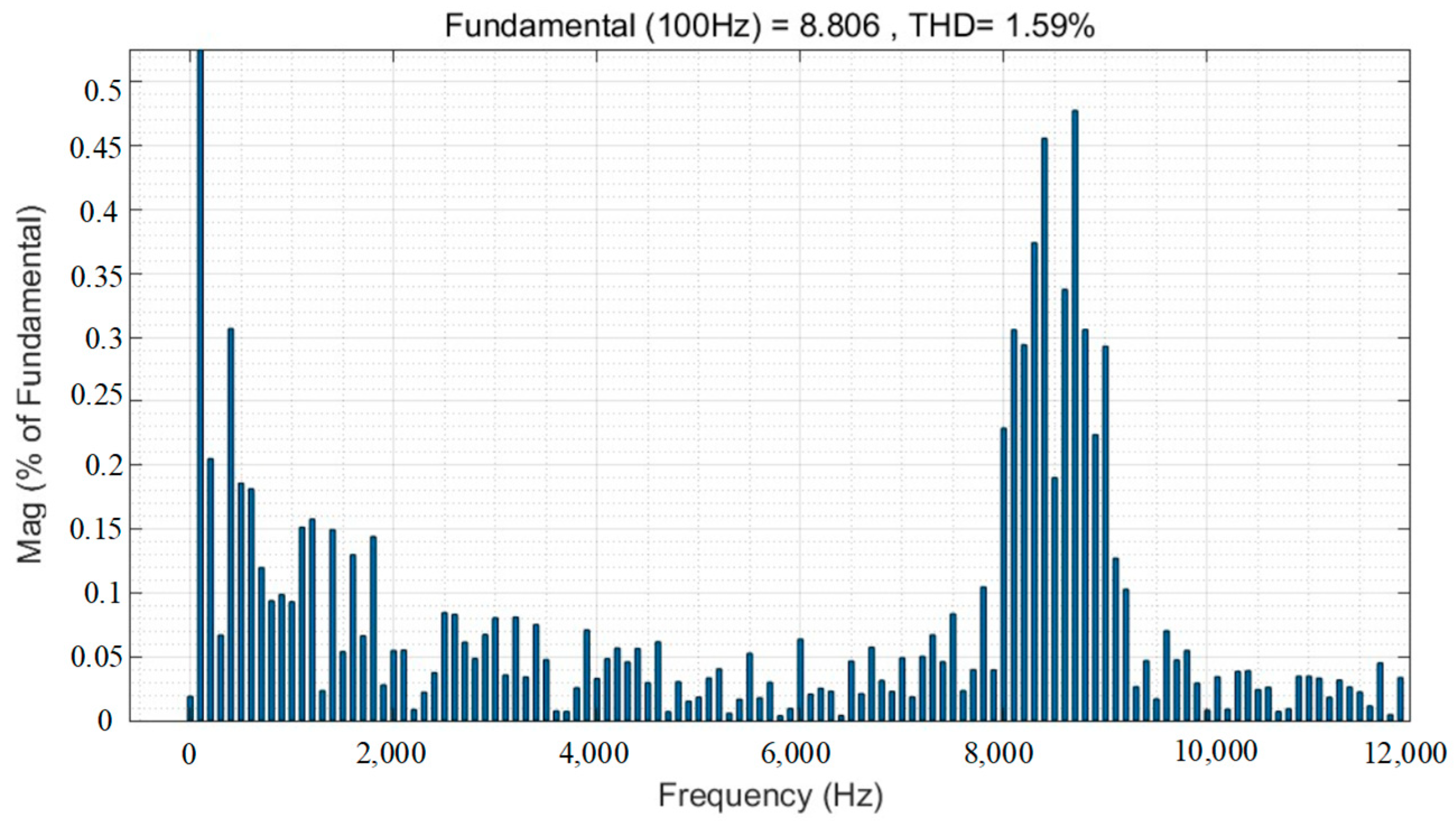
- Simulation results show that for switching frequencies of 4 k, 6 k, 8 k, and 10 kHz, the amplitude suppression of high current harmonics by the random PWM technique reaches more than 20%. However, it increases the total harmonic distortion of the current by a maximum of 12%.
- (3)
- The experimental results demonstrate that the control strategy employing both the PPWM and RPWM techniques significantly reduces the amplitude of high-frequency harmonic components in the current supplied by the inverter, as well as the motor vibrations induced by these harmonics. This attenuation occurs around the carrier frequency fc and its integer multiples mfc (where m ≥ 2), which in turn can greatly weaken the sharp high-frequency noise, reducing the amplitude by more than 60%. However, the random PWM techniques cannot reduce the total vibration levels compared with conventional PWM.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bracikowski, N.; Fakam, M.; Hecquet, M.; Brochet, P.; Lanfranchi, V. Characterisation of radial vibration force and electromagnetic noise behaviour of a PWM-fed permanent magnet synchronous machine. In Proceedings of the XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012. [Google Scholar]
- Vijayraghavan, P.; Krishnan, R. Noise in electric machines: A review. IEEE Trans. Ind. Appl. 1999, 35, 1007–1013. [Google Scholar] [CrossRef]
- Bonthu, S.S.R.; Tarek, M.T.B.; Choi, S. Optimal Torque Ripple Reduction Technique for Outer Rotor Permanent Magnet Synchronous Reluctance Motors. IEEE Trans. Energy Convers. 2017, 33, 1184–1192. [Google Scholar]
- Lo, W.C.; Chan, C.C.; Zhu, Z.; Xu, L.; Howe, D.; Chau, K.T. Acoustic noise radiated by PWM-controllel induction machine drives. IEEE Trans. Ind. Electron. 2000, 47, 880. [Google Scholar] [CrossRef]
- Lin, F.; Zuo, S.; Deng, W.; Wu, S. Modeling and analysis of electromagnetic force, vibration, and noise in permanent-magnet synchronous motor considering current harmonics. IEEE Trans. Ind. Electron. 2016, 63, 7455–7466. [Google Scholar] [CrossRef]
- Gamoudi, R.; Elhak Chariag, D.; Sbita, L. A Review of Spread- Spectrum-Based PWM Techniques A Novel Fast Digital Implementation. IEEE Trans. Power. Electron. 2018, 33, 10292–10307. [Google Scholar] [CrossRef]
- Nishimura, T.N. Reduction of vibration and acoustic noise in induction motor driven by three phase PWM AC chopper using static induction transistors. IEEE Trans. Power Electron. 2002, 4, 313. [Google Scholar] [CrossRef]
- Maria, C. Filtering technique to minimize the effect of long motor leads on PWM inverter drives. IEEE Trans. Electromagn. Compat. 2014, 56, 1067. [Google Scholar]
- Ferreira, J.A.; Dorlang, P.; Debeer, F.G. An active inline notch filter for reducing acoustic noise in drives. IEEE Trans. Ind. Appl. 2007, 43, 798. [Google Scholar] [CrossRef]
- Li, D.Y.; Chen, Q.F.; Jia, Z.C.; Ke, J. A novel active power filter with fundamental magnetic flux compensation. IEEE Trans. Power Deliv. 2004, 19, 799. [Google Scholar] [CrossRef]
- Quang, N.P.; Dittrich, J.A. Inverter Control with Space Vector Modulation; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Jui, Y.C. On Acoustic-Noise-Reduction Control Using Random Switching Technique for Switch-Mode Rectifiers in PMSM Drive. IEEE Trans. Ind. Electron. 2008, 55, 1295. [Google Scholar]
- Kirlin, R.L.; Lascu, C.; Trzynadlowski, A.M. Shaping the Noise Spectrum in Power Electronic Converters. IEEE Trans. Ind. Electron. 2011, 58, 2780–2788. [Google Scholar]
- Lim, Y.C.; Wi, S.O.; Kim, J.N.; Jung, Y.G. A Pseudorandom Carrier Modulation Scheme. IEEE Trans. Power Electron. 2010, 25, 797–805. [Google Scholar]
- Wang, G.; Yang, L.; Yuan, B.; Wang, B.; Zhang, G.; Xu, D. Pseudo-random high-frequency square-wave voltage injection based sensorless control of IPMSM drives for audible noise reduction. IEEE Trans. Ind. Electron. 2016, 63, 7423. [Google Scholar] [CrossRef]
- Peyghambari, A.; Dastfan, A.; Ahmadyfard, A. Selective voltage noise cancellation in three-Phase inverter using random SVPWM. IEEE Trans. Power Electron. 2016, 31, 4604. [Google Scholar] [CrossRef]
- Miyama, Y.; Ishizuka, M.; Kometani, H.; Akatsu, K. Vibration reduction by applying carrier phase-shift PWM on dual three-phase winding permanent magnet synchronous motor. IEEE Trans. Ind. Appl. 2018, 54, 5998. [Google Scholar] [CrossRef]
- Ruiz, G.A.; Vargas, M.F.; Heredia, L.J.; Meco-Gutierrez, M.J.; Perez-Hidalgo, F. Application of slope PWM strategies to reduce acoustic noise radiated by inverter-fed induction motors. IEEE Trans. Ind. Electron. 2013, 60, 2555. [Google Scholar]
- Le, B.J.; Lanfranchi, V.; Hecquet, M.; Brochet, P. Characterization and reduction of audible magnetic noise due to PWM supply in induction machines. IEEE Trans. Ind. Electron. 2010, 57, 1288. [Google Scholar]
- Jarin, T.; Subburaj, P.; Bright, S.J.V. Performance Evaluation and Experimental Validation of Random Pulse Position Pwm for Industrial Drives. SSRN Electron. J. 2015, 7, 137–146. [Google Scholar] [CrossRef]
- Huang, J.; Xiong, R. Study on modulating carrier frequency twice in SPWM single-phase inverter. IEEE Trans. Power Electron. 2014, 29, 3384. [Google Scholar]
- Huang, J.; Li, K. Suppressing the maximum EMI spectral peak through asynchronous carriers in the three-phase inverter with the periodic CFM. IEEE Trans. Power Electron. 2022, 37, 3702–3707. [Google Scholar]

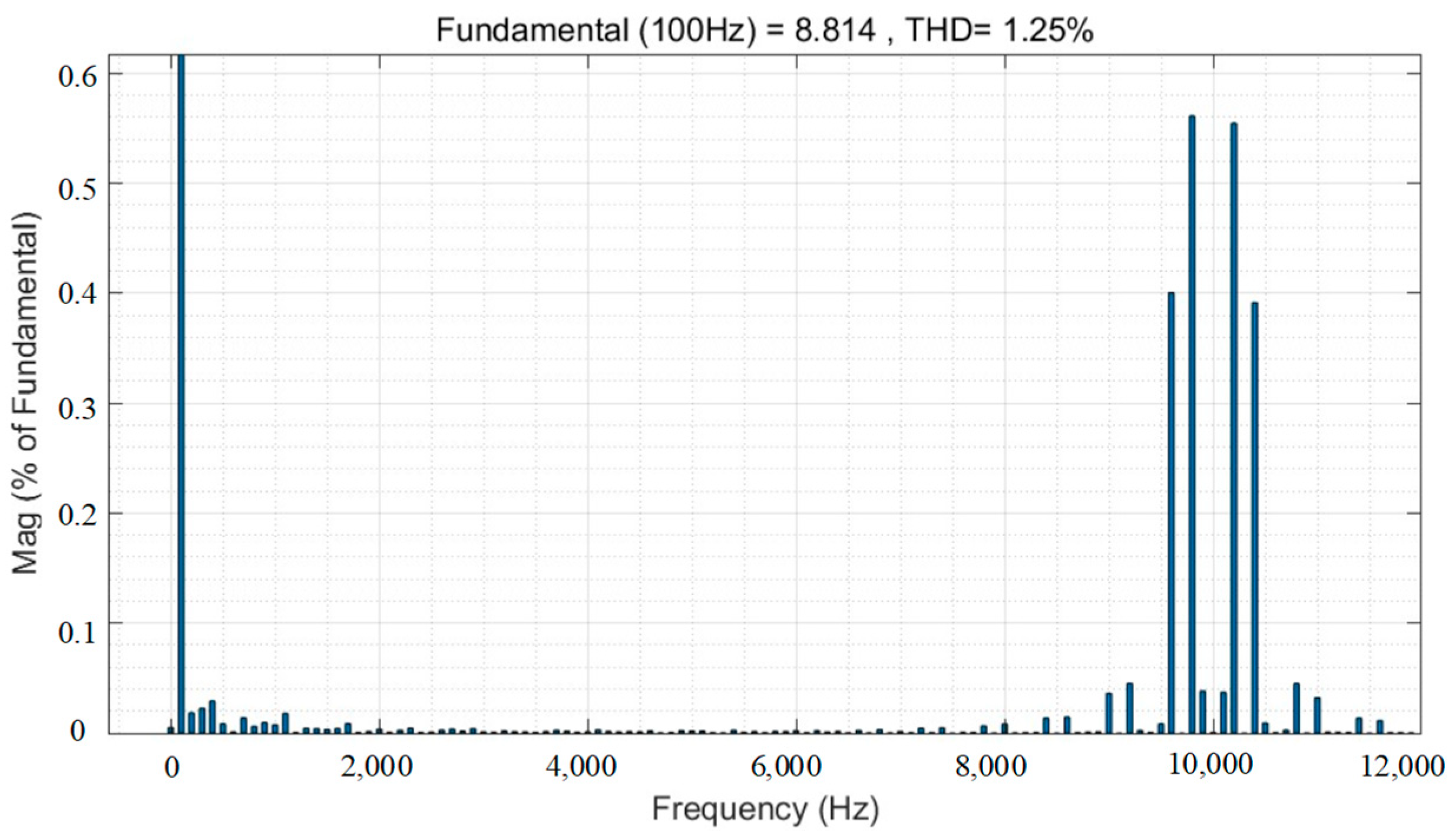
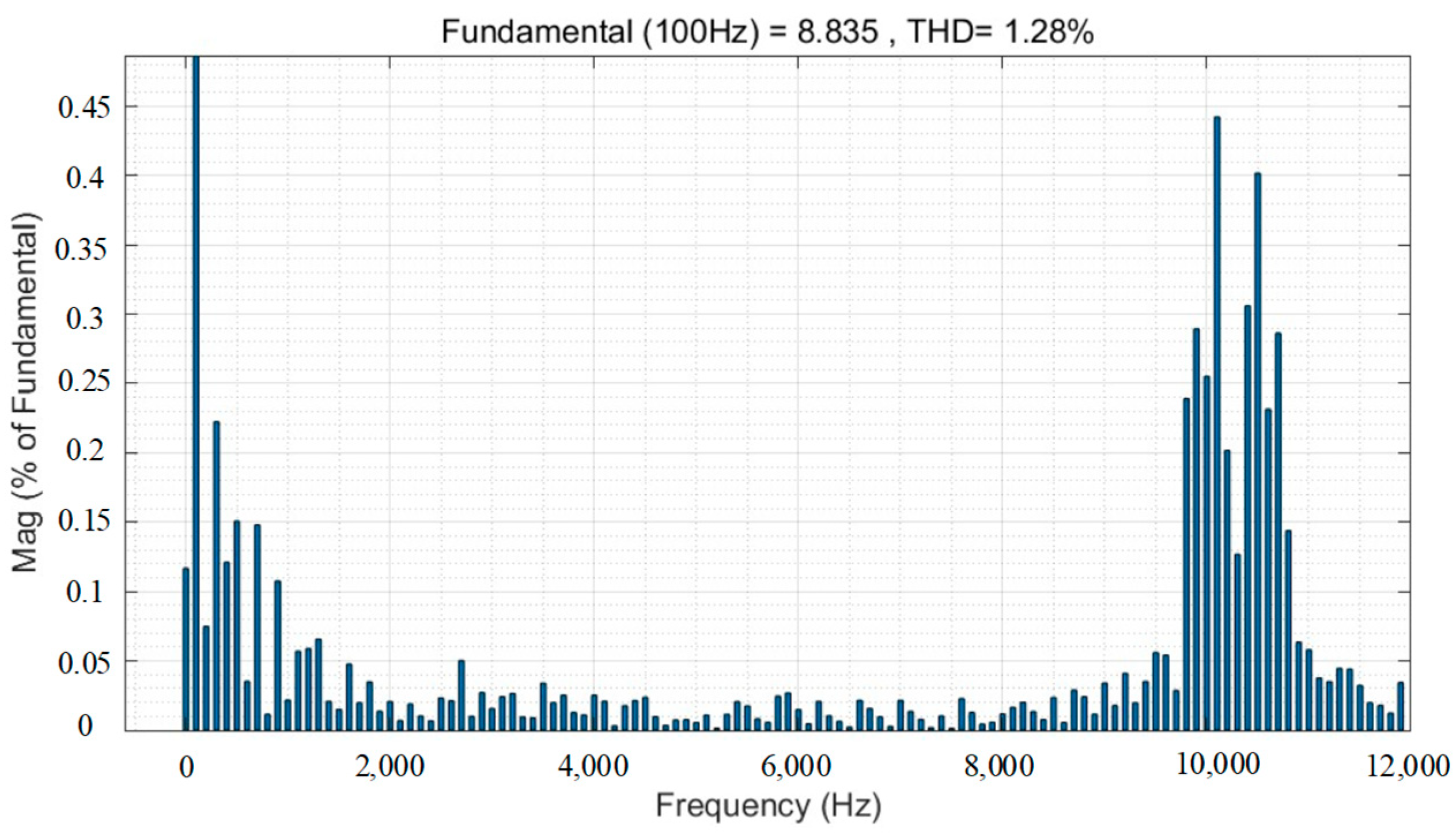
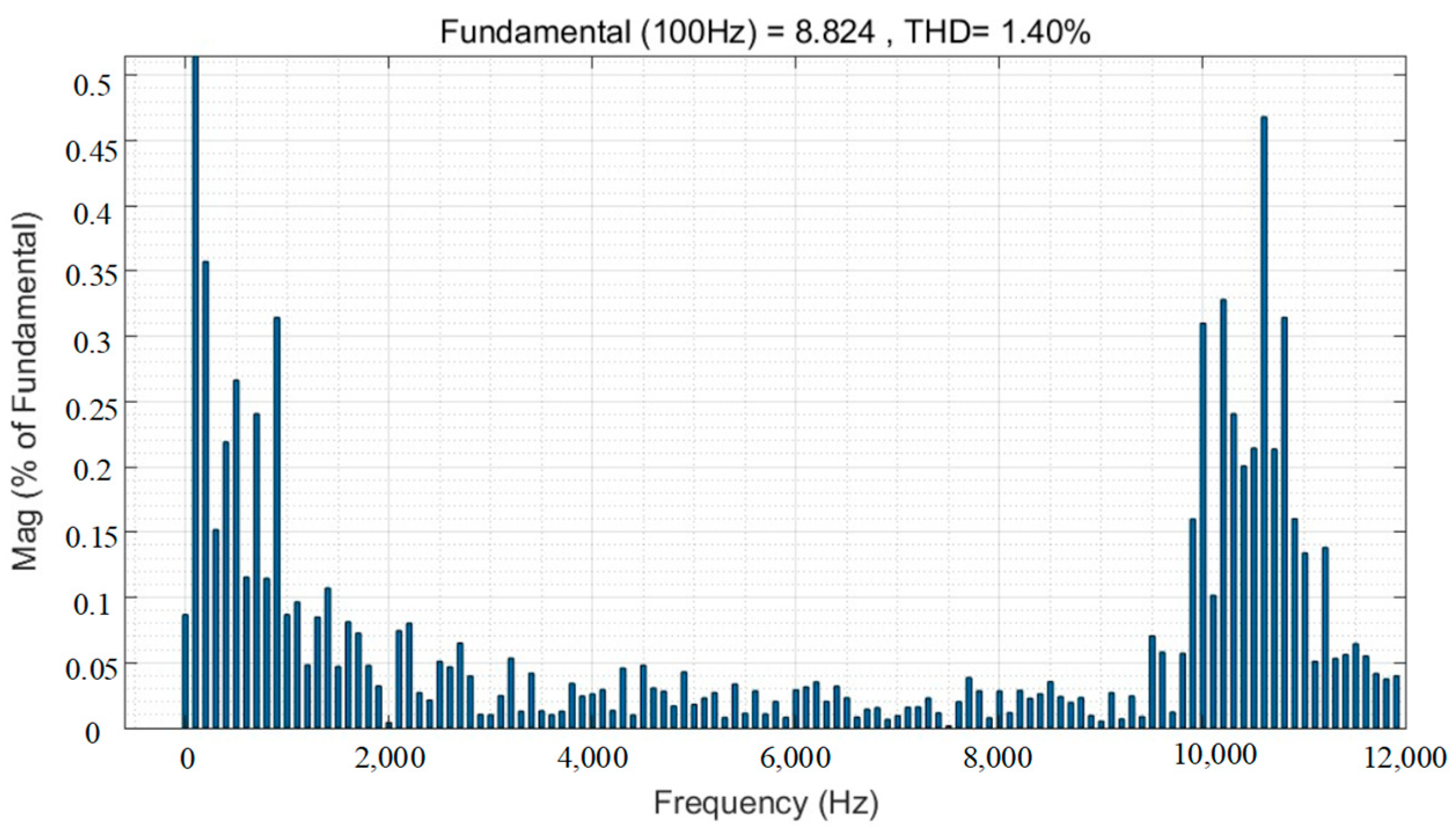

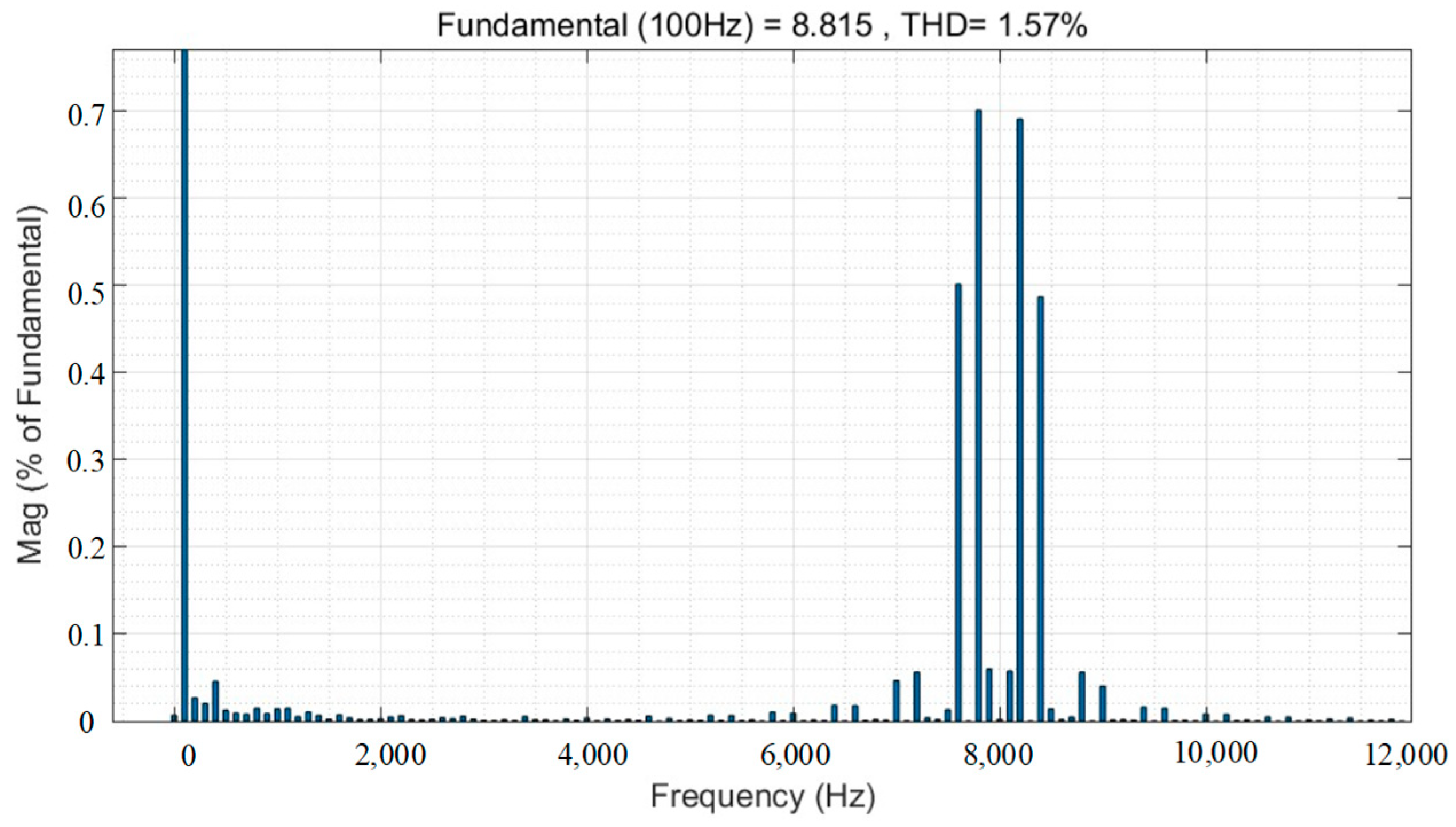



| Switching Frequency | Amplitude Reduction | Reduction Ratio in Amplitude | Elevated THD |
|---|---|---|---|
| 10 kHz | 0.011 A | 21.4% | 0.15 |
| 8 kHz | 0.02 A | 32.9% | 0.13 |
| 6 kHz | 0.03 A | 37% | 0.56 |
| 4 kHz (at 4 kHz) | 0.035 A | 28.6% | 0.7 |
| 4 kHz (at 8 kHz) | 0.067 A | 63.3% | 0.7 |
| Switching Frequency | Base Wave Current Amplitude = 0 | Base Wave Current Amplitude = 0.5 kHz | Base Wave Current Amplitude = 1 kHz |
|---|---|---|---|
| 10 kHz | 8.814 A | 8.835 A | 8.824 A |
| 8 kHz | 8.815 A | 8.826 A | 8.806 A |
| 6 kHz | 8.816 A | 8.817 A | 8.831 A |
| 4 kHz | 8.817 A | 8.841 A | 8.847 A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Wang, Y.; Chen, H.; Hong, J.; Wang, Y. Analysis of Electromagnetic Vibration in Permanent Magnet Motors Based on Random PWM Technology. Machines 2025, 13, 259. https://doi.org/10.3390/machines13040259
Ma C, Wang Y, Chen H, Hong J, Wang Y. Analysis of Electromagnetic Vibration in Permanent Magnet Motors Based on Random PWM Technology. Machines. 2025; 13(4):259. https://doi.org/10.3390/machines13040259
Chicago/Turabian StyleMa, Chi, Yongxiang Wang, Huang Chen, Jianfeng Hong, and Yi Wang. 2025. "Analysis of Electromagnetic Vibration in Permanent Magnet Motors Based on Random PWM Technology" Machines 13, no. 4: 259. https://doi.org/10.3390/machines13040259
APA StyleMa, C., Wang, Y., Chen, H., Hong, J., & Wang, Y. (2025). Analysis of Electromagnetic Vibration in Permanent Magnet Motors Based on Random PWM Technology. Machines, 13(4), 259. https://doi.org/10.3390/machines13040259







