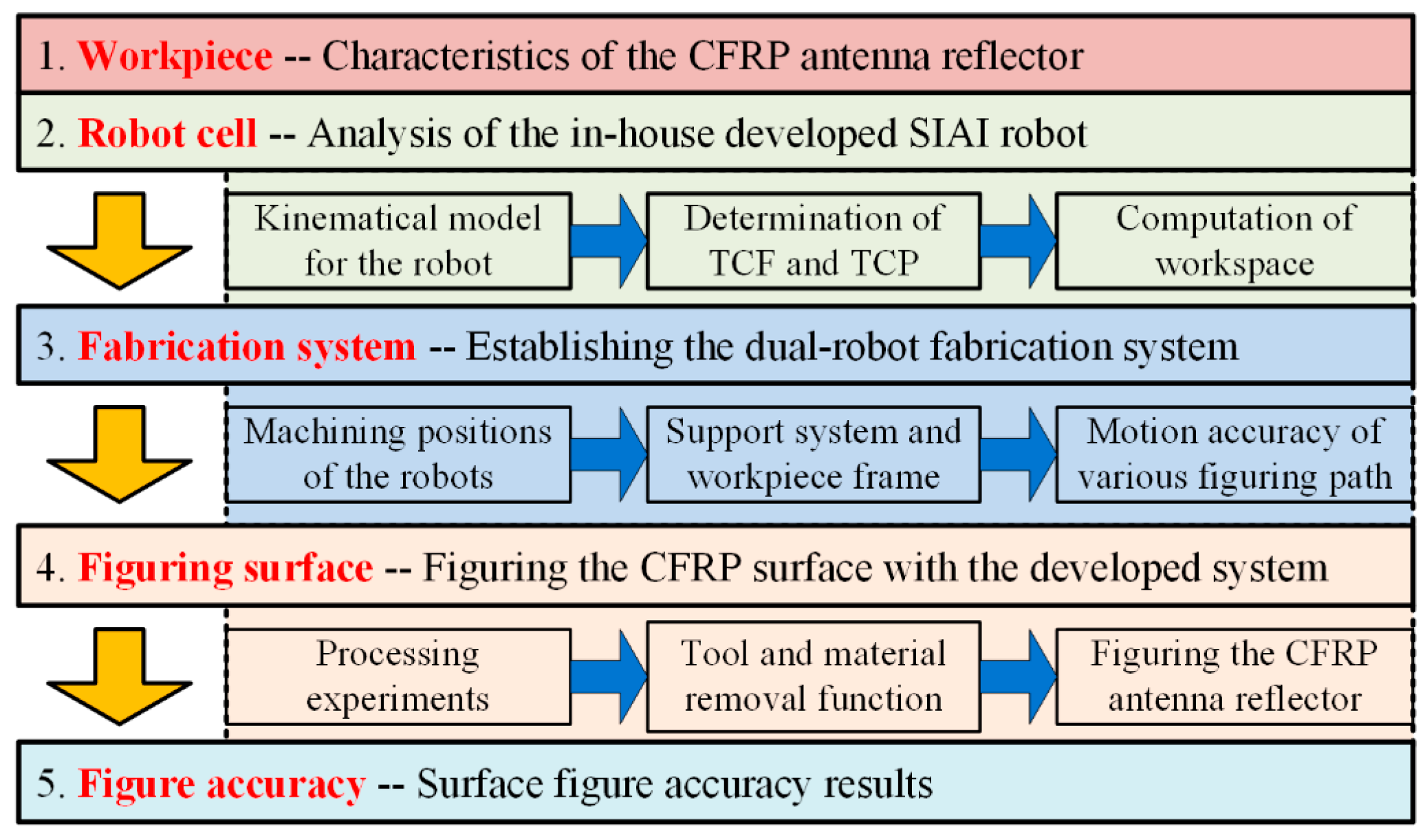
Development and Application of a Dual-Robot Fabrication System in Figuring of a 2.4 m × 4.58 m CFRP Antenna Reflector Surface †
Abstract
1. Introduction
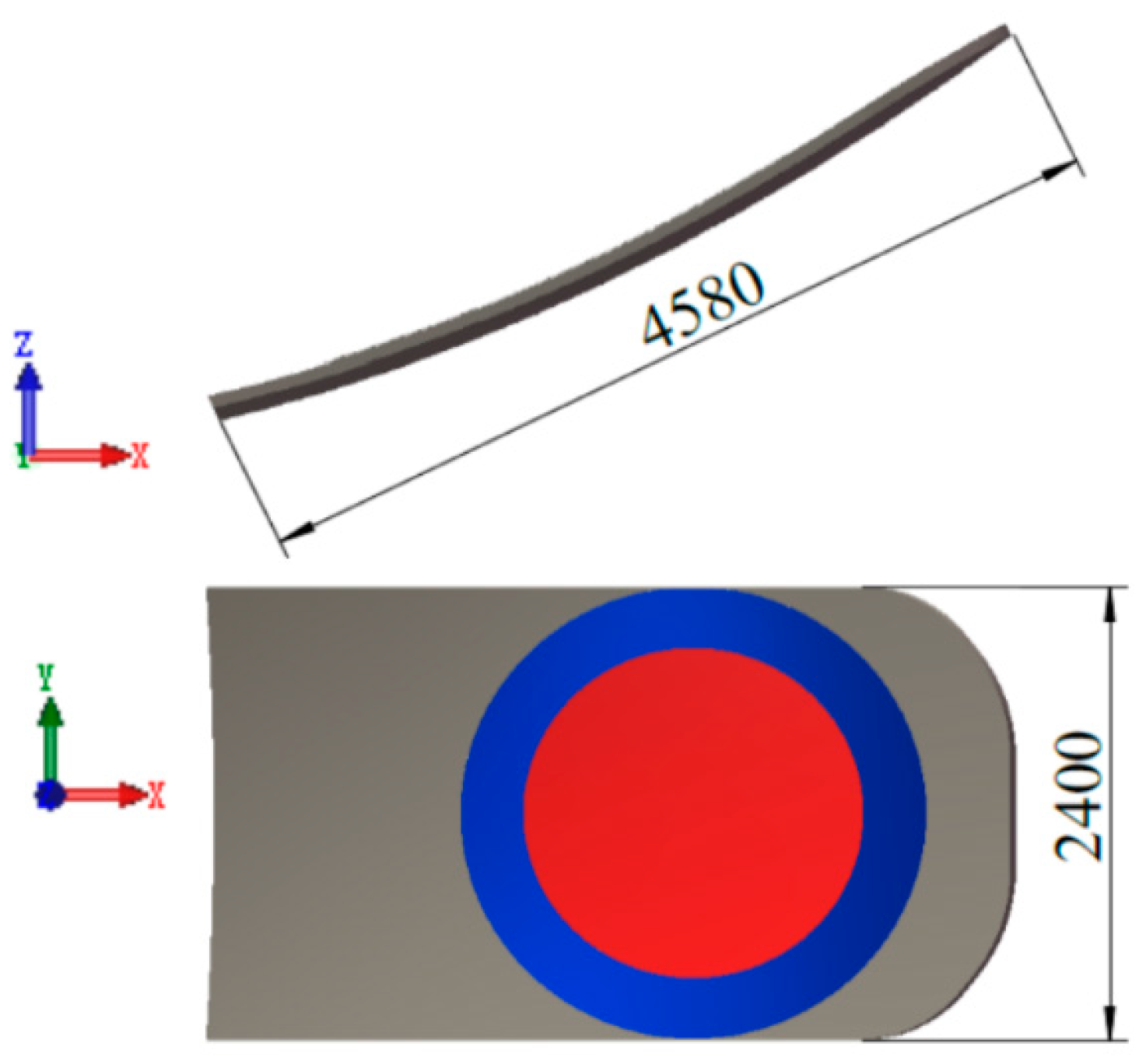
2. Characteristics of the CFRP Antenna Reflector
3. The In-House Developed SIAI Robot
3.1. Overview of SIAI Robot
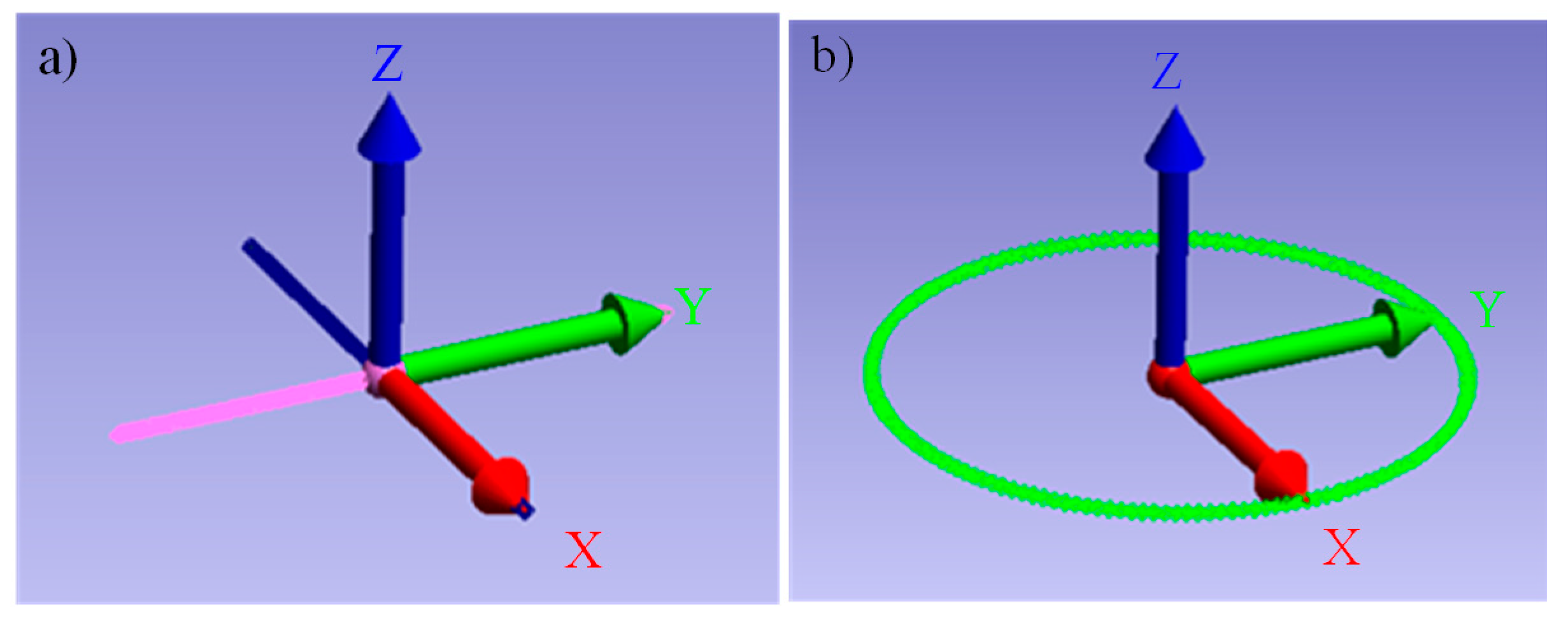
3.2. Determination of the Tool Center Point and Tool Control Frame
- Mount the base and SMR on the end of the polishing tool.
- Measure and set up the robot’s base frame using a laser tracker.
- Adjust the posture and orientation of the robot, deactivate the air valve, and ensure the telescopic link is in a contracted state. Record the joint parameters and the corresponding SMR position .
- Activate the air valve and ensure the telescopic link is in an extended state. Record the joint parameters and the corresponding SMR position .
3.3. Workspace for a Single SIAI Robot
4. Development of the Dual-Robot Fabrication System
4.1. Figuring Positions for the SIAI Robots
4.2. Support Structure for the CFRP Antenna Reflector
4.3. Work Frame for Figuring the CFRP Antenna Reflector
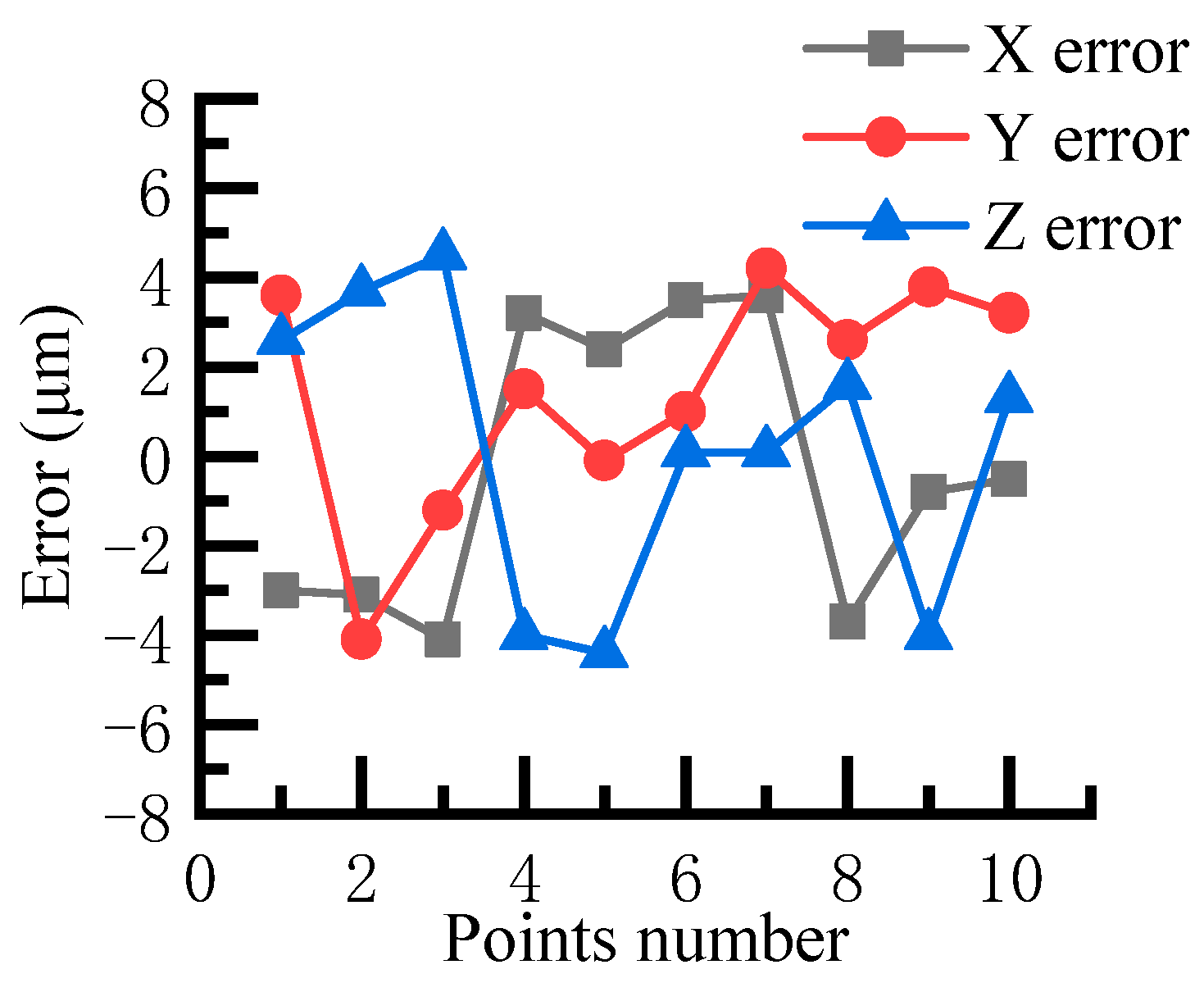
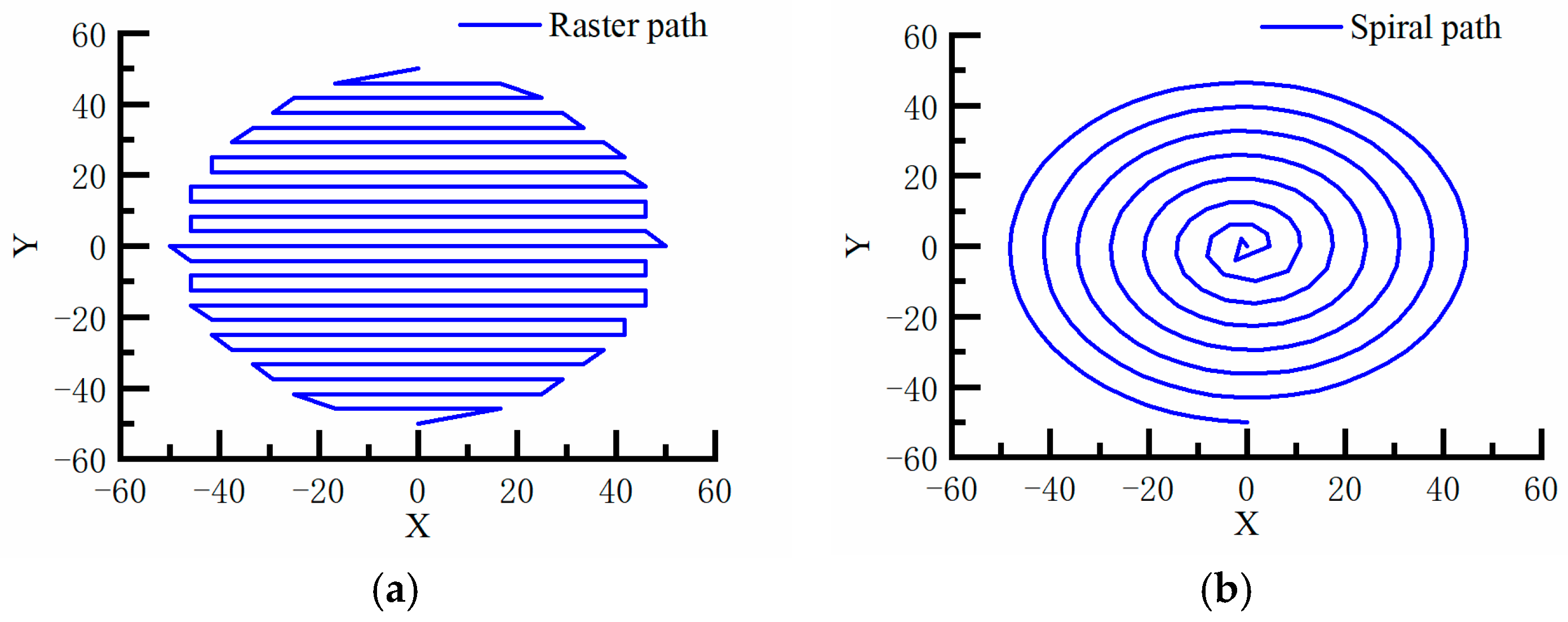
4.4. Surface Figuring Path Based on the SIAI Robot Motion Accuracy
5. Processing Experiments and Tool for Figuring the CFRP Antenna Reflector
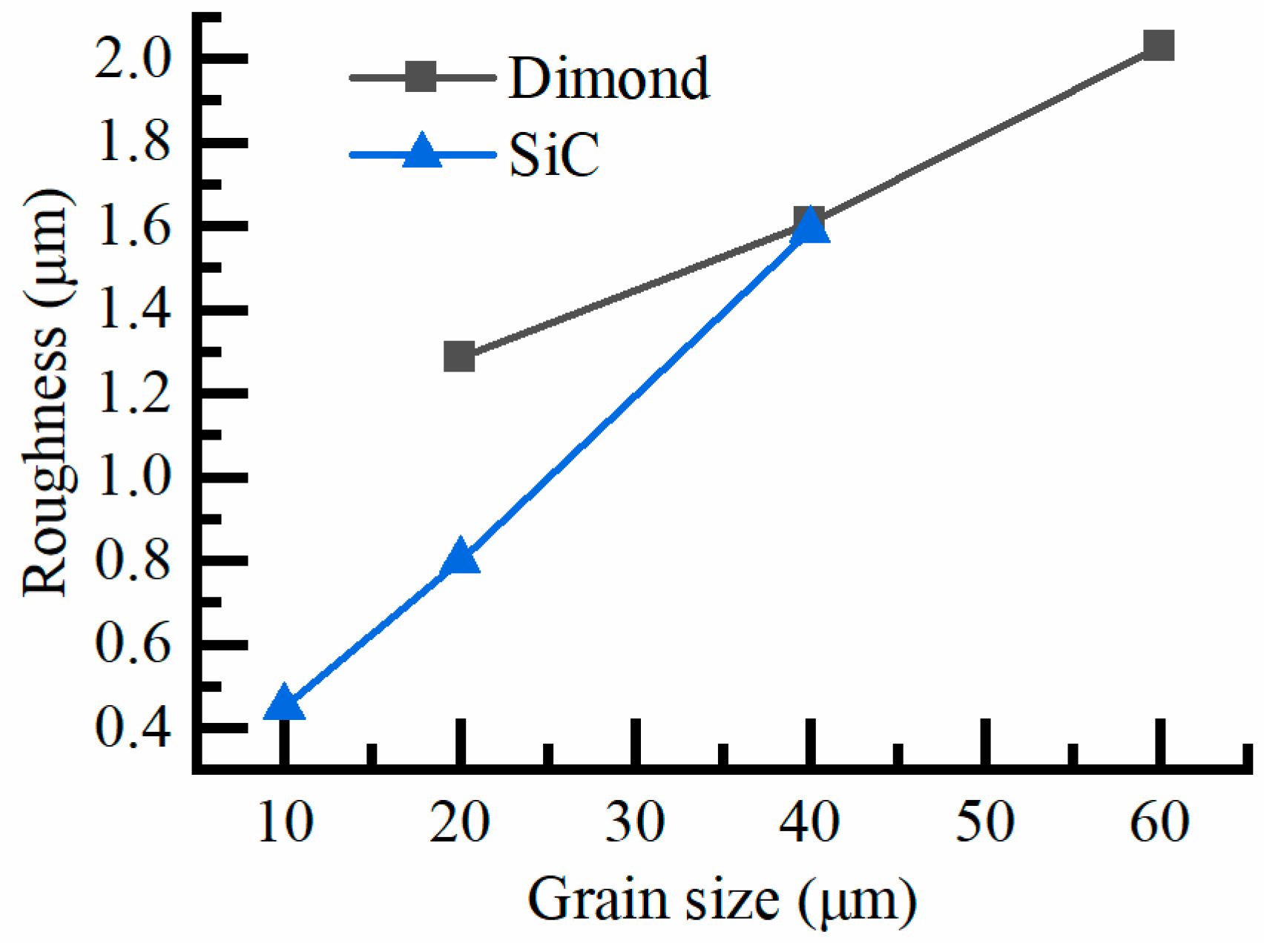
5.1. Processing Experiments to Obtain the Requested Surface Roughness for the CFRP Reflector
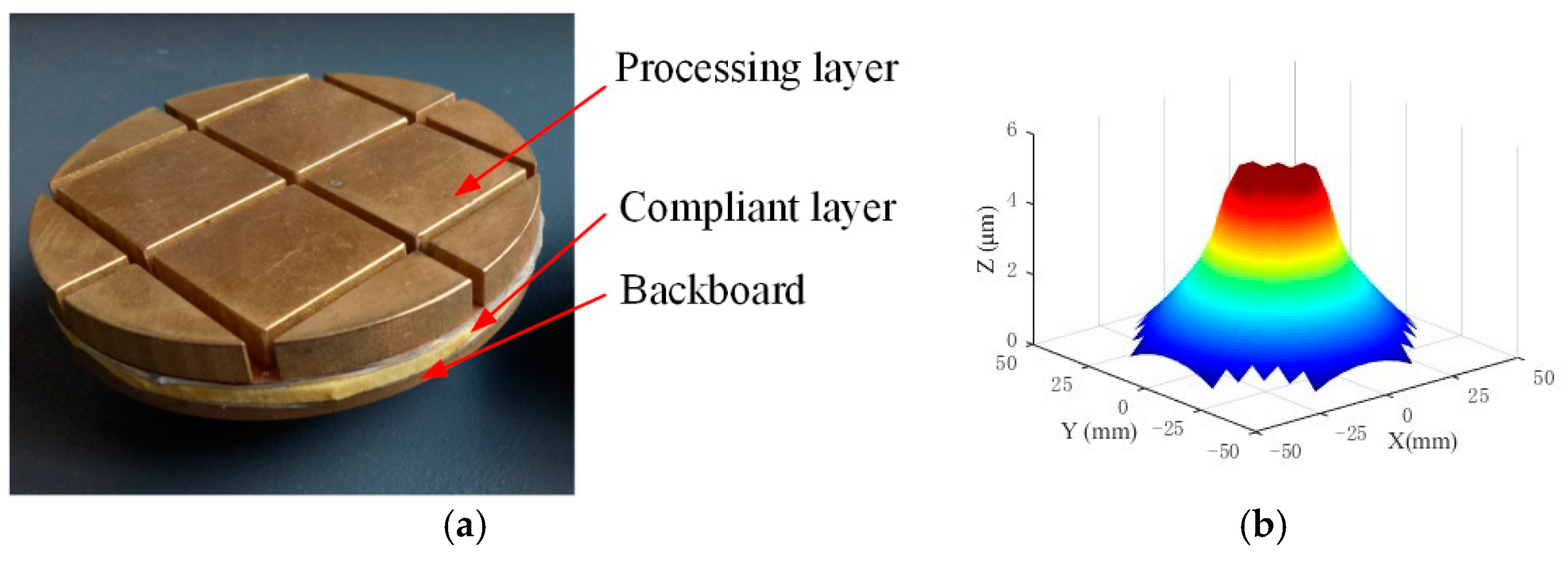
5.2. Tool for Figuring the Reflector Surface
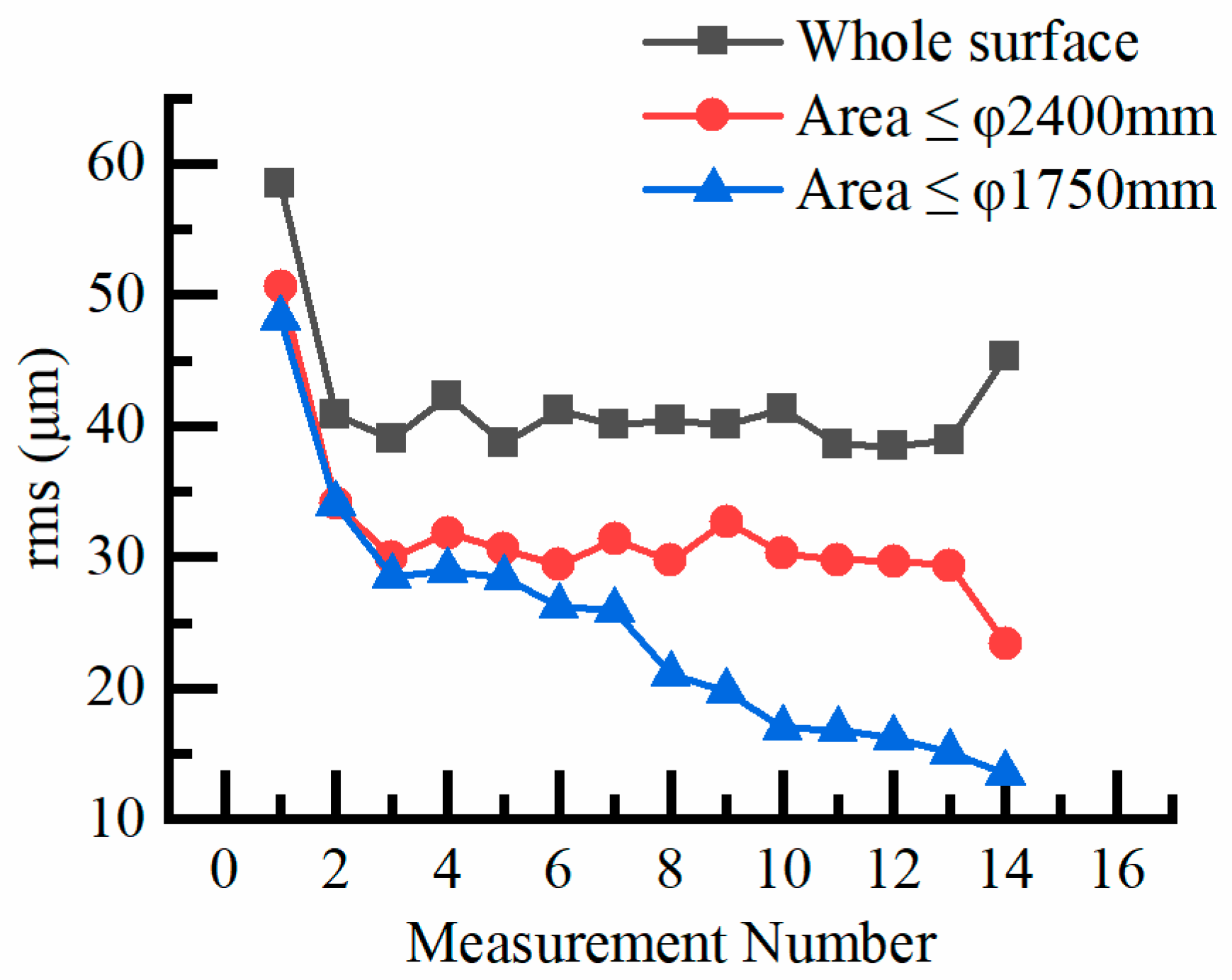
6. Results and Discussion for Figuring CFRP Reflector Surface by Using the Developed System
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bernstein, R.A.; McCarthy, P.J.; Raybould, K.; Bigelow, B.C.; Bouchez, A.H.; Filgueira, J.M.; Jacoby, G.; Johns, M.; Sawyer, D.; Shectman, S.; et al. Overview and status of the Giant Magellan Telescope project. In Proceedings of the Ground-Based and Airborne Telescopes V, Montreal, QC, Canada, 22–27 June 2014; Volume 9145, pp. 494–509. [Google Scholar]
- Graves, L.R.; Smith, G.A.; Apai, D.; Kim, D.W. Precision Optics Manufacturing and Control for Next-Generation Large Telescopes. Nanomanufacturing Metrol. 2019, 2, 65–90. [Google Scholar]
- Martin, H.M.; Burge, J.H.; Davis, J.M.; Kim, D.W.; Kingsley, J.S.; Law, K.; Loeff, A.; Lutz, R.D.; Merrill, C.; Strittmatter, P.A.; et al. Status of mirror segment production for the Giant Magellan Telescope. In Proceedings of the Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II, Edinburgh, UK, 26 June–1 July 2016; Volume 9912, pp. 266–277. [Google Scholar]
- Cayrel, M. E-ELT optomechanics: Overview. In Proceedings of the SPIE—The International Society for Optical Engineering, Amsterdam, The Netherlands, 1–6July 2012; Volume 8444, pp. 674–691. [Google Scholar]
- Rajan, R.T.; Boonstra, A.-J.; Bentum, M.; Klein-Wolt, M.; Belien, F.; Arts, M.; Saks, N.; van der Veen, A.-J. Space-based aperture array for ultra-long wavelength radio astronomy. Exp. Astron. 2016, 41, 271–306. [Google Scholar]
- National Academy of Engineering. Frontiers of Engineering: Reports on Leading-Edge Engineering from the 2015 Symposium; The National Academies Press: Washington, DC, USA, 2016. [Google Scholar]
- Hegde, S.; Satish Shenoy, B.; Chethan, K.N. Review on carbon fiber reinforced polymer (CFRP) and their mechanical performance. Mater. Today Proc. 2019, 19, 658–662. [Google Scholar]
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, present and future prospective of global carbon fibre composite developments and applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar]
- Wu, W.; Li, S.; Qin, X.; Fu, G.; Bao, Z.; Li, H.; Zhao, Q. Tool wear influence on surface roughness, burrs and cracks in milling unidirectional carbon fiber reinforced plastics (UD-CFRP). J. Mater. Res. Technol. 2024, 30, 3052–3065. [Google Scholar]
- Li, J.; Kang, R.; Tian, J.; Dong, Z.; Yan, B. The influence of precision polishing parameters on surface roughness of resin-rich layer on antenna reflective surface. Diam. Abras. Eng. 2023, 43, 250. [Google Scholar]
- Qian, Y.; Kan, F.W.; Sarawit, A.T.; Lou, Z.; Cheng, J.-Q.; Wang, H.-R.; Zuo, Y.-X.; Yang, J. Conceptual Design of the Aluminum Reflector Antenna for DATE5. Res. Astron. Astrophys. 2016, 16, 6. [Google Scholar]
- Qian, Y.; Lou, Z.; Hao, X.; Zhu, J.; Cheng, J.; Wang, H.; Zuo, Y.; Yang, J. Initial development of high-accuracy CFRP panel for DATE5 antenna. Adv. Opt. Mech. Technol. Telesc. Instrum. II 2016, 9912, 475–482. [Google Scholar]
- Qian, Y.; Hao, X.; Shi, Y.; Cai, D.a.; Wu, N.; Lou, Z.; Zuo, Y. Deformation behavior of high accuracy carbon fiber-reinforced plastics sandwiched panels at low temperature, Journal of Astronomical Telescopes. Instrum. Syst. 2019, 5, 034003. [Google Scholar]
- Perez, R.; Gutierrez, S.C.; Zotovic, R. A study on robot arm machining: Advance and future challenges. In Proceedings of the 29th International DAAAM Symposium, Zadar, Croatia, 24–27 October 2018; Volume 29, pp. 931–940. [Google Scholar]
- Torres, R.; Mata, S.; Iriarte, X.; Barrenetxea, D. Robotic Belt Finishing with Process Control for Accurate Surfaces. J. Manuf. Mater. Process. 2023, 7, 124. [Google Scholar] [CrossRef]
- Pedroso, A.F.V.; Sebbe, N.P.V.; Silva, F.J.G.; Campilho, R.D.S.G.; Sales-Contini, R.C.M.; Costa, R.D.F.S.; Sánchez, I.I. An overview on the recent advances in robot-assisted compensation methods used in machining lightweight materials. Robot. Comput.-Integr. Manuf. 2025, 91, 102844. [Google Scholar] [CrossRef]
- Caro, S.; Dumas, C.; Garnier, S.; Furet, B. Workpiece placement optimization for machining operations with a KUKA KR270-2 robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2921–2926. [Google Scholar]
- Iglesias, I.; Sebastián, M.A.; Ares, J.E. Overview of the State of Robotic Machining: Current Situation and Future Potential. Procedia Eng. 2015, 132, 911–917. [Google Scholar] [CrossRef]
- Barosz, P.; Gołda, G.; Kampa, A. Efficiency Analysis of Manufacturing Line with Industrial Robots and Human Operators. Appl. Sci. 2020, 10, 2862. [Google Scholar] [CrossRef]
- Ji, W.; Wang, L. Industrial Robotic Machining: A Review. Int. J. Adv. Manuf. Technol. 2019, 103, 1239–1255. [Google Scholar]
- Chen, H.; Yaseer, A.; Zhang, Y. Top Surface Roughness Modeling for Robotic Wire Arc Additive Manufacturing. J. Manuf. Mater. Process. 2022, 6, 39. [Google Scholar] [CrossRef]
- Walker, D.; Wang, W.; Xu, M.; Yu, G. Coordinate transformation of an industrial robot and its application in deterministic optical polishing. Opt. Eng. 2014, 53, 055102. [Google Scholar]
- Xin, Q.; Liu, H.; Wu, J.; Tang, L.; Wang, D.; Wan, Y. Surface Figuring of Large Carbon Fiber Reinforced Polymer Antenna Reflector with A Dual-robots Fabrication System. EPJ Web Conf. 2019, 215, 05005. [Google Scholar]
- Li, H.; Walker, D.; Zheng, X.; Yu, G.; Reynolds, C.; Zhang, W.; Li, T. Advanced techniques for robotic polishing of aluminum mirrors. In Proceedings of the SPIE Optical Systems Design, Frankfurt, Germany, 14–17 May 2018; Volume 10692, pp. 152–163. [Google Scholar]
- Yao, Y.; Ma, Z.; Ding, J.; Chen, Q.; Fan, X.; Shen, L.; Li, Q. Heavy-calibre off-axis aspheric surface polishing by industrial robot. In Proceedings of the 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Meta-Surface-Wave and Planar Optics, Chengdu, China, 26–29 June 2018; Volume 10838, pp. 16–24. [Google Scholar]
- Wan, S.; Zhang, X.; Xu, M.; Wang, W.; Jiang, X. Region-adaptive path planning for precision optical polishing with industrial robots. Opt. Express 2018, 26, 23782–23795. [Google Scholar]
- Hasirden; Zeng, Z.; Liu, H.; Zhao, H. Measurement and analyses on positioning accuracy for optical processing robots. Opto-Electron. Eng. 2017, 44, 516–522. [Google Scholar]
- Liu, H.; Wan, Y.; Zeng, Z.; Xu, L.; Zhao, H.; Fang, K. Freeform surface grinding and polishing by CCOS based on industrial robot. In Proceedings of the Eighth International Symposium on Advanced Optical Manufacturing and Testing Technology (AOMATT2016), Suzhou, China, 26–29 April 2016; Volume 9683, pp. 587–593. [Google Scholar]
- Brooks, D.R.; Brunelle, M.; Lynch, T.; Medicus, K. Manufacturing of a large, extreme freeform, conformal window with robotic polishing. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 19–23 August 2018; Volume 10742, pp. 126–133. [Google Scholar]
- Zhao, Q.; Zhang, K.; Zhu, S.; Xu, H.; Cao, D.; Zhao, L.; Zhang, R.; Yin, W. Review on the Electrical Resistance/Conductivity of Carbon Fiber Reinforced Polymer. Appl. Sci. 2019, 9, 2390. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, X.; Du, D.; Kong, X.; Qin, G. Low Deformation Optimized Design of CFRP Antenna Reflector. Spacecr. Eng. 2018, 27, 83–88. [Google Scholar]
- Utsunomiya, S.; Kamiya, T.; Shimizu, R. Development of CFRP mirrors for space telescopes. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation, San Diego, CA, USA, 25–29 August 2013; Volume 8837, pp. 206–211. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Chen, Y.; Dong, F. Robot machining: Recent development and future research issues. Int. J. Adv. Manuf. Technol. 2013, 66, 1489–1497. [Google Scholar]
- Park, K.-S.; Lee, J.H.; Youn, S.-K. Lightweight mirror design method using topology optimization. Opt. Eng. 2005, 44, 053002. [Google Scholar]
- Wang, H.; Lou, Z.; Qian, Y.; Zheng, X.; Zuo, Y. Hybrid optimization methodology of variable densities mesh model for the axial supporting design of wide-field survey telescope. Opt. Eng. 2016, 55, 035105. [Google Scholar] [CrossRef]
- Luo, X.; Qi, E.; Hu, H.; Hu, H.; Ford, V.G.; Cole, G. Fabrication and metrology study for M3MP of TMT. In Proceedings of the Eighth International Symposium on Advanced Optical Manufacturing and Testing Technology (AOMATT2016), Suzhou, China, 26–29 April 2016; Volume 9682, pp. 49–57. [Google Scholar]
- Vázquez, E.; Gomar, J.; Ciurana, J.; Rodríguez, C.A. Evaluation of machine-tool motion accuracy using a CNC machining center in micro-milling processes. Int. J. Adv. Manuf. Technol. 2015, 76, 219–228. [Google Scholar]
- Chen, T.; Gao, F.; Li, S.; Liu, X. The Comparative Study on Cutting Performance of Different-Structure Milling Cutters in Machining CFRP. Appl. Sci. 2018, 8, 1353. [Google Scholar] [CrossRef]
- Nam, H.-S.; Kim, G.-C.; Kim, H.-S.; Rhee, H.-G.; Ghim, Y.-S. Modeling of edge tool influence functions for computer controlled optical surfacing process. Int. J. Adv. Manuf. Technol. 2016, 83, 911–917. [Google Scholar] [CrossRef]
- Haitao, L.; Zhige, Z.; Fan, W.; Bin, F.; Yongjian, W. Study on active lap tool influence function in grinding 1.8 m primary mirror. Appl. Opt. 2013, 52, 7504–7511. [Google Scholar]











| Range of Motion | |||||
|---|---|---|---|---|---|
| 1 | 0 | 1021 | 0 | −145°~145° | |
| 2 | 0 | 0 | 0 | −5 mm~904 mm | |
| 3 | 1402.08 | −229 | 0 | −156°~156° | |
| 4 | 0 | 1400.7 | 90 | −183°~183° | |
| 5 | 0 | 0 | −90 | −120~120° | |
| 6 | 0 | 344 | 90 | −195°~195° | |
| 7 | 0 | 0 | −90 | −90 | 0 |
| Error | Motion Along X Direction (μm) | Motion Along Y Direction (μm) | Circular Motion (μm) |
|---|---|---|---|
| Mean | 54.472 | 25.016 | 144.746 |
| rms | 63.408 | 27.769 | 160.801 |
| Maximum | 138.125 | 57.276 | 324.909 |
| Minimum | 5.947 | 1.822 | 10.158 |
| Measurement No. | rms Accuracy (μm) | ||
|---|---|---|---|
| ≤φ1750 mm | ≤φ2400 mm | Whole Surface | |
| 1st | 13.4 | 23.4 | 45.8 |
| 2nd | 13.5 | 24 | 42.8 |
| 3rd | 13.7 | 24.2 | 41.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, Q.; Liu, H.; Wu, J.; Lu, L.; Hao, X.; Zeng, Z.; Wan, Y. Development and Application of a Dual-Robot Fabrication System in Figuring of a 2.4 m × 4.58 m CFRP Antenna Reflector Surface. Machines 2025, 13, 268. https://doi.org/10.3390/machines13040268
Xin Q, Liu H, Wu J, Lu L, Hao X, Zeng Z, Wan Y. Development and Application of a Dual-Robot Fabrication System in Figuring of a 2.4 m × 4.58 m CFRP Antenna Reflector Surface. Machines. 2025; 13(4):268. https://doi.org/10.3390/machines13040268
Chicago/Turabian StyleXin, Qiang, Haitao Liu, Jieli Wu, Liming Lu, Xufeng Hao, Zhige Zeng, and Yongjian Wan. 2025. "Development and Application of a Dual-Robot Fabrication System in Figuring of a 2.4 m × 4.58 m CFRP Antenna Reflector Surface" Machines 13, no. 4: 268. https://doi.org/10.3390/machines13040268
APA StyleXin, Q., Liu, H., Wu, J., Lu, L., Hao, X., Zeng, Z., & Wan, Y. (2025). Development and Application of a Dual-Robot Fabrication System in Figuring of a 2.4 m × 4.58 m CFRP Antenna Reflector Surface. Machines, 13(4), 268. https://doi.org/10.3390/machines13040268






