Decentralized Adaptive Control of Closed-Kinematic Chain Mechanism Manipulators
Abstract
:1. Introduction
2. Synchronization Control
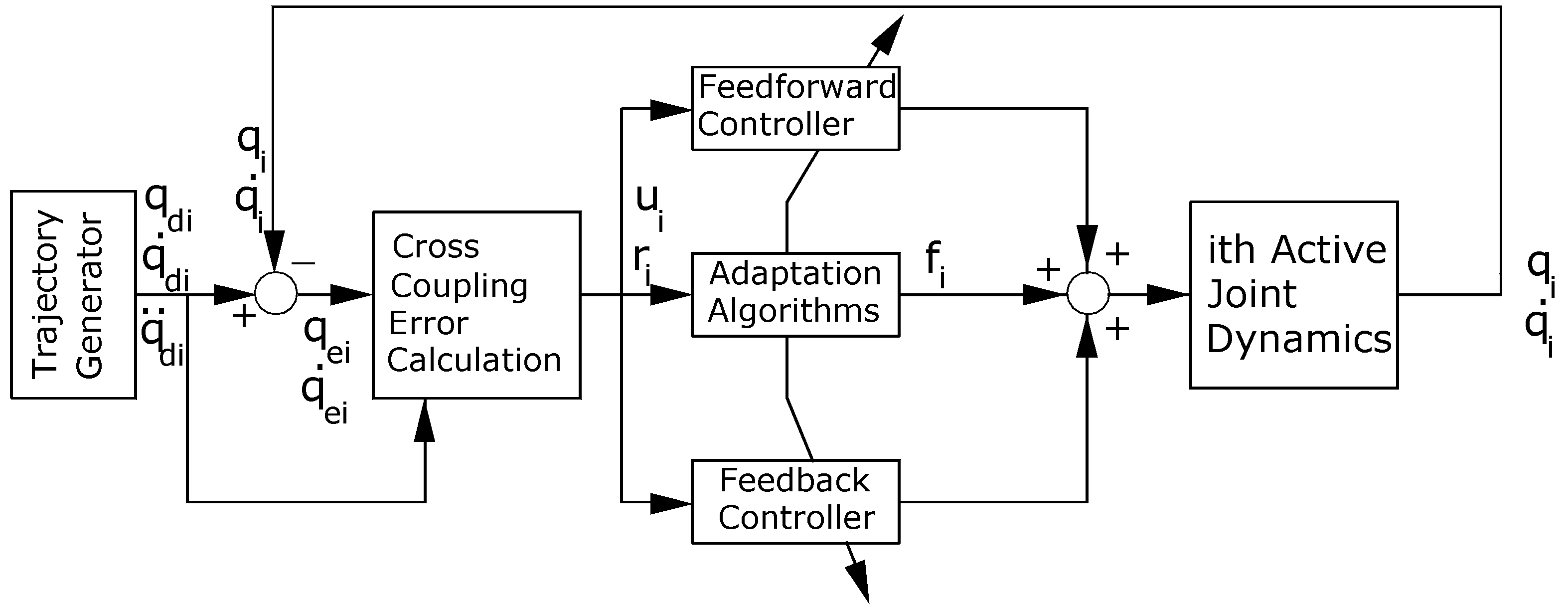
3. Development of the DASCS
- The first term represents auxiliary signal to improve the tracking performance and partly compensate for disturbance .
- The second term = represents the PID feedback controller.
- The last term represent the feedforward controller.
4. Computer Simulation Study of a 6-DOF CKCM Manipulator
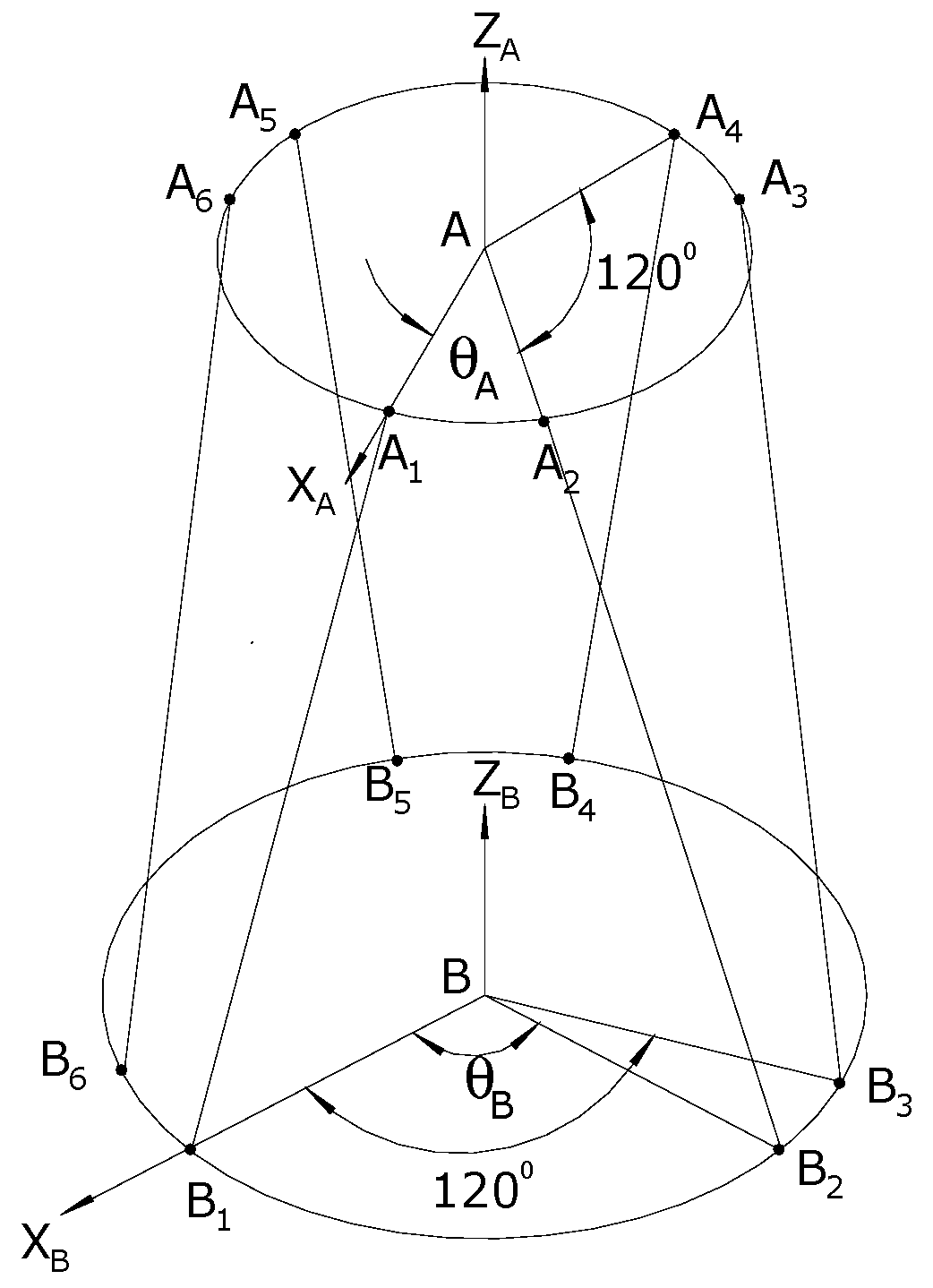
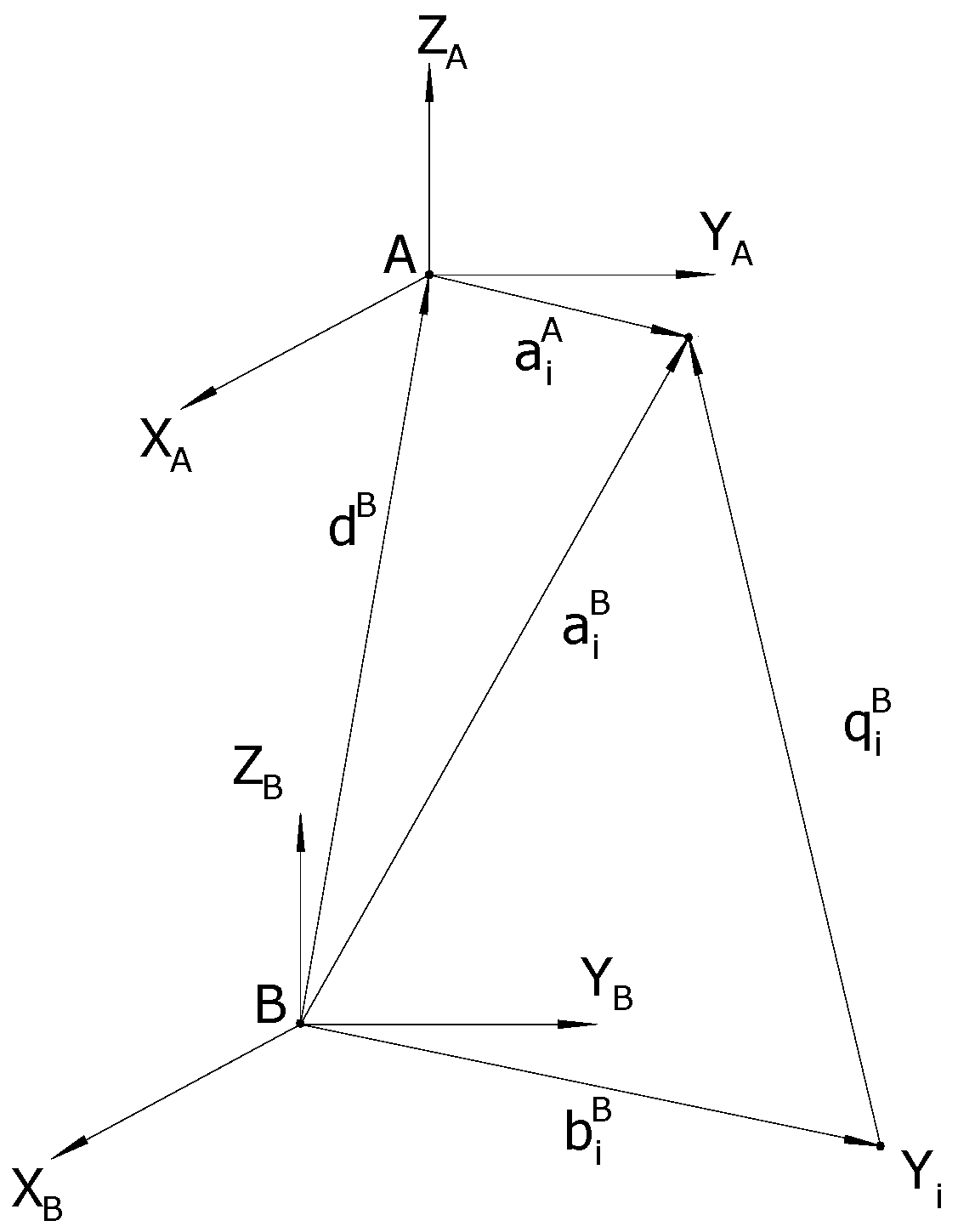
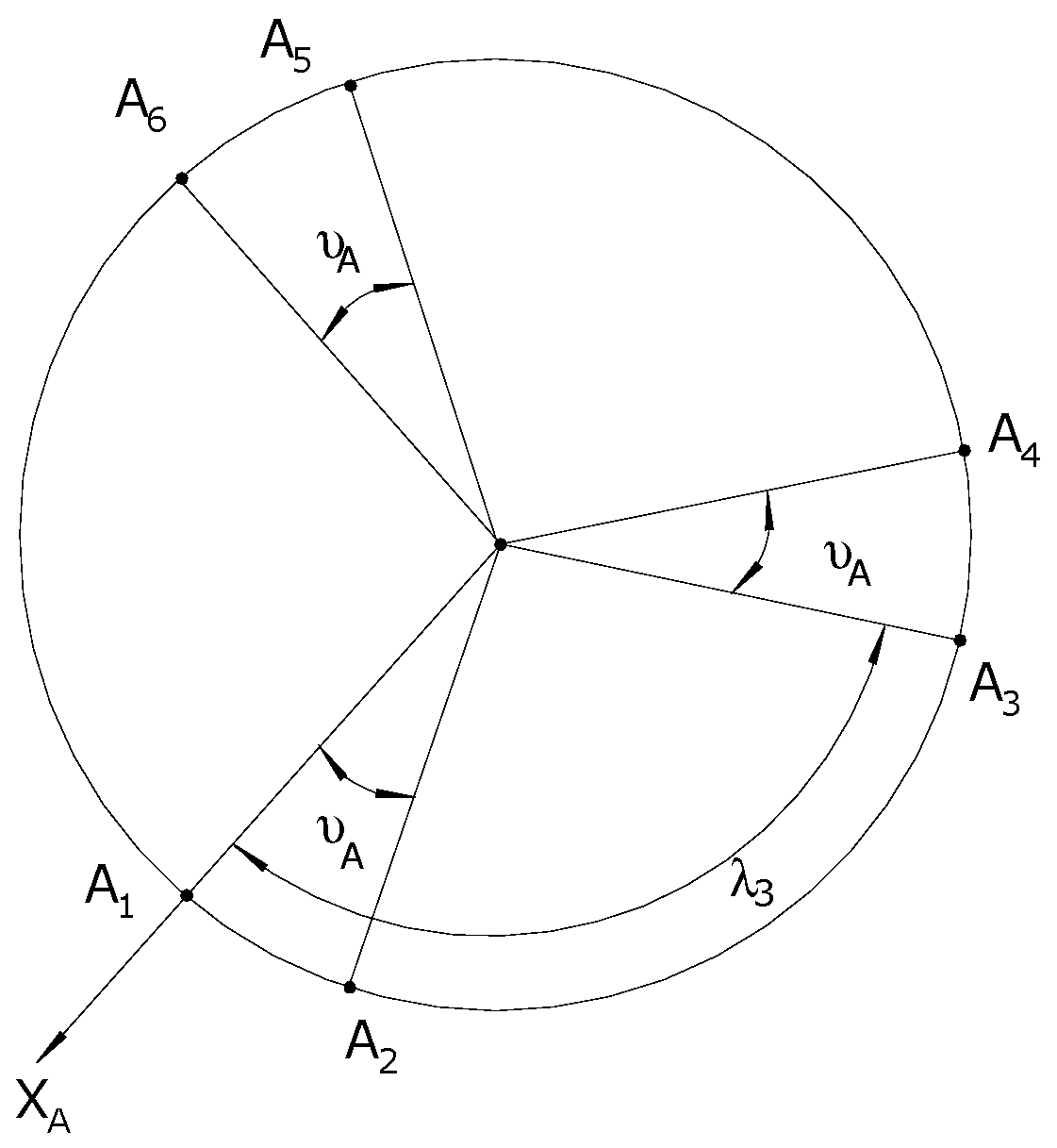
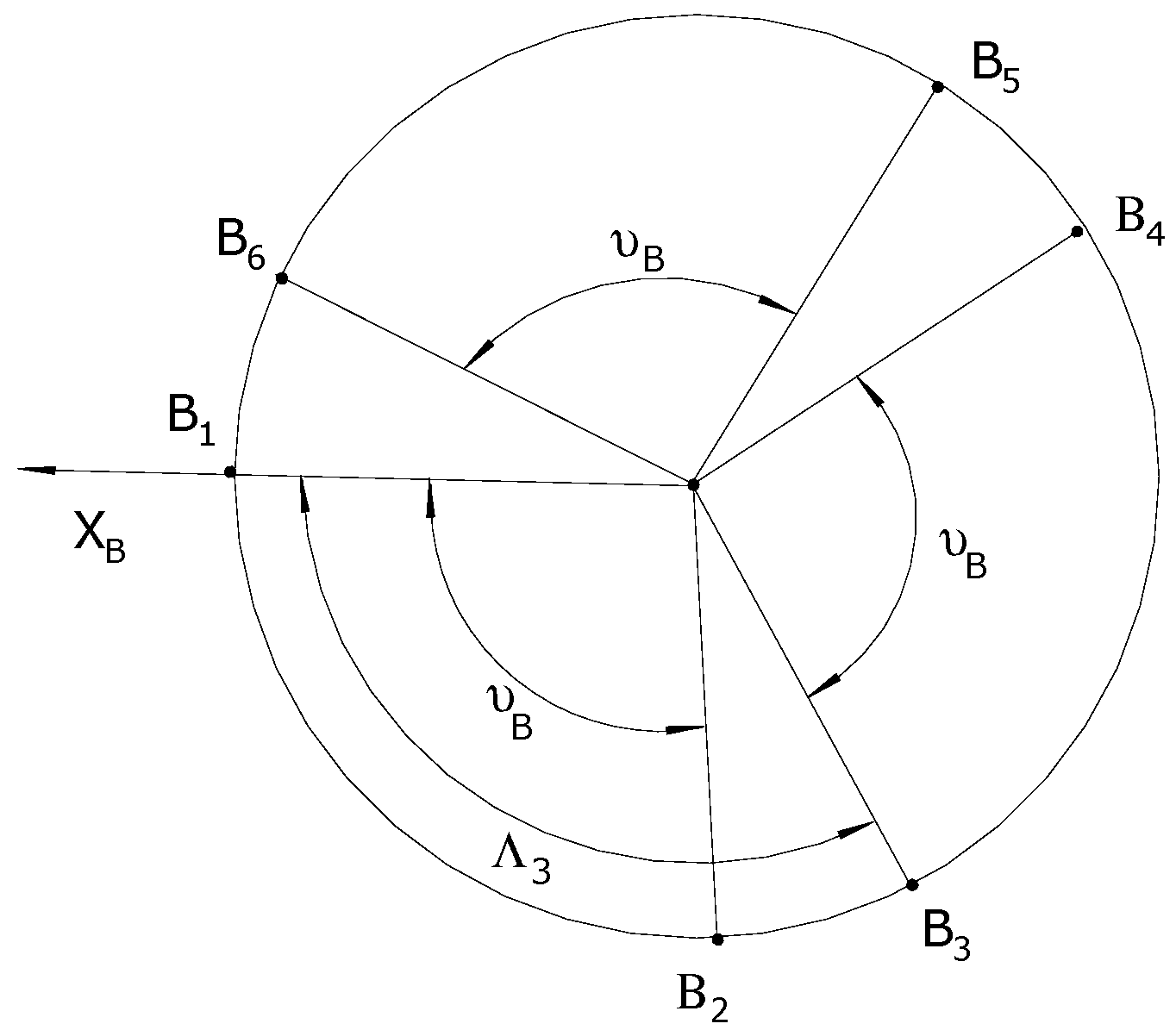
4.1. Kinematic Analysis of the 6-DOF CKCM Manipulator
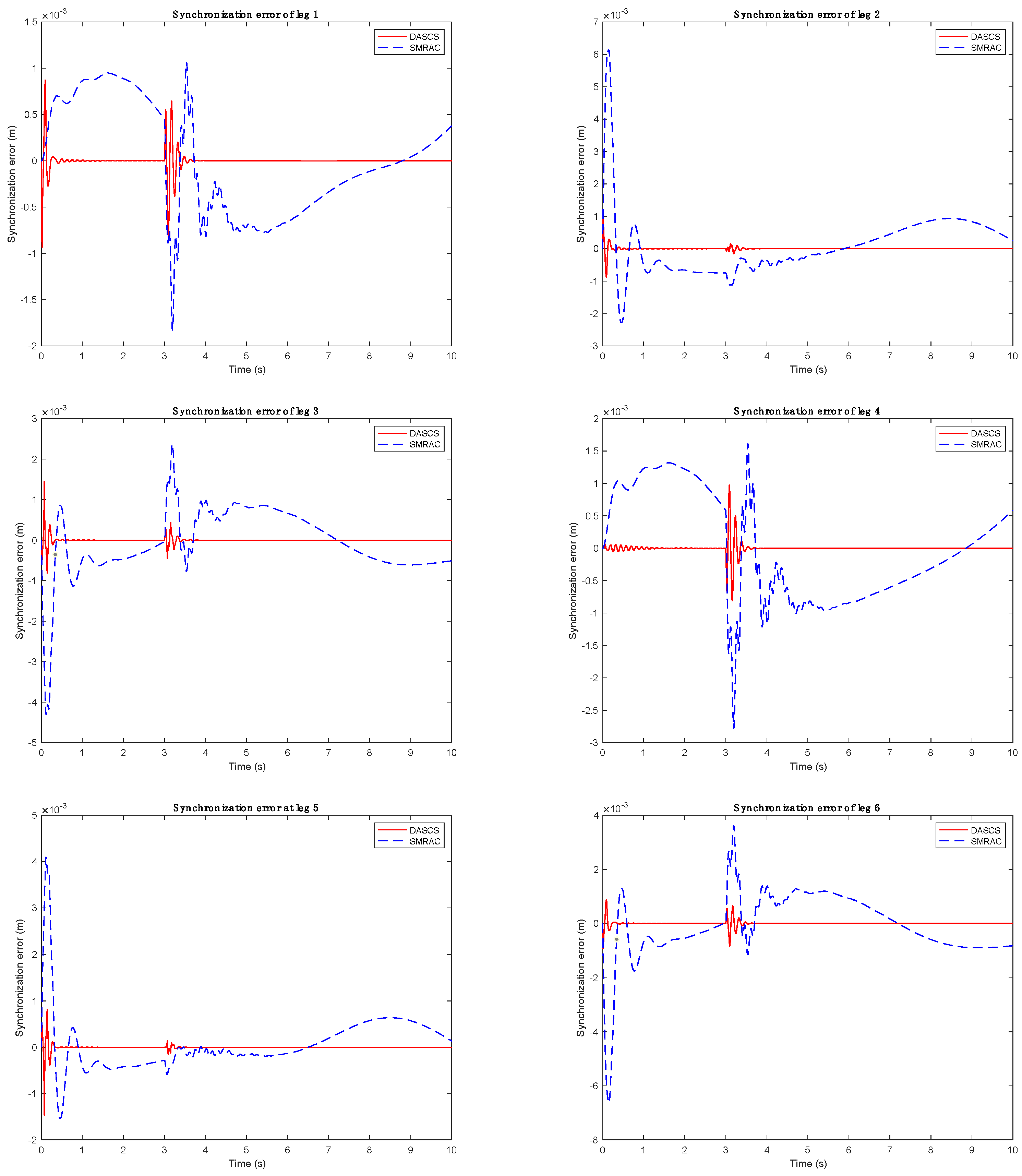
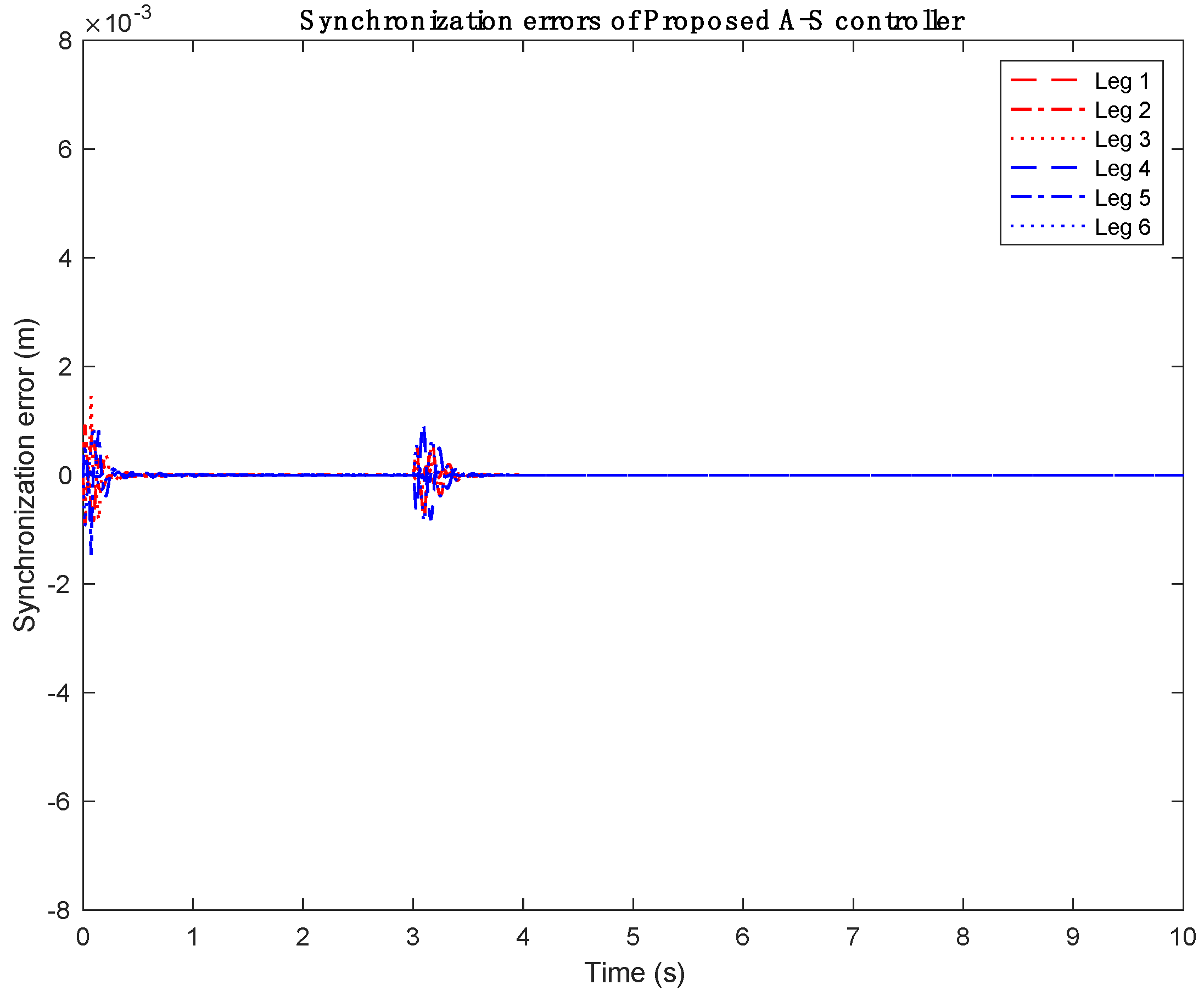
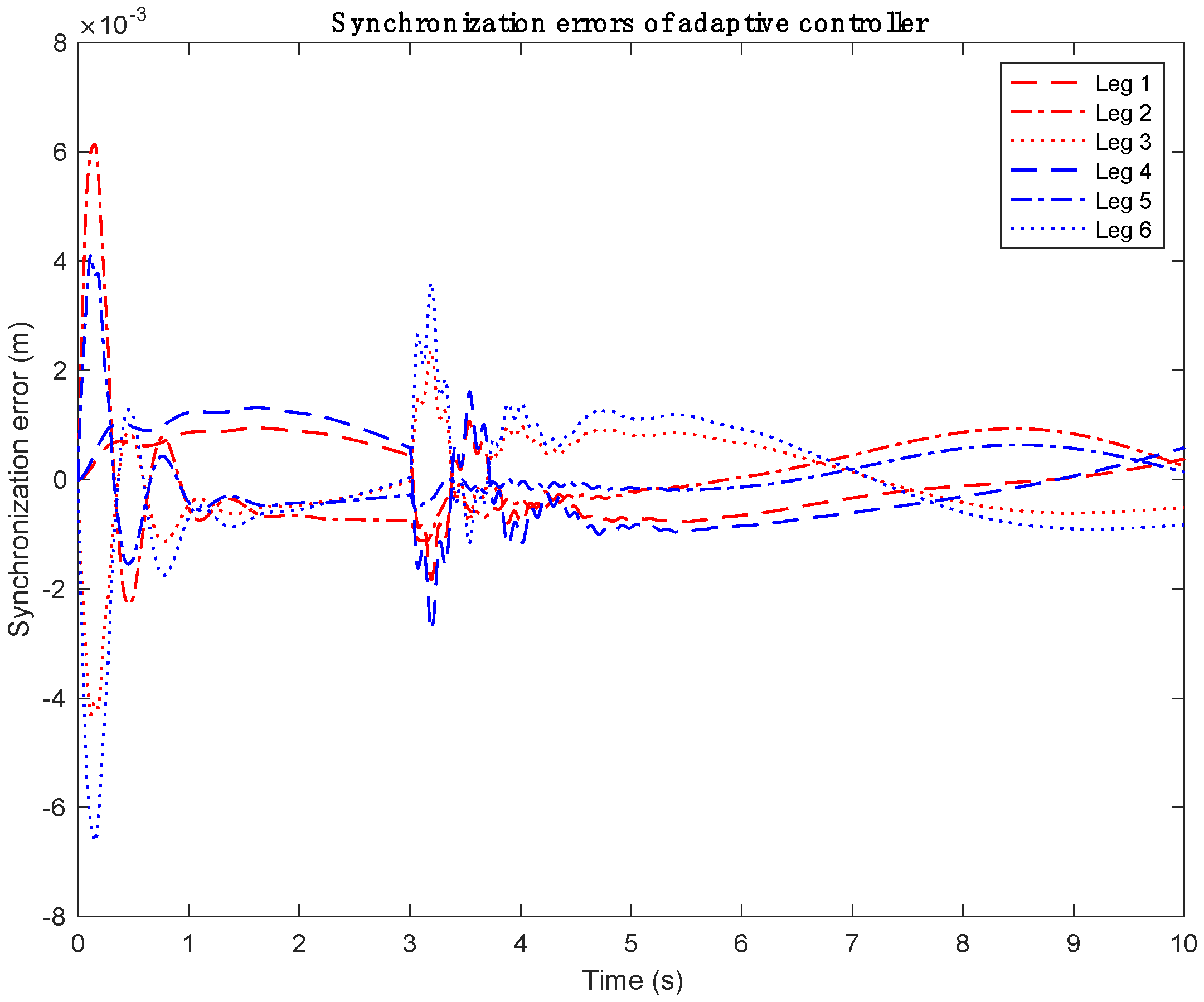
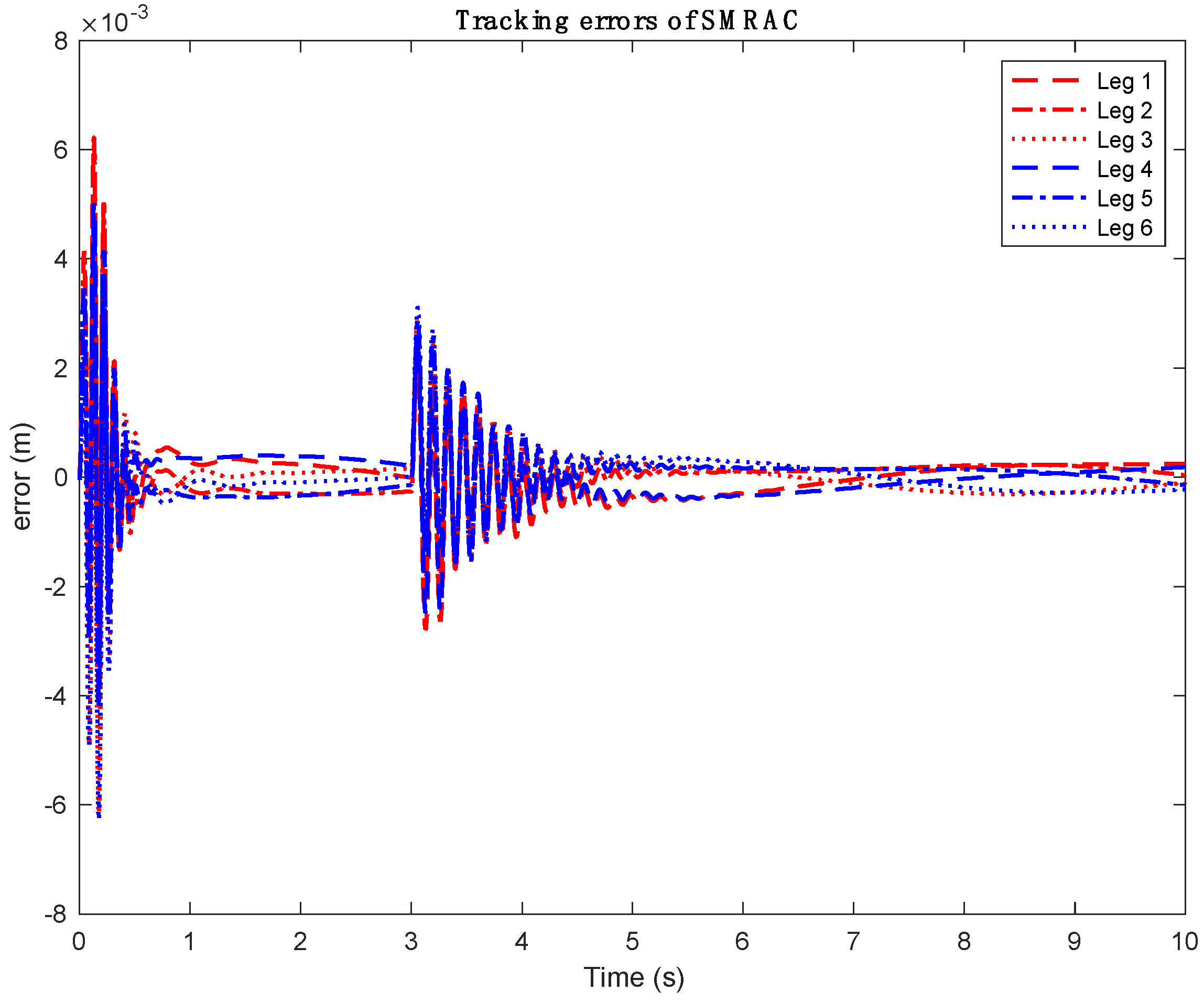
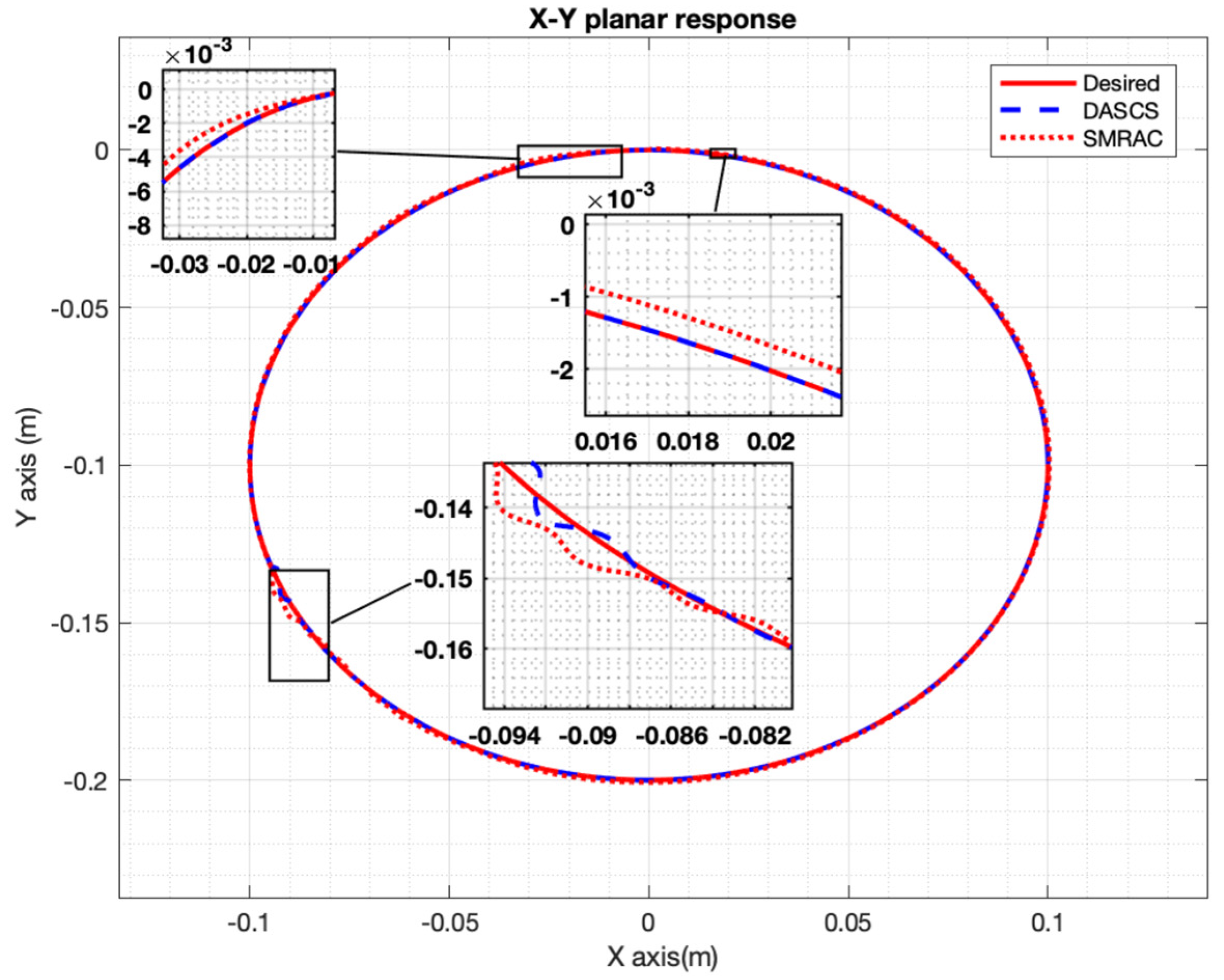
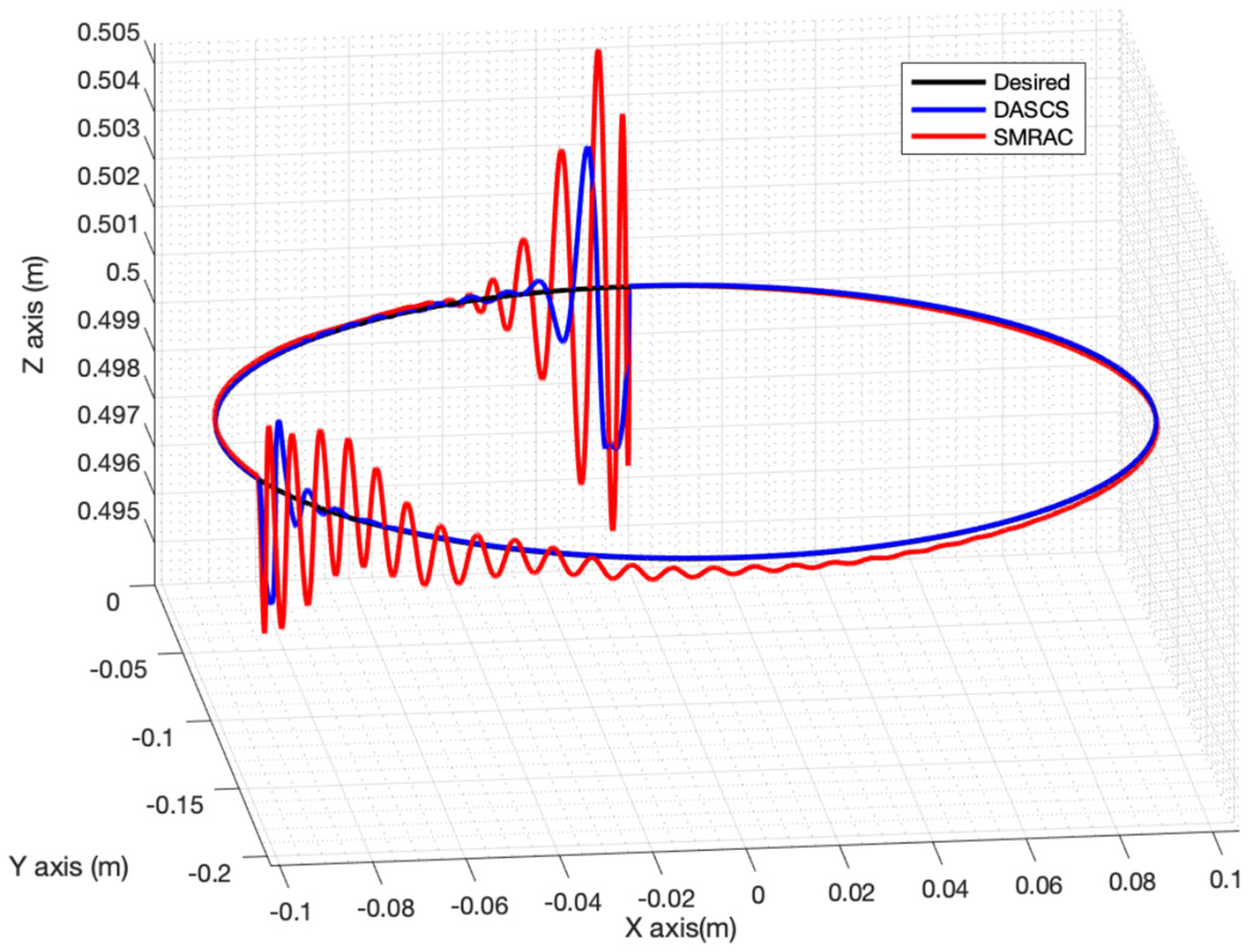
4.2. Computer Simulation Results
5. Conclusions
- Experimental investigation of the performance of DASC on real CKCM manipulators in comparison with other conventional MRAC schemes.
- Application of DASCS on OKCM manipulators and evaluation of its performance using computer simulation and experimentation.
- Combination of DASC with other intelligent control methods including fuzzy control, neuro fuzzy control, and neural network control to improve performance.
- Addressing robustness and resilience of synchronized error control of robot manipulators.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bi, Z.M.; Lin, Y.; Zhang, W.J. The general architecture of adaptive robotic systems for manufacturing applications. Robot. Comput.-Integr. Manuf. 2010, 26, 461–470. [Google Scholar] [CrossRef]
- Wu, F.X.; Zhang, W.J.; Li, Q.; Ouyang, P.R. Integrated design and PD control of high-speed closed-loop mechanisms. J. Dyn. Syst. Meas. Control 2002, 124, 522–528. [Google Scholar] [CrossRef]
- Merlet, J.P. Parallel Robots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 128. [Google Scholar]
- Dasgupta, B.; Mruthyunjaya, T.S. The Stewart platform manipulator: A review. Mech. Mach. Theory 2000, 35, 15–40. [Google Scholar] [CrossRef]
- Stewart, D. A Platform with Six Degrees of Freedom. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Tsai, L.W. Robot Analysis: The Mechanics of Serial and Parallel Manipulators; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Yanna, Y.; Huiying, W.; Lu, S.; Wei, H. The Influence of Road Geometry on Vehicle Rollover and Skidding. Int. J. Environ. Res. Public Health 2020, 17, 1648. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, X. Coupled Dynamics of Vehicle-Bridge Interaction System Using High Efficiency Method. Adv. Civ. Eng. 2021, 2021, 1964200. [Google Scholar] [CrossRef]
- Kelly, R.; Davila, V.S.; Perez, J.A.L. Control of Robot Manipulators in Joint Space; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Koren, Y. Cross-coupled biaxial computer control for manufacturing systems. J. Dyn. Syst. Meas. Control 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Li, Y.; Nielsen, C. Position synchronized path following for a mobile robot and manipulator. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 3541–3546. [Google Scholar]
- Do, K.D. Synchronization motion tracking control of multiple underactuated ships with collision avoidance. IEEE Trans. Ind. Electron. 2016, 63, 2976–2989. [Google Scholar] [CrossRef]
- Bouteraa, Y.; Ghommam, J.; Poisson, G.; Derbel, N. Distributed synchronization control to trajectory tracking of multiple robot manipulators. J. Robot. 2011, 2011, 652785. [Google Scholar] [CrossRef]
- Wang, C.; Sun, D. A synchronization control strategy for multiple robot systems using shape regulation technology. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 467–472. [Google Scholar]
- Sun, D.; Shao, X.; Feng, G. A model-free cross-coupled control for position synchronization of multi-axis motions: Theory and experiments. IEEE Trans. Control Syst. Technol. 2007, 15, 306–314. [Google Scholar] [CrossRef]
- Ouyanga, P.R.; Dam, T.; Huang, J.; Zhang, W.J. Contour tracking control in position domain. Mechatronics 2012, 22, 934–944. [Google Scholar] [CrossRef]
- Shang, W.; Cong, S.; Ge, Y. Coordination motion control in the task space for parallel manipulators with actuation redundancy. IEEE Trans. Autom. Sci. Eng. 2012, 10, 665–673. [Google Scholar] [CrossRef]
- Sun, D.; Wang, C.; Shang, W.; Feng, G. A synchronization approach to trajectory tracking of multiple mobile robots while maintaining time-varying formations. IEEE Trans. Robot. 2009, 25, 1074–1086. [Google Scholar]
- Sun, D.; Mills, J.K. Adaptive synchronized control for coordination of two robot manipulators. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), Washington, DC, USA, 11–15 May 2002; Cat. No. 02CH37292. Volume 1, pp. 976–981. [Google Scholar]
- Zhu, W.H. On adaptive synchronization control of coordinated multi robots with flexible/rigid constraints. IEEE Trans. Robot. 2005, 21, 520–552. [Google Scholar]
- Wang, H. Task-space synchronization of networked robotic systems with uncertain kinematics and dynamics. IEEE Trans. Autom. Control 2013, 58, 3169–3174. [Google Scholar] [CrossRef]
- Long, Y.; Yang, X.J. Robust adaptive fuzzy sliding mode synchronous control for a planar redundantly actuated parallel manipulator. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 2264–2269. [Google Scholar]
- Fuh, C.C.; Tsai, H.H.; Huang, C.C.A. fuzzy cross-coupled linear quadratic regulator for improving the contour accuracy of bi-axis machine tools. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 4156–4161. [Google Scholar]
- Zhao, D.; Zhu, Q.; Li, N.; Li, S. Neural networked based synchronized control for multiple robotic manipulators. In Proceedings of the10th IEEE International Conference on Control and Automation (ICCA), Hangzhou, China, 12–14 June 2013; pp. 1950–1955. [Google Scholar]
- Yang, G.; Yao, J. Multilayer neurocontrol of high-order uncertain nonlinear systems with active disturbance rejection. Int. J. Robust Nonlinear Control 2024, 34, 2972–2987. [Google Scholar] [CrossRef]
- Le, D.K.; Ahn, K.K. Synchronization algorithm for controlling 3-R planar parallel pneumatic artificial muscle robot. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Republic of Korea, 26–29 October 2011; pp. 1588–1593. [Google Scholar]
- Su, Y.X.; Sun, D.; Ren, L.; Wang, X.; Mills, J.K. Nonlinear PD synchronized control for parallel manipulators. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1374–1379. [Google Scholar]
- Sun, D.; Tong, M.C. A synchronization approach for the minimization of contouring errors of CNC machine tools. IEEE Trans. Autom. Sci. Eng. 2009, 6, 720–729. [Google Scholar]
- Zhao, D.; Li, S.; Gao, F. Fully adaptive feedforward feedback synchronized tracking control for Stewart Platform systems. Int. J. Control Autom. Syst. 2008, 6, 689–701. [Google Scholar]
- Seraji, H. Decentralized adaptive control of manipulators: Theory, simulation, and experimentation. IEEE Trans. Robot. Autom. 1989, 5, 183–201. [Google Scholar] [CrossRef]
- Sun, D.; Mills, J.K. Adaptive Synchronized Control for Coordination of Multirobot Assembly Tasks. IEEE Trans. Robot. Autom. 2002, 18, 498–510. [Google Scholar]
- Sun, D. Position synchronization of multiple motion axes with adaptive coupling control. Automatic 2003, 39, 997–1005. [Google Scholar] [CrossRef]
- Craig, J. Robotics: Mechanics and Control; Addison-Wesley: Reading, MA, USA, 1986. [Google Scholar]
- Slotine, J.J.E.; Li, W. On the adaptive control of robot manipulators. Int. J. Robot. Res. 1987, 6, 49–59. [Google Scholar] [CrossRef]
- O’Searcoid, M. Metric Spaces; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 3. [Google Scholar]
- Nguyen, C.C.; Zhou, Z.; Antrazi, S.S.; Campbell, C.E. Efficient computation of forward kinematics and Jacobian matrix of a Stewart platform-based manipulator. In Proceedings of the IEEE Proceedings of the SOUTHEASTCON ′91, Williamsburg, VA, USA, 7–10 April 1991; Volume 2, pp. 869–874. [Google Scholar]
- Merlet, J.P. Solving the forward kinematics of a Gough-type parallel manipulator with interval analysis. Int. J. Robot. Res. 2004, 23, 221–235. [Google Scholar] [CrossRef]



| Plant Parameters | Value |
|---|---|
| Base radius (m) | 0.36 |
| Platform radius(m) | 0.27 |
| Initial height (m) | 0.5 |
| Base offset angle (deg) | 2.5 |
| Platform offset angle (deg) | 10 |
| Mass of the platform (kg) | 4.92 |
| Mass of the leg cylinder (kg) | 10.29 |
| Inertia coefficient of the platform, Ixx (kg*m2) | 0.09 |
| Inertia coefficient of the platform, Iyy (kg*m2) | 0.09 |
| Inertia coefficient of the platform, Izz (kg*m2) | 0.18 |
| Maximum Errors | Average Errors | |||
|---|---|---|---|---|
| SMRAC | DASCS | SMRAC | DASCS | |
| 4.6 | 0.9602 | 0.508 | 0.0226 | |
| 1.8 | 1.63 | 0.501 | 0.0284 | |
| 5.1 | 3.37 | 0.28 | 0.0947 | |
| 6.2 | 3.0340 | 0.379 | 0.0988 | |
| 6.1 | 3.0347 | 0.323 | 0.0905 | |
| 6.2 | 3.3442 | 0.318 | 0.0909 | |
| 5 | 3.2212 | 0.375 | 0.0972 | |
| 4.8 | 2.93 | 0.331 | 0.0832 | |
| 6.3 | 3.3394 | 0.341 | 0.0860 | |
| 1.8325 | 0.9329 | 0.5109 | 0.0021 | |
| 6.1393 | 0.9292 | 0.6637 | 0.0122 | |
| 4.3010 | 1.4477 | 0.6245 | 0.0156 | |
| 2.7799 | 0.9756 | 0.7342 | 0.0176 | |
| 4.098 | 1.47 | 0.3961 | 0.0117 | |
| 6.6267 | 0.9329 | 0.8946 | 0.0211 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.T.; Nguyen, C.C.; Nguyen, T.M.; Duong, T.T.C.; Ngo, H.T.T.; Sun, L. Decentralized Adaptive Control of Closed-Kinematic Chain Mechanism Manipulators. Machines 2025, 13, 331. https://doi.org/10.3390/machines13040331
Nguyen TT, Nguyen CC, Nguyen TM, Duong TTC, Ngo HTT, Sun L. Decentralized Adaptive Control of Closed-Kinematic Chain Mechanism Manipulators. Machines. 2025; 13(4):331. https://doi.org/10.3390/machines13040331
Chicago/Turabian StyleNguyen, Tri T., Charles C. Nguyen, Tuan M. Nguyen, Tu T. C. Duong, Ha Tang T. Ngo, and Lu Sun. 2025. "Decentralized Adaptive Control of Closed-Kinematic Chain Mechanism Manipulators" Machines 13, no. 4: 331. https://doi.org/10.3390/machines13040331
APA StyleNguyen, T. T., Nguyen, C. C., Nguyen, T. M., Duong, T. T. C., Ngo, H. T. T., & Sun, L. (2025). Decentralized Adaptive Control of Closed-Kinematic Chain Mechanism Manipulators. Machines, 13(4), 331. https://doi.org/10.3390/machines13040331







