Meshing Performance Analysis of a Topologically Modified and Formed Internal Helical Gear Pair
Abstract
1. Introduction
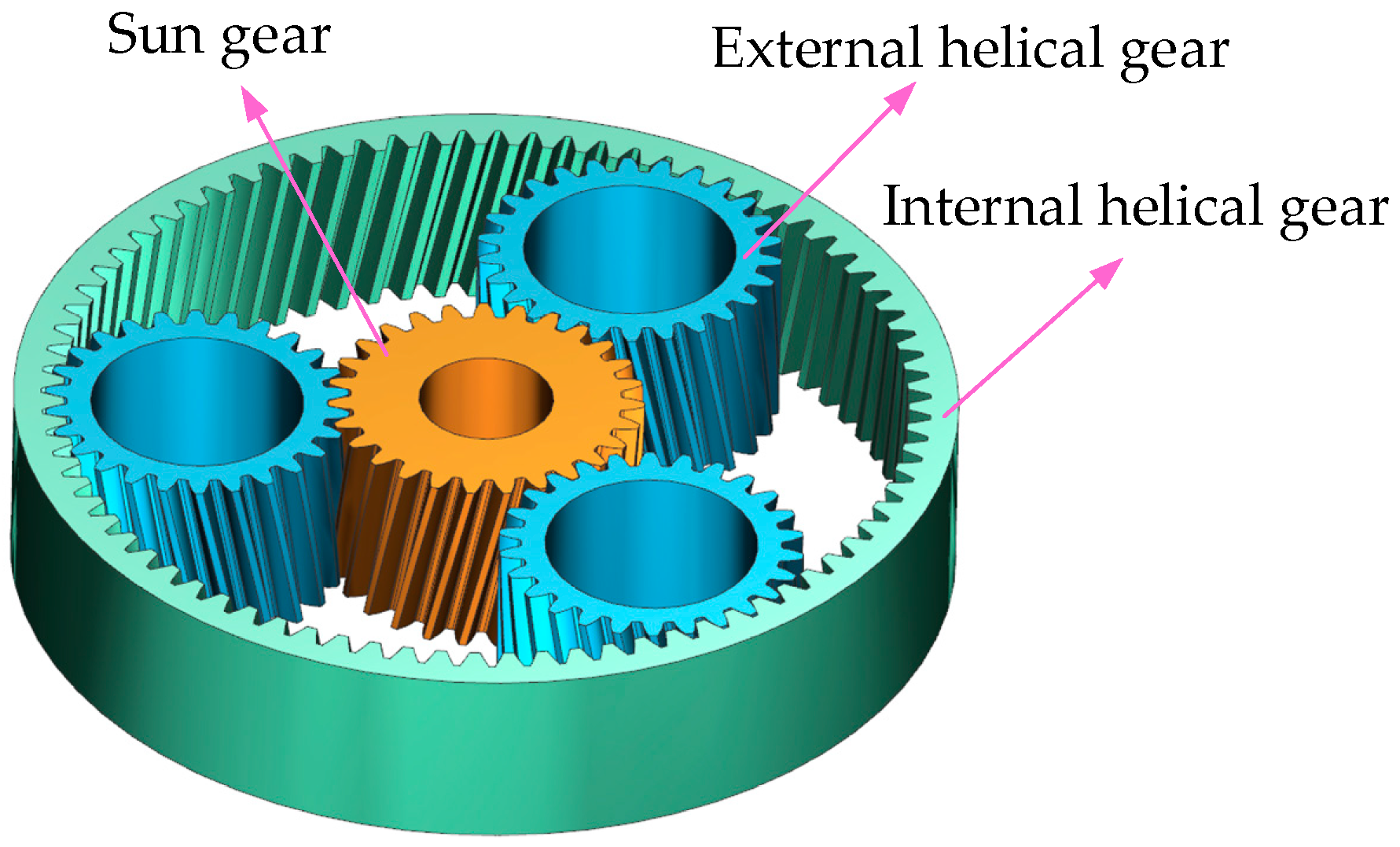
2. Mathematical Modeling of Internal Helical Gears Pair
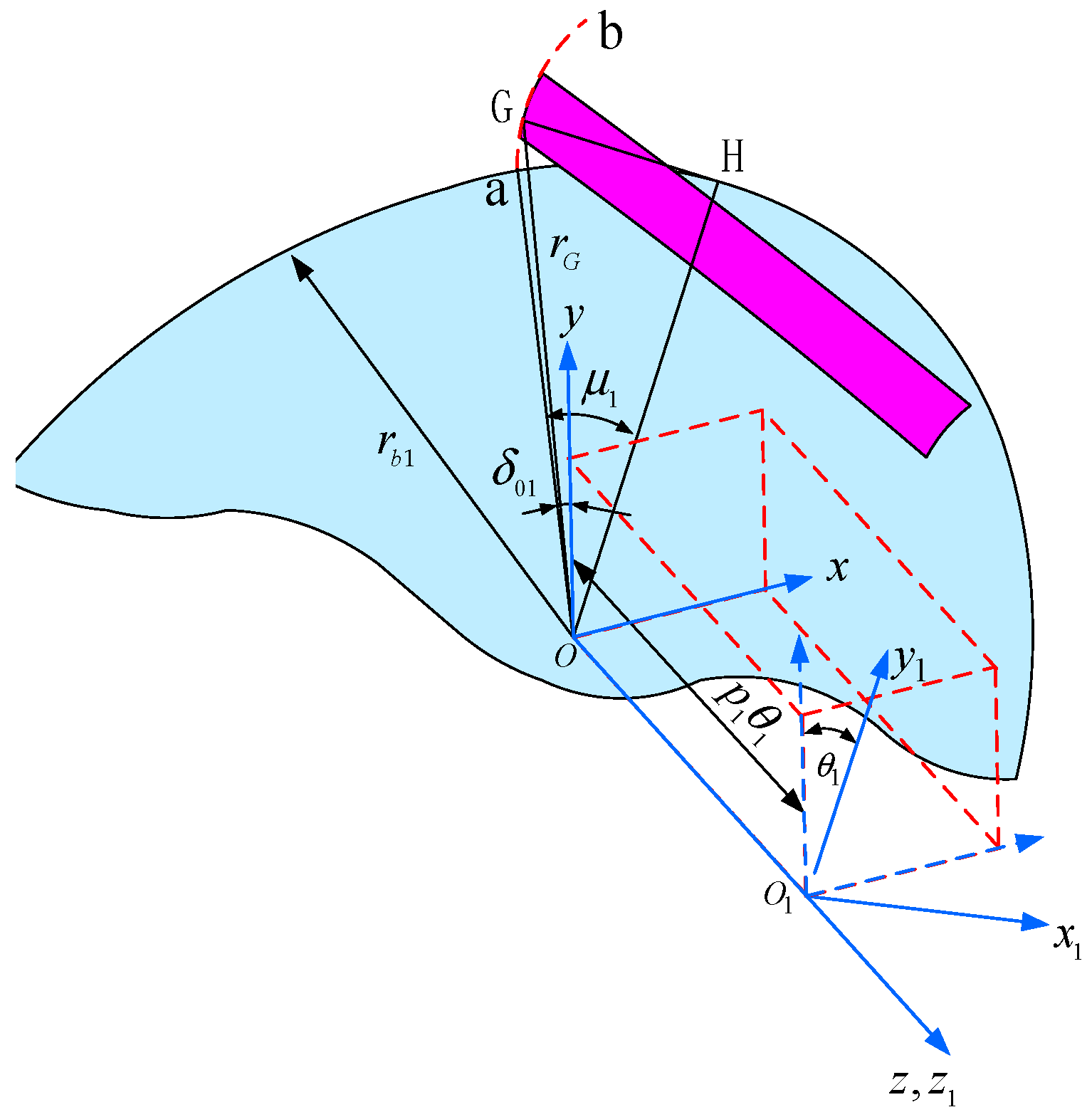
2.1. Internal Helical Gear Tooth Equation
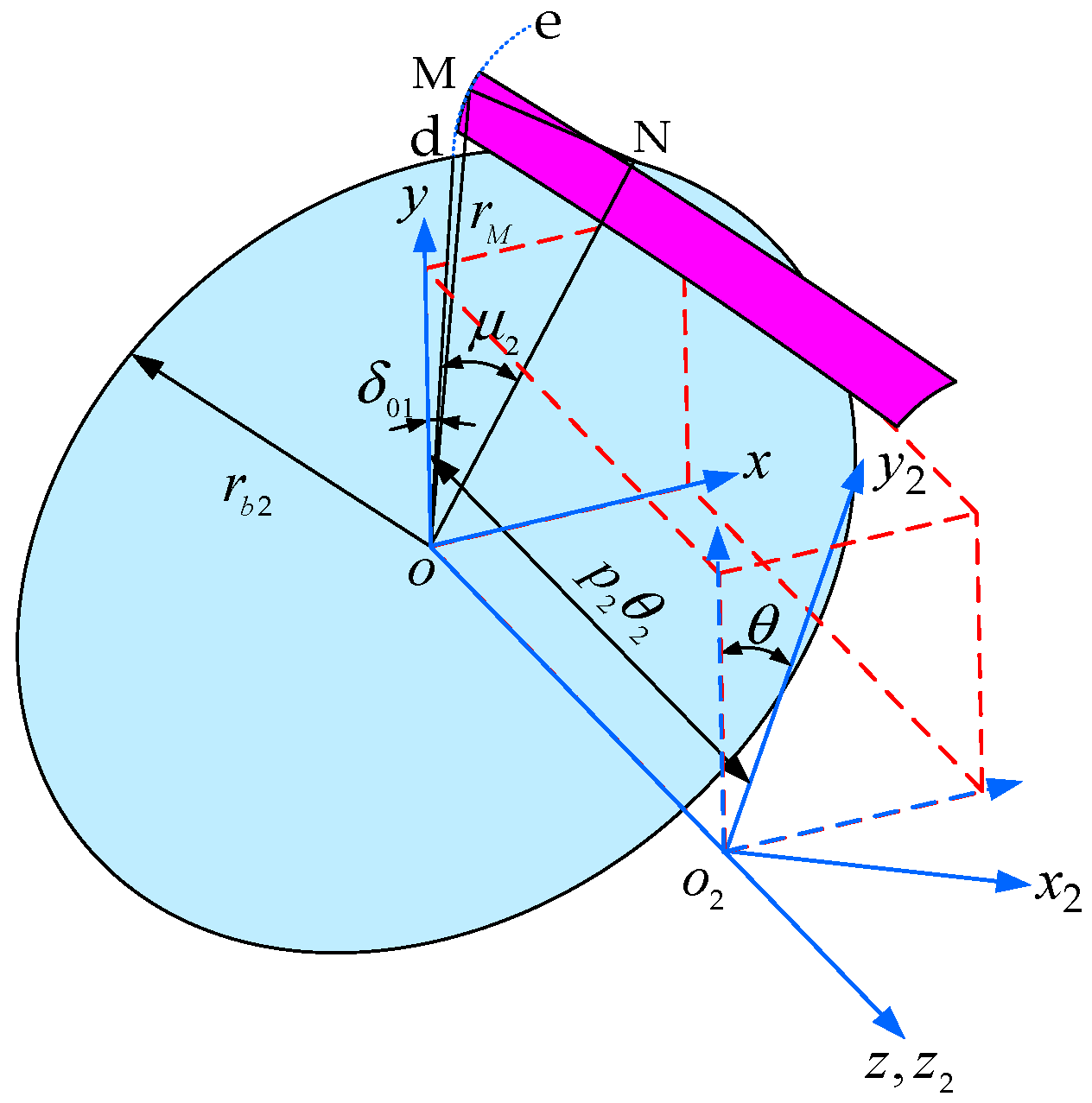
2.2. External Helical Gear Tooth Equations
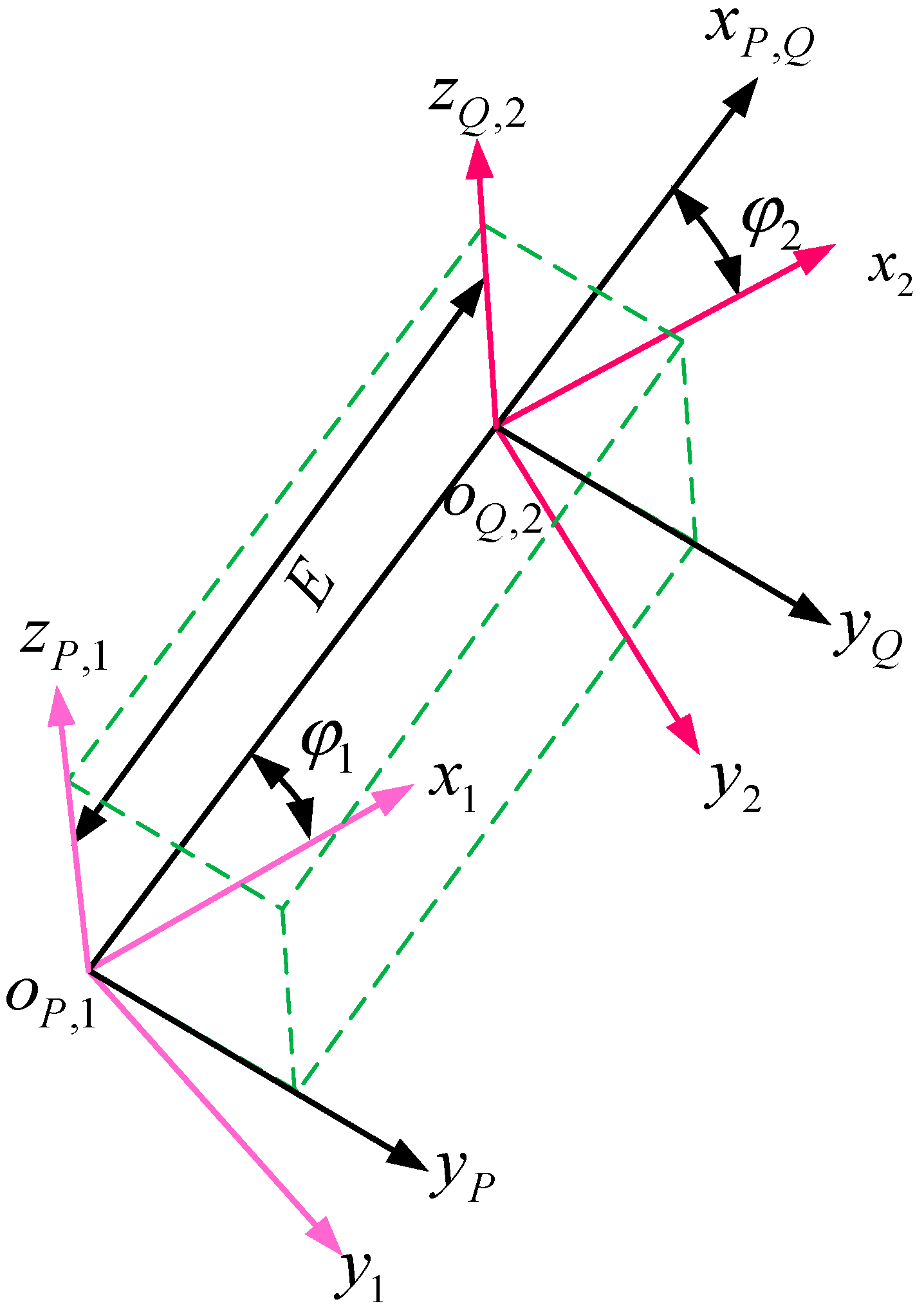
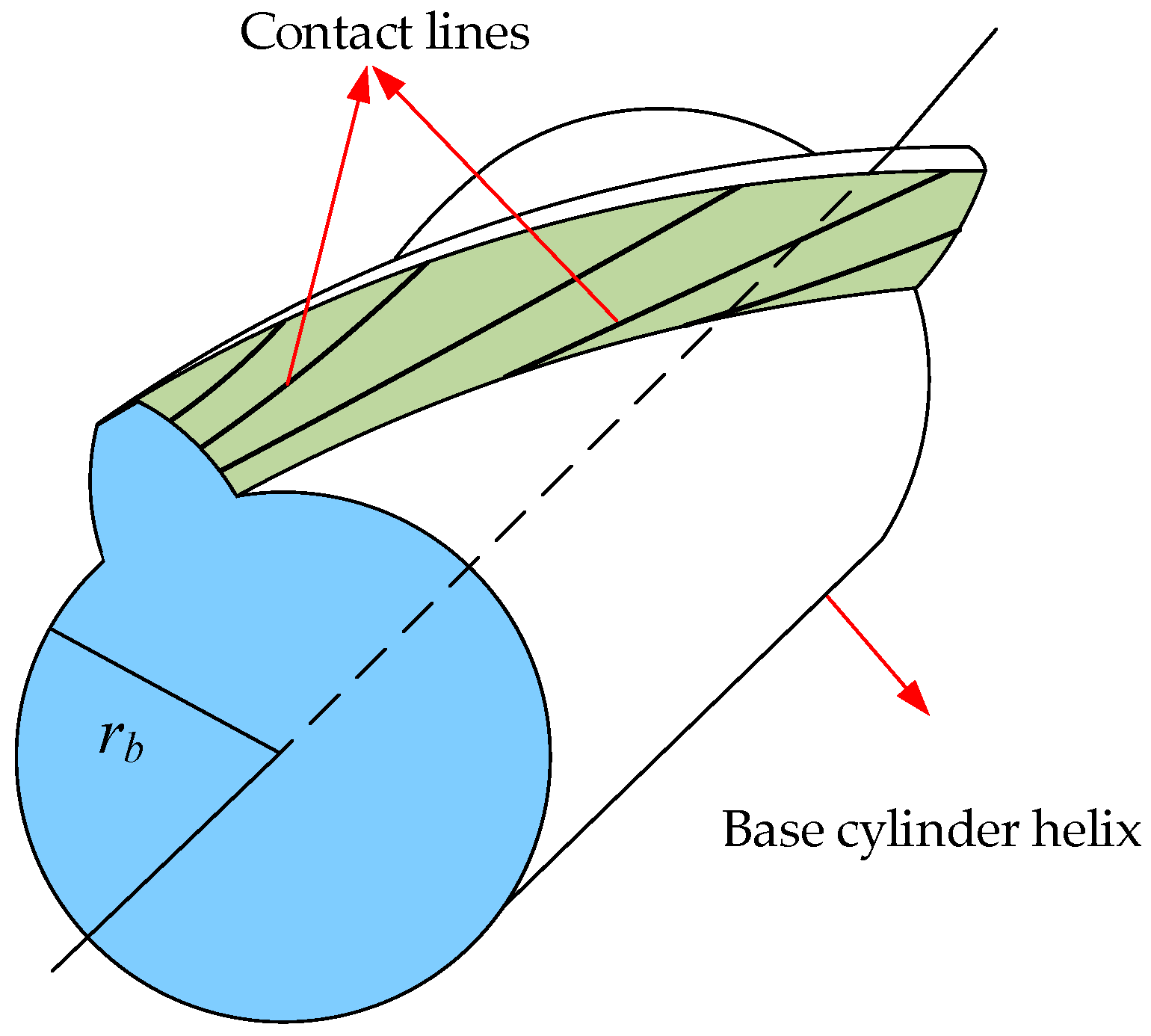
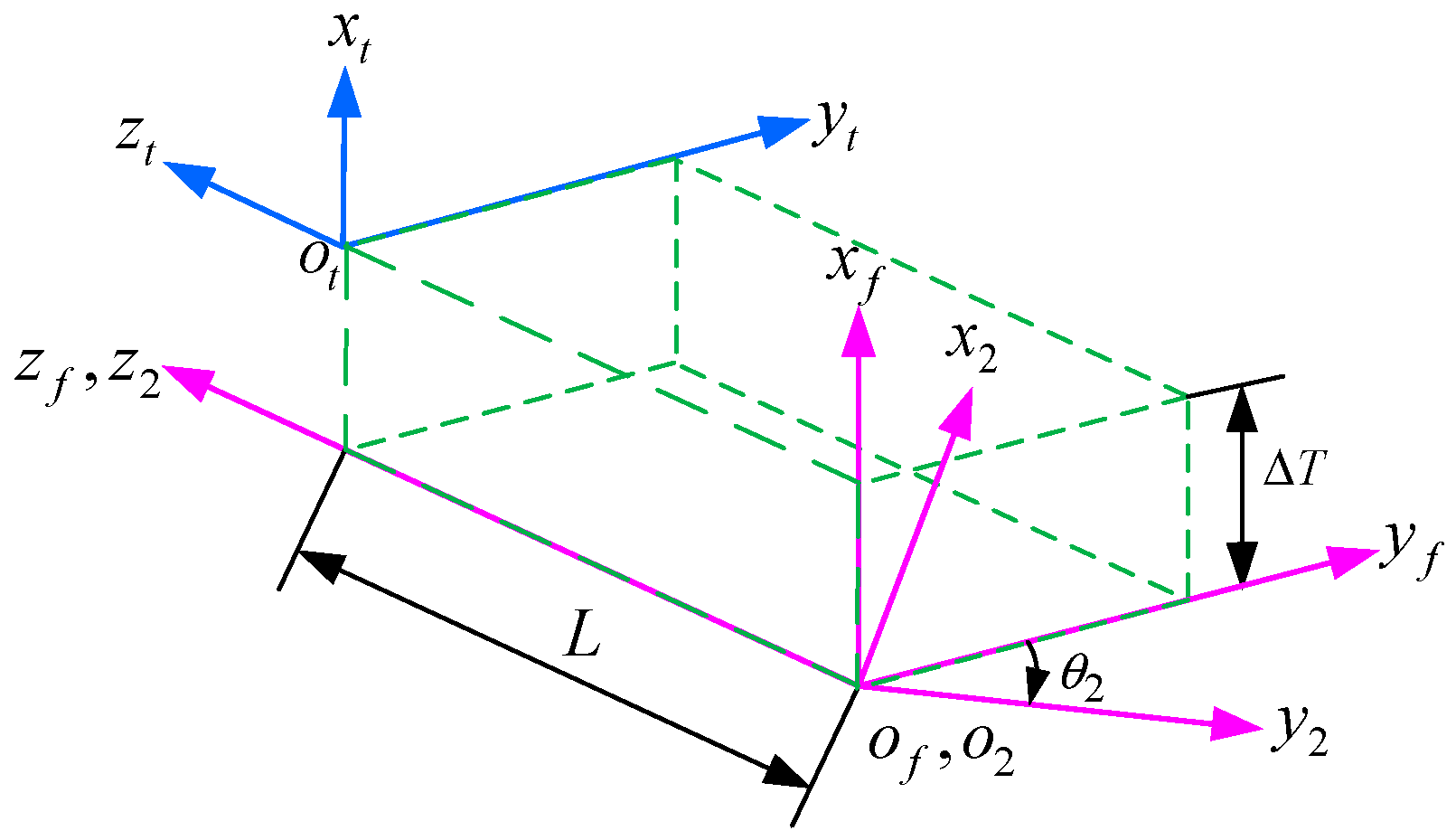
2.3. Internal Helical Gear Pair Meshing Coordinate System
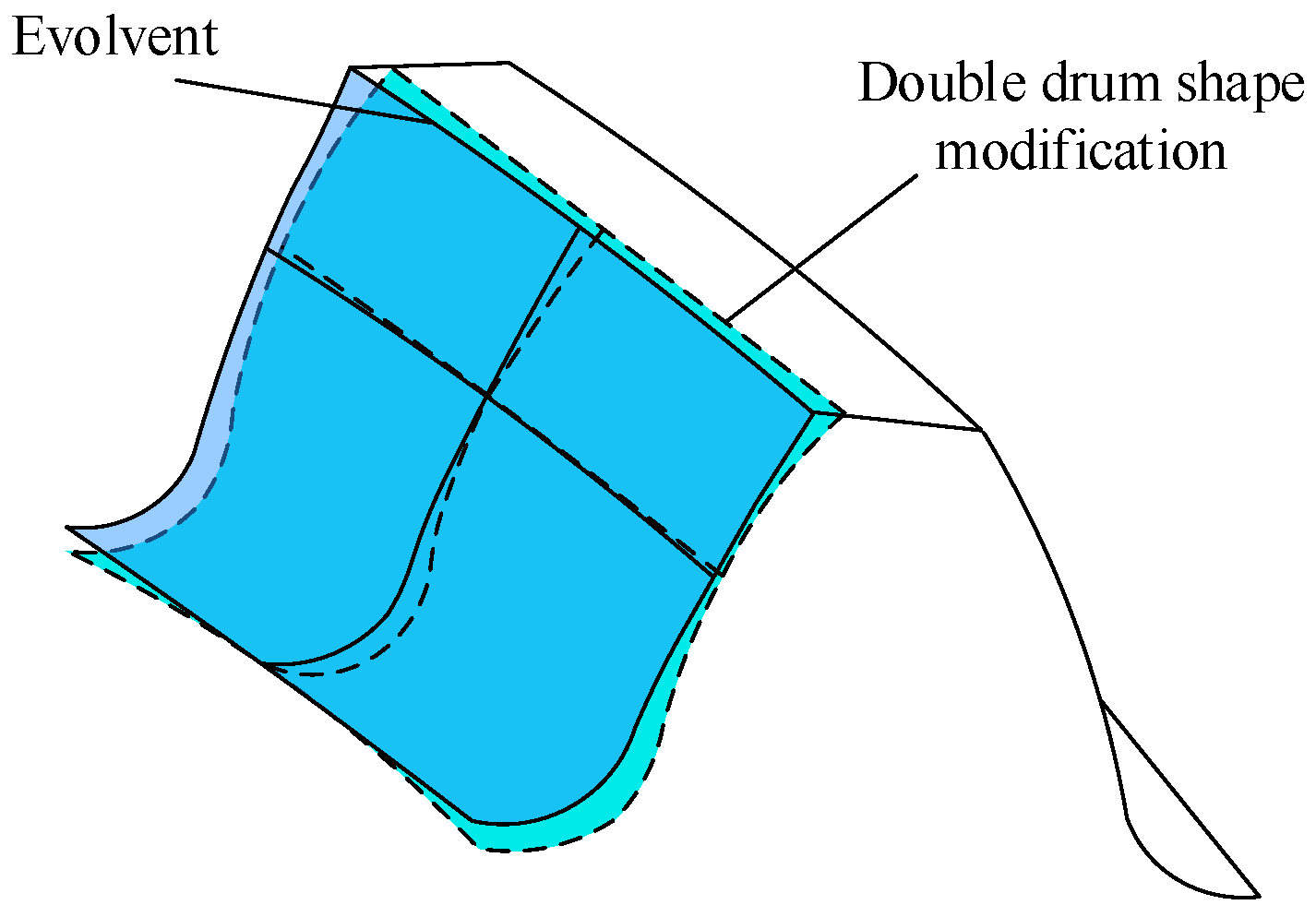
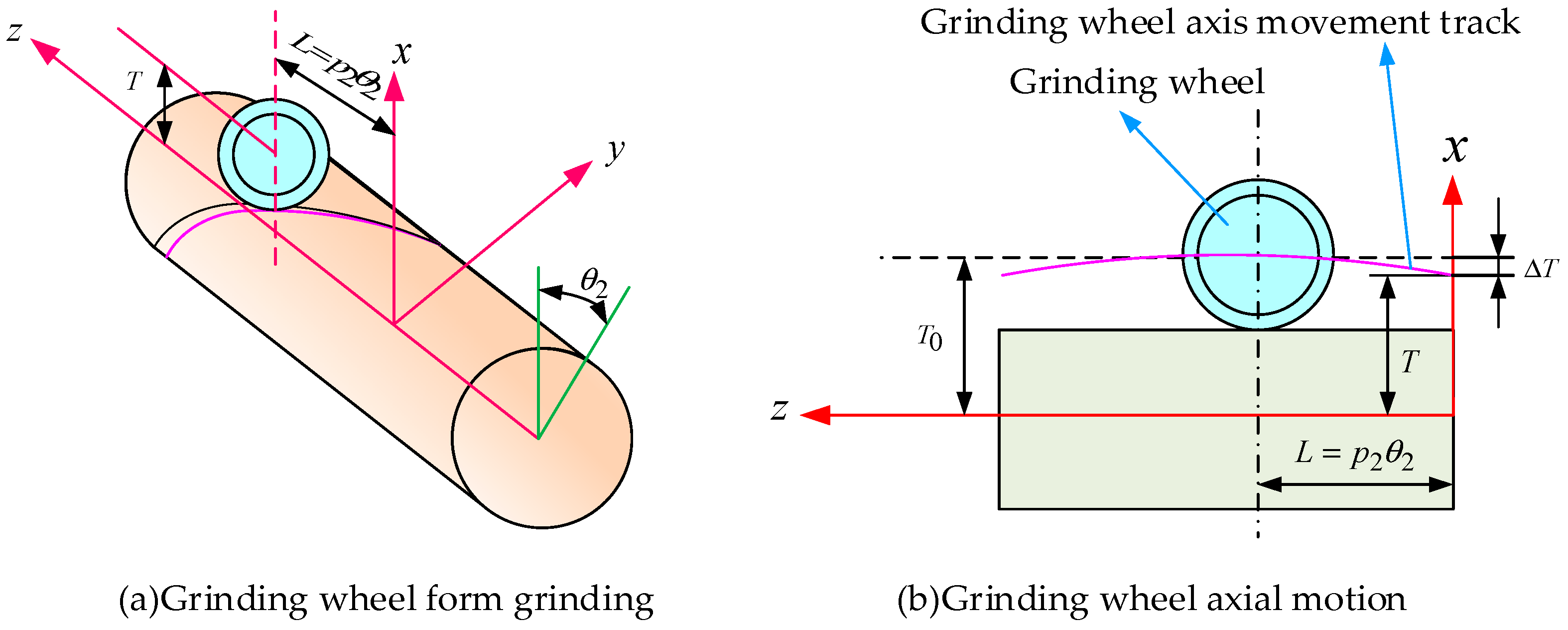
3. Topological Modification of Internal Helical Gear
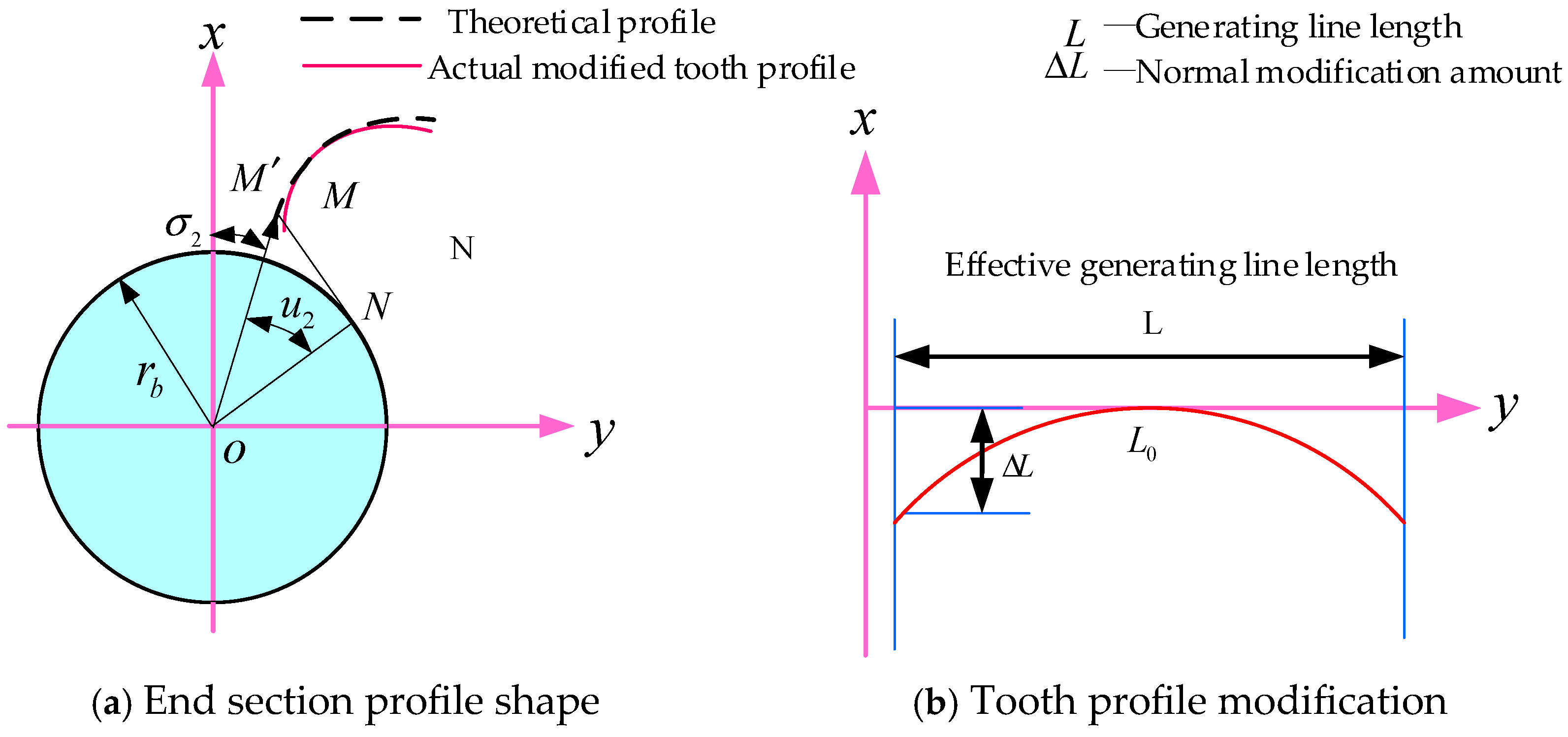
3.1. Modification of External Helical Gear
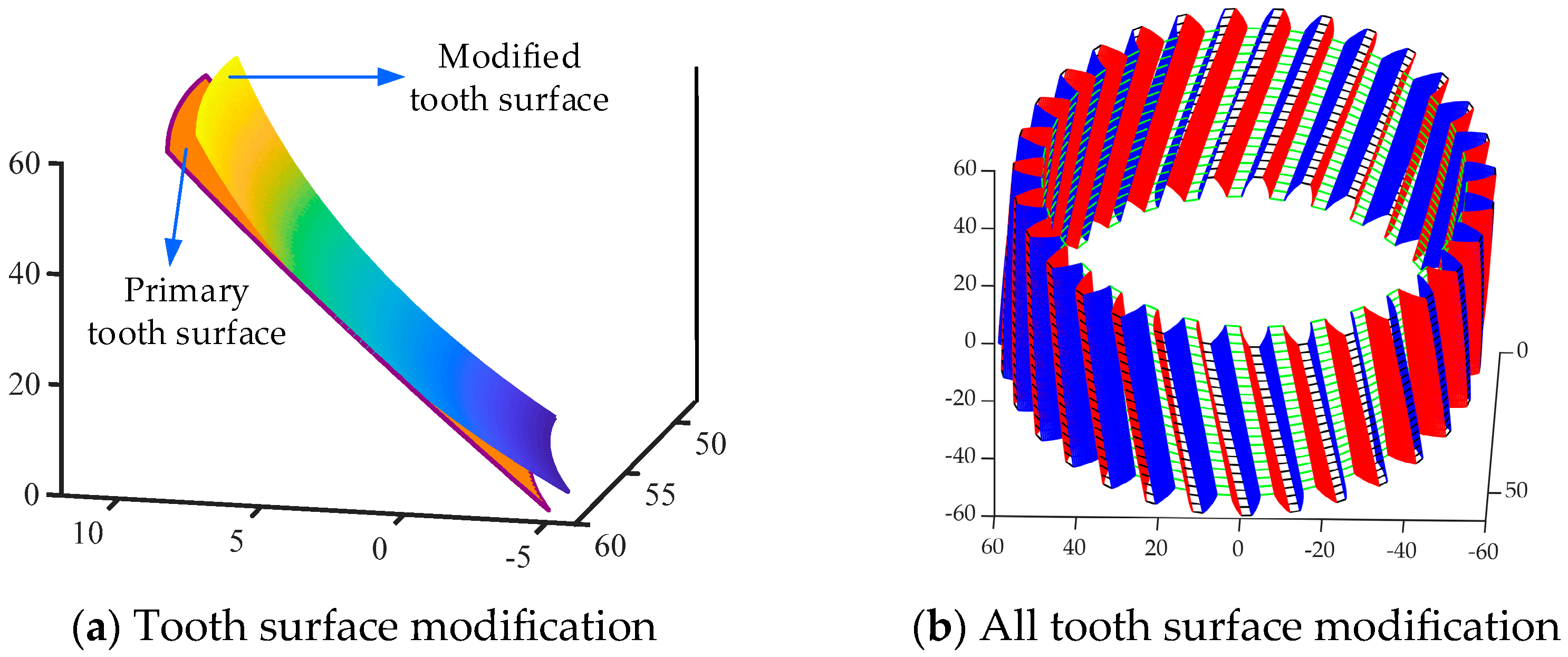
3.2. Topologically Modified Tooth Equations
3.2.1. Tooth Equation of Profile-Modification External Helical Gear
3.2.2. Tooth Equations of Ground and Modified External Helical Gear
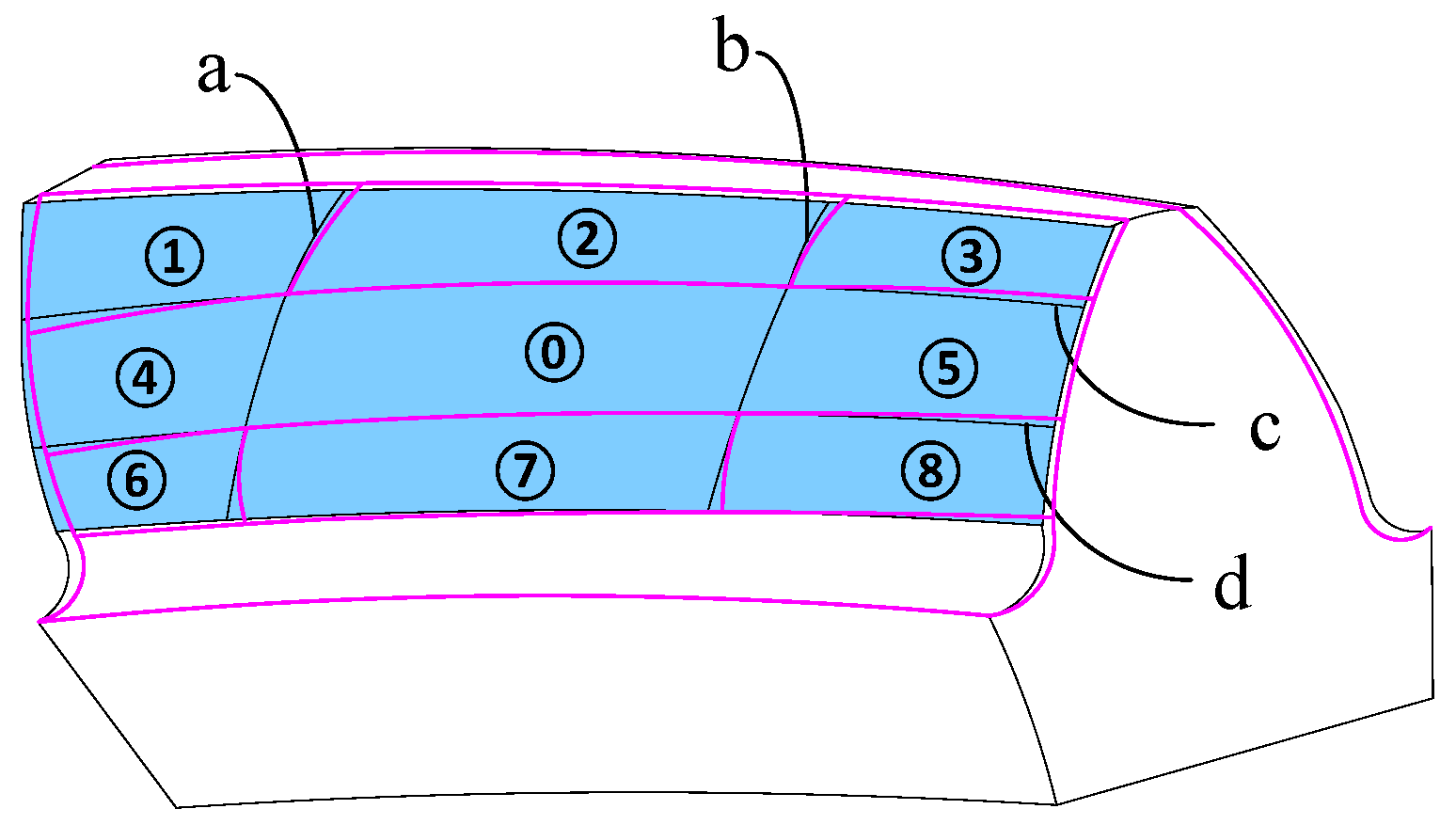
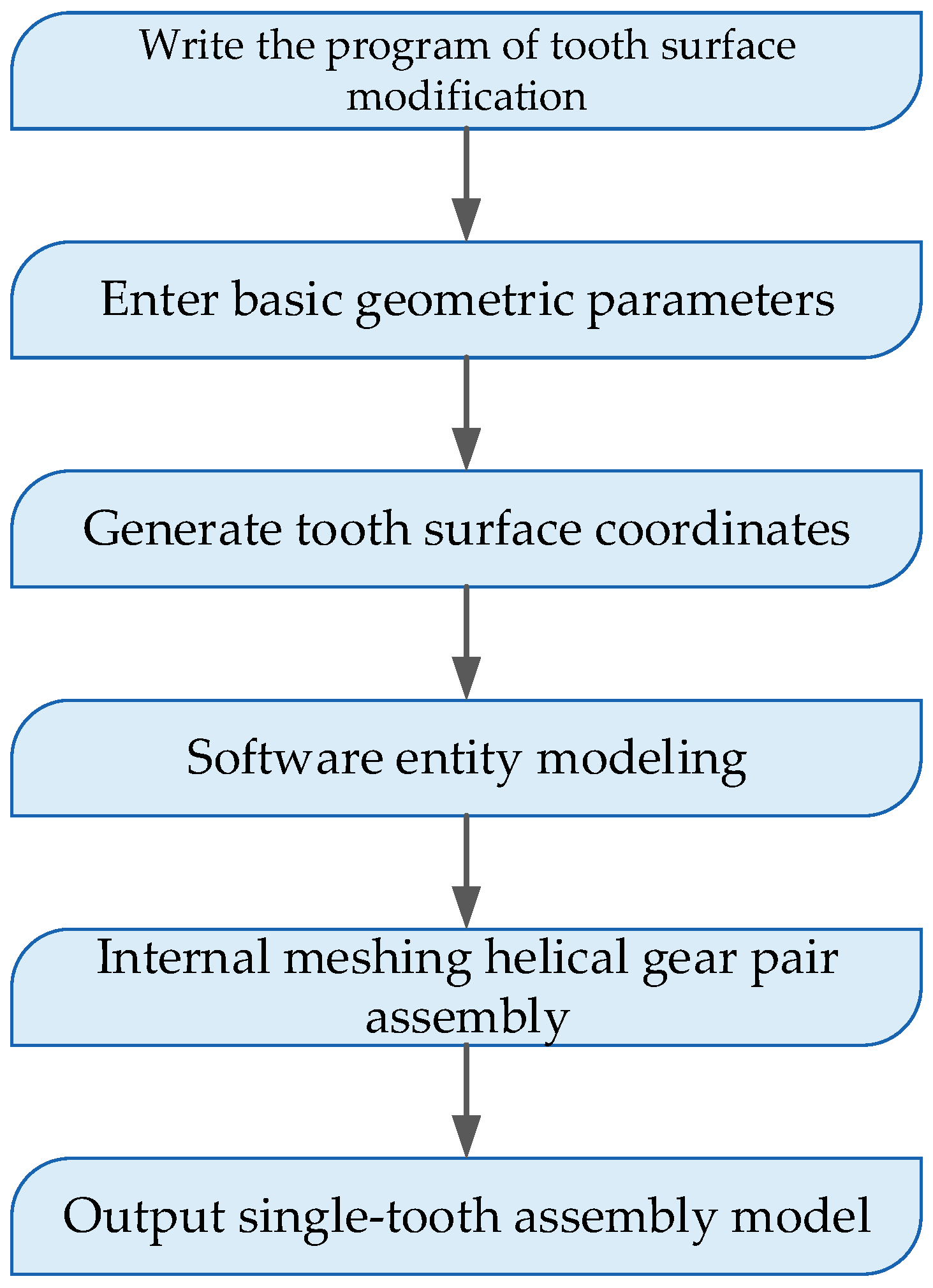
4. Digital Modeling of an Internal Helical Gear Pair
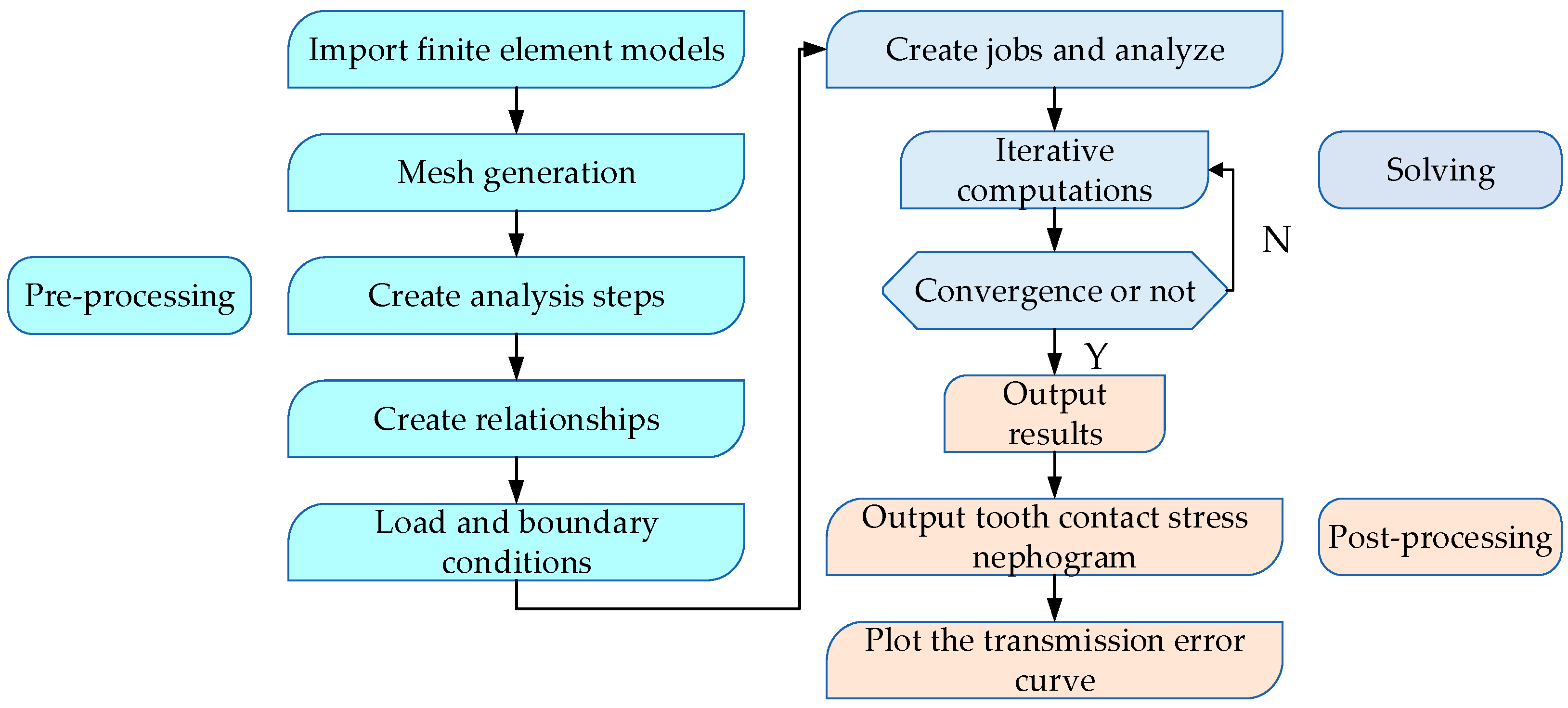
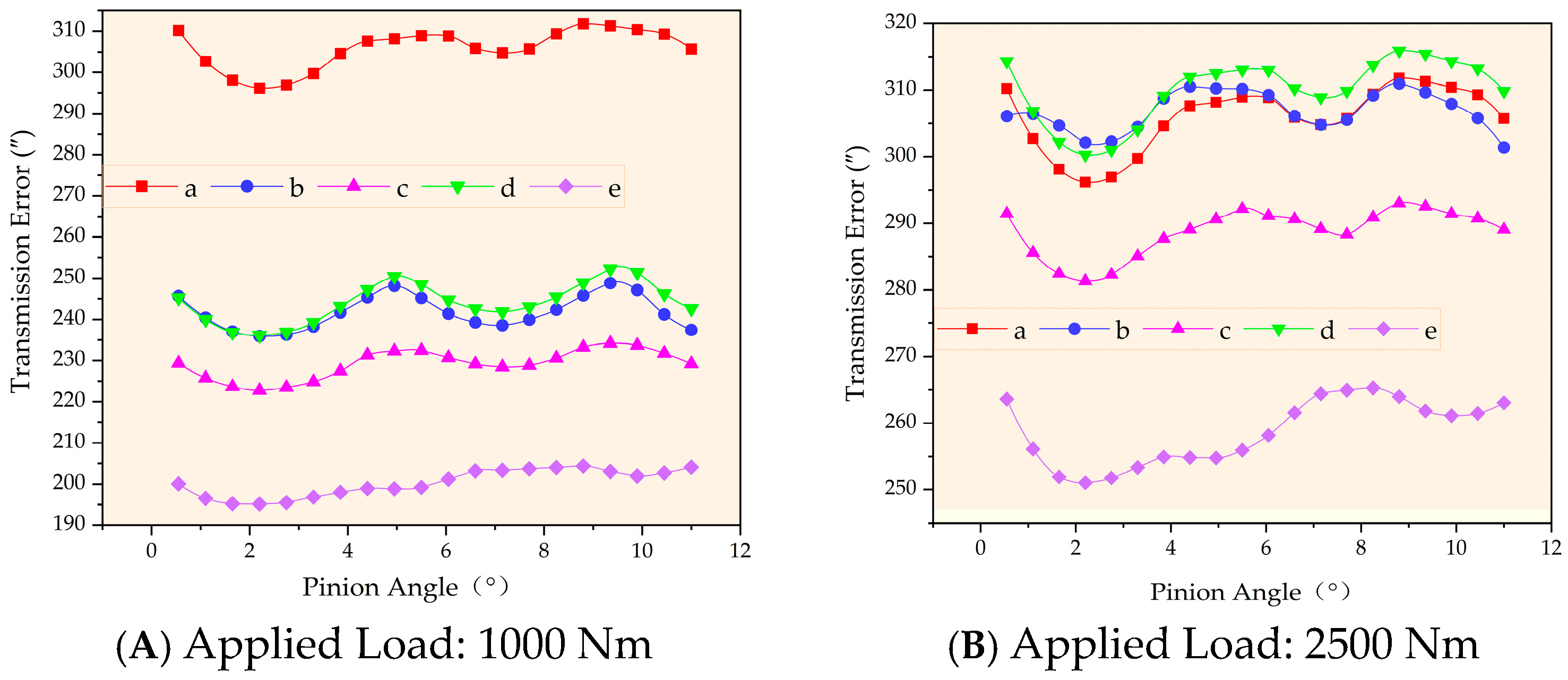
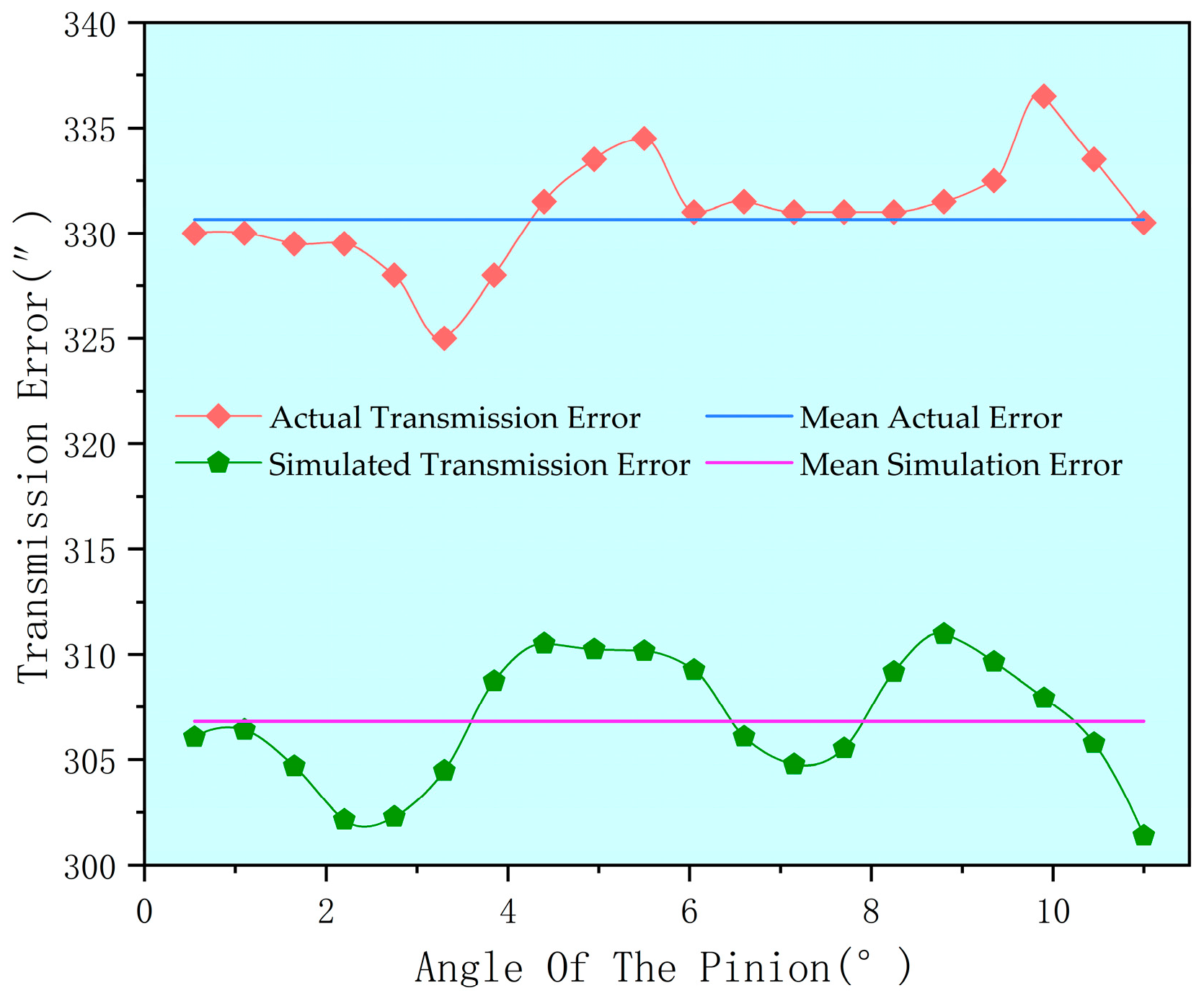
5. Experimental Verification
6. Conclusions
- This study proposes a variable-diameter helical modification method for longitudinal correction, where the tooth width center remains unmodified while both sides undergo material reduction. Combined with tooth profile modification, this approach is used to study the influence of modification on the transmission performance of an internal helical gear pair.
- The simulation results demonstrate that maintaining the longitudinal modification coefficient constant while increasing the profile modification coefficient shifts the maximum contact stress toward the tooth root. Concurrently, the meshing area expands longitudinally, significantly affecting the peak contact stress distribution. Conversely, keeping the profile modification coefficient constant while increasing the longitudinal modification coefficient narrows the contact area and lowers the stress concentration. Notably, the longitudinal modification coefficient has a greater influence on transmission error than the profile modification coefficient, as it decreases the meshing area, thereby increasing transmission instability during gear engagement and disengagement.
- The modified gear pair exhibited a 28.4% lower simulated transmission error than the unmodified version under 2500 Nm loading conditions. The amplitude of the experiment transmission error curve reached 12.5″. Based on these results, prototype gears were manufactured and tested. The experiments confirmed the modification effectiveness, demonstrating improved performance in the internal helical gear pair.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, R.Y.; Yang, J.W.; Wang, J.H. Study on the effect of displacement design on the dynamic characteristics of helical gear system. Mech. Transm. 2024, 48, 1–8. [Google Scholar]
- Jia, B. Research on the Dynamic Characteristics Analysis and Shape Optimization of Helical Gears for High-Speed Trains under Multiple Working Conditions. Master Thesis, Dalian Jiaotong University, Dalian, China, 2023. [Google Scholar]
- Zhao, H.Y.; Zhi, Z.G.; Cao, J.F. Design analysis of helical gear trimming for aerospace gearboxes based on KISSsoft. Mech. Res. Appl. 2023, 36, 67–70. [Google Scholar]
- Lin, T.; He, Z. Analytical method for coupled transmission error of helical gear system with machining errors, assembly errors and tooth modifications. Mech. Syst. Signal Process. 2017, 91, 167–182. [Google Scholar] [CrossRef]
- Wang, H.L. Helical Gear Topology Trimming Method Based on Functional Requirements and Its Gear Grinding Realization. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2016. [Google Scholar]
- Hua, X.J.; Du, H.; Xie, X.; Huang, W.P.; Tian, Z.X.; Yin, B.F.; Liu, J.F. Noise reduction analysis of involute helical gears with short profile trimming. Appl. Acoust. 2020, 39, 430–437. [Google Scholar]
- Zhao, Z.Q. Topological Modification and Load Bearing Contact Analysis of Helical Gears Ground by Forming Method. Master Thesis, Henan University of Science and Technology, Luoyang, China, 2020. [Google Scholar]
- Chen, J.J.; Zhu, R.P.; Chen, W.F.; Li, M.M.; Yin, X.M.; Zhang, X.X. General Meshing Modeling and Dynamic Characteristics Analysis of Helical Gear Pair with Tooth Surface Deviation. Iran. J. Sci. Technol. Trans. Mech. Eng. 2024, 48, 1623–1641. [Google Scholar] [CrossRef]
- Jiang, J.K.; Fang, Z.D.; Su, J.Z. Design and machining of helical gear trimming with high-order transmission error. J. Harbin Inst. Technol. 2014, 46, 43–49. [Google Scholar]
- Yang, J.J.; Wang, J.J.; Mao, S.M. Analysis of Transmission Performance of Helical Gear Based on High-Order Modification Design. Appl. Mech. Mater. 2013, 2773, 236–240. [Google Scholar] [CrossRef]
- Yan, P.F.; Liu, H.; Gao, P.; Zhang, X.; Zhan, Z.B.; Zhang, C. Optimization of distributed axial dynamic modification based on the dynamic characteristics of a helical gear pair and a test verification. Mech. Mach. Theory 2021, 163, 104371. [Google Scholar] [CrossRef]
- Wu, Y.J.; Wang, J.J.; Han, Q.K. Static/dynamic contact FEA and experimental study for tooth profile modification of helical gears. J. Mech. Sci. Technol. 2012, 26, 1409–1417. [Google Scholar] [CrossRef]
- Zhang, X.J.; Jia, C.; Hou, X.Y.; Guo, F.; Zhai, J. Topological modification and simulation of helical gears with axial angle error. J. Xi’an Univ. Technol. 2018, 38, 28–34. [Google Scholar]
- Jia, C.; Fang, Z.D.; Yao, L.G.; Zhang, J. Tooth flank modification to reduce transmission error and mesh-in impact force in consideration of contact ratio for helical gears. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 4475–4493. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Liu, Y.; Tang, W.; Liu, P. Parametric finite element modeling and tooth contact analysis of spur and helical gears including profile and lead modifications. Eng. Comput. 2017, 34, 2877–2898. [Google Scholar] [CrossRef]
- Zhao, Z.F.; Yang, Y.; Ma, H.; Wang, H.X.; Tian, H.X.; Han, C.Y. Meshing characteristics of spur gear pairs with tooth modification under different assembly errors and sensitivity analysis for impact factors. J. Mech. Sci. Technol. 2022, 37, 149–162. [Google Scholar] [CrossRef]
- Bejar, F.; Perret-Liaudet, J.; Bareille, O.; Ichchou, M.; Fontana, M. Review and benchmarking study of different gear contact analysis software in terms of the static transmission error response. Results Eng. 2024, 22, 102286. [Google Scholar] [CrossRef]
- Ahmad, H.; Cheng, W.; Xing, J.; Wang, W.T.; Du, S.H.; Li, L.Y.; Zhang, R.Y.; Chen, X.F.; Lu, J.Q. Deep learning-based fault diagnosis of planetary gearbox: A systematic review. J. Manuf. Syst. 2024, 77, 730–745. [Google Scholar] [CrossRef]
- Pedrero, J.I.; Sánchez-Espiga, J.; Sánchez, M.B.; Pleguezuelos, M.; Fernández-Del-Rincón, A.; Viadero, F. Simulation and validation of the transmission error, meshing stiffness, and load sharing of planetary spur gear transmissions. Mech. Mach. Theory 2024, 203, 105800. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A.; Gonzalez-Perez, I.; Carvenali, L.; Kawasaki, K.; Handschuh, R.F. Modified involute helical gears: Computerized design, simulation of meshing and stress analysis. Comput. Methods Appl. Mech. Eng. 2003, 192, 3619–3655. [Google Scholar] [CrossRef]
- Nie, S.W.; Chen, J.Y.; Liu, S.H. Research on noise reduction of drive axle hypoid gear based on tooth surface mismatch modification. Adv. Mech. Eng. 2024, 16, 16878132241228195. [Google Scholar] [CrossRef]

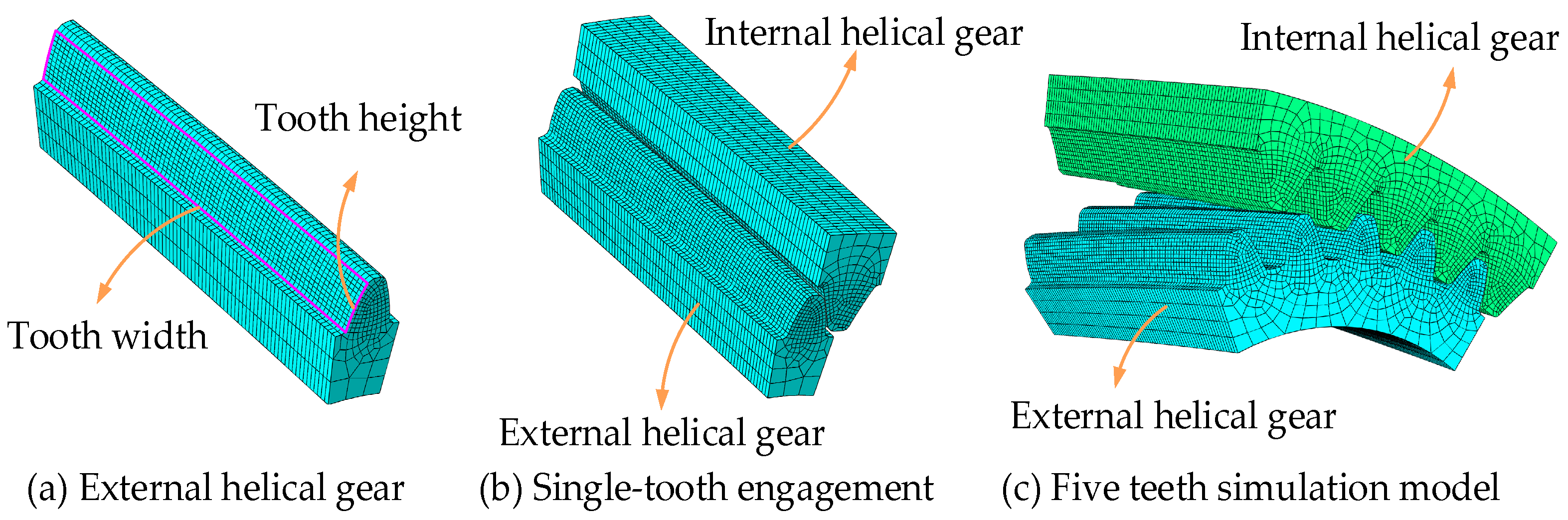
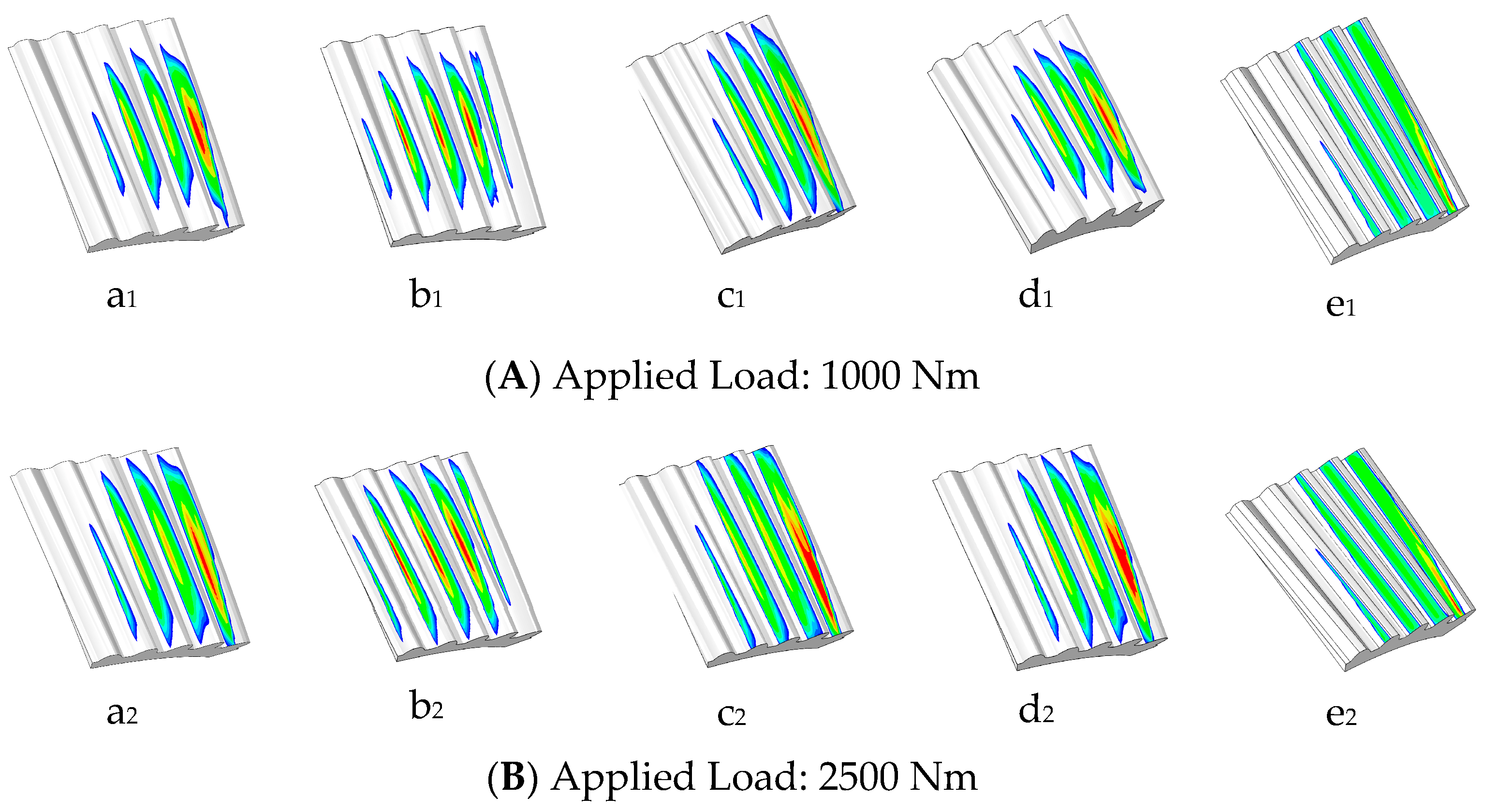
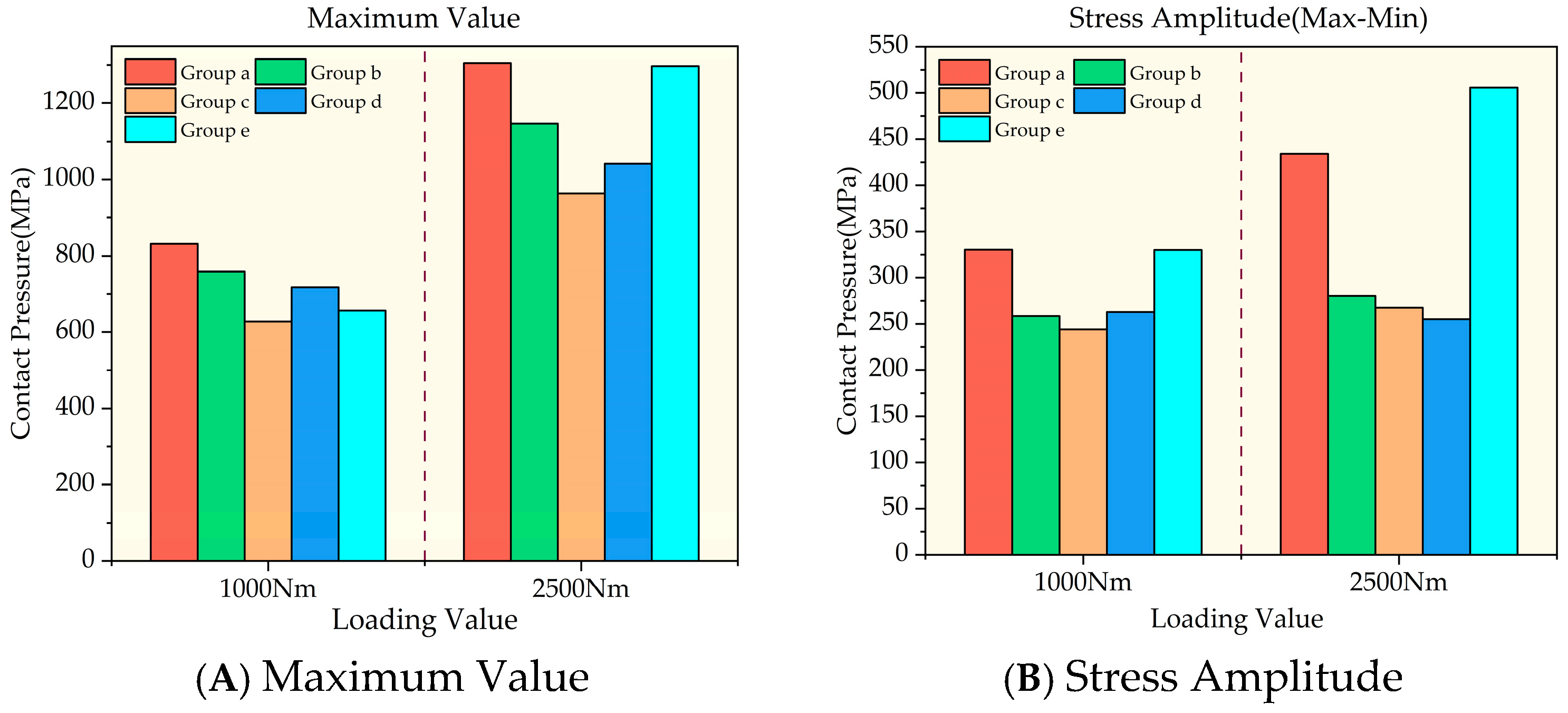



| Items | Helical Gear | Internal Helical Gear |
|---|---|---|
| Number of teeth | 31 | 79 |
| Helix direction | left-hand | left-hand |
| Module | 3.5 | 3.5 |
| Pressure angle/(°) | 20 | 20 |
| Helix angle/(°) | 12 | 12 |
| Tooth width/mm | 60 | 60 |
| Group | Tooth Profile Modification Factor () | Tooth Modification Coefficient Factor () |
|---|---|---|
| A | 0.00003 | 0.0001 |
| B | 0.00008 | 0.0001 |
| C | 0.00004 | 0.00003 |
| D | 0.00004 | 0.0001 |
| E | 0.0 | 0.0 |
| Item | Value |
|---|---|
| Material density/kg/m3 | 7.85 × 103 |
| Poisson’s ratio | 0.29 |
| Modulus of elasticity/MPa | 2.05 × 105 |
| Unit type | C3D8I |
| Friction factor | 0.06 |
| Number of seeds localized in tooth width | 80 |
| Number of seeds localized in tooth height | 10 |
| Loading value/Nm | 1000; 2500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Wei, X.; Lian, S.; Xu, J. Meshing Performance Analysis of a Topologically Modified and Formed Internal Helical Gear Pair. Machines 2025, 13, 340. https://doi.org/10.3390/machines13050340
Su J, Wei X, Lian S, Xu J. Meshing Performance Analysis of a Topologically Modified and Formed Internal Helical Gear Pair. Machines. 2025; 13(5):340. https://doi.org/10.3390/machines13050340
Chicago/Turabian StyleSu, Jianxin, Xiao Wei, Shilin Lian, and Jiewei Xu. 2025. "Meshing Performance Analysis of a Topologically Modified and Formed Internal Helical Gear Pair" Machines 13, no. 5: 340. https://doi.org/10.3390/machines13050340
APA StyleSu, J., Wei, X., Lian, S., & Xu, J. (2025). Meshing Performance Analysis of a Topologically Modified and Formed Internal Helical Gear Pair. Machines, 13(5), 340. https://doi.org/10.3390/machines13050340






