Bayesian Optimization Design of Inlet Volute for Supercritical Carbon Dioxide Radial-Flow Turbine
Abstract
:1. Introduction
2. Volute Design Method
3. The Three-Dimensional Simulation Model of the Volute
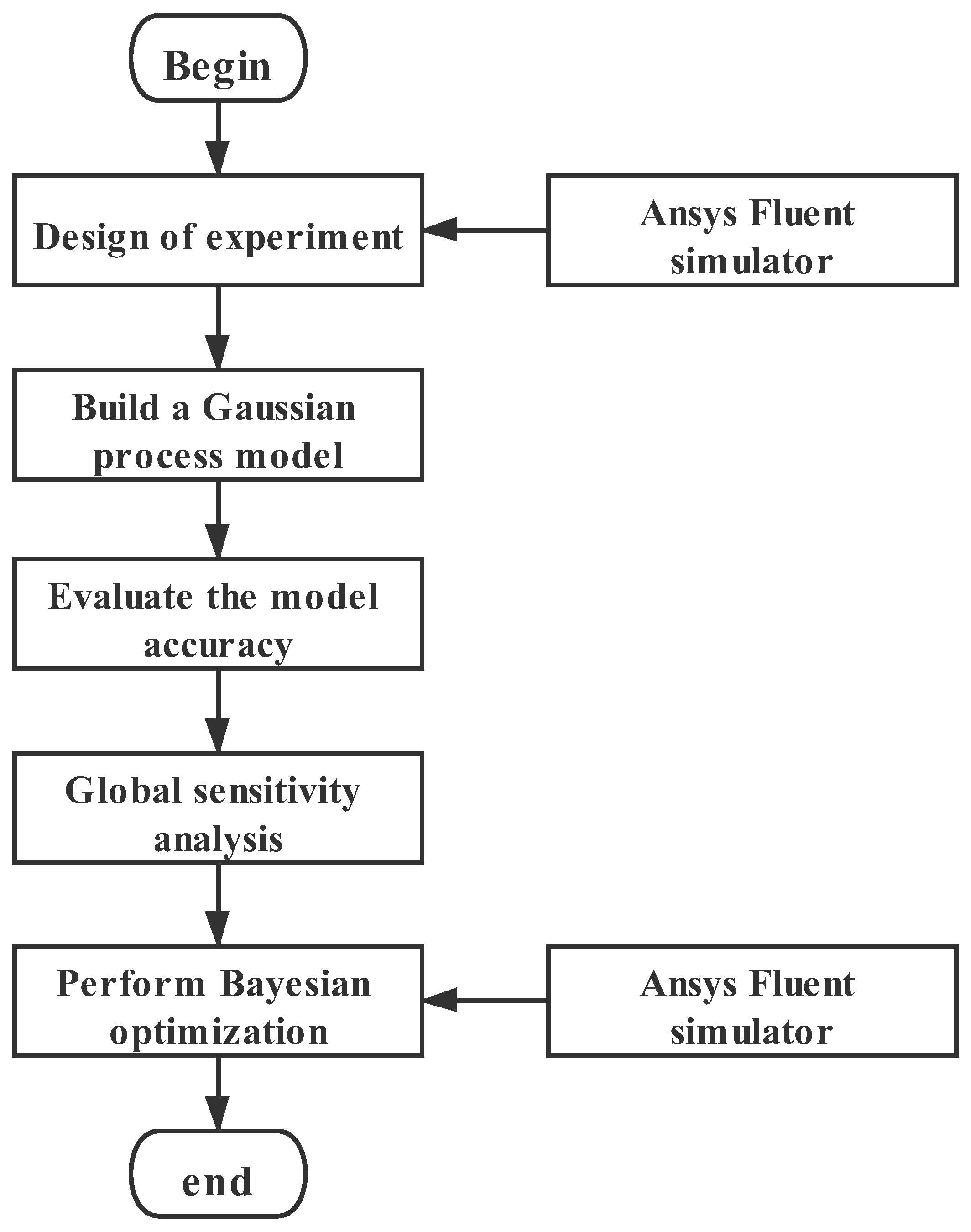
4. Bayesian Optimization Framework for the Design of Volute
4.1. Optimization Object Description
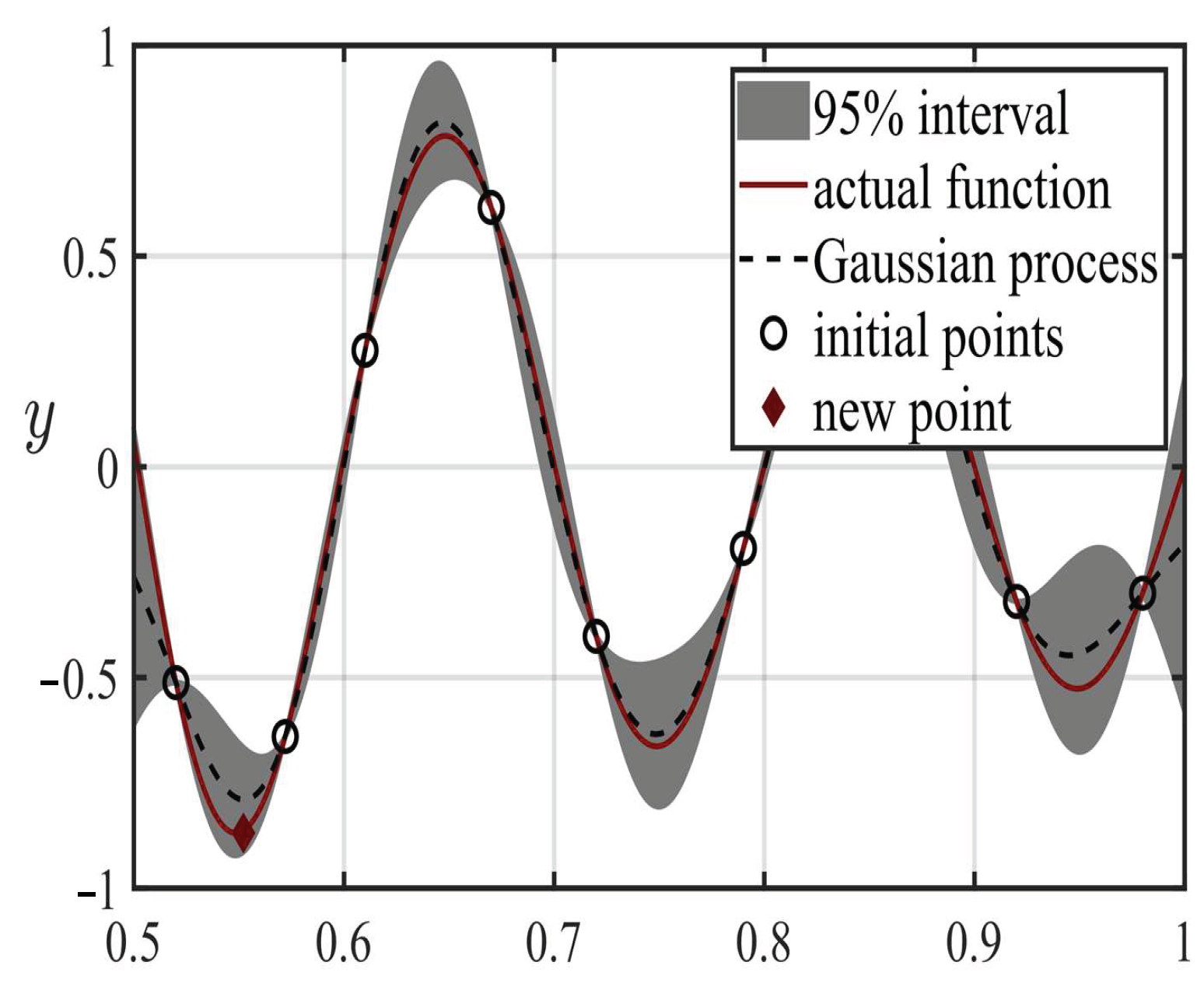
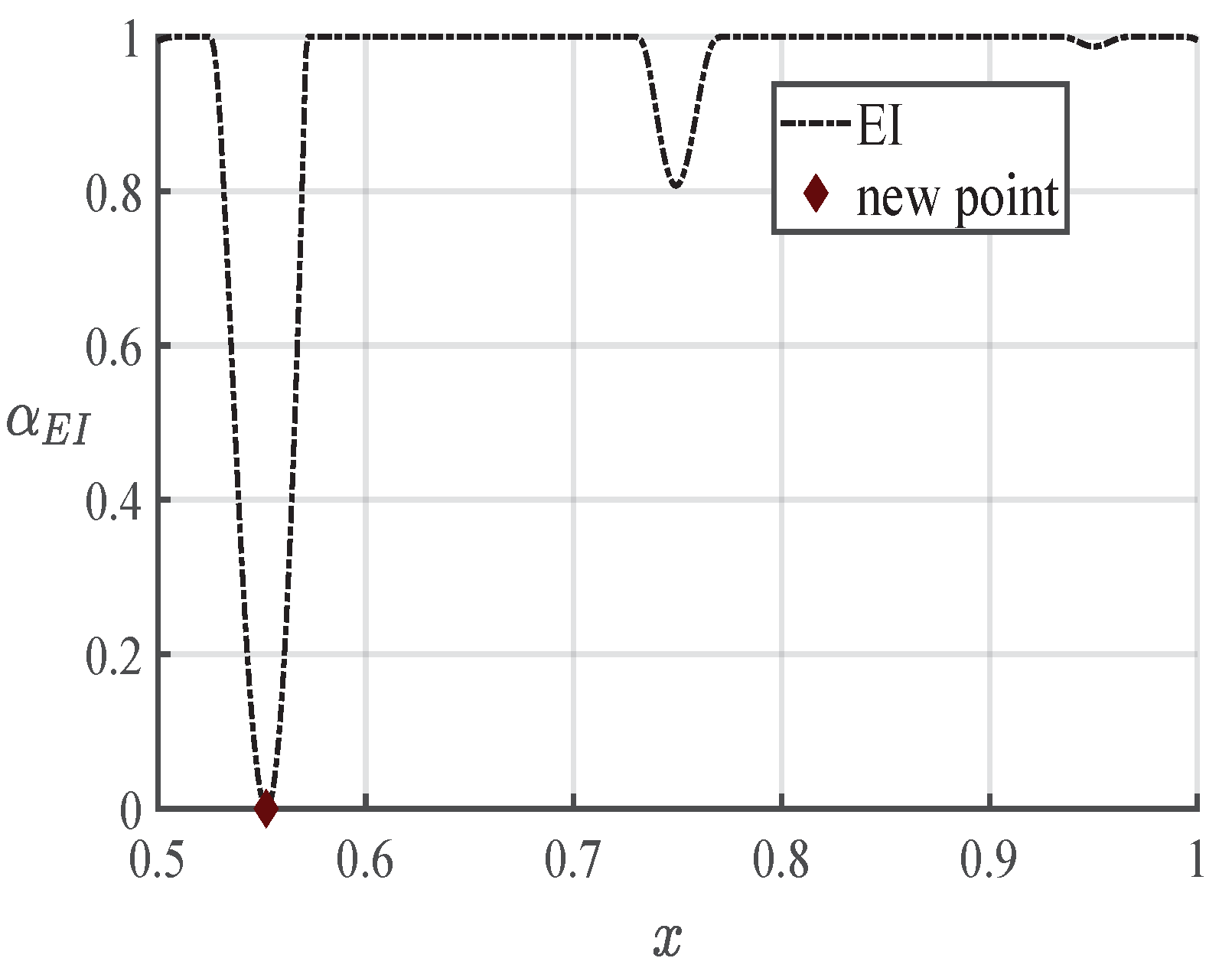
4.2. Optimization Framework Introduction
5. Results and Discussion
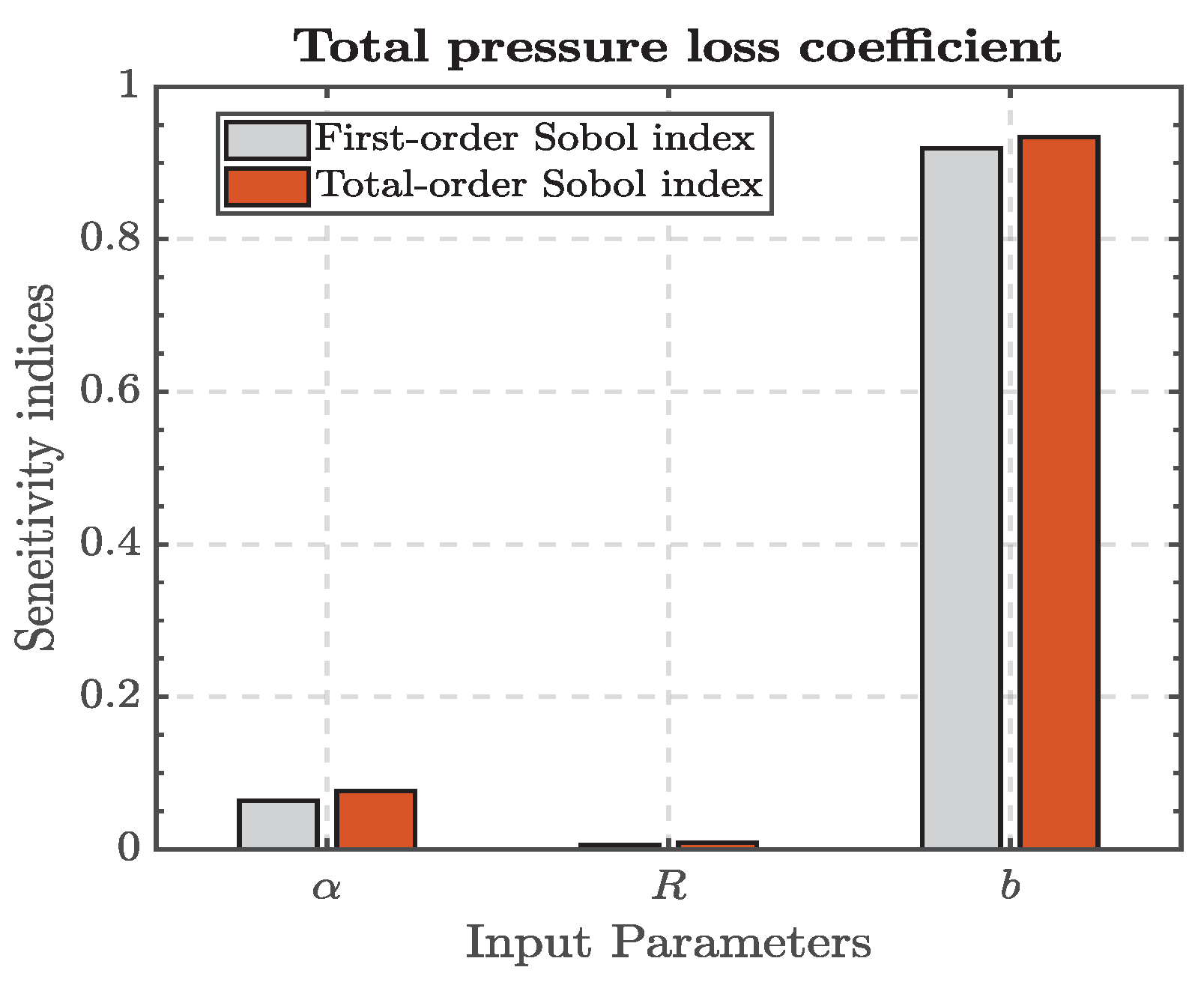
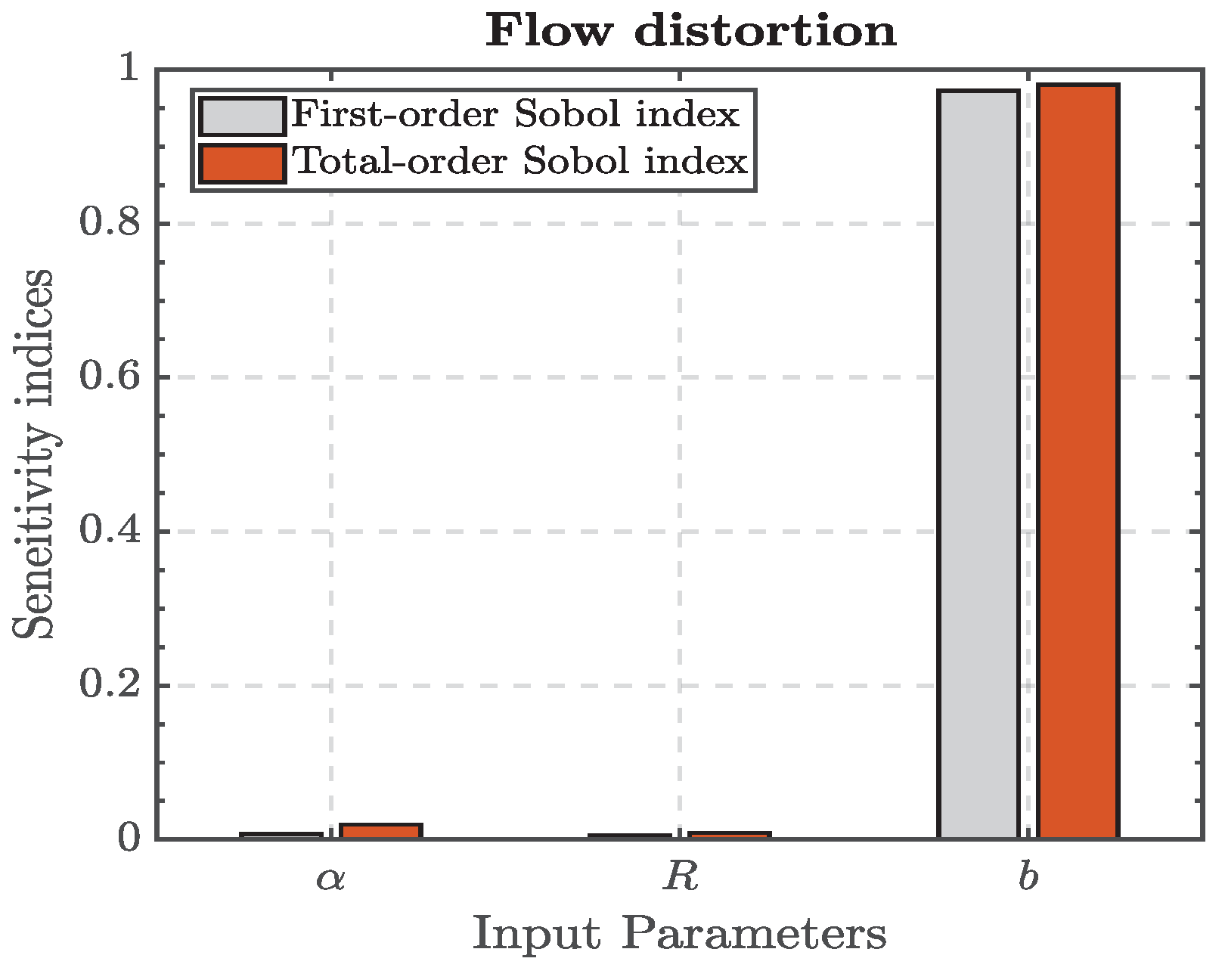
5.1. Sensitivity Analysis of Volute Optimization Parameters
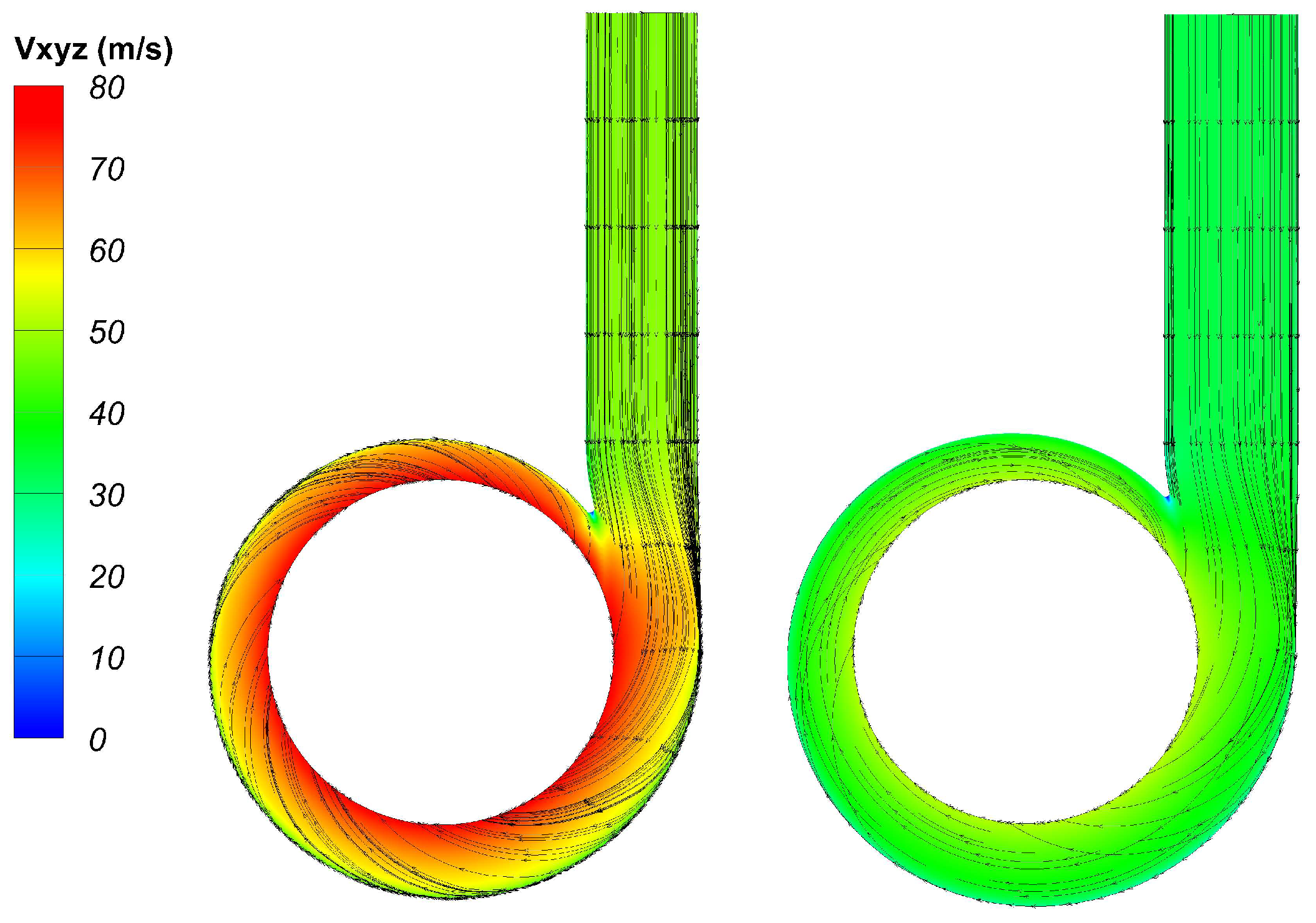
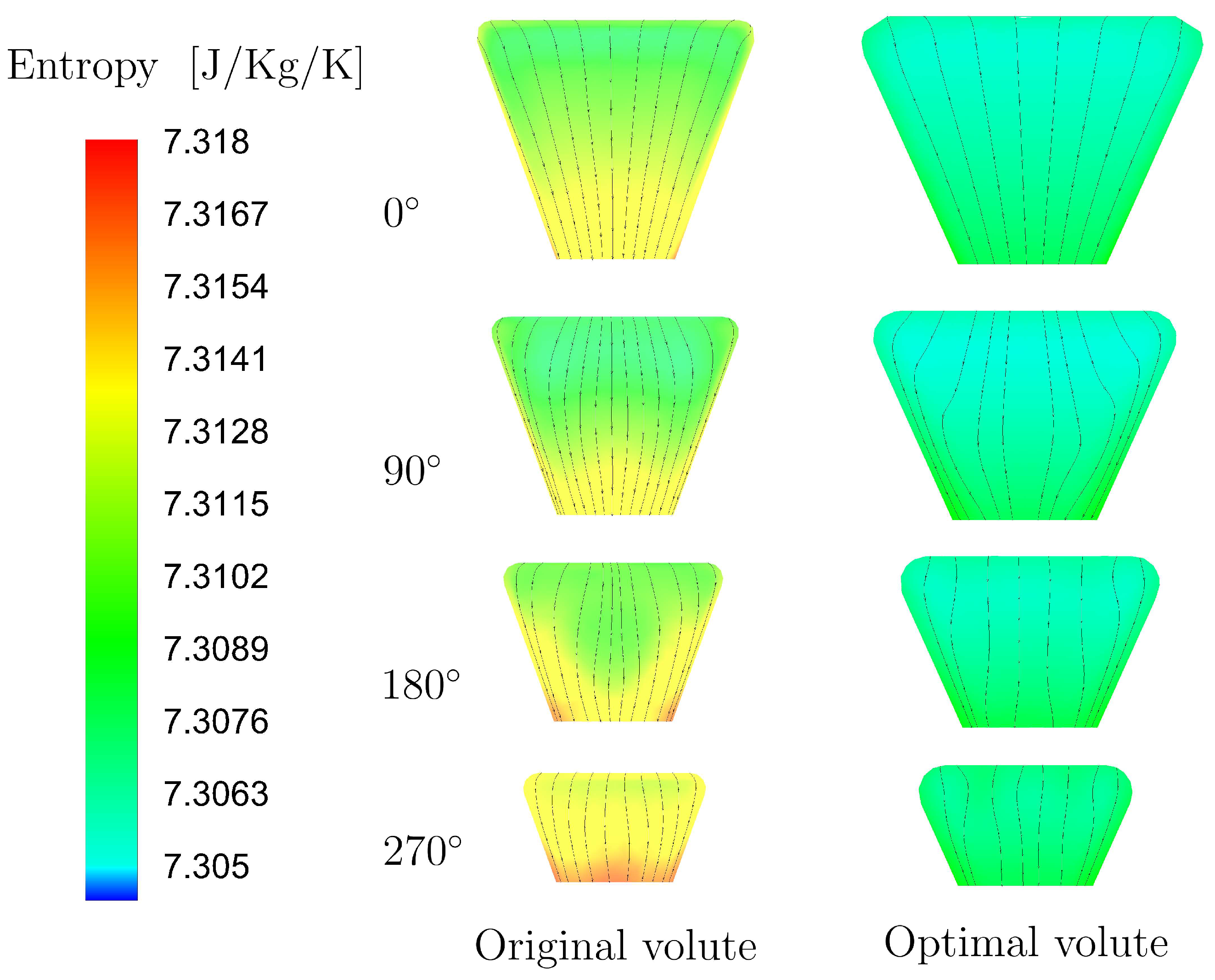
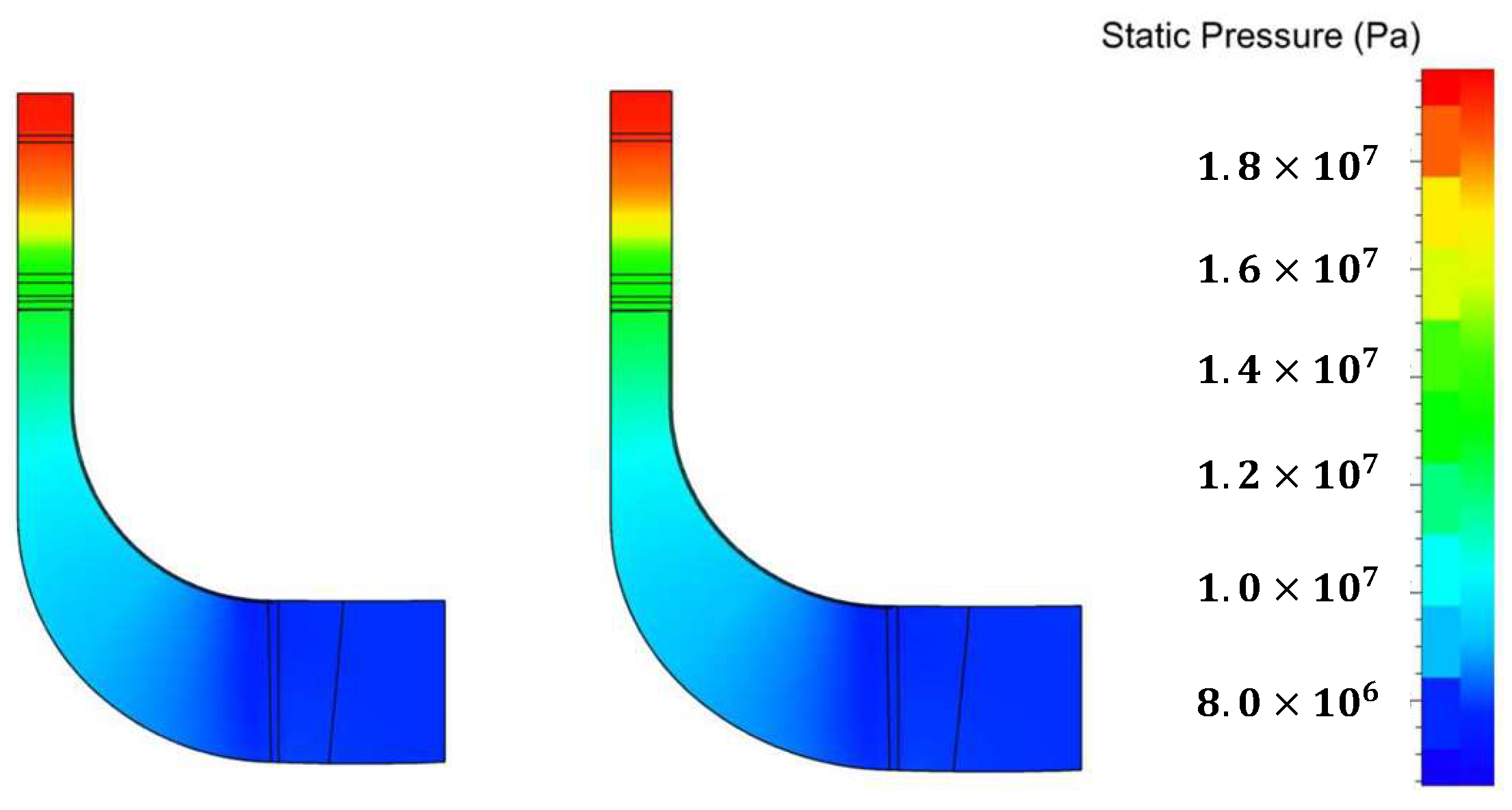
5.2. Performance Analysis of the Optimal Volute
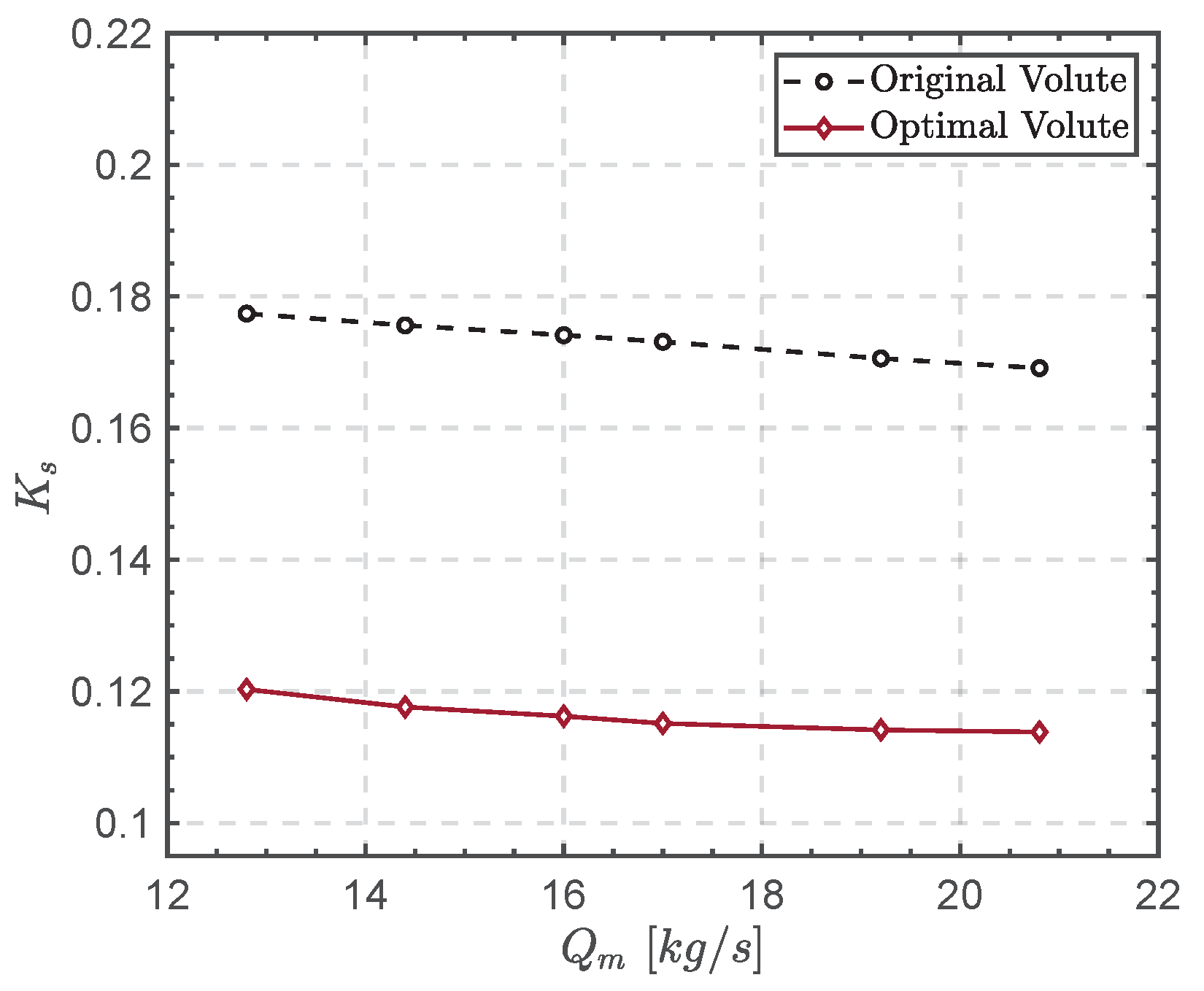
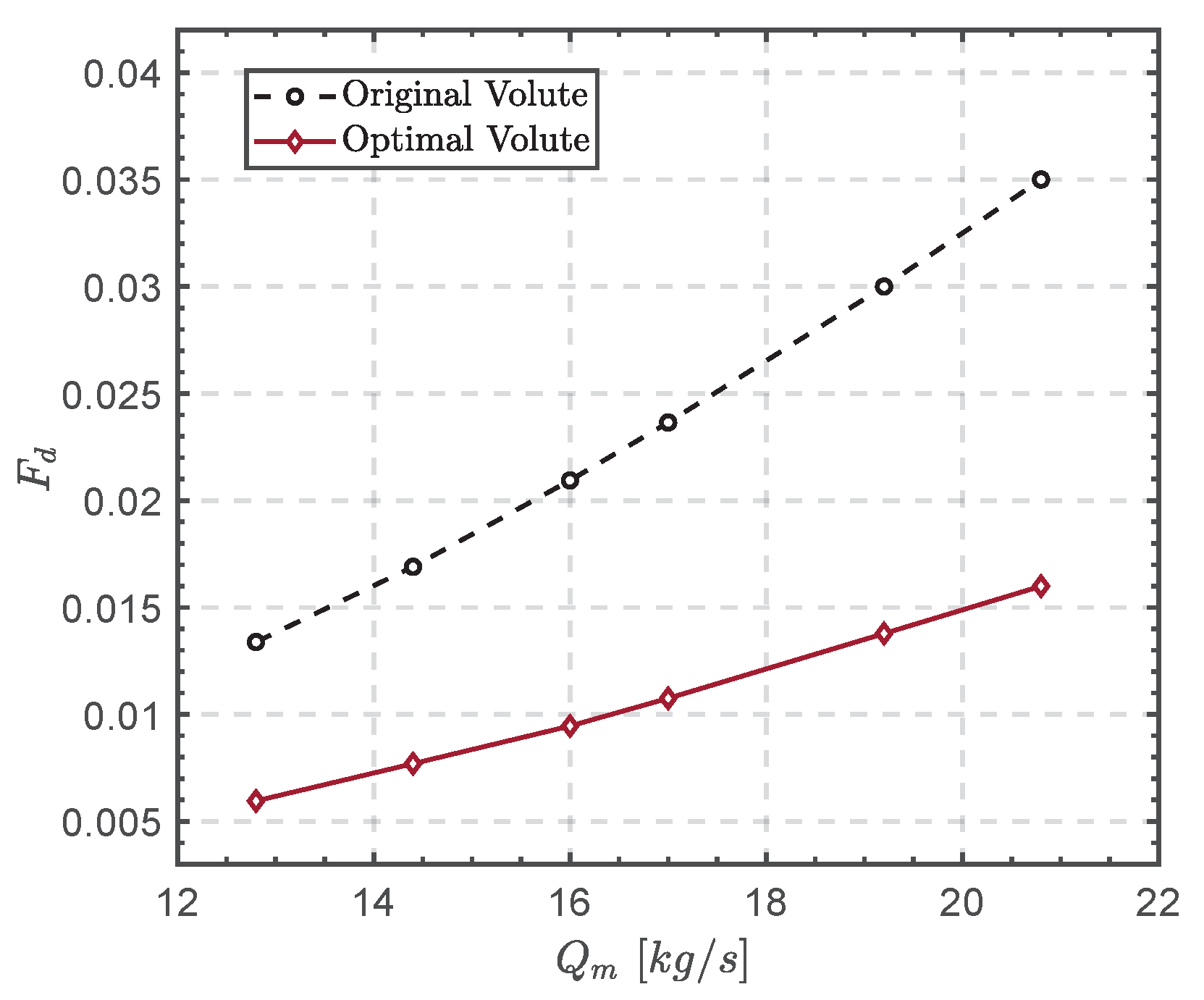
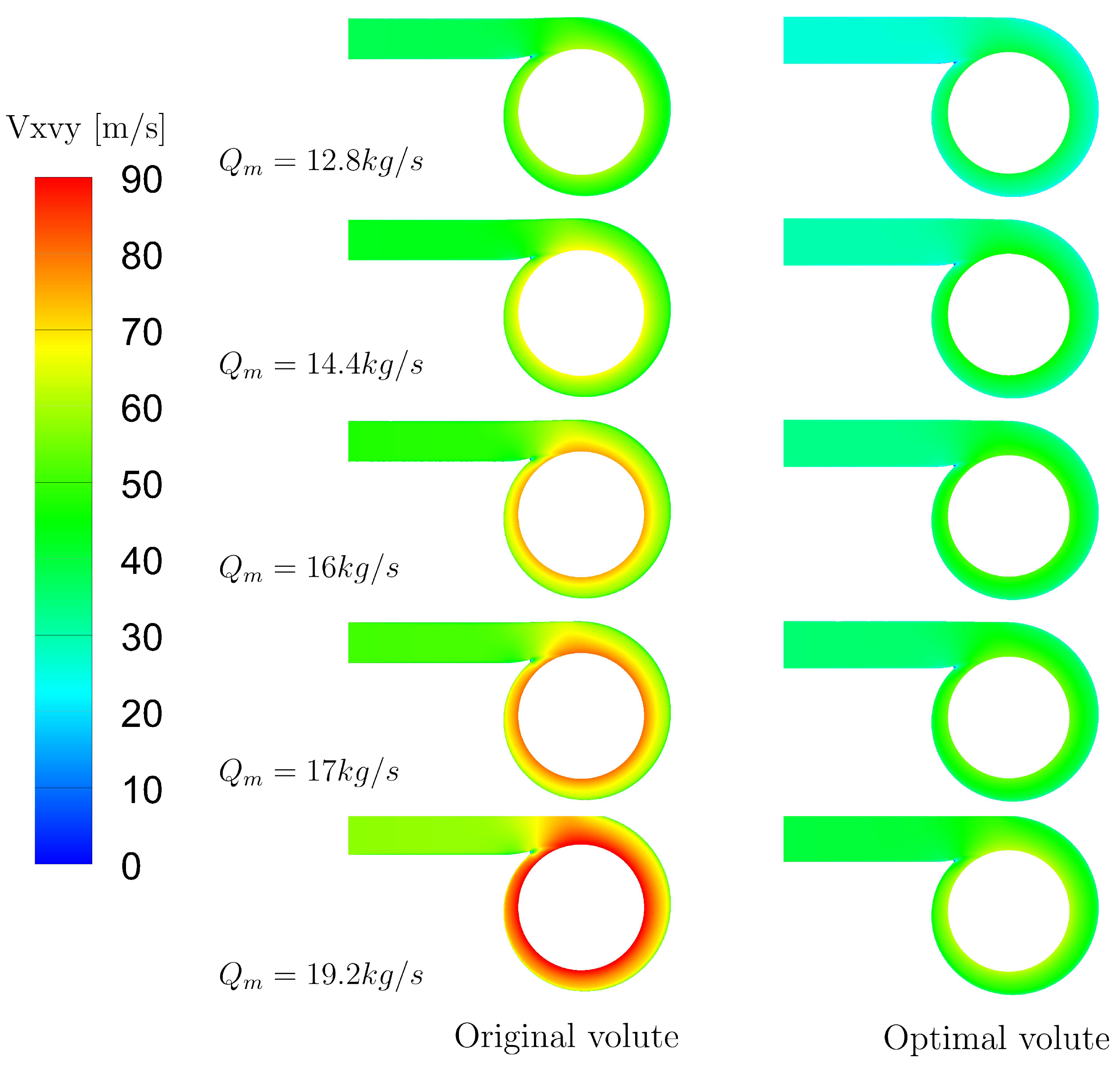
5.3. Off Design Performance Analysis of Optimal Volute
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| - | Supercritical carbon dioxide |
| BO | Bayesian optimization |
| CFD | Computational fluid dynamics |
| SA | Spalart–Allmaras |
| NIST | The national institute of standards and technology |
| ICEM | The integrated computer engineering and manufacturing code |
| RMSE | Root mean square error |
| MAE | Maximum absolute error |
| MRE | Maximum relative error |
| EI | Expected improvement |
| PI | Probability of improvement |
| GA | Genetic algorithm |
| DOE | Design of experiment |
| GP | Gaussian processes |
| RBF | Radial basis function |
| PRS | Polynomial response surface |
| MARS | Multivariate adaptive regression splines |
References
- Apostolos, A.G.; Anastassios, M.S.; Anestis, I.K. Recuperators Investigation for High Temperature Supercritical Carbon Dioxide Power Generation Cycles. Appl. Therm. Eng. 2017, 125, 1094–1102. [Google Scholar]
- Chen, Y. Thermodynamic Cycles using Carbon Dioxide as Working Fluid: CO2 Transcritical Power Cycle Study. Toxicol. In Vitro 2017, 25, 206–212. [Google Scholar]
- Dostal, V.; Driscoll, M.J.; Hejzlar, P. Advanced Nuclear Power Technology Program. In A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors; MIT: Cambridge, MA, USA, 2004. [Google Scholar]
- Sienicki, J.J.; Moisseytsev, A.; Fuller, R.L.; Wright, S.A.; Pickard, P.S. Scale Dependencies of Supercritical Carbon Dioxide Brayton Cycle Technologies and the Optimal Size for a Next-Step Supercritical CO2 Cycle Demonstration. In Proceedings of the SCO2 Power Cycle Symposium, Boulder, CO, USA, 24–25 May 2011; pp. 24–25. [Google Scholar]
- Simpson, A.T.; Stephen, S.; John, W. A Comparison of the Flow Structures and Losses Within Vaned and Vaneless Stators for Radial Turbines. J. Turbomach.-Trans. ASME 2009, 131, 031010. [Google Scholar] [CrossRef]
- Suhrmann, J.F.; Peitsch, D.; Gugau, M.; Heuer, T. On the Effect of Volute Tongue Design on Radial Turbine Performance. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 891–901. [Google Scholar]
- Lee, S.P.; Jupp, M.L.; Nickson, A.K. The Influence of Secondary Flow Structures in a Turbocharger Turbine Housing in Steady State and Pulsating Flow Conditions. In Proceedings of the 2016 7th International Conference on Mechanical and Aerospace Engineering (ICMAE), London, UK, 18–20 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 154–159. [Google Scholar]
- Yang, M.; Martinez-Botas, R.; Rajoo, S.; Yokoyama, T.; Ibaraki, S. An Investigation of Volute Cross-Sectional Shape on Turbocharger Turbine under Pulsating Conditions in Internal Combustion Engine. Energy Convers. Manag. 2015, 105, 167–177. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.P.; Barrans, S.M.; Jupp, M.L.; Nickson, A.K. The Impact of Volute Aspect Ratio on the Performance of a Mixed Flow Turbine. Aircr. Eng. Aerosp. Technol. 2017, 4, 56. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.P.; Jupp, M.L.; Nickson, A.K.; Allport, J.M. Analysis of a Tilted Turbine Housing Volute Design under Pulsating Inlet Conditions. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Huang, J.; Xu, S.; Liu, H.; Wang, X. Robust Performance Optimization of Centrifugal Compressor Volute with a Rectangular Cross-Section. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15 June 2015. [Google Scholar]
- Du, X.; Yu, D.; Luo, D.; Huang, D. Supercritical Carbon Dioxide Centripetal Compressor—Aerodynamic Design and Analysis of Off Design Conditions. J. Nucl. Eng. Radiat. Sci. 2019, 5, 041209. [Google Scholar] [CrossRef]
- Zhu, C.; Shao, W.Y.; Ma, Z.Y.; Lv, G.C.; Wang, X.F. Investigation on Interaction between Geometry and Performance and Design of S-CO2 Radial Inflow Turbine’s Vaneless Inlet Volute. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1081, 012009. [Google Scholar] [CrossRef]
- Liu, H.; Xu, S.; Wang, X.; Wu, J.; Song, Y. A Global Optimization Algorithm for Simulation-Based Problems via the Extended DIRECT Scheme. Eng. Optim. 2015, 47, 1441–1458. [Google Scholar] [CrossRef]
- Liu, H.; Ong, Y.S.; Cai, J. A Survey of Adaptive Sampling for Global Metamodeling in Support of Simulation-Based Complex Engineering Design. Struct. Multidiscip. Optim. 2018, 57, 393–416. [Google Scholar] [CrossRef]
- Moustapha, H. Axial and Radial Turbines; Concepts NREC: White River Junction, VT, USA, 2003. [Google Scholar]
- Chen, H. Design Methods of Volute Casings for Turbocharger Turbine Applications. Proc. Inst. Mech. Eng. Part A J. Power Energy 1996, 210, 149–156. [Google Scholar] [CrossRef]
- Owarish, H.O.; Ilyas, M.; Bhinder, F.S. A Two-Dimensional Flow Analysis Model for Designing a Nozzle-less Volute Casing for Radial Flow Gas Turbines. J. Turbomach.-Trans. ASME 1992, 114, 402–410. [Google Scholar] [CrossRef]
- Ayder, E.; Van den Braembussche, R.; Brasz, J.J. Experimental and Theoretical Analysis of the Flow in a Centrifugal Compressor Volute. J. Turbomach.-Trans. ASME 1993, 115, 582–589. [Google Scholar] [CrossRef]
- Ayder, E.; Van den Braembussche, R. Numerical Analysis of the Three-Dimensional Swirling Flow in Centrifugal Compressor Volutes. J. Turbomach.-Trans. ASME 1994, 116, 462–468. [Google Scholar] [CrossRef]
- Lv, G.; Yang, J.; Shao, W.; Wang, X. Aerodynamic Design Optimization of Radial-Inflow Turbine in Supercritical CO2 Cycles using a One-Dimensional Model. Energy Convers. Manag. 2018, 165, 827–839. [Google Scholar] [CrossRef]
- Roache, P.J.; Ghia, K.; White, F. Editorial Policy Statement on the Control of Numerical Accuracy. ASME J. Fluids Eng. 1986, 108, 2. [Google Scholar] [CrossRef] [Green Version]
- Eça, L.; Hoekstra, M.; Roache, P. Verification of Calculations: An Overview of the 2nd Lisbon Workshop. In Proceedings of the 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007. [Google Scholar]
- Abedi, M.; Askari, R.; Sepahi-Younsi, J.; Soltani, M.R. Axisymmetric and Three-Dimensional Flow Simulation of a Mixed Compression Supersonic Air Inlet. Propuls. Power Res. 2020, 9, 51–61. [Google Scholar] [CrossRef]
- Joe, S.; Kuo, F.Y. Constructing Sobol Sequences with Better Two-Dimensional Projections. SIAM J. Sci. Comput. 2008, 30, 2635–2654. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005; pp. 1–30. [Google Scholar]
- Karkee, M.; Steward, B.L. Local and Global Sensitivity Analysis of a Tractor and Single Axle Grain Cart Dynamic System Model. Biosyst. Eng. 2010, 106, 352–366. [Google Scholar] [CrossRef]
- Burnaev, E.; Panin, I.; Sudret, B. Efficient Design of Experiments for Eensitivity Analysis Based on Polynomial Chaos Expansions. Ann. Math. Artif. Intell. 2017, 81, 187–207. [Google Scholar] [CrossRef] [Green Version]
- Sobolá, I.M. Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Al, R.; Behera, C.R.; Zubov, A.; Gernaey, K.V.; Sin, G. Meta-Modeling Based Efficient Global Sensitivity Analysis for Wastewater Treatment Plants—An Application to the BSM2 Model. Comput. Chem. Eng. 2019, 127, 233–246. [Google Scholar] [CrossRef]
- Letham, B.; Karrer, B.; Ottoni, G.; Bakshy, E. Constrained Bayesian Optimization with Noisy Experiments. Bayesian Anal. 2019, 14, 495–519. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2951–2959. [Google Scholar]
- Ghosh, S.; Mondal, S.; Fernandez, E.; Kapat, J.S.; Roy, A. Parametric Shape Optimization of Pin-Fin Arrays Using a Surrogate Model-Based Bayesian Method. J. Thermophys. Heat Transf. 2021, 35, 245–255. [Google Scholar] [CrossRef]
- Bonfiglio, L.; Perdikaris, P.; Brizzolara, S.; Karniadakis, G.E. Multi-Fidelity Optimization of Super-Cavitating Hydrofoils. Comput. Methods Appl. Mech. Eng. 2018, 332, 63–85. [Google Scholar] [CrossRef]
- Tran, A.; Sun, J.; Furlan, J.M.; Pagalthivarthi, K.V.; Visintainer, R.J.; Wang, Y. pBO-2GP-3B: A Batch Parallel Known/Unknown Constrained Bayesian Optimization with Feasibility Classification and Its Applications in Computational Fluid Dynamics. Comput. Methods Appl. Mech. Eng. 2019, 347, 827–852. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]

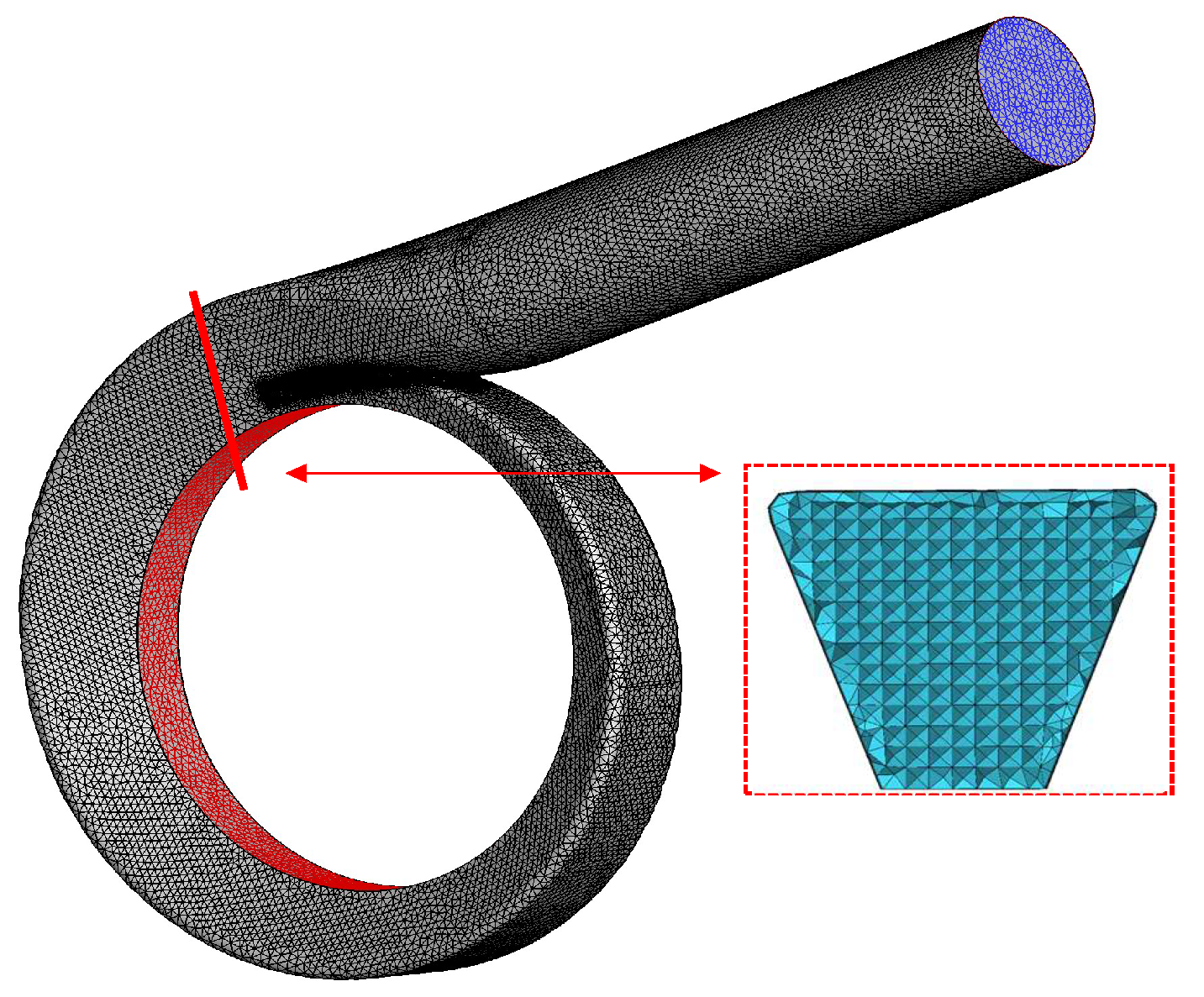



| Item | Symbol | Unit | Value |
|---|---|---|---|
| Inlet total temperature | K | 773.15 | |
| Inlet total pressure | MPa | 20 | |
| Outlet static pressure | MPa | 19.62 | |
| Mass flow rate | kg/s | 16 |
| Item | Symbol | Value |
|---|---|---|
| Grid refinement ratio between and | 1.28 | |
| Grid refinement ratio between and | 1.30 | |
| The order of convergence | P | 1.0520 |
| The extrapolated values between and | 19,882,247 (Pa) | |
| The extrapolated values between and | 19,980,611 (Pa) | |
| Approximate relative error between and | 0.004405 | |
| Approximate relative error between and | 0.004205 | |
| Extrapolated relative error between and | 0.035960 | |
| Extrapolated relative error between and | 0.032185 | |
| The fine-grid convergence index between and | 0.032185 | |
| The fine-grid convergence index between and | 0.308447 |
| Symbol | Range | Parameter | Unit |
|---|---|---|---|
| [10, 30] | Global spread angle of the volute | ° | |
| R | [70, 200] | Corner radius factor of the volute cross-section | mm |
| b | [200, 300] | Outlet size factor of the volute | mm |
| Symbol | Surrogate Model | RMSE | MAE | MRE | |
|---|---|---|---|---|---|
| GP | 0.9861 | 0.0046 | 0.0101 | 0.0513 | |
| RBF | 0.9596 | 0.0079 | 0.0146 | 0.1007 | |
| PRS | 0.9847 | 0.0049 | 0.0079 | 0.0643 | |
| MARS | 0.9638 | 0.0075 | 0.0129 | 0.0658 | |
| GP | 0.9980 | 0.0004 | 0.0008 | 0.0515 | |
| RBF | 0.9633 | 0.0016 | 0.0036 | 0.2643 | |
| PRS | 0.9847 | 0.0005 | 0.0079 | 0.0642 | |
| MARS | 0.9637 | 0.0075 | 0.0129 | 0.0658 |
| (°) | R (mm) | b (mm) | Relative Error (%) | ||
|---|---|---|---|---|---|
| BO | Numerical Calculation | ||||
| 24.25 | 200 | 300 | 0.1177 | 0.1162 | 1.25% |
| Item | (°) | R (mm) | b (mm) | ||
|---|---|---|---|---|---|
| original | 20 | 135 | 250 | 0.0209 | 0.1741 |
| optimal | 24.25 | 200 | 300 | 0.0095 | 0.1162 |
| Improvement | / | / | / | 54.55% | 33.26% |
| Item | Total Pressure Ratio | Isentropic Efficiency |
|---|---|---|
| Impeller matching original volute | 0.4197 | 0.9095 |
| Impeller matching optimal volute | 0.4195 | 0.9111 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, C.; Zhang, S.; Yang, J.; Liu, H.; Zhao, F.; Wang, X. Bayesian Optimization Design of Inlet Volute for Supercritical Carbon Dioxide Radial-Flow Turbine. Machines 2021, 9, 218. https://doi.org/10.3390/machines9100218
Bian C, Zhang S, Yang J, Liu H, Zhao F, Wang X. Bayesian Optimization Design of Inlet Volute for Supercritical Carbon Dioxide Radial-Flow Turbine. Machines. 2021; 9(10):218. https://doi.org/10.3390/machines9100218
Chicago/Turabian StyleBian, Chao, Shaojie Zhang, Jinguang Yang, Haitao Liu, Feng Zhao, and Xiaofang Wang. 2021. "Bayesian Optimization Design of Inlet Volute for Supercritical Carbon Dioxide Radial-Flow Turbine" Machines 9, no. 10: 218. https://doi.org/10.3390/machines9100218
APA StyleBian, C., Zhang, S., Yang, J., Liu, H., Zhao, F., & Wang, X. (2021). Bayesian Optimization Design of Inlet Volute for Supercritical Carbon Dioxide Radial-Flow Turbine. Machines, 9(10), 218. https://doi.org/10.3390/machines9100218







