Modeling the Dynamics of a Gyroscopic Rigid Rotor with Linear and Nonlinear Damping and Nonlinear Stiffness of the Elastic Support
Abstract
:1. Introduction
2. Materials and Methods
2.1. Related Work
2.2. Equations of Motion and Their Solutions
2.3. Nonlinear Frequency Characteristics
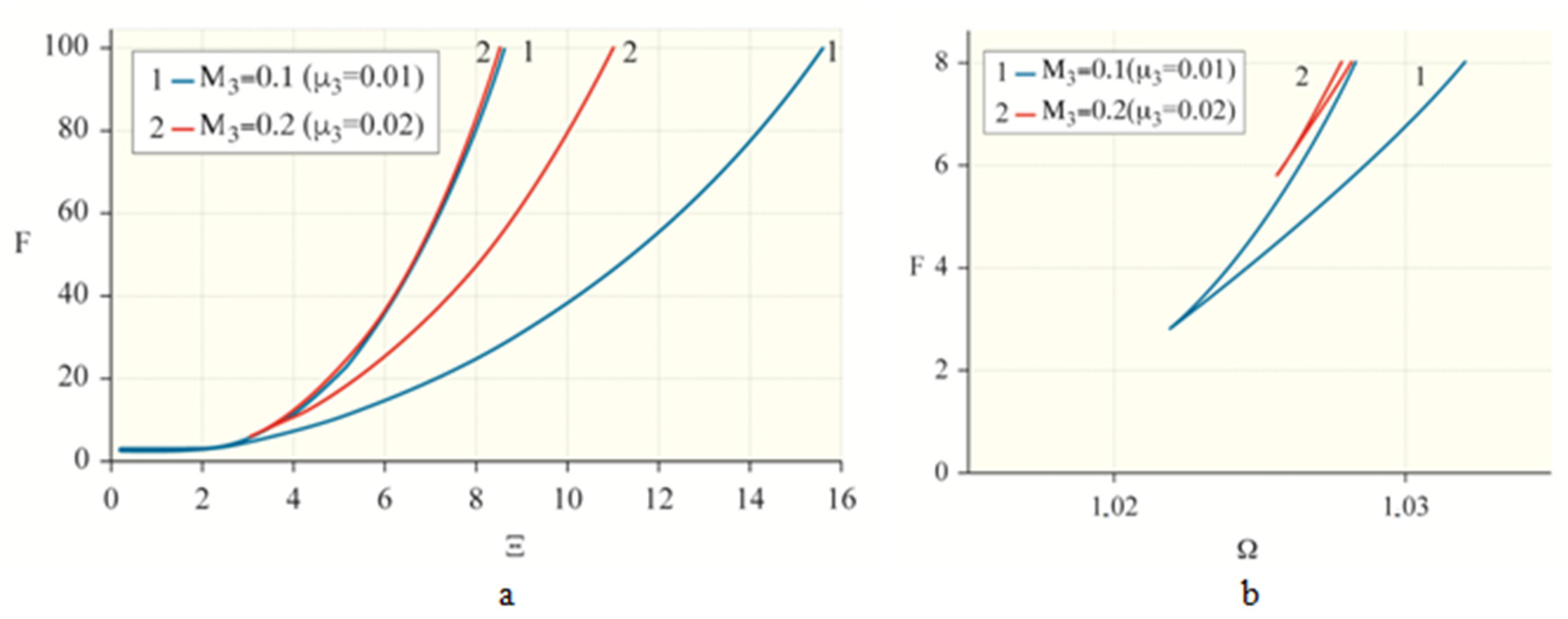
2.4. Analysis of Solutions of Motion Equations
2.5. Stability of Stationary Motion
2.6. Non-Stationary Oscillations
3. Results
3.1. Stability of Stationary Motion
3.2. Non-Stationary Oscillations
3.3. Methodology for Measuring and Identification of Damping Coefficients
4. Discussion
5. Conclusions
- The combined effect of linear and nonlinear cubic damping of an elastic support with nonlinear stiffness on the dynamics of a vertical rigid gyroscopic rotor was investigated by analytical and numerical modeling methods.
- It was shown that the combined linear and nonlinear cubic damping significantly reduces the oscillation amplitudes, including the maximum resonant amplitude, and has a greater effect on the boundaries of the bistability region—on the amplitudes and frequencies (shaft rotation speeds) corresponding to jumps—than the linear damping of the support material.
- A methodology has been developed for determining and identifying the coefficients of linear damping and nonlinear cubic damping of the support material, at which nonlinear jumping effects disappear, for a harmonically forced weakly nonlinear gyroscopic rigid rotor system with a disk with a predominant transverse moment of inertia.
- It is shown that if linear damping shifts the left boundary of the instability region towards large amplitudes and speeds of shaft rotation, then nonlinear cubic damping can completely eliminate it. In this case, the stability criterion has been obtained by the method of analysis of the characteristic equation in the form of Jacobi and the results of studies of the region of specific points.
- The resonant transitions and the influence of nonlinear stiffness and nonlinear cubic damping of the support material on the frequency characteristics of a non-stationary process are considered because the VAM was employed to study the response of the rotor system, supplemented by the concept of “slow” time and the parameter “slowly” by changing the angular velocity of rotation.
- The analytical solutions and numerical solutions of the equations of motion of the rotor show agreement.
- The results of analytical solutions of the equations of motion are in satisfactory agreement with the results of numerical solutions.
- The subject of research for the near future is the experimental measurement of parameters of elastic and damping characteristics of samples of material for support and determination of values and and theidentification of these parameters, comparison of the results obtained with the results of other models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Nomenclature
| vibration amplitude, rad | |
| vibration amplitude in stationary motion mode, rad | |
| linear eccentricity, m | |
| linear eccentricity, dimensionless | |
| disc weight, N | |
| disc weight, dimensionless | |
| polar moment of inertia, kgm2 | |
| polar moment of inertia, dimensionless | |
| polar moment of inertia, comparative, dimensionless | |
| transverse moment of inertia, kgm2 | |
| transverse moment of inertia, dimensionless | |
| coefficient of linear stiffness, N/m | |
| coefficient of linear stiffness, dimensionless | |
| linear stiffness coefficient, comparative, dimensionless | |
| coefficient of nonlinear stiffness, N/m3 | |
| coefficient of nonlinear stiffness, dimensionless | |
| distance between supports, m | |
| l | distance between supports, dimensionless |
| shaft length, m | |
| disc mass, kg | |
| time, dimensionless | |
| angular coordinates, rad | |
| vibration phase, rad | |
| coefficient of linear viscous damping, Nms/rad | |
| coefficient of linear viscous damping, dimensionless | |
| coefficient of nonlinear cubic viscous damping, N ms3/rad3 | |
| coefficient of nonlinear cubic viscous damping, dimensionless | |
| angular acceleration, dimensionless | |
| frequency detuning, rad | |
| frequency detuning taking into account the gyroscopic moment, rad | |
| slow time, dimensionless | |
| shaft speed, rad/s | |
| shaft speed, dimensionless | |
| the natural frequency of the rotary system, rad/s | |
| the natural frequency of the rotary system, dimensionless |
References
- Zakaria, A.A.; Rustighi, E.; Ferguson, N.S. A numerical investigation into the effect of the supports on the vibration of rotating shafts. In Dynamics of Rotating Systems, Proceedings of the 11th International Conference on Engineering Vibration, Ljubljana, Slovenia, 7–10 September 2015; Boltear, M., Slavi£, J., Wiercigroch, M., Eds.; Faculty for Mechanical Engineering: Ljubljana, Slovenia, 2015; Volume 57, pp. 539–552. [Google Scholar]
- Gil-Negrete, N.; Vinolas, J.; Kari, L. A Nonlinear Rubber Material Model Combining Fractional Order Viscoelasticity and Amplitude Dependent Effects. J. Appl. Mech. 2009, 76, 011009. [Google Scholar] [CrossRef]
- Richards, C.M.; Singh, R. Experimental characterization of nonlinear rubber isolators in a multi-degree-of-freedom system configuration. J. Acoust. Soc. Am. 1999, 106, 2178. [Google Scholar] [CrossRef]
- Matsubara, M.; Teramoto, S.; Nagatani, A.; Kawamura, S.; Tsujiuchi, N.; Ito, A.; Kobayashi, M.; Furuta, S. Effect of Fiber Orientation on Nonlinear Damping and Internal Microdeformation in Short-Fiber-Reinforced Natural Rubber. Exp. Tech. 2021, 45, 37–47. [Google Scholar] [CrossRef]
- Ravindra, B.; Mallik, A. Performance of Non-linear Vibration Isolators Under Harmonic Excitation. J. Sound Vib. 1994, 170, 325–337. [Google Scholar] [CrossRef]
- Peng, Z.; Meng, G.; Lang, Z.; Zhang, W.; Chu, F. Study of the effects of cubic nonlinear damping on vibration isolations using Harmonic Balance Method. Int. J. Non-Linear Mech. 2012, 47, 1073–1080. [Google Scholar] [CrossRef]
- Lang, Z.; Jing, X.; Billings, S.; Tomlinson, G.; Peng, Z. Theoretical study of the effects of nonlinear viscous damping on vibration isolation of sdof systems. J. Sound Vib. 2009, 323, 352–365. [Google Scholar] [CrossRef]
- Xiao, Z.; Jing, X.; Cheng, L. The transmissibility of vibration isolators with cubic nonlinear damping under both force and base excitations. J. Sound Vib. 2013, 332, 1335–1354. [Google Scholar] [CrossRef]
- Iskakov, Z. Resonant Oscillations of a Vertical Hard Gyroscopic Rotor with Linear and Non-linear Damping. In Advances in Mechanism and Machine Science; Mechanisms and Machine Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 73, pp. 3353–3362. [Google Scholar] [CrossRef]
- Iskakov, Z.; Bissembayev, K. The nonlinear vibrations of a vertical hard gyroscopic rotor with nonlinear characteristics. Mech. Sci. 2019, 10, 529–544. [Google Scholar] [CrossRef]
- Al-Solihat, M.K.; Behdinan, K. Force transmissibility and frequency response of a flexible shaft–disk rotor supported by a nonlinear suspension system. Int. J. Non-Linear Mech. 2020, 124, 103501. [Google Scholar] [CrossRef]
- Fujiwara, H.; Nakaura, H.; Watanabei, K. The vibration behavior of flexibly fixed rotating machines. In Rotor Dynamics, Proceedings of the 14th IFToMM World Congress, 25–30 October 2015; Chang, S.H., Ceccarelli, M., Sung, C.K., Chang, J.Y., Liu, T., Eds.; Airily Library: Taipei, Taiwan, 2015; pp. 517–522. [Google Scholar] [CrossRef]
- Li, D.; Shaw, S.W. The effects of nonlinear damping on degenerate parametric amplification. Nonlinear Dyn. 2020, 102, 2433–2452. [Google Scholar] [CrossRef]
- Mofidian, S.M.M.; Bardaweel, H. Displacement transmissibility evaluation of vibration isolation system employing nonlinear-damping and nonlinear-stiffness elements. J. Vib. Control 2018, 24, 4247–4259. [Google Scholar] [CrossRef]
- Iskakov, Z. Resonant Oscillations of a Vertical Unbalanced Gyroscopic Rotor with Non-linear Characteristics. In Rotor Dynamics, Proceedings of the 14th IFToMM World Congress, Taipei, Taiwan, 25–30 October 2015; Chang, S.H., Ceccarelli, M., Eds.; Airily Library: Taipei, Taiwan, 2015; pp. 505–513. [Google Scholar] [CrossRef]
- Iskakov, Z. Dynamics of a Vertical Unbalanced Gyroscopic Rotor with Non-linear Characteristics. In New advances in Mechanisms, Mechanical Transmissions and Robotics; Mechanisms and Machine Science; Springer International Publishing: Cham, Switzerland, 2017; Volume 46, pp. 107–114. [Google Scholar] [CrossRef]
- Donmez, A.; Cigeroglu, E.; Ozgen, G.O. The effect of stiffness and loading deviations in a nonlinear isolator having quasi zero stiffness and geometrically nonlinear damping. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017. [Google Scholar]
- Balaji, P.S.; Selvakumar, K.K. Applications of Nonlinearity in Passive Vibration Control: A Review. J. Vib. Eng. Technol. 2021, 9, 183–213. [Google Scholar] [CrossRef]
- Liao, X.; Sun, X.J.; Wang, Y. Modeling and dynamic analysis of hydraulic damping rubber mount for cab under larger amplitude excitation. J. Vibroeng. 2021, 23, 542–558. [Google Scholar]
- Menga, N.; Bottiglione, F.; Carbone, G. Nonlinear viscoelastic isolation for seismic vibration mitigation. Mech. Syst. Signal Process. 2021, 157, 107626. [Google Scholar] [CrossRef]
- Dai, Q.; Liu, Y.; Qin, Z.; Chu, F. Nonlinear Damping and Forced Response of Laminated Composite Cylindrical Shells with Inherent Material Damping. Int. J. Appl. Mech. 2021, 13. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Yu, Y.; Li, Y. Modified Adaptive Negative Stiffness Device with Variable Negative Stiffness and Geometrically Nonlinear Damping for Seismic Protection of Structures. Int. J. Struct. Stab. Dyn. 2021, 21, 2150107. [Google Scholar] [CrossRef]
- Kong, X.; Li, H.; Wu, C. Dynamics of 1-dof and 2-dof energy sink with geometrically nonlinear damping: Application to vibration suppression. Nonlinear Dyn. 2018, 91, 733–754. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, X.; Yue, C.; Xiong, H. Dynamic analysis of 1-dof and 2-dof nonlinear energy sink with geometrically nonlinear damping and combined stiffness. Nonlinear Dyn. 2021, 105, 167–190. [Google Scholar] [CrossRef]
- Taghipour, J.; Dardel, M.; Pashaei, M.H. Vibration mitigation of a nonlinear rotor system with linear and nonlinear vibration absorbers. Mech. Mach. Theory 2018, 128, 586–615. [Google Scholar] [CrossRef]
- Mojahed, A.; Moore, K.; Bergman, L.A.; Vakakis, A.F. Strong geometric softening–hardening nonlinearities in an oscillator composed of linear stiffness and damping elements. Int. J. Non-Linear Mech. 2018, 107, 94–111. [Google Scholar] [CrossRef]
- Liu, Y.; Mojahed, A.; Bergman, L.A.; Vakakis, A.F. A new way to introduce geometrically nonlinear stiffness and damping with an application to vibration suppression. Nonlinear Dyn. 2019, 96, 1819–1845. [Google Scholar] [CrossRef]
- Le Guisquet, S.; Amabili, M. Identification by means of a genetic algorithm of nonlinear damping and stiffness of continuous structures subjected to large-amplitude vibrations. Part I: Single-degree-of-freedom responses. Mech. Syst. Signal Process. 2021, 153, 107470. [Google Scholar] [CrossRef]
- Civera, M.; Grivet-Talocia, S.; Surace, C.; Fragonara, L.Z. A generalised power-law formulation for the modelling of damping and stiffness nonlinearities. Mech. Syst. Signal Process. 2021, 153, 107531. [Google Scholar] [CrossRef]
- Chatterjee, A.; Chintha, H.P. Identification and parameter estimation of cubic nonlinear damping using harmonic probing and volterra series. Int. J. Non-Linear Mech. 2020, 125, 103518. [Google Scholar] [CrossRef]
- Chatterjee, A.; Chintha, H.P. Identification and Parameter Estimation of Asymmetric Nonlinear Damping in a Single-Degree-of-Freedom System Using Volterra Series. J. Vib. Eng. Technol. 2021, 9, 817–843. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Ferrari, G.; Amabili, M. Identification of the viscoelastic response and nonlinear damping of a rubber plate in nonlinear vibration regime. Mech. Syst. Signal Process. 2018, 111, 376–398. [Google Scholar] [CrossRef]
- Amabili, M.; Balasubramanian, P.; Ferrari, G. Nonlinear vibrations and damping of fractional viscoelastic rectangular plates. Nonlinear Dyn. 2021, 103, 3581–3609. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear damping in large-amplitude vibrations: Modelling and experiments. Nonlinear Dyn. 2018, 93, 5–18. [Google Scholar] [CrossRef]
- Lisitano, D.; Bonisoli, E. Direct identification of nonlinear damping: Application to a magnetic damped system. Mech. Syst. Signal Process. 2021, 146, 107038. [Google Scholar] [CrossRef]
- Lu, Z.-Q.; Hu, G.-S.; Ding, H.; Chen, L.-Q. Jump-based estimation for nonlinear stiffness and damping parameters. J. Vib. Control. 2019, 25, 325–335. [Google Scholar] [CrossRef]
- Al-Hababi, T.; Cao, M.; Saleh, B.; Alkayem, N.F.; Xu, H. A Critical Review of Nonlinear Damping Identification in Structural Dynamics: Methods, Applications, and Challenges. Sensors 2020, 20, 7303. [Google Scholar] [CrossRef]
- Parshakov, A.N. Physics of Vibratory Motion; Publishing House of Perm State University: Perm, Russia, 2010; pp. 79–90. [Google Scholar]
- Grobov, V.A. Asymptotic Methods for Calculating Bending Vibrations of Turbomachine Shafts; Publishing House of the Academy of Science of the USSR: Moscow, Russia, 1961; pp. 39–79, 95–102. [Google Scholar]
- Kuznetsov, A.P.; Kuznetsov, S.P.; Ryskin, N.M. Non-linear vibrations. In Lectures on the Theory of Vibration and Waves; Publishing House of Saratov State University named after Chernyshevsky: Saratov, Russia, 2011; pp. 219–229. [Google Scholar]
- Mendeley Date. Available online: https://data.mendeley.com/drafts/ngntc2944b (accessed on 31 October 2021). [CrossRef]
- Mendeley Date. Available online: https://data.mendeley.com/drafts/b33zrddfdh (accessed on 31 October 2021). [CrossRef]
- Mendeley Date. Available online: http//www.doi.org/10.17632/kcgzh2s5kx (accessed on 31 October 2021). [CrossRef]
- Mendeley Date. Available online: https://data.mendeley.com/drafts/f286br875d (accessed on 31 October 2021). [CrossRef]


































| K3 | μ3 | A | Ω | K3 | μ3 | A | Ω |
|---|---|---|---|---|---|---|---|
| 0.1 | 0.010 | 1.360 | 1.075 | −0.1 | 0.010 | 1.163 | 0.960 |
| 0.020 | 1.125 | 1.060 | 0.020 | 1.050 | 0.967 | ||
| 0.043 | 0.910 | 1.041 | 0.043 | 0.900 | 0.980 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iskakov, Z.; Bissembayev, K.; Jamalov, N.; Abduraimov, A. Modeling the Dynamics of a Gyroscopic Rigid Rotor with Linear and Nonlinear Damping and Nonlinear Stiffness of the Elastic Support. Machines 2021, 9, 276. https://doi.org/10.3390/machines9110276
Iskakov Z, Bissembayev K, Jamalov N, Abduraimov A. Modeling the Dynamics of a Gyroscopic Rigid Rotor with Linear and Nonlinear Damping and Nonlinear Stiffness of the Elastic Support. Machines. 2021; 9(11):276. https://doi.org/10.3390/machines9110276
Chicago/Turabian StyleIskakov, Zharilkassin, Kuatbay Bissembayev, Nutpulla Jamalov, and Azizbek Abduraimov. 2021. "Modeling the Dynamics of a Gyroscopic Rigid Rotor with Linear and Nonlinear Damping and Nonlinear Stiffness of the Elastic Support" Machines 9, no. 11: 276. https://doi.org/10.3390/machines9110276
APA StyleIskakov, Z., Bissembayev, K., Jamalov, N., & Abduraimov, A. (2021). Modeling the Dynamics of a Gyroscopic Rigid Rotor with Linear and Nonlinear Damping and Nonlinear Stiffness of the Elastic Support. Machines, 9(11), 276. https://doi.org/10.3390/machines9110276






