Flux Estimator for Salient Pole Synchronous Machines Driven by the Cycloconverter Based on Enhanced Current and Voltage Model of the Machine with Fuzzy Logic Transition
Abstract
:1. Introduction
- Salient pole synchronous machine flux estimator based on current and voltage model with fuzzy logic set of rules to ensure the smooth transition between the models.
- The flux estimator uses only basic machine parameters, which makes it ideal for industry applications where a limited amount of machine data is available.
- Specially designed for the drives with high voltage and current ripple, e.g., cycloconverters.
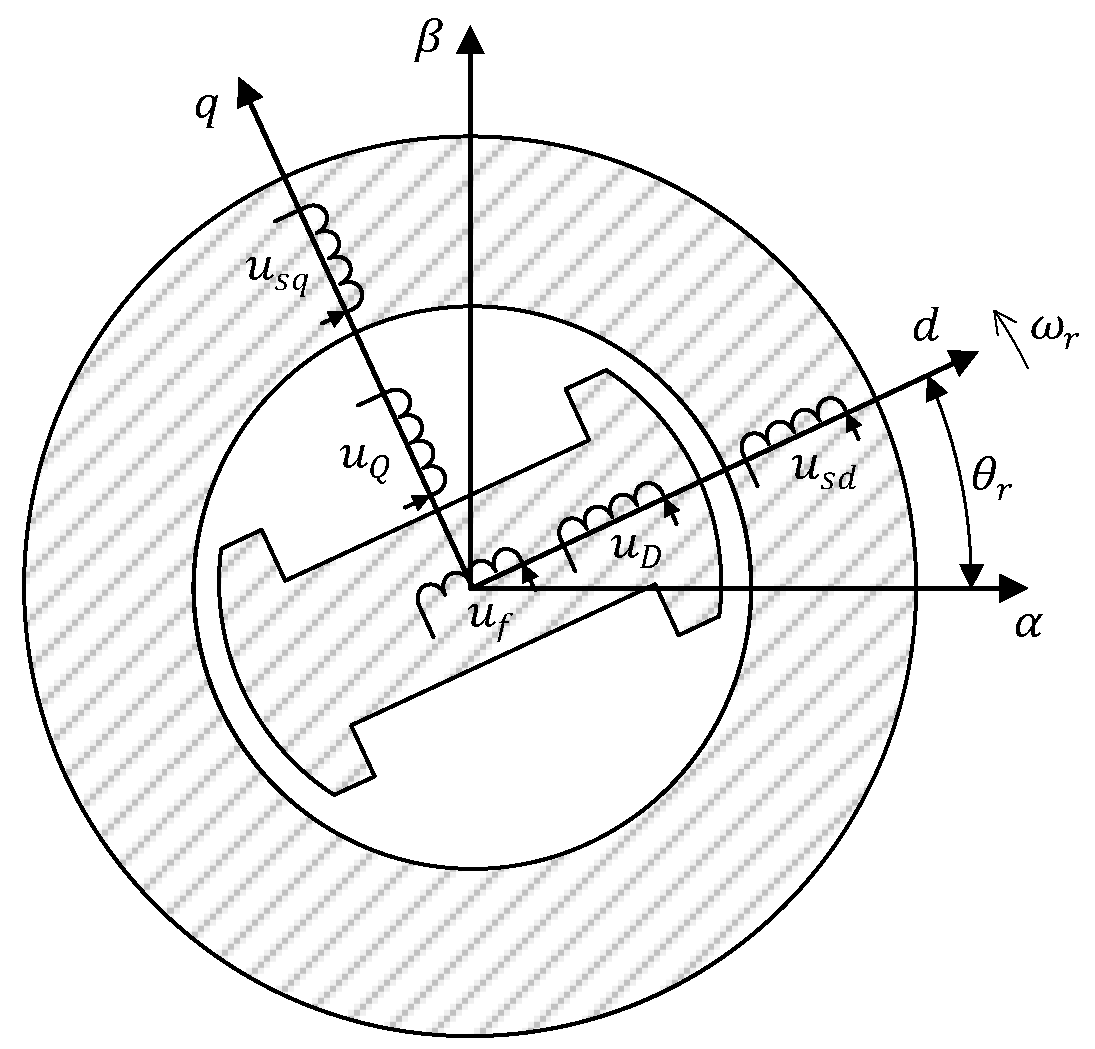
2. Mathematical Model of Salient Pole Synchronous Machine
3. Hybrid Model
3.1. Overview of the Proposed Flux Hybrid Model
3.2. Flux Estimator Based on Current Model of the Machine
3.3. Flux Estimator Based on Voltage Model of the Machine
3.4. Design of the Fuzzy Transition between the Flux Estimator Based on Current and Voltage Model
- IF (Speed is Small) AND (Torque is Small) THEN
- IF (Speed is High) AND (Torque is High) THEN
4. Experimental Verification of the Proposed Flux Estimator
4.1. System Setup
4.2. Experimental Results and Analysis
4.3. Analyisis of the Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Rated power | 18.5 | kW | |
| Rated stator voltage | 400 | V | |
| Rated stator current | 29.2 | A | |
| Rated excitation voltage | 65 | V | |
| Rated excitation current | 11 | A | |
| Rated stator frequency | 30 | Hz | |
| Number of pole pairs | 2 | - | |
| Stator resistance | 0.244 | Ω | |
| Stator leakage inductance | 0.0076 | H | |
| Unsaturated magnetizing inductance in the direct axis | 0.04 | H | |
| Unsaturated magnetizing inductance in the quadrature axis | 0.035 | H | |
| Damping winding resistance in the direct axis | 1.08 | Ω | |
| Damping winding resistance in the quadrature axis | 1.26 | Ω | |
| Damper winding leakage inductance in the direct axis | 0.0048 | H | |
| Damper winding leakage inductance in the quadrature axis | 0.0058 | H |

References
- Leonhard, W. Control of Electrical Drives, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Vas, P. Vector Control of AC Machines; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Vas, P. Sensorless Vector and Direct Torque Control; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Han, Y.; Wu, X.; He, G.; Hu, Y.; Ni, K. Nonlinear Magnetic Field Vector Control with Dynamic-Variant Parameters for High-Power Electrically Excited Synchronous Motor. IEEE Trans. Power Electron. 2020, 35, 11053–11063. [Google Scholar] [CrossRef]
- Zhou, Y.; Long, S. Sensorless Direct Torque Control for Electrically Excited Synchronous Motor Based on Injecting High-Frequency Ripple Current into Rotor Winding. IEEE Trans. Energy Convers. 2015, 30, 246–253. [Google Scholar] [CrossRef]
- Koteich, M. Flux estimation algorithms for electric drives: A comparative study. In Proceedings of the 3rd International Conference on Renewable Energies for Developing Countries (REDEC), Zouk Mosbeh, Lebanon, 13–15 July 2016. [Google Scholar]
- Pyrhönen, J.; Hrabovcová, V.; Semken, R.S. Electrical Machine Drives Control, 1st ed.; John Wiley & Sons: Chichester, UK, 2016. [Google Scholar]
- Levi, E. Saturation modelling in d-q axis models of salient pole synchronous machines. IEEE Trans. Energy Convers. 1999, 14, 44–50. [Google Scholar] [CrossRef]
- Levi, E.; Levi, V.A. Impact of dynamic cross-saturation on accuracy of saturated synchronous machine models. IEEE Trans. Energy Convers. 2000, 15, 224–230. [Google Scholar] [CrossRef]
- Jeong, I.; Gu, B.G.; Kim, J.; Nam, K.; Kim, Y. Inductance Estimation of Electrically Excited Synchronous Motor via Polynomial Approximations by Least Square Method. IEEE Trans. Ind. Appl. 2015, 51, 1526–1537. [Google Scholar] [CrossRef]
- Kar, N.C.; El-Serafi, A.M. Measurement of the saturation characteristic in the quadrature axis of synchronous machines. IEEE Trans. Energy Convers. 2006, 21, 690–698. [Google Scholar] [CrossRef]
- Kaukonen, J. Salient Pole Synchronous Machine Modelling in an Industrial Direct Torque Controlled Drive Application. Ph.D. Thesis, Lappeenranta University of Technology, Lappeenranta, Finland, 26 March 1999. [Google Scholar]
- Hu, J.; Wu, B. New integration algorithms for estimating motor flux over a wide speed range. IEEE Trans. Power Electron. 1998, 13, 969–977. [Google Scholar]
- Wang, D.; Lu, K.; Rasmussen, P.O. Improved Closed-Loop Flux Observer Based Sensorless Control Againts System Oscillation for Synchronous Reluctance Machine Drives. IEEE Trans. Power Electron. 2019, 34, 4593–4602. [Google Scholar] [CrossRef] [Green Version]
- Stojić, D.; Milinković, M.; Veinović, S.; Klasnić, I. Improved Stator Flux Estimator for Speed Sensorless Induction Motor Drives. IEEE Trans. Power Electron. 2015, 30, 2363–2371. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Gharehpetian, G.B. Five Approaches to Deal with Problem of DC Offset in Phase-Locked Loop Algorithms: Design Considerations and Performance Evaluations. IEEE Trans. Power Electron. 2016, 31, 648–661. [Google Scholar] [CrossRef] [Green Version]
- Sevilmis, F.; Karaca, H. Performance Analysis of Dual Second Order Generalized Integrator Phase Locked Loop for Grid Interactive Inverter. In Proceedings of the 6th International Conference on Advanced Technology & Sciences (ICAT’Riga), Riga, Latvia, 12–15 September 2017. [Google Scholar]
- Li, Q.; Jiang, D.; Zhang, Y. Analysis and Calculation of Current Ripple Considering Inductance Saturation and Its Application to Variable Switching Frequency PWM. IEEE Trans. Power Electron. 2019, 34, 12262–12273. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, D.; He, X. Integration of Improved Flux Linkage Observer and I-f Starting Method for Wide-Speed-Range Sensorless SPMSM Drives. IEEE Trans. Power Electron. 2020, 35, 8374–8383. [Google Scholar] [CrossRef]
- Aliaskari, A.; Davari, S.A. A new closed-loop voltage model flux observer for sensorless DTC method. In Proceedings of the 8th Power Electronics, Drive Systems & Technologies Conference (PEDSTC), Mashhad, Iran, 14–16 February 2017. [Google Scholar]
- Pelly, B.R. Thyristor Phase-Controlled Converters and Cycloconverters; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- Lei, M.; Li, C.; Duan, W.; Zhang, Y.; Li, F. Research on the control methods of large-power cyclo-converter under the discontinuous conduction mode. In Proceedings of the IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009. [Google Scholar]
- Sangsefidi, Y.; Ziaeinejad, S.; Mehrizi-Sani, A. Sensorless Speed Control of Synchronous Motors: Analysis and Mitigation of Stator Resistance Error. IEEE Trans. Energy Convers. 2016, 31, 540–548. [Google Scholar] [CrossRef]













| Torque | ||||
|---|---|---|---|---|
| Small | Medium | High | ||
| Speed | Small | 0 | 0 | 0.5 |
| Medium | 0.5 | 0.5 | 0.5 | |
| High | 1 | 1 | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cikač, D.; Turk, N.; Bulić, N.; Barbanti, S. Flux Estimator for Salient Pole Synchronous Machines Driven by the Cycloconverter Based on Enhanced Current and Voltage Model of the Machine with Fuzzy Logic Transition. Machines 2021, 9, 279. https://doi.org/10.3390/machines9110279
Cikač D, Turk N, Bulić N, Barbanti S. Flux Estimator for Salient Pole Synchronous Machines Driven by the Cycloconverter Based on Enhanced Current and Voltage Model of the Machine with Fuzzy Logic Transition. Machines. 2021; 9(11):279. https://doi.org/10.3390/machines9110279
Chicago/Turabian StyleCikač, Dominik, Nikola Turk, Neven Bulić, and Stefano Barbanti. 2021. "Flux Estimator for Salient Pole Synchronous Machines Driven by the Cycloconverter Based on Enhanced Current and Voltage Model of the Machine with Fuzzy Logic Transition" Machines 9, no. 11: 279. https://doi.org/10.3390/machines9110279
APA StyleCikač, D., Turk, N., Bulić, N., & Barbanti, S. (2021). Flux Estimator for Salient Pole Synchronous Machines Driven by the Cycloconverter Based on Enhanced Current and Voltage Model of the Machine with Fuzzy Logic Transition. Machines, 9(11), 279. https://doi.org/10.3390/machines9110279






