An Improved Invariant Kalman Filter for Lie Groups Attitude Dynamics with Heavy-Tailed Process Noise
Abstract
:1. Introduction
2. Primaries and Problem Definition
2.1. The Attitude Estimation System on the Special Orthogonal Group SO(3)
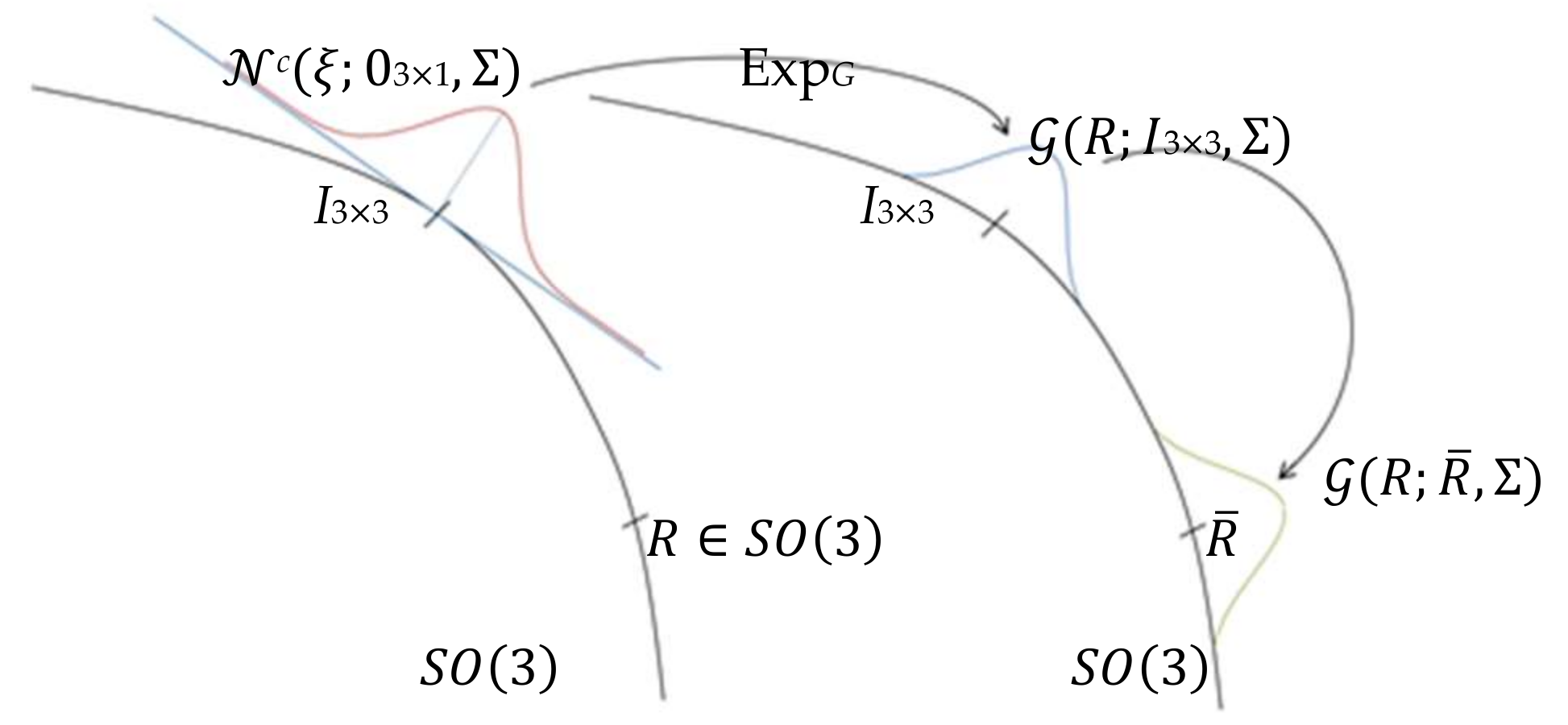
2.2. Model Projection Based on the Invariance Property of Attitude Estimation System
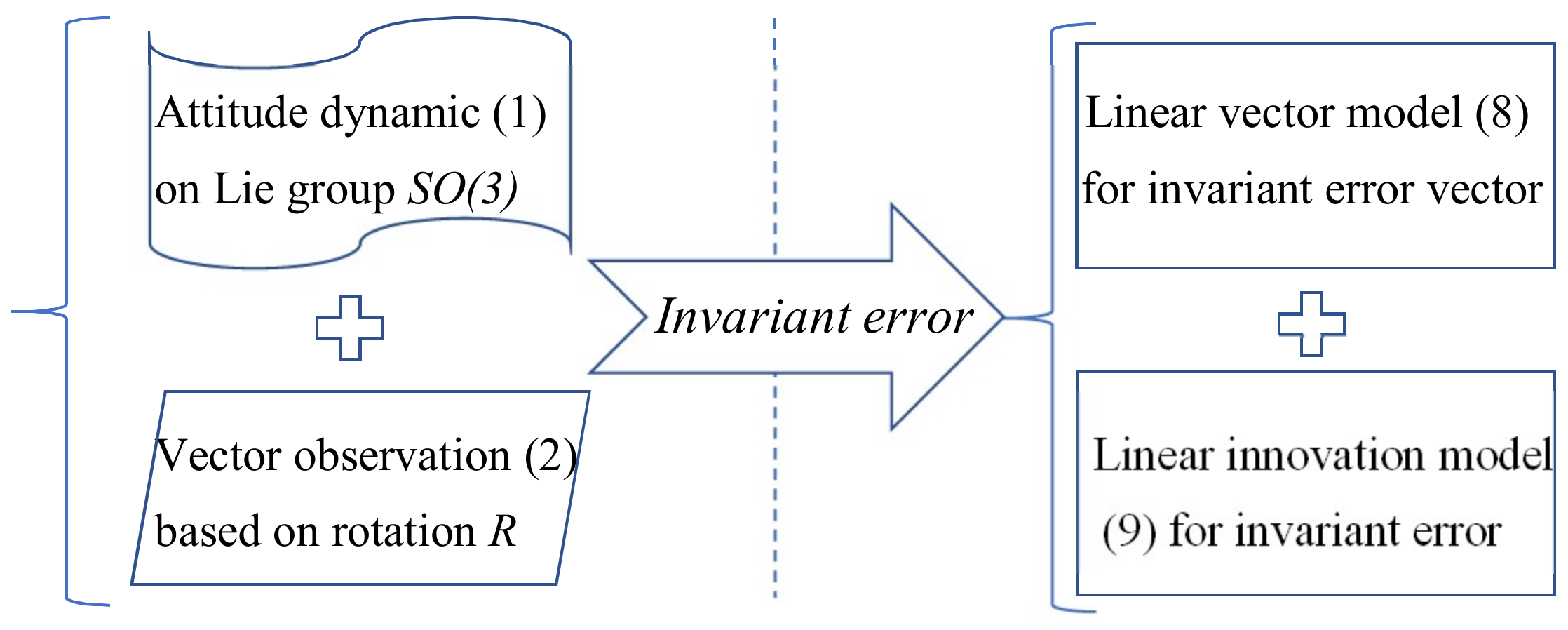
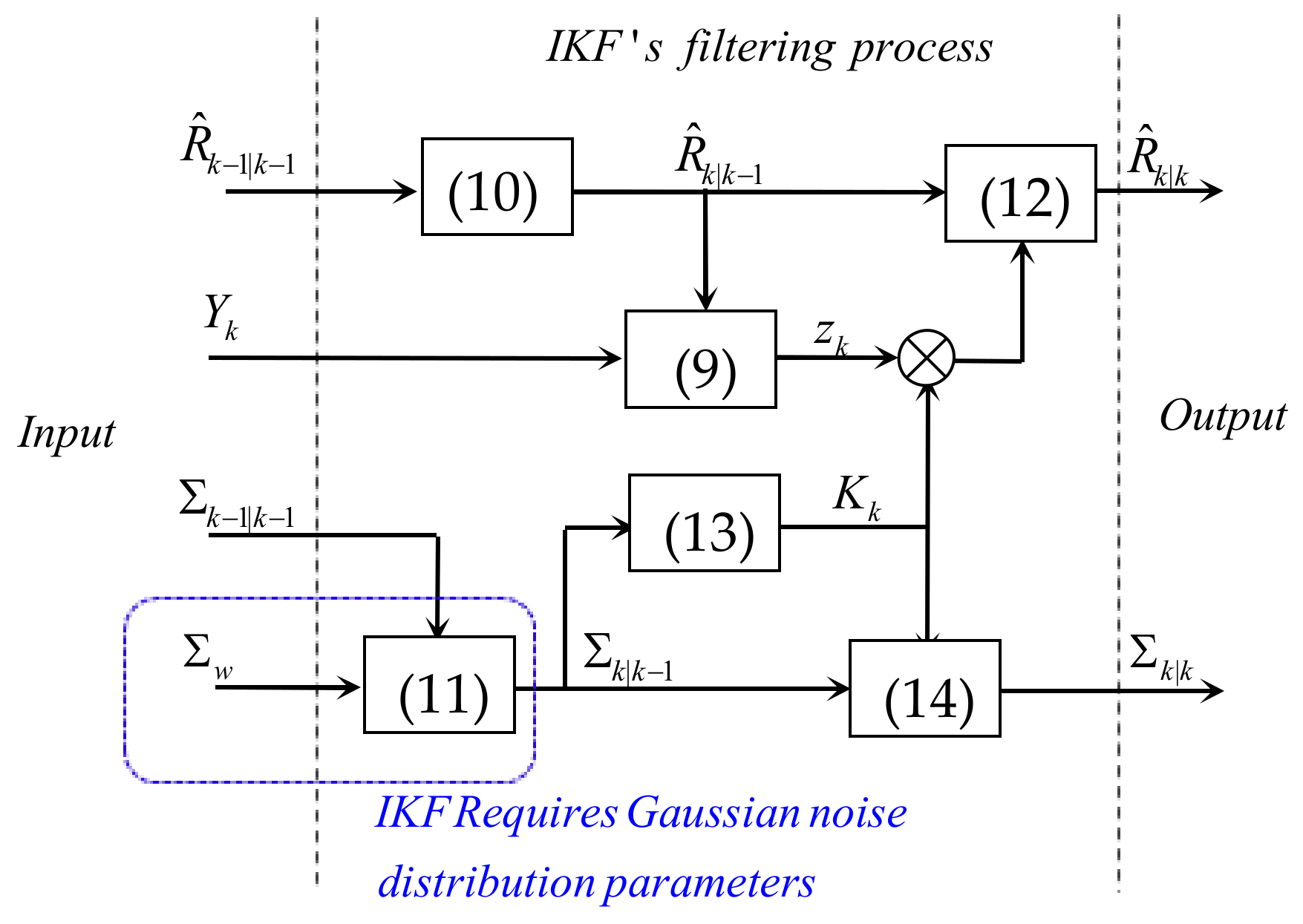
2.3. The Invariant Kalman Filter for Attitude Estimation
2.4. The Attitude Estimation Problem with the Trouble of Heavy-Tailed Process Noise
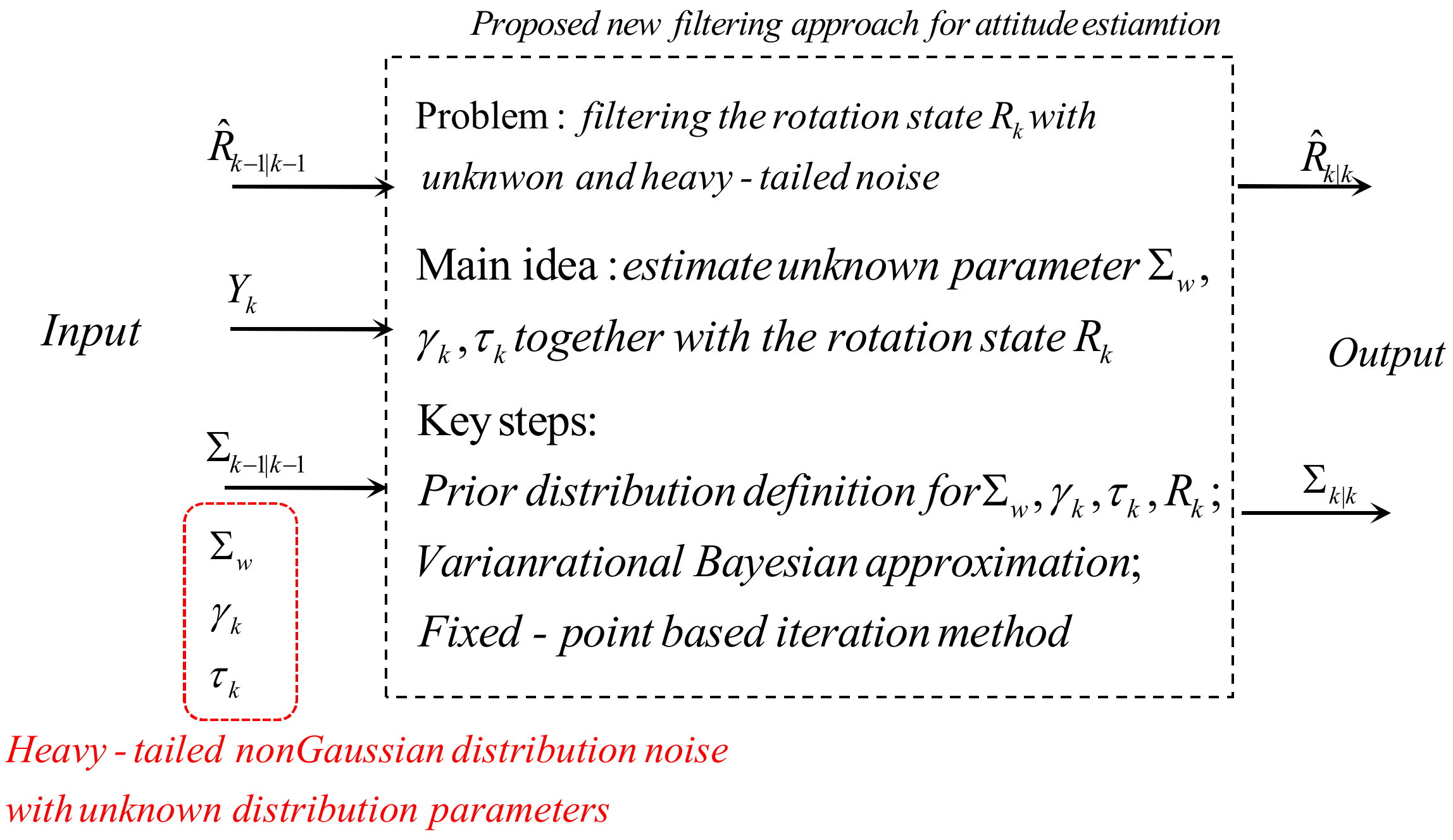
3. Robust Student’s t Based Invariant Kalman Filter for Attitude Estimation on SO(3)
3.1. Probability View of Attitude Estimation with Heavy-Tailed Process Noise
- (1)
- With the student’s t distribution process noise, the probability density function in classical invariant Kalman filter depends on the auxiliary random variable and becomes the hierarchical form in (20) and (21).
- (2)
- For the unpredictable disturbances or outliers induced by severely maneuvering operations, the accurate scale matrix and degree of freedom are usually unavailable but essential to propagate the posterior estimates.
3.2. Prior Probability Definition for the Parameters of Student’s t Distribution
3.3. Variational Beayesian Approximations of Posterior Probability Density Function
3.4. Fixed-Point Iteration of the System State and Distribution Parameters
3.4.1. Fixed-Point Iteration of the Invariant Error
3.4.2. Fixed-Point Iteration of the Auxiliary Random Variable
3.4.3. Fixed-Point Iteration of the Prior Estimate for Covariance Matrix
3.4.4. Fixed-Point Iteration of the Prior Estimate for Parameter
3.5. The Variational Beayesian Iteration Based Robust Student’s t Invariant Kalman Filter
| Algorithm 1. The filtering steps of one time instant in the proposed approach for attitude estimation. |
| Inputs:,,,,,,,, 1. Predict the nominal invariant error and rotation according to (8) and (10) , 2. Predict the nominal prior error covariance according to (11) 3. Calculate the converted innovation according to (9) 4. Initialize the prior parameters ,, 5. Calculate initial expectations according to (24) and (25) , for i = 0:N − 1 6. Update according to (36)~(40) ,, , 7. Update according to (44)~(46) , 8. Update according to (48)~(51) ,, 9. Update expectations , and according to (57)~(59) ,, 10. Update according to (55) and (56) , 11. Calculate the expectation according to (60) end for 12. Update the posterior rotation group and its covariance according to (63) , |
| Outputs: , |
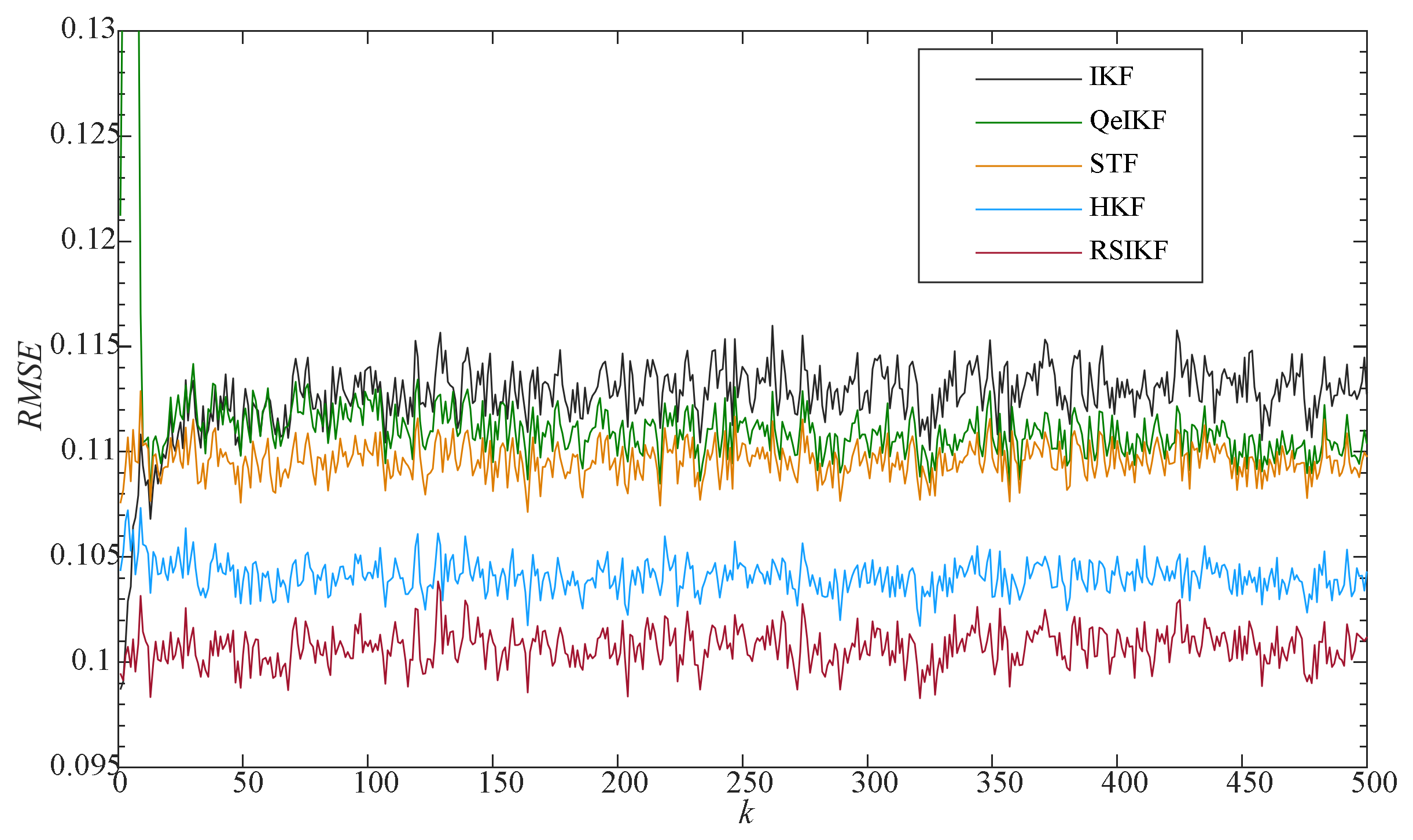
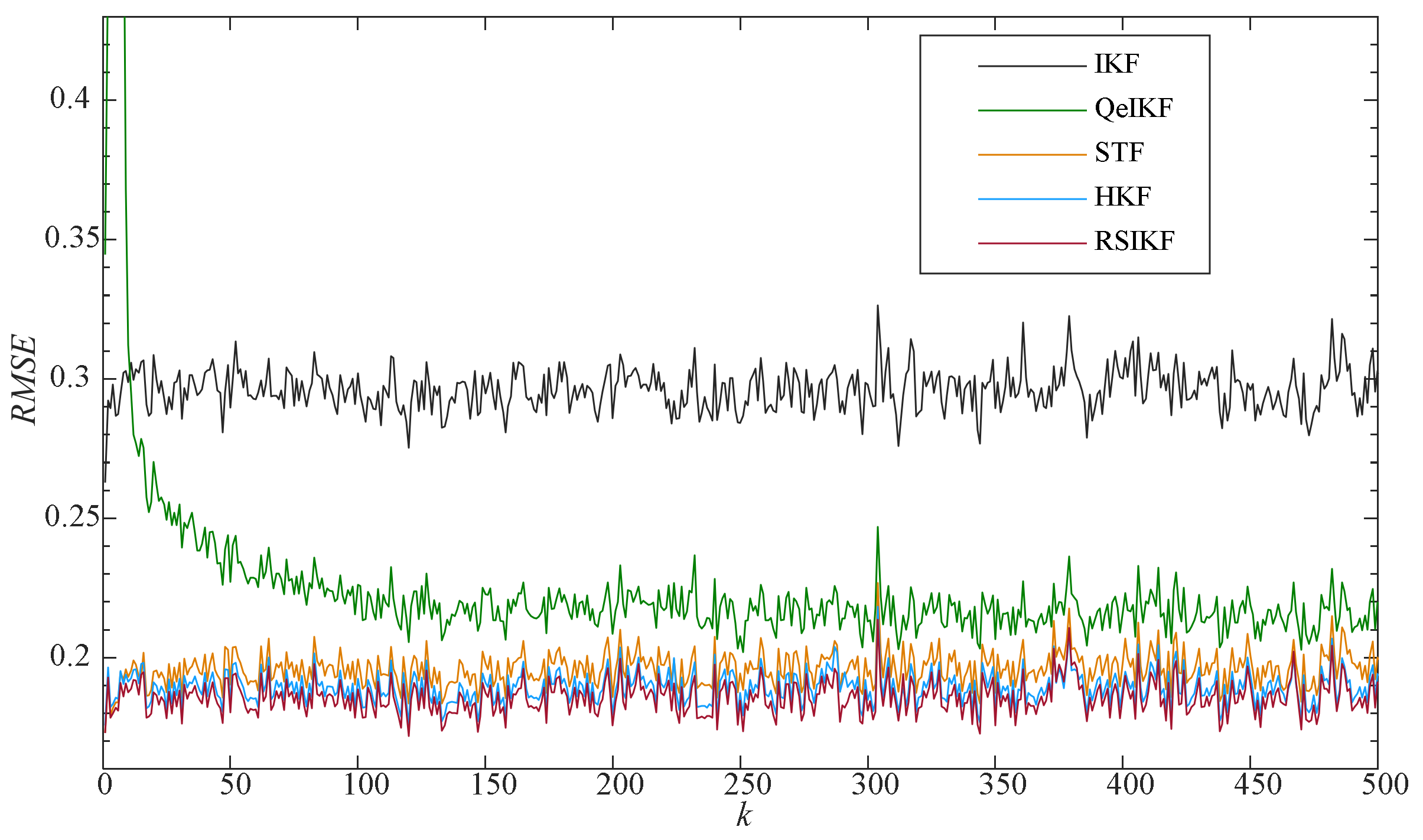
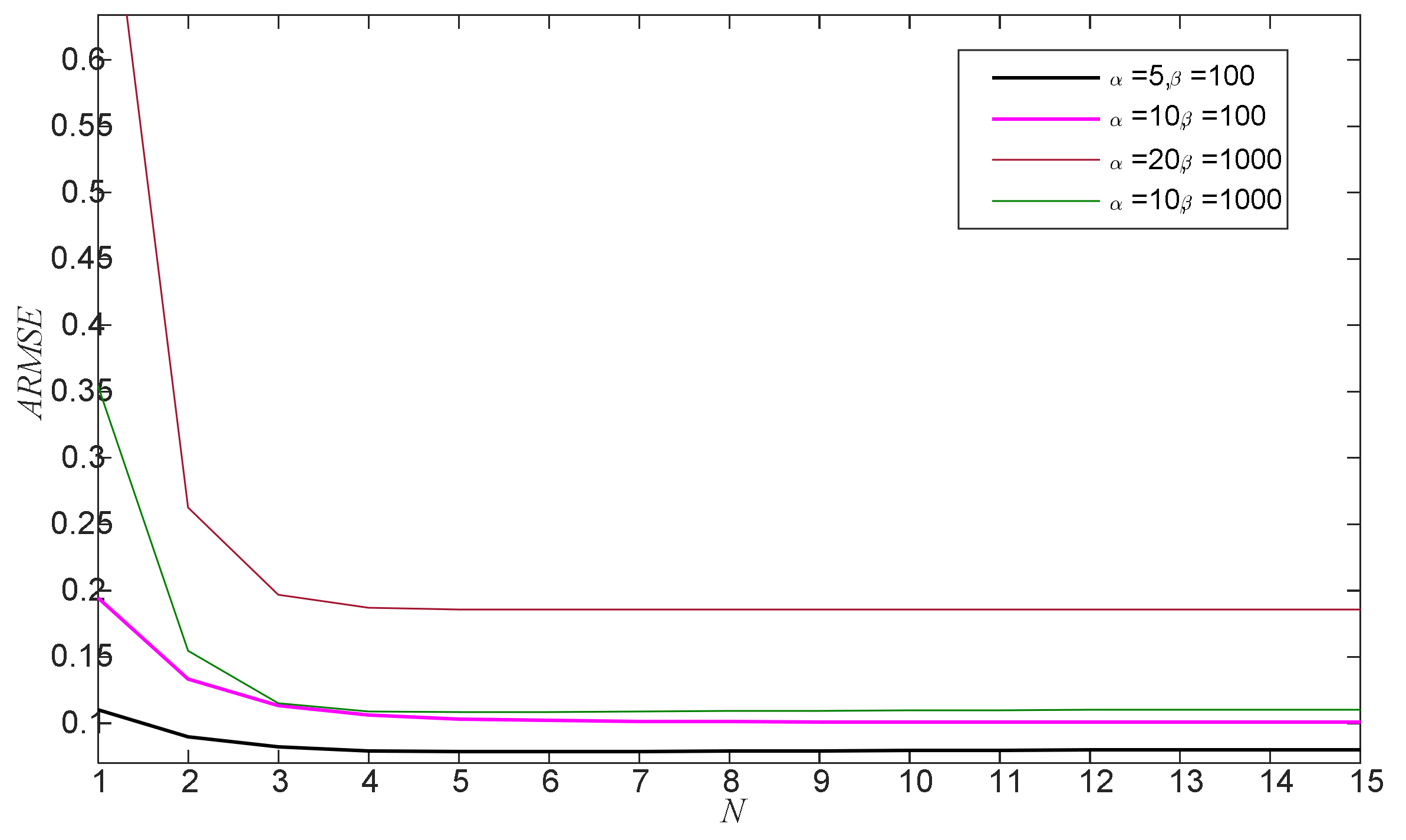
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Shan, S. Dot Product Equality Constrained Attitude Determination from Two Vector Observations: Theory and Astronautical Applications. Aerospace 2019, 6, 102. [Google Scholar] [CrossRef] [Green Version]
- Phisannupawong, T.; Kamsing, P.; Torteeka, P.; Channumsin, S.; Sawangwit, U.; Hematulin, W.; Jarawan, T.; Somjit, T.; Yooyen, S.; Delahaye, D.; et al. Vision-Based Spacecraft Pose Estimation via a Deep Convolutional Neural Network for Noncooperative Docking Operations. Aerospace 2020, 7, 126. [Google Scholar] [CrossRef]
- Soken, H.E.; Sakai, S.-I.; Asamura, K.; Nakamura, Y.; Takashima, T.; Shinohara, I. Filtering-Based Three-Axis Attitude Determination Package for Spinning Spacecraft: Preliminary Results with Arase. Aerospace 2020, 7, 97. [Google Scholar] [CrossRef]
- Carletta, S.; Teofilatto, P.; Farissi, M.S. A Magnetometer-Only Attitude Determination Strategy for Small Satellites: Design of the Algorithm and Hardware-in-the-Loop Testing. Aerospace 2020, 7, 3. [Google Scholar] [CrossRef] [Green Version]
- Louédec, M.; Jaulin, L. Interval Extended Kalman Filter-Application to Underwater Localization and Control. Algorithms 2021, 14, 142. [Google Scholar] [CrossRef]
- Pan, C.; Qian, N.; Li, Z.; Gao, J.; Liu, Z.; Shao, K. A Robust Adaptive Cubature Kalman Filter Based on SVD for Dual-Antenna GNSS/MIMU Tightly Coupled Integration. Remote Sens. 2021, 13, 1943. [Google Scholar] [CrossRef]
- Zheng, L.; Zhan, X.; Zhang, X. Nonlinear Complementary Filter for Attitude Estimation by Fusing Inertial Sensors and a Camera. Sensors 2020, 20, 6752. [Google Scholar] [CrossRef]
- Deibe, Á.; Antón Nacimiento, J.A.; Cardenal, J.; López Peña, F. A Kalman Filter for Nonlinear Attitude Estimation Using Time Variable Matrices and Quaternions. Sensors 2020, 20, 6731. [Google Scholar] [CrossRef]
- Guo, H.; Liu, H.; Hu, X.; Zhou, Y. A Global Interconnected Observer for Attitude and Gyro Bias Estimation with Vector Measurements. Sensors 2020, 20, 6514. [Google Scholar] [CrossRef] [PubMed]
- Ayala, V.; Román-Flores, H.; Torreblanca Todco, M.; Zapana, E. Observability and Symmetries of Linear Control Systems. Symmetry 2020, 12, 953. [Google Scholar] [CrossRef]
- Bonnabel, S.; Martin, P.; Salaun, E. Invariant Extended Kalman Filter: Theory and application to a velocity-aided attitude estimation problem. In Proceedings of the IEEE Conference on Decision & Control, Shanghai, China, 15–18 December 2009. [Google Scholar] [CrossRef] [Green Version]
- Vasconcelos, J.; Cunha, R.; Silvestre, C.; Oliveira, P. A nonlinear position and attitude observer on SE(3) using landmark measurements. Syst. Control Lett. 2010, 59, 155–166. [Google Scholar] [CrossRef]
- Chaturvedi, N.; Sanyal, A.; Mcclamroch, A. Rigid-body attitude control using rotation matrices for continuous singularity-free control laws. IEEE Control Syst. Mag. 2011, 31, 30–51. [Google Scholar]
- Barrau, A.; Bonnabel, S. Intrinsic filtering on Lie groups with applications to attitude estimation. IEEE Trans. Autom. Contr. 2014, 60, 436–449. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. The invariant extended Kalman filter as a stable observer. IEEE Trans. Autom. Contr. 2017, 62, 1797–1812. [Google Scholar] [CrossRef] [Green Version]
- Barrau, A.; Bonnabel, S. Invariant Kalman filtering. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 237–257. [Google Scholar] [CrossRef]
- Batista, P.; Silvestre, C.; Oliveira, P. A GES attitude observer with single vector observations. Automatica 2012, 49, 388–395. [Google Scholar] [CrossRef]
- Chirikjian, G.; Kobilarov, M. Gaussian approximation of non-linear measurement models on lie groups. In Proceedings of the IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014. [Google Scholar]
- Barfoot, T.; Furgale, P. Associating uncertainty with three- dimensional poses for use in estimation problems. IEEE Trans. Robot. 2014, 30, 679–693. [Google Scholar] [CrossRef]
- Said, S.; Manton, J. Extrinsic mean of Brownian distributions on compact lie groups. IEEE Trans. Inf. Theory 2012, 58, 3521–3535. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Zhang, Y. A New Process Uncertainty Robust Student’s t Based Kalman Filter for SINS/GPS Integration. IEEE Access 2017, 5, 14391–14404. [Google Scholar] [CrossRef]
- Karasalo, M.; Hu, X. An optimization approach to adaptive Kalman filtering. Automatica 2011, 47, 1785–1793. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, J.; Zhang, D.; Shao, X.; Chen, G. Kalman filtering through the feedback adaption of prior error covariance. Signal. Process. 2018, 152, 47–53. [Google Scholar] [CrossRef]
- Feng, B.; Fu, M.; Ma, H.; Xia, Y.; Wang, B. Kalman filter with recursive covariance Estimation--sequentially estimating process noise covariance. IEEE Trans. Ind. Electron. 2014, 61, 6253–6263. [Google Scholar] [CrossRef]
- Zanni, L.; Le Boudec, J.; Cherkaoui, R.; Paolone, M. A prediction-error covariance estimator for adaptive Kalman filtering in step-varying processes: Application to power-system state estimation. IEEE Trans. Contr. Syst. Technol. 2017, 25, 1683–1697. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.; Schwarz, K. Adaptive Kalman Filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Ardeshiri, T.; Özkan, E.; Orguner, U.; Gustafsson, F. Approximate Bayesian smoothing with unknown process and measurement noise covariance. IEEE Signal Process. Lett. 2015, 22, 2450–2454. [Google Scholar] [CrossRef] [Green Version]
- Assa, A.; Plataniotinos, K. Adptive Kalman filtering by covariance sampling. IEEE Signal Process. Lett. 2017, 24, 1288–1292. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices. IEEE Trans. Autom. Contr. 2018, 63, 594–601. [Google Scholar] [CrossRef] [Green Version]
- Tronarp, F.; Karvonen, T.; Särkkä, S. Student′s t-Filters for Noise Scale Estimation. IEEE Signal Process. Lett. 2019, 26, 352–356. [Google Scholar] [CrossRef]
- Dong, P.; Jing, Z.; Leung, H.; Shen, K.; Wang, J. Student-t mixture labeled multi-Bernoulli filter for multi-target tracking with heavy-tailed noise. Signal Process. 2018, 152, 331–339. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Li, N.; Wu, Z.; Chambers, J. A novel robust student’s t-based Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1545–1554. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Zhang, Y.; Li, N.; Chambers, J. Robust student’s t based nonlinear filter and smoother. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2586–2596. [Google Scholar] [CrossRef] [Green Version]
- Ćesić, J.; Markovi, I.; Petrovi, I. Mixture Reduction on Matrix Lie Groups. IEEE Signal Process. Lett. 2017, 24, 1719–1723. [Google Scholar] [CrossRef] [Green Version]
- Ćesić, J.; Markovi, I.; Bukal, M.; Petrović, I. Extended Information Filter on Matrix Lie Groups. Automatica 2017, 82, 226–234. [Google Scholar] [CrossRef]
- Kang, D.; Jang, C.; Park, F. Unscented Kalman Filtering for Simultaneous Estimation of Attitude and Gyroscope Bias. IEEE/ASME Trans. Mechatron. 2019, 24, 350–360. [Google Scholar] [CrossRef]
- Bourmaud, G.; Mégret, R.; Arnaudon, M.; Giremus, A. Continuous-Discrete Extended Kalman Filter on Matrix Lie Groups Using Concentrated Gaussian Distributions. J. Math. Imaging Vis. 2015, 51, 209–228. [Google Scholar] [CrossRef] [Green Version]
- Tzikas, D.; Likas, A.; Galatsanos, N. The Variational Approximation for Bayesian Inference. IEEE Signal Process. Mag. 2008, 25, 131–146. [Google Scholar] [CrossRef]
- Pavliotis, G.A. Applied Stochastic Processe; Springer: London, UK, 2009. [Google Scholar]
- Hagan, T.; Forster, J.J. Kendall’s Advanced Theory of Statistics; Arnold: London, UK, 2004. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2007. [Google Scholar]
- Huang, Y.; Zhang, Y.; Li, N.; Chambers, J. A Robust Gaussian Approximate Fixed-Interval Smoother for Nonlinear Systems With Heavy-Tailed Process and Measurement Noises. IEEE Signal Process. Lett. 2016, 23, 468–472. [Google Scholar] [CrossRef] [Green Version]
- Roth, M.; Ozkan, E.; Gustafsson, F. A Student’s t filter for heavy tailed process and measurement noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 5770–5774. [Google Scholar]
- Karlgaard, C.D.; Schaub, H. Huber-Based Divided Difference Filtering. J. Guid. Control Dyn. 2012, 30, 885–891. [Google Scholar] [CrossRef]


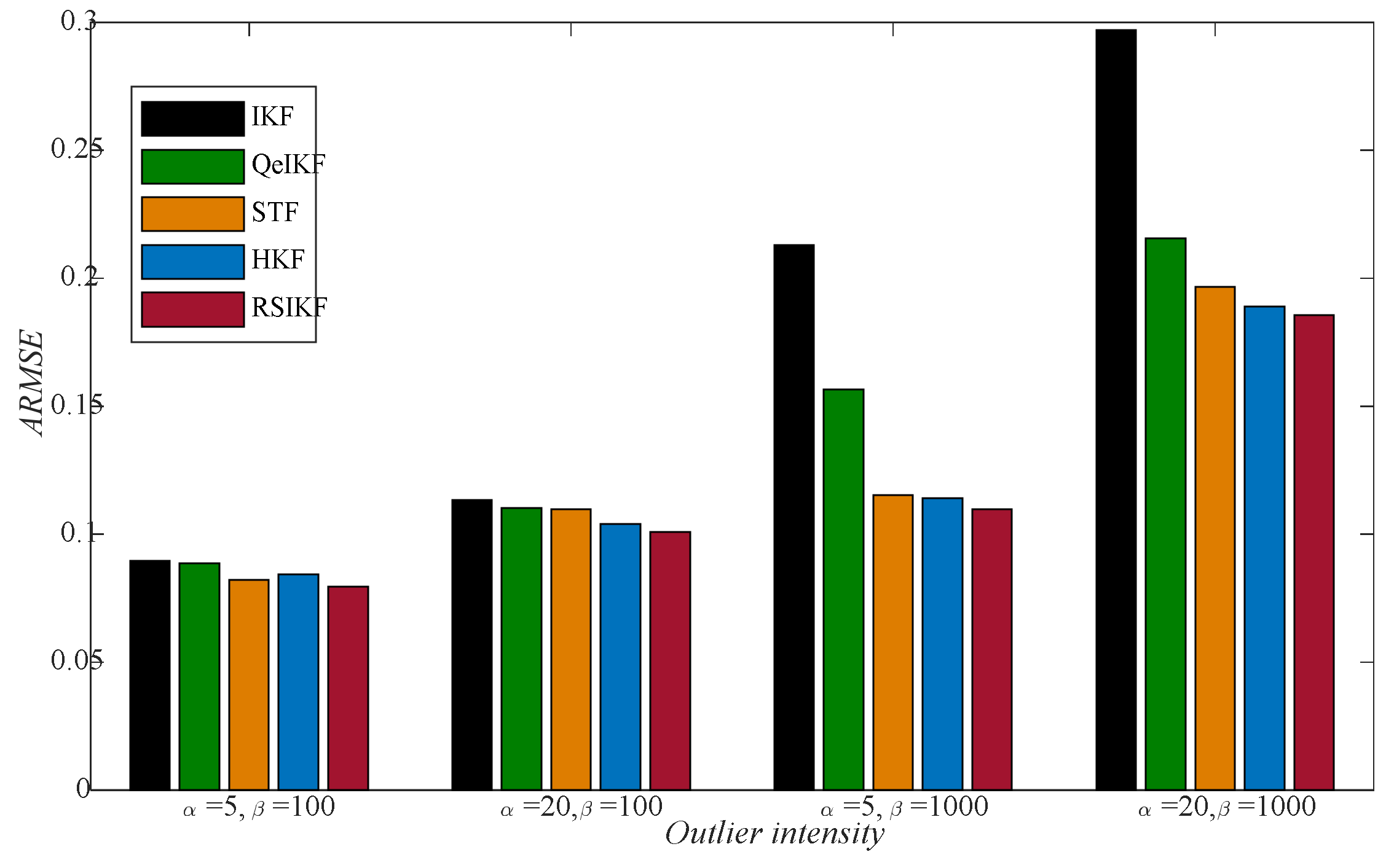


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, C.; Wu, J.; Liu, M. An Improved Invariant Kalman Filter for Lie Groups Attitude Dynamics with Heavy-Tailed Process Noise. Machines 2021, 9, 182. https://doi.org/10.3390/machines9090182
Wang J, Zhang C, Wu J, Liu M. An Improved Invariant Kalman Filter for Lie Groups Attitude Dynamics with Heavy-Tailed Process Noise. Machines. 2021; 9(9):182. https://doi.org/10.3390/machines9090182
Chicago/Turabian StyleWang, Jiaolong, Chengxi Zhang, Jin Wu, and Ming Liu. 2021. "An Improved Invariant Kalman Filter for Lie Groups Attitude Dynamics with Heavy-Tailed Process Noise" Machines 9, no. 9: 182. https://doi.org/10.3390/machines9090182





