Track Structure Components: Characterizing Energy Deposited in Spherical Cells from Direct and Peripheral HZE Ion Hits
Abstract
1. Introduction
2. Methods
2.1. Simulation of Volume Irradiation by Stochastic Radiation Tracks
2.2. Effects of the Irradiated Volume Size on Dose Calculations
2.2.1. Restricted LET
2.2.2. PBCs
2.3. Single-Ion Energy Deposition Spectra
2.4. Calculation of the Indirect Dose Contribution Using the Local Effect Model
3. Results and Discussion
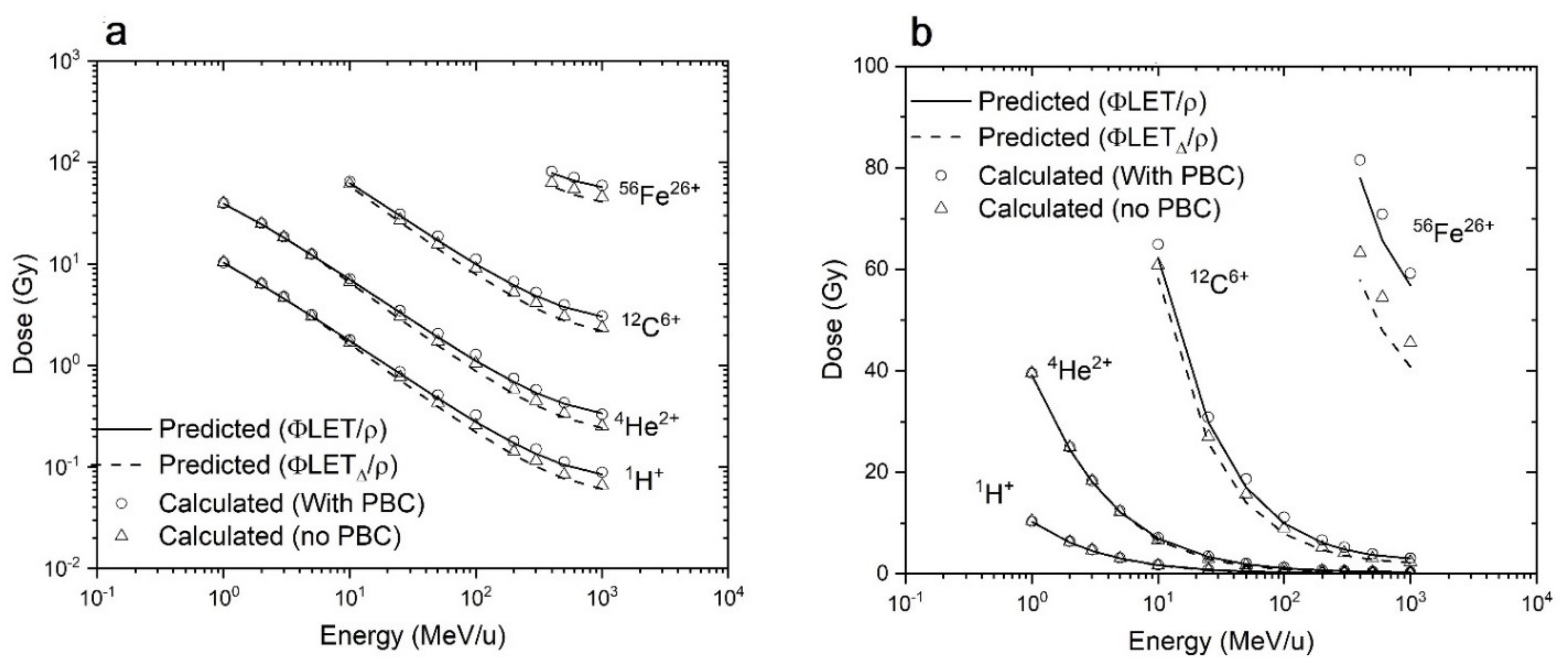
3.1. RITRACKS Microdosimetry Benchmark
3.1.1. Comparison of Average Dose in Targets with Theoretical Predictions
3.1.2. Comparison with Published Results
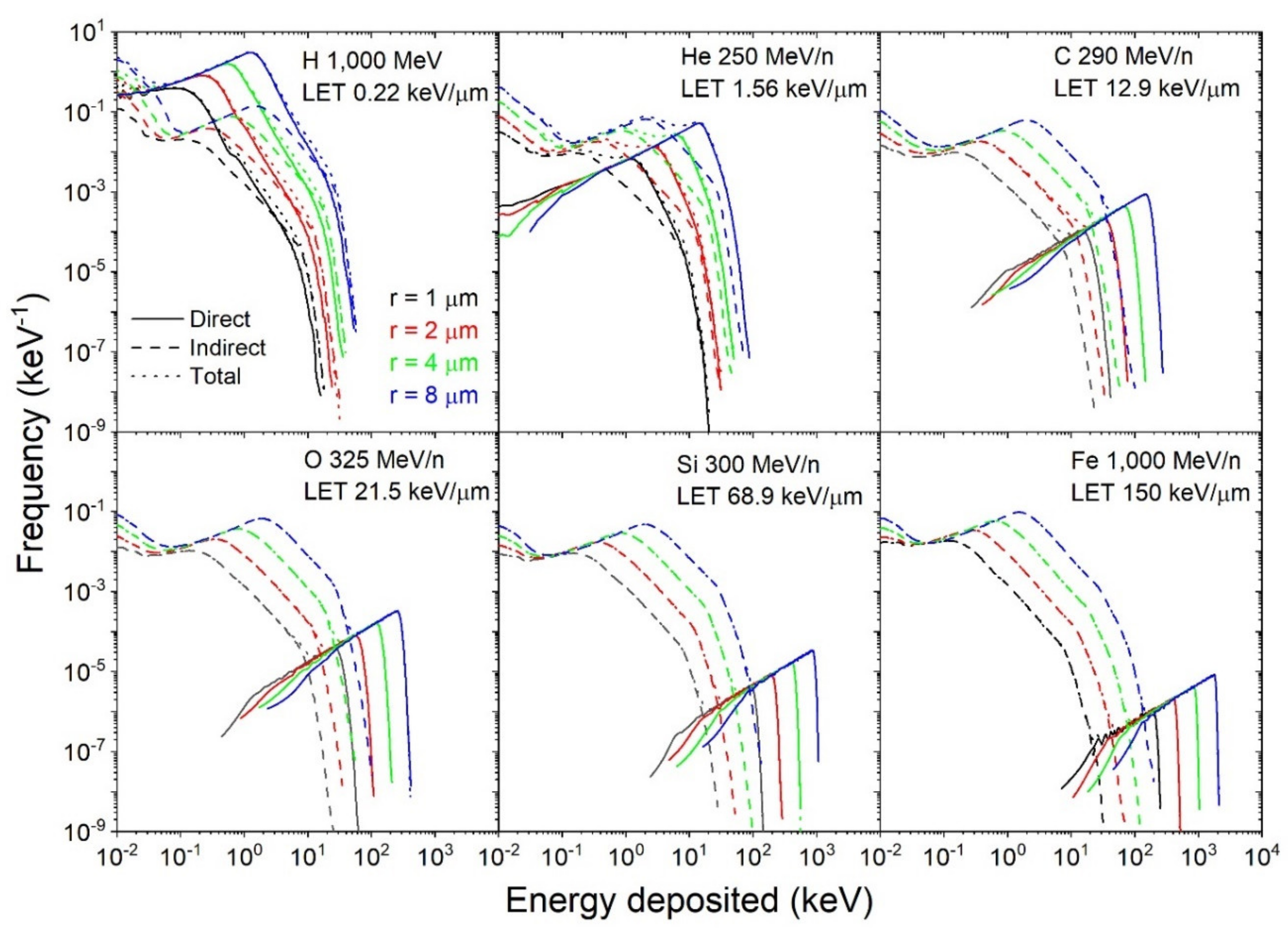
3.2. Single-Ion Energy Distribution Spectra
3.2.1. Direct and Indirect Contributions
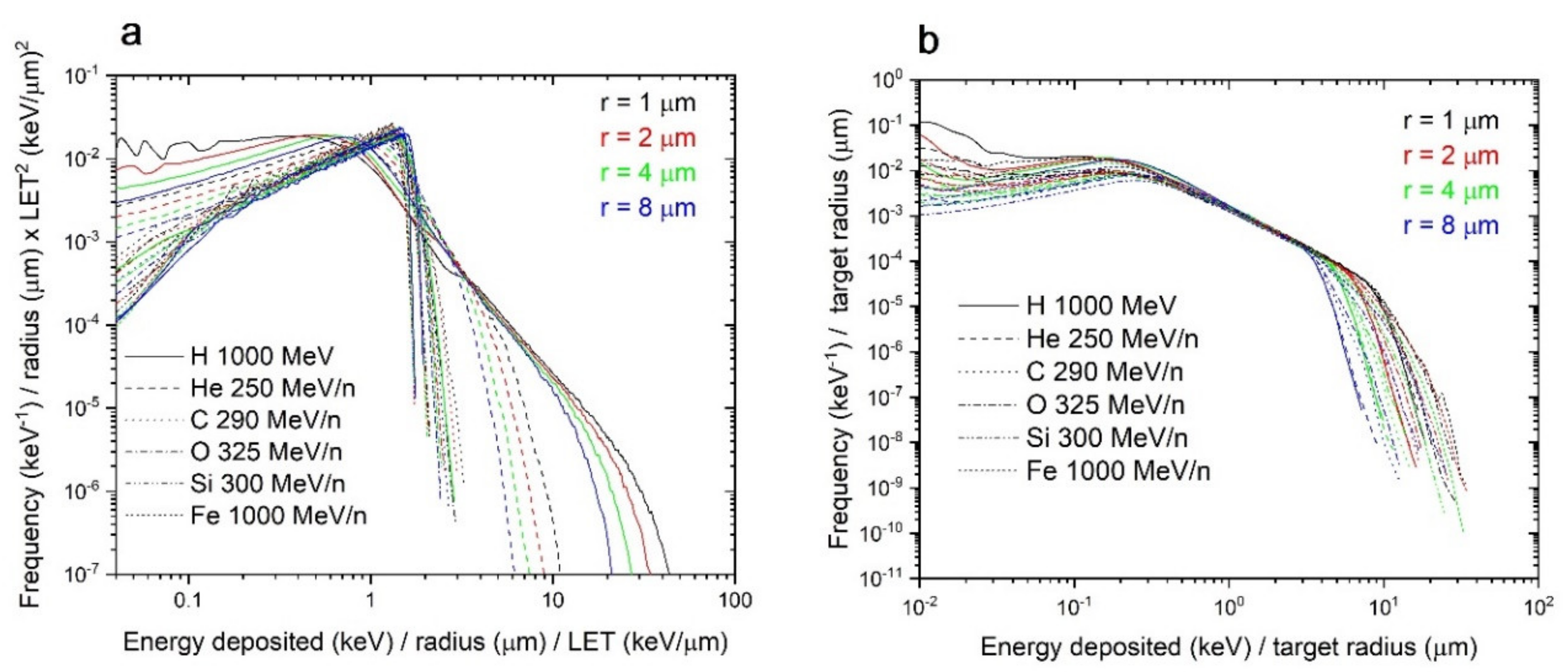
3.2.2. Variation with Dose, Radius, and LET
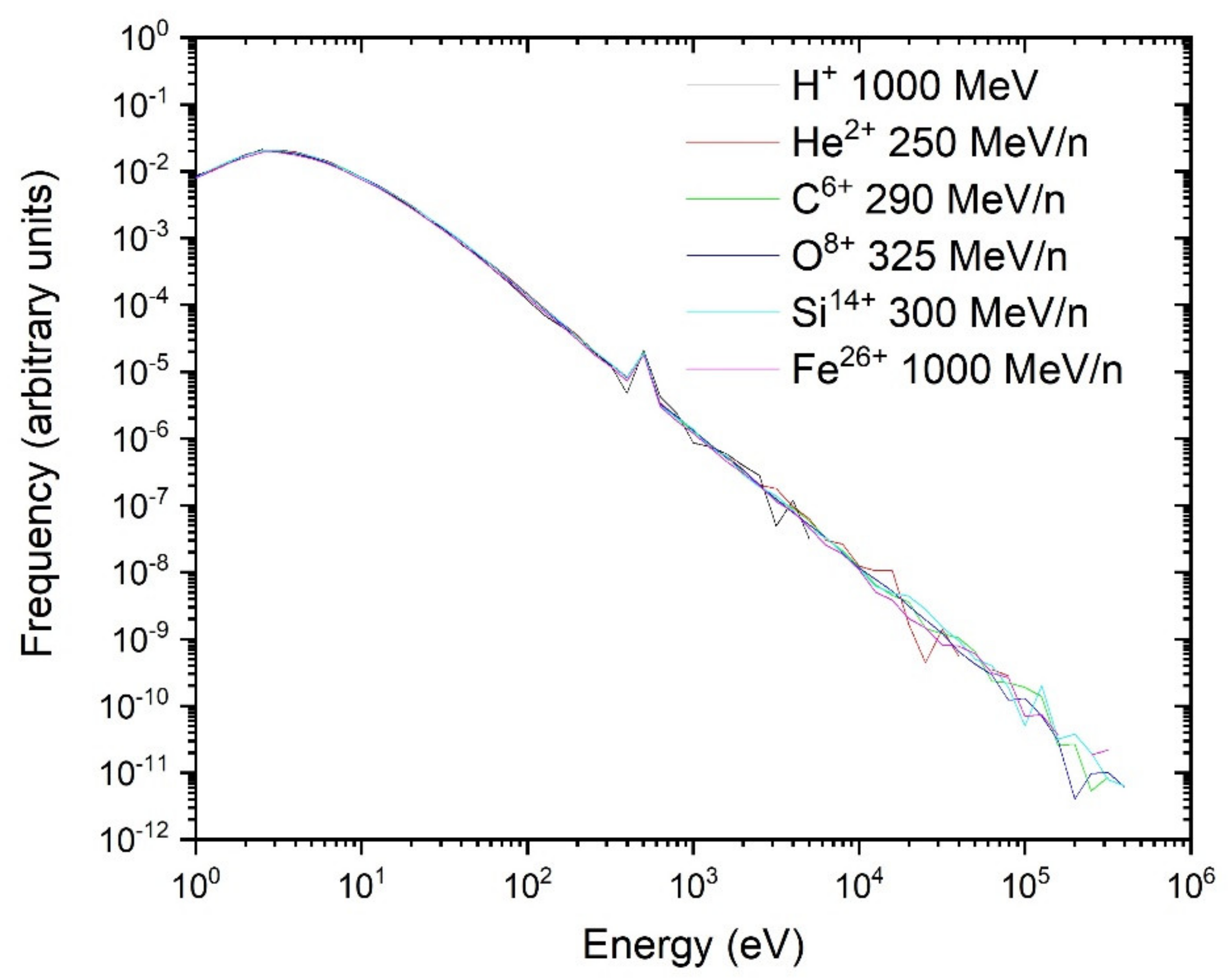
3.2.3. Scaling of the Single-Ion Spectra
4. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- LaVerne, J.A. Track effects of heavy ions in liquid water. Radiat. Res. 2000, 153, 487–496. [Google Scholar] [CrossRef]
- Rossi, H.; Zaider, M. Microdosimetry and Its Applications; Springer: Berlin/Heidelberg, Germany, 1996; pp. 205–278. [Google Scholar]
- Kellerer, A.M.; Chmelevsky, D. Concepts of Microdosimetry, I. Quantities. Radiat. Environ. Biophys. 1975, 12, 61–69. [Google Scholar] [CrossRef]
- Kellerer, A.M.; Chmelevsky, D. Concepts of Microdosimetry II. Probability distributions of the microdosimetric variables. Radiat. Environ. Biophys. 1975, 12, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Kellerer, A.M.; Chmelevsky, D. Concepts of Microdosimetry III. Mean values of microdosimetric distributions. Radiat. Environ. Biophys. 1975, 12, 321–335. [Google Scholar] [CrossRef] [PubMed]
- Zaider, M.; Brenner, D.J. On the microdosimetric definition of Quality Factors. Radiat. Res. 1985, 103, 302–316. [Google Scholar] [CrossRef]
- ICRU. Microdosimetry; ICRU Report 36; International Commission on Radiological Units and Measurements: Bethesda, MD, USA, 1983. [Google Scholar]
- Inaniwa, T.; Furukawa, T.; Kase, Y.; Matsufuji, N.; Toshito, T.; Matsumoto, Y.; Furusawa, Y.; Noda, K. Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model. Phys. Med. Biol. 2010, 55, 6721–6737. [Google Scholar] [CrossRef] [PubMed]
- Bellinzona, V.E.; Cordoni, F.; Missiaggia, M.; Tommasino, F.; Scifoni, E.; La Tessa, C.; Attili, A. Linking Microdosimetric Measurements to Biological Effectiveness in Ion Beam Therapy: A review of theoretical aspects of MKM and other models. Front. Phys. 2021, 8, 578492. [Google Scholar] [CrossRef]
- Brogan, J. Benchmarking Computations Using the Monte Carlo Code RITRACKS with Data from a Tissue Equivalent Proportional Counter. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2015. [Google Scholar]
- Kellerer, A.M. An assessment of wall effects in microdosimetric measurements. Radiat. Res. 1971, 47, 377–386. [Google Scholar] [CrossRef]
- Glass, W.A.; Braby, L.A. A wall-less detector for measuring energy deposition spectra. Radiat. Res. 1969, 39, 230–240. [Google Scholar] [CrossRef]
- Friedrich, T.; Ilicic, K.; Greubel, C.; Girst, S.; Reindl, J.; Sammer, M.; Schwarz, B.; Siebenwirth, C.; Walsh, D.W.; Schmid, T.E.; et al. DNA damage interactions on both nanometer and micrometer scale determine overall cellular damage. Sci. Rep. 2018, 8, 16063. [Google Scholar] [CrossRef]
- Goodhead, D.T.; Nikjoo, H. Track structure analysis of ultrasoft X-rays compared to high- and low-LET radiations. Int. J. Radiat. Biol. 1989, 55, 513–529. [Google Scholar] [CrossRef]
- Ponomarev, A.L.; George, K.; Cucinotta, F.A. Computational model of chromosome aberration yield induced by high- and low-LET radiation exposures. Radiat. Res. 2012, 177, 727–737. [Google Scholar] [CrossRef]
- Cunha, M.; Monini, C.; Testa, E.; Beuve, M. NanOx, a new model to predict cell survival in the context of particle therapy. Phys. Med. Biol. 2017, 62, 1248–1268. [Google Scholar] [CrossRef]
- Stewart, R.D.; Stewart, R.D.; Carlson, D.J.; Butkus, M.P.; Hawkins, R.; Friedrich, T.; Scholz, M. A comparison of mechanism-inspired models for particle relative biological effectiveness (RBE). Med. Phys. 2018, 45, e925–e952. [Google Scholar] [CrossRef]
- Plante, I.; Cucinotta, F.A. Monte-Carlo Simulation of Ionizing Radiation Tracks in Applications of Monte Carlo Methods in Biology, Medicine and Other Fields of Science; Mode, C.B., Ed.; InTech: Rijeka, Croatia, 2011; pp. 315–356. [Google Scholar] [CrossRef]
- Plante, I.; Ponomarev, A.L.; Cucinotta, F.A. 3D visualisation of the stochastic patterns of the radial dose in nano-volumes by a Monte Carlo simulation of HZE ion track structure. Radiat. Prot. Dosim. 2011, 143, 156–161. [Google Scholar] [CrossRef]
- Plante, I.; Cucinotta, F.A. Energy deposition and relative frequency of hits of cylindrical nanovolume in medium irradiated by ions: Monte-Carlo simulations of track structure. Radiat. Environ. Biophys. 2010, 49, 5–13. [Google Scholar] [CrossRef]
- Plante, I.; Ponomarev, A.L.; Patel, Z.; Slaba, T.; Hada, M. RITCARD: Radiation-Induced Tracks, Chromosome Aberrations, Repair and Damage. Radiat. Res. 2019, 192, 282–298. [Google Scholar] [CrossRef] [PubMed]
- Turner, J. Atoms, Radiation and Radiation Protection, 3rd ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1988; pp. 278–320. [Google Scholar]
- Meesungnoen, J.; Jay-Gerin, J.-P.; Filali-Mouhim, A.; Mankhetkorn, S. Low-energy electron penetration range in Liquid Water. Radiat. Res. 2002, 158, 657–660. [Google Scholar] [CrossRef]
- Chen, J.; Kellerer, A.M.; Rossi, H. Radially restricted linear energy transfer for high-energy protons: A new analytical approach. Radiat. Environ. Biophys. 1994, 33, 181–187. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Van Kerm, P. Adaptive kernel density estimation. Stata J. 2003, 3, 148–156. [Google Scholar] [CrossRef]
- Kiefer, J.; Straaten, H. A model of ion track structure based on classical collision dynamics. Phys. Med. Biol. 1986, 31, 1201–1209. [Google Scholar] [CrossRef]
- Kobetich, E.J.; Katz, R. Energy deposition by electron beams and δ rays. Phys. Rev. 1968, 170, 391–396. [Google Scholar] [CrossRef]
- Wang, H.; Vassiliev, O.N. Radial dose distributions from carbon ions of therapeutic energies calculated with Geant4-DNA. Phys. Med. Biol. 2017, 62, N219–N227. [Google Scholar] [CrossRef] [PubMed]
- Elsässer, T.; Cunrath, R.; Krämer, M.; Scholz, M. Impact of track structure calculations on biological treatment planning in ion radiotherapy. New J. Phys. 2008, 10, 075005. [Google Scholar] [CrossRef]
- Xarpos, M. A spatially restricted linear energy transfer equation. Radiat. Res. 1992, 132, 232–287. [Google Scholar] [CrossRef]
- Heitler, V. The Quantum Theory of Radiation; Dover Publications: Mineola, NY, USA, 1953; pp. 362–400. [Google Scholar]
- Nikjoo, H.; Khvostunov, I.K.; Cucinotta, F.A. The response of tissue-equivalent proportional counters to heavy ions. Radiat. Res. 2002, 157, 435–445. [Google Scholar] [CrossRef]
- Shinn, J.L.; Badhwar, G.D.; Xapsos, M.A.; Cucinotta, F.A.; Wilson, J.T. An analysis of energy deposition in a tissue equivalent proportional counter onboard the space shuttle. Radiat. Meas. 1999, 30, 19–28. [Google Scholar] [CrossRef]
- Olko, P.; Booz, J. Energy deposition by protons and alpha particles in spherical sites of nanometer to micrometer diameter. Radiat. Environ. Biophys. 1990, 28, 1–17. [Google Scholar] [CrossRef]
- Perales, Á.; Baratto-Roldán, A.; Kimstrand, P.; Cortés-Giraldo, M.A.; Carabe, A. Parameterising microdosimetric distributions of mono-energetic proton beams for fast estimates of yD and y*. Biomed. Phys. Eng. Express 2019, 5, 045014. [Google Scholar] [CrossRef]
- Newpower, M.; Patel, D.; Bronk, L.; Guan, F.; Chaudhary, P.; McMahon, S.J.; Prise, K.M.; Schettino, G.; Grosshans, D.R.; Mohan, R. Using the proton energy spectrum and microdosimetry to model proton relative biological effectiveness. Int. J. Radiat. Oncol. Biol. Phys. 2019, 104, 316–324. [Google Scholar] [CrossRef]
- Nikitaki, Z.; Nikolov, V.; Mavragani, I.V.; Plante, I.; Emfietzoglou, D.; Iliakis, G.; Georgakilas, A.G. Non-DSB clustered DNA lesions. Does theory colocalize with the experiment? Radiat. Phys. Chem. 2016, 128, 26–35. [Google Scholar] [CrossRef]
- Watanabe, R.; Rahmanian, S.; Nikjoo, H. Spectrum of radiation-induced clustered non-DSB damage—A Monte Carlo track structure modeling and calculations. Radiat. Res. 2015, 183, 525–540. [Google Scholar] [CrossRef]
- McMahon, S.J.; Schuemann, J.; Paganetti, H.; Prise, K.M. Mechanistic modelling of DNA repair and cellular survival following radiation-induced DNA damage. Sci. Rep. 2016, 6, 33290. [Google Scholar] [CrossRef] [PubMed]
- Kalospyros, S.A.; Nikitaki, Z.; Kyriakou, I.; Kokkoris, M.; Emfietzoglou, D.; Georgakilas, A.G. A mathematical radiobiological model (MRM) to predict complex DNA Damage and Cell Survival for Ionizing Particle Radiations of Varying Quality. Molecules 2021, 26, 840. [Google Scholar] [CrossRef] [PubMed]
- Simonsen, L.C.; Slaba, T.C.; Guida, P.; Rusek, A. NASA’s first ground-based Galactic Cosmic Ray Simulator: Enabling a new era in space radiobiology research. PLoS Biol. 2020, 18, e3000669. [Google Scholar] [CrossRef]




| Box Size | Direct | Indirect | Sum | |||
|---|---|---|---|---|---|---|
| µm | eV | Gy | eV | Gy | eV | Gy |
| 2 | 20,175 | 0.7707 | 191 | 0.0073 | 20,366 | 0.7780 |
| 3 | 20,156 | 0.7700 | 691 | 0.0264 | 20,847 | 0.7963 |
| 4 | 20,448 | 0.7811 | 1001 | 0.0382 | 21,449 | 0.8194 |
| 5 | 20,393 | 0.7790 | 1159 | 0.0443 | 21,552 | 0.8233 |
| 10 | 20,566 | 0.7856 | 1612 | 0.0616 | 22,178 | 0.8472 |
| 20 | 20,794 | 0.7943 | 1872 | 0.0715 | 22,666 | 0.8658 |
| Box Size | Direct | Indirect | Sum | |||
|---|---|---|---|---|---|---|
| µm | eV | Gy | eV | Gy | eV | Gy |
| 2 | 19,603 | 0.7488 | 5885 | 0.2248 | 25,489 | 0.9737 |
| 3 | 20,146 | 0.7700 | 6071 | 0.2319 | 26,217 | 1.0015 |
| 4 | 20,258 | 0.7739 | 6192 | 0.2365 | 26,540 | 1.0138 |
| 5 | 20,328 | 0.7765 | 6140 | 0.2345 | 26,470 | 1.0111 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plante, I.; Poignant, F.; Slaba, T. Track Structure Components: Characterizing Energy Deposited in Spherical Cells from Direct and Peripheral HZE Ion Hits. Life 2021, 11, 1112. https://doi.org/10.3390/life11111112
Plante I, Poignant F, Slaba T. Track Structure Components: Characterizing Energy Deposited in Spherical Cells from Direct and Peripheral HZE Ion Hits. Life. 2021; 11(11):1112. https://doi.org/10.3390/life11111112
Chicago/Turabian StylePlante, Ianik, Floriane Poignant, and Tony Slaba. 2021. "Track Structure Components: Characterizing Energy Deposited in Spherical Cells from Direct and Peripheral HZE Ion Hits" Life 11, no. 11: 1112. https://doi.org/10.3390/life11111112
APA StylePlante, I., Poignant, F., & Slaba, T. (2021). Track Structure Components: Characterizing Energy Deposited in Spherical Cells from Direct and Peripheral HZE Ion Hits. Life, 11(11), 1112. https://doi.org/10.3390/life11111112







