Musculoskeletal Modeling of the Wrist via a Multi Body Simulation
Abstract
:1. Introduction
2. Material and Methods
2.1. General Approach of Modelling
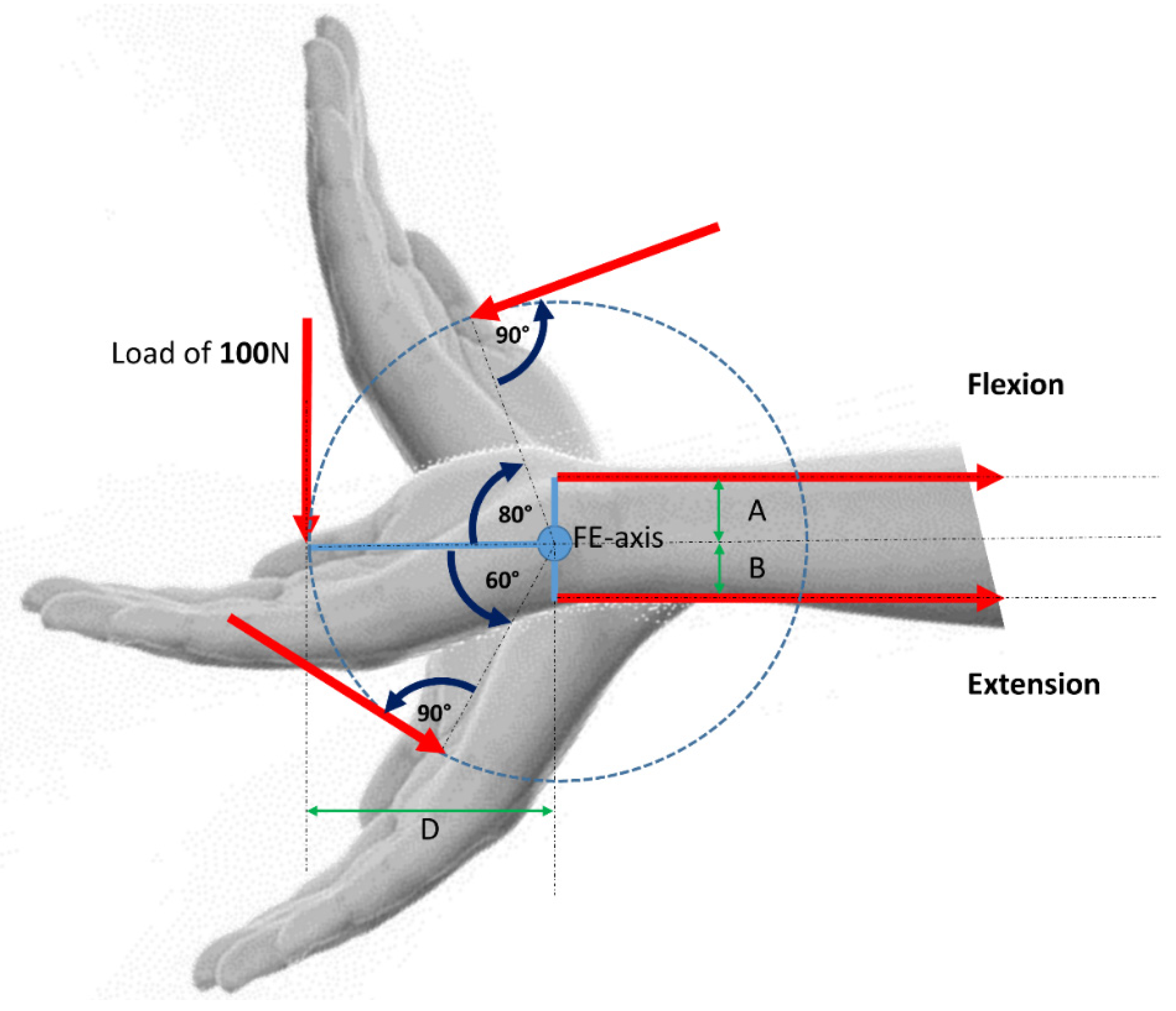
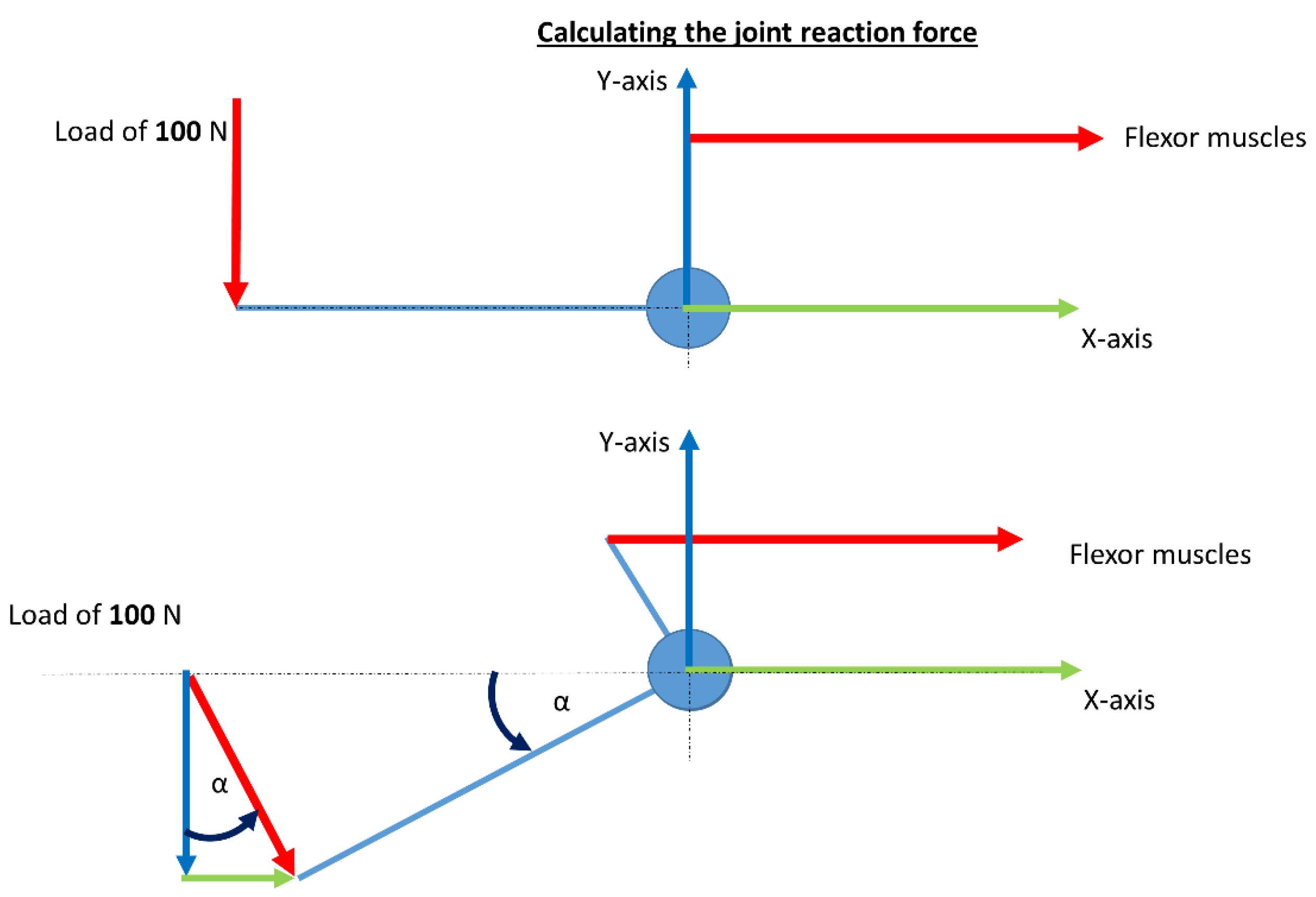
2.2. Simple Mechanical Wrist Model
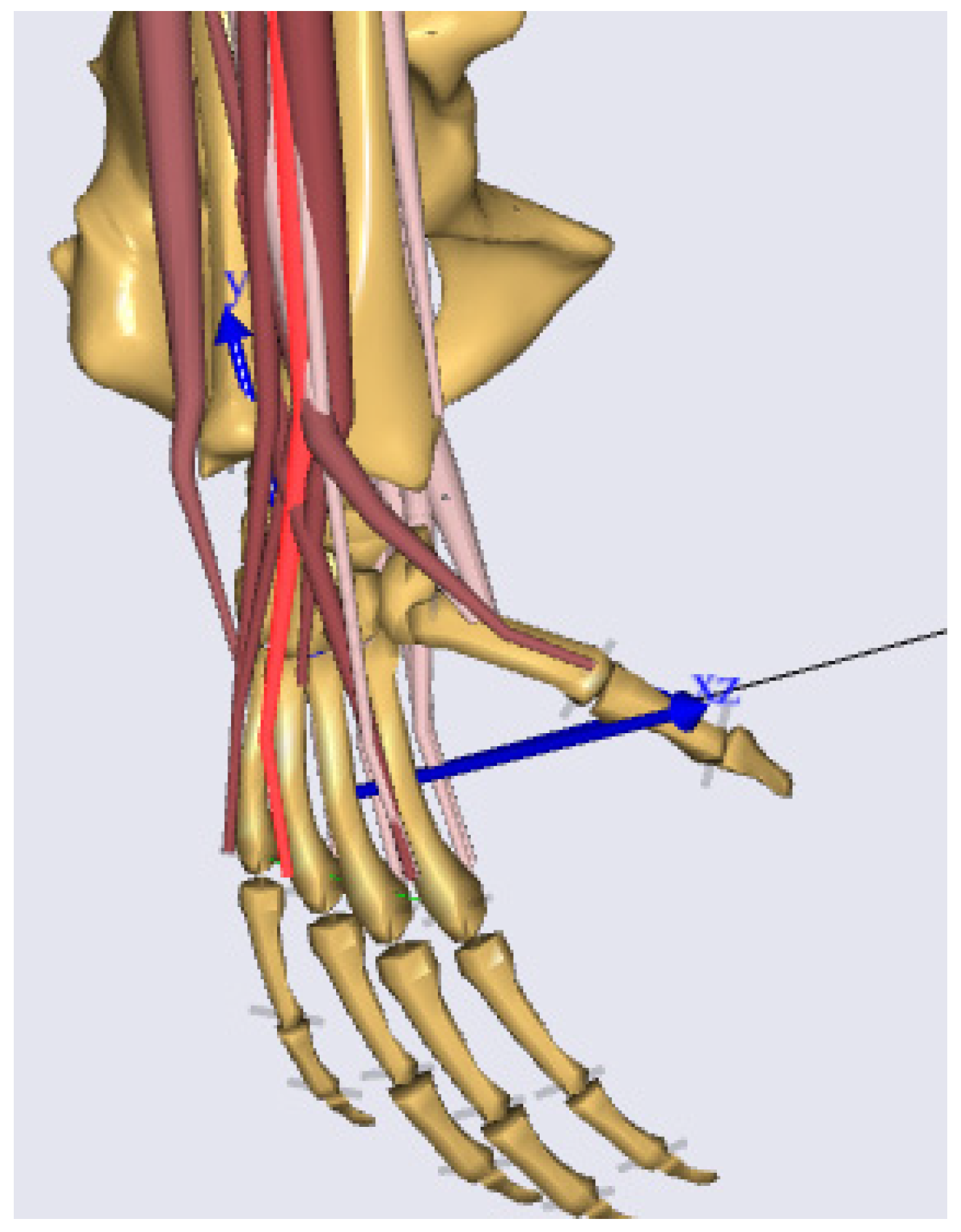
2.3. Musculoskeletal Model of the Standard Wrist Developed in AnyBody
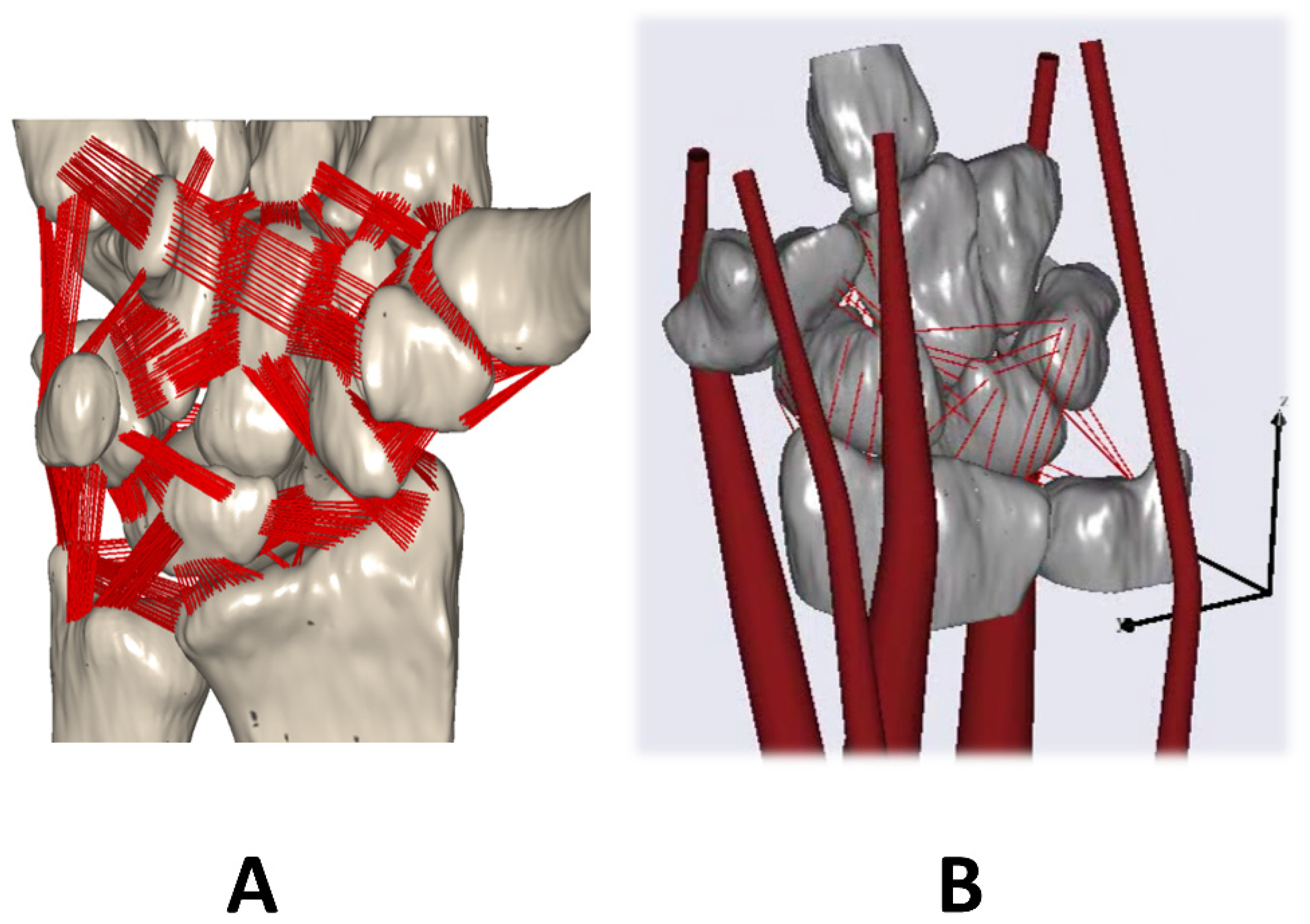
2.4. Musculoskeletal Model of a Complex Wrist Developed in AnyBody
3. Results
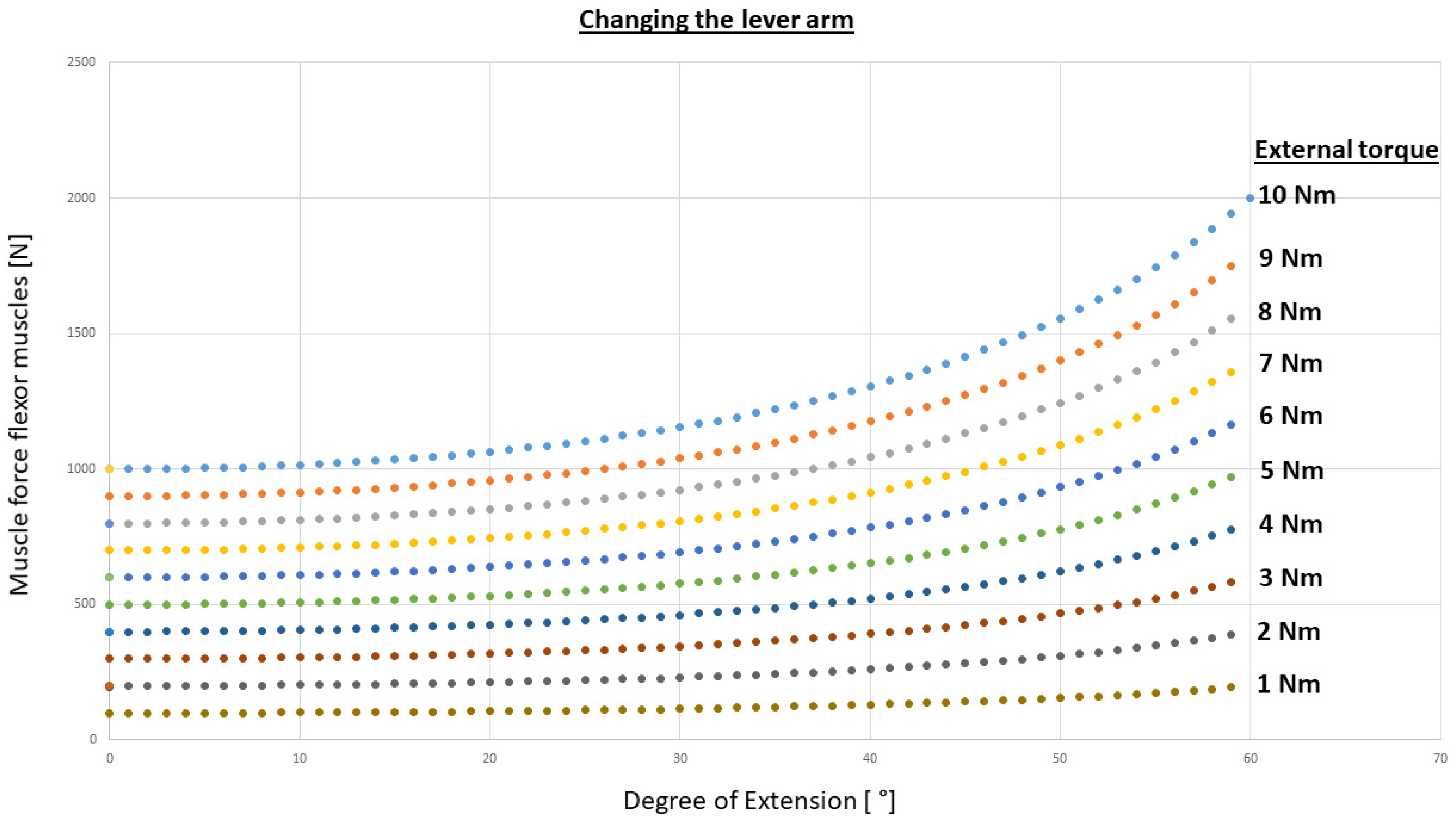
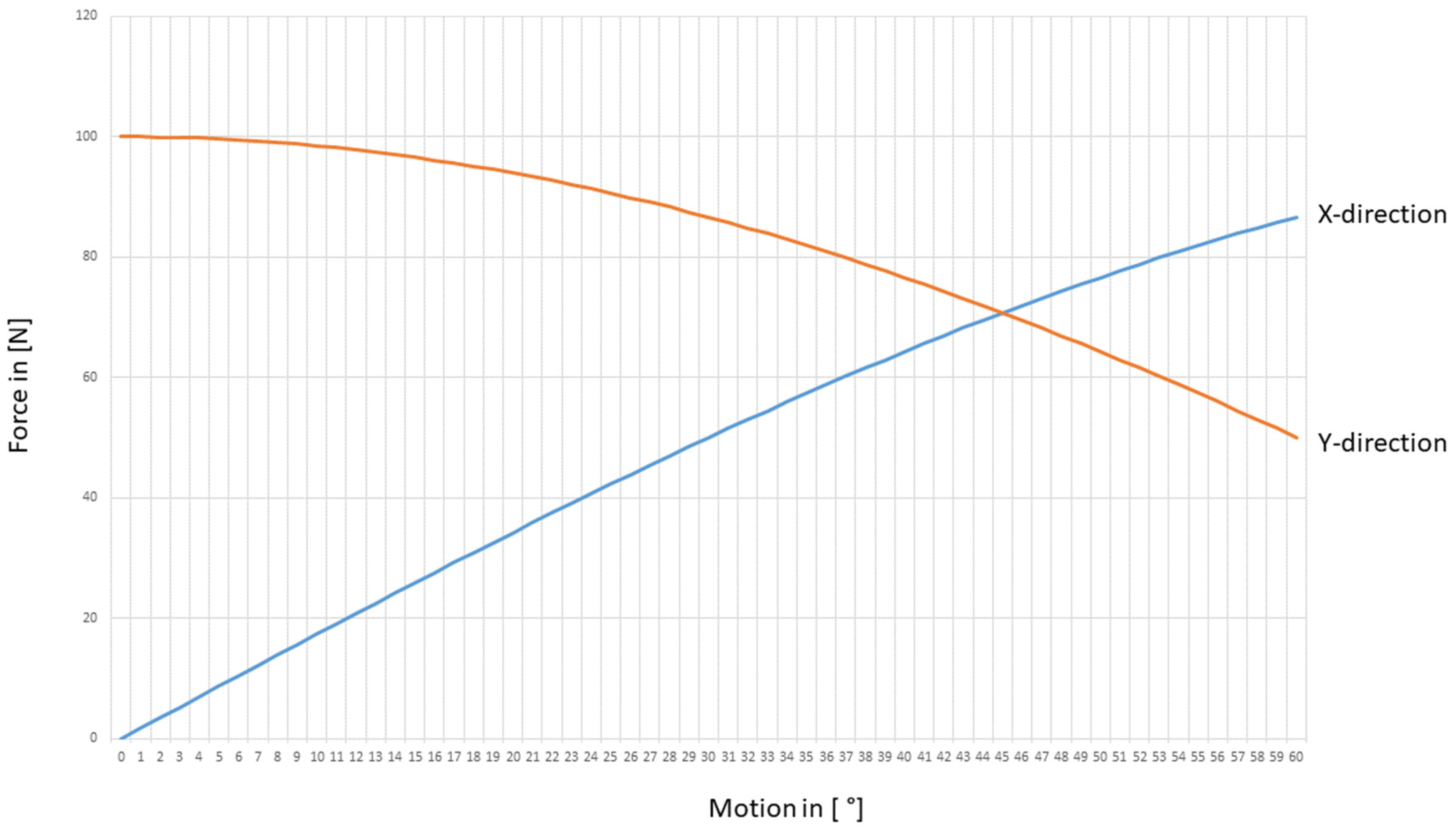
3.1. Simple Mechanical Wrist Model
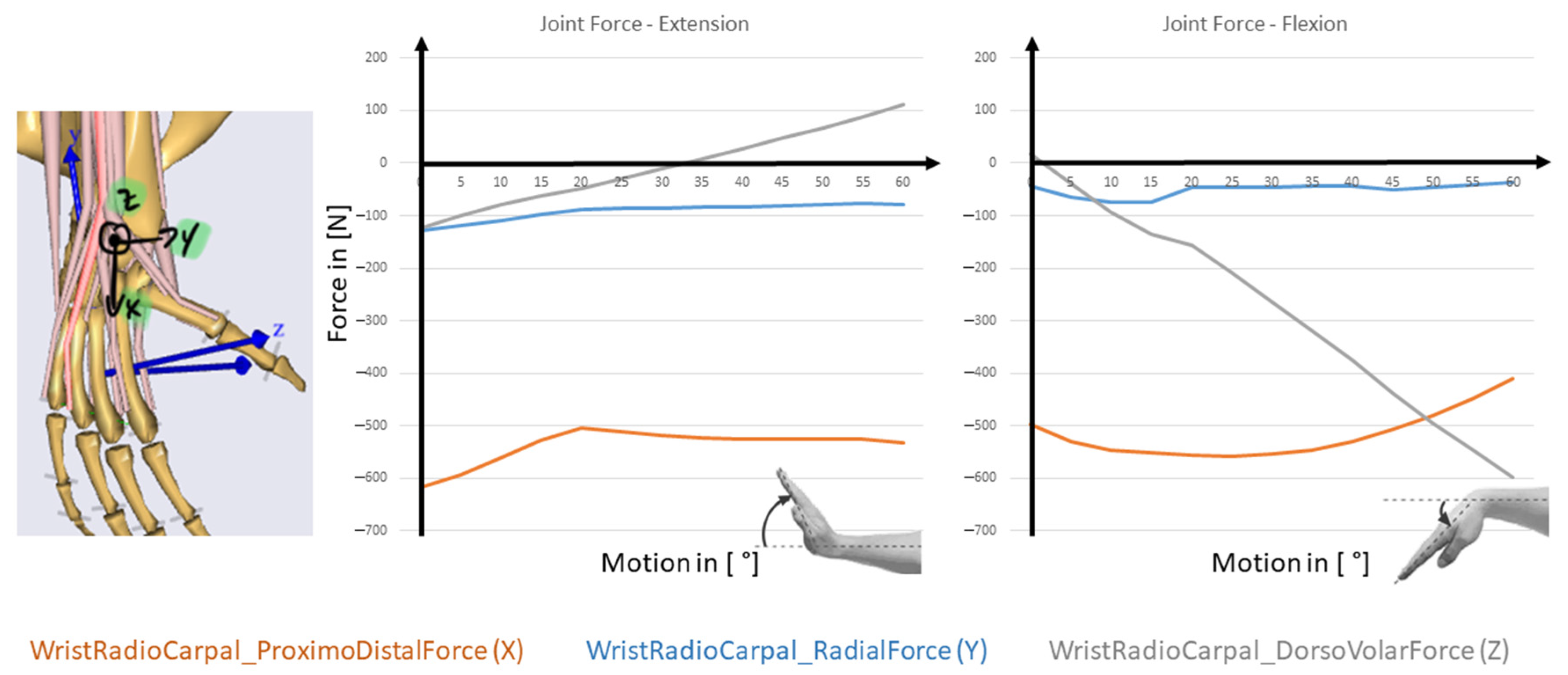
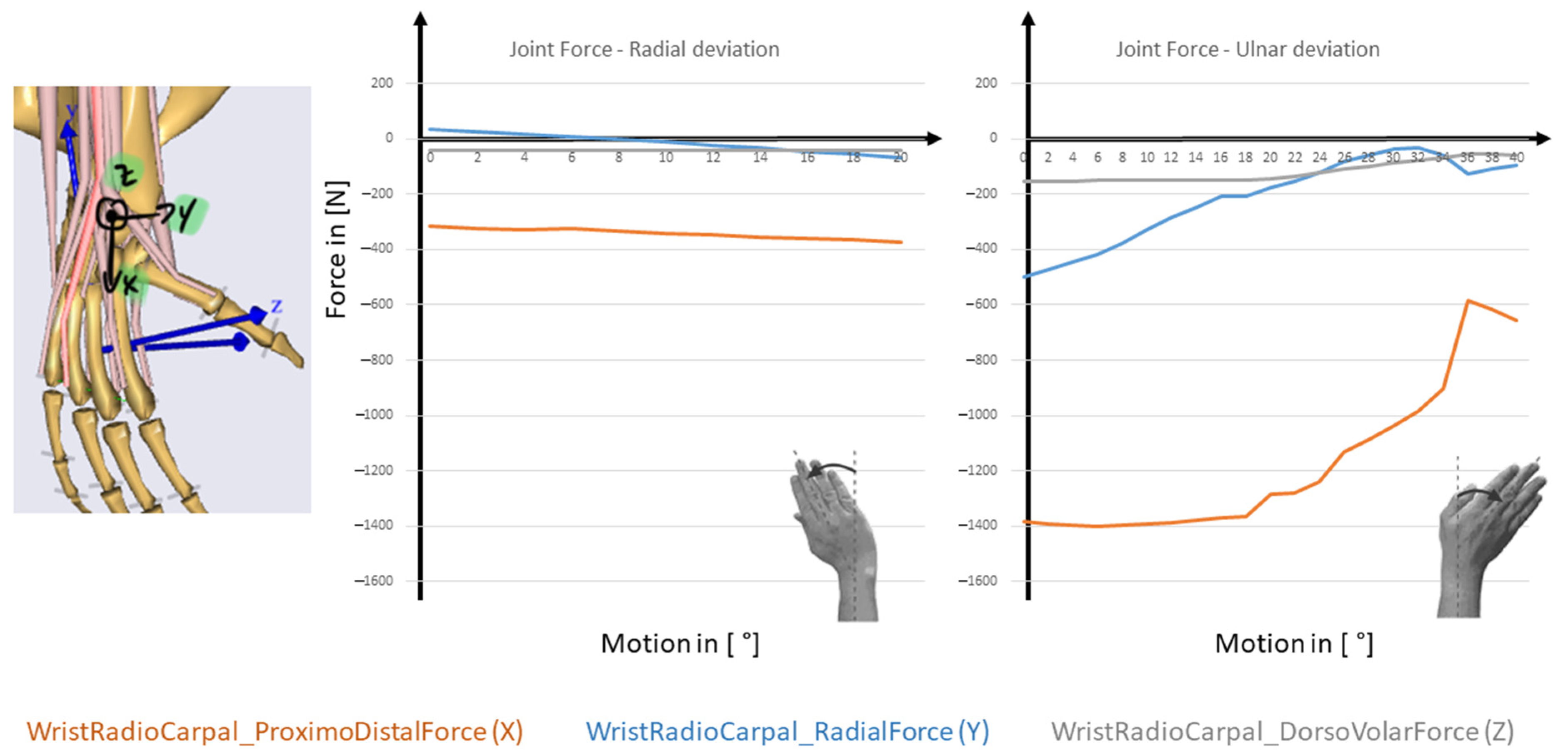
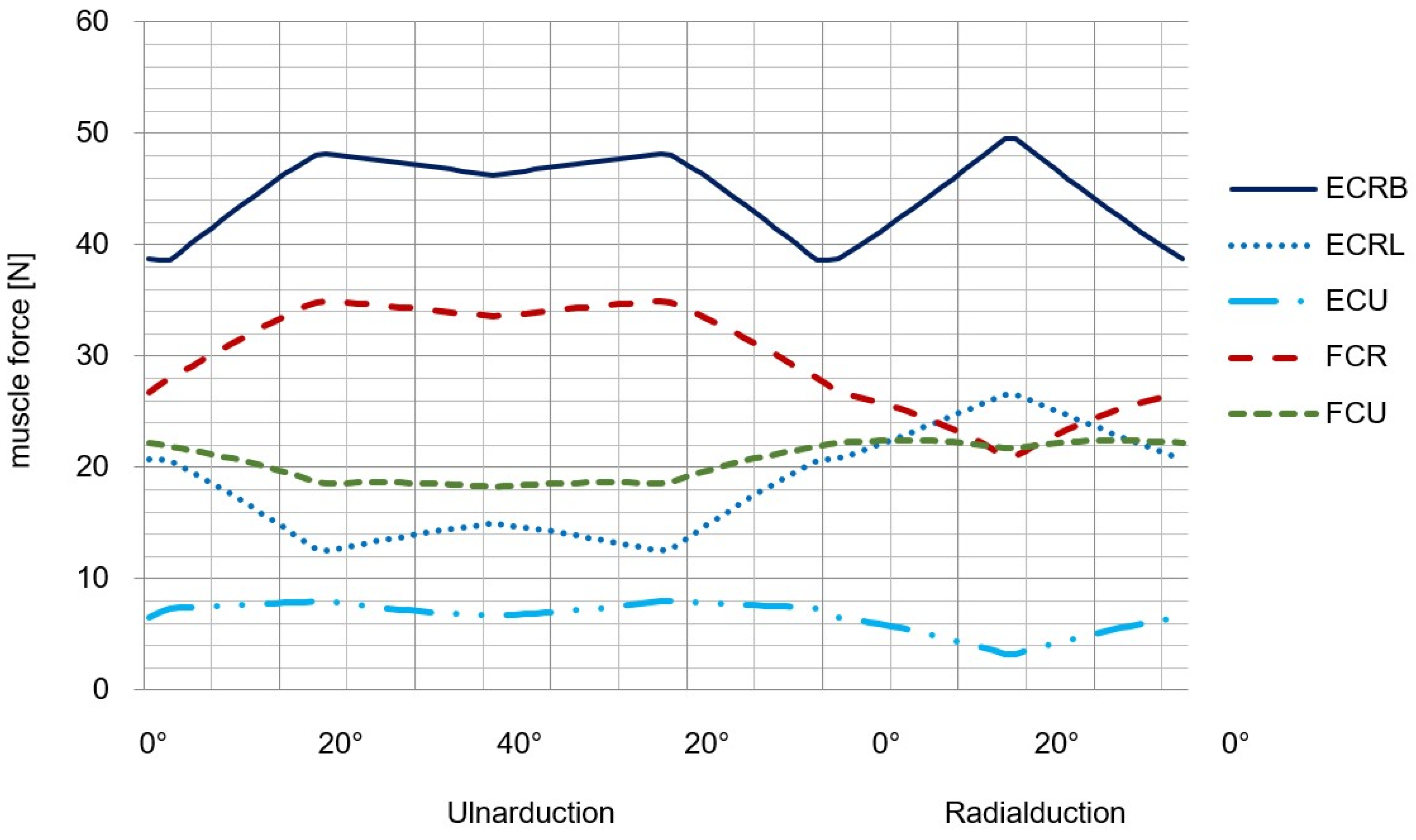
3.2. Musculoskeletal Standard Model of the Wrist in AnyBody
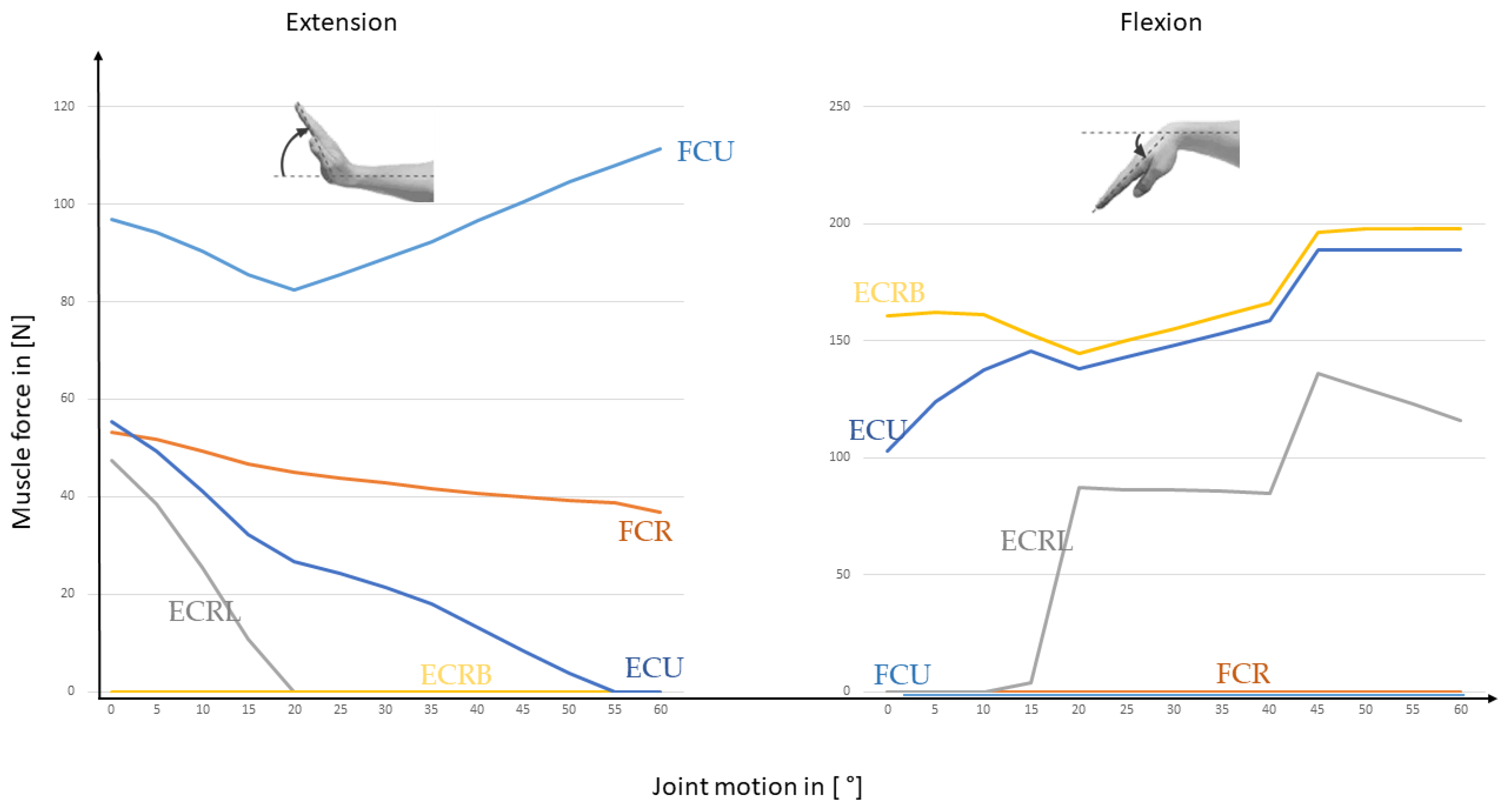
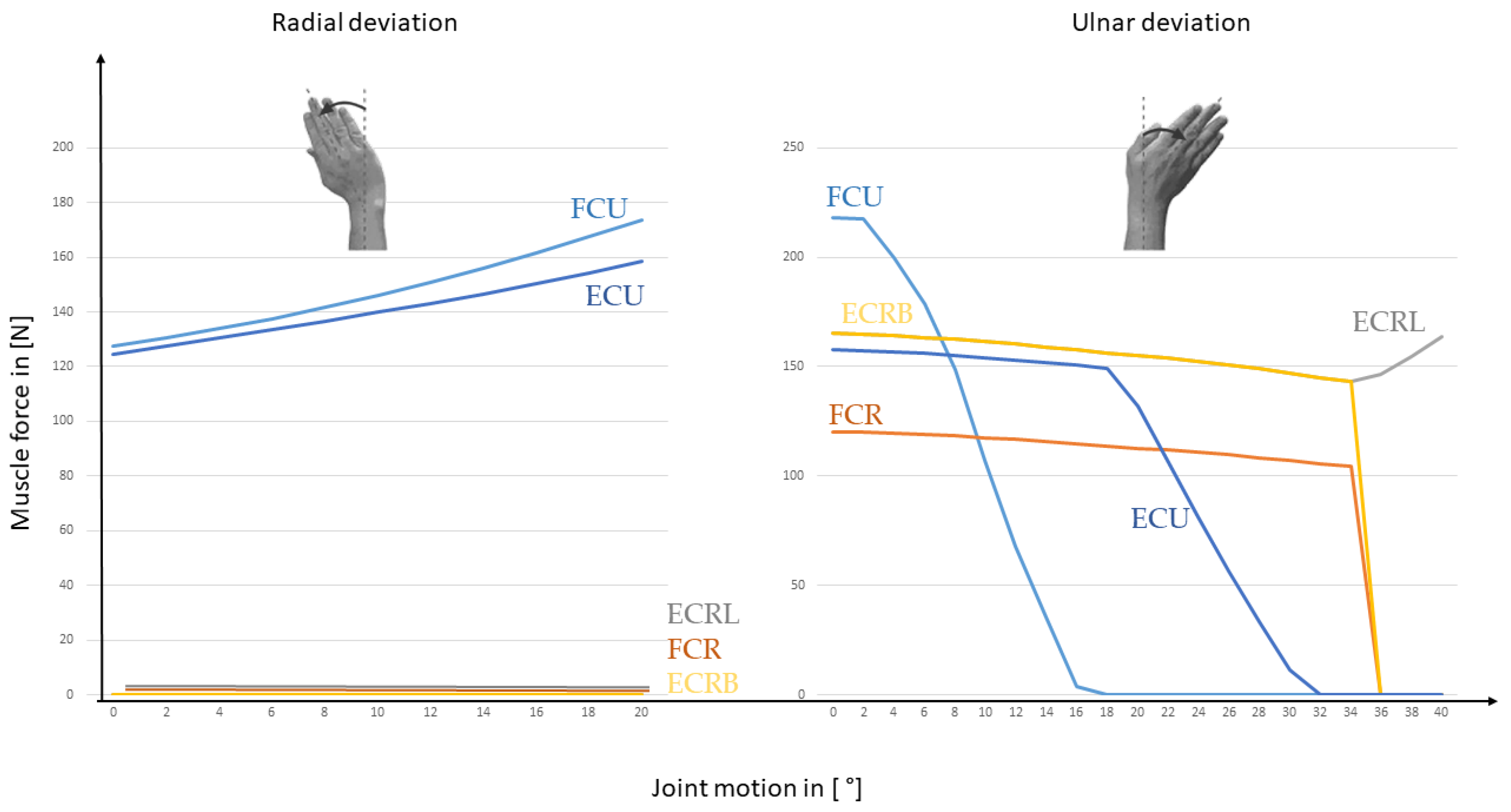
3.3. Musculoskeletal Model of the Complex Wrist Developed in AnyBody
3.4. Data for Validation of the Muscle Forces
4. Discussion
4.1. Simple Mechanical Model
4.2. AMS standard MBS Wrist Model
4.3. Complex MBS Wrist Model
4.4. Limitations
4.5. Examples of Possible Use Cases
- It is possible to show the change of the resulting joint load in case of osteotomies. Via simulation the joint load could be calculated (preoperatively) for different surgical scenarios, and the surgeon could directly see which influence the surgical intervention will have (e.g., [34]).
- You can investigate the influence changing the degrees of freedom (DOF) of a joint. In the case of e.g., a four corner fusion in the wrist you can visualize the new kinematic with reduced DOF and calculate additionally the resulting joint load [37]. Also the load on the implant itself could be calculated.
4.6. Examples of Validation Possibilities
- For example, there exist checklist and methodology for verification and validation focused on FEA models [25].
- For the huge joints in the human body (knee, hip, shoulder, and spine) the online database Orthoload (www.orthoload.com, accessed on 13 April 2022) is a perfect approach to use their information to validate own models. Furthermore, kinematic investigation is an alternative method to use the acquired motion trajectories for model validation [38].
- Also the methods like e.g., sensitivity studies (A sensitivity study quantifies how the uncertainty in the output of a model can be divided and allocated to different sources of uncertainty in its inputs), can be a powerful tool to get an impression of the validity of the model [24].
4.7. Ongoing Work in the Case of the Complex MBS Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Nichols, J.A.; Bednar, M.S.; Wohlman, S.J.; Murray, W.M. Connecting the wrist to the hand: A simulation study exploring changes in thumb-tip endpoint force following wrist surgery. J. Biomech. 2017, 58, 97–104. [Google Scholar] [CrossRef] [PubMed]
- Brand, R.A.; Pedersen, D.R.; Davy, D.T.; Kotzar, G.M.; Heiple, K.G.; Goldberg, V.M. Comparison of hip force calculations and measurements in the same patient. J. Arthroplast. 1994, 9, 45–51. [Google Scholar] [CrossRef]
- Gelberman, R.H.; Cooney, W.P.; Szabo, R.M. Carpal instability. Instr. Course Lect. 2001, 50, 123–134. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.E.; Wolfe, S.W. Scapholunate instability: Current concepts in diagnosis and management. J. Hand Surg. Am. 2012, 33, 998–1013. [Google Scholar] [CrossRef]
- Schmidt, H.-M.; Lanz, U. Chirurgische Anatomie der Hand, 2nd ed.; Thieme: Stuttgart, Germany, 2003; ISBN 3131306920. [Google Scholar]
- Sennwald, G. Das Handgelenk; Springer: Berlin/Heidelberg, Germany, 1987; ISBN 0387180257. [Google Scholar]
- Laulan, J.; Marteau, E.; Bacle, G. Wrist osteoarthritis. Orthop. Traumatol. Surg. Res. 2015, 101, S1–S9. [Google Scholar] [CrossRef] [Green Version]
- Palmer, A.K.; Werner, F.W.; Murphy, D.; Glisson, R. Functional wrist motion: A biomechanical study. J. Hand Surg. Am. 1985, 10, 39–46. [Google Scholar] [CrossRef]
- Nelson, D.L.; Mitchell, M.A.; Groszewski, P.G.; Pennick, S.L.; Manske, P.R. Wrist Range of Motion in Activities of Daily Living. In Advances in the Biomechanics of the Hand and Wrist; Schuind, F., An, K.N., Cooney, W.P., Garcia-Elias, M., Eds.; Springer: Boston, MA, USA, 1994; pp. 329–334. ISBN 978-1-4757-9107-5. [Google Scholar]
- Erdemir, A.; McLean, S.; Herzog, W.; van den Bogert, A.J. Model-based estimation of muscle forces exerted during movements. Clin. Biomech. 2007, 22, 131–154. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, R.V.; Buchanan, T.S.; Delp, S.L. How muscle architecture and moment arms affect wrist flexion-extension moments. J. Biomech. 1996, 30, 705–712. [Google Scholar] [CrossRef]
- Eschweiler, J.; Li, J.; Quack, V.; Rath, B.; Baroncini, A.; Hildebrand, F.; Migliorini, F. Anatomy, Biomechanics, and Loads of the Wrist Joint. Life 2022, 12, 188. [Google Scholar] [CrossRef]
- Garcia-Elias, M.; Lluch, A.L.; Stanley, J.K. Three-ligament tenodesis for the treatment of scapholunate dissociation: Indications and surgical technique. J. Hand Surg. Am. 2006, 31, 125–134. [Google Scholar] [CrossRef]
- Marqués, R.; Melchor, J.; Sánchez-Montesinos, I.; Roda, O.; Rus, G.; Hernández-Cortés, P. Biomechanical Finite Element Method Model of the Proximal Carpal Row and Experimental Validation. Front. Physiol. 2021, 12, 749372. [Google Scholar] [CrossRef] [PubMed]
- Genda, E.; Horii, E. Theoretical stress analysis in wrist joint--neutral position and functional position. J. Hand Surg. Br. 2000, 25, 292–295. [Google Scholar] [CrossRef] [PubMed]
- Eschweiler, J.; Stromps, J.-P.; Fischer, M.; Schick, F.; Rath, B.; Pallua, N.; Radermacher, K. A biomechanical model of the wrist joint for patient-specific model guided surgical therapy: Part 2. Proc. Inst. Mech. Eng. Part H 2016, 230, 326–334. [Google Scholar] [CrossRef] [PubMed]
- Eschweiler, J.; Stromps, J.-P.; Fischer, M.; Schick, F.; Rath, B.; Pallua, N.; Radermacher, K. Development of a biomechanical model of the wrist joint for patient-specific model guided surgical therapy planning: Part 1. Proc. Inst. Mech. Eng. Part H 2016, 230, 310–325. [Google Scholar] [CrossRef]
- Fischli, S.; Sellens, R.W.; Beek, M.; Pichora, D.R. Simulation of extension, radial and ulnar deviation of the wrist with a rigid body spring model. J. Biomech. 2009, 42, 1363–1366. [Google Scholar] [CrossRef]
- Iwasaki, N.; Genda, E.; Minami, A.; Kaneda, K.; Chao, E.Y. Force transmission through the wrist joint in Kienböck’s disease: A two-dimensional theoretical study. J. Hand Surg. Am. 1998, 23, 415–424. [Google Scholar] [CrossRef]
- Majors, B.J.; Wayne, J.S. Development and validation of a computational model for investigation of wrist biomechanics. Ann. Biomed. Eng. 2011, 39, 2807–2815. [Google Scholar] [CrossRef]
- Manal, K.; Lu, X.; Nieuwenhuis, M.K.; Helders, P.J.M.; Buchanan, T.S. Force transmission through the juvenile idiopathic arthritic wrist: A novel approach using a sliding rigid body spring model. J. Biomech. 2002, 35, 125–133. [Google Scholar] [CrossRef]
- Schuind, F.; Cooney, W.P.; Linscheid, R.L.; An, K.N.; Chao, E.Y. Force and pressure transmission through the normal wrist. A theoretical two-dimensional study in the posteroanterior plane. J. Biomech. 1995, 28, 587–601. [Google Scholar] [CrossRef]
- Sirkett, D.M.; Mullineux, G.; Giddins, G.E.B.; Miles, A.W. A kinematic model of the wrist based on maximization of joint contact area. Proc. Inst. Mech. Eng. Part H 2004, 218, 349–359. [Google Scholar] [CrossRef]
- Henninger, H.B.; Reese, S.P.; Anderson, A.E.; Weiss, J.A. Validation of computational models in biomechanics. Proc. Inst. Mech. Eng. Part H 2010, 224, 801–812. [Google Scholar] [CrossRef] [PubMed]
- Oefner, C.; Herrmann, S.; Kebbach, M.; Lange, H.-E.; Kluess, D.; Woiczinski, M. Reporting checklist for verification and validation of finite element analysis in orthopedic and trauma biomechanics. Med. Eng. Phys. 2021, 92, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Pauwels, F. Osteoarthritis: Biomechanics of the Normal and Diseased Hip: Theoretical Foundation, Technique, and Results of Treatment; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Brand, R.A. Hip osteotomies: A biomechanical consideration. JAAOS-J. Am. Acad. Orthop. Surg. 1997, 5, 282–291. [Google Scholar] [CrossRef] [PubMed]
- Eschweiler, J.; Fieten, L.; Dell’Anna, J.; Kabir, K.; Gravius, S.; Tingart, M.; Radermacher, K. Application and evaluation of biomechanical models and scores for the planning of total hip arthroplasty. Proc. Inst. Mech. Eng. Part H 2012, 226, 955–967. [Google Scholar] [CrossRef] [PubMed]
- Eschweiler, J.; Asseln, M.; Damm, P.; Quack, V.; Rath, B.; Bergmann, G.; Tingart, M.; Radermacher, K. Evaluierung von biomechanischen Modellen zur Therapieplanung für die Hüftendoprothesenversorgung-direkter Vergleich zwischen Berechnungsergebnissen und In-vivo-Messungen. Z. Orthop. Unfall. 2014, 152, 603–615. [Google Scholar] [CrossRef] [PubMed]
- Eschweiler, J.; Migliorini, F.; Siebers, H.; Tingart, M.; Rath, B. Biomechanische Modellierung und ihre Bedeutung für die Hüftendoprothetik. Der Orthop. 2019, 48, 282–291. [Google Scholar] [CrossRef]
- Andersen, M.S.; Damsgaard, M.; Rasmussen, J. Force-dependent kinematics: A new analysis method for non-conforming joints. In Proceedings of the XIII International Symposium on Computer Simulation in Biomechanics, Leuven, Belgium, 30 June–2 July 2011. [Google Scholar]
- Andersen, M.S.; Rasmussen, J. Total knee replacement musculoskeletal model using a novel simulation method for non-conforming joints. In Proceedings of the International Society of Biomechanics Conference, International Society of Biomechanics (ISB), Brussels, Belgium, 3–7 July 2011. [Google Scholar]
- Debottis, D.P.; Werner, F.W.; Sutton, L.G.; Harley, B.J. 4-corner arthrodesis and proximal row carpectomy: A biomechanical comparison of wrist motion and tendon forces. J. Hand Surg. Am. 2013, 38, 893–898. [Google Scholar] [CrossRef]
- Holzbaur, K.R.S.; Murray, W.M.; Delp, S.L. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Ann. Biomed. Eng. 2005, 33, 829–840. [Google Scholar] [CrossRef]
- Eschweiler, J.; Hawlitzky, J.; Quack, V.; Tingart, M.; Rath, B. Biomechanical model based evaluation of Total Hip Arthroplasty therapy outcome. J. Orthop. 2017, 14, 582–588. [Google Scholar] [CrossRef]
- Rath, B.; Eschweiler, J.; Betsch, M.; Quack, V.; Lüring, C.; Tingart, M. Hüftendoprothetik nach korrigierenden Osteotomien: Becken und proximales Femur. Der Orthop. 2016, 45, 678–686. [Google Scholar] [CrossRef]
- Fan, S.; Padmore, C.; Kadar, A.; Chambers, S.; Langohr, G.D.G.; Suh, N. The effect of four-corner fusion and proximal row carpectomy on uniplanar and multiplanar wrist motion: A biomechanical study. J. Orthop. 2021, 24, 102–110. [Google Scholar] [CrossRef] [PubMed]
- Eschweiler, J.; Stromps, J.P.; Rath, B.; Pallua, N.; Radermacher, K. Analysis of wrist bone motion before and after SL-ligament resection. Biomed. Eng./Biomed. Tech. 2016, 61, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Akhbari, B.; Moore, D.C.; Laidlaw, D.H.; Weiss, A.-P.C.; Akelman, E.; Wolfe, S.W.; Crisco, J.J. Predicting Carpal Bone Kinematics Using an Expanded Digital Database of Wrist Carpal Bone Anatomy and Kinematics. J. Orthop. Res. 2019, 37, 2661–2670. [Google Scholar] [CrossRef] [PubMed]
- Akhbari, B.; Morton, A.M.; Shah, K.N.; Molino, J.; Moore, D.C.; Weiss, A.-P.C.; Wolfe, S.W.; Crisco, J.J. Proximal-distal shift of the center of rotation in a total wrist arthroplasty is more than twice of the healthy wrist. J. Orthop. Res. 2020, 38, 1575–1586. [Google Scholar] [CrossRef]
- Akhbari, B.; Morton, A.M.; Shah, K.N.; Molino, J.; Moore, D.C.; Weiss, A.-P.C.; Wolfe, S.W.; Crisco, J.J. In vivo articular contact pattern of a total wrist arthroplasty design. J. Biomech. 2021, 121, 110420. [Google Scholar] [CrossRef]
- Moore, D.C.; Crisco, J.J.; Trafton, T.G.; Leventhal, E.L. A digital database of wrist bone anatomy and carpal kinematics. J. Biomech. 2007, 40, 2537–2542. [Google Scholar] [CrossRef]
- Hughes, R.E.; Bean, J.C.; Chaffin, D.B. Evaluating the effect of co-contraction in optimization models. J. Biomech. 1995, 28, 875–878. [Google Scholar] [CrossRef]
- Saxby, D.J.; Killen, B.A.; Pizzolato, C.; Carty, C.P.; Diamond, L.E.; Modenese, L.; Fernandez, J.; Davico, G.; Barzan, M.; Lenton, G.; et al. Machine learning methods to support personalized neuromusculoskeletal modelling. Biomech. Model. Mechanobiol. 2020, 19, 1169–1185. [Google Scholar] [CrossRef]


| PM: | PM: | |
|---|---|---|
| Contact Matching | 0.6 × 1010 N/m3 | 1.2 × 1010 N/m3 |
| Resulting Contact | Resulting Contact | |
| Force (N) | Force (N) | |
| Scaphoid-Radius | 124.0 | 185.9 |
| Lunate-Radius | 49.0 | 66.8 |
| Lunate-Ulna | 5.5 | 9.4 |
| FR | 178.5 | 262.1 |
| Wrist Motion | ECU | ECRB | ECRL | FCR | FCU |
|---|---|---|---|---|---|
| FE | 54 (15) | 26 (7) | 60 (22) | 32 (12) | 33 (5) |
| RUD | 34 (9) | 16 (7) | 51 (9) | 12 (7) | 34 (12) |
| Wrist Motion | ECU | ECRB | ECRL | FCR | FCU |
|---|---|---|---|---|---|
| FE | 23 (2) | 11 (6) | 25 (6) | 17 (3) | 15 (5) |
| RUD | 21 (4) | 5 (3) | 27 (3) | 6 (4) | 18 (3) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eschweiler, J.; Praster, M.; Quack, V.; Michalik, R.; Hildebrand, F.; Rath, B.; Migliorini, F. Musculoskeletal Modeling of the Wrist via a Multi Body Simulation. Life 2022, 12, 581. https://doi.org/10.3390/life12040581
Eschweiler J, Praster M, Quack V, Michalik R, Hildebrand F, Rath B, Migliorini F. Musculoskeletal Modeling of the Wrist via a Multi Body Simulation. Life. 2022; 12(4):581. https://doi.org/10.3390/life12040581
Chicago/Turabian StyleEschweiler, Jörg, Maximilian Praster, Valentin Quack, Roman Michalik, Frank Hildebrand, Björn Rath, and Filippo Migliorini. 2022. "Musculoskeletal Modeling of the Wrist via a Multi Body Simulation" Life 12, no. 4: 581. https://doi.org/10.3390/life12040581
APA StyleEschweiler, J., Praster, M., Quack, V., Michalik, R., Hildebrand, F., Rath, B., & Migliorini, F. (2022). Musculoskeletal Modeling of the Wrist via a Multi Body Simulation. Life, 12(4), 581. https://doi.org/10.3390/life12040581









