Nucleic Acid Thermodynamics Derived from Mechanical Unzipping Experiments
Abstract
:1. Introduction
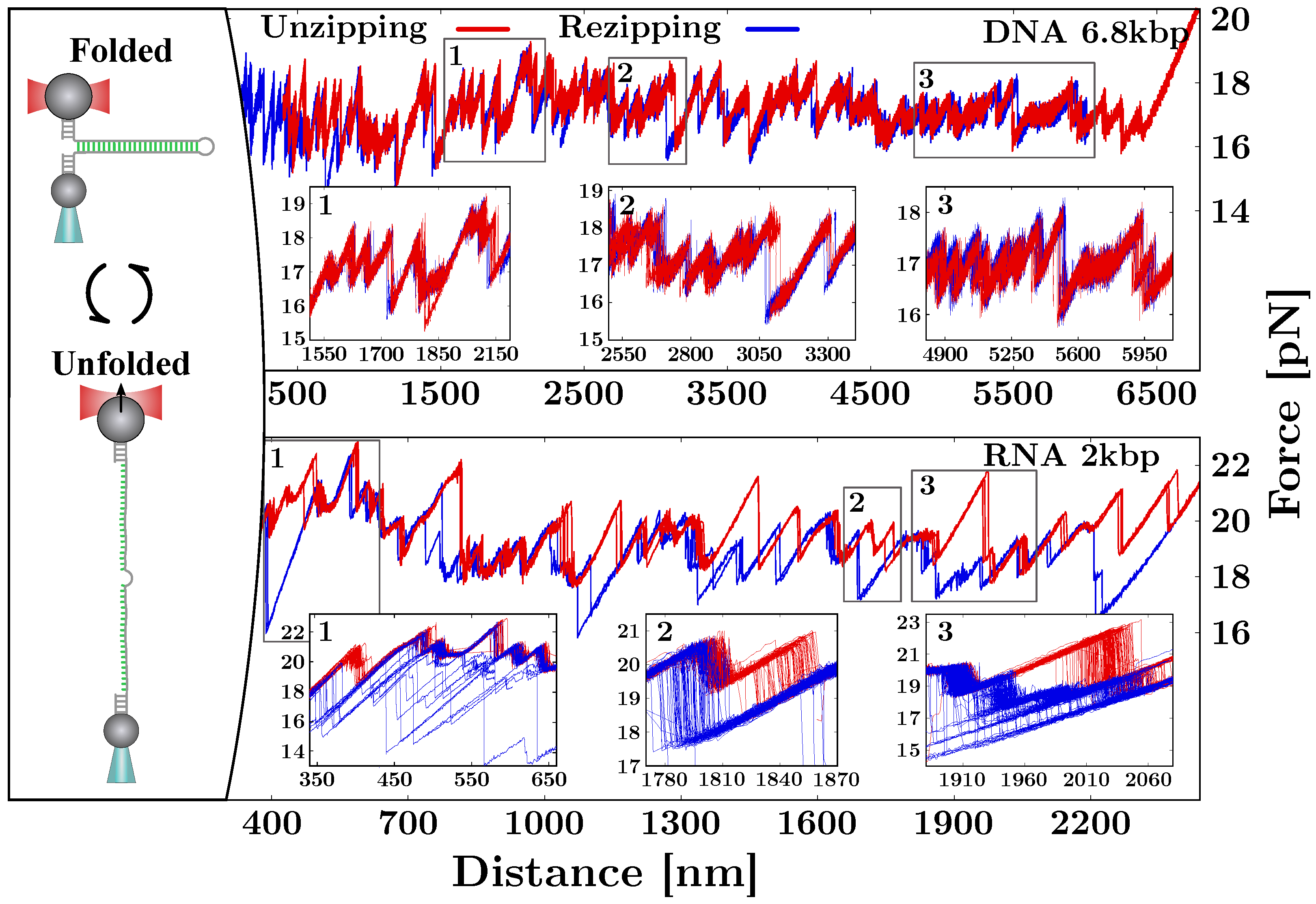
2. Mechanical Unzipping of Nucleic Acids (NAs)
3. Modeling the Unzipping Experiment
3.1. Bases Hybridization and Nearest-Neighbors Model
3.2. Computation of the System Free-Energy
3.3. The Equilibrium FDC
4. Derivation of the NNBP Free-Energies
5. Out-of-Equilibrium Processes and Kinetics Effects
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bryngelson, J.D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aabert, B.; Johnson, A.L.J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Englander, S.W.; Mayne, L.; Krishna, M.M. Protein folding and misfolding: Mechanism and principles. Q. Rev. Biophys. 2007, 40, 1–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Englander, S.W.; Mayne, L. The nature of protein folding pathways. Proc. Natl. Acad. Sci. USA 2014, 111, 15873–15880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rico-Pasto, M.; Zaltron, A.; Davis, S.J.; Frutos, S.; Ritort, F. Molten globule–like transition state of protein barnase measured with calorimetric force spectroscopy. Proc. Natl. Acad. Sci. USA 2022, 119, e2112382119. [Google Scholar] [CrossRef] [PubMed]
- Felsenfeld, G.; Miles, H.T. The physical and chemical properties of nucleic acids. Annu. Rev. Biochem. 1967, 36, 407–448. [Google Scholar] [CrossRef]
- Shamsi, M.H.; Kraatz, H.B. Interactions of metal ions with DNA and some applications. Inorg. Organomet. Polym. Mater. 2013, 23, 4–23. [Google Scholar] [CrossRef]
- Cantor, C.R.; Schimmel, P.R. Biophysical Chemistry: Part II: Techniques for the Study of Biological Structure and Function; Macmillan: New York, NY, USA, 1980. [Google Scholar]
- SantaLucia, J. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. USA 1998, 95, 1460–1465. [Google Scholar] [CrossRef] [Green Version]
- Xia, T.; SantaLucia, J., Jr.; Burkard, M.E.; Kierzek, R.; Schroeder, S.J.; Jiao, X.; Cox, C.; Turner, D.H. Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson-Crick base-pairs. Biochemistry 1998, 37, 14719–14735. [Google Scholar] [CrossRef] [Green Version]
- Zuker, M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003, 31, 3406–3415. [Google Scholar] [CrossRef]
- Neupane, K.; Foster, D.A.; Dee, D.R.; Yu, H.; Wang, F.; Woodside, M.T. Direct observation of transition paths during the folding of proteins and nucleic acids. Science 2016, 352, 239–242. [Google Scholar] [CrossRef]
- Treiber, D.K.; Williamson, J.R. Exposing the kinetic traps in RNA folding. Curr. Opin. Struct. Biol. 1999, 9, 339–345. [Google Scholar] [CrossRef]
- Johnson, S.M.; Wiseman, R.L.; Sekijima, Y.; Green, N.S.; Adamski-Werner, S.L.; Kelly, J.W. Native state kinetic stabilization as a strategy to ameliorate protein misfolding diseases: A focus on the transthyretin amyloidoses. Acc. Chem. Res. 2005, 38, 911–921. [Google Scholar] [CrossRef] [PubMed]
- Manosas, M.; Junier, I.; Ritort, F. Force-induced misfolding in RNA. Phys. Rev. E 2008, 78, 061925. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russell, R. RNA misfolding and the action of chaperones. Front. Biosci. 2008, 13, 1–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodgers, M.L.; Woodson, S.A. A roadmap for rRNA folding and assembly during transcription. Trends Biochem. Sci. 2021, 46, 889–901. [Google Scholar] [CrossRef]
- Jain, A.; Vale, R.D. RNA phase transitions in repeat expansion disorders. Nature 2017, 546, 243–247. [Google Scholar] [CrossRef] [Green Version]
- Błaszczyk, L.; Rypniewski, W.; Kiliszek, A. Structures of RNA repeats associated with neurological diseases. Wiley Interdiscip. Rev. RNA 2017, 8, e1412. [Google Scholar] [CrossRef]
- Zhao, X.; Usdin, K. (Dys) function follows form: Nucleic acid structure, repeat expansion, and disease pathology in FMR1 disorders. Int. J. Mol. Sci. 2021, 22, 9167. [Google Scholar] [CrossRef]
- Shashkova, S.; Leake, M.C. Single-molecule fluorescence microscopy review: Shedding new light on old problems. Biosci. Rep. 2017, 37, BSR20170031. [Google Scholar] [CrossRef] [Green Version]
- Meller, A.; Nivon, L.; Branton, D. Voltage-driven DNA translocations through a nanopore. Phys. Rev. Lett. 2001, 86, 3435. [Google Scholar] [CrossRef] [Green Version]
- Neuman, K.C.; Nagy, A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2008, 5, 491. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Mourou, G.; Strickland, D. The 2018 Nobel Prize in Physics: A gripping and extremely exciting tale of light. Curr. Sci. 2018, 115, 1844. [Google Scholar]
- Junier, I.; Mossa, A.; Manosas, M.; Ritort, F. Recovery of free energy branches in single molecule experiments. Phys. Rev. Lett. 2009, 102, 070602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tinoco, I.; Li, P.T.; Bustamante, C. Determination of thermodynamics and kinetics of RNA reactions by force. Q. Rev. Biophys. 2006, 39, 325–360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bustamante, C.; Liphardt, J.; Ritort, F. The nonequilibrium thermodynamics of small systems. Phys. Today 2005, 58, 43. [Google Scholar] [CrossRef] [Green Version]
- Bosco, A.; Camunas-Soler, J.; Ritort, F. Elastic properties and secondary structure formation of single-stranded DNA at monovalent and divalent salt conditions. Nucleic Acids Res. 2014, 42, 2064–2074. [Google Scholar] [CrossRef]
- Camunas-Soler, J.; Ribezzi-Crivellari, M.; Ritort, F. Elastic properties of nucleic acids by single-molecule force spectroscopy. Annu. Rev. Biophys. 2016, 45, 65–84. [Google Scholar] [CrossRef]
- Viader-Godoy, X.; Pulido, C.; Ibarra, B.; Manosas, M.; Ritort, F. Cooperativity-dependent folding of single-stranded DNA. Phys. Rev. X 2021, 11, 031037. [Google Scholar] [CrossRef]
- Best, R.B.; Paci, E.; Hummer, G.; Dudko, O.K. Pulling direction as a reaction coordinate for the mechanical unfolding of single molecules. J. Phys. Chem. B 2008, 112, 5968–5976. [Google Scholar] [CrossRef]
- Dudko, O.K.; Hummer, G.; Szabo, A. Theory, analysis, and interpretation of single-molecule force spectroscopy experiments. Proc. Natl. Acad. Sci. USA 2008, 105, 15755–15760. [Google Scholar] [CrossRef] [Green Version]
- Huguet, J.M.; Bizarro, C.V.; Forns, N.; Smith, S.B.; Bustamante, C.; Ritort, F. Single-molecule derivation of salt dependent base-pair free energies in DNA. Proc. Natl. Acad. Sci. USA 2010, 107, 15431–15436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huguet, J.M.; Ribezzi-Crivellari, M.; Bizarro, C.V.; Ritort, F. Derivation of nearest-neighbor DNA parameters in magnesium from single molecule experiments. Nucleic Acids Res. 2017, 45, 12921–12931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rissone, P.; Bizarro, C.V.; Ritort, F. Stem–loop formation drives RNA folding in mechanical unzipping experiments. Proc. Natl. Acad. Sci. USA 2022, 119, e2025575119. [Google Scholar] [CrossRef] [PubMed]
- Liphardt, J.; Onoa, B.; Smith, S.B.; Tinoco, I., Jr.; Bustamante, C. Reversible unfolding of single RNA molecules by mechanical force. Science 2001, 292, 733–737. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.J.; Dill, K.A. RNA folding energy landscapes. Proc. Natl. Acad. Sci. USA 2000, 97, 646–651. [Google Scholar] [CrossRef] [Green Version]
- Woodson, S.A. Compact intermediates in RNA folding. Annu. Rev. Biophys. 2010, 39, 61–77. [Google Scholar] [CrossRef]
- Liphardt, J.; Dumont, S.; Smith, S.B.; Tinoco, I., Jr.; Bustamante, C. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski’s equality. Science 2002, 296, 1832–1835. [Google Scholar] [CrossRef] [Green Version]
- Alemany, A.; Mossa, A.; Junier, I.; Ritort, F. Experimental free-energy measurements of kinetic molecular states using fluctuation theorems. Nat. Phys. 2012, 8, 688. [Google Scholar] [CrossRef]
- Koch, S.J.; Shundrovsky, A.; Jantzen, B.C.; Wang, M.D. Probing protein-DNA interactions by unzipping a single DNA double helix. Biophys. J. 2002, 83, 1098–1105. [Google Scholar] [CrossRef] [Green Version]
- Camunas-Soler, J.; Alemany, A.; Ritort, F. Experimental measurement of binding energy, selectivity, and allostery using fluctuation theorems. Science 2017, 355, 412–415. [Google Scholar] [CrossRef] [Green Version]
- Suren, T.; Rutz, D.; Mößmer, P.; Merkel, U.; Buchner, J.; Rief, M. Single-molecule force spectroscopy reveals folding steps associated with hormone binding and activation of the glucocorticoid receptor. Proc. Natl. Acad. Sci. USA 2018, 115, 11688–11693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bizarro, C.V.; Alemany, A.; Ritort, F. Non-specific binding of Na+ and Mg2+ to RNA determined by force spectroscopy methods. Nucleic Acids Res. 2012, 40, 6922–6935. [Google Scholar] [CrossRef] [Green Version]
- Calladine, C.R.; Drew, H. Understanding DNA: The Molecule and How It Works; Academic Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Saenger, W. Principles of Nucleic Acid Structure; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Yakovchuk, P.; Protozanova, E.; Frank-Kamenetskii, M.D. Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Res. 2006, 34, 564–574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DeVoe, H.; Tinoco, I., Jr. The stability of helical polynucleotides: Base contributions. J. Mol. Biol. 1962, 4, 500–517. [Google Scholar] [CrossRef]
- Crothers, D.M.; Zimm, B.H. Theory of the melting transition of synthetic polynucleotides: Evaluation of the stacking free energy. J. Mol. Biol. 1964, 9, 1–9. [Google Scholar] [CrossRef]
- Breslauer, K.J.; Frank, R.; Blöcker, H.; Marky, L.A. Predicting DNA duplex stability from the base sequence. Proc. Natl. Acad. Sci. USA 1986, 83, 3746–3750. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.F.; Benight, A.S. How many numbers are required to specify sequence-dependent properties of polynucleotides? Biopolymers 1992, 32, 1679–1693. [Google Scholar] [CrossRef]
- Licinio, P.; Guerra, J.C.O. Irreducible representation for nucleotide sequence physical properties and self-consistency of nearest-neighbor dimer sets. Biophys. J. 2007, 92, 2000–2006. [Google Scholar] [CrossRef] [Green Version]
- Gray, D.M.; Tinoco, I., Jr. A new approach to the study of sequence-dependent properties of polynucleotides. Biopolymers 1970, 9, 223–244. [Google Scholar] [CrossRef]
- Mathews, D.H.; Sabina, J.; Zuker, M.; Turner, D.H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999, 288, 911–940. [Google Scholar] [CrossRef] [Green Version]
- Walter, A.E.; Turner, D.H.; Kim, J.; Lyttle, M.H.; Müller, P.; Mathews, D.H.; Zuker, M. Coaxial stacking of helixes enhances binding of oligoribonucleotides and improves predictions of RNA folding. Proc. Natl. Acad. Sci. USA 1994, 91, 9218–9222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freier, S.M.; Kierzek, R.; Jaeger, J.A.; Sugimoto, N.; Caruthers, M.H.; Neilson, T.; Turner, D.H. Improved free-energy parameters for predictions of RNA duplex stability. Proc. Natl. Acad. Sci. USA 1986, 83, 9373–9377. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Severino, A.; Monge, A.M.; Rissone, P.; Ritort, F. Efficient methods for determining folding free energies in single-molecule pulling experiments. J. Stat. Mech. Theory Exp. 2019, 2019, 124001. [Google Scholar] [CrossRef] [Green Version]
- Woodside, M.T.; Anthony, P.C.; Behnke-Parks, W.M.; Larizadeh, K.; Herschlag, D.; Block, S.M. Direct measurement of the full, sequence-dependent folding landscape of a nucleic acid. Science 2006, 314, 1001–1004. [Google Scholar] [CrossRef] [Green Version]
- Forns, N.; de Lorenzo, S.; Manosas, M.; Hayashi, K.; Huguet, J.M.; Ritort, F. Improving signal/noise resolution in single-molecule experiments using molecular constructs with short handles. Biophys. J. 2011, 100, 1765–1774. [Google Scholar] [CrossRef] [Green Version]
- Bustamante, C.; Marko, J.; Siggia, E.; Smith, S. Entropic elasticity of λ-phage DNA. Proc. Nati. Acad. Sci. USA 1991, 88, 10009. [Google Scholar] [CrossRef] [Green Version]
- Lipfert, J.; Skinner, G.M.; Keegstra, J.M.; Hensgens, T.; Jager, T.; Dulin, D.; Köber, M.; Yu, Z.; Donkers, S.P.; Chou, F.C.; et al. Double-stranded RNA under force and torque: Similarities to and striking differences from double-stranded DNA. Proc. Natl. Acad. Sci. USA 2014, 111, 15408–15413. [Google Scholar] [CrossRef] [Green Version]
- Tan, Z.J.; Chen, S.J. RNA helix stability in mixed Na+/Mg2+ solution. Biophys. J. 2007, 92, 3615–3632. [Google Scholar] [CrossRef] [Green Version]
- Owczarzy, R.; Moreira, B.G.; You, Y.; Behlke, M.A.; Walder, J.A. Predicting stability of DNA duplexes in solutions containing magnesium and monovalent cations. Biochemistry 2008, 47, 5336–5353. [Google Scholar] [CrossRef] [Green Version]
- Lipfert, J.; Doniach, S.; Das, R.; Herschlag, D. Understanding nucleic acid–ion interactions. Annu. Rev. Biochem. 2014, 83, 813–841. [Google Scholar] [CrossRef] [Green Version]
- Markham, N.R.; Zuker, M. DINAMelt web server for nucleic acid melting prediction. Nucleic Acids Res. 2005, 33, W577–W581. [Google Scholar] [CrossRef] [PubMed]
- Markham, N.; Zuker, M.; Keith, J. UNAFold: Software for nucleic acid folding and hybridization. Bioinformatics 2008, 2, 3–31. [Google Scholar]
- Montanari, A.; Mézard, M. Hairpin formation and elongation of biomolecules. Phys. Rev. Lett. 2001, 86, 2178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dessinges, M.N.; Maier, B.; Zhang, Y.; Peliti, M.; Bensimon, D.; Croquette, V. Stretching single stranded DNA, a model polyelectrolyte. Phys. Rev. Lett. 2002, 89, 248102. [Google Scholar] [CrossRef]
- Viader-Godoy, X.; Manosas, M.; Ritort, F. Sugar-Pucker Force-Induced Transition in Single-Stranded DNA. Int. J. Mol. Sci. 2021, 22, 4745. [Google Scholar] [CrossRef]
- Collin, D.; Ritort, F.; Jarzynski, C.; Smith, S.B.; Tinoco, I.; Bustamante, C. Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature 2005, 437, 231–234. [Google Scholar] [CrossRef]
- De Lorenzo, S.; Ribezzi-Crivellari, M.; Arias-Gonzalez, J.R.; Smith, S.B.; Ritort, F. A temperature-jump optical trap for single-molecule manipulation. Biophys. J. 2015, 108, 2854–2864. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.N.; Vincent, A.; Neupane, K.; Yu, H.; Wang, F.; Woodside, M.T. Experimental validation of free-energy-landscape reconstruction from non-equilibrium single-molecule force spectroscopy measurements. Nat. Phys. 2011, 7, 631–634. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rissone, P.; Ritort, F. Nucleic Acid Thermodynamics Derived from Mechanical Unzipping Experiments. Life 2022, 12, 1089. https://doi.org/10.3390/life12071089
Rissone P, Ritort F. Nucleic Acid Thermodynamics Derived from Mechanical Unzipping Experiments. Life. 2022; 12(7):1089. https://doi.org/10.3390/life12071089
Chicago/Turabian StyleRissone, Paolo, and Felix Ritort. 2022. "Nucleic Acid Thermodynamics Derived from Mechanical Unzipping Experiments" Life 12, no. 7: 1089. https://doi.org/10.3390/life12071089
APA StyleRissone, P., & Ritort, F. (2022). Nucleic Acid Thermodynamics Derived from Mechanical Unzipping Experiments. Life, 12(7), 1089. https://doi.org/10.3390/life12071089






