A Necessary Condition for Coexistence of Autocatalytic Replicators in a Prebiotic Environment
Abstract
:1. Introduction
2. Background
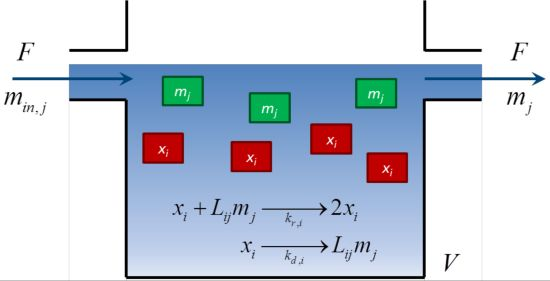
2.1. Mathematical Model of a Fed-Batch Bioreactor



2.2. A Mathematical Condition for Sustained Diversity






3. Analysis
| Variable | Description | Units | Value |
|---|---|---|---|
| x0,1 | Initial concentration, x1 | mol/m3 | 0.1 |
| x0,2 | Initial concentration, x2 | mol/m3 | 0.1 |
| m0,a | Initial concentration, ma | mol/m3 | 0.5 |
| m0,b | Initial concentration, mb | mol/m3 | 0.5 |
| min,a | Inlet concentration, ma | mol/m3 | 0.5 |
| min,b | Inlet concentration, mb | mol/m3 | 0.5 |
| F | Inlet flow rate | m3/s | 1 |
| V | Reactor volume | m3 | 1 |
| tf | Simulation time | s | 1 × 107 |
| Lia + Lib | Total replicator size | monomers | 20 |
4. Results
4.1. Growth of Replicators under a Constant Monomer Supply

 . Therefore, the linear replicator profiles are based on how the reaction orders, αij, and the composition parameters, Lij, are used to manage the shared monomer resources.
. Therefore, the linear replicator profiles are based on how the reaction orders, αij, and the composition parameters, Lij, are used to manage the shared monomer resources. 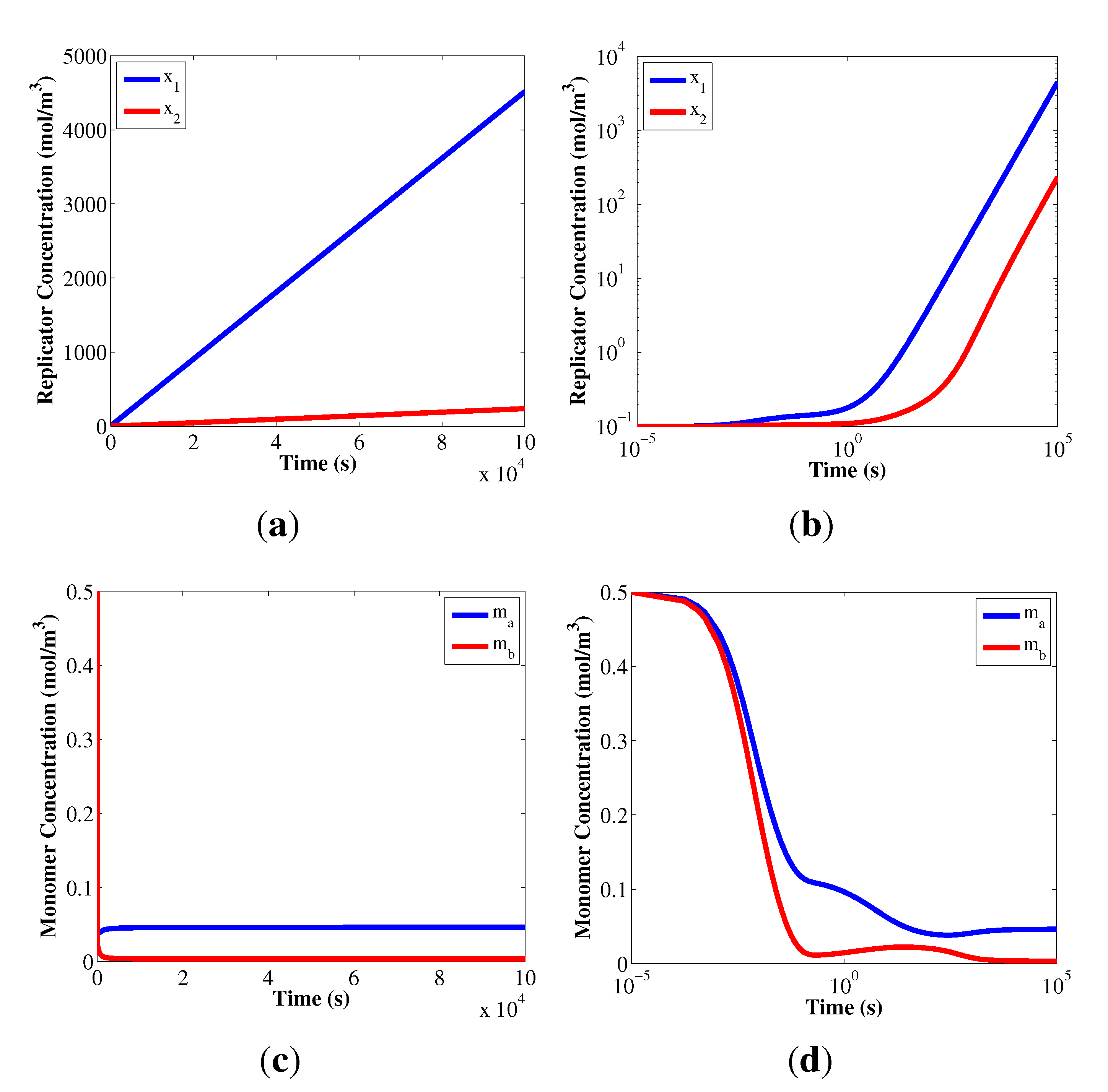
4.2. Condition of Coexistence for Autocatalytic Replicators
| Observed | Screening | Total | ||
|---|---|---|---|---|
| c1 < 0 c2 < 0 | c1 > 0, c2 < 0 c1 < 0, c2 > 0 | c1 > 0 c2 > 0 | ||
| Extinction | 1.87% | 34.89% | 0.00% | 36.76% |
| Single Winner | 0.00% | 53.96% | 0.83% | 54.79% |
| Coexistence | 0.00% | 0.00% | 0.90% | 0.90% |
| Extinction | Single Winner | Coexistence | Total |
|---|---|---|---|
| 2.18% | 3.19% | 0.00 | 5.27% |

| kr,1 = 4.3692 | kr,2 = 1.6605 |
| kd,1 = 4.16 × 10−4 | kd,2 = 4.83 × 10−4 |
| α1a = 0.2914 | α2a = 0.3585 |
| α1b = 2.6602 | α2b = 0.7387 |
5. Discussion
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Eigen, M.; Schuster, P. The hypercycle, a principle of natural self-organization. Part A: Emergence of the hypercycle. Naturwissenschaften 1977, 64, 541–565. [Google Scholar]
- Chen, I.A.; Nowak, M.A. From prelife to life: How chemical kinetics become evolutionary dynamics. Acc. Chem. Res. 2012, 45, 2088–2096. [Google Scholar] [CrossRef] [PubMed]
- Pross, A.; Khodorkovsky, V. Extending the concept of kinetic stability: Toward a paradigm for life. J. Phys. Org. Chem. 2004, 17, 312–316. [Google Scholar] [CrossRef]
- Lifson, S.; Lifson, H. A model of prebiotic replication: Survival of the fittest versus extinction of the unfittest. J. Theor. Biol. 1999, 199, 425–433. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.I.; Grover, M.A.; Hud, N.V. Universal sequence replication,reversible polymerization and early functional biopolymers: A model for the initiation of prebiotic sequence evolution. PLoS One 2012, 7, e34166. [Google Scholar] [CrossRef] [PubMed]
- Yarus, M. Darwinian behavior in a cold,sporadically fed pool of ribonucleotides. Astrobiology 2012, 12, 870–883. [Google Scholar] [CrossRef] [PubMed]
- King, G. Was there a prebiotic soup? J. Theor. Biol. 1986, 123, 493–498. [Google Scholar] [CrossRef]
- Chacon, P.; Nuno, J. Spatial dynamics of a model for prebiotic evolution. Phys. D 1995, 81, 398–410. [Google Scholar] [CrossRef]
- Li, X.; Zhan, Z.Y.J.; Knipe, R.; Lynn, D.G. DNA-catalyzed polymerization. J. Am. Chem. Soc. 2002, 124, 746–747. [Google Scholar] [CrossRef] [PubMed]
- Ura, Y.; Beierle, J.; Leman, L.; Orgel, L.; Ghadiri, M. Self-assembling sequence-adaptive peptide nucleic acids. Science 2009, 325, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Bean, H.; Anet, F.; Gould, I.; Hud, N. Glyoxylate as a backbone linkage for a prebiotic ancestor of RNA. Orig. Life Evol. B 2006, 36, 39–63. [Google Scholar] [CrossRef]
- Carnall, J.M.A.; Waudby, C.A.; Belenguer, A.M.; Stuart, M.C.A.; Peyralans, J.J.P.; Otto, S. Mechanosensitive self-replication driven by self-organization. Science 2010, 327, 1502–1506. [Google Scholar] [CrossRef] [PubMed]
- Hong, L.; Qi, X.; Zhang, Y. Dissecting the kinetic process of amyloid fiber formation through asymptotic analysis. J. Phys. Chem. B 2012, 116, 6611–6617. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, J.T.; Østergaard, J.; Rozlosnlk, N.; Gammelgaard, B.; Heegaard, N.H. Cu (II) mediates kinetically distinct, non-amyloidogenic aggregation of amyloid-β peptides. J. Biol. Chem. 2011, 286, 26952–26963. [Google Scholar]
- Morris, A.M.; Watzky, M.A.; Agar, J.N.; Finke, R.G. Fitting neurological protein aggregation kinetic data via a 2-Step,minimal/Ockhams razor model: The Finke-Watzky mechanism of nucleation followed by autocatalytic surface growth. Biochemistry 2008, 47, 2413–2427. [Google Scholar] [CrossRef] [PubMed]
- Martin, O.; Horvath, J.E. Biological evolution of replicator systems: Towards a quantitative approach. Orig. Life Evol. B 2013, 43, 151–160. [Google Scholar] [CrossRef]
- Szathmary, E.; Smith, J.M. From replicators to reproducers: The first major transitions leading to life. J. Theor. Biol. 1997, 187, 555–571. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Higgs, P.G. Origin of self-replicating biopolymers: Autocatalytic feedback can jump-start the RNA world. J. Mol. Evol. 2009, 69, 541–554. [Google Scholar] [CrossRef] [PubMed]
- Scheuring, I.; Szathmary, E. Survival of replicators with parabolic growth tendency and exponential decay. J. Theor. Biol. 2001, 212, 99–105. [Google Scholar] [CrossRef] [PubMed]
- Bailey, J.E.; Ollis, D.F. Biochemical Engineering Fundamentals, 2nd ed.; McGraw-Hill Company: New York, NY, USA, 1986; Chapter 9; p. 533. [Google Scholar]
- Nauman, E.B. Chemical Reactor Design,Optimization and Scaleup, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008; Chapter 12; p. 445. [Google Scholar]
- Wright, D.H. A simple,stable model of mutualism incorporating handling time. Am. Nat. 1989, 134, 664–667. [Google Scholar] [CrossRef]
- Hsu, S.B.; Hwang, T.W.; Kuang, Y. Rich dynamics of a ratio-dependent one-prey two-predators model. J. Math. Biol. 2001, 43, 377–396. [Google Scholar] [CrossRef] [PubMed]
- Xie, C.; Fan, M.; Zhao, W. Dynamics of a discrete stoichiometric two predators one prey model. J. Biol. Syst. 2010, 18, 649–667. [Google Scholar] [CrossRef]
- Ko, W.; Ahn, I. A diffusive one-prey and two-competing-predator system with a ratio-dependent functional response: I,long time behavior and stability of equilibria. J. Math. Anal. Appl. 2013, 397, 9–28. [Google Scholar] [CrossRef]
- Deck, C.; Jauker, M.; Richert, C. Efficient enzyme-free copying of all four nucleobases templated by immobilized RNA. Nat. Chem. 2011, 3, 603–608. [Google Scholar] [CrossRef] [PubMed]
- Luther, A.; Brandsch, R.; von Kiedrowski, G. Surface-promoted replication and exponential amplification of DNA analogues. Nature 1998, 396, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 4th ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2005; Chapter 12; pp. 833–834. [Google Scholar]
- Von Kiedrowski, G. Minimal replocator theory I: Parabolic versus exponential growth. Bioorg. Chem. Front. 1993, 3, 113–146. [Google Scholar]
- Szathmary, E.; Gladkih, I. Sub-exponential growth and coexistence of non-enzymatically replicating templates. J. Theor. Biol. 1989, 138, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, N.; Hogeweg, P. Evolutionary dynamics of RNA-like replicator systems: A bioinformatic approach to the origin of life. J. Mol. Evol. 2012, 9, 219–263. [Google Scholar]
- Takeuchi, N.; Hogeweg, P. Multilevel selection in models of prebiotic evolution II: A direct comparison of compartamentalization and spatial self-organization. PLoS Comp. Biol. 2009, 5, e1000542. [Google Scholar] [CrossRef]
- McKay, M.; Beckman, R.; Conover, W. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hernandez, A.F.; Grover, M.A. A Necessary Condition for Coexistence of Autocatalytic Replicators in a Prebiotic Environment. Life 2013, 3, 403-420. https://doi.org/10.3390/life3030403
Hernandez AF, Grover MA. A Necessary Condition for Coexistence of Autocatalytic Replicators in a Prebiotic Environment. Life. 2013; 3(3):403-420. https://doi.org/10.3390/life3030403
Chicago/Turabian StyleHernandez, Andres F., and Martha A. Grover. 2013. "A Necessary Condition for Coexistence of Autocatalytic Replicators in a Prebiotic Environment" Life 3, no. 3: 403-420. https://doi.org/10.3390/life3030403