Relativistic Signatures of Flux Eruption Events near Black Holes
Abstract
:1. Introduction
2. Toy Model
2.1. Description of the Model
2.2. Photon Ring Flux Ratios
3. GRMHD
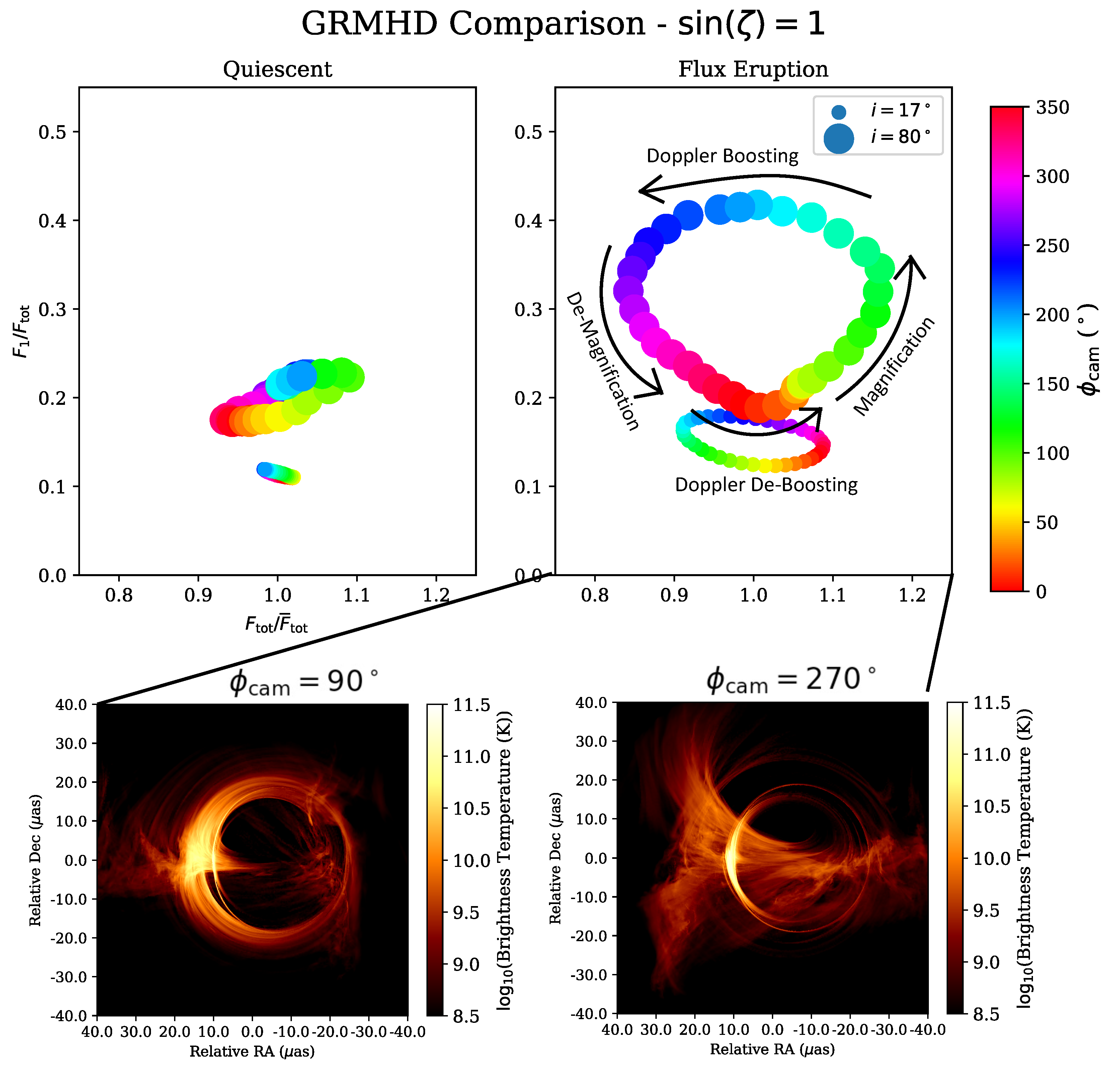
3.1. Procedure
3.2. Photon Ring Flux Ratios
4. Magnetic Fields
4.1. Background
4.2. Effects of Magnetic Field Direction on GRMHD PFR’s
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BH | Black Hole |
| EHT | Event Horizon Telescope |
| FOV | Field Of View |
| GRMHD | General Relativistic Magneto Hydro Dynamic |
| GRRT | General Relativistic Ray Tracing |
| ISCO | Inner Stable Circular Orbit |
| MAD | Magnetically Arrested Disk |
| ngEHT | next generation Event Horizon Telescope |
| PFR | Photon ring Flux Ratio |
| SMBH | Super Massive Black Hole |
| VLBI | Very Long Baseline Interferometry |
Appendix A. Magnetic Flux Eruptions in GRMHD

| 1 | We use natural units, i.e., , and the length and time units are both defined only in terms of the black hole mass M. |
| 2 | The effects of black hole spin on these conclusions are minimal, and these results are very similar for a Schwarzschild () black hole. In the Schwarzschild case, Doppler effects vanish completely, as the zero-angular momentum frame is motionless everywhere. |
| 3 | By flares, we refer to transient bright emission usually observed at wavelengths much smaller than sub-millimeter, e.g., X-ray flares in Sgr A[25]. |
References
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Luminet, J.P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228–235. [Google Scholar]
- de Vries, A. The apparent shape of a rotating charged black hole, closed photon orbits and the bifurcation set A4. Class. Quantum Gravity 2000, 17, 123–144. [Google Scholar] [CrossRef]
- Takahashi, R. Shapes and Positions of Black Hole Shadows in Accretion Disks and Spin Parameters of Black Holes. Astrophys. J. 2004, 611, 996–1004. [Google Scholar] [CrossRef]
- Beckwith, K.; Done, C. Extreme gravitational lensing near rotating black holes. Mon. Not. R. Astron. Soc. 2005, 359, 1217–1228. [Google Scholar] [CrossRef] [Green Version]
- Johannsen, T.; Psaltis, D. Testing the No-hair Theorem with Observations in the Electromagnetic Spectrum. II. Black Hole Images. Astrophys. J. 2010, 718, 446–454. [Google Scholar] [CrossRef] [Green Version]
- Gralla, S.E.; Holz, D.E.; Wald, R.M. Black hole shadows, photon rings, and lensing rings. Phys. Rev. D 2019, 100, 024018. [Google Scholar] [CrossRef] [Green Version]
- Johnson, M.D.; Lupsasca, A.; Strominger, A.; Wong, G.N.; Hadar, S.; Kapec, D.; Narayan, R.; Chael, A.; Gammie, C.F.; Galison, P.; et al. Universal interferometric signatures of a black hole’s photon ring. Sci. Adv. 2020, 6, eaaz1310. [Google Scholar] [CrossRef] [Green Version]
- Darwin, C. The Gravity Field of a Particle. Proc. R. Soc. Lond. Ser. A 1959, 249, 180–194. [Google Scholar] [CrossRef]
- Ohanian, H.C. The black hole as a gravitational “lens”. Am. J. Phys. 1987, 55, 428–432. [Google Scholar] [CrossRef]
- Broderick, A.E.; Pesce, D.W.; Tiede, P.; Pu, H.Y.; Gold, R. Hybrid Very Long Baseline Interferometry Imaging and Modeling with THEMIS. Astrophys. J. 2020, 898, 9. [Google Scholar] [CrossRef]
- Tiede, P.; Broderick, A.E.; Palumbo, D.C.M.; Chael, A. Measuring the Ellipticity of M 87* Images. arXiv 2022, arXiv:2210.13499. [Google Scholar]
- Porth, O.; Chatterjee, K.; Narayan, R.; Gammie, C.F.; Mizuno, Y.; Anninos, P.; Baker, J.G.; Bugli, M.; Chan, C.k.; Davelaar, J.; et al. The Event Horizon General Relativistic Magnetohydrodynamic Code Comparison Project. Astrophys. J. Suppl. Ser. 2019, 243, 26. [Google Scholar] [CrossRef] [Green Version]
- Gold, R.; Broderick, A.E.; Younsi, Z.; Fromm, C.M.; Gammie, C.F.; Mościbrodzka, M.; Pu, H.Y.; Bronzwaer, T.; Davelaar, J.; Dexter, J.; et al. Verification of Radiative Transfer Schemes for the EHT. Astrophys. J. 2020, 897, 148. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. Lett. 2019, 875, L5. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. Astrophys. J. Lett. 2022, 930, L16. [Google Scholar] [CrossRef]
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. Publ. Astron. Soc. Jpn. 2003, 55, L69–L72. [Google Scholar] [CrossRef] [Green Version]
- Igumenshchev, I.V.; Narayan, R.; Abramowicz, M.A. Three-dimensional Magnetohydrodynamic Simulations of Radiatively Inefficient Accretion Flows. Astrophys. J. 2003, 592, 1042–1059. [Google Scholar] [CrossRef]
- Ripperda, B.; Liska, M.; Chatterjee, K.; Musoke, G.; Philippov, A.A.; Markoff, S.B.; Tchekhovskoy, A.; Younsi, Z. Black Hole Flares: Ejection of Accreted Magnetic Flux through 3D Plasmoid-mediated Reconnection. Astrophys. J. Lett. 2022, 924, L32. [Google Scholar] [CrossRef]
- Wielgus, M.; Moscibrodzka, M.; Vos, J.; Gelles, Z.; Martí-Vidal, I.; Farah, J.; Marchili, N.; Goddi, C.; Messias, H. Orbital motion near Sagittarius A*. Constraints from polarimetric ALMA observations. Astron. Astrophys. 2022, 665, L6. [Google Scholar] [CrossRef]
- Narayan, R.; Chael, A.; Chatterjee, K.; Ricarte, A.; Curd, B. Jets in magnetically arrested hot accretion flows: Geometry, power, and black hole spin-down. Mon. Not. R. Astron. Soc. 2022, 511, 3795–3813. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First Sagittarius A* Event Horizon Telescope Results. II. EHT and Multiwavelength Observations, Data Processing, and Calibration. Astrophys. J. Lett. 2022, 930, L13. [Google Scholar] [CrossRef]
- Wielgus, M.; Marchili, N.; Martí-Vidal, I.; Keating, G.K.; Ramakrishnan, V.; Tiede, P.; Fomalont, E.; Issaoun, S.; Neilsen, J.; Nowak, M.A.; et al. Millimeter Light Curves of Sagittarius A* Observed during the 2017 Event Horizon Telescope Campaign. Astrophys. J. Lett. 2022, 930, L19. [Google Scholar] [CrossRef]
- Haggard, D.; Nynka, M.; Mon, B.; de la Cruz Hernandez, N.; Nowak, M.; Heinke, C.; Neilsen, J.; Dexter, J.; Fragile, P.C.; Baganoff, F.; et al. Chandra Spectral and Timing Analysis of Sgr A*’s Brightest X-ray Flares. Astrophys. J. 2019, 886, 96. [Google Scholar] [CrossRef] [Green Version]
- Abuter, R. et al. [GRAVITY Collaboration]. Constraining particle acceleration in Sgr A☆ with simultaneous GRAVITY, Spitzer, NuSTAR, and Chandra observations. Astron. Astrophys. 2021, 654, A22. [Google Scholar] [CrossRef]
- Gelles, Z.; Himwich, E.; Johnson, M.D.; Palumbo, D.C.M. Polarized image of equatorial emission in the Kerr geometry. Phys. Rev. D 2021, 104, 044060. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F. IPOLE—Semi-analytic scheme for relativistic polarized radiative transport. Mon. Not. R. Astron. Soc. 2018, 475, 43–54. [Google Scholar] [CrossRef] [Green Version]
- Gelles, Z.; Prather, B.S.; Palumbo, D.C.M.; Johnson, M.D.; Wong, G.N.; Georgiev, B. The Role of Adaptive Ray Tracing in Analyzing Black Hole Structure. Astrophys. J. 2021, 912, 39. [Google Scholar] [CrossRef]
- Liska, M.; Chatterjee, K.; Tchekhovskoy, A.; Yoon, D.; van Eijnatten, D.; Hesp, C.; Markoff, S.; Ingram, A.; van der Klis, M. H-AMR: A New GPU-accelerated GRMHD Code for Exascale Computing With 3D Adaptive Mesh Refinement and Local Adaptive Time-stepping. arXiv 2019, arXiv:1912.10192. [Google Scholar] [CrossRef]
- Narayan, R.; Palumbo, D.C.M.; Johnson, M.D.; Gelles, Z.; Himwich, E.; Chang, D.O.; Ricarte, A.; Dexter, J.; Gammie, C.F.; Chael, A.A.; et al. The Polarized Image of a Synchrotron-emitting Ring of Gas Orbiting a Black Hole. Astrophys. J. 2021, 912, 35. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Ricarte, A.; Gammie, C.; Narayan, R.; Prather, B.S. Probing Plasma Physics with Spectral Index Maps of Accreting Black Holes on Event Horizon Scales. arXiv 2022, arXiv:2202.02408. [Google Scholar]
- Boyce, H.; Haggard, D.; Witzel, G.; Fellenberg, S.v.; Willner, S.P.; Becklin, E.E.; Do, T.; Eckart, A.; Fazio, G.G.; Gurwell, M.A.; et al. Multiwavelength Variability of Sagittarius A* in 2019 July. Astrophys. J. 2022, 931, 7. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; Borrel, V.; et al. Fast Variability of Tera-Electron Volt γ Rays from the Radio Galaxy M87. Science 2006, 314, 1424–1427. [Google Scholar] [CrossRef] [Green Version]
- Broderick, A.E.; Loeb, A. Imaging bright-spots in the accretion flow near the black hole horizon of Sgr A*. Mon. Not. R. Astron. Soc. 2005, 363, 353–362. [Google Scholar] [CrossRef] [Green Version]
- Broderick, A.E.; Loeb, A. Imaging optically-thin hotspots near the black hole horizon of Sgr A* at radio and near-infrared wavelengths. Mon. Not. R. Astron. Soc. 2006, 367, 905–916. [Google Scholar] [CrossRef]
- Chael, A.A.; Johnson, M.D.; Narayan, R.; Doeleman, S.S.; Wardle, J.F.C.; Bouman, K.L. High-resolution Linear Polarimetric Imaging for the Event Horizon Telescope. Astrophys. J. 2016, 829, 11. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Stanzione, D.; West, J.; Evans, R.T.; Minyard, T.; Ghattas, O.; Panda, D.K. Frontera: The Evolution of Leadership Computing at the National Science Foundation. In Proceedings of the Practice and Experience in Advanced Research Computing, PEARC’20, Portland, OR, USA,, 26–30 July 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 106–111. [Google Scholar]
- Leung, P.K.; Gammie, C.F.; Noble, S.C. Numerical Calculation of Magnetobremsstrahlung Emission and Absorption Coefficients. Astrophys. J. 2011, 737, 21. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gelles, Z.; Chatterjee, K.; Johnson, M.; Ripperda, B.; Liska, M. Relativistic Signatures of Flux Eruption Events near Black Holes. Galaxies 2022, 10, 107. https://doi.org/10.3390/galaxies10060107
Gelles Z, Chatterjee K, Johnson M, Ripperda B, Liska M. Relativistic Signatures of Flux Eruption Events near Black Holes. Galaxies. 2022; 10(6):107. https://doi.org/10.3390/galaxies10060107
Chicago/Turabian StyleGelles, Zachary, Koushik Chatterjee, Michael Johnson, Bart Ripperda, and Matthew Liska. 2022. "Relativistic Signatures of Flux Eruption Events near Black Holes" Galaxies 10, no. 6: 107. https://doi.org/10.3390/galaxies10060107
APA StyleGelles, Z., Chatterjee, K., Johnson, M., Ripperda, B., & Liska, M. (2022). Relativistic Signatures of Flux Eruption Events near Black Holes. Galaxies, 10(6), 107. https://doi.org/10.3390/galaxies10060107





