Abstract
In the past few years, the Event Horizon Telescope (EHT) has provided the first-ever event horizon-scale images of the supermassive black holes (BHs) M87 and Sagittarius A (Sgr A). The next-generation EHT project is an extension of the EHT array that promises larger angular resolution and higher sensitivity to the dim, extended flux around the central ring-like structure, possibly connecting the accretion flow and the jet. The ngEHT Analysis Challenges aim to understand the science extractability from synthetic images and movies to inform the ngEHT array design and analysis algorithm development. In this work, we compare the accretion flow structure and dynamics in numerical fluid simulations that specifically target M87 and Sgr A, and were used to construct the source models in the challenge set. We consider (1) a steady-state axisymmetric radiatively inefficient accretion flow model with a time-dependent shearing hotspot, (2) two time-dependent single fluid general relativistic magnetohydrodynamic (GRMHD) simulations from the H-AMR code, (3) a two-temperature GRMHD simulation from the BHAC code, and (4) a two-temperature radiative GRMHD simulation from the KORAL code. We find that the different models exhibit remarkably similar temporal and spatial properties, except for the electron temperature, since radiative losses substantially cool down electrons near the BH and the jet sheath, signaling the importance of radiative cooling even for slowly accreting BHs such as M87. We restrict ourselves to standard torus accretion flows, and leave larger explorations of alternate accretion models to future work.
1. Introduction
With the advent of the Event Horizon Telescope ([EHT; [1,2]), imaging the near-horizon structure of supermassive black holes (BHs) is now a reality. The primary targets of the EHT and the future next-generation EHT (or ngEHT1) are M87 (the supermassive BH in the elliptical galaxy M87; [1]) and Sgr A in the Galactic Center [2], which are two of the most well-studied low-luminosity active galactic nuclei. Extracting information about the event horizon-scale accretion flows in these two sources using the EHT’s enormous resolving power is an active area of research. With the ngEHT, we will achieve unprecedented levels of angular resolution and sensitivity to low-flux regions, with the dynamic range in flux expected to increase to ∼1000 compared to the EHT’s current dynamic range of ∼10 (e.g., [3]). This would enable us to investigate the BH shadow shape with higher precision as well as provide a crucial connection between the accretion flow and the jet launching region. The expected advances in sensitivity require deeper investigations of feature extraction from simulated synthetic reconstructions of BH systems. Hence, we designed the ngEHT analysis challenges 2 [4] to test our ability to capture the complex dynamics of gas and magnetic fields around M87 and Sgr A using the ngEHT reference array (e.g., [5]) with various analysis methods.
Black hole accretion and jet physics have been intensively studied over the past few decades (e.g., [6,7,8,9,10,11,12,13,14,15]). In the context of M87 and Sgr A, we expect the accretion flow to be highly sub-Eddington, radiatively inefficient, and geometrically thick, popularly known as radiatively inefficient accretion flows (RIAFs). This accretion flow solution has been used to successfully model the multiwavelength spectrum of Sgr A (e.g., [16]). On the other hand, semi-analytical models of jets are preferred to explain the spectrum of M87 (e.g., [17]). Thus, these two sources already provide a means to probe two different components of BH accretion, namely, the inner accretion flow structure and turbulence in Sgr A and the prominent jet feature in M87. The first three EHT numerical simulation papers [18,19,20] already provide us with important clues about the horizon-scale conditions of these BH systems based on numerical simulations: (1) these BHs probably have non-zero spin, (2) the accretion disk is expected to have colder electrons than the jet sheath, and (3) the observations favor the presence of dynamically important magnetic fields close to the BH. All of these results point us toward the magnetically arrested disk (MAD; [10,21]) state, an accretion mode where the BH magnetosphere becomes over-saturated with magnetic flux and exhibits quasi-periodic explosions of vertical magnetic field bundles. MAD flows around spinning BHs also have powerful relativistic jets, where the jet power can exceed the input accretion power [13], which is a definite signature of BH spin energy extraction via the Blandford and Znajek [22] process.
Building on the semi-analytical RIAF models, the time-dependent general relativistic magneto-hydrodynamic (GRMHD) simulations have become important tools for deciphering BH accretion physics in a variety of astrophysical systems (e.g., [11,13,23,24,25,26,27]). Indeed, the EHT regularly uses the libraries of GRMHD simulations to model the observed horizon-scale BH images of M87 and Sgr A as well as larger-scale jet images (such as for Centaurus A; [28]) in order to constrain the time-variable plasma properties. In designing the ngEHT reference array, it is therefore crucial to use GRMHD simulations for understanding the attainability of specific science goals, such as resolving the photon ring and the disk-jet connection region as well as tracing out time-variable features via the ngEHT analysis challenges.
In this work, we discuss the numerical fluid simulations that were used as source models for the ngEHT analysis challenges. In particular, our objective is to compare between the models that incorporate increasingly complicated levels of accretion and electron physics, focusing on M87 and Sgr A. Our model set consists of a time-dependent shearing hotspot stitched to a steady-state RIAF solution, two standard GRMHD simulations of MAD accretion flows, a GRMHD MAD simulation with electron heating via incorporating two-temperature physics, and a fully radiative, two-temperature, GRMHD MAD simulation. We describe the equations and setup of our numerical models in Section 2, show our comparison results in Section 3, and, finally, conclude in Section 4.
2. Numerical Simulations
In this section, we provide a brief description of the semi-analytical stationary RIAF and shearing hotspot model as well as the (two-temperature/radiative) GRMHD simulations used for the ngEHT analysis challenges.
2.1. RIAF + Hotspot Solutions
RIAF models attempt to describe the time and azimuthally averaged appearance of accretion flows. This is performed using a set of building blocks. The specific RIAF models used in the challenges are based on Yuan et al. [16], Broderick and Loeb [29], Broderick and McKinney [30] approach. We decompose the accretion flow into a set of phenomenological models that describe the electron density, temperature, magnetic field, and velocity profile. We have a cylindrical coordinate system . The electron density profile is defined in terms of the cylindrical radius and vertical displacement , and is provided by
where X denotes the population of electrons. The disk height h is set to unity for this work. For the challenge dataset, we included both thermal synchrotron emitting (, and non-thermal synchrotron () emitting electrons. The thermal electrons have and , while the non-thermal electrons are provided by , . These numbers are from Tiede et al. [31] and are set to match the best-fit parameters for the Sgr A spectrum from Broderick et al. [32] and Broderick et al. [33].
The temperature profile of the thermal electrons is also provided by a radial power law with a Gaussian envelope describing the height:
where, for the challenge data, we set K.
Following Pu et al. [34], we define the gas pressure by assuming that the ultra-relavistic protons are in roughly virial equilibrium with the gravitational force providing:
where , G, and are the proton mass, gravitational constant, and the black hole mass.
For the local magnetic field, we then assume a constant plasma, which, combined with Equation (3), provide us the magnetic field strength. The orientation of the magnetic field is then provided by a purely toroidal configuration, relative to the plasma observer. Finally, we extract the emission and absorption coefficients from the synchrotron self-absorption model in Broderick and Blandford [35] for both the thermal and non-thermal synchrotron electrons. For the non-thermal electrons, we use a power law prescription with radiation coefficients from Jones and O’Dell [36], and a photon spectral power law index of 1.25 (see [31] for more details).
We follow the velocity field prescription from Pu et al. [34] to describe the accretion flow dynamics. Using the notation from Tiede et al. [31], the velocity field is provided by
where denotes the Keplerian velocity field, is the free-fall velocity field, and and , i.e., the hotspot rotates with Keplerian angular velocity and is weakly free-falling. For , we have a Keplerian orbit, whereas, for , we have free-fall. The remaining component is provided by the normalization condition . The radial component outside the inner stable circular orbit (ISCO) is as the disk is in steady-state. However, inside the ISCO, we use plunging geodesics that are specified by matching the angular momentum and energy at the ISCO.
The hotspot evolution follows the model from Tiede et al. [31] (also see [29]), where we assume that the hotspot travels passively along the accretion flow velocity field Equation (4). This implies that the equation of motion is provided by the conservation of particle number Equation (6). For the emission, we assume a non-thermal synchrotron hotspot, with an initial Gaussian density profile
where we have set , hotspot size , and is the displacement from the hotspot center.
2.2. GRMHD Simulations
Over the previous two decades, multiple GRMHD codes have been developed and utilized to model black hole accretion and jet launching physics over long dynamical timescales. The wide usage of GRMHD simulations is particularly encouraging since this allows for verification of code-specific numerical choices that users usually have to make even while solving the same base set of GRMHD equations. Indeed, recently, there was a community-wide effort to benchmark these codes against each other for a standard problem: evolving a weakly magnetized torus of gas around a spinning black hole [26]. It was found that these codes largely provide similar solutions, though some disk quantities remain unconverged with increasing grid resolutions, suggesting more investigation is required. For this work, we employ three different GRMHD codes to probe black hole accretion, increasing the complexity of the equations solved at each step: (1) single fluid GRMHD simulations from the H-AMR code [37], (2) a two-temperature single fluid GRMHD simulation from the BHAC code [38], and (3) a two-temperature radiative GRMHD simulation from the KORAL code [39].
First, we describe the set of GRMHD Equations (e.g., from [23,26]). We have the conservation of particle number and energy-momentum:
Here, is the rest-mass gas density and can also be written in the form of , where m is the mean rest–mass per particle and n is the particle number density. We also have the four-velocity , stress–energy tensor , metric determinant , and the metric connection . Note that the index t refers to the temporal component of the vector or tensor and i denotes the spatial indices.
The stress-energy tensor is provided as
where and are the gas internal energy and pressure, related by the ideal gas equation: assuming a gas adiabatic index . We also have the magnetic pressure and the magnetic field 4-vector , which can be defined in terms of the magnetic field 3-vector :
Here, we included a factor of into the definition of . We evolve the magnetic field using the spatial components of the induction equation,
while the temporal component provides the no monopoles constraint,
These equations are numerically integrated in the conservative form [23] to obtain the physically relevant quantities , , , and . We refer the reader to the corresponding code papers for more information on the numerical techniques used to evolve these equations over space and time.
In this work, we use two GRMHD simulations performed with the H-AMR code, one targeting M87 and the other Sgr A. These simulations employ logarithmic Kerr–Schild coordinates and the grid resolutions are for the M87 simulation and for the Sgr A simulation. All the simulations in this work adopt the geometrical unit convention, and using , normalizing the length scale to the gravitational radius . The M87 GRMHD simulation evolves a MAD flow around a black hole with spin . The Sgr A model also simulates a MAD flow but around a black hole with spin . H-AMR uses outflowing radial boundary conditions (BCs), transmissive polar BCs, and periodic azimuthal BCs (for more details, see [40]).
Since GRMHD simulations are scale-free, we determine the gas density code-to-CGS units conversion factor (hereafter, “density scaling”) by raytracing the simulation at 230 GHz for a target source and flux. We use the general relativistic ray-tracing codes BHOSS [41] and IPOLE [42] to compute images at 230 GHz and set the compact flux to be approximately 0.5 Jy for M87 [1] and 2.4 Jy for Sgr A [2]. We use the black hole masses and distances of and Mpc for M87 (e.g., [18,43] and references therein) and and kpc for Sgr A [20,44,45].
GRMHD simulations evolve a single temperature fluid. At the low accretion rates seen in M87 and Sgr A, Coulomb coupling between ions and electrons is inefficient and, therefore, the two particle species are not in thermal equilibrium. Since ions are much heavier than electrons, the ions dominate the single fluid thermodynamics evolved in GRMHD simulations. Hence, to calculate the radiative output from GRMHD simulations, we calculate the electron temperature using sub-grid models such as the prescription [46] based on local gas plasma- ():
For the ngEHT analysis challenges, we select values of 160 and 40 and source inclinations of and for the M87 and Sgr A simulations, respectively. We assume a thermal relativistic Maxwell–Jüttner distribution for describing the electron energy distribution in the Sgr A model, and a hybrid thermal+non-thermal distribution (e.g., [47,48]) for the M87 model. The model images are shown in Roelofs et al. [4].
2.3. Two-Temperature Physics
Two-temperature GRMHD (or 2t-GRMHD) simulations (e.g., [49,50]) evolve the ion and electron entropy equation separately and, hence, provide the ion and electron temperature in a self-consistent manner. The main advantage of this method is that we remove the electron temperature as a free parameter when constructing images. However, we do have to make a choice about the sub-grid prescription that determines the fraction of local dissipative energy that heats the electrons. There are two heating mechanisms that are thought to be applicable to global accretion flows: turbulent heating [51,52], and magnetic reconnection [53,54]. For the ngEHT analysis challenges, we focus only on one simulation with reconnection heating, from Mizuno et al. [55], as heating via magnetic reconnection in equatorial current sheets formed in magnetically arrested flows, captured by the Rowan et al. [54] heating model, is arguably more important than heating via small-scale turbulent eddies that are more prevalent in weakly magnetized disks.
We assume that the number densities and velocities of ions and electrons are equal, i.e., and , thus maintaining charge neutrality. The electron entropy equation is provided as
where the electron entropy is , with and as the electron pressure and adiabatic index. The total heating rate Q is calculated by comparing the total internal energy of the gas and the internal energy obtained from the electron entropy conservation Equation (see [49] for more details). The fraction of dissipative heating that contributes to electron heating is provided by . For this particular simulation, is designed to capture electron/ion heating via magnetic reconnection from Rowan et al. [54]:
where , defined using the hot gas magnetization and the specific gas enthalpy .
The 2t-GRMHD simulation from Mizuno et al. [55] assumes modified Kerr–Schild coordinates and a black hole spin of . The grid resolution is . The accretion mode is of a magnetically arrested flow and the simulation is raytraced (using BHOSS) once the near-horizon flow has reached steady state. The target source is M87, assuming a black hole mass of and distance of 16.9 Mpc [1]. The accretion rate is normalized such that the 230 GHz compact flux density is 0.8 Jy. We assume a thermal electron distribution everywhere except in the jet sheath where we adopt a distribution. More details about the image are provided in Roelofs et al. [4].
2.4. Radiative GRMHD
Two temperature GRMHD simulations do not include radiative cooling and, hence, are thought to be appropriate for low luminosity supermassive black holes such as M87 and Sgr A. To verify this assumption, we consider a two-temperature radiative GRMHD (2t-GRRMHD hereafter) simulations from Chael et al. [25]. This simulation accounts for self-consistent radiation physics, incorporating both particle heating via magnetic reconnection (as in Section 2.3) and radiative cooling via bremsstrahlung, synchrotron, Compton, and Coulomb losses. The simulation is run using the 2t-GRRMHD code KORAL [39,56,57], which evolves a two-temperature magnetized fluid and treats the radiation field as a second fluid [58]. The conservation equations solved in 2t-GRRMHD are different from that of GRMHD:
where is the frequency-integrated radiation field, defined as,
Here, the radiation field is described by its rest-frame energy density and four-velocity following the M1 closure scheme. The ion and electron entropy equations are
where is the dissipative heating rate and is the Coulomb coupling rate that captures the exchange of energy between ions and electrons. The heating fraction is from Rowan et al. [54] (see Chael et al. [57] for more details), same as the 2t-GRMHD simulation. Finally, G is the radiative cooling rate [39]. For further details about the equations, see Sądowski et al. [39], Chael et al. [57], Sądowski et al. [58].
The simulation assumes a black hole spin of and mass , targeting M87. The gas density is scaled to physical CGS units such that the compact emission at 230 GHz is roughly 0.98 Jy [59,60]. The simulation uses modified Kerr–Schild coordinates with a grid resolution of . See Chael et al. [25] for more details about the simulation, while not utilized for the ngEHT analysis challenges, we included this simulation in this work since this model captures the coupling between gas and radiation, necessary for black holes accreting close the Eddington limit. Further, this model has been used in previous ngEHT reference array papers [3,5].
3. Results
We perform a series of comparisons focused on the time-evolution of horizon-scale quantities and radial dependence of disk and jet properties. The diagnostics are chosen such that any trends we find can inform EHT/ngEHT science applications, such as horizon-scale morphology and variability of the accretion flow. Further, the quantities are similar to those reported in the GRMHD code comparison project [26] and, thus, can be directly compared. There is a total of five models: three (2t-radiative) GRMHD simulations targeting M87 *, and one RIAF solution and one GRMHD simulation for Sgr A *. We further note that all three numerical simulations of M87 * have the same BH spin, favoring direct comparisons of the horizon-scale gas properties.
3.1. Temporal Behavior of Horizon Fluxes
We calculate the mass, magnetic, angular momentum and energy fluxes in the radial direction as follows:
where all quantities are calculated at the event horizon radius . We note that there could be a substantial contribution of density floors when calculating the mass accretion rate for MAD systems. However, this radius was chosen for simplicity when comparing to previous simulations in the literature. Figure 1 shows the mass accretion rate in units of solar masses per year (/yr), the dimensionless magnetic flux , the outflow power , and the specific angular momentum flux for simulations targeting M87 * and Sgr A *. The RIAF solution being a steady-state solution is excluded from this section (though the hotspot evolves with time). The quantities from the 2t-GRRMHD simulation are only shown for , i.e., the time period over which the simulation was raytraced in Chael et al. [25]. Remarkably, despite the difference in electron the physics complexity, the simulations behave very similarly. The factor of 2 difference in between the M87 non-radiative simulations and the 2t-GRRMHD simulation can be explained by the lower electron temperatures in the near-horizon accretion flow due to radiative cooling (see Section 3.2) as well as the higher 230 GHz flux normalization used for the radiative model.
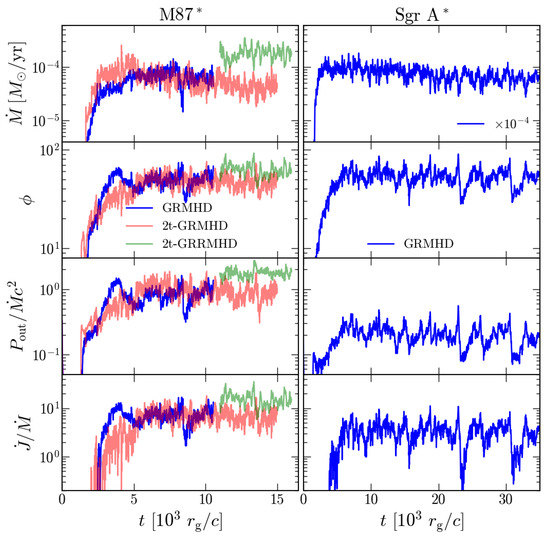
Figure 1.
We show the mass accretion rate , dimensionless magnetic flux , the outflow efficiency , and specific radial flux of the angular momentum over time. Values are calculated at the event horizon.
The accretion rate in all simulations show large variation with quasi-periodic sharp drops. These drops in occur due to the emergence of magnetic flux eruptions, a characteristic feature of the magnetically arrested disks [61,62,63,64]. These eruptions also lower the value of since magnetic flux bundles escape from the vicinity of the BH, carrying away the magnetic flux accumulated in the BH magnetosphere. We see that often crosses the magnetic flux saturation value of 50 [13], overwhelming the BH magnetosphere with strong magnetic fields that eventually reconnect and trigger flux eruptions (see [63] for the detailed mechanism). Figure 2 shows a series of equatorial snapshots from the M87 2t-GRMHD simulation where we follow a particular magnetic flux eruption by the rotating gas that is hot ( K), has low density ( in code units), and primarily consists of vertical field lines. As these field line bundles move out and interact with the disk, they (1) hinder accretion, lowering , (2) remove magnetic flux from near the BH, lowering the jet power, and (3) push gas outwards, reducing the inward angular momentum flux. Curiously, we see larger drops in the specific angular momentum flux for the Sgr A GRMHD model. This is possibly due to the smaller BH spin ( as opposed to for the M87 models) as the weakly powered jet does not carry away angular momentum as efficiently as the higher BH spin models and flux eruptions play a bigger role in regulating disk angular momentum transport. Additionally, the reconnection events that trigger these eruptions accelerate electrons to higher energies, and are, thus, crucial for understanding flare activity in BH sources.
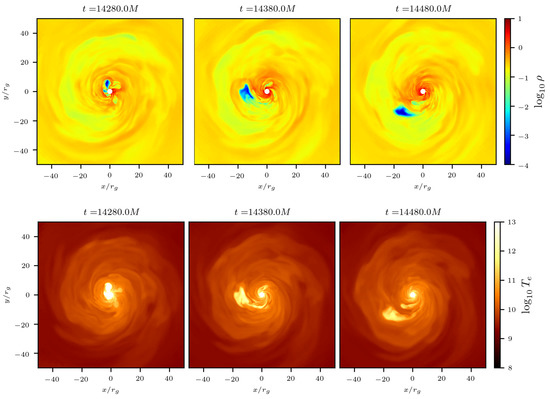
Figure 2.
We show equatorial cross-sections of gas density (in arbitrary code units) and electron temperature (in Kelvin) during a magnetic flux eruption in the 2t-GRMHD simulation of M87. Magnetic flux eruptions, a characteristic feature of magnetically arrested disks, eject bundles of vertical magnetic fields filled with relativistically hot, low-density plasma. These flux bundles spiral around the black hole and may be responsible for high-energy flares [63]. The time unit M is equivalent to .
To quantify the time-variability of the horizon-fluxes, we calculate the modulation index MI, which is defined as the ratio of the standard deviation and the mean of the quantity over time [20]. We show the MI for the different fluxes in Table 1. The MI() is usually a good proxy for the variability of the sub-millimeter (sub-mm) emission in these slowly accreting optically thin black hole sources (e.g., [65]). The MI() values we see from the simulations are ∼0.23–0.29 and are larger than expected from Sgr A 230 GHz lightcurves (where MI ∼ 0.1; [66]). This suggests that careful analysis of the electron distribution function is needed to understand if we are substantially over-predicting the 230 GHz lightcurve variability. Further, in general, weakly magnetized accretion flows exhibit lower MI() values due to the absence of flux eruptions, which suggests that further study of the accretion mode in Sgr A is also necessary. It is encouraging to note that our MI values for and are consistent with the MI values from longer time-evolved GRMHD simulations of BHs in Narayan et al. [27], indicating that our simulations are sufficiently converged with respect to horizon-scale quantities.

Table 1.
GRMHD simulations considered in this work. Simulation grid resolution, simulation time period over which raytracing was performed, modulation index (MI) of the mass accretion rate , dimensionless magnetic flux , outflow efficiency , and the specific angular momentum flux for each GRMHD model. The MI is calculated over the final in runtime and at the event horizon (see Figure 1).
3.2. Disk-Averaged Quantities
Here, we calculate the disk-averaged properties of each model, namely gas density , thermal pressure , magnetic pressure , radial velocity , azimuthal velocity , angular momentum , disk scale height , ion temperature , and the electron temperature . We define disk-averaging of a quantity q as
where . Further definitions follow:
where and u are the adiabatic index and the internal energy of the gas.
Figure 3 and Figure 4 show the respective disk-averaged radial profiles for each model, including the Sgr A RIAF solution. The density profiles in the inner few tens of converge roughly to a profile, matching the RIAF density profile as well as the longer time-evolved MAD simulations [64]. The M87 2t-GRRMHD density is larger by a factor of ≈2 from the GRMHD/2t-GRMHD, as is expected from the difference in the mass accretion rate (Figure 1). The 2t-GRRMHD simulation exhibits a slightly more magnetized inflow within the inner , but, overall, the GRMHD simulations have a similar plasma- disk profile. The stronger magnetic field seen in the 2t-GRRMHD model could explain the higher values of the horizon magnetic flux seen in Figure 1. The RIAF model assumes a constant disk plasma-, (see Section 2.1), which is substantially higher when compared to the MAD GRMHD models. This value of plasma- is chosen in order to match the observed 230 GHz flux density of Sgr A. As we see from the disk scale height in Figure 4, the RIAF model has a much thicker disk than the GRMHD models, and, therefore, produces a lot more sub-mm emission even with a low electron temperature and weak magnetic field strength.
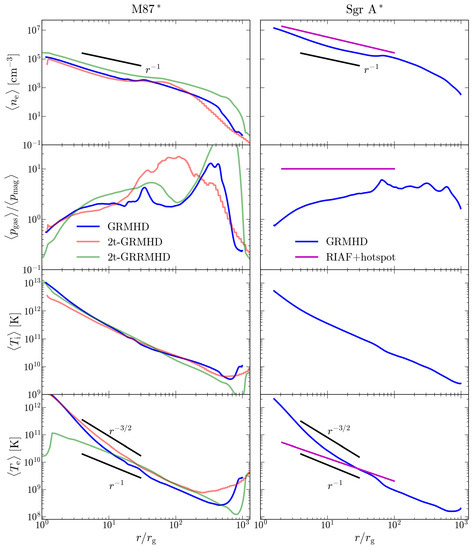
Figure 3.
We show the radial profiles of gas density , plasma, proton temperature , and electron temperature . Quantities are disk-averaged and time-averaged over the raytracing period.
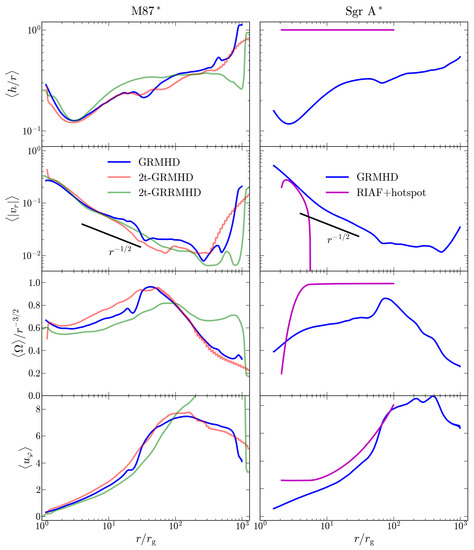
Figure 4.
We show the radial profiles of disk scale height , radial velocity , angular velocity , and specific angular momentum . Quantities are disk-averaged and time-averaged over the raytracing period.
Next, we see that the disk-averaged electron temperature in the 2t-GRRMHD M87 model is more than an order of magnitude lower than the other GRMHD models within the inner , but actually matches the Sgr A RIAF profile and has a shallower profile instead of . It is also interesting to note that the disk ion temperatures are very similar in all the GRMHD simulations shown here. Therefore, despite the same reconnection-driven heating mechanism captured in both the 2t-GRMHD and the 2t-GRRMHD models, the radiative cooling of hot electrons plays a crucial role in determining the eventual . Due to the low , the required accretion rate normalization is higher in the 2t-GRRMHD, as we noted in the previous subsection.
In Figure 4, we show the average disk scale height , the radial and angular velocities ( and and the specific angular momentum ). The MAD simulations all show very similar disk properties. The 0.1–0.3 with a sharp increase within where the inflow becomes vertically supported by strong poloidal magnetic fields. The radial velocity has a profile of , similar to the scaling relation found in ADAF solutions assuming a constant viscosity parameter [67,68]. The parameter profile depends on how magnetized the accretion flow is, with for the weakly magnetized flows and close to constant for the MAD-like flows (e.g., [64,69]). We also see highly sub-Keplerian angular velocity profiles in the GRMHD models, typical for magnetically supported disks. For the RIAF model, the RIAF disk is not infalling and has a constant Keplerian angular velocity. Instead, the hotspot, added to the RIAF solution, undergoes shearing and disappears into the BH with a radial velocity similar to the values found in the GRMHD MAD disks. This occurs because the hotspot is designed to travel along plunging geodesics (see Section 2.1), similar to rapid gas infall close to the BH in the GRMHD models. The angular momentum in the GRMHD models looks sub-Keplerian as expected for MADs.
3.3. Jet Properties
Here, we calculate the radial profiles of the jet half width and Lorentz factor :
where is the specific radial energy density and . We calculate the average jet radius by integrating over the total surface area covered by the two jets over a shell at a particular radius, and assume that the total surface area is approximately . We define the jet boundary as , i.e., the region over which the jet still remains highly energized. This definition of the jet boundary is quite similar to the condition , which is widely used in the literature (e.g., [27]). Since , our condition also incorporates regions where the jet might not be magnetically dominated but is relativistically hot or fast. Since we restrict our jet profiles to within , the jet radius is primarily determined by the jet magnetization.3
Figure 5 shows the jet radius and Lorentz factor as a function of the radial distance from the BH for the M87 GRMHD and 2t-GRRMHD models as well as the Sgr A GRMHD model. The M87 jet radius from our models matches the observed jet width from M87 (gray circles) quite well, with the radial profile roughly proportional to , which is the fitted powerlaw for the M87 jet [70], though the index value has also been reported to be slightly smaller in some works (0.57; [71,72]). The power law index of 0.625 is larger than that found using the condition from Narayan et al. [27], where the authors found a power law index of 0.428 for their MAD spin GRMHD model. It is possible that we find larger jet radii as we incorporate a part of the hot jet sheath region within our definition of (as suggested by Figure 7 in [73]). For the Sgr A model, we also find a similar profile. While there are no detections of an extended jet in Sgr A (e.g., [74]), semi-analytical and GRMHD models of Sgr A largely favor a jet component from a spinning BH (e.g., [20,75]).
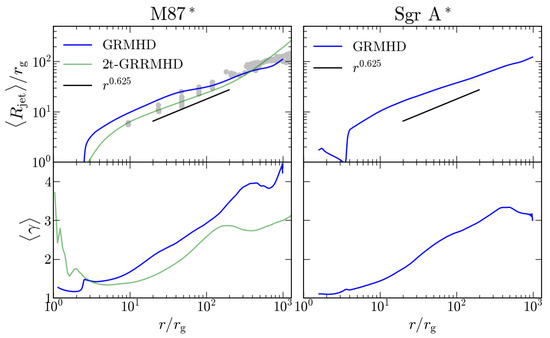
Figure 5.
We show the jet radius and the jet Lorentz factor from the M87 GRMHD and 2t-GRRMHD models, and the Sgr A GRMHD model. The gray circles indicates the deprojected jet radius of the M87 jet assuming a BH mass of and a source inclination of [70]. The data points are a compilation of various papers [59,60,71,77,78,79].
We also show the Lorentz factor in Figure 5. Mostly, the jets accelerate to 3–4 by in all of our GRMHD models. It is difficult to compare our profiles with values inferred from observations of the M87 jet (e.g., [76]) since our values are biased toward the jet spine while the observations generally capture the velocities of localized features in the sub-relativistic jet sheath/disk wind, especially at small distances from the BH. Indeed, both simulations and observations show that the jet Lorentz factor varies greatly as a function of jet radius (e.g., see [73]). We speculate that a better approach might be to calculate emissivity-weighted Lorentz factors in order to compare to the measured from M87. Since our focus is on the comparison between GRMHD simulations, we leave direct comparisons to observational data to future work.
3.4. Axisymmetrized Profiles
In the previous sections, we found that the largest differences between the GRMHD models occur in electron temperature distribution. Figure 6 shows the time and azimuthally averaged 2D vertical plots of gas density and electron temperature . We show the normalized so as to capture the relative change in the disk/wind density distribution, which would provide us information about the disk structure. The large difference in disk scale height is immediately apparent between the RIAF and the MAD GRMHD models (also see Figure 4). The presence of a prominent wide jet component in MADs squeezes the inner disk and pushes against the accretion flow, a feature which is not captured in the constant RIAF model. However, the RIAF model roughly reproduces the density profile of the disk midplane region, suggesting that the RIAF model could represent non/weakly jetted, quasi-spherical accretion flows quite well. For sources such as M87, where we see a prominent jet component, the density gradient in the vertical direction is expected to be steeper as strong magnetic stresses power winds carry gas away from the disk (e.g., [64]).
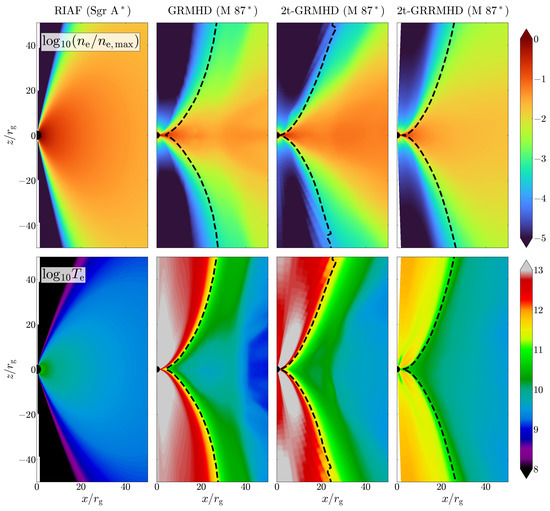
Figure 6.
We show t- and -averaged data: electron number density (top row) and temperature (bottom row). We also denote the jet boundary with (black lines). The time-averaging is performed over the for each model. RIAF plots are for Sgr A while the rest are for M87. The Sgr A GRMHD model produces similar plots of and as the M87 model, and, hence, we do not show it here.
Overall, the disk/wind density distribution among the GRMHD models look similar with small differences in the lateral extension of the wind region and the steepness of the vertical gradient in density. For example, if we compare the 2t-GRRMHD model with the other two simulations, the density in the wind region is larger in the radiative model. The reason for the shallow vertical density profile in the 2t-GRRMHD model is unclear since the weakly magnetized thick disk simulations tell us that radiative cooling would lead to the loss of gas pressure in the disk and would result in the disk collapsing to a relatively dense structure in the midplane (e.g., [80,81]). However, in the presence of strong poloidal magnetic fields, i.e., in the MAD state, the plasma- decreases to 0.2–1 in the disk midplane (see Figure 3, third row, left panel), and can reach even lower values in the upper layers of the accretion flow. The high magnetic pressure could help support the disk against collapse while sufficiently strong magnetic stresses could power disk winds. Such behavior is also seen in recent GRMHD simulations of near-Eddington, geometrically thin, strongly magnetized disks, where the inner disk (or corona) has a larger than the outer disk due to magnetic pressure support [82,83,84]. To verify how radiative cooling affects the inner disk/wind structure in highly sub-Eddington accretion flows such as M87 and Sgr A, we require longer 2t-GRRMHD simulations such that the disk is in an inflow–outflow equilibrium out to a radius of at least .
The 2D temperature plot of the RIAF model also looks vastly different in the inner disk () when compared to the GRMHD and 2t-GRMHD simulations, but is similar to the temperature distribution in the 2t-GRRMHD disk midplane (also seen in the plot of Figure 3). The RIAF model does not capture gas heating in the jet sheath region (the region just outside of the jet boundary indicated by the dashed line) and, therefore, drops as we move away from the midplane toward the poles. In the GRMHD models, the jet sheath is as hot, if not hotter, than the inner accretion flow as temperatures reach K. For the GRMHD simulation, the electron temperature is provided as a fraction of the fluid temperature, where the fraction depends on how magnetized the gas is in the region, as per the prescription from Equation (14). For the M87 model, we chose a value of 160 to have a jet-dominated sub-mm image. This choice of suppresses the electron temperature in the disk, focusing higher temperatures in the jet sheath. Comparing the GRMHD model with the 2t-GRMHD model, the jet sheath region exhibits very similar values, but the disk midplane is hotter by a factor of a few in the 2t-GRMHD model. We note that this difference in in the midplane is more noticeable in the 2D plot rather than in the disk-averaged profile shown in Figure 3 as the upper layers of the disk become substantially hotter in the GRMHD model.
For the radiative 2t-GRRMHD model, the inner regions of the disk are cooler as electrons heated by magnetic reconnection quickly cool via synchrotron and Compton losses. From Figure 3, the drop in for the 2t-GRRMHD model is shown to be as large as an order of magnitude when compared to the (2t-) GRMHD models. Another interesting feature is that the hot region ( K) in the jet sheath is much narrower in the 2t-GRRMHD model, which could have a significant bearing on the ray-traced image, possibly producing a thinner jet sheath. Finally, the difference in in the jet body between the GRMHD models is due to the different density/internal energy floor setups used by the corresponding codes. Since the gas in the jet sheath and the jet body undergo mixing due to boundary instabilities (e.g., [73,85]), it is possible that the choice of floors could affect the overall electron temperature in the jet sheath. Such a study is outside the scope of our paper and is left to future work.
3.5. Orbiting Hotspot in a RIAF Model
High-energy flares are commonly observed in AGNs, with GeV and MeV flares seen in M87 (e.g., [86,87]) and quasi-daily nIR and X-ray flares in Sgr A (e.g., [44,88,89,90,91,92,93,94]). A number of attempts have been performed to explain the origin of flaring, such as magnetic reconnection in turbulent gas flows in the disk and the jet [65,73,95,96,97] and magnetic flux eruptions [61,63,98,99]. For Sgr A, the semi-analytical models found that we require high-energy electrons, assumed to be accelerated via an ad hoc process such as a large magnetic reconnection event or shocks, to describe the large flaring events [100,101,102]. The near-infrared observations from the GRAVITY telescope provided further evidence for orbiting hotspot features in the accretion flow [103] that may be linked to acceleration events. It has also been recently shown that orbiting hotspots can be used to model double-peaked X-ray flares [94,104] and prominent Stokes Q-U loops in the sub-mm emission of Sgr A [105]. These results provide us with considerable motivation to test the capability of the ngEHT to detect hotspot formation in accretion flows around black holes.
Instead of isolating a particular magnetic flux eruption event in our simulations, we added a shearing hotspot to the RIAF solution as detailed in Section 2.1. Figure 7 shows the temporal evolution of the azimuthally averaged electron number density of the hotspot. We begin with a Gaussian distribution of gas that undergoes shearing as the gas falls in closer to the BH. The overall density normalization is much lower than in the RIAF disk since the optically thin hotspot gas produces a large enough non-thermal synchrotron emissivity. The hotspot is evolved over , but the gas distribution comes to a near-steady-state profile within the first , which is roughly one hour for Sgr A. The shearing of the hotspot gas has a significant impact on the evolution of the 230 GHz image [4,31]. From Figure 4 (right column), we see that the radial velocity matches the disk-averaged gas velocity from the GRMHD model, showing nearly free-fall speeds, while the azimuthal velocity becomes highly sub-Keplerian. The velocity profiles show that our hotspot model should be able to reproduce the expected hotspot motion from the GRMHD models, and is ideal for investigating multiwavelength flare lightcurves. Emami et al. [106], a companion paper, goes into further details about how current dynamical reconstruction techniques can be used to trace out the motion and morphology of the shearing hotspot in the context of ngEHT observations. These hotspot models and reconstruction methods would be integral in deciphering the more complex gas dynamics of magnetic flux eruption events in MADs, which have been shown to produce a significant variation in the image structure of M87 at 230 GHz (e.g., [107]).
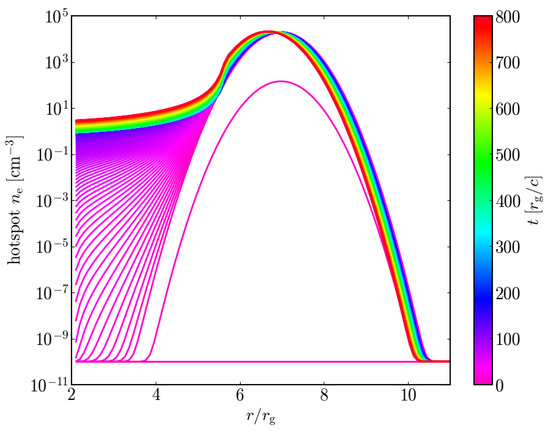
Figure 7.
We show the averaged hotspot electron number density as a function of radius and time. The hotspot falls into the BH and becomes sheared over time.
4. Conclusions
In this work, for the first time, we compare a series of numerical solutions with increasing complexity that were specifically constructed to understand the accretion flow around the supermassive black holes M87 and Sgr A. We include a time-independent radiatively inefficient accretion flow (RIAF) model as well as fully 3D GRMHD simulations of accreting black holes, incorporating the effects of electron heating and cooling losses via two-temperature and radiation physics. In addition, each of our simulations are run with different GRMHD codes, which is similar to the approach of another community-wide code comparison effort [26]. We found that the simulations exhibit remarkably similar properties given that the simulations incorporate varying levels of complexity in electron physics. The notable exception is the electron temperature, where radiative cooling decreases the temperature by a factor of ≲10 within the inner 10 gravitational radii, the region that produces the bulk of the 230 GHz emission in M87, one of the two primary targets of the EHT and the ngEHT (the other being Sgr A). The main goal of this work is to understand the variation in the underlying accretion flow and jet properties in our models since synthetic ray-traced images constructed from these models are used as “truth” images of M87 and Sgr A for the ngEHT Analysis Challenges [4]. The ngEHT Analysis Challenges are an effort to determine how much information about the accretion flow and jet dynamics we can glean from the proposed ngEHT reference array, and what modifications in the image reconstruction tools are necessarily required to decode future ngEHT observational data.
Our paper deals with numerical models designed to investigate hotspot evolution, turbulent inspiralling gas flows, and extended powerful jets, targeting M87 and Sgr A. We restricted our model set to the community-standard setup: a rotating, geometrically thick, optically thin torus of magnetized gas around a spinning black hole, which is the fiducial model choice of the EHT [18,19,20]. This model choice leaves out the exploration of multiple new setups of black hole accretion, such as quasi-spherical wind-fed inflows (e.g., [108,109]), strongly wind-fed accretion (e.g., [110,111]), geometrically thin accretion disks (e.g., [83,84,112]), puffy radiation-dominated super-Eddington disks (e.g., [113,114]), and misaligned accretion disks (e.g., [24,40,115,116]). Apart from varying the accretion mode, the high resolution of the images from EHT and ngEHT could potentially help distinguish between different space–time metrics [117]. To date, only a limited number of non-Kerr GRMHD simulations have only been performed (e.g., [118,119,120]). The future of numerical studies is bright, given their rising popularity in the astrophysics community and the increase in computational resources. The breadth of the current investigations in accretion physics would result in a plethora of variable structures that should be thoroughly studied keeping the observational capabilities of the ngEHT in mind.
Author Contributions
Conceptualization, K.C.; Methodology, K.C., P.T., Y.M. and F.R.; Software, K.C., A.C., P.T. and Y.M.; Formal analysis, K.C. and P.T.; Investigation, K.C., Y.M., R.E., C.F., A.R. (Angelo Ricarte), L.B., F.R., P.A., A.F., J.K., N.K., G.L., H.M., N.P., A.R. (Alexander Raymond), E.T. and J.V.; Writing—original draft, K.C. and P.T.; Writing—review & editing, K.C., A.C. and A.R. (Angelo Ricarte); Visualization, K.C.; Supervision, M.D.J. and S.S.D. All authors have read and agreed to the published version of the manuscript.
Funding
We thank the National Science Foundation (AST-1716536, AST-1935980 and AST-2034306) and the Gordon and Betty Moore Foundation (GBMF-10423) for financially supporting this work. This work was supported in part by the Black Hole Initiative, which is funded by grants from the John Templeton Foundation (JTF-61497) and the Gordon and Betty Moore Foundation (GBMF-8273) to Harvard University. K.C. is also supported in part by the Black Hole PIRE program (NSF grant OISE-1743747). R.E. acknowledges the support by the Institute for Theory and Computation at the Center for Astrophysics as well as grant numbers 21-atp21-0077, NSF AST-1816420, and HST-GO-16173.001-A for very generous supports. H.M. received financial support for this research from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. This research is supported by the DFG research grant “Jet physics on horizon scales and beyond” (Grant No. FR 4069/2-1), the ERC synergy grant “BlackHoleCam: Imaging the Event Horizon of Black Holes” (Grant No. 610058), and ERC advanced grant “JETSET: Launching, propagation and emission of relativistic jets from binary mergers and across mass scales” (Grant No. 884631). J.K. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany´s Excellence Strategy—EXC 2094—390783311. Y.M. is supported by the National Natural Science Foundation of China (No. 12273022) and the Shanghai pilot program of international scientists for basic research (No. 22JC1410600).
Data Availability Statement
The data shown in this study has been generated using the following codes: BHAC [38], BHOSS [41], H-AMR [37], IPOLE [42], KORAL [39], with access provided upon request to the corresponding authors.
Acknowledgments
We thank the anonymous referees for their suggestions that greatly improved the text. This research was enabled by support provided by grant no. NSF PHY-1125915 along with INCITE and ASCR Leadership Computing Challenge (ALCC) programs under the award PHY129, using resources from the Oak Ridge Leadership Computing Facility, Summit, which is a US Department of Energy office of Science User Facility supported under contract DE-AC05- 00OR22725, as well as Calcul Quebec and Compute Canada under award xsp-772-ab (PI: D. Haggard).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the studyl in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Notes
| 1 | https://www.ngeht.org/ (accessed on 22 November 2022). |
| 2 | https://challenge.ngeht.org/ (accessed on 22 November 2022). |
| 3 | Specific enthalpy includes the rest-mass energy contribution in our definition from Section 2.3. |
References
- Akiyama, K. et al. [Event Horizon Telescope Collaboration]. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration]. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Doeleman, S.; Blackburn, L.; Dexter, J.; Gomez, J.L.; Johnson, M.D.; Palumbo, D.C.; Weintroub, J.; Farah, J.R.; Fish, V.; Loinard, L.; et al. Studying Black Holes on Horizon Scales with VLBI Ground Arrays. Bulletin of the AAS, 2019, Volume 51. Available online: https://baas.aas.org/pub/2020n7i256 (accessed on 22 November 2022).
- Roelofs, F.; Blackburn, L.; Lindahl, G.; Doeleman, S.S.; Johnson, M.D.; Arras, P.; Chatterjee, K.; Emami, R.; Fromm, C.; Fuentes, A.; et al. The ngEHT Analysis Challenges. Galaxies 2022, 11, 12. [Google Scholar] [CrossRef]
- Raymond, A.W.; Palumbo, D.; Paine, S.N.; Blackburn, L.; Córdova Rosado, R.; Doeleman, S.S.; Farah, J.R.; Johnson, M.D.; Roelofs, F.; Tilanus, R.P.J.; et al. Evaluation of New Submillimeter VLBI Sites for the Event Horizon Telescope. Astrophys. J. Suppl. Ser. 2021, 253, 5. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Reprint of 1973A&A....24..337S. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 500, 33–51. [Google Scholar]
- Rees, M.J.; Phinney, E.S.; Begelman, M.C.; Blandford, R.D. Ion-supported tori and the origin of radio jets. Nature 1982, 295, 17–21. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I.; Mahadevan, R. Explaining the spectrum of Sagittarius A* with a model of an accreting black hole. Nature 1995, 374, 623–625. [Google Scholar] [CrossRef]
- Quataert, E.; Gruzinov, A. Convection-dominated Accretion Flows. Astrophys. J. 2000, 539, 809–814. [Google Scholar] [CrossRef]
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. PASJ 2003, 55, L69–L72. [Google Scholar] [CrossRef]
- McKinney, J.C. General relativistic magnetohydrodynamic simulations of the jet formation and large-scale propagation from black hole accretion systems. Mon. Not. R. Astron. Soc. 2006, 368, 1561–1582. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Barkov, M.V.; Vlahakis, N.; Königl, A. Magnetic acceleration of relativistic active galactic nucleus jets. Mon. Not. R. Astron. Soc. 2007, 380, 51–70. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Narayan, R.; Sa̧dowski, A.; Penna, R.F.; Kulkarni, A.K. GRMHD simulations of magnetized advection-dominated accretion on a non-spinning black hole: Role of outflows. Mon. Not. R. Astron. Soc. 2012, 426, 3241–3259. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Bromberg, O. Three-dimensional relativistic MHD simulations of active galactic nuclei jets: Magnetic kink instability and Fanaroff–Riley dichotomy. Mon. Not. R. Astron. Soc. 2016, 461, L46–L50. [Google Scholar] [CrossRef]
- Yuan, F.; Quataert, E.; Narayan, R. Nonthermal Electrons in Radiatively Inefficient Accretion Flow Models of Sagittarius A*. Astrophys. J. 2003, 598, 301–312. [Google Scholar] [CrossRef]
- Lucchini, M.; Krauß, F.; Markoff, S. The unique case of the active galactic nucleus core of M87: A misaligned low-power blazar? Mon. Not. R. Astron. Soc. 2019, 489, 1633–1643. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration]. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. Lett. 2019, 875, L5. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration]. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration]. First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. Astrophys. J. Lett. 2022, 930, L16. [Google Scholar] [CrossRef]
- Igumenshchev, I.V.; Narayan, R.; Abramowicz, M.A. Three-dimensional Magnetohydrodynamic Simulations of Radiatively Inefficient Accretion Flows. Astrophys. J. 2003, 592, 1042–1059. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Gammie, C.F.; McKinney, J.C.; Tóth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 444–457. [Google Scholar] [CrossRef]
- Fragile, P.C.; Blaes, O.M.; Anninos, P.; Salmonson, J.D. Global General Relativistic Magnetohydrodynamic Simulation of a Tilted Black Hole Accretion Disk. Astrophys. J. 2007, 668, 417–429. [Google Scholar] [CrossRef]
- Chael, A.; Narayan, R.; Johnson, M.D. Two-temperature, Magnetically Arrested Disc simulations of the jet from the supermassive black hole in M87. Mon. Not. R. Astron. Soc. 2019, 486, 2873–2895. [Google Scholar] [CrossRef]
- Porth, O.; Chatterjee, K.; Narayan, R.; Gammie, C.F.; Mizuno, Y.; Anninos, P.; Baker, J.G.; Bugli, M.; Chan, C.k.; Davelaar, J.; et al. The Event Horizon General Relativistic Magnetohydrodynamic Code Comparison Project. Astrophys. J. Suppl. Ser. 2019, 243, 26. [Google Scholar] [CrossRef]
- Narayan, R.; Chael, A.; Chatterjee, K.; Ricarte, A.; Curd, B. Jets in magnetically arrested hot accretion flows: Geometry, power, and black hole spin-down. Mon. Not. R. Astron. Soc. 2022, 511, 3795–3813. [Google Scholar] [CrossRef]
- Janssen, M.; Falcke, H.; Kadler, M.; Ros, E.; Wielgus, M.; Akiyama, K.; Baloković, M.; Blackburn, L.; Bouman, K.L.; Chael, A.; et al. Event Horizon Telescope observations of the jet launching and collimation in Centaurus A. Nat. Astron. 2021, 5, 1017–1028. [Google Scholar] [CrossRef]
- Broderick, A.E.; Loeb, A. Imaging optically thin hotspots near the black hole horizon of Sgr A* at radio and near-infrared wavelengths. Mon. Not. R. Astron. Soc. 2006, 367, 905–916. [Google Scholar] [CrossRef]
- Broderick, A.E.; McKinney, J.C. Parsec-scale Faraday Rotation Measures from General Relativistic Magnetohydrodynamic Simulations of Active Galactic Nucleus Jets. Astrophys. J. 2010, 725, 750–773. [Google Scholar] [CrossRef]
- Tiede, P.; Pu, H.Y.; Broderick, A.E.; Gold, R.; Karami, M.; Preciado-López, J.A. Spacetime Tomography Using the Event Horizon Telescope. Astrophys. J. 2020, 892, 132. [Google Scholar] [CrossRef]
- Broderick, A.E.; Fish, V.L.; Doeleman, S.S.; Loeb, A. Evidence for Low Black Hole Spin and Physically Motivated Accretion Models from Millimeter-VLBI Observations of Sagittarius A*. Astrophys. J. 2011, 735, 110. [Google Scholar] [CrossRef]
- Broderick, A.E.; Fish, V.L.; Johnson, M.D.; Rosenfeld, K.; Wang, C.; Doeleman, S.S.; Akiyama, K.; Johannsen, T.; Roy, A.L. Modeling Seven Years of Event Horizon Telescope Observations with Radiatively Inefficient Accretion Flow Models. Astrophys. J. 2016, 820, 137. [Google Scholar] [CrossRef]
- Pu, H.Y.; Akiyama, K.; Asada, K. The Effects of Accretion Flow Dynamics on the Black Hole Shadow of Sagittarius A*. Astrophys. J. 2016, 831, 4. [Google Scholar] [CrossRef]
- Broderick, A.; Blandford, R. Covariant magnetoionic theory—II. Radiative transfer. Mon. Not. R. Astron. Soc. 2004, 349, 994–1008. [Google Scholar] [CrossRef]
- Jones, T.W.; O’Dell, S.L. Transfer of polarized radiation in self-absorbed synchrotron sources. I. Results for a homogeneous source. Astrophys. J. 1977, 214, 522–539. [Google Scholar] [CrossRef]
- Liska, M.T.P.; Chatterjee, K.; Issa, D.; Yoon, D.; Kaaz, N.; Tchekhovskoy, A.; van Eijnatten, D.; Musoke, G.; Hesp, C.; Rohoza, V.; et al. H-AMR: A New GPU-accelerated GRMHD Code for Exascale Computing with 3D Adaptive Mesh Refinement and Local Adaptive Time Stepping. Astrophys. J. Suppl. Ser. 2022, 263, 26. [Google Scholar] [CrossRef]
- Porth, O.; Olivares, H.; Mizuno, Y.; Younsi, Z.; Rezzolla, L.; Moscibrodzka, M.; Falcke, H.; Kramer, M. The black hole accretion code. Comput. Astrophys. Cosmol. 2017, 4, 1. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R.; Tchekhovskoy, A.; Zhu, Y. Semi-implicit scheme for treating radiation under M1 closure in general relativistic conservative fluid dynamics codes. Mon. Not. R. Astron. Soc. 2013, 429, 3533–3550. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S. Formation of precessing jets by tilted black hole discs in 3D general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2018, 474, L81–L85. [Google Scholar] [CrossRef]
- Younsi, Z.; Porth, O.; Mizuno, Y.; Fromm, C.M.; Olivares, H. Modelling the polarised emission from black holes on event horizon-scales. Proc. IAU 2020, 14, 9–12. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F. IPOLE - semi-analytic scheme for relativistic polarized radiative transport. Mon. Not. R. Astron. Soc. 2018, 475, 43–54. [Google Scholar] [CrossRef]
- Gebhardt, K.; Adams, J.; Richstone, D.; Lauer, T.R.; Faber, S.M.; Gültekin, K.; Murphy, J.; Tremaine, S. The Black Hole Mass in M87 from Gemini/NIFS Adaptive Optics Observations. Astrophys. J. 2011, 729, 119. [Google Scholar] [CrossRef]
- Do, T.; Witzel, G.; Gautam, A.K.; Chen, Z.; Ghez, A.M.; Morris, M.R.; Becklin, E.E.; Ciurlo, A.; Hosek, M., Jr.; Martinez, G.D.; et al. Unprecedented Near-infrared Brightness and Variability of Sgr A *. Astrophys. J. Lett. 2019, 882, L27. [Google Scholar] [CrossRef]
- Abuter, R. et al. [GRAVITY Collaboration]. A geometric distance measurement to the Galactic center black hole with 0.3% uncertainty. Astron. Astrophys. 2019, 625, L10. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H.; Shiokawa, H. General relativistic magnetohydrodynamical simulations of the jet in M87. A&A 2016, 586, A38. [Google Scholar] [CrossRef]
- Xiao, F. Modelling energetic particles by a relativistic kappa-loss-cone distribution function in plasmas. Plasma Phys. Control. Fusion 2006, 48, 203–213. [Google Scholar] [CrossRef]
- Davelaar, J.; Mościbrodzka, M.; Bronzwaer, T.; Falcke, H. General relativistic magnetohydrodynamical κ-jet models for Sagittarius A*. Astron. Astrophys. 2018, 612, A34. [Google Scholar] [CrossRef]
- Ressler, S.M.; Tchekhovskoy, A.; Quataert, E.; Chandra, M.; Gammie, C.F. Electron thermodynamics in GRMHD simulations of low-luminosity black hole accretion. Mon. Not. R. Astron. Soc. 2015, 454, 1848–1870. [Google Scholar] [CrossRef]
- Dexter, J.; Jiménez-Rosales, A.; Ressler, S.M.; Tchekhovskoy, A.; Bauböck, M.; de Zeeuw, P.T.; Eisenhauer, F.; von Fellenberg, S.; Gao, F.; Genzel, R.; et al. A parameter survey of Sgr A * radiative models from GRMHD simulations with self-consistent electron heating. Mon. Not. R. Astron. Soc. 2020, 494, 4168–4186. [Google Scholar] [CrossRef]
- Howes, G.G. A prescription for the turbulent heating of astrophysical plasmas. Mon. Not. R. Astron. Soc. 2010, 409, L104–L108. [Google Scholar] [CrossRef]
- Kawazura, Y.; Barnes, M.; Schekochihin, A.A. Thermal disequilibration of ions and electrons by collisionless plasma turbulence. Proc. Natl. Acad. Sci. USA 2019, 116, 771–776. [Google Scholar] [CrossRef] [PubMed]
- Werner, G.R.; Uzdensky, D.A.; Begelman, M.C.; Cerutti, B.; Nalewajko, K. Non-thermal particle acceleration in collisionless relativistic electron-proton reconnection. Mon. Not. R. Astron. Soc. 2018, 473, 4840–4861. [Google Scholar] [CrossRef]
- Rowan, M.E.; Sironi, L.; Narayan, R. Electron and Proton Heating in Transrelativistic Magnetic Reconnection. Astrophys. J. 2017, 850, 29. [Google Scholar] [CrossRef]
- Mizuno, Y.; Fromm, C.M.; Younsi, Z.; Porth, O.; Olivares, H.; Rezzolla, L. Comparison of the ion-to-electron temperature ratio prescription: GRMHD simulations with electron thermodynamics. Mon. Not. R. Astron. Soc. 2021, 506, 741–758. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R. Photon-conserving Comptonization in simulations of accretion discs around black holes. Mon. Not. R. Astron. Soc. 2015, 454, 2372–2380. [Google Scholar] [CrossRef]
- Chael, A.; Rowan, M.; Narayan, R.; Johnson, M.; Sironi, L. The role of electron heating physics in images and variability of the Galactic Centre black hole Sagittarius A*. Mon. Not. R. Astron. Soc. 2018, 478, 5209–5229. [Google Scholar] [CrossRef]
- Sądowski, A.; Wielgus, M.; Narayan, R.; Abarca, D.; McKinney, J.C.; Chael, A. Radiative, two-temperature simulations of low-luminosity black hole accretion flows in general relativity. Mon. Not. R. Astron. Soc. 2017, 466, 705–725. [Google Scholar] [CrossRef]
- Doeleman, S.S.; Fish, V.L.; Schenck, D.E.; Beaudoin, C.; Blundell, R.; Bower, G.C.; Broderick, A.E.; Chamberlin, R.; Freund, R.; Friberg, P.; et al. Jet-Launching Structure Resolved Near the Supermassive Black Hole in M87. Science 2012, 338, 355. [Google Scholar] [CrossRef]
- Akiyama, K.; Lu, R.; Fish, V.L.; Doeleman, S.S.; Broderick, A.E.; Dexter, J.; Hada, K.; Kino, M.; Nagai, H.; Honma, M.; et al. 230 GHz VLBI Observations of M87: Event-horizon-scale Structure during an Enhanced Very-high-energy γ-Ray State in 2012. Astrophys. J. 2015, 807, 150. [Google Scholar] [CrossRef]
- Porth, O.; Mizuno, Y.; Younsi, Z.; Fromm, C.M. Flares in the Galactic Centre - I. Orbiting flux tubes in magnetically arrested black hole accretion discs. Mon. Not. R. Astron. Soc. 2021, 502, 2023–2032. [Google Scholar] [CrossRef]
- Begelman, M.C.; Scepi, N.; Dexter, J. What really makes an accretion disc MAD. Mon. Not. R. Astron. Soc. 2022, 511, 2040–2051. [Google Scholar] [CrossRef]
- Ripperda, B.; Liska, M.; Chatterjee, K.; Musoke, G.; Philippov, A.A.; Markoff, S.B.; Tchekhovskoy, A.; Younsi, Z. Black Hole Flares: Ejection of Accreted Magnetic Flux through 3D Plasmoid-mediated Reconnection. Astrophys. J. Lett. 2022, 924, L32. [Google Scholar] [CrossRef]
- Chatterjee, K.; Narayan, R. Flux Eruption Events Drive Angular Momentum Transport in Magnetically Arrested Accretion Flows. Astrophys. J. 2022, 941, 30. [Google Scholar] [CrossRef]
- Chatterjee, K.; Markoff, S.; Neilsen, J.; Younsi, Z.; Witzel, G.; Tchekhovskoy, A.; Yoon, D.; Ingram, A.; van der Klis, M.; Boyce, H.; et al. General relativistic MHD simulations of non-thermal flaring in Sagittarius A*. Mon. Not. R. Astron. Soc. 2021, 507, 5281–5302. [Google Scholar] [CrossRef]
- Wielgus, M.; Marchili, N.; Martí-Vidal, I.; Keating, G.K.; Ramakrishnan, V.; Tiede, P.; Fomalont, E.; Issaoun, S.; Neilsen, J.; Nowak, M.A.; et al. Millimeter Light Curves of Sagittarius A* Observed during the 2017 Event Horizon Telescope Campaign. Astrophys. J. Lett. 2022, 930, L19. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated accretion: A self-similar solution. Astrophys. J. Lett. 1994, 428, L13–L16. [Google Scholar] [CrossRef]
- Narayan, R.; Mahadevan, R.; Quataert, E. Advection-dominated accretion around black holes. In Theory of Black Hole Accretion Disks; Abramowicz, M.A., Bjornsson, G., Pringle, J.E., Eds.; Cambridge University Press: Cambridge, UK, 1998; pp. 138–182. [Google Scholar] [CrossRef]
- Liska, M.; Tchekhovskoy, A.; Quataert, E. Large-scale poloidal magnetic field dynamo leads to powerful jets in GRMHD simulations of black hole accretion with toroidal field. Mon. Not. R. Astron. Soc. 2020, 494, 3656–3662. [Google Scholar] [CrossRef]
- Nakamura, M.; Asada, K.; Hada, K.; Pu, H.Y.; Noble, S.; Tseng, C.; Toma, K.; Kino, M.; Nagai, H.; Takahashi, K.; et al. Parabolic Jets from the Spinning Black Hole in M87. Astrophys. J. 2018, 868, 146. [Google Scholar] [CrossRef]
- Asada, K.; Nakamura, M. The Structure of the M87 Jet: A Transition from Parabolic to Conical Streamlines. ApJL 2012, 745, 5. [Google Scholar] [CrossRef]
- Nokhrina, E.E.; Gurvits, L.I.; Beskin, V.S.; Nakamura, M.; Asada, K.; Hada, K. M87 black hole mass and spin estimate through the position of the jet boundary shape break. Mon. Not. R. Astron. Soc. 2019, 489, 1197–1205. [Google Scholar] [CrossRef]
- Chatterjee, K.; Liska, M.; Tchekhovskoy, A.; Markoff, S.B. Accelerating AGN jets to parsec scales using general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2019, 490, 2200–2218. [Google Scholar] [CrossRef]
- Issaoun, S.; Johnson, M.D.; Blackburn, L.; Brinkerink, C.D.; Mościbrodzka, M.; Chael, A.; Goddi1, C.; Martí-Vidal, I.; Wagner, J.; Doeleman, S.S. The Size, Shape, and Scattering of Sagittarius A* at 86 GHz: First VLBI with ALMA. Astrophys. J. 2019, 871, 30. [Google Scholar] [CrossRef]
- Markoff, S.; Bower, G.C.; Falcke, H. How to hide large-scale outflows: Size constraints on the jets of Sgr A *. Mon. Not. R. Astron. Soc. 2007, 379, 1519–1532. [Google Scholar] [CrossRef]
- Mertens, F.; Lobanov, A.P.; Walker, R.C.; Hardee, P.E. Kinematics of the jet in M87 on scales of 100–1000 Schwarzschild radii. Astron. Astrophys. 2016, 595, A54. [Google Scholar] [CrossRef]
- Hada, K.; Kino, M.; Doi, A.; Nagai, H.; Honma, M.; Hagiwara, Y.; Giroletti, M.; Giovannini, G.; Kawaguchi, N. The Innermost Collimation Structure of the M87 Jet Down to 10 Schwarzschild Radii. Astrophys. J. 2013, 775, 70. [Google Scholar] [CrossRef]
- Nakamura, M.; Asada, K. The Parabolic Jet Structure in M87 as a Magnetohydrodynamic Nozzle. Astrophys. J. 2013, 775, 118. [Google Scholar] [CrossRef]
- Hada, K.; Kino, M.; Doi, A.; Nagai, H.; Honma, M.; Akiyama, K.; Tazaki, F.; Lico, R.; Giroletti, M.; Giovannini, G.; et al. High-sensitivity 86 GHz (3.5 mm) VLBI Observations of M87: Deep Imaging of the Jet Base at a Resolution of 10 Schwarzschild Radii. Astrophys. J. 2016, 817, 131. [Google Scholar] [CrossRef]
- Fragile, P.C.; Meier, D.L. General Relativistic Magnetohydrodynamic Simulations of the Hard State as a Magnetically Dominated Accretion Flow. Astrophys. J. 2009, 693, 771–783. [Google Scholar] [CrossRef]
- Yoon, D.; Chatterjee, K.; Markoff, S.B.; van Eijnatten, D.; Younsi, Z.; Liska, M.; Tchekhovskoy, A. Spectral and imaging properties of Sgr A * from high-resolution 3D GRMHD simulations with radiative cooling. Mon. Not. R. Astron. Soc. 2020, 499, 3178–3192. [Google Scholar] [CrossRef]
- Sadowski, A. Magnetic flux stabilizing thin accretion discs. Mon. Not. R. Astron. Soc. 2016, 462, 960–965. [Google Scholar] [CrossRef]
- Liska, M.T.P.; Musoke, G.; Tchekhovskoy, A.; Porth, O.; Beloborodov, A.M. Formation of Magnetically Truncated Accretion Disks in 3D Radiation-Transport Two-Temperature GRMHD Simulations. arXiv 2022, arXiv:2201.03526. [Google Scholar] [CrossRef]
- Mishra, B.; Fragile, P.C.; Anderson, J.; Blankenship, A.; Li, H.; Nalewajko, K. The Role of Strong Magnetic Fields in Stabilizing Highly Luminous Thin Disks. Astrophys. J. 2022, 939, 31. [Google Scholar] [CrossRef]
- Wong, G.N.; Du, Y.; Prather, B.S.; Gammie, C.F. The Jet-disk Boundary Layer in Black Hole Accretion. Astrophys. J. 2021, 914, 55. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; Borrel, V.; et al. Fast Variability of Tera-Electron Volt γ Rays from the Radio Galaxy M87. Science 2006, 314, 1424–1427. [Google Scholar] [CrossRef] [PubMed]
- Acciari, V.A.; Aliu, E.; Arlen, T.; Aune, T.; Beilicke, M.; Benbow, W.; Boltuch, D.; Bradbury, S.M.; Buckley, J.H.; Bugaev, V.; et al. Veritas 2008-2009 Monitoring of the Variable Gamma-ray Source M 87. Astrophys. J. 2010, 716, 819–824. [Google Scholar] [CrossRef]
- Baganoff, F.K.; Bautz, M.W.; Brandt, W.N.; Chartas, G.; Feigelson, E.D.; Garmire, G.P.; Maeda, Y.; Morris, M.; Ricker, G.R.; Townsley, L.K.; et al. Rapid X-ray flaring from the direction of the supermassive black hole at the Galactic Centre. Nature 2001, 413, 45–48. [Google Scholar] [CrossRef]
- Eckart, A.; Baganoff, F.K.; Schödel, R.; Morris, M.; Genzel, R.; Bower, G.C.; Marrone, D.; Moran, J.M.; Viehmann, T.; Bautz, M.W.; et al. The flare activity of Sagittarius A*. New coordinated mm to X-ray observations. Astron. Astrophys. 2006, 450, 535–555. [Google Scholar] [CrossRef]
- Hornstein, S.D.; Matthews, K.; Ghez, A.M.; Lu, J.R.; Morris, M.; Becklin, E.E.; Rafelski, M.; Baganoff, F.K. A Constant Spectral Index for Sagittarius A* during Infrared/X-ray Intensity Variations. Astrophys. J. 2007, 667, 900–910. [Google Scholar] [CrossRef]
- Nowak, M.A.; Neilsen, J.; Markoff, S.B.; Baganoff, F.K.; Porquet, D.; Grosso, N.; Levin, Y.; Houck, J.; Eckart, A.; Falcke, H.; et al. Chandra/HETGS Observations of the Brightest Flare Seen from Sgr A *. Astrophys. J. 2012, 759, 95. [Google Scholar] [CrossRef]
- Neilsen, J.; Nowak, M.A.; Gammie, C.; Dexter, J.; Markoff, S.; Haggard, D.; Nayakshin, S.; Wang, Q.D.; Grosso, N.; Porquet, D.; et al. A Chandra/HETGS Census of X-ray Variability from Sgr A * during 2012. Astrophys. J. 2013, 774, 42. [Google Scholar] [CrossRef]
- Witzel, G.; Martinez, G.; Hora, J.; Willner, S.P.; Morris, M.R.; Gammie, C.; Becklin, E.E.; Ashby, M.L.N.; Baganoff, F.; Carey, S.; et al. Variability Timescale and Spectral Index of Sgr A * in the Near Infrared: Approximate Bayesian Computation Analysis of the Variability of the Closest Supermassive Black Hole. Astrophys. J. 2018, 863, 15. [Google Scholar] [CrossRef]
- Haggard, D.; Nynka, M.; Mon, B.; de la Cruz Hernandez, N.; Nowak, M.; Heinke, C.; Neilsen, J.; Dexter, J.; Fragile, P.C.; Baganoff, F.; et al. Chandra Spectral and Timing Analysis of Sgr A *’s Brightest X-ray Flares. Astrophys. J. 2019, 886, 96. [Google Scholar] [CrossRef]
- Dodds-Eden, K.; Sharma, P.; Quataert, E.; Genzel, R.; Gillessen, S.; Eisenhauer, F.; Porquet, D. Time-Dependent Models of Flares from Sagittarius A*. Astrophys. J. 2010, 725, 450–465. [Google Scholar] [CrossRef]
- Dibi, S.; Markoff, S.; Belmont, R.; Malzac, J.; Barrière, N.M.; Tomsick, J.A. Exploring plasma evolution during Sagittarius A* flares. Mon. Not. R. Astron. Soc. 2014, 441, 1005–1016. [Google Scholar] [CrossRef]
- Nathanail, A.; Fromm, C.M.; Porth, O.; Olivares, H.; Younsi, Z.; Mizuno, Y.; Rezzolla, L. Plasmoid formation in global GRMHD simulations and AGN flares. Mon. Not. R. Astron. Soc. 2020, 495, 1549–1565. [Google Scholar] [CrossRef]
- Dexter, J.; Tchekhovskoy, A.; Jiménez-Rosales, A.; Ressler, S.M.; Bauböck, M.; Dallilar, Y.; de Zeeuw, P.T.; Eisenhauer, F.; von Fellenberg, S.; Gao, F.; et al. Sgr A * near-infrared flares from reconnection events in a magnetically arrested disc. Mon. Not. R. Astron. Soc. 2020, 497, 4999–5007. [Google Scholar] [CrossRef]
- Scepi, N.; Dexter, J.; Begelman, M.C. Sgr A * X-ray flares from non-thermal particle acceleration in a magnetically arrested disc. Mon. Not. R. Astron. Soc. 2022, 511, 3536–3547. [Google Scholar] [CrossRef]
- Markoff, S.; Falcke, H.; Yuan, F.; Biermann, P.L. The Nature of the 10 kilosecond X-ray flare in Sgr A *. Astron. Astrophys. 2001, 379, L13–L16. [Google Scholar] [CrossRef]
- Dibi, S.; Markoff, S.; Belmont, R.; Malzac, J.; Neilsen, J.; Witzel, G. Using infrared/X-ray flare statistics to probe the emission regions near the event horizon of Sgr A *. Mon. Not. R. Astron. Soc. 2016, 461, 552–559. [Google Scholar] [CrossRef]
- Gutiérrez, E.M.; Nemmen, R.; Cafardo, F. A Nonthermal Bomb Explains the Near-infrared Superflare of Sgr A *. Astrophys. J. Lett. 2020, 891, L36. [Google Scholar] [CrossRef]
- Bauböck, M. et al. [Gravity Collaboration]. Modeling the orbital motion of Sgr A *’s near-infrared flares. Astron. Astrophys. 2020, 635, A143. [Google Scholar] [CrossRef]
- Ball, D.; Özel, F.; Christian, P.; Chan, C.K.; Psaltis, D. A Plasmoid model for the Sgr A * Flares Observed With Gravity and CHANDRA. Astrophys. J. 2021, 917, 8. [Google Scholar] [CrossRef]
- Wielgus, M.; Moscibrodzka, M.; Vos, J.; Gelles, Z.; Martí-Vidal, I.; Farah, J.; Marchili, N.; Goddi, C.; Messias, H. Orbital motion near Sagittarius A*. Constraints from polarimetric ALMA observations. Astron. Astrophys. 2022, 665, L6. [Google Scholar] [CrossRef]
- Emami, R.; Tiede, P.; Doeleman, S.S.; Roelofs, F.; Wielgus, M.; Blackburn, L.; Liska, M.; Chatterjee, K.; Ripperda, B.; Fuentes, A.; et al. Tracing Hot Spot Motion in Sagittarius A* Using the Next-Generation Event Horizon Telescope (ngEHT). Galaxies 2023, 11, 23. [Google Scholar] [CrossRef]
- Gelles, Z.; Chatterjee, K.; Johnson, M.; Ripperda, B.; Liska, M. Relativistic Signatures of Flux Eruption Events near Black Holes. Galaxies 2022, 10, 107. [Google Scholar] [CrossRef]
- Ressler, S.M.; White, C.J.; Quataert, E.; Stone, J.M. Ab Initio Horizon-scale Simulations of Magnetically Arrested Accretion in Sagittarius A* Fed by Stellar Winds. Astrophys. J. Lett. 2020, 896, L6. [Google Scholar] [CrossRef]
- Lalakos, A.; Gottlieb, O.; Kaaz, N.; Chatterjee, K.; Liska, M.; Christie, I.M.; Tchekhovskoy, A.; Zhuravleva, I.; Nokhrina, E. Bridging the Bondi and Event Horizon Scales: 3D GRMHD Simulations Reveal X-shaped Radio Galaxy Morphology. Astrophys. J. Lett. 2022, 936, L5. [Google Scholar] [CrossRef]
- Cruz-Osorio, A.; Sánchez-Salcedo, F.J.; Lora-Clavijo, F.D. Relativistic Bondi-Hoyle-Lyttleton accretion in the presence of small rigid bodies around a black hole. Mon. Not. R. Astron. Soc. 2017, 471, 3127–3134. [Google Scholar] [CrossRef]
- Kaaz, N.; Murguia-Berthier, A.; Chatterjee, K.; Liska, M.; Tchekhovskoy, A. Jet Formation in 3D GRMHD Simulations of Bondi-Hoyle-Lyttleton Accretion. arXiv 2022, arXiv:2201.11753. [Google Scholar]
- Avara, M.J.; McKinney, J.C.; Reynolds, C.S. Efficiency of thin magnetically arrested discs around black holes. Mon. Not. R. Astron. Soc. 2016, 462, 636–648. [Google Scholar] [CrossRef]
- Sadowski, A.; Narayan, R. Three-dimensional simulations of supercritical black hole accretion discs - luminosities, photon trapping and variability. Mon. Not. R. Astron. Soc. 2016, 456, 3929–3947. [Google Scholar] [CrossRef]
- Curd, B.; Narayan, R. GRRMHD simulations of tidal disruption event accretion discs around supermassive black holes: Jet formation, spectra, and detectability. Mon. Not. R. Astron. Soc. 2019, 483, 565–592. [Google Scholar] [CrossRef]
- White, C.J.; Quataert, E.; Blaes, O. Tilted Disks around Black Holes: A Numerical Parameter Survey for Spin and Inclination Angle. Astrophys. J. 2019, 878, 51. [Google Scholar] [CrossRef]
- Chatterjee, K.; Younsi, Z.; Liska, M.; Tchekhovskoy, A.; Markoff, S.B.; Yoon, D.; van Eijnatten, D.; Hesp, C.; Ingram, A.; van der Klis, M.B.M. Observational signatures of disc and jet misalignment in images of accreting black holes. Mon. Not. R. Astron. Soc. 2020, 499, 362–378. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration]. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
- Mizuno, Y.; Younsi, Z.; Fromm, C.M.; Porth, O.; De Laurentis, M.; Olivares, H.; Falcke, H.; Kramer, M.; Rezzolla, L. The current ability to test theories of gravity with black hole shadows. Nat. Astron. 2018, 2, 585–590. [Google Scholar] [CrossRef]
- Olivares, H.; Younsi, Z.; Fromm, C.M.; De Laurentis, M.; Porth, O.; Mizuno, Y.; Falcke, H.; Kramer, M.; Rezzolla, L. How to tell an accreting boson star from a black hole. Mon. Not. R. Astron. Soc. 2020, 497, 521–535. [Google Scholar] [CrossRef]
- Nampalliwar, S.; Yfantis, A.I.; Kokkotas, K.D. Extending GRMHD for thin disks to non-Kerr spacetimes. Phys. Rev. D 2022, 106, 063009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).