The Relative Position of the Solar Magnetic Dipole Axis and Rotation Axis of the Sun
Abstract
1. Introduction
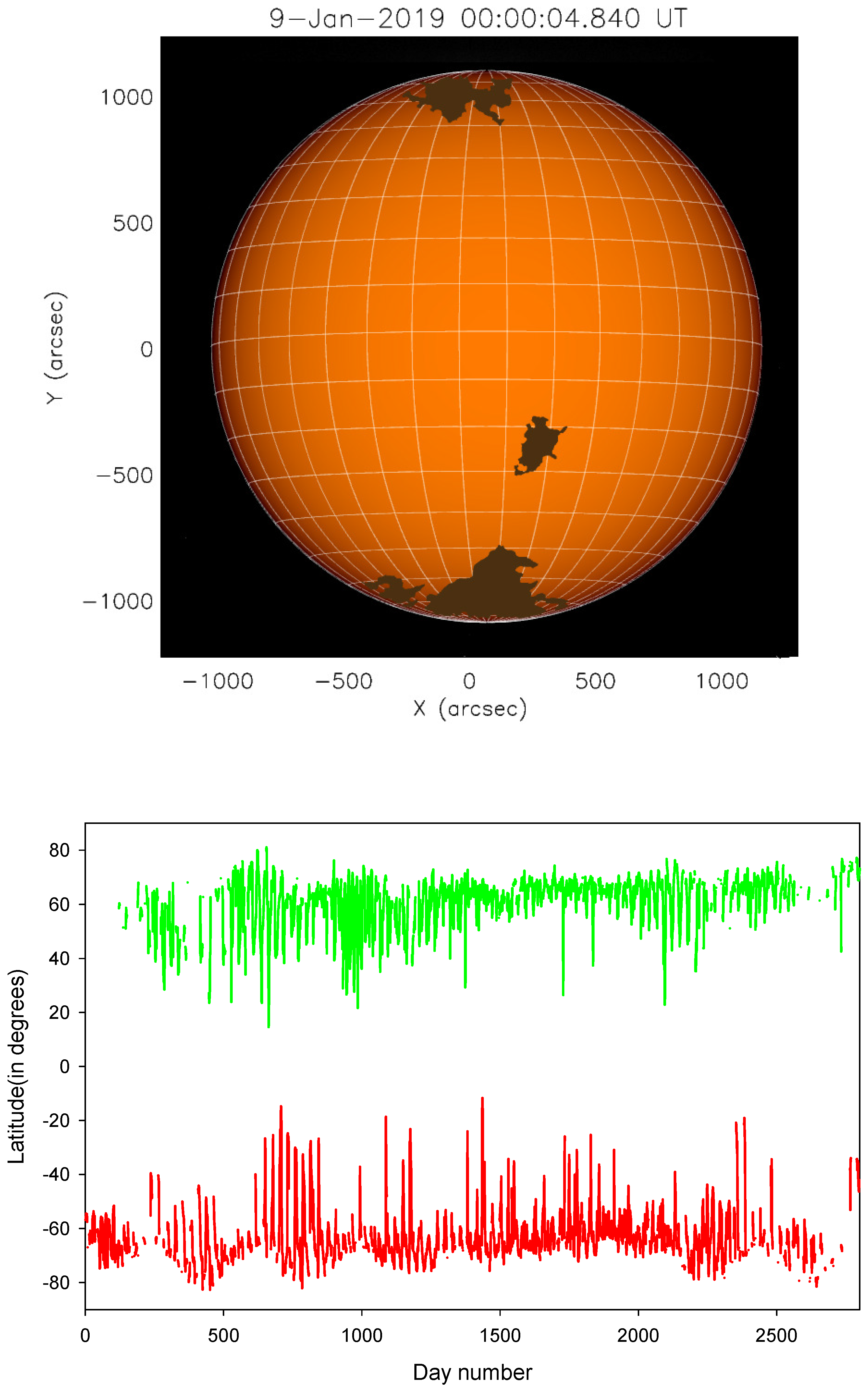
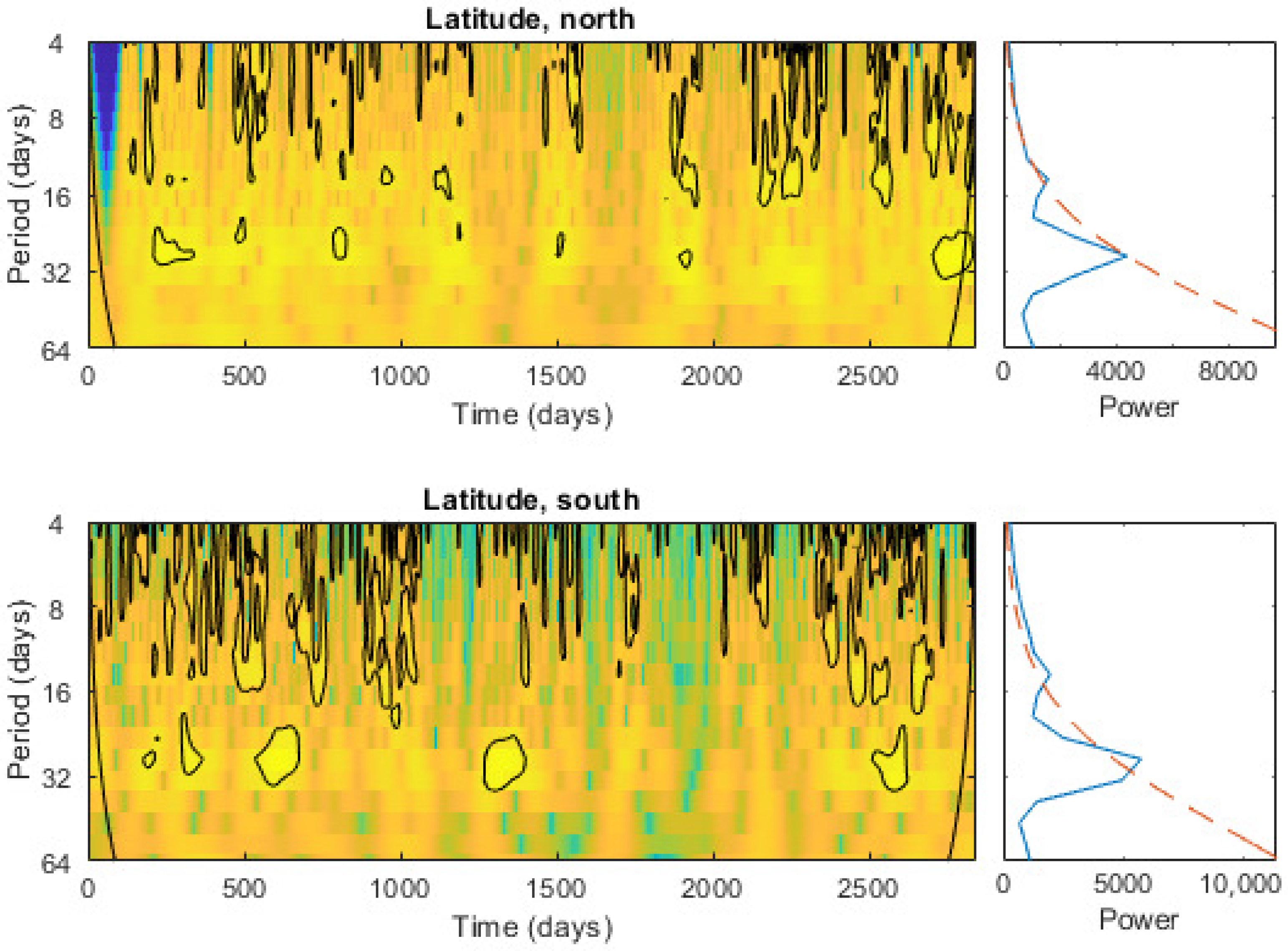
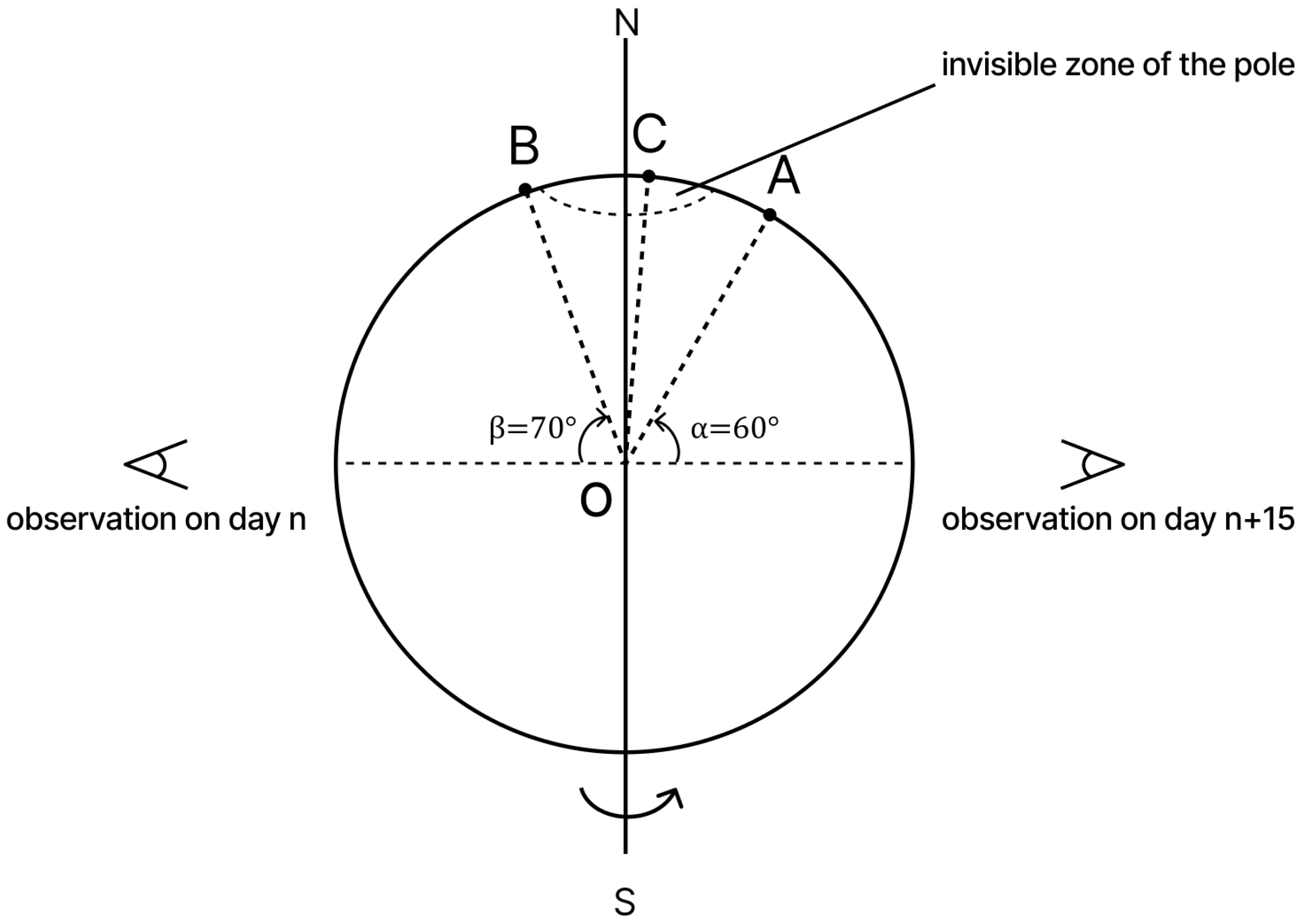
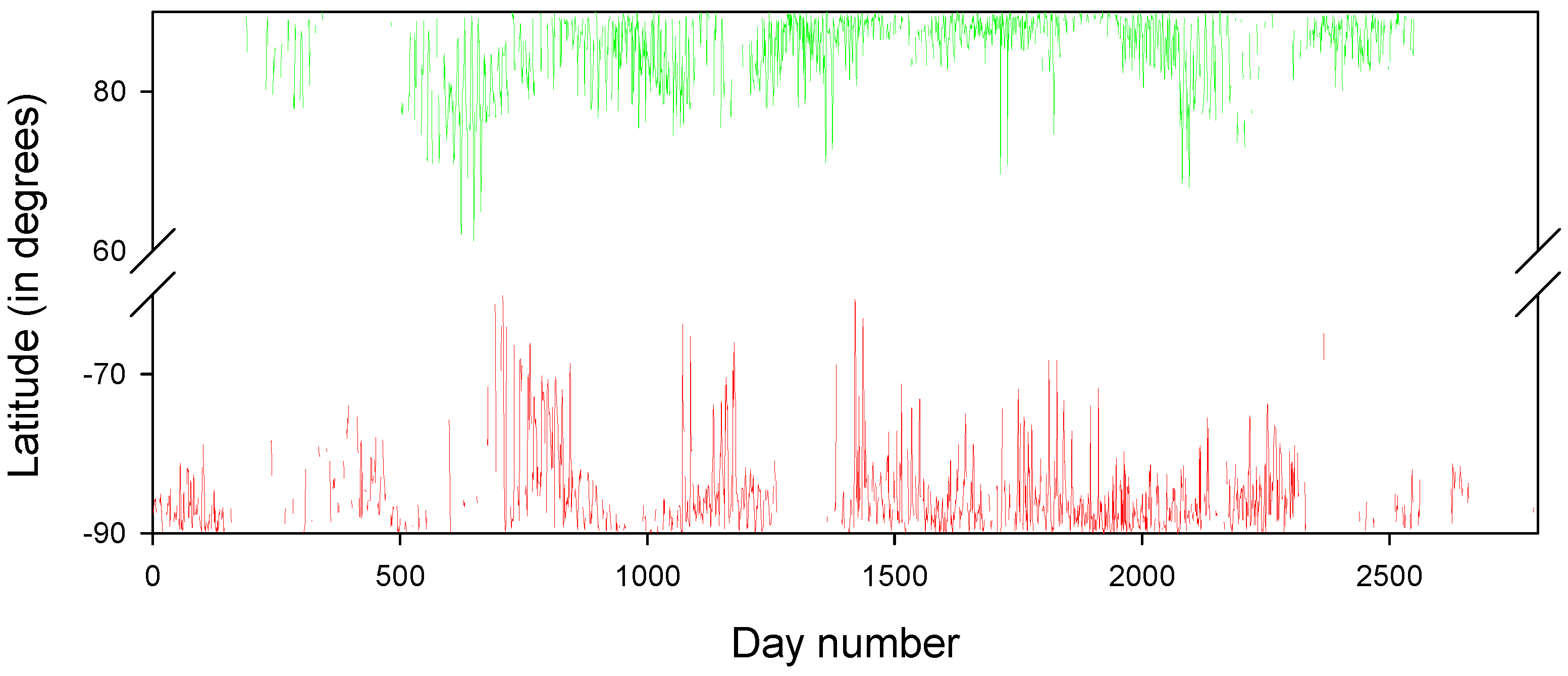
2. Methods and Observations
3. Results and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Babcock, H.W. The Topology of the Sun’s Magnetic Field and the 22-Year Cycle. Astrophys. J. 1961, 133, 572. [Google Scholar] [CrossRef]
- Leighton, R.B. A Magneto-Kinematic Model of the Solar Cycle. Astrophys. J. 1969, 156, 1. [Google Scholar] [CrossRef]
- Cowling, T.G. The Magnetic Field of Sunspots. Mon. Not. R. Astron. Soc. 1933, 94, 39–48. [Google Scholar] [CrossRef]
- James, R.W.; Winch, D.E.; Roberts, P.H. The Cowling anti-dynamo theorem. Geophys. Astrophys. Fluid Dyn. 1980, 15, 149–160. [Google Scholar] [CrossRef]
- Jones, C.A. Course 2 Dynamo theory. In Dynamos; Cardin, P., Cugliandolo, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 88, pp. 45–135. [Google Scholar] [CrossRef]
- Norton, A.A.; Raouafi, N.E.; Petrie, G.J.D. The Tilted Solar Dipole as Observed and Modeled during the 1996 Solar Minimum. Astrophys. J. 2008, 682, 1306–1314. [Google Scholar] [CrossRef]
- Norton, A.A.; Raouafi, N.E. The Tilted Solar Dipole: Coronal Streamer and Polar Cap Geometry Observed Near Solar Minimum. In Proceedings of the Subsurface and Atmospheric Influences on Solar Activity; Howe, R., Komm, R.W., Balasubramaniam, K.S., Petrie, G.J.D., Eds.; Astronomical Society of the Pacific Conference Series: San Francisco, CA, USA, 2008; Volume 383, p. 405. [Google Scholar]
- Pastor Yabar, A.; Martinez Gonzalez, M.J.; Collados, M. Where are the solar magnetic poles? Mon. Not. R. Astron. Soc. Lett. 2015, 453, L69–L72. [Google Scholar] [CrossRef]
- Mancuso, S.; Garzelli, M.V. Assessing the tilt of the solar magnetic field axis through Faraday rotation observations. Astron. Astrophys. 2007, 466, L5–L8. [Google Scholar] [CrossRef]
- Borovikov, S.N.; Pogorelov, N.V.; Ebert, R.W. Solar Rotation Effects on the Heliosheath Flow near Solar Minima. Astrophys. J. 2012, 750, 42. [Google Scholar] [CrossRef]
- Cranmer, S.R. Coronal Holes. Living Rev. Sol. Phys. 2009, 6, 3. [Google Scholar] [CrossRef]
- Heinemann, S.G.; Jerčić, V.; Temmer, M.; Hofmeister, S.J.; Dumbović, M.; Vennerstrom, S.; Verbanac, G.; Veronig, A.M. A statistical study of the long-term evolution of coronal hole properties as observed by SDO. Astron. Astrophys. 2020, 638, A68. [Google Scholar] [CrossRef]
- Abramenko, V.; Yurchyshyn, V.; Watanabe, H. Parameters of the Magnetic Flux inside Coronal Holes. Sol. Phys. 2009, 260, 43–57. [Google Scholar] [CrossRef]
- Hofmeister, S.J.; Veronig, A.M.; Poedts, S.; Samara, E.; Magdalenic, J. On the Dependency between the Peak Velocity of High-speed Solar Wind Streams near Earth and the Area of Their Solar Source Coronal Holes. Astrophys. J. 2020, 897, L17. [Google Scholar] [CrossRef]
- Jain, R.N.; Choudhary, R.K.; Ambili, K.M.; Roopa, M.V.; Dai, B.K. Impact of the high-speed solar wind stream over the low-latitude ionospheric system - a study combining Indian MOM and InSWIM observations. Mon. Not. R. Astron. Soc. Lett. 2024, 534, 117–127. [Google Scholar] [CrossRef]
- Ervin, T.; Jaffarove, K.; Badman, S.T.; Huang, J.; Rivera, Y.J.; Bale, S.D. Characteristics and Source Regions of Slow Alfvénic Solar Wind Observed by Parker Solar Probe. Astrophys. J. 2024, 975, 156. [Google Scholar] [CrossRef]
- Tokumaru, M.; Fujiki, K. Coronal Magnetic-Field Configuration Associated with Pseudostreamer and Slow Solar Wind. Sol. Phys. 2024, 299, 160. [Google Scholar] [CrossRef]
- Harvey, K.L.; Recely, F. Polar Coronal Holes During Cycles 22 and 23. Sol. Phys. 2002, 211, 31–52. [Google Scholar] [CrossRef]
- Riehokainen, A.; Smirnova, V.; Solov’ev, A.; Tlatov, A.; Zhivanovich, I.; Al-Hamadani, F.; Strekalova, P. Variations in Daily Maximum Areas and Longitudinal Widths of Solar Coronal Holes in 2017–2020. Universe 2022, 8, 158. [Google Scholar] [CrossRef]
- Horbury, T.S.; Laker, R.; Rodriguez, L.; Steinvall, K.; Maksimovic, M.; Livi, S.; Berghmans, D.; Auchere, F.; Zhukov, A.N.; Khotyaintsev, Y.V.; et al. Signatures of coronal hole substructure in the solar wind: Combined Solar Orbiter remote sensing and in situ measurements. arXiv 2021, arXiv:2104.14960. [Google Scholar] [CrossRef]
- Telloni, D.; Antonucci, E.; Adhikari, L.; Zank, G.P.; Giordano, S.; Vai, M.; Zhao, L.L.; Andretta, V.; Burtovoi, A.; Capuano, G.E.; et al. First polar observations of the fast solar wind with the Metis—Solar Orbiter coronagraph: Role of 2D turbulence energy dissipation in the wind acceleration. Astron. Astrophys. 2023, 670, L18. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Q.; Xia, L.; Feng, L.; Fu, H.; Liu, W.; Sun, M.; Qi, Y.; Liu, D.; Zhang, Q.; et al. Population of Bright Plume Threads in Solar Polar Coronal Holes. Sol. Phys. 2021, 296, 22. [Google Scholar] [CrossRef]
- Morton, R.J.; Cunningham, R. The Fine-scale Structure of Polar Coronal Holes. Astrophys. J. 2023, 954, 90. [Google Scholar] [CrossRef]
- Stepanian, N.N.; Shtertser, N.I. Polar coronal holes in the solar activity cycle. Adv. Space Res. 2015, 55, 795–797. [Google Scholar] [CrossRef]
- Shrestha, B.L.; Zirnstein, E.J.; McComas, D.J. Tracking the Rapid Opening and Closing of Polar Coronal Holes through IBEX ENA Observations. Astrophys. J. 2023, 943, 34. [Google Scholar] [CrossRef]
- Korolkova, O.A.; Solov’ev, A.A. Large-Scale Magnetostatic Structures in the Solar Corona and a Model of the Polar Coronal Hole. Geomagn. Aeron. 2018, 58, 953–958. [Google Scholar] [CrossRef]
- Wang, Q.; Song, X.; Jiang, Z. An Improved Image Segmentation Method Using Three-dimensional Region Growing Algorithm. In Proceedings of the 2013 International Conference on Information Science and Computer Applications, Changsha, China, 8–9 November 2013; Atlantis Press: Dordrecht, The Netherlands, 2013; pp. 148–152. [Google Scholar] [CrossRef]
- Tlatov, A.G.; Vasil’eva, V.V.; Makarova, V.V.; Otkidychev, P.A. Applying an Automatic Image-Processing Method to Synoptic Observations. Sol. Phys. 2014, 289, 1403–1412. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Obridko, V.N.; Shelting, B.D. Structure of the Heliospheric Current Sheet derived for the interval 1915–1916. Sol. Phys. 1999, 184, 187–200. [Google Scholar] [CrossRef]
- Vasil’Eva, V.V.; Makarov, V.I.; Tlatov, A.G. Rotation Cycles of the Sector Structure of the Solar Magnetic Field and Its Activity. Astron. Lett. 2002, 28, 199–205. [Google Scholar] [CrossRef]
- Du, A.M.; Xu, W.Y.; Feng, X.S. Dependence of the IMF sector structure on the solar dipole tilt angle. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
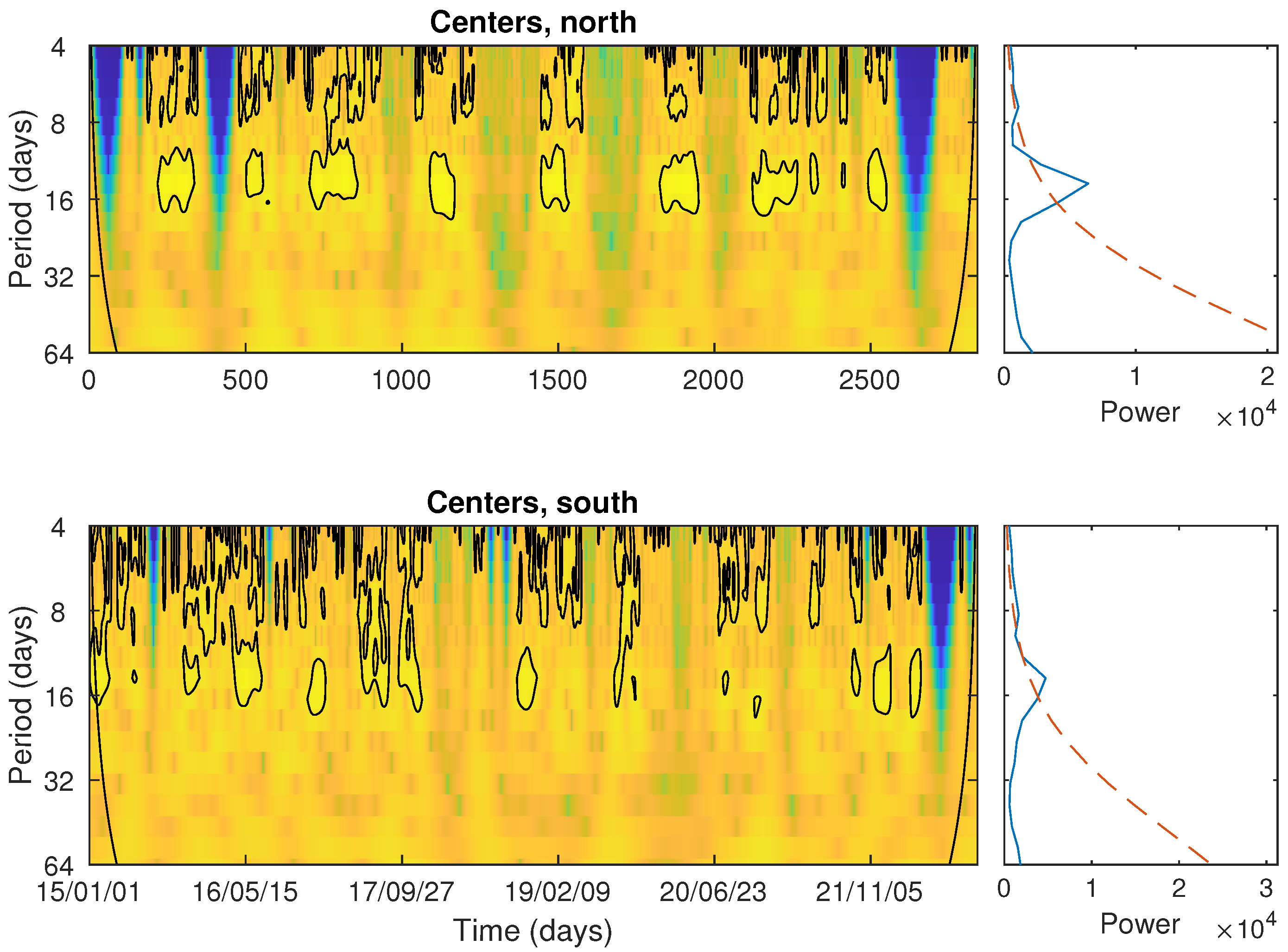
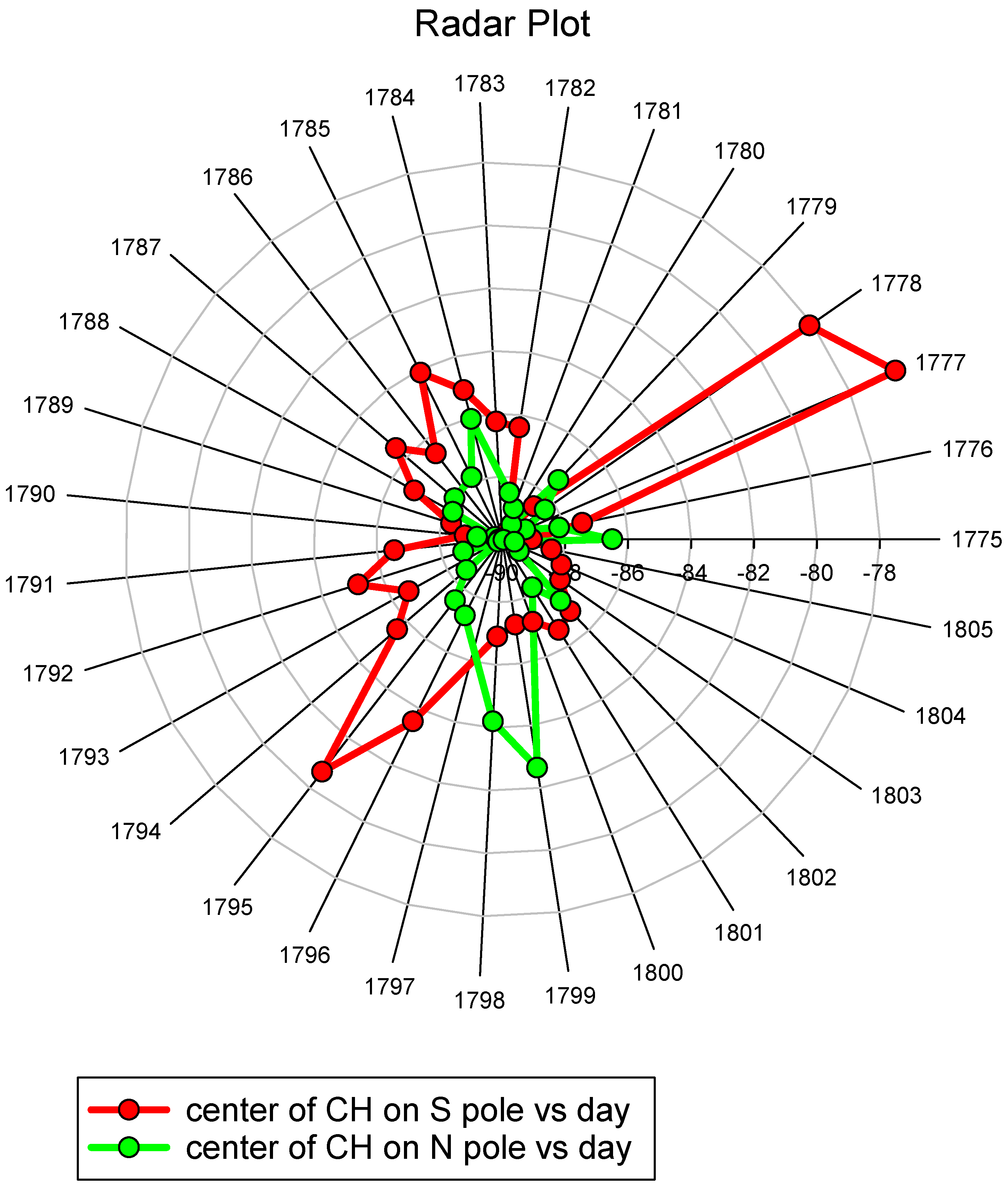
| Mean | Median | Std.Dev | Std.Err | 95% Conf |
|---|---|---|---|---|
| −85.009 | −86.55 | 5.075 | 0.1304 | 0.256 |
| 85.513 | 86.95 | 4.271 | 0.1074 | 0.211 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riehokainen, A.; Smirnova, V.; Solov’ev, A.; Strekalova, P. The Relative Position of the Solar Magnetic Dipole Axis and Rotation Axis of the Sun. Galaxies 2025, 13, 24. https://doi.org/10.3390/galaxies13020024
Riehokainen A, Smirnova V, Solov’ev A, Strekalova P. The Relative Position of the Solar Magnetic Dipole Axis and Rotation Axis of the Sun. Galaxies. 2025; 13(2):24. https://doi.org/10.3390/galaxies13020024
Chicago/Turabian StyleRiehokainen, Alexandr, Victoria Smirnova, Alexander Solov’ev, and Polina Strekalova. 2025. "The Relative Position of the Solar Magnetic Dipole Axis and Rotation Axis of the Sun" Galaxies 13, no. 2: 24. https://doi.org/10.3390/galaxies13020024
APA StyleRiehokainen, A., Smirnova, V., Solov’ev, A., & Strekalova, P. (2025). The Relative Position of the Solar Magnetic Dipole Axis and Rotation Axis of the Sun. Galaxies, 13(2), 24. https://doi.org/10.3390/galaxies13020024






