1. Introduction
Variation of physical constants is a subject that is marred with semantics: What exactly is varying and how is it being measured? There is an ongoing debate about dimensionful and dimensionless constants (e.g., Uzan [
1,
2], Duff [
3], Chiba [
4]). Our approach therefore would be to work mostly with easily comprehensible dimensionful constants and later on see if a meaningful relationship can be established for a common dimensionless parameter and how it evolves with time. The physical constants considered in this work are primarily the speed of light
, the Newton’s gravitational constant
, the Einstein’s cosmological constant
, the Planck’s constant
ħ, the Hubble constant
, and the fine structure constant
. There is a plethora of literature discussing the variation, or lack thereof, of these physical constants and others, and there are excellent reviews on the subject [
1,
2,
3,
4,
5,
6]. We will therefore limit ourselves to a selected few with direct relevance to our work. In addition, we will focus only on the time variation of physical constants in the spirit of the cosmological principle, which assumes the universe to be isotropic and homogeneous in space at large scale.
Varying physical constant theories gained traction after Dirac [
7,
8] in 1937 suggested such variation based on his large number hypothesis that related ratios of certain scales in the universe to that of the forces of nature. Magueijo [
6] reviewed the variable speed of light (VSL) theories and their limitations in 2003 that included theories based on hard breaking of Lorentz invariance, biometric models, local Lorentz invariance, color dependent speed of light, extra dimension (e.g., brane-world) induced variation, and field functions. Farrell and Dunning-Davis [
9] discussed in 2004 the VSL theories that were used as alternatives to the inflationary model of the universe and reviewed evidence for the same.
Maharaj and Naidoo [
10] introduced variable
and
in Einstein field equation using Robertson-Walker metric in 1993. Belenchon and Chakrabarty [
11] added the variation of
to develop a perfect fluid cosmological model in 2003. Recently (2017) Franzmann [
12] developed an approach that included space as well as time dependence of the constants. More recently Barrow and Magueijo [
13] proposed that the constants be considered as quantum observables in a kinematical Hilbert space. These works are mostly theoretical and do not directly offer how much exactly they vary and if they can directly explain some observations or measurements. Our focus will be to develop a model that can be used to explain certain anomalies, hitherto not explained satisfactorily, as well as the redshift vs distance modulus data on supernovae 1a better than alternative models.
The possible variation of the fine structure constant
has been of great interest as it is perhaps the most basic dimensionless constant in physics. Rosenband et al. [
14] have put a constraint on the
derived from the constancy of the ratio of aluminum and mercury single-ion optical clock frequencies. More recently Gohar [
15], using his entropic model of the universe and data on supernovae 1a, baryon acoustic oscillations, and cosmic microwave background, has established even more stringent constraint on the variation of
. Additionally, he states that in his model
and
should be increasing with the evolution of the universe, which corroborates our findings in this work. Similar constraints on
were shown by Songaila and Cowie [
16] from the observation of narrow quasar absorption lines at redshift
. There is a significant amount of work on the subject, most of it can be found referenced in the papers cited above.
If does vary, no matter how small the variation, it is normal to ask what causes its variation—electric charge , or ħ? We will show that since and ħ variations cancel out, it is that should be considered responsible for the variation of if there is any.
We will solve the Einstein field equation with varying
and
with Robertson-Walker metric in
Section 2, and show that
and
where
is the Hubble parameter. Based on the Hofmann and Müller’s [
17] determination of a very tight constraint on the variation of
from the analysis of laser lunar ranging data of more than 40 years, we will establish in
Section 3 that
and
.
Section 4 is devoted to the derivation of the expression for distance modulus
of an intergalactic light emitting source in terms of its redshift
.
Section 5 delineates the methodology for fitting the
data and applying the same to the new model, the variable
and
(VcG
model, and for comparison also to the standard
CDM model. Having shown that the VcG
model fits the supernovae 1a
data almost as well as the
CDM model and has predictive capability better than the latter, we will proceed to demonstrate that the model can explain the three astrometric anomalies that have not yet been explained satisfactorily. All we need to explain these anomalies is
and
at current time with
as the Hubble constant.
The first anomaly we will consider here is the Pioneer anomaly, which refers to the near constant acceleration back towards the sun, observed when a spacecraft cruises on a hyperbolic path away from the solar system (Anderson et al., 1998 [
18]). Many explanations have been given for such an anomaly but none appears to be satisfactory and they are difficult to incorporate in the models used for real time spacecraft astrodynamics. Principal among these explanations are as follows: (a) Turyshev et al. [
19] in 2012 tried to explain the anomaly as being due to the recoil force associated with an anisotropic emission of thermal radiation off the spacecraft. However, it is not clear why it should be the same for Pioneer 10/11, Galileo and Ulysses spacecrafts. (b) Feldman and Anderson [
20] in 2015 used “the theory of inertial centers” [
21] to develop a model to compute the anomaly. (c) Kopeikim [
22] in 2012 used Hubble expansion of the universe to address the anomaly and gave a reason why one should see deceleration rather than acceleration of the spacecraft due the expansion of the universe. These approaches are rather circuitous and depend on many assumptions to explain the anomaly. Feldman and Anderson [
20] allocated 12% of the total anomalous acceleration of
m
to various thermal contributions, leaving
m
that requires other explanations. In
Section 6 we will try to explain this unexplained Pioneer acceleration.
The lunar laser ranging technique has improved to the extent that it can determine the lunar orbit with an accuracy of better than a centimeter. The moon’s orbit has an eccentricity that depends on the tidal forces due to surficial and the geophysical processes interior to Earth and the moon. After all the known sources responsible for the eccentricity
were included, Williams and Dickey [
23] in 2003 estimated that there remained a discrepancy of
between the observed and calculated values. This value was revised downward by Williams and Boggs [
24] in 2009 to
and by Williams, Turyshev and Boggs [
25] in 2014 to
with updated data and tidal models. With additional terrestrial tidal modeling, William and Boggs [
26] in 2016 were able to further reduce the number and stated that it might even be negative. While these authors possibly felt that unexplained secular increase of the eccentricity was due to the deficiency in their model and therefore a better tidal modeling should eliminate it, others feel that the anomaly may be pointing to some unknown physical process. There have been attempts to resolve the anomaly using Newtonian, relativistic and modified gravity approaches [
27,
28,
29] as well as using some unfamiliar gravitational effects [
27]. Reviews by Anderson and Nieto [
30] in 2009 and Iorio [
31] in 2015 have covered the above and additional attempts to solve the problem. It appears that none of the models secularly affect the lunar eccentricity. Attempts of cosmological origin were also not successful [
22,
29,
32,
33]. We attempt to explain this anomaly in
Section 7 with the varying
and
approach developed here.
The anomalous secular increase of astronomical unit
AU was first reported by Krasinsky and Brumberg [
34] in 2004 as d
AU/dt = (15 ± 4) m cy
−1 from the analysis of all radiometric measurements of distances between Earth and the major planets they had available over the period 1971–2003, which included the observations of Martian landers and orbiters. They noted that unexplained secular increase in
AU might point to some fundamental features of space time that are beyond the current cosmological understanding according to which the Hubble expansion yields d
AU/dt = 1 km cy
−1. This value is almost two orders of magnitude higher than observed. Their theoretical analysis revealed that the relativistic calculations that included the gravitational shift of proper time gave null results. Anderson and Nieto [
30] in 2009 corroborated Krasinsky and Brumberg’s [
34] findings. They showed that the effect of the loss of solar mass on
AU is miniscule and will cause the
AU to shrink rather than increase (d
AU/dt = −0.34 cm cy
−1). Iorio [
31] in 2015 reviewed the status of the
AU anomaly in significant details and concluded that, considering the various unsatisfactory attempts to explain the anomaly and the new IAU definition of astronomical unit, the anomaly no longer exists (just by virtue of new definition). We show in
Section 8 that the AU anomaly based on the old definition can be easily explained with the new approach.
Section 9 shows how we obtain the variation of
from the null result on the variation of fine structure constant. We explore the relationship between Planck units and Hubble units in
Section 10, and show that all units have the same constant relating them, and then determine how this constant evolves in time.
Section 11 is devoted to discussion and
Section 12 to conclusions.
2. Evolutionary Constants Model
We will develop our model in the general relativistic domain starting from the Robertson-Walker metric with the usual coordinates
where
is the scale factor and
determines the spatial geometry of the universe:
(closed), 0 (flat), +1 (open). The Einstein field equations may be written in terms of the Einstein tensor
metric tensor
, energy-momentum tensor
, cosmological constant
, gravitational constant
and speed of light
as:
When solved for the Robertson-Walker metric, we get the following non-trivial equations for the flat universe (
of interest to us here, with
as the pressure and
as the energy density [
10]:
If we do not regard
,
and
to be constant and define
we may easily derive the continuity equation by taking time derivative of Equation (4) and substituting in Equation (3) (see
Appendix A):
This reduces to the standard continuity equation when
and
are held constant. And since the Einstein field equations require that the covariant derivative of the energy-momentum tensor
be zero, we can interpret Equation (5) as comprising of two continuity equations [
10], viz:
This separation simplifies the solution of the field equations (Equations (3) and (4)). Equation (6) yields the standard solution for the energy density . Here is the equation of state parameter defined as with for matter, 1/3 for radiation and for .
As has been explicitly delineated by Magueijo in several of his papers (e.g., reference [
35]), this approach is not generally Lorentz invariant albeit relativistic. Strictly speaking we should have used the Einstein-Hilbert action to obtain correct Einstein equations with variable
and
as scalar fields. Thus, one may consider the current formulation quasi-phenomenological.
Since the expansion of the universe is determined by
, it is natural to assume the time dependence of any time dependent parameter to be proportional to
(the so called Machian scenario—Magueijo [
6]). Let us therefore write:
where
,
and
are the proportionality constants, and subscript zero indicates the parameter value at present
. With this substitution in Equation (4) we may write:
Comparing the exponents of the only time dependent parameter a of all the terms, we may write , and with for matter, we have . Thus, if we know , we know and .
We can now have a closed analytical solution of Equation (10) as follows (since
):
where
is the deceleration parameter. It may be noticed that
does not depend on time, i.e.,
. As we know the radiation energy density is negligible at present, and dark energy
Λ is implicitly included in the above formulation, so we need to be concerned with the matter only solutions, i.e., with
.
The deceleration parameter
has been analytically determined on the premise that expansion of the universe and the tired light phenomena are jointly responsible for the observed redshift, especially in the limit of very low redshift [
36]. One could see it as if the tired light effect is superimposed on the Einstein de Sitter’s matter only universe rather than the cosmological constant [
37]. By equating the expressions for the proper distance of the source of the redshift for the two, one gets
. Then from Equation (12) we get
, and also
and
. We thus have from Equation (8)
,
and
.
3. Varying G and c Formulation
Having determined the value of
, and since the Hubble parameter is defined as
, we may write from Equations (8) and (9):
We may also write explicitly:
Taking at the present time as km Mpc−1 (2.27 ) we get .
The findings from the Lunar Laser Ranging (LLR) data analysis provides the limits on the variation of
(
) [
17], which is considered to be about three orders of magnitude lower than was expected [
7,
8,
38]. However, the LLR data analysis is based on the assumption that the distance measuring tool, i.e., the speed of light, is constant and non-evolutionary. If this constraint were dropped then the finding would be very different.
As is well known [
39], a time variation of
should show up as an anomalous evolution of the orbital period
of astronomical bodies expressed by Kepler’s 3rd law:
where
is semi-major axis of the orbit,
is the gravitational constant and
is the mass of the bodies involved in the orbital motion considered. If we take time derivative of Equation (15), divide by
and rearrange, we get:
If we write
then
. Here
may be considered associated with the Hubble time (i.e.,
), as are other quantities. We may now rewrite Equation (16) as:
Since LLR measures the time of flight of the laser photons, it is the right hand side of Equation (17) that is determined from LLR data analysis [
17] to be
and not the right hand side of Equation (16).
Then, taking the right hand side of Equation (17) as 0 and combining it with Equation (14), one can solve the two equations and get
and
. It should be emphasized that both
and
are positive and thus both of them are
increasing with time rather than decreasing, as is generally believed (e.g., [
7,
8,
40]). This may be considered as the most significant observational finding of cosmological consequences just by studying the Earth–moon system.
4. Redshift vs. Distance Modulus
The distance
of a light emitting source in a distant galaxy is determined from the measurement of its bolometric flux
and comparing it with a known luminosity
. The luminosity distance
is defined as:
In a flat universe the measured flux could be related to the luminosity
with an inverse square relation
. However, this relation needs to be modified to take into account the flux losses due to the expansion of the universe through the scale factor
, the redshift
and all other phenomena that can result in the loss of flux. Generally accepted flux loss phenomena are as follows [
41]:
Increase in the wavelength causes a flux loss proportional to .
In an expanding universe, an increase in detection time between two consecutive photons emitted from a source leads to a reduction of flux proportional to , i.e., proportional to .
Therefore, in an expanding universe the necessary flux correction required is proportional to
. The measured bolometric flux
and the luminosity distance
may thus be written as:
How does
compare with and without varying
? Let us first consider the case of non-expanding universe. The distance from the point of emission at time
to the point of observation at time
may be written as
Therefore for constant
:
When
and since
from Equation (11), we may write:
The ratio of the two distances may be considered the normalization factor
when using the variable
in calculating the proper distance of a source. Since
, we may write for the source of redshift
with emission time
Now the proper distance of the source with variable
may be defined as [
41] (page 105):
From Equation (11)
. Therefore:
Thus the expression for to be substituted in Equation (20) to determine the luminosity distance of the source is
Since the observed quantity is distance modulus
rather than the luminosity distance
, we will use the relation:
where
and all the distances are in Mpc. It is the only free parameter in Equation (28).
We will compare the new model, hereafter referred to as the VcG
(variable
and
) model, with the standard
CDM model, which is the most accepted model for explaining cosmological phenomena, and thus may be considered the reference models for all the other models. Ignoring the contribution of radiation density at the current epoch, we may write the distance modulus
for redshift
in a flat universe for the
CDM model as follows [
42]:
Here is the current matter density relative to critical density and is the current dark energy density relative to critical density.
5. Supernovae Ia z-µ Data Fit
We tried the VcG
model developed here to see how well it fits the best supernovae Ia data [
43] as compared to the standard ΛCDM model. The data fit is shown in
Figure 1. The VcG
model requires only one parameter to fit all the data (
km
), whereas the ΛCDM model requires two parameters (
km
and
).
The data used in this work is the so-called Pantheon Sample of 1048 supernovae Ia in the range of
[
43]. The data is in terms of the apparent magnitude and we added 19.35 to it to obtain normal luminosity distance numbers as suggested by Scolnic [
43]. To test the fitting and predictive capability of the two models, we divided the data in 6 subsets: (a)
; (b)
; (c)
; (d)
; (e)
and (f)
. The idea is to parameterize a model with a low redshift data subset and then see how the model, using parameters thus obtained, fits the remaining redshift data. In addition, we considered the fits for the whole data. The models were parameterized with subsets (a), (b) and (c). The parameterized models were then tried to fit the data in the subsets that contained data with z values higher than in the parameterized subset. For example if the models were parameterized with data subset (a)
, then the models were fitted with the data subsets (d)
(e)
and (f)
to examine the models’ predictive capability.
The Matlab curve fitting tool was used to fit the data by minimizing
and the latter was used for determining the corresponding
probability [
44]
. Here
is the weighted summed square of residual of
:
where
is the number of data points,
is the weight of the
th data point
determined from the measurement error
in the observed distance modulus
using the relation
, and
is the model calculated distance modulus dependent on parameters
and all other model dependent parameter
etc. As an example, for the
CDM models considered here,
and there is no other unknown parameter.
We then quantified the goodness-of-fit of a model by calculating the
probability for a model whose
has been determined by fitting the observed data with known measurement error as above. This probability
for a
distribution with
degrees of freedom (DOF), the latter being the number of data points less the number of fitted parameters, is given by:
where
is the well know gamma function that is generalization of the factorial function to complex and non-integer numbers. The lower the value of
the better the fit, but the real test of the goodness-of-fit is the
probability
; the higher the value of
for a model, the better the model’s fit to the data. We used an online calculator to determine
from the input of
and DOF [
45]. Our primary findings are presented in
Table 1. The unit of the Hubble distance
is Mpc and that of the Hubble constant
is km s
−1 Mpc
−1. The table is divided into four categories vertically and four categories horizontally. Vertical division is based on the parameterizing data subset indicated in the second row and discussed above. The parameters determined for each model are in the first horizontal category. The remaining horizontal categories show the goodness-of-fit parameters for higher redshift subsets than those used for parameterizing the models. Thus this table shows the relative predictive capability of the two models. The model cells with the highest probability in each category are shown in bold and highlighted.
6. Pioneer Anomaly
Having determined the values of
and
we can now proceed to calculate the anomalous acceleration towards the sun of Pioneer 10 and 11 spacecraft [
20]. Since the gravitational pull of the sun on the spacecraft decreases according the inverse square law,
cannot be expected to give a constant acceleration independent of the distance of the spacecraft. If the acceleration is denoted by
, one can easily work out, using the Newtonian relation
, that
, which yields negligible anomalous acceleration. Thus, we need to only consider the effect of
from a different perspective. If the spacecraft is at a distance
from Earth then the signal from Earth will have a two way transit time
given by
assuming
as the speed of light. But, if the speed of light is evolving as
near
, i.e., as
during the transit time, then the actual transit time will be shorter than
(since
for
). Because of the shorter actual transit time, an observer would consider the spacecraft to be nearer to Earth than it actually is and thus would think that there is a deceleration of the spacecraft due to some unaccounted-for cause.
We could write the proper distance of the spacecraft
and its apparent distance
as:
Thus the acceleration is − m, and since it is negative, it is towards the observer at Earth.
Out of m anomalous acceleration of Pioneer 10 and 11 towards the sun (truly towards Earth) we are able to analytically account for m, leaving only m as the anomaly.
It should be mentioned that Kopeikin [
22] has obtained essentially the same result and explained it as due to the cosmological effect of quadratic divergence between the electromagnetic and atomic time scales governing the propagation of radio waves in the Doppler tracking system and the atomic clock on Earth, respectively. However, his approach is not conducive to explaining the other two anomalies.
7. The Moon’s Eccentricity Anomaly
The eccentricity
of the orbit of the moon may be written as [
46]:
where
is the specific orbital energy,
here the gravitational parameter for the Earth–moon system,
is the specific relative angular momentum,
is the semi-major axis of the orbit,
is mass of Earth,
is the mass of the moon,
is the radius vector and
is the velocity vector of the moon, and
is the reduced mass. Taking
and assuming
, we may write Equation (34) as:
Differentiating this equation with respect to time, assuming the mass factor to be constant, and dividing by the same equation, we get:
and, since
e ≪ 1:
Since
is measured by electromagnetic waves, the measuring tool for distance, the speed of light, enters in it, i.e.,
or
or
. Since all the parameters are expressed at current time,
in the denominator must be expressed in terms of the Hubble time
. However, it is better to write
where
is the small factor very close to 0 that may be considered to correct for the approximations made in our model (
here is not pressure). We can also determine
:
, assuming
as constant. Thus
. We may therefore write Equation (37) as:
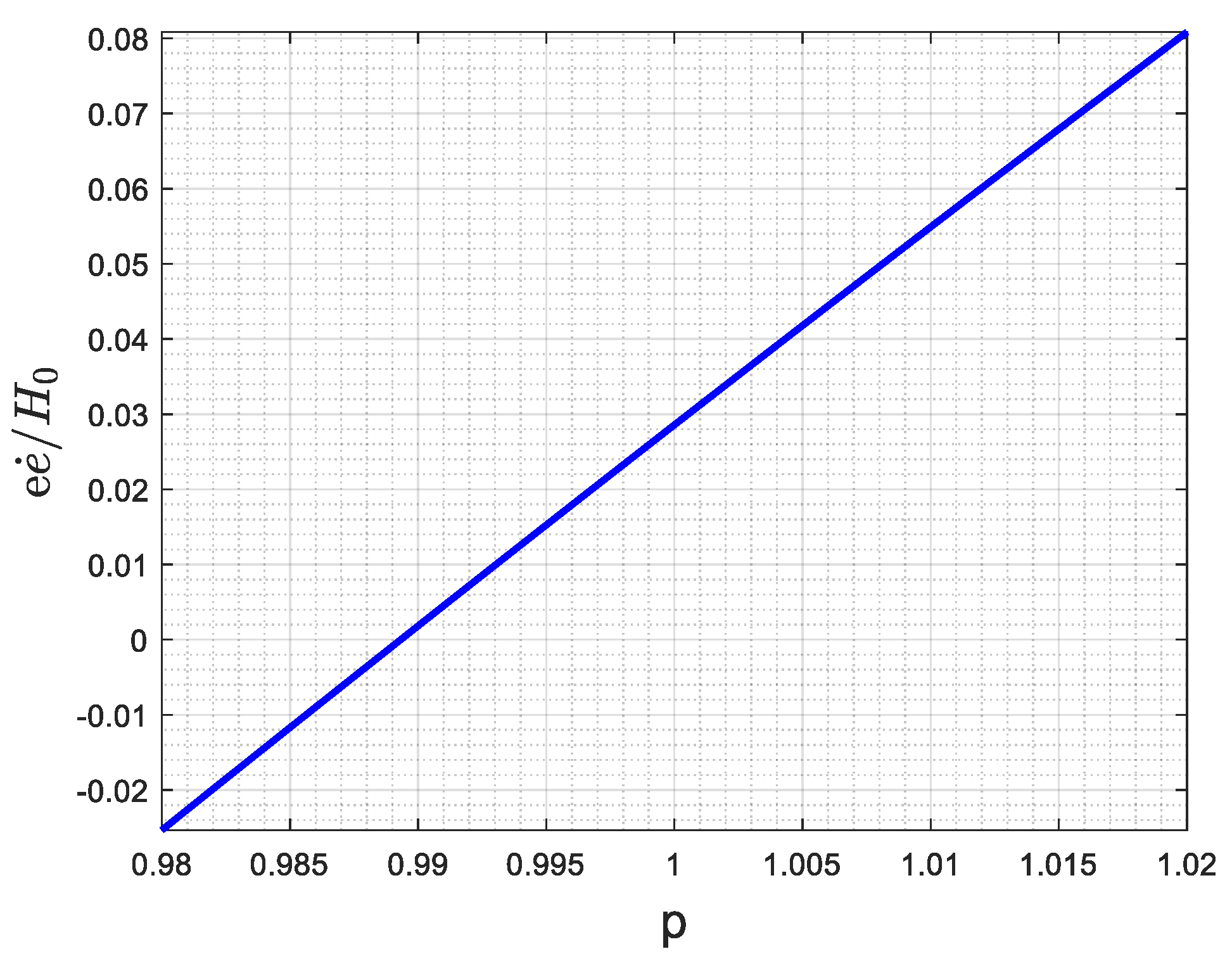
For and taking , and for the moon, we get . This is about twice the original value of the anomalous rate of eccentricity increase.
The value determined is very sensitive to the value of the parameter
. We have therefore plotted dimensionless eccentricity variation
against
in
Figure 2. It can be approximated near
with the expression:
There are three values of that are significant here:
originally estimated by Williams and Dickey in 2003 [
23]; it gives
.
, the updated value using more data and ‘better’ tidal effect model by Williams and Boggs in 2009 [
24]; it gives
.
the updated value with even more data and ‘even better’ tidal effect model by Williams et al. in 2014 [
25]; it gives
.
All the values of
are very close to 1, indicating that our model is a very good approximation to the exact solution of the Einstein field equations, at least locally, with variable
. Even lower and negative values of
derived by Williams and Boggs in 2016 [
26] can be easily explained with this approach. The question remains—is it the tidal model’s deficiency that is being corrected or is it presumed that there could be no other cause for the anomaly?
11. Discussion
As should be expected, the two-parameter CDM model is able to fit any data set better than the one-parameter VcG model. What is unexpected is that when parameterized with a relatively low redshift data the VcG model is able to fit the higher redshift data better than the CDM model. This shows that the second parameter in the latter, while trying to fit a limited dataset as best as possible, compromises the model fit for data not used for parameterizing. This means that the CDM model does not have as good a predictive capability (i.e., the capability to fit the data that is not included for determining the model parameters) as the VcG model, despite having twice as many parameters as the VcGmodel. In addition, the VcG model has the analytical expression for the distance modulus unlike the CDM model, which must be evaluated numerically.
One would notice that while (and hence values are relatively stable with the parameterizing dataset containing higher and higher redshift values, varying no more than 0.35%, the variation in the is up to 9.4%, i.e., 27 time larger. This confirms that the parameter, and hence through , is an artificially introduced parameter to fit the data rather than being fundamental to the CDM model. In contrast, is an integral part of the VcG model. Since () and are related through Equation (7), one could easily derive that the term contributes 60% for the VcG model against 70% for the CDM model.
We have established that the supernovae 1a data is compatible with the variable constants proposition. This is contrary to the findings of Mould and Uddin [
49] in 2014 who considered only the variation of
in their work. We believe most of the negative findings on the variation of physical constants are possibly due to the variation of a constant being considered in isolation rather than holistically for all the constants involved. We have established that the physical constants not only vary but also how much they vary:
,
,
and
. In addition, from the null results on the variation of the fine structure constant [
14,
15], we have shown that
. We urge that they be used in union rather than in isolation. This indeed was not possible until now when one knows the exact form of the variation of each as above.
One basic question naturally arises—what is the consequences of the findings here? It is clear from the above that at time the dark energy parameter was infinity, whereas and were zero. Existence of any baryonic matter and radiation was irrelevant since they did not provide any energy density due to and all being zero. We may need to explore how the universe would evolve from such a state against the state assumed in the standard model.
One may wonder how the physical constants’ variation could be measured experimentally. The most accurate device developed to date to measure the variation of fine structure constant
is atomic clock based on the hyperfine trasitions of certain atoms at microwave and optical frequencies. The transitions are also used for tests of quantum electrodynamics, general relativity and the equivalence principle, searches for dark matter, dark energy and extra forces, and tests of the spin-statistics theorem [
50,
51,
52]. However, tests related to the variation of
and
as presented here are not possible using the atomic transitions since the latter are dependent on the variation of α, which is already assumed to be zero in our theory.
Spinning bodies cause spacetime to rotate around it causing the nearby angular momentum vector to precess. This so-called frame-dragging phenomenon causes the electromagnetic signal from an orbiting spacecraft to register a redshift
given by [
53]:
where
is the mass of the spinning body and
is its spinning period. If
and
evolve in time as determined in this paper then
will not vary in time due to the variation of these constants, and therefore this method is not suitable for measuring their variation.
If we could isolate all the perturbative and relativistic effects on a high eccentricity satellite orbit then any residual increase in its eccentricity and orbit size may be attributed to the variation of and , and Equations (40) and (43) may be adapted to the satellite parameters. In addition, any spacecraft receding from Earth should experience anomalous deceleration similar to Pioneer’s. The spacecraft may be designed to eliminate or minimize the thermal radiation anisotropy. One could possibly design other experiments that could test the variability of constants when all the constants discussed here are simultaneously varying.
Existence of the parameter in estimating eccentricity increase can be seen as a deficiency of the quasi-phenomenological model we have used. Since the Moon eccentricity involves Earth and Moon whereas the AU increase involves Earth and Sun, and since the masses of the two systems are enormously different, the parameter may be considered to take this difference into account. We will need to develop a fully relativistic theory to eliminate this arbitrariness in for estimating the two anomalies with varying and . Until then it would be prudent to leave and just be contended that the variable and theory is able to estimate the anomalies within a factor of 2.