Static and Dynamic Characteristics of Rough Porous Rayleigh Step Bearing Lubricated with Couple Stress Fluid
Abstract
:1. Introduction
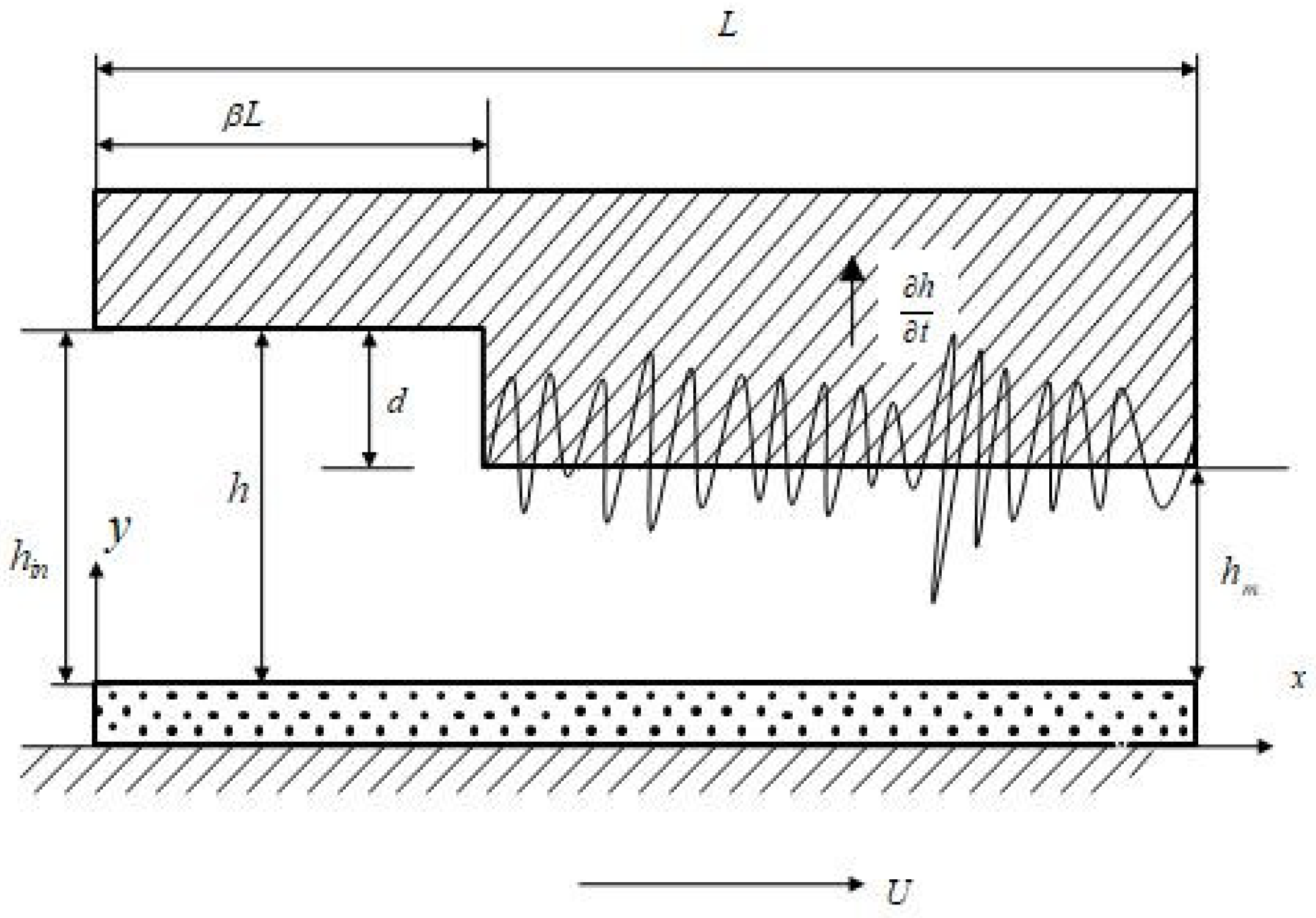
2. Mathematical Formulation
3. Results
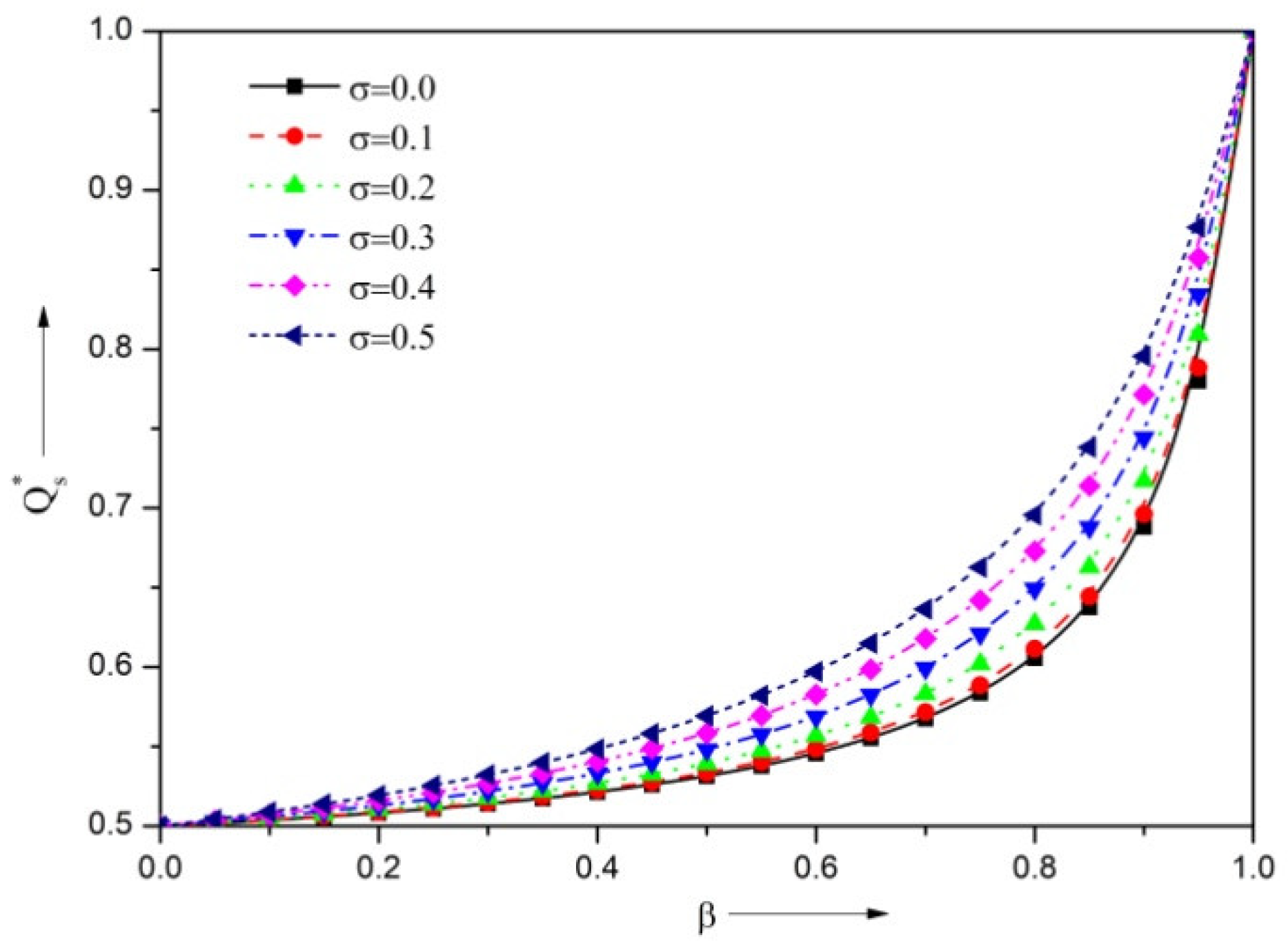
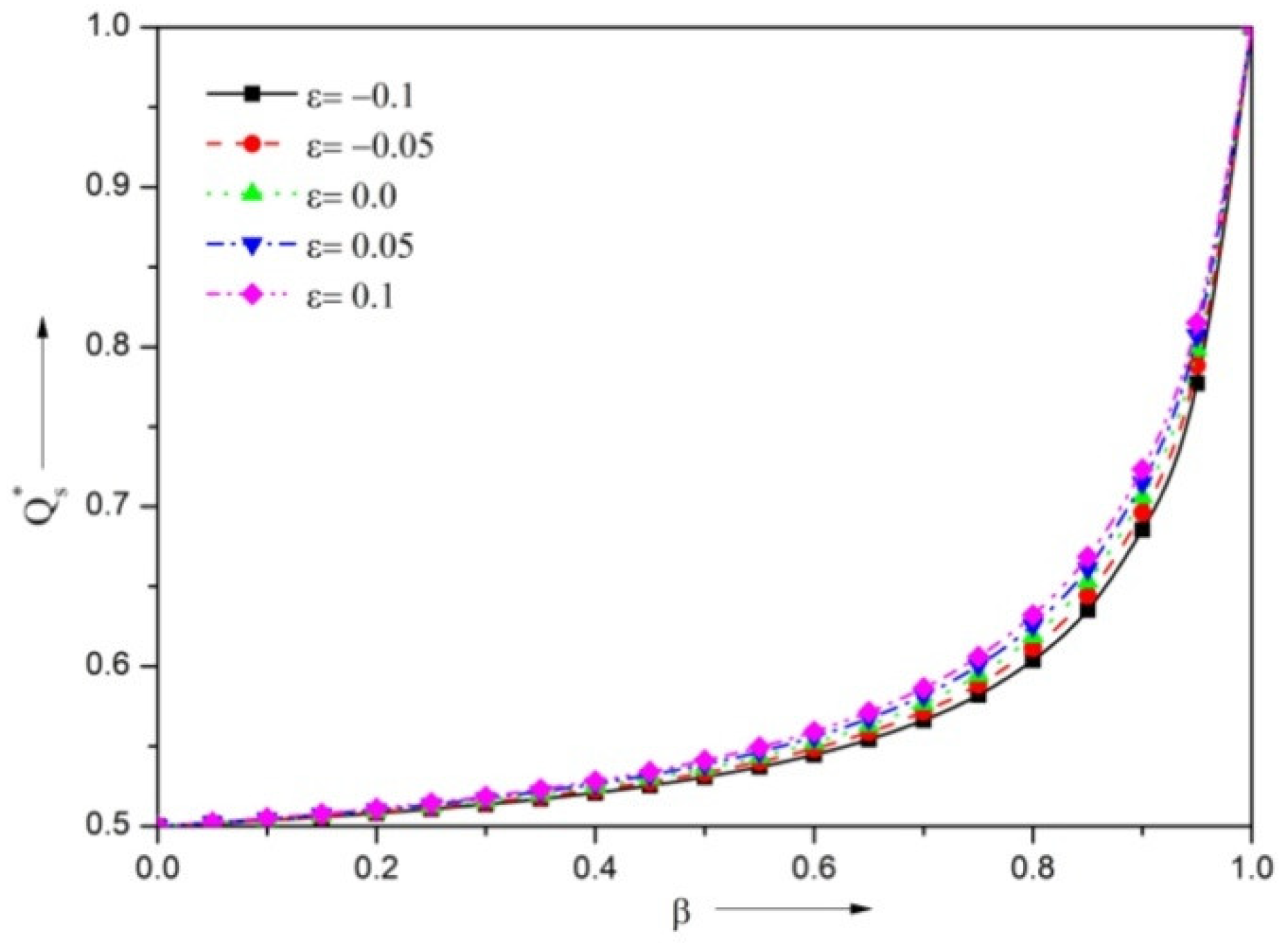
3.1. Volume Flow Rate
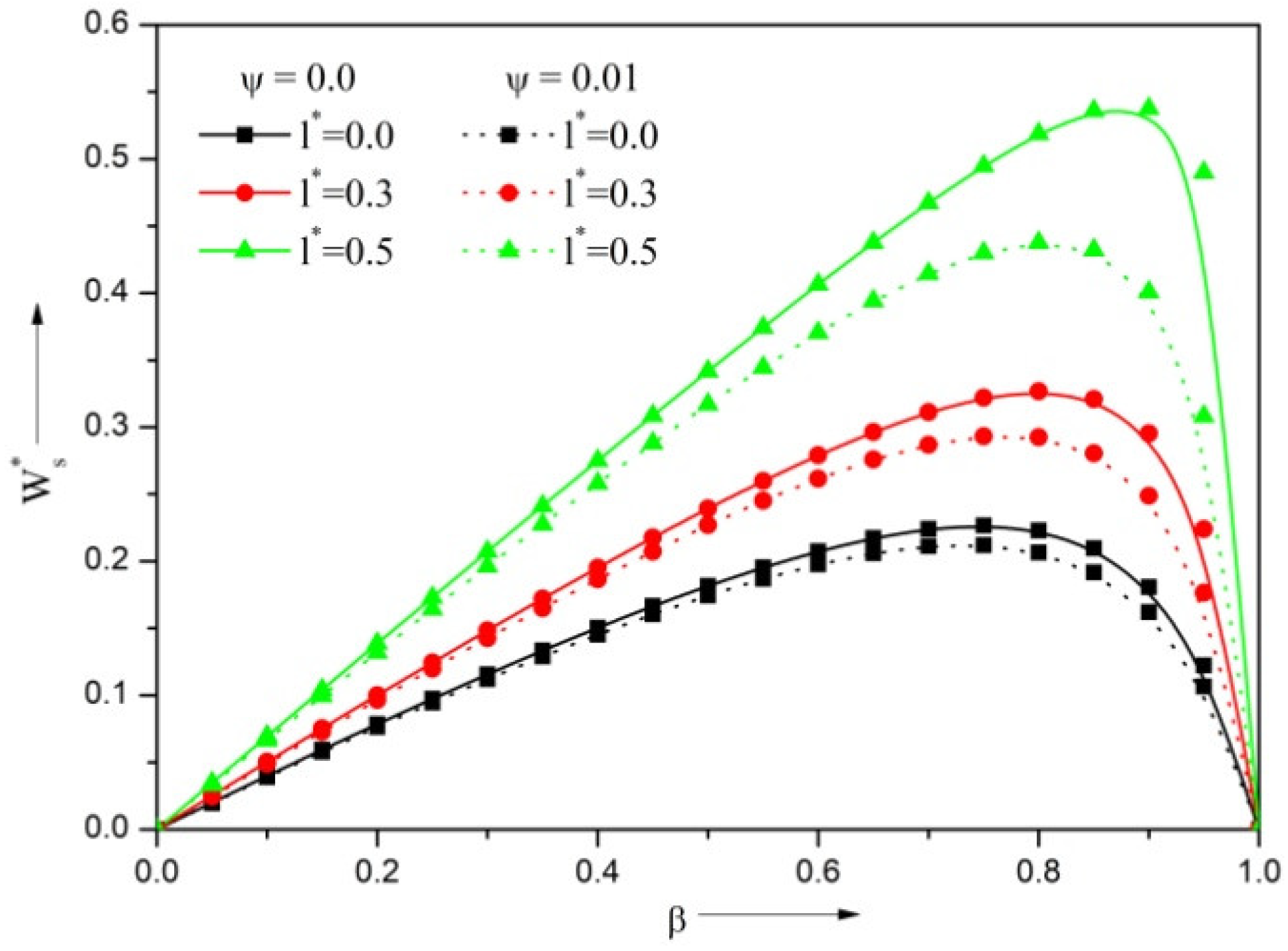
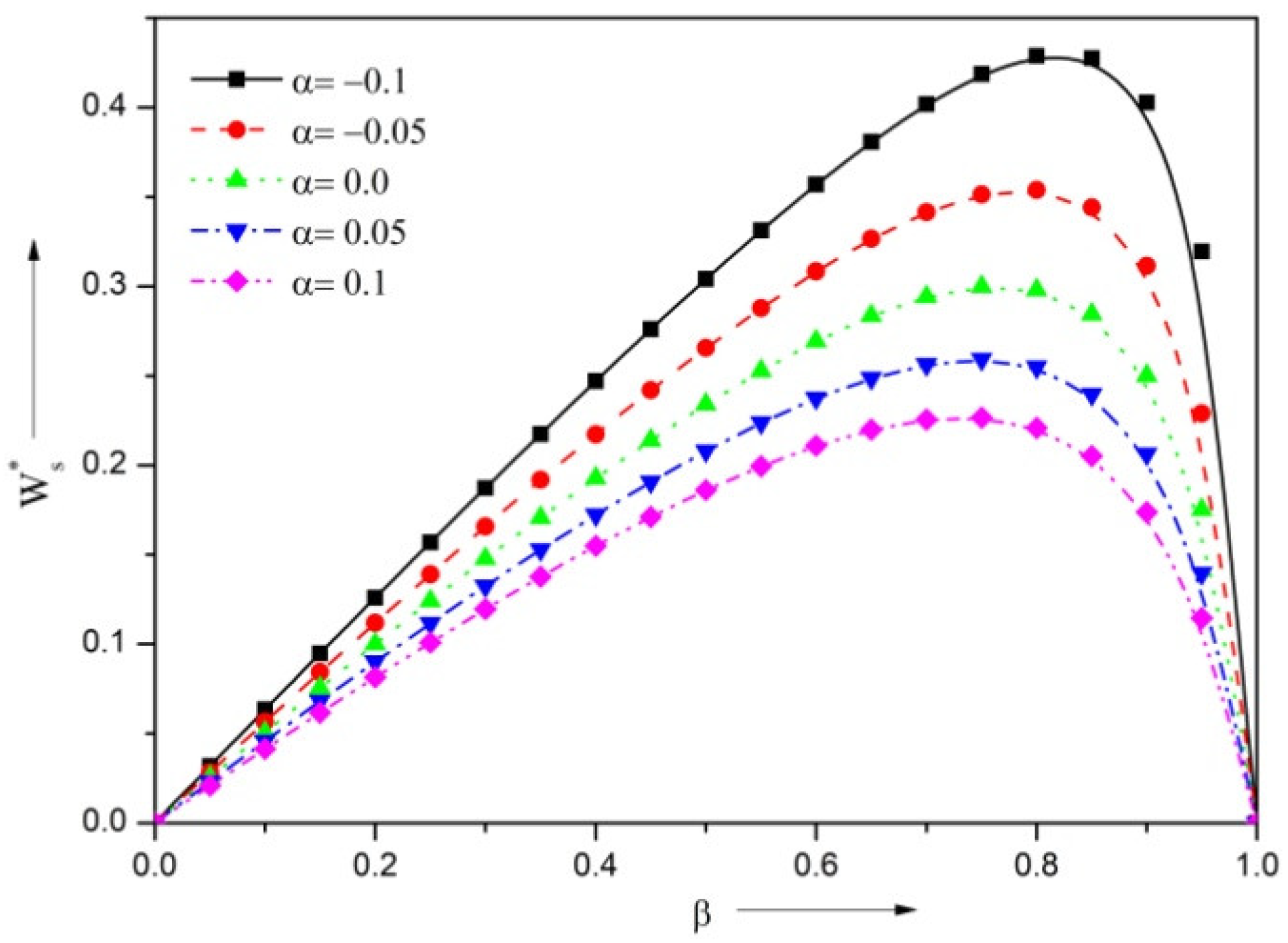
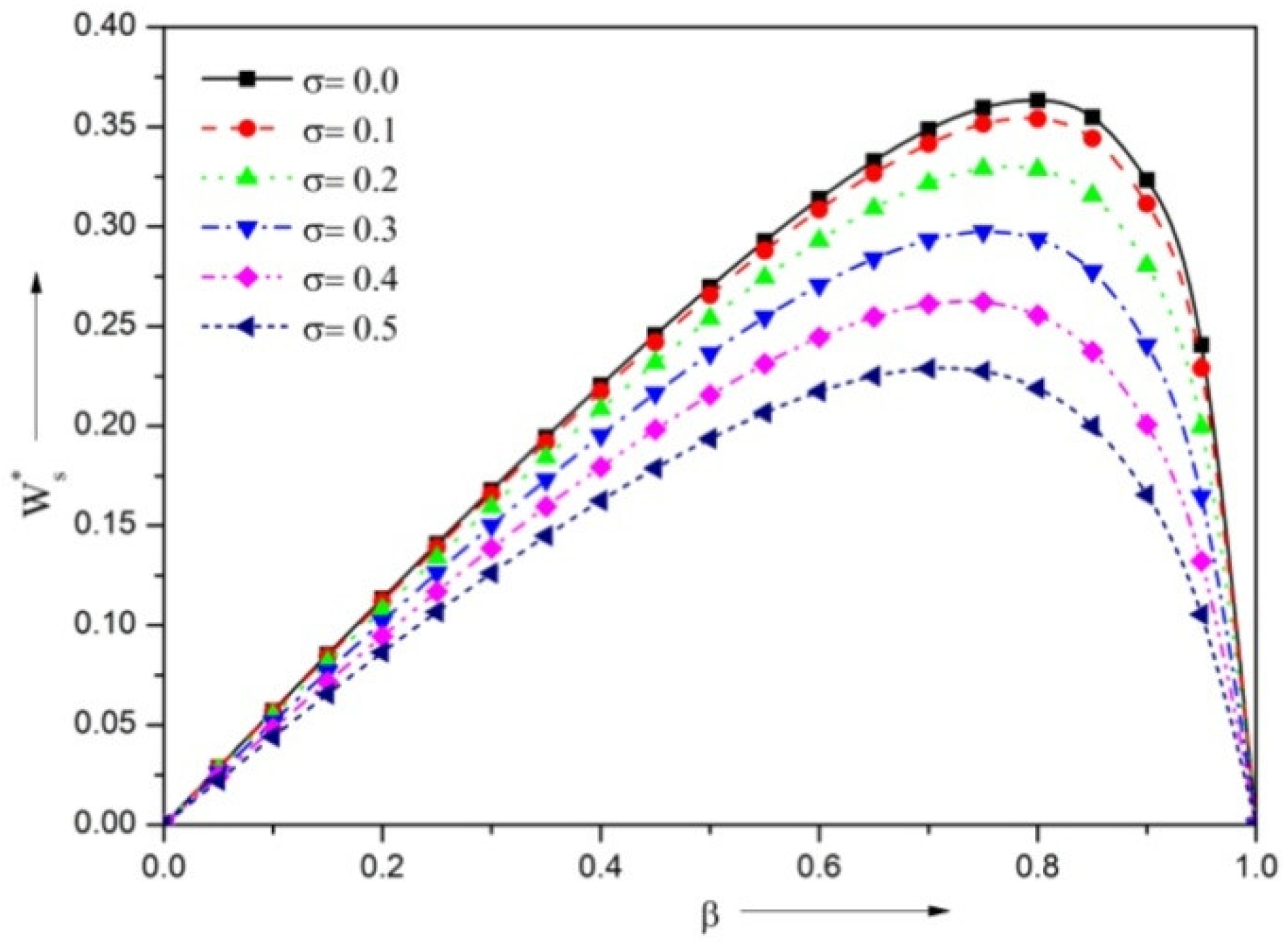
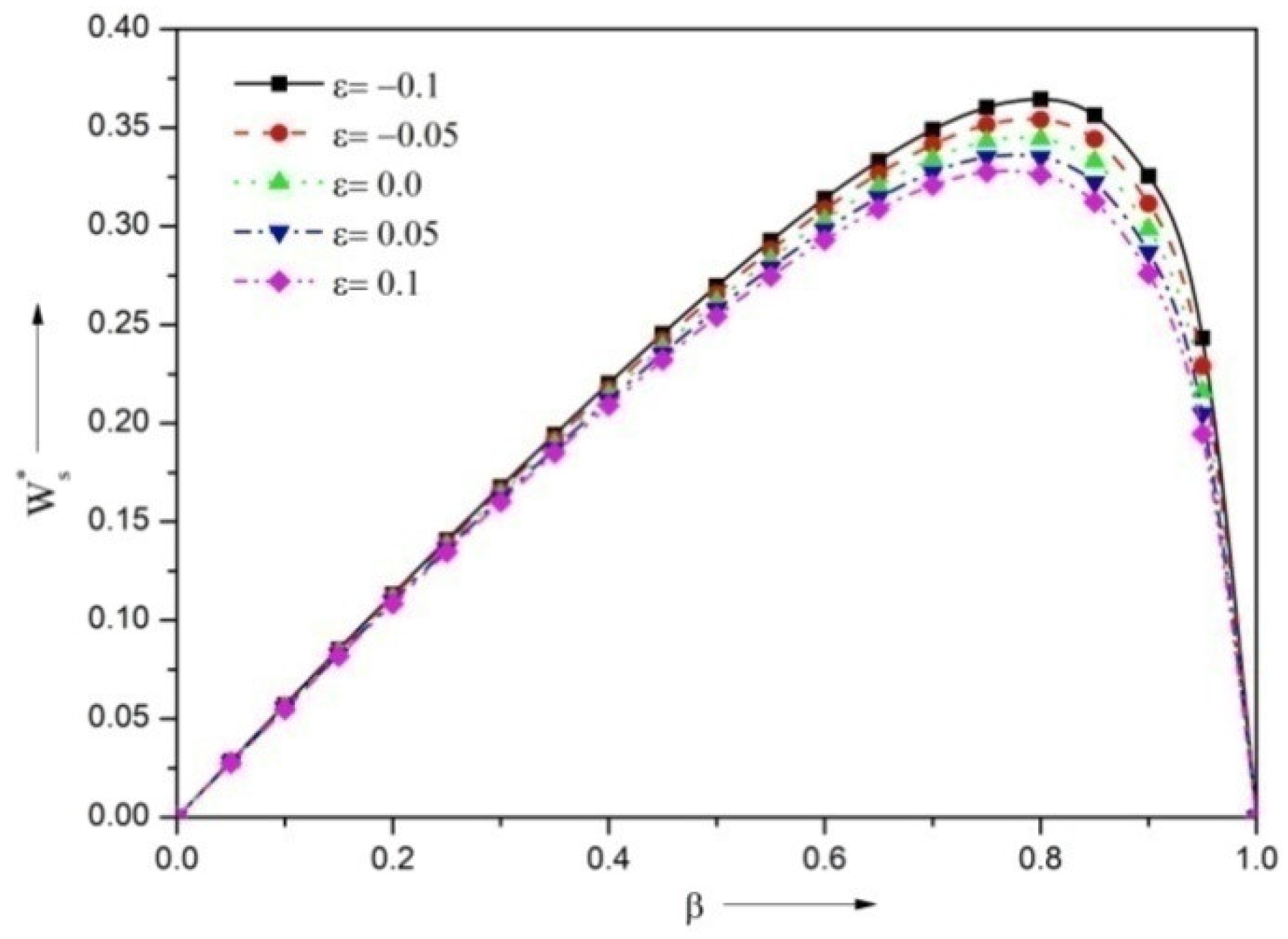
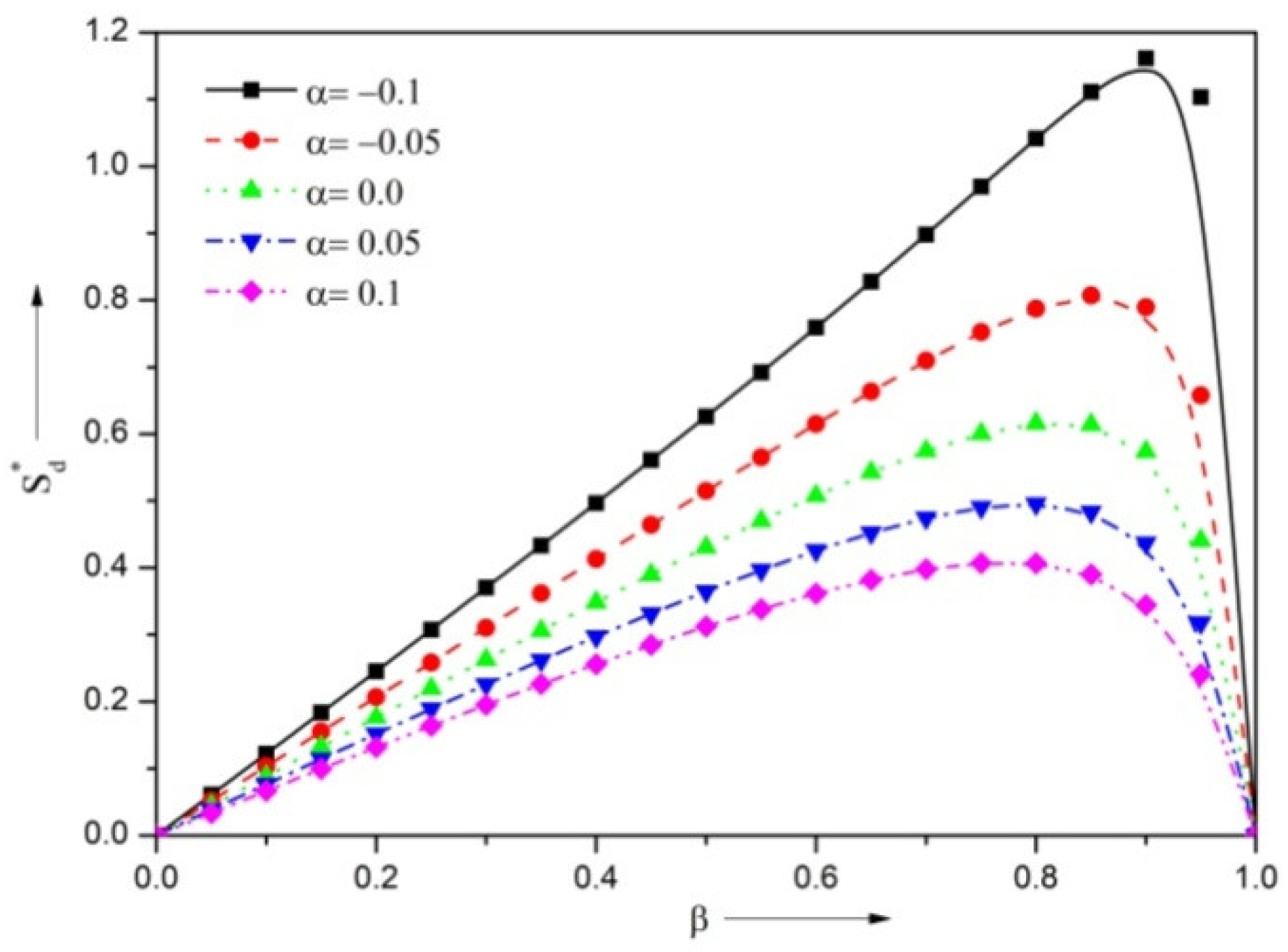
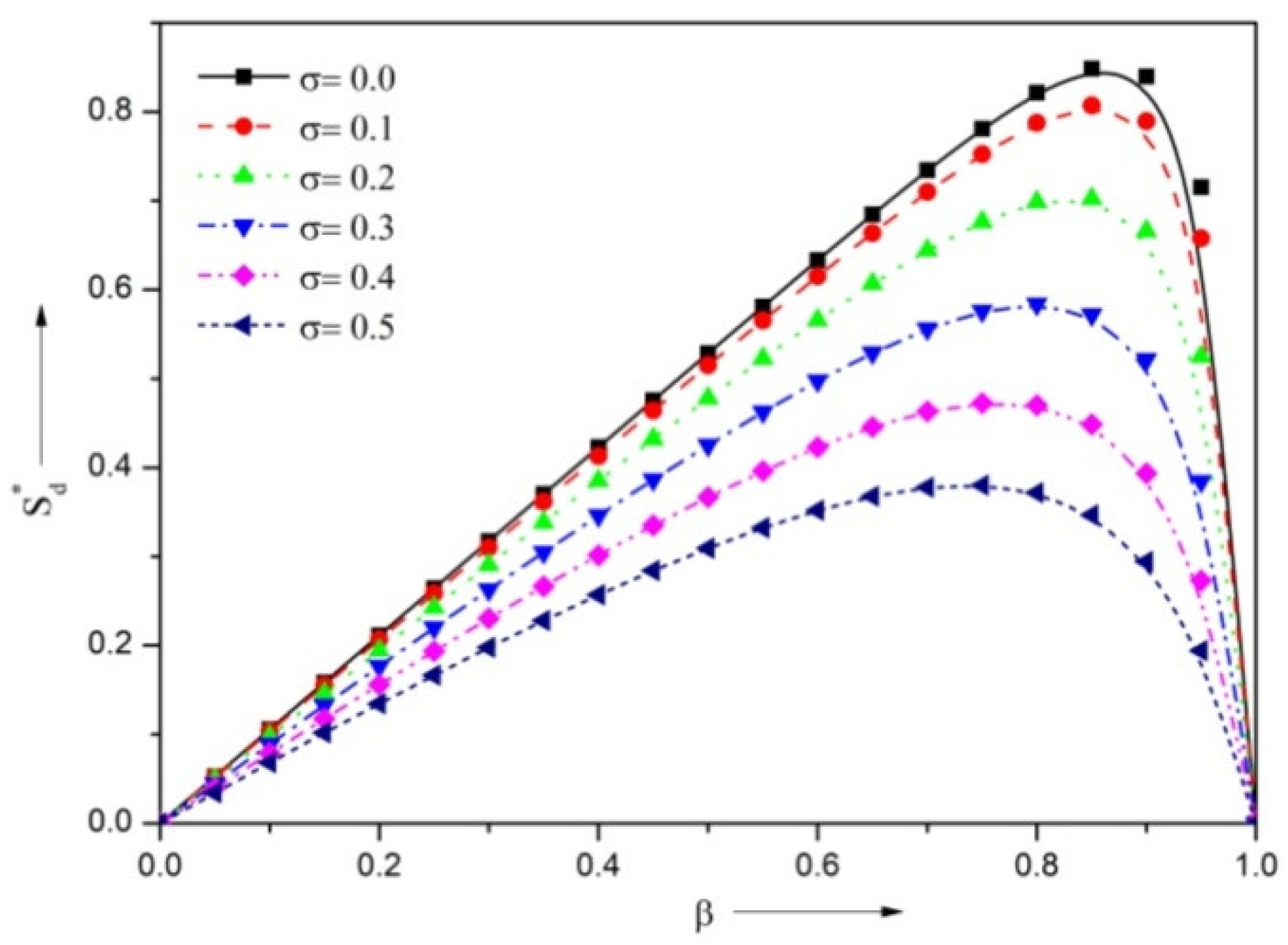
3.2. Steady Load-Carrying Capacity
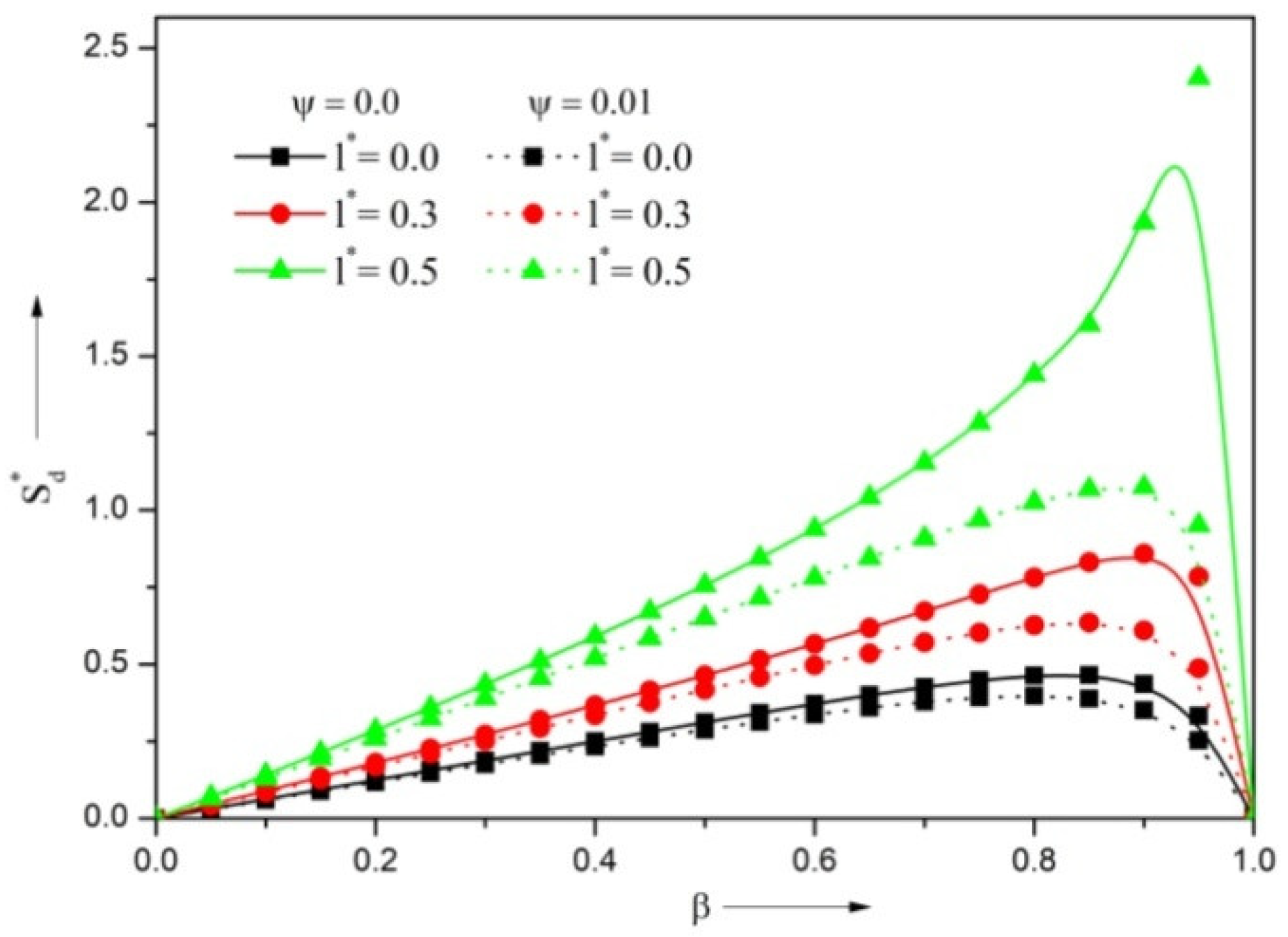
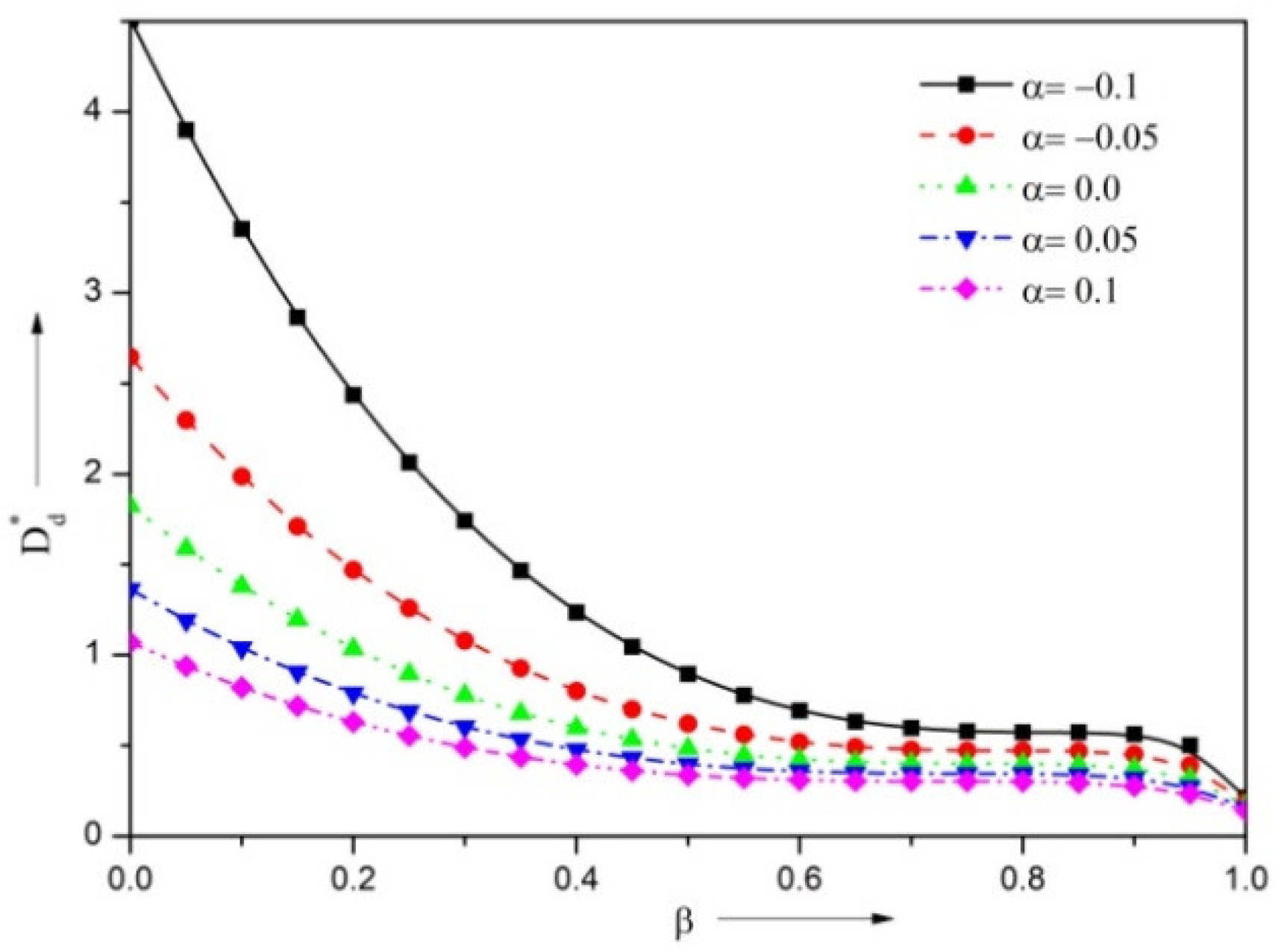
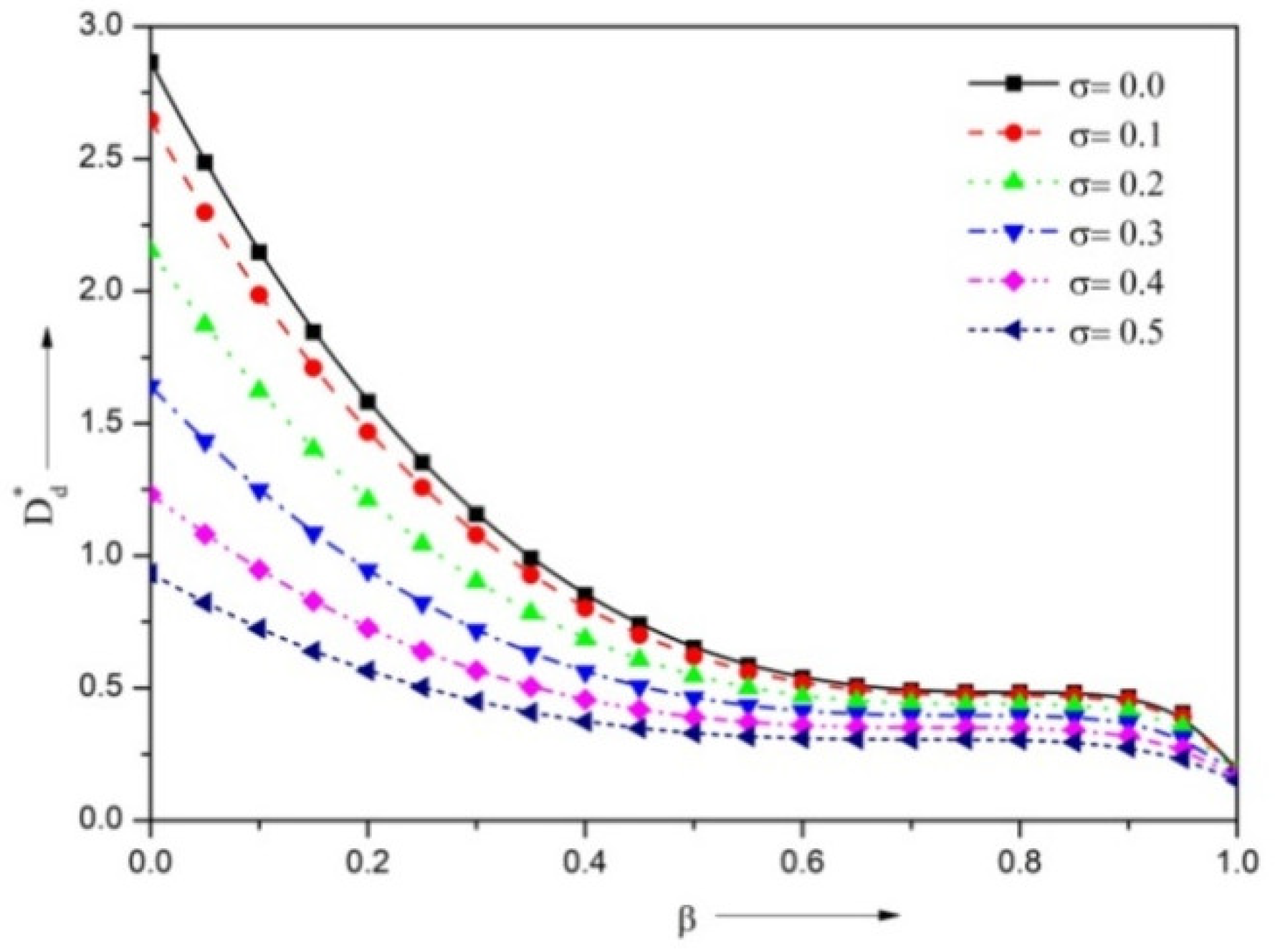
3.3. Dynamic Stiffness Coefficient
3.4. Dynamic Damping Coefficient
4. Conclusions
- The presence of microstructure additives in the lubricant enhances the LCC, DSC and DDC of the RSB and diminishes the VFR. There is a 7% decrease in VFR, and 14.12%, 16.06%, and 5.52%increase in LCC, DSC and DDC, respectively.
- The porous facing on the Rayleigh step slider bearing structure increases the VFR by 6.2% and decreases the LCC by 10.7%, DSC by 20.2% and DDC by 14.3%.
- The reduction in LCC caused by the porous facing can be compensated for by using lubricants that contain additives of the proper size. With this, bearing performance is enhanced.
- The presence of the negatively skewed surface roughness structure provides a reduction in the VFR, and higher steady LCC, DSC and DDC, whereas the positively skewed roughness enhances the VFR, and diminishes the load, stiffness, and damping coefficient.
- The presence of the surface roughness structure improves the LCC, DSC and DDC in comparison with the smooth surface case.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| difference between the inlet-outlet film thicknesses, | |
| bearing width | |
| DDC, | |
| dynamic film force, | |
| integration functions, | |
| film thickness, | |
| inlet film thickness, | |
| steady inlet film thickness, | |
| outlet film thickness, | |
| steady outlet film thickness | |
| couple stress parameter, | |
| length of the bearing | |
| dynamic pressure, | |
| VFR, | |
| steady VFR, | |
| DSC, | |
| time, | |
| velocity components in the and directions | |
| sliding velocity of the lower part | |
| non-dimensional squeezing velocity, | |
| steady LCC, | |
| Cartesian coordinates | |
| non-dimensional coordinate, | |
| mean defined by | |
| riser location parameter | |
| shoulder parameter, | |
| skewness parameter defined by | |
| couple stress fluid material constant | |
| lubricant viscosity | |
| standard deviation defined by |
Appendix A
References
- Lord Rayleigh, O.M.F.R.S. I. Notes on the theory of lubrication. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1918, 35, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Stokes, V.K. Couple stresses in fluids. Phys. Fluids 1966, 9, 1709. [Google Scholar] [CrossRef]
- Bujurke, N.M.; Naduvinamani, N.B.; Jagadeeswar, M. Porous Rayleigh step bearing with second-order fluid. J. Appl. Math. Mech. 1990, 70, 517–526. [Google Scholar] [CrossRef]
- Naduvinamani, N.B. Non-Newtonian effects of second-order fluids on double-layered porous Rayleigh-step bearings. Fluid Dyn. Res. 1997, 21, 495–507. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Siddangouda, A. A note on porous Rayleigh step bearings lubricated with couple stress fluids. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 615–621. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Siddangouda, A. Porous inclined stepped composite bearings with micropolar fluid. Tribol.-Mater. Surf. Interfaces 2007, 1, 224–232. [Google Scholar] [CrossRef]
- Rahmani, R.; Shirvani, A.; Shirvani, H. Analytical analysis and optimization of the Rayleigh step slider bearing. Tribol. Int. 2009, 42, 666–674. [Google Scholar] [CrossRef] [Green Version]
- Vakilian, M.; Nassab, S.A.G.; Kheirandish, Z. Study of inertia effect on thermohydrodynamic characteristics of Rayleigh step bearings by CFD method. Mech. Ind. 2013, 14, 275–285. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Patil, S.; Siddapur, S.S. On the study of Rayleigh step slider bearings lubricated with non-Newtonian Robinowitsch fluid. Ind. Lubr. Tribol. 2017, 69, 666–672. [Google Scholar] [CrossRef]
- Shen, F.; Yan, C.J.; Dai, J.F.; Liu, Z.M. Recirculation flow and pressure distributions in a Rayleigh step bearing. Adv. Tribol. 2018, 2018, 9480636. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Nidal, H.A.; Goodarzi, M. Entropy optimization of first-grade viscoelastic Nanofluid flow over a stretching sheet by using classical Keller-Box scheme. Mathematics 2021, 9, 2563. [Google Scholar] [CrossRef]
- Patel, D.A.; Joshi, M.; Patel, D.B. Design of porous step bearing by considering different ferro fluid lubrication flow model. J. Manuf. Eng. 2021, 16, 108–114. [Google Scholar] [CrossRef]
- Jamshed, W.; Alanazi, A.K.; Isa, S.S.P.M.; Banerjee, R.; Eid, M.R.; Nisar, K.S.; Alshahrei, H.; Goodarzi, M. Thermal efficiency enhancement of solar aircraft by utilizing unsteady hybrid nanofluid: A single-phase optimized entropy analysis. Sustain. Energy Technol. Assess. 2022, 52, 101898. [Google Scholar] [CrossRef]
- ul Haq, M.R.; Hussain, M.; Bibi, N.; Shigidi, I.M.T.A.; Pashameah, R.A.; Alzahrani, E.; El-Shorbagy, M.A.; Safaei, M.R. Energy transport analysis of the magnetized forced flow of power-law nanofluid over a horizontal wall. J. Magn. Magn. Mater. 2022, 560, 169681. [Google Scholar] [CrossRef]
- Christensen, H. Stochastic models of hydrodynamic lubrication of rough surfaces. Proc. Inst. Mech. Eng. 1969, 184, 1013–1026. [Google Scholar] [CrossRef]
- Andharia, P.I.; Gupta, J.L.; Deheri, G.M. Effect of surface roughness on hydrodynamic lubrication of slider bearings. Tribol. Trans. 2001, 44, 291–297. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Kantli, M.H. Investigation of Couple Stress Fluid and Surface Roughness Effects in the Elastohydrodynamic Lubrication Problems using Wavelet-Based Decoupled Method. Lubricants 2016, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Dariush, B.; Deladi, E.L.; Aydar, A.; Matthijn, R.; Dirk, S. The Influence of Surface Texturing on the Frictional Behaviour of Parallel Sliding Lubricated Surfaces under Conditions of Mixed Lubrication. Lubricants 2018, 6, 91. [Google Scholar] [CrossRef] [Green Version]
- Andharia, P.I.; Pandya, H.M. Effect of Longitudinal Surface Roughness on the performance of RSB. Int. J. Appl. Eng. Res. 2018, 13, 14935–14941. Available online: https://www.ripublication.com/ijaer18/ijaerv13n21_17.pdf (accessed on 8 July 2021).
- Rao, P.S.; Agarwal, S. Theoretical study of couple stress fluid film in rough step slider bearing with assorted porous structure. J. Nanofluids 2018, 7, 92–99. [Google Scholar] [CrossRef]
- Marco, P.; Andrea, A.; Pietro, L. SPH Modeling of Hydrodynamic Lubrication along Rough Surfaces. Lubricants 2019, 7, 103. [Google Scholar] [CrossRef]
- Badescu, V. Two classes of sub-optimal shapes for one dimensional slider bearings with couple stress lubricants. Appl. Math. Model. 2020, 81, 887–909. [Google Scholar] [CrossRef]
- Vashi, Y.D.; Patel, R.M.; Deheri, G.B. Neuringer-Roseinweig model based longitudinally rough porous circular stepped plates in the existence of couple stress. Acta Polytech. 2020, 30, 259–267. [Google Scholar] [CrossRef]
- Wang, Y.; Azam, A.; Zhang, G.; Dorgham, A.; Liu, Y.; Wilson, M.C.T.; Neville, A. Understanding the Mechanism of Load-Carrying Capacity between Parallel Rough Surfaces through a Deterministic Mixed Lubrication Model. Lubricants 2022, 10, 12. [Google Scholar] [CrossRef]
- Lin, J.R. Static and dynamic behavior of externally pressurized circular step thrust bearings lubricated with couple stress fluids. Tribol. Int. 1999, 32, 207–216. [Google Scholar] [CrossRef]
- Lin, J.R.; Lu, R.F.; Chang, T.B. Derivation of Dynamic couple-stress Reynolds equation of sliding-squeezing surfaces and Numerical Solution of Plane Inclined Slider Bearings. Tribol. Int. 2003, 36, 679–685. [Google Scholar] [CrossRef]
- Lin, J.R.; Lu, R.-F.; Ho, M.-H.; Lin, M.-C. Dynamic characteristics of wide tapered-land slider bearings. J. Chin. Inst. Eng. 2006, 29, 543–548. [Google Scholar] [CrossRef]
- Lin, J.R.; Lu, R.F.; Ho, M.H.; Li, M.C. Dynamic characteristics of wide exponential film-shape slider bearings lubricated with a non-Newtonian couple stress fluid. J. Mar. Sci. Technol. 2006, 14, 93–101. [Google Scholar] [CrossRef]
- Lin, J.-R.; Chu, L.M.; Liaw, W.-L. Effects of non-Newtonian couple stress on the dynamic characteristics of wide Rayleigh step slider bearings. J. Mar. Sci. Technol. 2012, 20, 9. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Patil, S.B. Static and dynamic characteristics of finite exponential film shaped slider bearings lubricated with micropolar fluid. Tribol.-Mater. Surf. Interfaces 2009, 3, 110–117. [Google Scholar] [CrossRef]
- Singh, U.P.; Gupta, R.S. Dynamic performance characteristics of a curved slider bearing operating with ferrofluids. Adv. Tribol. 2012, 2012, 278723. [Google Scholar] [CrossRef]
- Siddangouda, A.; Naduvinamani, N.B.; Siddapur, S.S. Effect of surface roughness on the static characteristics of inclined plane slider bearing: Rabinowitsch fluid model. Tribol.-Mater. Surf. Interfaces 2017, 11, 125–135. [Google Scholar] [CrossRef]
- Dang, R.K.; Goyal, D.; Chauhan, A.; Dhami, S.S. Effect of non-Newtonian lubricants on static and dynamic characteristics of journal bearings. Mater. Today Proc. 2020, 28, 1345–1349. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Ashwini, A. On the dynamic characteristics of rough porous inclined slider bearing lubricated with micropolar fluid. Tribol. Online 2022, 17, 59–70. [Google Scholar] [CrossRef]
- Gu, Y.; Cheng, J.; Xie, C.; Li, L.; Zheng, C. Theoretical and Numerical Investigations on Static Characteristics of Aerostatic Porous Journal Bearings. Machines 2022, 10, 171. [Google Scholar] [CrossRef]
- Fang, C.; Zhu, A.; Zhou, W.; Peng, Y.; Meng, X. On the Stiffness and Damping Characteristics of Line Contacts under Transient Elastohydrodynamic Lubrication. Lubricants 2022, 10, 73. [Google Scholar] [CrossRef]






| Non-Porous Rough Surface | Porous Rough Surface | Non-Porous Rough Surface | Porous Rough Surface | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NSSR | PSSR | NSSR | PSSR | NSSR | PSSR | NSSR | PSSR | ||
| 0 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| 0.5 | 0.612961 | 0.623292 | 0.621158 | 0.628646 | 0.569021 | 0.610331 | 0.596764 | 0.620916 | |
| 1 | 0.626252 | 0.649364 | 0.642319 | 0.661148 | 0.554155 | 0.61458 | 0.588517 | 0.634438 | |
| 1.5 | 0.609108 | 0.636499 | 0.626454 | 0.650336 | 0.538447 | 0.593059 | 0.5666 | 0.613143 | |
| 2 | 0.588865 | 0.615334 | 0.604549 | 0.628555 | 0.528012 | 0.572678 | 0.549736 | 0.589958 | |
| 2.5 | 0.571852 | 0.595586 | 0.585248 | 0.607297 | 0.521175 | 0.557179 | 0.538049 | 0.57145 | |
| 3 | 0.558584 | 0.579297 | 0.569853 | 0.589395 | 0.516534 | 0.545788 | 0.529902 | 0.557526 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.5 | 0.202712 | 0.149249 | 0.18042 | 0.136804 | 0.501619 | 0.260817 | 0.384162 | 0.253665 | |
| 1 | 0.226563 | 0.18081 | 0.21193 | 0.171367 | 0.393575 | 0.270861 | 0.351423 | 0.281003 | |
| 1.5 | 0.195797 | 0.165237 | 0.188306 | 0.15987 | 0.279421 | 0.219986 | 0.26441 | 0.231931 | |
| 2 | 0.15947 | 0.139615 | 0.155687 | 0.136707 | 0.203581 | 0.171807 | 0.197455 | 0.180856 | |
| 2.5 | 0.128941 | 0.11571 | 0.126945 | 0.114101 | 0.153891 | 0.135169 | 0.151057 | 0.141432 | |
| 3 | 0.10513 | 0.095991 | 0.104019 | 0.095064 | 0.120164 | 0.108241 | 0.118714 | 0.112535 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.5 | 0.531458 | 0.341553 | 0.420996 | 0.286967 | 1.95344 | 0.682152 | 1.14572 | 0.507848 | |
| 1 | 0.44829 | 0.329102 | 0.392252 | 0.295624 | 0.943611 | 0.540175 | 0.752312 | 0.460935 | |
| 1.5 | 0.298172 | 0.239054 | 0.275793 | 0.223777 | 0.46872 | 0.335988 | 0.419848 | 0.307854 | |
| 2 | 0.194121 | 0.164385 | 0.185019 | 0.157608 | 0.261167 | 0.208737 | 0.245687 | 0.198222 | |
| 2.5 | 0.129902 | 0.113895 | 0.125912 | 0.110748 | 0.159793 | 0.135509 | 0.153962 | 0.131151 | |
| 3 | 0.0901384 | 0.080881 | 0.0882435 | 0.079326 | 0.104931 | 0.092197 | 0.102416 | 0.090203 | |
| 0 | 1.19635 | 0.807021 | 0.992749 | 0.708942 | 4.84507 | 1.57596 | 2.64674 | 1.24076 | |
| 0.5 | 0.562794 | 0.421535 | 0.507631 | 0.39037 | 1.33879 | 0.721327 | 1.04471 | 0.632911 | |
| 1 | 0.302087 | 0.241763 | 0.28299 | 0.229856 | 0.552039 | 0.36137 | 0.472845 | 0.33376 | |
| 1.5 | 0.177866 | 0.148018 | 0.169361 | 0.142651 | 0.2988 | 0.202675 | 0.253901 | 0.190768 | |
| 2 | 0.114836 | 0.097212 | 0.109655 | 0.094137 | 0.19713 | 0.127897 | 0.159563 | 0.120346 | |
| 2.5 | 0.0805295 | 0.068291 | 0.0765075 | 0.066079 | 0.149001 | 0.089316 | 0.113463 | 0.083156 | |
| 3 | 0.0605741 | 0.050941 | 0.0570036 | 0.049083 | 0.123353 | 0.067683 | 0.0884973 | 0.062033 | |
| Physical Quantity | Symbol | Value of the Physical Quantity |
|---|---|---|
| Bearing length | ||
| Inlet film thickness | ||
| Steady outlet film thickness | ||
| Length of the first part of the bearing | ||
| Lubricant viscosity | ||
| Shoulder parameter | ||
| Riser location parameter | ||
| Couple stress parameter | ||
| Couple stress material constant | ||
| Roughness parameters | −0.05 | |
| 0.1 | ||
| −0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naduvinamani, N.; Angadi, A. Static and Dynamic Characteristics of Rough Porous Rayleigh Step Bearing Lubricated with Couple Stress Fluid. Lubricants 2022, 10, 257. https://doi.org/10.3390/lubricants10100257
Naduvinamani N, Angadi A. Static and Dynamic Characteristics of Rough Porous Rayleigh Step Bearing Lubricated with Couple Stress Fluid. Lubricants. 2022; 10(10):257. https://doi.org/10.3390/lubricants10100257
Chicago/Turabian StyleNaduvinamani, Neminath, and Ashwini Angadi. 2022. "Static and Dynamic Characteristics of Rough Porous Rayleigh Step Bearing Lubricated with Couple Stress Fluid" Lubricants 10, no. 10: 257. https://doi.org/10.3390/lubricants10100257





