Elastic Contact Analysis of Shot-Peened Rough Surfaces
Abstract
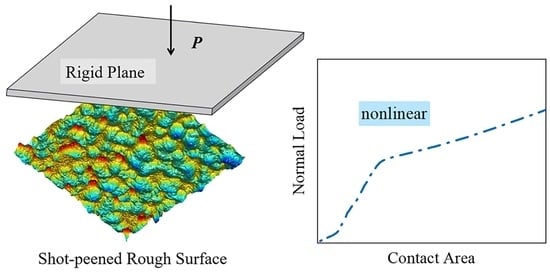
:1. Introduction
2. Sample Preparation and Experimental Measurement
3. Methods
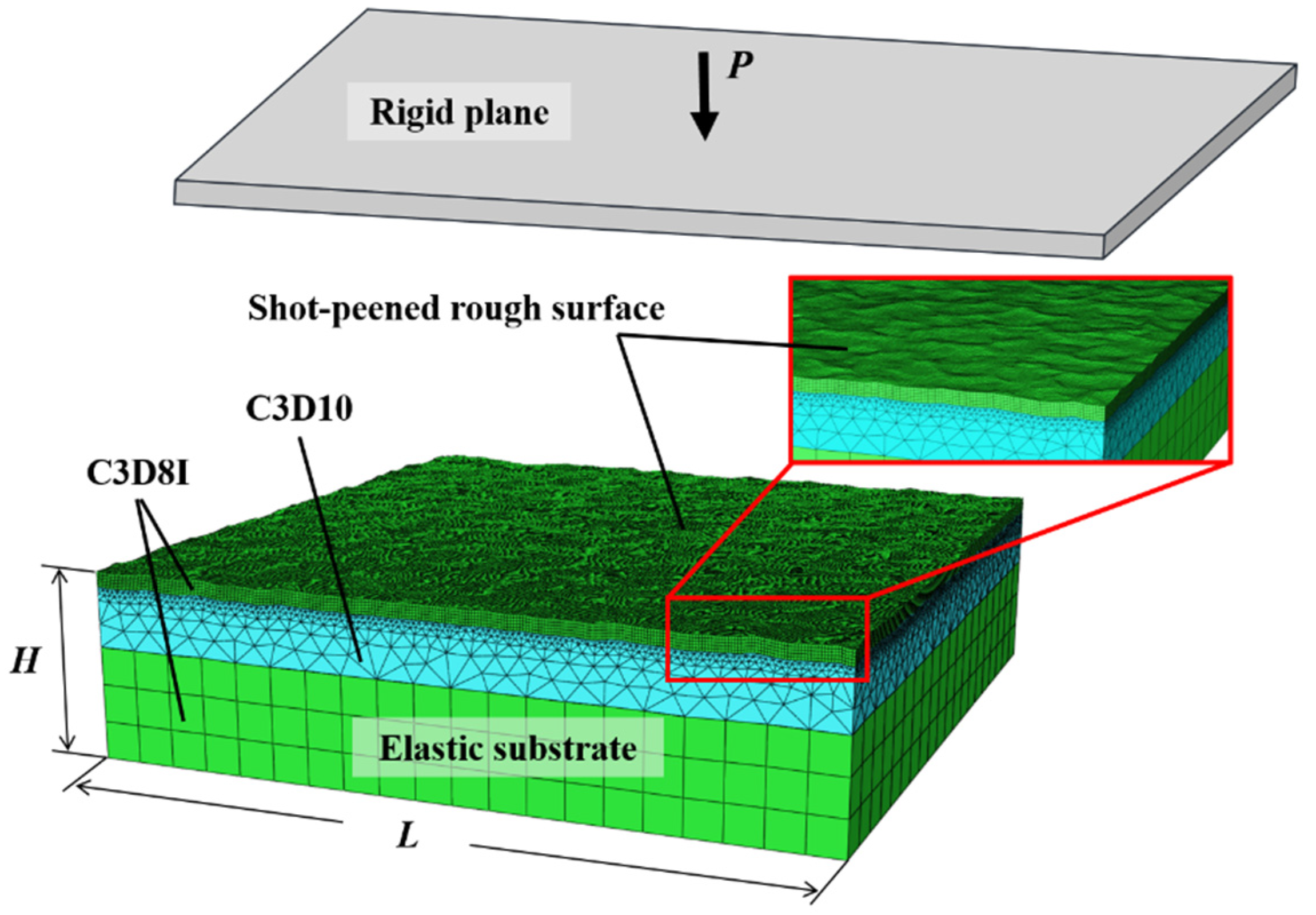
3.1. Finite Element Analysis
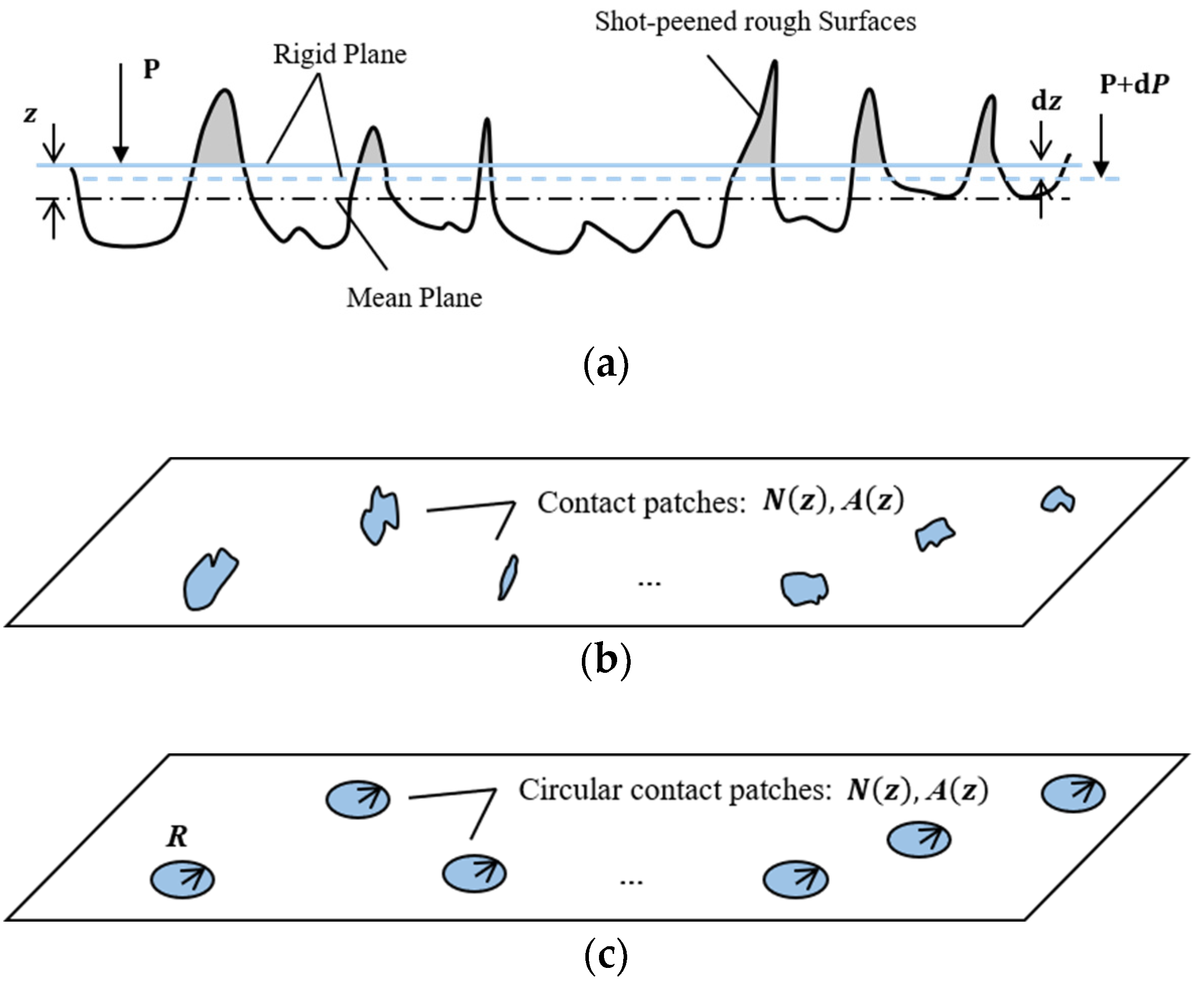
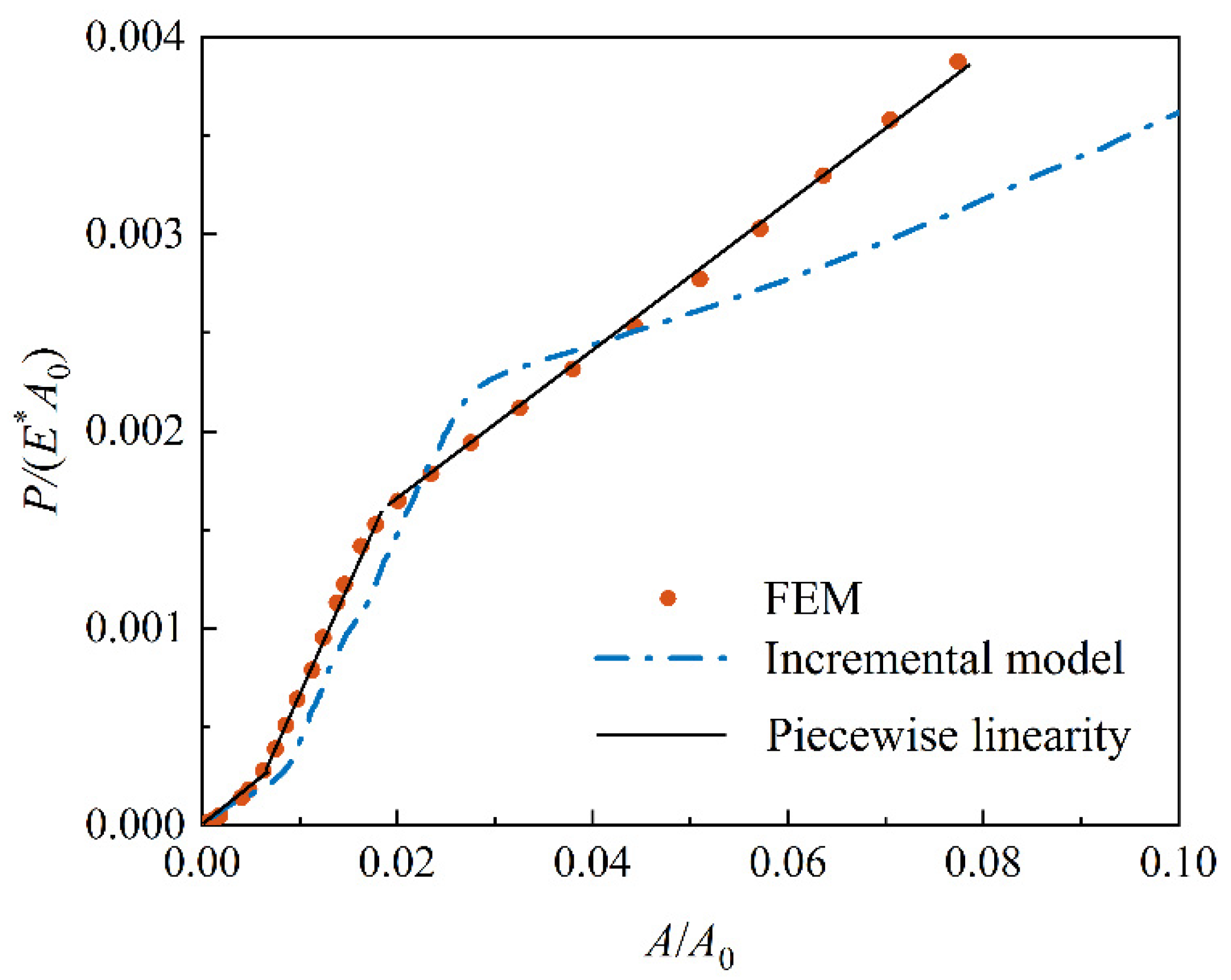
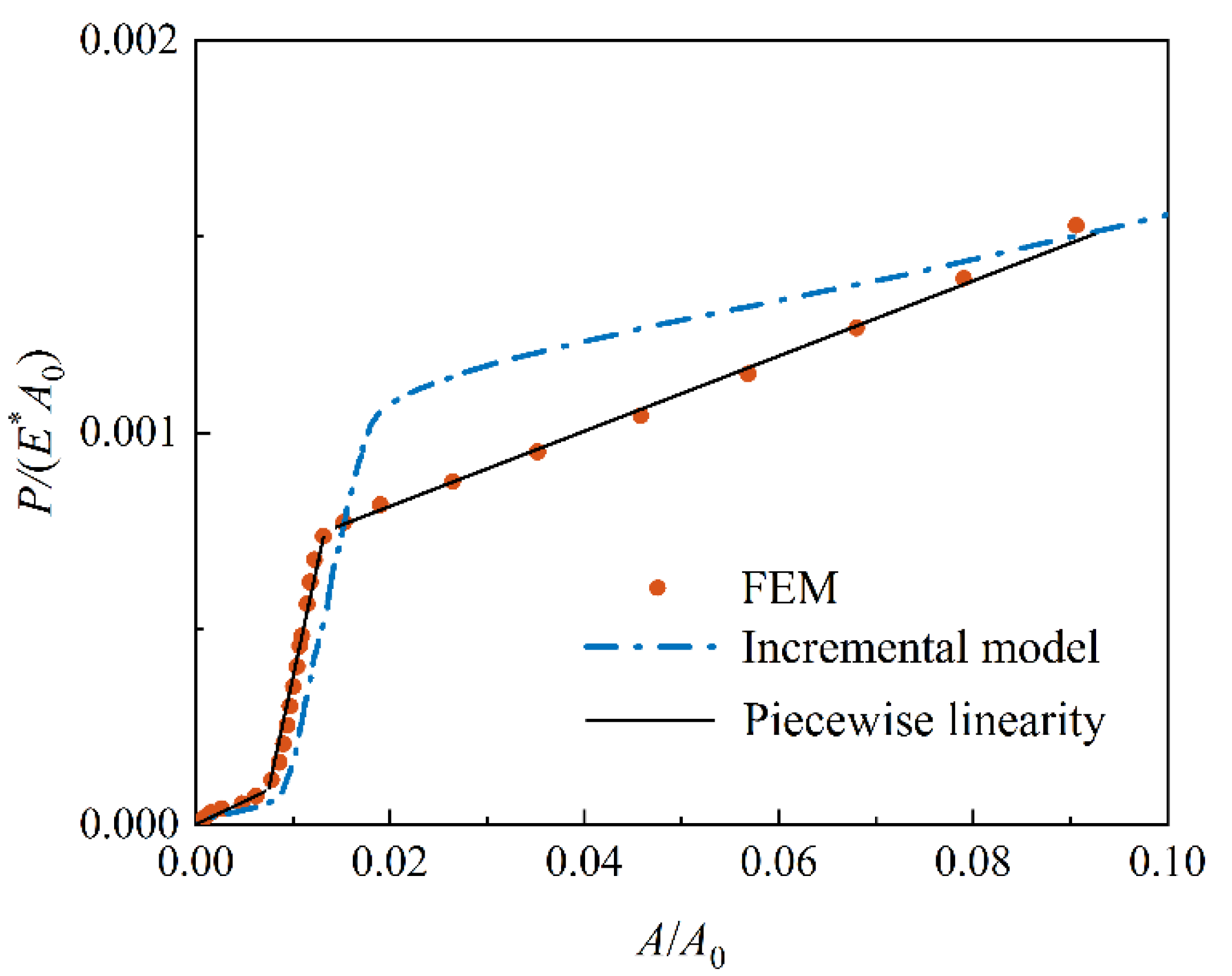
3.2. Incremental Contact Model
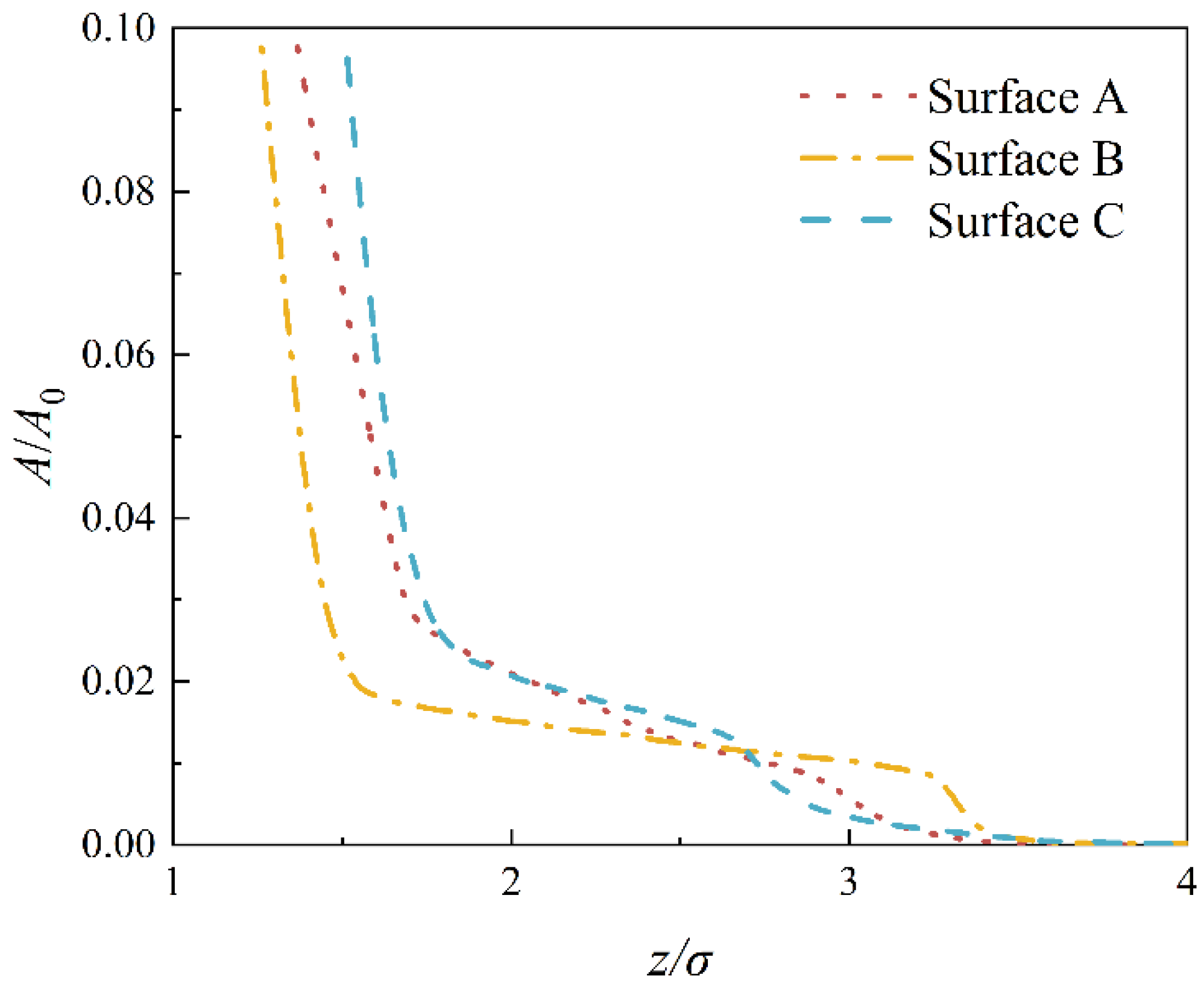
4. Results and Discussion
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Hu, Y.; Gong, C.; Yao, Z.; Hu, J. Investigation on the non-homogeneity of residual stress field induced by laser shock peening. Surf. Coat. Technol. 2009, 203, 3503–3508. [Google Scholar] [CrossRef]
- Bagherifard, S.; Slawik, S.; Fernández-Pariente, I.; Pauly, C.; Mücklich, F.; Guagliano, M. Nanoscale surface modification of AISI 316L stainless steel by severe shot peening. Mater. Des. 2016, 102, 68–77. [Google Scholar] [CrossRef]
- Wu, D.; Yao, C.; Zhang, D. Surface characterization and fatigue evaluation in GH4169 superalloy: Comparing results after finish turning; shot peening and surface polishing treatments. Int. J. Fatigue 2018, 113, 222–235. [Google Scholar] [CrossRef]
- Soyama, H. Comparison between the improvements made to the fatigue strength of stainless steel by cavitation peening, water jet peening, shot peening and laser peening. J. Mater. Process. Technol. 2019, 269, 65–78. [Google Scholar] [CrossRef]
- Taylor, R.I. Rough surface contact modelling-A Review. Lubricants 2022, 10, 98. [Google Scholar] [CrossRef]
- Vakis, A.I.; Yastrebov, V.A.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Archard, J.F. Elastic deformation and the laws of friction. Proc. R. Soc. Lond. 1957, 243, 190–205. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. A 1966, 295, 300–319. [Google Scholar]
- Nayak, P.R. Random process model of rough surfaces. J. Lubr. Technol. 1971, 93, 398–407. [Google Scholar] [CrossRef]
- Nayak, P.R. Random process model of rough surfaces in plastic contact. Wear 1973, 26, 305–333. [Google Scholar] [CrossRef]
- Bush, A.W.; Gibson, R.D.; Thomas, T.R. The elastic contact of a rough surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- Bush, A.W.; Gibson, R.D.; Keogh, G.P. Strongly anisotropic rough surfaces. J. Tribol. 1979, 101, 15–20. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Persson, B.N.J. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef] [Green Version]
- Carbone, G.; Bottiglione, F. Asperity contact theories: Do they predict linearity between contact area and load? J. Mech. Phys. Solids 2008, 56, 2555–2572. [Google Scholar] [CrossRef]
- Bagherifard, S.; Ghelichi, R.; Guagliano, M. Numerical and experimental analysis of surface roughness generated by shot peened. Appl. Surf. Sci. 2012, 258, 6831–6840. [Google Scholar] [CrossRef]
- Hyun, S.; Pei, L.; Molinari, J.F.; Robbins, M.O. Finite-element analysis of contact between elastic self-affine surfaces. Phys. Rev. E 2004, 70, 026117. [Google Scholar] [CrossRef] [Green Version]
- Pei, L.; Hyun, S.; Molinari, J.F.; Robbins, M.O. Finite element modeling of elasto-plastic contact between rough surfaces. J. Mech. Phys. Solids 2005, 53, 2385–2409. [Google Scholar] [CrossRef]
- Song, H.; Van der Giessen, E.; Liu, X. Strain gradient plasticity analysis of elasto-plastic contact between rough surfaces. J. Mech. Phys. Solids 2016, 96, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.F.; Liang, X.M.; Yan, D. An incremental equivalent circular contact model for rough surfaces. J. Tribol. 2021, 143, 081503. [Google Scholar] [CrossRef]
- Wang, S.H.; Yuan, W.K.; Liang, X.M.; Wang, G.F. A new analytical model for the flattening of Gaussian rough surfaces. Eur. J. Mech.-A/Solids 2022, 94, 104578. [Google Scholar] [CrossRef]
- Tiwari, A.; Almqvist, A.; Persson, B.N.J. Plastic deformation of rough metallic surfaces. Tribol. Lett. 2020, 68, 129. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Almqvist, A. On the stiffness of surfaces with non-Gaussian height distribution. Sci. Rep. 2021, 11, 1863. [Google Scholar] [CrossRef] [PubMed]
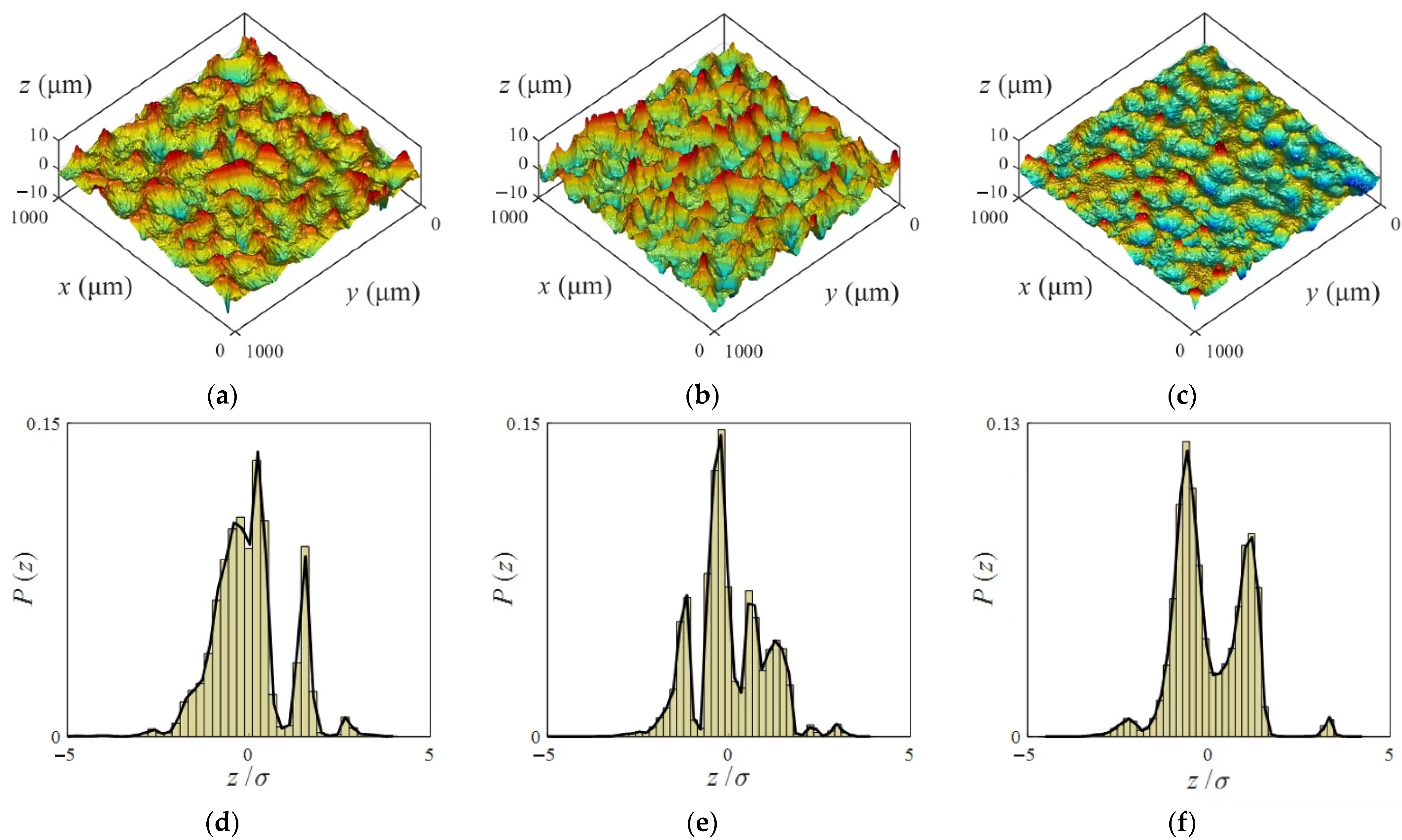


| Shot Material | Shot Diameter (mm) | Pressure (MPa) | Rate of Flow (kg/min) |
|---|---|---|---|
| ASH 230 steel | 0.58–0.71 | 0.12 | 12 |
| Ceramic | 0.61–0.84 | 0.20 | 10 |
| Global Size | RMS Roughness, σ (μm) | Mechanical Parameter | ||||
|---|---|---|---|---|---|---|
| L (mm) | H (mm) | Surface A | Surface B | Surface C | E (GPa) | ν |
| 1.04 | 0.26 | 1.3803 | 1.9868 | 0.8808 | 91 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, W.; Yuan, W.; Wang, G. Elastic Contact Analysis of Shot-Peened Rough Surfaces. Lubricants 2022, 10, 331. https://doi.org/10.3390/lubricants10120331
Dai W, Yuan W, Wang G. Elastic Contact Analysis of Shot-Peened Rough Surfaces. Lubricants. 2022; 10(12):331. https://doi.org/10.3390/lubricants10120331
Chicago/Turabian StyleDai, Wanlin, Weike Yuan, and Gangfeng Wang. 2022. "Elastic Contact Analysis of Shot-Peened Rough Surfaces" Lubricants 10, no. 12: 331. https://doi.org/10.3390/lubricants10120331
APA StyleDai, W., Yuan, W., & Wang, G. (2022). Elastic Contact Analysis of Shot-Peened Rough Surfaces. Lubricants, 10(12), 331. https://doi.org/10.3390/lubricants10120331