SACGNet: A Remaining Useful Life Prediction of Bearing with Self-Attention Augmented Convolution GRU Network

Abstract

In recent years, the development of deep learning-based remaining useful life (RUL) prediction methods of bearings has flourished because of their high accuracy, easy implementation, and lack of reliance on a priori knowledge. However, there are two challenging issues concerning the prediction accuracy of existing methods. The run-to-failure sequential data and its RUL labels are almost inaccessible in real-world scenarios. Meanwhile, the existing models usually capture the general degradation trend of bearings while ignoring the local information, which restricts the model performance. To tackle the aforementioned problems, we propose a novel health indicator derived from the original vibration signals by combining principal components analysis with Euclidean distance metric, which was motivated by the desire to resolve the dependency on RUL labels. Then, we design a novel self-attention augmented convolution GRU network (SACGNet) to predict the RUL. Combining a self-attention mechanism with a convolution framework can both adaptively assign greater weights to more important information and focus on local information. Furthermore, Gated Recurrent Units are used to parse the long-term dependencies in weighted features such that SACGNet can utilize the important weighted features and focus on local features to improve the prognostic accuracy. The experimental results on the PHM 2012 Challenge dataset and the XJTU-SY bearing dataset have demonstrated that our proposed method is superior to the state of the art.

1. Introduction

Bearings are one of the key components in a rotating machinery system. The remaining useful life (RUL) of a bearing is often defined as the length of a bearing from the current time to failure [1]. If the damage time or the trend of the vibration signal can be predicted from the collected vibration signal of a bearing, it is beneficial for identifying the adverse running condition in time to avoid the sudden danger of bearings. Thus, the RUL of a bearing is essential for the maintenance and management of mechanical systems [1,2].

In general, the RUL prediction of bearings can be sorted into two different directions: physics-based methods and data-driven methods. Physics-based methods focus on physical and mathematical models, e.g., partial differential equations and state-space models, which require extensive prior knowledge [3,4,5,6].

Data-driven RUL methods directly use historical data to model the degradation process of bearings without any prior knowledge.

Deep learning is a popular approach among data-driven methods, which can directly build a deep neural network to model the degradation process as a functional relationship between health states and original sensory data [7].

Deep learning-based RUL approaches typically include the steps of data acquisition, health indicator (HI) construction, and remaining useful life prediction [7].

Data acquisition is to collect the run-to-failure signals from different sensors that can reflect the degradation process of bearings. The complete lifecycle data of a bearing are usually high-dimension and nonlinear. Therefore, a suitable processing method to retain the degradation features (i.e., HI) is necessary.

Health indicators such as the RUL labels are constructed by selecting the appropriate characteristics from the original sensory signal. Since the damage extent of bearings cannot be directly observed, the RUL labels are almost inaccessible in real-world scenarios. Thereby, the critical information from the original data are extracted as HI to train the prediction model, which is a crucial issue to the model [8].

Afterwards, several deep neural networks are designed to extract deep features from the original sensory data and then predict the RUL. The prevalent models include RNN, LSTM, CNN, etc. RNN are often used for predicting the time-series data. The prevalent RNNs are mainly LSTM, GRU, and their variants, which can learn the general degradation trend of the input data. However, they often overlook the local features in input data. With respect to the sequence vibration signal of the bearing, these vibration data have merely small fluctuations in long time series. Until the end of the bearing’s life, the vibration fluctuates dramatically, which is often difficult to predict; hence, the existing models cannot obtain satisfactory prediction results [9].

To tackle the aforementioned issues, we propose a novel health indicator-based remaining useful life prediction approach of bearings. The main contributions of this paper are summarized as follows:

• We combine the PCA with Euclidean distance metric methods to construct a health indicator to tackle the problem of lack of RUL labels. Facing the high-dimensional and long-term series data, PCA can reduce the data dimensionality while retaining sufficient useful features. The Euclidean distance is to measure the similarity between data to distinguish the different degradation stages. Compared with the existing linear RUL labels, our HI is not only capable of representing the general degradation trend of bearings, but it also can retain more local features from the original vibration signal, which benefit the corresponding model’s learning and calculations.
• We design a novel self-attention augmented convolution GRU network (SACGNet) to predict the RUL. Combining the self-attention mechanism with a convolution framework can both adaptively assign greater weights to more important information and focus on local information. Furthermore, Gated Recurrent Units (GRU) are used to parse the long-term dependencies in weighted features so that SACGNet can utilize the important weighted features and focus on local features to improve the prognostic accuracy.
• Based on the designed HI and SACGNet, a novel remaining useful life prediction approach is proposed. We conduct ablation experiments and different comparison experiments on the PHM 2012 Challenge dataset and XJTU-SY bearing dataset. The experimental results prove the superiority of our proposed method.

The remaining part of this paper is organized as follows: In Section 2, we introduce related works in the field of RUL prediction. We describe our proposed method in detail in Section 3. The experimental results are discussed in Section 4. Finally, we conclude the paper in Section 5.

2. Related Works

2.1. Health Indicator Construction

In deep learning-based RUL methods, HI construction currently has two branches in general. One approach extracts simple physical fault characterization from the original vibration signals as HI, using statistical methods or signal processing methods. For instance, the root mean square (RMS) of the original vibration signal [10] or the percentage of useful life (the current life divided by the total useful life) [11,12,13,14]. However, such HIs cannot represent enough useful degradation information of the original data. Thereby, using such HIs as model input makes the model fail to accurately capture the degradation trend for RUL prediction.

The other branch constructs the virtual HI by fusing multiple physical characteristics or multi-sensor signals. These HI can filter out abnormal trends in the early degradation stages, which is more suitable for model learning [15,16,17,18]. Guo et al. selected six related-similarity features and combined eight time-frequency features so as to form an original feature set that contains rich degradation signatures of bearings. Then, the selected features are fused into an HI through an RNN [19]. Li et al. used KPCA to integrate multiple features and introduced the EWMA to reduce the fluctuations for the constructed HI [20]. Li et al. designed the generative adversarial network to learn the data distribution in the health states of machine, using the output of the discriminator as HI [21]. Liang et al. proposed a novel index by calculating offset distance and offset angle between the current state and normal state of devices [22].

In summary, the existing HI can only represent the global degradation process of the vibration signal, but it fails to retain more local features. In order to extract more representative features from the vibration signal and facilitate for the model learning, a more effective HI construction method is proposed in this paper.

2.2. Prediction Model

With respect to regression model design, LSTM, GRU, CNN, and the attention mechanism have been successively introduced into the field of RUL prediction.

LSTM uses input gates, forgetting gates, and output gates to regulate the information of the input sequence, which enables the network to learn the long-term dependence of the data and gain favorable results. Hinchi et al. used convolutional layers to directly extract local features from sensor data, combined them with LSTM layers to capture the degradation process of the bearing, and finally output the prediction values [23]. Whereas LSTM solves the problem of gradient disappearance of traditional RNN to some extent, the deliberate design of LSTM for RUL prediction is very time consuming [24,25].

GRU is a variant of LSTM, whose structure is further simplified to show better performance than LSTM in smaller datasets [26,27]. Cao et al. use the BiGRU model to solve the problem of distribution discrepancy [28]. However, with regard to LSTM and GRU, they only use the features learned in the previous time step for regression prediction and often do not pay attention to local features in the long time series [29].

CNN can extract features with less computational effort because of the sparsity of parameter sharing of the convolutional kernel and inter-layer connectivity. More importantly, CNN focuses on the local features in the original vibration signal, which is suitable for RUL prediction [30,31,32,33]. Wang et al. proposed a multi-scale convolutional network to improve the domain adaptation capability of the RUL prediction model [34].

It is noted that the original vibration signal often contains different features with different levels of importance. The features that contain more important information should be paid more attention. Hence, an attention mechanism is introduced to RUL prediction of bearing to adaptively extract input features [35]. The self-attention mechanism aims to correlate different states of sequences, which reduces the dependence on external information and is more suitable for capturing the internal relevance of data or features [36,37]. Chen et al. constructed an encoder–decoder model based on the attention mechanism to mine useful degradation information from a long historical vibration signal [38]. Chen et al. proposed an attention-based deep learning framework for RUL prediction, which adopted LSTM to extract features, and then combined with the attention layer to fusion the features, LSTM extracted and manually extracted features [39].

3. Proposed Method

Without loss of generality, given a bearing, vibration signals $V=\{v_1,v_2,\dots v_m\}$, input V to the health indicator construction module and get the $HI=\{h_1,h_2,\dots h_m\}$. We expect the model to predict the $h_{t+1}$ value after input $h_1,h_2,\dots h_t$.

Then, our proposed SACGNet learns the deep features in HI:

$$F(h_1,h_2,\dots ,h_t,\theta ):h\to h_{t+1}$$

(1)

where $\theta$ is the parameter on the model.

There is also a testing dataset of the vibration signal $V^{\prime }=\{v_1^{\prime },v_2^{\prime },\dots v_m^{\prime }\}$, which after HI construction obtains $H^{\prime }=\{h_1^{\prime },h_2^{\prime },\dots h_n^{\prime }\}$.

Finally, inputing the $H^{\prime }$ to the trained SACGNet, the model will predict the correct value: $\widehat{y_t^{\prime }}=F(h_1^{\prime },h_2^{\prime },\dots ,h_t^{\prime })$, where $\widehat{y_t^{\prime }}$ is the model’s prediction value.

The whole structure of SACGNet is shown in Figure 1, including the health indicator construction module and remaining useful life prediction module. First, input the original signal of the bearings to the health indicator construction module to obtain the HI. After data normalization and sliding window processing, input it to SACGNet for training. In the testing stage, the predicted values are output by autoregression.

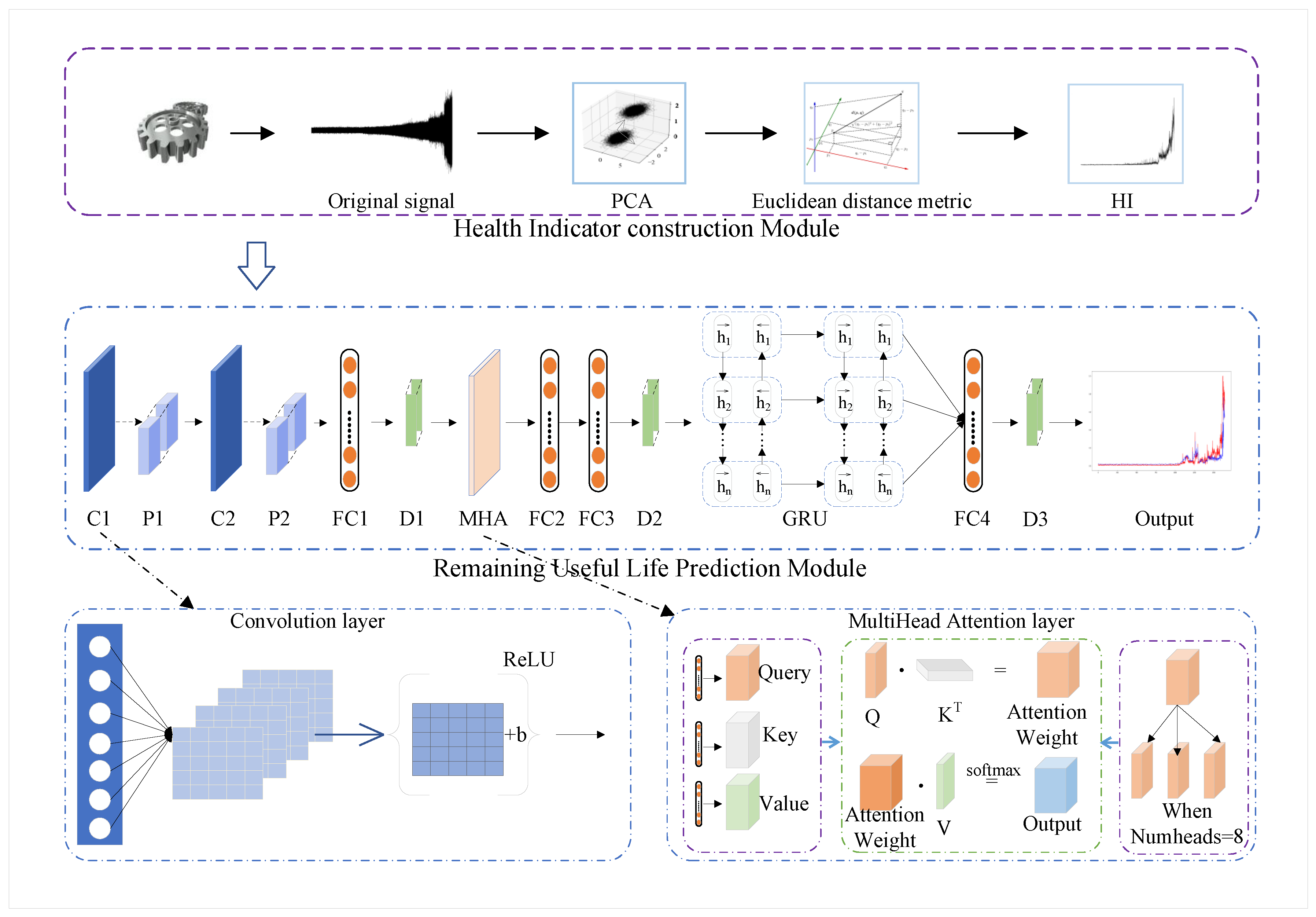
3.1. Health Indicator Construction Module

If the dimension of the original signal is set to d, the matrix form of the original vibration signal $V=\{v_1,v_2,\dots v_m\}$, where $v_i$ denoted an acquired vibration data that can be written as:

$$V=\left(\begin{array}{ccc}{v}_{11}& ...& v_{1d}\\ ⋮& \ddots & ⋮\\ v_{m1}& \dots & v_{md}\end{array}\right).$$

(2)

Principal components analysis (PCA) linearly transforms the data into a new coordinate system such that the first major variance of any data projection is at the first coordinate (called the first principal component), the second major variance is at the second coordinate, and so on.

$V^T$ is the de-averaged data. The singular value decomposition of V is:

$$V=W\sum H^T$$

(3)

where the matrix W is the eigenvector matrix of $V{V}^T$, ∑ is a non-negative rectangular diagonal matrix, and H is the eigenvector matrix of $V^{T}V$.

Assuming zero empirical means, the principal component $w\left(1\right)$ of the dataset V can be defined as:

$$w\left(1\right)=argma{x}_{\parallel w\parallel =1}Var\left\{W^{T}V\right\}.$$

(4)

To obtain the k-th principal component, the previous k−1 principal components must first be subtracted from V.

$$\widehat{V_{k-1}}=V-\sum _{i-1}^{k-1}{w}_i{w}_i^{T}V$$

(5)

Then, the k-th principal component is obtained to update a new dataset and continue to search for principal components.

$$w_k=argma{x}_{\parallel w\parallel =1}E\left\{{\left(w^T\widehat{V_{k-1}}\right)}^2\right\}$$

(6)

Through PCA, we can reduce the original vibration signal’s dimensionality from d to k. We retain the k principal components of the original signals; thus, the dimension of $V_{pca}$ is k, which can be abbreviated as $\{v_{pca1},v_{pca2},v_{pca3},\dots ,v_{pcan}\}$.

$$V_{pca}=pca\left(V\right)=\left(\begin{array}{ccc}{w}_{11}& \dots & w_{1k}\\ ⋮& \ddots & ⋮\\ w_{m1}& \dots & w_{mk}\end{array}\right)=\{v_{pca1},v_{pca2},v_{pca3}\dots ,v_{pcam}\}$$

(7)

Using standard PCA to reduce the dimensionality of the original vibration data, we can only retain the principal components of the data. In this paper, based on PCA, to reduce the dimensionality of vibration data, we use Euclidean distance to calculate the distance between the low-dimensional data to construct HI. The metric Euclidean distance can obtain the similarity between one data in the time series and the neighboring points, which can better reflect the trend of the neighboring data in the original vibration signal, which means “capturing local features” we mentioned.

By calculating the average of the Euclidean distance from each point in $V_{pca}$ to the sequential neighboring points, we can obtain the HI corresponding to each point. HI = $\{h_1,h_2,\dots h_m\}$. The calculation process of $h_i$ is as follows:

$$h_i=\frac{1}{2}(\sqrt{\sum _{j=1}^k{(v_{pca{i}_j}-v_{pca{(i+1)}_j})}^2}+\sqrt{\sum _{j=1}^k{(v_{pca{i}_j}-v_{pca{(i-1)}_j})}^2}).$$

(8)

HI will be input to the constructed SACGNet to make the model learn the relationship between them. In order to make HI meet the dimensionality requirements of the model input, a sliding window is set to process the data into the shape required by the model, with a sliding window size of 20. Then, we obtain the $X=\{x_1,x_2,\dots x_n\}$.

3.2. Remaining Useful Life Prediction Module

In this section, we describe our SACGNet in detail, as shown in the

Table 1. The architecture of SACGNet.

No	Symobl	Operator	Kernel Size	Dimension
1	Input	Input signal	/	(None, 20, 2)
2	C1	Convolution	4 × 4	(None, 20, 80)
3	P1	Average pooling	1 × 1	(None, 20, 80)
4	C2	Convolution	4 × 4	(None, 20, 80)
5	P2	Average pooling	1 × 1	(None, 20, 80)
6	FC1	Fully connected	80 × 1	(None, 20, 80)
7	D1	Dropout	/	(None, 20, 80)
8	MHA	Multi-Head Attention	/	(None, 20, 80)
9	FC2	Fully connected	80 × 1	(None, 20, 80)
10	FC3	Fully connected	80 × 1	(None, 20, 80)
11	D2	Dropout	/	(None, 20, 80)
12	GRU	Gated recurrent units	/	(None, 80)
13	D3	Dropout	/	(None, 80)
14	FC4	Fully connected	1 × 1	(None, 1)

. We combine a 1D convolution (Conv1d) block with self-attention mechanisms to extract deep features from the input data. The Conv1d block focuses more on local features, and the self-attention mechanism can extract global features of the data. GRU can identify long-term features in the input data, which is beneficial to adapt the bearings under different operating conditions, thereby improving the prediction accuracy of our model [40,41].

For convenience, we use C, P, FC, D, MHA, and GRU to denote the Conv1d layer, the pooling layer, the fully connected layer, the dropout layer, Multi-Head attention layer, and the GRU layer, respectively.

In the convolution layer, the calculation of the input data can be written as follows:

$$X_c=ReLU(X\odot f_i+b_i)$$

(9)

where ⊙ represents convolution operation. $f_i$ represents the ith convolution filter, and $b_i$ is the bias. The convolution layers used $ReLU$ as the activation function. Compared to images, the vibration signal is time-series data; hence, the one-dimensional convolution (Conv1d) neural network can be used to perform convolutional operations. The filters of the Conv1d layer are set to 80, the kernel size is set to 4, the stride is set to 1. In our paper, we select the average pooling layer.

The specific calculation process of the self-attention mechanism can be summarized into two processes: calculation the weight coefficients based on the Query and Key, and summation of the weight values based on the weight coefficients. The first process can further include the following: first, calculate the similarity or relevance between Query and Key, and then normalize the found relevance. Its attention function can be described as mapping a Query and a pair of key-value pairs to an output, where Queries, Keys, and values are vectors and the output is computed as a weighted sum of values, where the weight assigned to each value is computed by the compatibility function of the Query with the corresponding Key.

In order to learn the expression of multiple meanings, the input data will be transformed; $W_Q,W_K,W_V$ is the matrix of assigned weights. Self-attention represents a focus on itself, so the equation can be denoted as follows:

$$\left\{\begin{array}{c}Q=X_c{W}_Q=Linear\left(X_c\right)\hfill \\ K=X_c{W}_K=Linear\left(X_c\right)\hfill \\ V=X_c{W}_V=Linear\left(X_c\right).\hfill \end{array}\right.$$

(10)

The output matrix of self-attention is expressed as:

$$Attention(Q,K,V)=softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

(11)

where $d_k$ is the dimension of K, and the use of $\sqrt{d_k}$ is to change the attention matrix into a standard normal distribution.

Multi-head attention can make the model pay attention to the information from different representational subspaces; the output of the self-attention mechanism layer is three-dimensional vectors, which are written as $X_a$:

$$X_a=Multi-Head(Q,K,V)=Concat(hea{d}_1,\dots hea{d}_h)W.$$

(12)

In this paper, we choose h = 8, $d_k=d_q=d_v=80,W\in R^{h{d}_v\times d_{model}}$, which are the empirical values selected in the experiment.

Gated Recurrent Units (GRUs) are a gating mechanism in recurrent neural networks. The calculation of the GRU can be written as follows:

$$\left\{\begin{array}{c}{X}_a=\{a_1,a_2,\dots a_n\}\hfill \\ z_t={\sigma }_g(W_z{a}_t+U_z{h}_{t-1}+b_z)\hfill \\ r_t={\sigma }_g(W_r{a}_t+U_r{h}_{t-1}+b_r)\hfill \\ \widehat{h_t}={\varphi }_h(W_h{x}_t+U_h\ast (r_t\ast h_{t-1})+b_h)\hfill \\ h_t=(1-z_t)\ast h_{t-1}+z_t\ast \widehat{h_t}.\hfill \end{array}\right.$$

(13)

Among them, $a_t$ is input vector $X_a$ at time t, $h_t$ is output vector, $\widehat{h_t}$ is the candidate activation vector, $z_t$ is the update gate vector, $r_t$ is reset gate vector, W, U, and b are the parameter matrices, vector ${\sigma }_g$ is a sigmoid function, and ${\varphi }_h$ is a hyperbolic tangent. The GRU layer receives the features extracted from the Conv1d layer and the Multi-Head attention layer and then outputs the prediction value. The units of GRU are set to 80.

Finally, after the fully connected layer, the final output is obtained:

$$\widehat{y_t}=FCN\left(h_t\right).$$

(14)

SACGNet is trained using the error back-propagation algorithm and gradient descent method. The loss function of the training process is the mean square error function:

$$\mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2$$

(15)

where $y_i$ is the true value, $\widehat{y_i}$ is the prediction value, and n is the total number of samples.

In addition, Adam is chosen as the optimizer of this paper, and the learning rate is set to ${10}^{-3}$ [42].

Dropout is added to our SACGNet with the parameter set to 0.5 in order to reduce overfitting by preventing complex co-adaptations on training data. The algorithm pseudo-code is shown in as follow Algorithm 1.

Algorithm 1: Proposed SACGNet.

1. The SACGNet algorithm for training is defined

as follows:

Input: Hyper-parameters of model (batch size, epoch,

dropout rate, learning rate, etc.), original signal $V=\{v_1,v_2,v_3,\dots v_m\}$

2. $HI=\{h_1,h_2,\dots h_m\}$

3. By sliding window processing:

$HI=\{h_1,h_2,\dots h_m\}\to X=\{x_1,x_2,\dots x_n\}$

Each x represents a batch h, the number of a batch is i

4. $Y=\{y_1,y_2,\dots y_n\}=\{h_{i+1},h_{i+2},\dots h_m\}$

5. For $i=1,2,\dots n$ do:

$X=\frac{x_i-Min\left(X\right)}{Max\left(X\right)-Min\left(X\right)}$,$Y=\frac{y_i-Min\left(Y\right)}{Max\left(Y\right)-Min\left(Y\right)}$

end

6. Build SACGNet model

7. w (parameters of the SACGNet) and b (biases) are initialized to zeros

8. Input X and Y to train SACGNet

$X_c=Conv\left(X\right)$

$Q=X_c{W}_Q=Linear\left(X_c\right)$$K=X_c{W}_K=Linear\left(X_c\right)$$V=X_c{W}_V=Linear\left(X_c\right)$

$Attention(Q,K,V)=softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$

$X_a=Multi-Head(Q,K,V)$

$Output=GRU\left(X_a\right)$

$ComputeMSEby\left(15\right)$

$w\leftarrow Adam(MSE,w)$

$b\leftarrow Adam(MSE,b)$

$end$

Output: Trained SACGNet model for prediction

END

4. Experiments and Results

In this section, we use the IEEE PHM Challenge 2012 bearing dataset and the XJTU-SY Bearing dataset to validate the effectiveness of our method.

4.1. Dataset Description

The IEEE PHM 2012 Challenge dataset was collected from the PRONOSTIA testbed, as shown in Figure 2.

The PRONOSTIA test platform contains a rotating part, load part, and data collection part. The motor power of the rotating part is 250 W. The power is transferred to the bearing by the axis of rotation. The load part provides a load of 4000 N to make the bearing degrade quickly. The acceleration sensor is placed on a bearing seat in horizontal and vertical directions to select the vibration signals. The sampling frequency of the acceleration sensor is 25.6 kHz. When the test platform starts to work, the vibration signal is recorded every 10 s, and the sampling time is 0.1 s [43].

The data provided by IEEE PHM Challenge 2012 include three different operating conditions. Seven bearings (bearings 1-1 to 1-7) work in the first condition, the motor speed is 1800 rpm, and the load is 4000 N. Seven bearings (bearings 2-1 to 2-7) work in the second condition, the motor speed is 1650 rpm, and the load is 4200 N. Three bearings (bearings 3-1 to 3-3) work in the third condition, the motor speed is 1500 rpm, and the load is 5000 N.

Table 2. The detail of the PHM dataset.

Working Condition	Rotation Speed	Load	Dataset	Sample Number	Bearing Lifetime	Division
1	1800 rpm	4000 N	Bearing 1-1	2803	7 h 47 m	training
			Bearing 1-2	871	2 h 25 m	training
			Bearing 1-3	1802	5 h 10 s	testing
			Bearing 1-4	1139	3 h 9 m 40 s	testing
			Bearing 1-5	2302	6 h 23 m 30 s	testing
			Bearing 1-6	2302	6 h 23 m 29 s	testing
			Bearing 1-7	1502	4 h 10 m 11 s	testing
2	1650 rpm	4200 N	Bearing 2-1	911	2 h 31 m 40 s	training
			Bearing 2-2	797	2 h 12 m 40 s	training
			Bearing 2-3	1202	3 h 20 m 10 s	testing
			Bearing 2-4	612	1 h 41 m 50 s	testing
			Bearing 2-5	2002	5 h 33 m 30 s	testing
			Bearing 2-6	572	1 h 35 m 10 s	testing
			Bearing 2-7	172	28 m 30 s	testing
3	1500 rpm	5000 N	Bearing 3-1	515	1 h 25 m 40 s	training
			Bearing 3-2	1637	4 h 32 m 40 s	training
			Bearing 3-3	352	58 m 30 s	testing

illustrates the details of the PHM 2012 dataset.

In this paper, the vibration dada of bearings 1-1, 1-2, 2-1, 2-2, and 3-1 are selected, respectively, as the training set, while the rest of the bearings are selected as the testing set. Table 2 illustrates the details of the PHM dataset.

The XJTU-SY bearing dataset is provided by the Institute of Design Science and Fundamental Research of Xi’an Jiaotong University and contains the run-to-failure vibration data from 15 rolling bearings [44].

As shown in Figure 3, the bearing testbed is composed of an alternating current (AC) induction motor, a motor speed controller, a support shaft, two support bearings (heavy duty roller bearings), and a hydraulic loading system. This testbed is designed to conduct the accelerated degradation tests of the testing bearings under different operating conditions (i.e., different radial force and rotating speed). The radial force is generated by the hydraulic loading system and applied to the housing of tested bearings, and the rotating speed is set and kept by the speed controller of the AC induction motor [44].

Three different operating conditions are set in the accelerated degradation experiments, and five bearings are used under each operating condition. The sampling frequency is 25.6 kHz, and the sampling period is 1 min.

Table 3. The details of the XJTU-SY dataset.

Working Condition	Rotation Speed	Load	Dataset	Sample Number	Bearing Lifetime	Division
1	2100 rpm	12,000 N	Bearing 1-1	123	2 h 3 m	training
			Bearing 1-2	161	2 h 41 m	training
			Bearing 1-3	158	2 h 38 m	testing
			Bearing 1-4	122	2 h 2 m	testing
			Bearing 1-5	52	52 m	testing
2	2250 rpm	11,000 N	Bearing 2-1	491	8 h 11 m	training
			Bearing 2-2	161	2 h 41 m	training
			Bearing 2-3	533	8 h 53 m	testing
			Bearing 2-4	42	42 m	testing
			Bearing 2-5	339	5 h 39 m	testing
3	2400 rpm	10,000 N	Bearing 3-1	2538	42 h 18 m	training
			Bearing 3-2	2496	41 h 36 m	training
			Bearing 3-3	371	6 h 11 m	testing
			Bearing 3-4	1515	25 h 15 m	testing
			Bearing 3-5	114	1 h 54 m	testing

illustrates the details of the XJTU-SY dataset.

In this paper, the mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) are used to evaluate the prediction accuracy. They are respectively computed as follows:

$$\mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2$$

(16)

$$\mathrm{RMSE}=\sqrt{\mathrm{MSE}}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{(y_i-\widehat{y_i})}^2}$$

(17)

$$\mathrm{MAE}=\frac{1}{n}\sum _{i=1}^n|y_i-\widehat{y_i}|$$

(18)

$$\mathrm{MAPE}=\frac{1}{n}\sum _{i=1}^n\left|\frac{y_i-\widehat{y_i}}{y_i}\right|.$$

(19)

In Equations (18)–(21), $y_i$ is the label, $\widehat{y_i}$ is the model’s prediction value, and n is the total number of samples.

4.2. Different HIs Results

In this section, we compare different HI construction methods to validate the superiority of our proposed HI construction method.

Figure 4 shows the results of different HI construction methods on the bearing 1-3 of the PHM dataset. It can be clearly observed from Figure 4a that the original vibration signal of the bearing 1-3 is in a very smooth state with little fluctuation when the bearing has just begun to work. In the degradation state, the vibration signal usually fluctuates slightly, whereas the overall trend is upward. The signal fluctuation will increase sharply when the bearing finally completely degrades.

As shown in Figure 4b–h, the HIs constructed by the combination of TSNE and other distance metrics basically do not have any regular change trend. Meanwhile, the methods of SAE and Euclidean distance metric can retain the change trend of the original vibration signal, but the early degradation and complete degradation stage of the bearing cannot be completely distinguished. For the vibration signal of the bearing, PCA is a linear transformation method for each of its principal components. Specifically, the linearity of each point is calculated to obtain the principal components and then downscaled; thus, the global trend of the original signal can be retained. Meanwhile, SAE is a nonlinear learning model that requires a lot of training data to get a satisfactory performance. In contrast, our proposed method, as shown in Figure 4i, is more suitable to reflect the change trend of the original signal and can distinguish the early degradation and complete degradation stage of the bearing, which is beneficial for SACGNet to improve its prediction accuracy.

In order to further illustrate the superiority of our HI construct method, we use the percentage of the use life as the HI; then, we compare the RUL prediction results with our proposed methods on the PHM dataset. The red lines are true values of HI, and the blue lines are the prediction values of the model. Figure 5a–c is the RUL results of comparison HI, while Figure 5d–f is the RUL results of our methods.

It can be seen that when the bearing true remaining useful life percentage is used as the HI label, the model fails to learn the degradation trend of the bearing vibration signal, and the final prediction results are not well-fitted. In contrast, using our proposed HI for prediction, the degradation trend of the vibrtion data is depicted more accurately, and the prediction accuracy of the model is improved. Note that our model can properly predict RUL in the stages of rapid degradation of bearing operation, which is of great value for the actual industrial scenarios.

4.3. Ablation Experiments

In order to observe the effects of the different layers in the proposed model, we conduct ablation experiments on the PHM dataset and the XJTU-SY dataset. We let the model constructs remain and respectively remove the Conv1d layer and Multi-Head Attention layer for comparison models. We call them the NoAttention model and NoConv1d model, respectively.

As seen in

Table 4. Ablation experiments in PHM dataset.

Metric		Bearing 1-3	Bearing 1-4	Bearing 1-5	Bearing 1-6	Bearing 1-7	Bearing 2-3	Bearing 2-4	Bearing 2-5	Bearing 2-6	Bearing 2-7	Bearing 3-3
MSE	SACGNet	0.010	0.053	0.039	0.042	0.012	0.017	0.042	0.066	0.042	0.061	0.078
	NoAttention	0.203	0.138	0.212	0.193	0.223	0.049	0.063	0.064	0.061	0.062	0.162
	NoConv1d	0.055	0.099	0.160	0.060	0.069	0.162	0.110	0.161	0.129	0.076	0.095
RMSE	SACGNet	0.101	0.230	0.197	0.205	0.108	0.131	0.204	0.202	0.205	0.397	0.280
	NoAttention	0.451	0.372	0.461	0.439	0.472	0.220	0.250	0.253	0.246	0.249	0.403
	NoConv1d	0.236	0.314	0.401	0.245	0.263	0.403	0.332	0.402	0.359	0.276	0.309
MAE	SACGNet	0.041	0.157	0.077	0.079	0.022	0.033	0.081	0.071	0.083	0.220	0.161
	NoAttention	0.373	0.304	0.382	0.359	0.394	0.201	0.148	0.225	0.167	0.096	0.368
	NoConv1d	0.216	0.215	0.273	0.203	0.256	0.387	0.271	0.375	0.303	0.178	0.205
MAPE	SACGNet	1.300	1.461	5.800	2.707	2.526	13.290	14.128	15.778	48.944	188.952	11.879
	NoAttention	26.616	3.542	64.021	38.050	86.298	89.249	33.654	47.493	83.542	11.724	22.317
	NoConv1d	16.809	2.627	33.060	19.339	47.315	175.061	62.932	77.439	140.799	78.596	15.225

, with respect to the PHM dataset, our method achieved the best results in 10 of the 11 bearing data for MSE, RMSE, MAE, and MAPE metrics. Using the MSE metric, our model did not achieve the best result for bearing 2-5; the discrepancy with respect to the best results (i.e., NoAttention model) is 0.002. For the RMSE, MAE, and MAPE metrics, our model does not achieve the optimal results for bearing 2-7, the discrepancy with respect to the best results (i.e., the NoAttention model) is 0.148, 0.124, and 177.228, respectively.

Furthermore, we also conducted the ablation experiment on the XJTU-SY dataset, and the results are shown in

Table 5. Ablation experiments in the XJTU-SY dataset.

Metric		Bearing 1-3	Bearing 1-4	Bearing 1-5	Bearing 2-3	Bearing 2-4	Bearing 2-5	Bearing 3-3	Bearing 3-4	Bearing 3-5
MSE	SACGNet	0.022	0.028	0.129	0.102	0.261	0.116	0.134	0.037	0.249
	NoAttention	0.071	0.045	0.151	0.099	0.238	0.189	0.150	0.050	0.252
	NoConv1d	0.282	0.141	0.150	0.262	0.292	0.122	0.147	0.093	0.254
RMSE	SACGNet	0.147	0.166	0.360	0.320	0.511	0.341	0.369	0.193	0.500
	NoAttention	0.266	0.212	0.388	0.315	0.488	0.435	0.387	0.223	0.502
	NoConv1d	0.531	0.376	0.387	0.512	0.540	0.350	0.383	0.304	0.504
MAE	SACGNet	0.117	0.088	0.206	0.307	0.428	0.249	0.256	0.069	0.447
	NoAttention	0.229	0.137	0.198	0.301	0.400	0.333	0.276	0.098	0.450
	NoConv1d	0.447	0.274	0.194	0.479	0.462	0.297	0.294	0.211	0.447
MAPE	SACGNet	12.904	0.714	3.217	12.090	0.862	8.714	17.105	31.240	1.251
	NoAttention	39.583	1.903	0.798	12.442	0.750	8.626	19.341	53.358	1.286
	NoConv1d	84.217	4.435	0.568	19.283	0.998	9.188	33.756	172.834	1.314

. Using the MAE and MAPE metrics, our model did not achieve the best results for bearings 1-5, 2-3, and 2-4 but only a discrepancy of 1.9% from the best results. Using the MSE and RMSE metrics, our model did not achieve the best results for bearings 2-3 and 2-4, but the discrepancy with the best results (i.e., NoAttention model) was only 3.03%. Except for the afore-mentioned results, the performance of our model is superior to the comparison models.

The results of the ablation experiments conducted on both bearing datasets prove that our proposed model achieves the best results on the largest number of testing bearings. In a comprehensive analysis, the degradation features of different bearings with different operating conditions are different, Conv1d can extract the local features of the original vibration signals, and the Self-Attention mechanism focuses on the global features, which can be integrated to achieve more excellent results.

4.4. Results of Different Models

In this section, we compare the overall prediction accuracy of our proposed model with state-of-the-art methods on the PHM dataset and XJTU-SY dataset. The compared models include CNN, RNN, LSTM, and GRU.

As shown in

Table 6. Different models’ result in the PHM dataset.

Metric		Bearing 1-3	Bearing 1-4	Bearing 1-5	Bearing 1-6	Bearing 1-7	Bearing 2-3	Bearing 2-4	Bearing 2-5	Bearing 2-6	Bearing 2-7	Bearing 3-3
MSE	SACGNet	0.010	0.053	0.039	0.042	0.012	0.017	0.042	0.066	0.042	0.061	0.078
	CNN	0.276	0.236	0.361	0.339	0.401	0.017	0.044	0.033	0.049	0.063	0.159
	RNN	0.087	0.079	0.191	0.167	0.089	0.098	0.107	0.102	0.106	0.052	0.080
	LSTM	0.051	0.154	0.099	0.088	0.100	0.134	0.126	0.080	0.129	0.153	0.232
	GRU	0.156	0.130	0.220	0.212	0.122	0.047	0.173	0.074	0.150	0.621	0.255
RMSE	SACGNet	0.101	0.230	0.197	0.205	0.108	0.131	0.204	0.202	0.205	0.397	0.280
	CNN	0.526	0.486	0.601	0.583	0.633	0.132	0.209	0.182	0.221	0.250	0.399
	RNN	0.295	0.282	0.437	0.409	0.299	0.313	0.327	0.319	0.326	0.229	0.282
	LSTM	0.227	0.393	0.315	0.296	0.317	0.366	0.354	0.283	0.360	0.392	0.482
	GRU	0.395	0.360	0.469	0.461	0.350	0.216	0.416	0.272	0.387	0.788	0.505
MAE	SACGNet	0.041	0.157	0.077	0.079	0.022	0.033	0.081	0.071	0.083	0.220	0.161
	CNN	0.431	0.401	0.492	0.473	0.529	0.079	0.121	0.127	0.129	0.094	0.361
	RNN	0.272	0.230	0.405	0.371	0.277	0.305	0.297	0.307	0.302	0.137	0.208
	LSTM	0.082	0.270	0.294	0.275	0.308	0.352	0.185	0.219	0.215	0.369	0.376
	GRU	0.378	0.315	0.449	0.282	0.337	0.163	0.250	0.167	0.220	0.744	0.433
MAPE	SACGNet	1.300	1.461	5.800	2.707	2.526	13.290	14.128	15.778	48.944	188.952	11.879
	CNN	34.128	4.702	84.794	68.833	116.331	34.082	26.482	26.338	66.653	10.532	21.550
	RNN	20.391	2.999	64.366	51.722	58.369	135.458	77.727	63.910	132.203	33.092	14.056
	LSTM	4.084	3.941	46.745	34.372	64.918	157.411	43.524	45.461	107.898	160.438	25.883
	GRU	28.107	4.765	52.206	52.417	70.271	72.181	63.668	35.833	110.955	364.585	28.784

, with respect to the PHM dataset, our model achieved the best results in nine out of 11 bearings for MSE and RMSE metrics, and in nine out of 11 bearings for MAE and MAPE metrics. Using the MSE and RMSE metrics, our model did not achieve the best results for bearings 2-5 and 2-7. Using the MAE and MAPE metrics, our model did not achieve the best values for bearings 2-7.

In order to indicate the superior performance of our model, we add the prediction results of all the comparison models in the PHM dataset. Without loss of generality, we visualize the prediction results for bearing 1-4, 1-5, and 1-6 in order to compare them with the previous prediction results, as shown in Figure 6.

From Figure 6a,d,g,j,m, it can be seen that CNN has the worst fitting results on the testing data. The difference between the CNN predicted values and the original signal is very obvious, because the single CNN models are unsuitable for processing the time-series data. The prediction results of RNN and GRU are slightly superior to those of CNN, but there is still a visible difference from the original vibration signal. Furthermore, the RNN performance is significantly inferior to LSTM on long-term series.

The prediction results of SACGNet and LSTM are similar on bearing 1-4, and the fitting results of SACGNet are more favorable when combined with the four evaluation metrics in Table 6. From Figure 6b,c,e,f,h,i,k,l,n,o, it can be seen that on bearing 1-5 and 1-6, SACGNet has superior prediction results, which is consistent with the comparison results of the four evaluation metrics in Table 6.

Upon observation of the original vibration signal of bearing 2-7, the early degradation states of bearing 2-7 show very sharp fluctuations, and the amplitude difference between the early degradation and the complete degradation stage is very small. The vibration fluctuation of the early degradation is even more severe than that of the complete degradation stage. That may be the reason why our model did not achieve optimal results on bearing 2-7.

As shown in

Table 7. Different models’ results in the XJTU-SY dataset.

Metric		Bearing 1-3	Bearing 1-4	Bearing 1-5	Bearing 2-3	Bearing 2-4	Bearing 2-5	Bearing 3-3	Bearing 3-4	Bearing 3-5
MSE	SACGNet	0.022	0.028	0.129	0.102	0.261	0.116	0.134	0.037	0.249
	CNN	0.024	0.036	0.151	0.060	0.276	0.190	0.161	0.041	0.255
	RNN	0.297	0.122	0.139	0.127	0.292	0.984	0.141	0.084	0.225
	LSTM	0.276	0.136	0.150	0.276	0.292	0.260	0.615	0.097	0.147
	GRU	0.276	0.144	0.150	0.123	0.292	0.107	0.170	0.331	0.236
RMSE	SACGNet	0.147	0.166	0.360	0.320	0.511	0.341	0.369	0.193	0.500
	CNN	0.154	0.191	0.389	0.244	0.525	0.436	0.401	0.203	0.505
	RNN	0.545	0.349	0.373	0.357	0.540	0.314	0.375	0.290	0.474
	LSTM	0.525	0.368	0.387	0.525	0.540	0.510	0.784	0.312	0.384
	GRU	0.526	0.380	0.387	0.351	0.540	0.331	0.413	0.575	0.486
MAE	SACGNet	0.117	0.088	0.206	0.307	0.428	0.249	0.256	0.069	0.447
	CNN	0.134	0.093	0.200	0.228	0.444	0.333	0.297	0.077	0.454
	RNN	0.469	0.249	0.194	0.332	0.462	0.231	0.311	0.252	0.421
	LSTM	0.442	0.280	0.194	0.520	0.462	0.457	0.730	0.135	0.297
	GRU	0.446	0.290	0.194	0.334	0.462	0.246	0.368	0.563	0.433
MAPE	SACGNet	12.904	0.714	3.217	12.090	0.862	8.714	17.105	31.240	1.251
	CNN	17.219	0.762	0.922	8.611	0.929	8.883	21.782	34.925	1.292
	RNN	85.029	4.089	1.628	14.217	0.998	8.480	29.475	184.134	1.257
	LSTM	84.945	4.599	0.568	19.232	0.998	15.022	90.756	77.418	1.546
	GRU	85.115	4.736	0.568	14.007	0.998	8.644	42.677	425.427	1.258

, with respect to the XJTU-SY dataset, it can be seen that our model has achieved the best resluts on most of the testing bearings, expect for the MSE of bearings 2-3 and 3-5, RMSE of bearings 2-3, 2-5 and 3-5, MAE of bearings 1-5, 2-3, 2-5, and 3-5, and MAPE of bearings 1-5, 2-3, and 2-5, respectively.

The reason for such results may be due to the fact that the experimental environment of 2-3, 2-5, and 3-5 is slightly different from the conditions of the bearing dataset we chose as the training set, and these datasets produce fluctuations in the degradation stage that are equal to or even higher than the final complete damage. Specifically, the CNN model achieved the best results on the bearing 2-3 dataset for four metrics, which may be because the degradation process of bearing 2-3 is filled with many small-scale local fluctuations, allowing the CNN to fit this process more directly. As for bearings 2-5 and 3-5, they do not show much sharp fluctuations and also due to the small amount of data compared to the other datasets, RNN and LSTM are able to parse their long-term serial relationships on these two datasets.

In summary, from the comparison experiments on the two datasets, in most of the cases, our model achieves the best prediction accuracy compared to the other existing models, which demonstrates that our proposed model is applicable for RUL prediction.

5. Conclusions

In this paper, we explored a health indicator-based remaining useful life prediction method. First, we combine principal component analysis (PCA) with Euclidean distance measurement to construct the health indicator for tackling the dependency on RUL labels. Then, we design a self-attention augmented convolution GRU network (SACGNet) to predict the RUL task, which utilizes the globe features as well as local important features to improve the prognostic accuracy. To verify the effectiveness of the model, we conducted extensive experiments on two bearing datasets, respectively, and the results demonstrate that SACGNet is superior to these existing models under several evaluation criteria. Meanwhile, the model has excellent generalization performance for multiple bearings.