A Minimal Input Engine Friction Model for Power Loss Prediction
Abstract
:1. Introduction
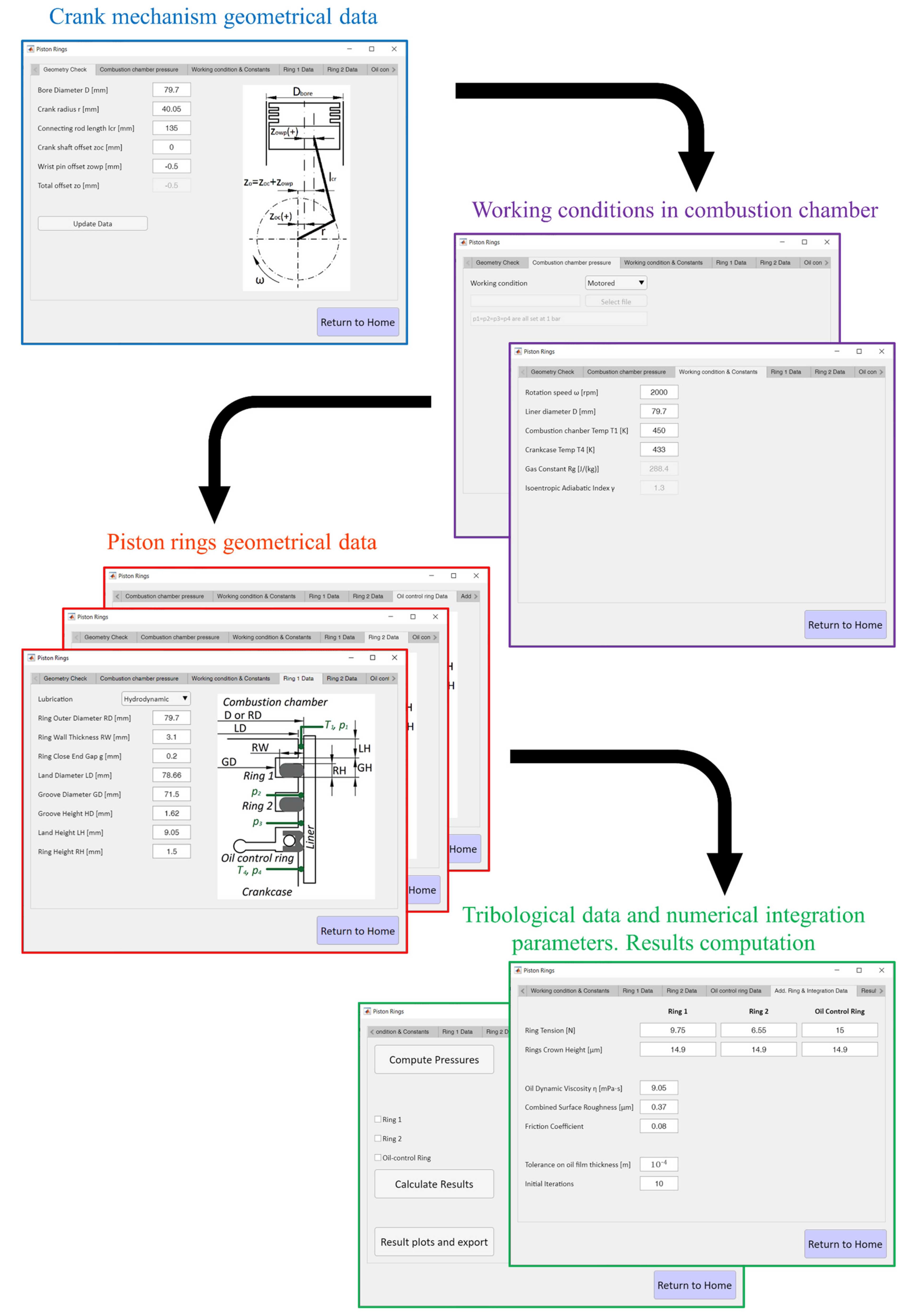
2. Design Tool Overview
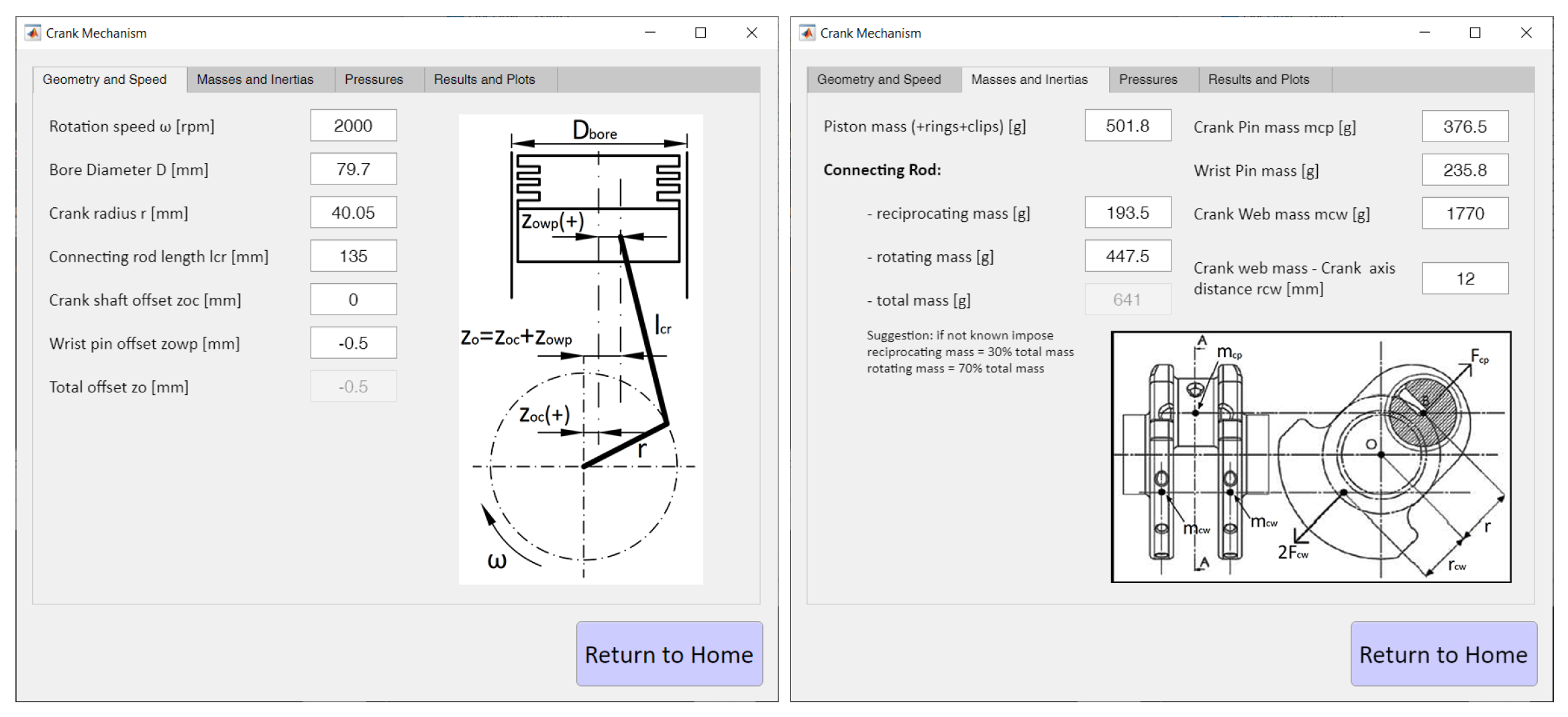
- Geometric (and inertial, if necessary) data of connecting rod-crank mechanism.
- Working conditions in the combustion chamber (motored or fired).
- Geometrical data and lubrication conditions of the component under examination.
- Tribological data of the lubricant and the modeled surfaces
- Parameters necessary to the numerical integration method.
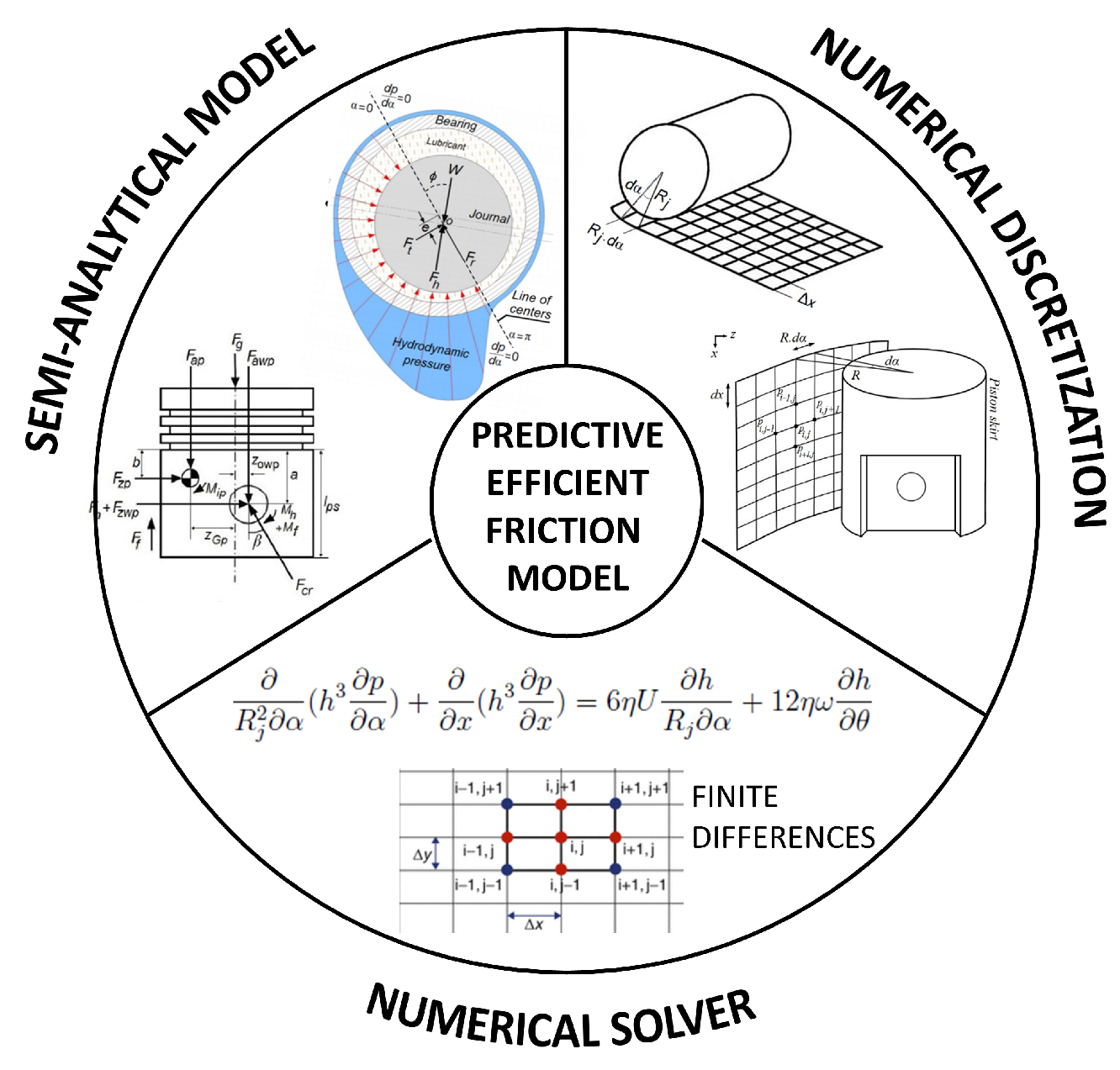
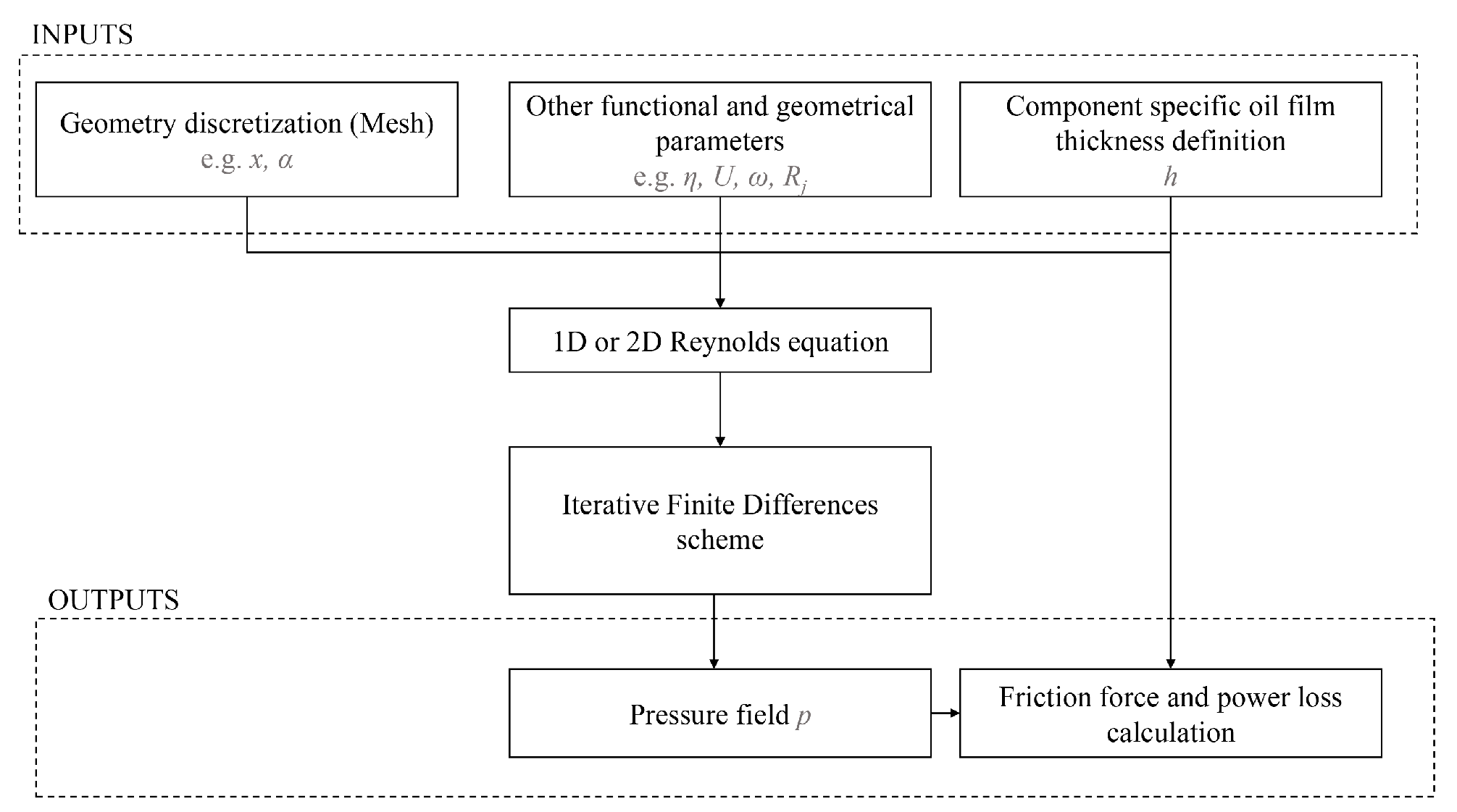
2.1. Modeling and Numerical Methods
- Necessary semianalytical model to define the relationship between external forces acting on the component, and the pressure and thickness present in the lubricant meatus.
- Numerical discretization (1D or 2D) to solve the Reynolds equation associated with the lubricant meatus.
- Numerical methods such as finite differences to solve the Reynolds equation, and algorithms to link equilibrium equations with meatus thickness h.
- crankshaft angular speed is constant;
- lubricant is Newtonian and incompressible;
- oil viscosity and density are constant;
- thermal and elastic deformation of the components are neglected.
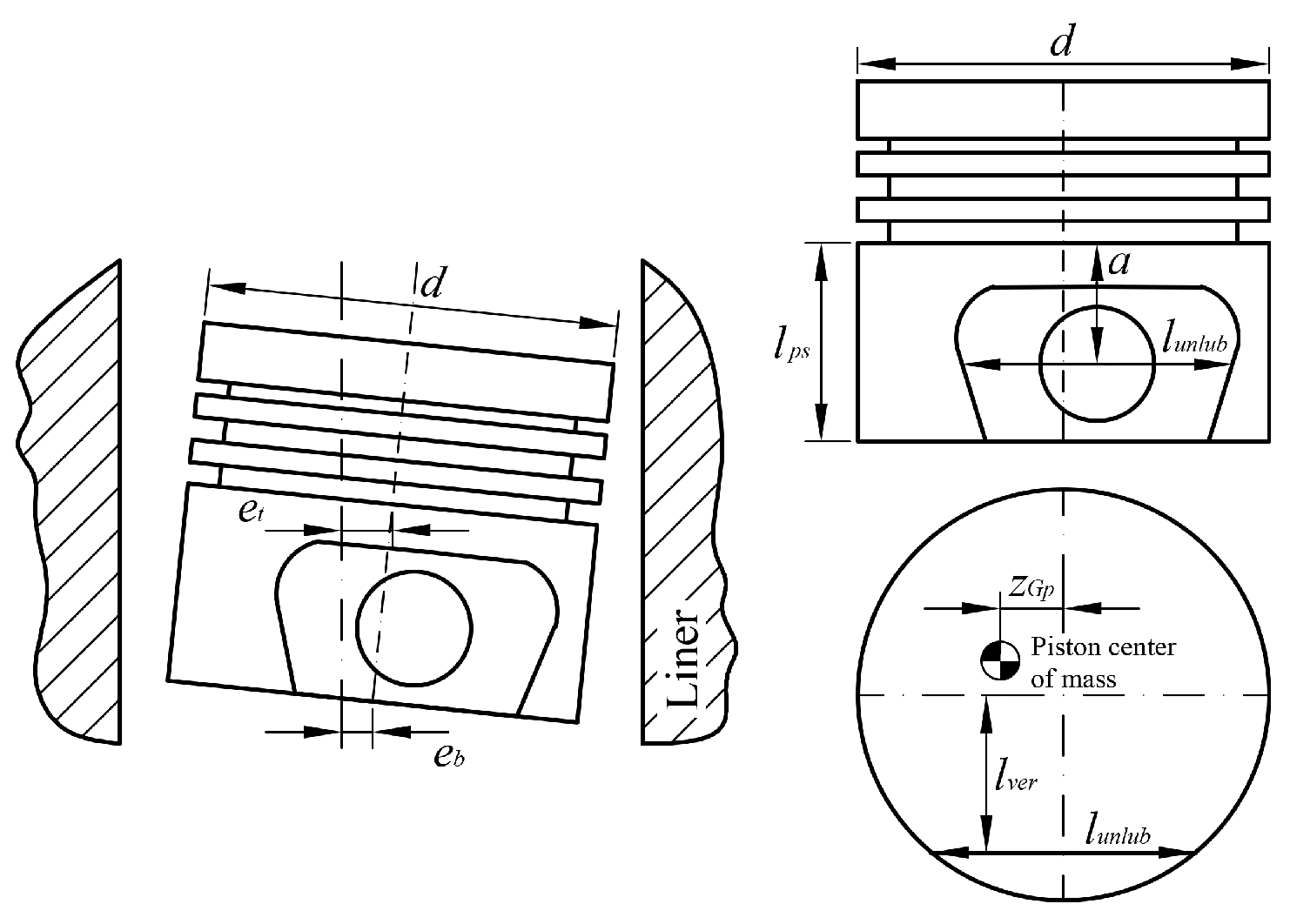
2.1.1. Piston Rings
2.1.2. Piston Skirt
2.1.3. Connecting Rod and Main Bearings
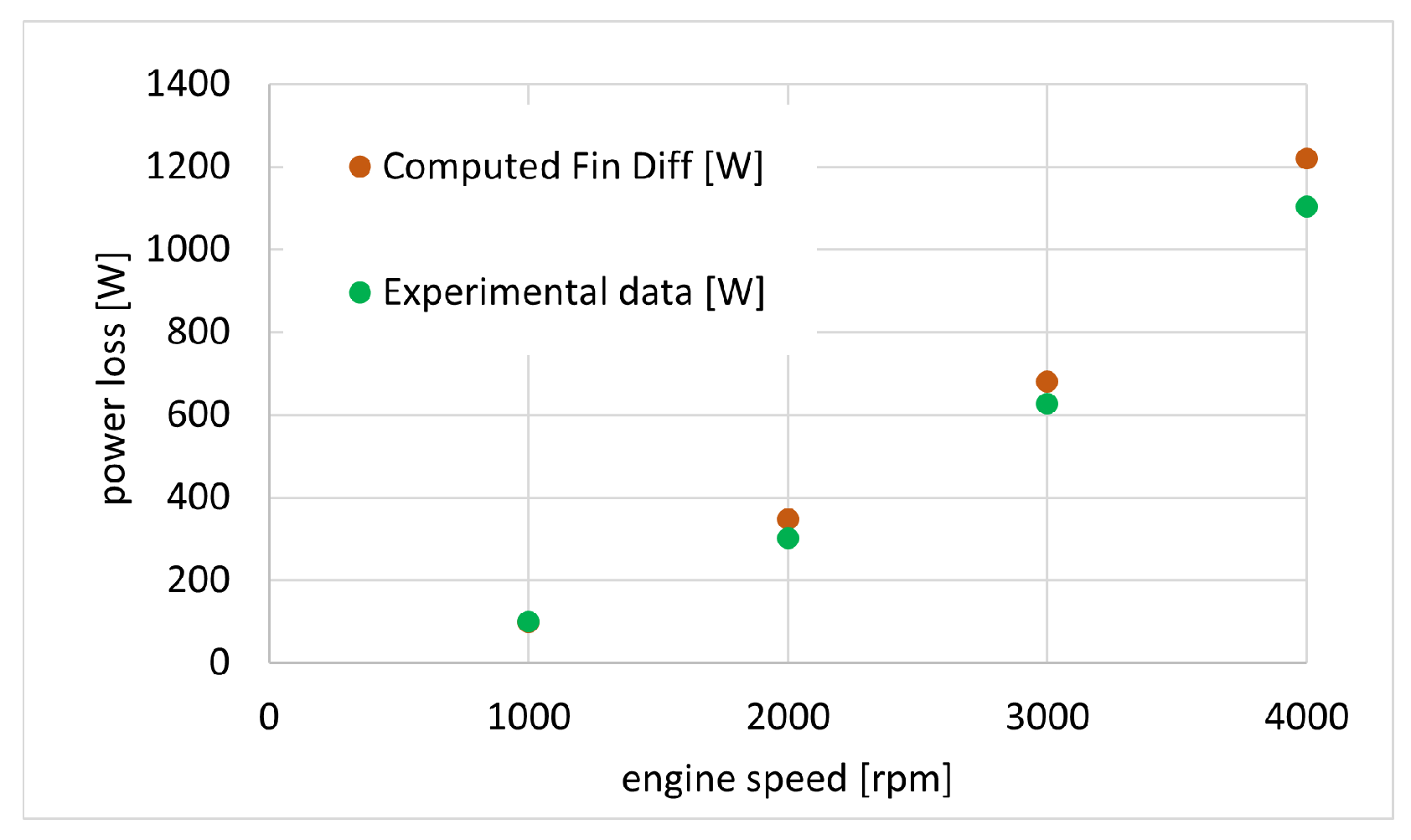
3. Results
- quantities directly related to the Reynolds equation such as oil film thickness and pressure distribution;
- frictional forces due to viscous shear stresses and the associated power loss (typically obtained as the integral of the frictional force).
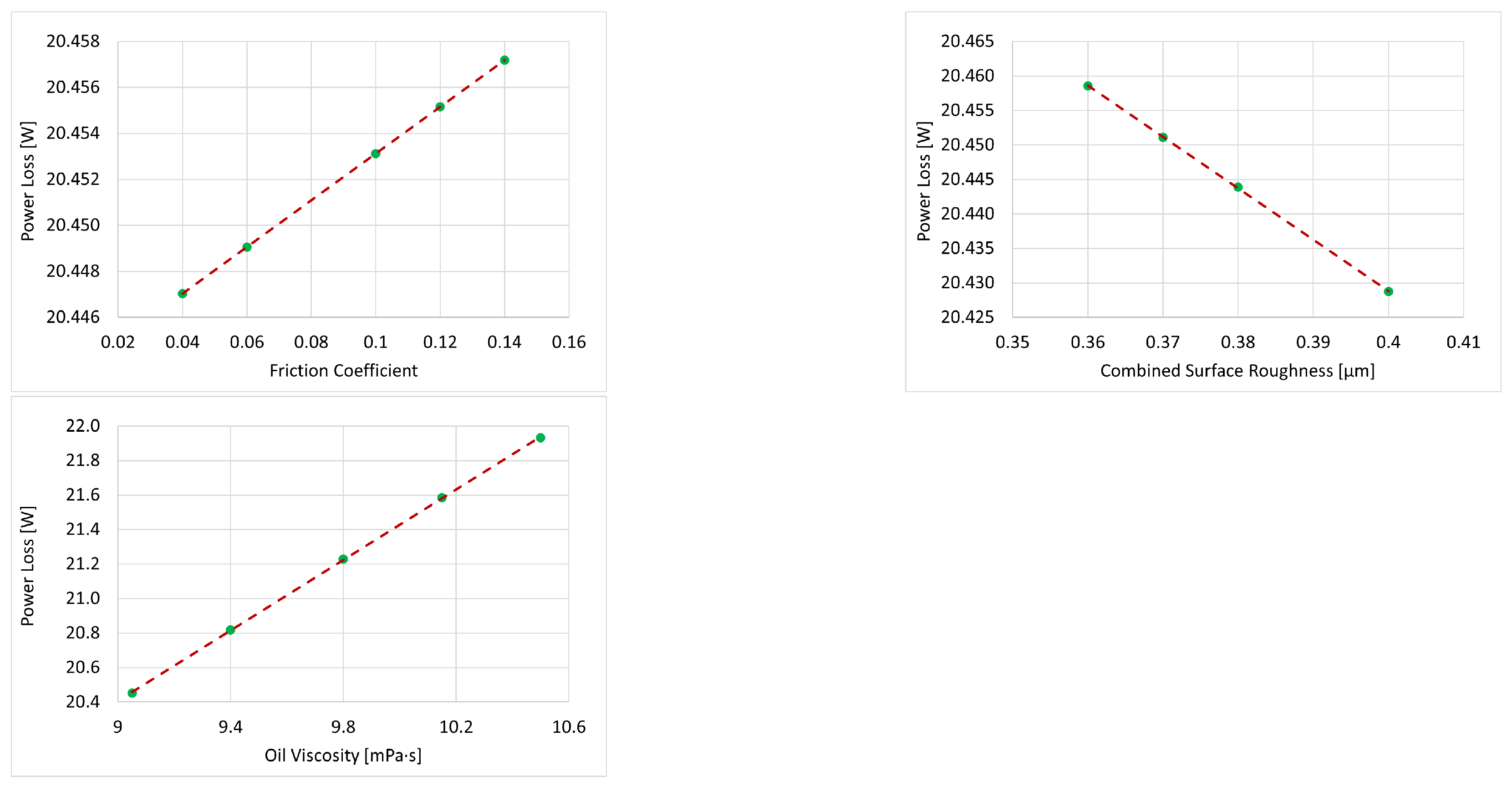
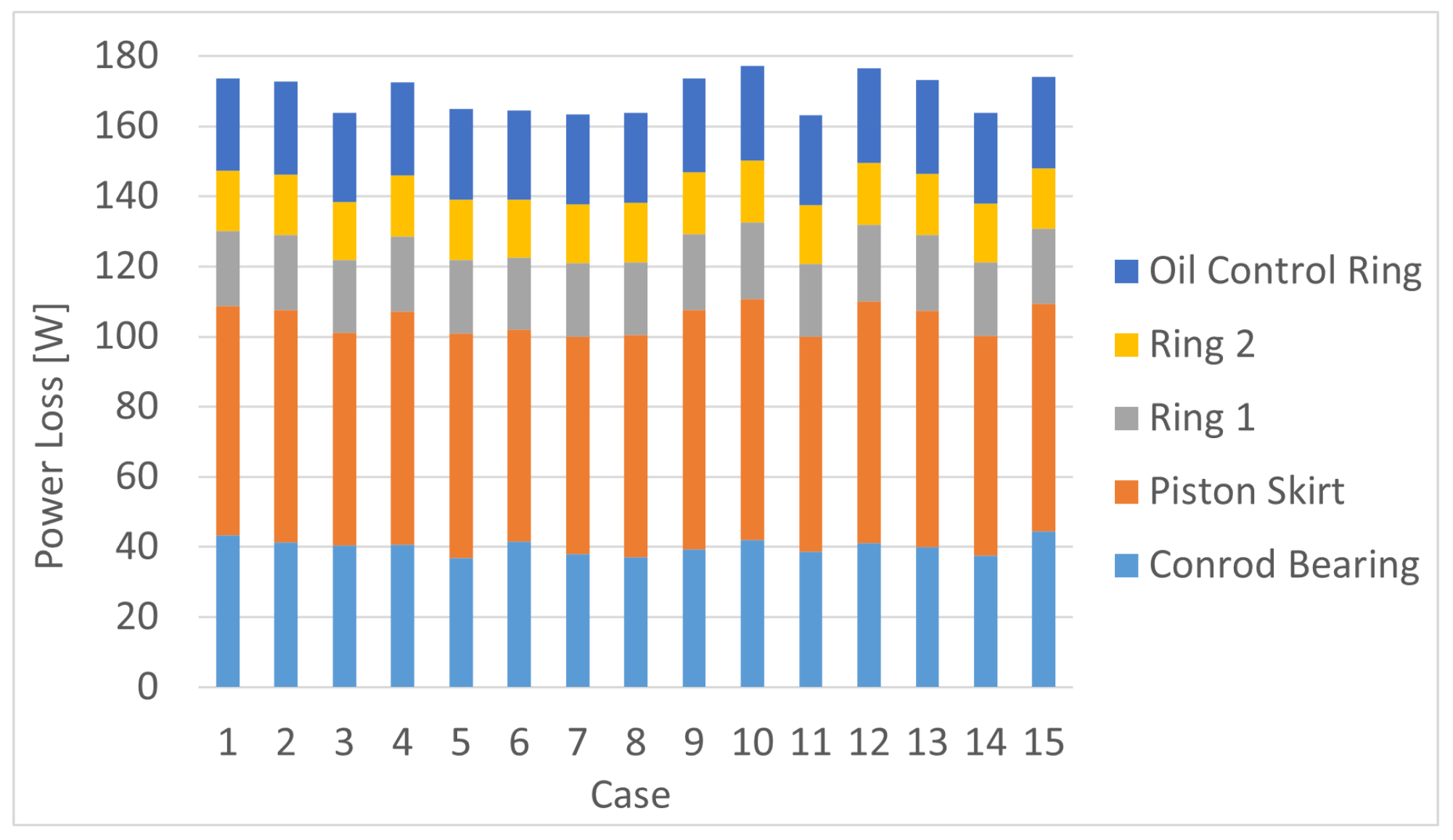
Sensitivity Analysis of Piston Assembly Power Losses to Uncertain Parameters
4. Conclusions
- use of the smallest possible number of inputs to calibrate the models, a necessary feature in the preliminary phase when not all design details are already available;
- use of semianalytical models with simple discretizations that guarantee low computational times;
- ease of use thanks to a graphical interface for data entry, and for the interpretation and export of results;
- proven predictive capabilities thanks to the experimental numerical comparison operated in different operating conditions;
- robustness of the model in the choice of uncertain parameters during the initial design phases of internal combustion engines, which guarantees limited variability in estimated power losses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rahnejat, H. Tribology and Dynamics of Engine and Powertrain: Fundamentals, Applications and Future Trends; Woodhead: Cambridge, UK, 2010. [Google Scholar]
- Delprete, C.; Razavykia, A. Piston dynamics, lubrication and tribological performance evaluation: A review. Int. J. Engine Res. 2018, 21, 725–741. [Google Scholar] [CrossRef]
- Taylor, C.M. Engine Tribology; Elsevier Science & Techn.: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Heywood, J. Internal Combustion Engine Fundamentals; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Miltsios, G.K.; Patterson, D.J.; Papanastasiou, T.C. Solution of the Lubrication Problem and Calculation of the Friction Force on the Piston Rings. J. Tribol. 1989, 111, 635–641. [Google Scholar] [CrossRef]
- Ma, M.T.; Smith, E.H.; Sherrington, I. A Three-Dimensional Analysis of Piston Ring Lubrication Part 1: Modelling. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 1995, 209, 1–14. [Google Scholar] [CrossRef]
- Ma, M.T.; Smith, E.H.; Sherrington, I. A Three-Dimensional Analysis of Piston Ring Lubrication Part 2: Sensitivity Analysis. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 1995, 209, 15–27. [Google Scholar] [CrossRef]
- Priest, M.; Dowson, D.; Taylor, C. Predictive wear modelling of lubricated piston rings in a diesel engine. Wear 1999, 231, 89–101. [Google Scholar] [CrossRef]
- Rodríguez, A.L.; Vølund, A.; Klit, P. Modeling of piston ring wear. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2020, 235, 629–638. [Google Scholar] [CrossRef]
- Stanley, R.; Taraza, D.; Henein, N.; Bryzik, W. A Simplified Friction Model of the Piston Ring Assembly; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 1999. [Google Scholar] [CrossRef]
- Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.; Fitzsimons, B. The influence of piston ring geometry and topography on friction. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2012, 227, 141–153. [Google Scholar] [CrossRef] [Green Version]
- Piao, Y.; Gulwadi, S.D. Numerical Investigation of the Effects of Axial Cylinder Bore Profiles on Piston Ring Radial Dynamics. J. Eng. Gas Turbines Power 2003, 125, 1081–1089. [Google Scholar] [CrossRef]
- Zavos, A. Effect of Coating and Low Viscosity Oils on Piston Ring Friction under Mixed Regime of Lubrication through Analytical Modelling. Lubricants 2021, 9, 124. [Google Scholar] [CrossRef]
- Jeng, Y.R. Theoretical Analysis of Piston-Ring Lubrication Part I—Fully Flooded Lubrication. Tribol. Trans. 1992, 35, 696–706. [Google Scholar] [CrossRef]
- Jeng, Y.R. Theoretical Analysis of Piston-Ring Lubrication Part II—Starved Lubrication and Its Application to a Complete Ring Pack. Tribol. Trans. 1992, 35, 707–714. [Google Scholar] [CrossRef]
- Bedajangam, S.K.; Jadhav, N.P. Friction Losses between Piston Ring-Liner Assembly ofInternal Combustion Engine: A Review. Int. J. Sci. Res. Publ. 2013, 3, 1–3. Available online: http://www.ijsrp.org/research-paper-0613.php?rp=P181298 (accessed on 29 March 2022).
- Oh, K.P.; Li, C.H.; Goenka, P.K. Elastohydrodynamic Lubrication of Piston Skirts. J. Tribol. 1987, 109, 356–362. [Google Scholar] [CrossRef]
- Smirnov, S.V.; Vorobyev, A.A. Hydrodynamic lubrication of a two-piece piston skirt considering deformations. In Proceedings of the III International Conference on Advanced Technologies in Materials Science, Mechanical and Automation Engineering, Krasnoyarsk, Russian, 29–30 April 2021; AIP Publishing: Melville, NY, USA, 2021. [Google Scholar] [CrossRef]
- Li, D.F.; Rohde, S.M.; Ezzat, H.A. An Automotive Piston Lubrication Model. ASLE Trans. 1983, 26, 151–160. [Google Scholar] [CrossRef]
- Liu, K.; Xie, Y.B.; Gui, C.L. A comprehensive study of the friction and dynamic motion of the piston assembly. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 1998, 212, 221–226. [Google Scholar] [CrossRef]
- Forero, J.D.; Ochoa, G.V.; Alvarado, W.P. Study of the Piston Secondary Movement on the Tribological Performance of a Single Cylinder Low-Displacement Diesel Engine. Lubricants 2020, 8, 97. [Google Scholar] [CrossRef]
- Ciulli, E. A Review of Internal Combustion Engine Losses Part 1: Specific Studies on the Motion of Pistons, Valves and Bearings. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 1992, 206, 223–236. [Google Scholar] [CrossRef]
- Thring, R.H. Engine Friction Modeling; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 1992. [Google Scholar] [CrossRef]
- Allmaier, H.; Priestner, C.; Six, C.; Priebsch, H.; Forstner, C.; Novotny-Farkas, F. Predicting friction reliably and accurately in journal bearings—A systematic validation of simulation results with experimental measurements. Tribol. Int. 2011, 44, 1151–1160. [Google Scholar] [CrossRef]
- Allmaier, H.; Priestner, C.; Reich, F.; Priebsch, H.; Forstner, C.; Novotny-Farkas, F. Predicting friction reliably and accurately in journal bearings – The importance of extensive oil-models. Tribol. Int. 2012, 48, 93–101. [Google Scholar] [CrossRef]
- Razavykia, A.; Delprete, C.; Baldissera, P. Numerical Study of Power Loss and Lubrication of Connecting Rod Big-End. Lubricants 2019, 7, 47. [Google Scholar] [CrossRef] [Green Version]
- Santos, N.D.S.A.; Roso, V.R.; Faria, M.T.C. Review of engine journal bearing tribology in start-stop applications. Eng. Fail. Anal. 2020, 108, 104344. [Google Scholar] [CrossRef]
- Sfyris, D.; Chasalevris, A. An exact analytical solution of the Reynolds equation for the finite journal bearing lubrication. Tribol. Int. 2012, 55, 46–58. [Google Scholar] [CrossRef]
- Chasalevris, A.; Sfyris, D. Evaluation of the finite journal bearing characteristics, using the exact analytical solution of the Reynolds equation. Tribol. Int. 2013, 57, 216–234. [Google Scholar] [CrossRef]
- Lozano, W.O.; Fonseca-Vigoya, M.D.S.; Pabón-León, J. Study of the Kinematics and Dynamics of the Ring Pack of a Diesel Engine by Means of the Construction of CFD Model in Conjunction with Mathematical Models. Lubricants 2021, 9, 116. [Google Scholar] [CrossRef]
- Delprete, C.; Razavykia, A. Modeling of Oil Film Thickness in Piston Ring/Liner Interface. Int. J. Mech. Eng. Robot. Res. 2017, 210–214. [Google Scholar] [CrossRef] [Green Version]
- Singhal, G. Computation methods for hydrodynamic problems (Reynold’s equation). Comput.-Aided Des. 1981, 13, 151–154. [Google Scholar] [CrossRef]
- Booker, J.F. Dynamically Loaded Journal Bearings: Mobility Method of Solution. J. Basic Eng. 1965, 87, 537–546. [Google Scholar] [CrossRef]
- Booker, J.F. Dynamically-Loaded Journal Bearings: Numerical Application of the Mobility Method. J. Lubr. Technol. 1971, 93, 168–174. [Google Scholar] [CrossRef]
- Myung-Rae, C.; Dae-Yoon, O.; Seung-Hyuk, R.; Dong-Chul, H. Load characteristics of engine main bearing: Comparison between theory and experiment. KSME Int. J. 2002, 16, 1095–1101. [Google Scholar] [CrossRef]
- Von Schnurbein, E. A New Method of Calculating Plain Bearings of Statically Indeterminate Crankshafts; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 1970. [Google Scholar] [CrossRef]
- Delprete, C.; Razavykia, A.; Baldissera, P. Detailed analysis of piston secondary motion and tribological performance. Int. J. Engine Res. 2020, 21, 1647–1661. [Google Scholar] [CrossRef]
- Chaudhari, T.; Sutaria, B. Investigation of friction characteristics in segmented piston ring liner assembly of IC engine. Perspect. Sci. 2016, 8, 599–602. [Google Scholar] [CrossRef] [Green Version]
- Westerfield, Z.; Liu, Y.; Kim, D.; Tian, T. A Study of the Friction of Oil Control Rings Using the Floating Liner Engine. SAE Int. J. Engines 2016, 9, 1807–1824. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]






| Module | Calculation Time [min] |
|---|---|
| Piston Rings | 8 |
| Piston Skirt | 40 |
| Journal Bearing | 10 |
| Component | [W] | [W μm] | [W mPa s] |
|---|---|---|---|
| Ring 1 | 0.102 | 0.74 | 1.022 |
| Ring 2 | 0.065 | −0.397 | 0.857 |
| Oil control ring | 0.132 | −0.782 | 1.277 |
| Conrod bearing | − | −10.614 | 1.791 |
| Piston skirt | − | − | 6.625 |
| Case | Oil Viscosity [mPa s] | Surface Rough. μm | Friction Coeff. [−] |
|---|---|---|---|
| 1 | 9.873 | 0.363 | 0.104 |
| 2 | 9.974 | 0.373 | 0.045 |
| 3 | 9.181 | 0.393 | 0.075 |
| 4 | 10.045 | 0.388 | 0.054 |
| 5 | 9.654 | 0.398 | 0.061 |
| 6 | 9.120 | 0.376 | 0.122 |
| 7 | 9.371 | 0.361 | 0.095 |
| 8 | 9.567 | 0.392 | 0.079 |
| 9 | 10.291 | 0.397 | 0.127 |
| 10 | 10.392 | 0.381 | 0.047 |
| 11 | 9.292 | 0.384 | 0.092 |
| 12 | 10.407 | 0.388 | 0.084 |
| 13 | 10.177 | 0.369 | 0.108 |
| 14 | 9.477 | 0.375 | 0.116 |
| 15 | 9.802 | 0.366 | 0.067 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delprete, C.; Gastaldi, C.; Giorio, L. A Minimal Input Engine Friction Model for Power Loss Prediction. Lubricants 2022, 10, 94. https://doi.org/10.3390/lubricants10050094
Delprete C, Gastaldi C, Giorio L. A Minimal Input Engine Friction Model for Power Loss Prediction. Lubricants. 2022; 10(5):94. https://doi.org/10.3390/lubricants10050094
Chicago/Turabian StyleDelprete, Cristiana, Chiara Gastaldi, and Lorenzo Giorio. 2022. "A Minimal Input Engine Friction Model for Power Loss Prediction" Lubricants 10, no. 5: 94. https://doi.org/10.3390/lubricants10050094
APA StyleDelprete, C., Gastaldi, C., & Giorio, L. (2022). A Minimal Input Engine Friction Model for Power Loss Prediction. Lubricants, 10(5), 94. https://doi.org/10.3390/lubricants10050094







